Как найти показатель воспроизводимости

6.2.1
Оценка показателя повторяемости методики
анализа

6.2.1.1 Рассчитывают
среднее арифметическое

и выборочную дисперсию

результатов единичного анализа содержания
компонента в т-м
ОО,
полученных в условиях повторяемости
(параллельных определений):

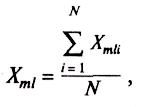
(5)

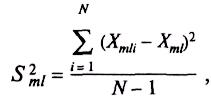
(6)

6.2.1.2 На
основе полученных значений выборочных
дисперсий

в
т-м
ОО
проверяют гипотезу о равенстве генеральных
дисперсий¹),
используя критерий Кохрена.

¹⁾
Дисперсии результатов единичного
анализа, полученные в различных
лабораториях, имеют различные значения.
Предполагают, что для аттестованной
методики анализа такие различия между
лабораториями невелики и что допустимо
установить одно общее (усредненное)
значение дисперсии для всех лабораторий,
применяющих данную методику.

Значение
критерия Кохрена

рассчитывают по формуле

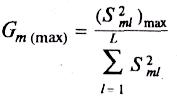
(7)

и
сравнивают его с табличным значением
этого критерия

для числа степеней свободы

соответствующего
максимальной дисперсии, и

,
соответствующего числу суммируемых
дисперсий, и
принятой
доверительной вероятности Р=
0,95
(значения

)
приведены в приложении Е, таблица Е.1)

Если

,
то соответствующее

из дальнейших расчетов исключают и
процедуру повторяют до следующего по
значению

и т. д. до тех пор, пока

не станет меньше либо равно

6.2.1.3 Не
исключенные из расчетов

считают однородными и по ним оценивают
средние квадратические отклонения
(далее – СКО), характеризующие повторяемость
результатов единичного анализа
(параллельных определений), полученных
для содержания, соответствующего
содержанию компонента в т-м
ОО.
Эти СКО –
рассчитывают
по формуле

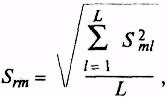
(8)

где
в числе слагаемых нет отброшенных
значений.

6.2.1.4 Показатель
повторяемости методики анализа в виде
СКО^1)-
для
содержания, соответствующего содержанию
компонента в т-м
ОО,
устанавливают, принимая равным

(9)

6.2.1.5 Показатель
повторяемости методики анализа в виде
предела повторяемости^2)-
для
содержания, соответствующего содержанию
компонента в т-м
ОО,
рассчитывают по формуле

(Ю)

где
п

число параллельных определений,
предусмотренных методикой анализа для
получения результата анализа,

=
2,77 при п
=2,
Р
=0,95;

Q(P,
п) = 3,31
при п
=
3, Р
= 0,95;

Q(P,
п) =
3,63 при п
=
4, Р
= 0,95;

Q(P,
п) =
3,86 при п
= 5,
Р
= 0,95.

6.2.2
Оценка показателя воспроизводимости
методики анализа

6.2.2.1
Рассчитывают выборочное СКО результатов
анализа т-го
ОО,
полученных в условиях воспроизводимости,-

по формуле

(11)

где

-общее среднее значение результатов
анализа, полученных в условиях
воспроизводимости,

рассчитывают по формуле

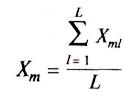
(12)

¹)
Стандартное отклонение повторяемости
по [1].

²)
Значение предела повторяемости
рассчитывают в случае, если методикой
анализа предусмотрено проведение
параллельных определений, и используют
при проверке приемлемости результатов
единичного анализа, полученных в условиях
повторяемости.

Примечание
– В случае, если методикой анализа не
предусмотрено проведение параллельных
определений (п
= 1)
и результат единичного анализа является
собственно результатом анализа,
выборочное СКО результатов анализа
т-го
ОО,
полученных в условиях воспроизводимости,
рассчитывают по формуле

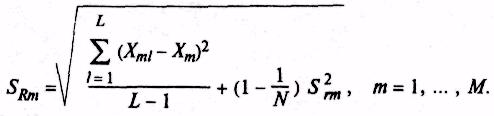
(13)

6.2.2.2
Оценка показателя воспроизводимости
методики анализа

Показатель
воспроизводимости методики анализа в
виде СКО¹⁾
–

для содержания, соответствующего
содержанию компонента в т-м
ОО,
устанавливают, принимая равным

(14)

Показатель
воспроизводимости методики анализа в
виде предела воспроизводимости²⁾–

для
содержания, соответствующего содержанию
компонента в т-м
ОО,
рассчитывают по формуле

(15)

где

=
2,77 при Р=
0,95.

Примечание
– В случае невозможности организации
эксперимента в разных лабораториях
экспериментальные данные получают в
одной лаборатории в условиях
внутрилабораторной прецизионности
(серии результатов единичного анализа
получают в разное время, разные операторы,
используя разные партии реактивов
одного типа, разные наборы мерной посуды
и т. п.). Результаты единичного анализа
внутри каждой серии получают в условиях
повторяемости. В этом случае показатель
воспроизводимости методики анализа в
виде СКО рассчитывают по формуле

(16)

где

–
выборочное СКО результатов анализа,
рассчитанное в соответствии с 6.2.2.1 на
основе результатов, полученных в условиях
внутрилабораторной прецизионности;

k
– коэффициент,
учитывающий условия проведения
эксперимента, k
может
принимать значения от 1,2 до 2,0.

6.3
Оценка показателя правильности методики
анализа

6.3.1 Рассчитывают
оценку математического ожидания
систематической погрешности методики
анализа –
как
разность между средним значением
результатов анализа

и аттестованным значением т-го
ОО
(СО или АС) –

(17)

6.3.2 Проверяют
значимость вычисленных значений
по
критерию Стьюдента. Для этого рассчитывают
значение r-критерия
для

:

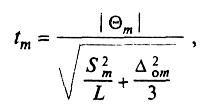
(18)

где

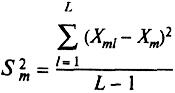
-дисперсия,
характеризующая разброс средних
арифметических значений результатов
единичного анализа

,
полученных в l-й
лаборатории,
относительного среднего значения
результатов анализа

–
погрешность аттестованного значения

¹⁾
Стандартное отклонение воспроизводимости
по [1].

²⁾
Значение предела воспроизводимости
используют при проверке приемлемости
результатов анализа, полученных в
условиях
воспроизводимости.

1. Полученное
   значение
   

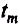
   сравнивают с
   

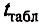
   при числе степеней свободы f
   = L
   –
   1 для доверительной вероятности Р
   = 0,95.
   Значения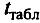

   

   приведены
   в приложении Е, таблица Е.2.

2. Если
   
   ,
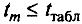
   то оценка систематической погрешности
   незначима на фоне случайного разброса,
   и в этом случае ее принимают равной
   нулю
   

3. Если
   
   ,
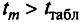
   то оценка систематической погрешности
   значима на фоне случайного разброса и
   для принятия решения о приемлемости
   методики анализа вводят еще один
   дополнительный критерий:

,

где

может
принимать значения от 0,5 до 1 в зависимости
от используемых в методике анализа
методе условий, средств измерений и т.
п., а также характеристик объекта анализа.

При
выполнении данного критерия может быть
принято решение (с учетом примечания к
6.4 о введении в результаты анализа,
получаемые при реализации данной
методики, поправки на значение

,
т. е. значение

,
соответствующее содержанию С
–

(С),
вычитают из любого результате анализа,
полученного по методике.

Если
данный критерий не выполняется, принимают
решение о доработке методики.

6.3.6 При
незначимости

или при принятом для методики анализа
решении о введении в результаты анализа
поправки показатель правильности
методики анализа [верхнюю
и
нижнюю
границы,
в которых неисключенная систематическая
погрешность методики анализа (для
содержания, соответствующего содержанию
определяемого компонента в т-м
ОО)
находится с принятой вероятностью Р-
0,95]
рассчитывают по формуле

(19)

Примечание
– При условии организации эксперимента
согласно примечанию к 6.2.2.2 показатель
правильности методики анализа (границы,
в которых неисключенная систематическая
погрешность методики анализа находится
с принятой вероятностью Р=
0,95)
рассчитывают по формуле

(20)

где

–
выборочное СКО результатов анализа,
рассчитанное в соответствии с 6.3.2 на
основе результатов, полученных в условиях
внутрилабораторной прецизионности;

k
–
коэффициент, учитывающий условия
проведения эксперимента, k
может
принимать значения от 1,2 до 2,0.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Протокол исследований с учетом знаний о метрологии

Термины и определения в метрологии

Как и любая другая наука, метрология имеет свой собственный язык – это термины и определения. Эти понятия используются дальше при знакомстве с нормативными документами и оценках результатов измерений или их сравнений. И нам необходимы эти знания, чтобы научиться правильно работать с нормативными документами, извлекая из них требуемую информацию.

В нормативном документе – рекомендациям по межгосударственной стандартизации «РМГ 29-2013 ГСИ Метрология. Основные термины и определения» дано пояснение и толкование 231 метрологическому понятию. Конечно, для наших целей такой список слишком велик. Наша цель – выделить тот их необходимый минимум, который позволит нам на практике правильно воспринимать и оценивать результаты измерений.

Рассмотрим пока всего только 9 самых важных понятий:

Метрология — Наука об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Комментарий: мы должны привлечь аппарат этой науки для целей объективной оценки качества измерений в измерительных лабораториях.

Результат измерения (РИ) – Множество значений величины, приписываемых измеряемой величине вместе с любой другой доступной и существенной информацией.
Комментарий: значения измеряемых показателей, которые мы видим, например, в протоколах испытаний/

Метрологические характеристики:

Погрешность РИ – Разность между измеренным значением величины и опорным значением величины.
Комментарий:на примере пакета с мукой: мы видим опорное значение (2 кг), а погрешность (разность с опорным значением) может достигать или 40 г, или 2% в зависимости от формы представления погрешности (см. ниже).

Абсолютная погрешность РИ – Погрешность измерения, выраженная в единицах измеряемой величины.
Комментарий: на примере пакета с мукой: абсолютная погрешность может составлять 40 г.

Относительная погрешность РИ – Погрешность измерения, выраженная отношением абсолютной погрешности измерения к опорному значению измеряемой величины.
Комментарий: на примере пакета с мукой: относительная погрешность прямо указана на его этикетке – 2%.

Границы абсолютной (относительной) погрешности: — Верхняя и нижняя границы интервала, внутри которого с заданной вероятностью находится значение погрешности измерений.
Комментарий: на примере пакета с мукой: видим на этикетке пакета границу относительной погрешности +/-2% или на этикетке может быть также указано +/-40 г в виде границы абсолютной погрешности.

Диапазон измерений – Множество значений величин одного рода, которые могут быть измерены данным средством измерений или измерительной системой с указанными инструментальной неопределенностью или указанными показателями точности при определенных условиях.
Комментарий: на примере пакета с мукой: например, весы для взвешивания пакетов с мукой могут обеспечивать указанную погрешность только в пределах от 100 г и до 10 кг (исходя из технических характеристик технических весов). Это и есть их рабочий диапазон измерений.

Повторяемость измерений (сходимость) – Прецизионность (точность) измерений в условиях повторяемости измерений (Один из наборов условий измерений, включающий применение одной и той же методики измерений, того же средства измерений, участие тех же операторов, те же рабочие условия, то же местоположение и выполнение повторных измерений на одном и том же или подобных объектах в течение короткого промежутка времени).
Комментарий: на примере лабораторных испытаний:допускаемый разброс результатов определений, по одной и той же пробе у одного и того же оператора, работающего на одной и той же измерительной установке в режиме непрерывных определений параметров пробы в одной и той же лаборатории.

Воспроизводимость измерений (прецизионность): — Прецизионность (точность) измерений в условиях воспроизводимости измерений (Один из наборов условий измерений, включающий разные местоположения, разные средства измерений, участие разных операторов и выполнение повторных измерений на одном и том же или аналогичных объектах).
Комментарий: на примере протокола лабораторных испытаний из 2-х или более лабораторий: допускаемый разброс результатов измерений, выполненных по одной и той же пробе в разных лабораториях у разных операторов, работающих на разных измерительных установках по одной и той же методике измерений.

Более наглядно указанные метрологические характеристики можно увидеть на нижеприведенных иллюстрациях, но перед этим снова обратимся к уже знакомому нам Протоколу испытаний:

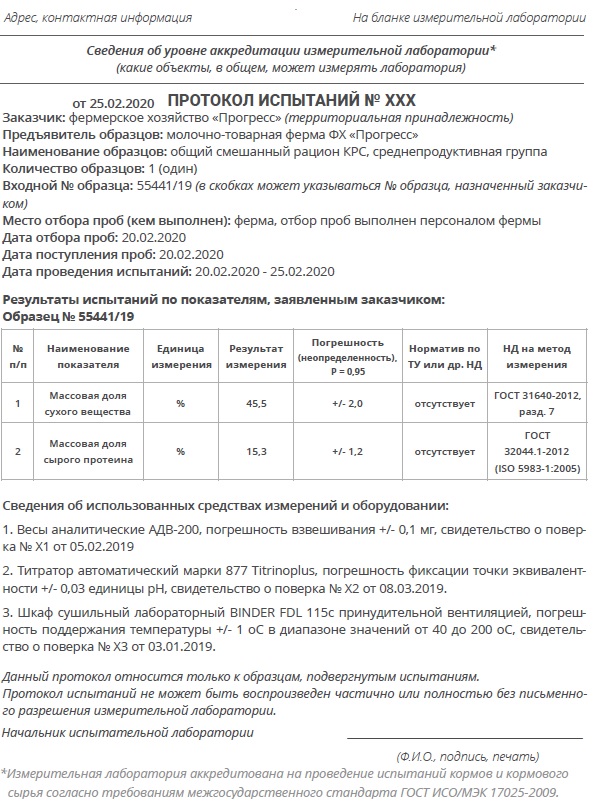
Рассмотрим в качестве примера более подробно метрологические характеристики метода определения содержания сухого вещества (далее по тексту – СВ) в общем смешанном рационе (далее по тексту – ОСР). В протоколе имеется ссылка на соответствующий нормативный документ — ГОСТ 31640-2012 Корма. Методы определения содержания сухого вещества (можно найти в Интернете в свободном доступе).

В разделе 3, Таблица 1 документа помещены метрологические характеристики этого метода:

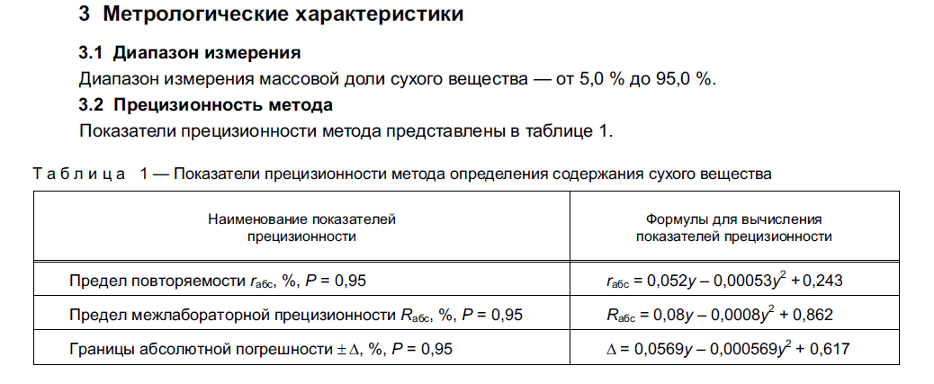
Используя формулы, приведенные в Таблице 1, и данные из Протокола по содержанию СВ в ОСР (y = 45,5%), можно выполнить расчет и оценить метрологические характеристики метода в его рабочем диапазоне измерений от 5% до 95% массовой доли СВ:

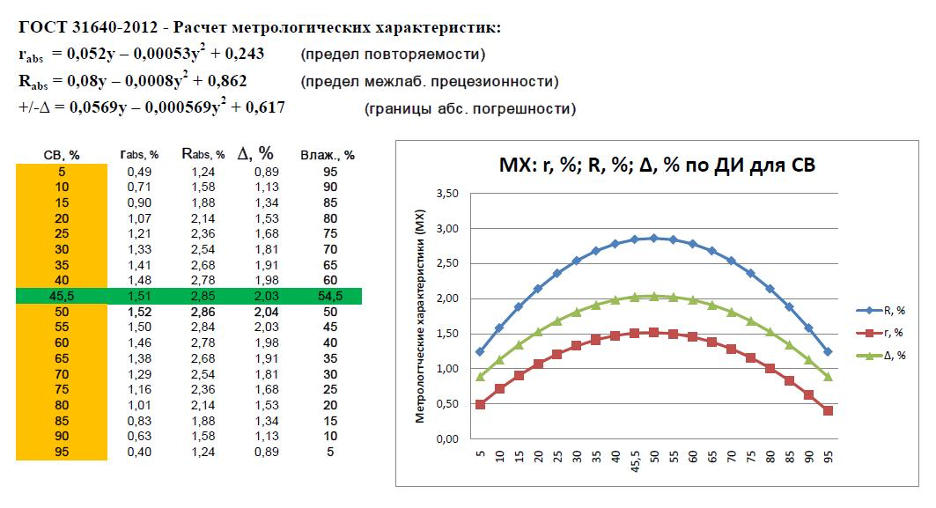
Итак, мы теперь можем разобрать 4 наиболее важные характеристики любого метода измерений: диапазон измерений, повторяемость, воспроизводимость и погрешность. В метрологии их принято представлять пределами или границами (см. пояснения по тексту ниже).

Диапазон измерений

Характеристика средства измерений (прибора) или методики выполнения измерений, описывающая допускаемый интервал значений для результатов измерений, простирающийся от минимального до максимального возможного значения измеряемой величины.

Так рабочий диапазон измерения этой линейки от 0 см и до 20 см. То же справедливо и для методик физико-химического анализа – каждая из них имеет свой диапазон измерений.

Что это означает на практике?

Например, в случае методики выполнения измерений содержания СВ в кормах по ГОСТ 31640-2012 диапазон измерения составляет от 5% и до 95%.

Зачем нужно его знать?

Это нужно для понимания: к каким именно образцам применим этот метод измерения. Для образцов содержанием СВ выше 95% или ниже 5% указанный метод применять нельзя, в этом случае надо искать другой метод, который обеспечивает измерения в более широком диапазоне содержания СВ.

Ответственность за выбор подходящего метода лежит на лаборатории, хотя заказчик, исходя из своих задач и требований, может также самостоятельно делать выбор конкретного метода измерения.

Сходимость (повторяемость) результатов измерений

Качество измерений, отражающее близость друг к другу результатов измерений (x1 и x2), выполненных в одинаковых условиях. Оценивается через предел сходимости (d) или предел повторяемости (r):

│x1 — x2│ ≤r или d

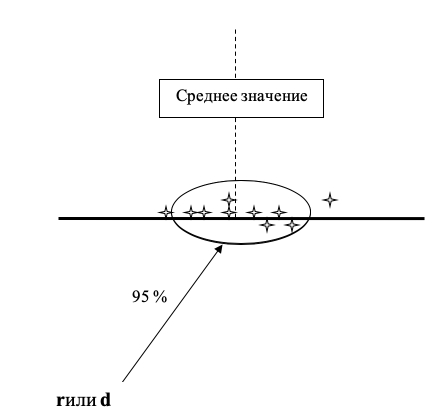
Предел сходимости (повторяемости) характеризует разброс единичных измерений, например, у одного оператора при выполнении измерений в серии при стабильных условиях.

При этом 95% единичных измерений укладывается в предел повторяемости.

Для наглядности снова обратимся ГОСТ 31640-2012. В Таблице 1 приводится формула для расчета предела повторяемости (r_abs, %, P = 0,95).

Как расшифровать эту запись? Она означает, что предел повторяемости по этой формуле будет выражен в абсолютных процентах от измеренного значения содержания СВ, а доверительная вероятность (P) при этом составляет 0,95. В пояснениях к Таблице 1 в ГОСТ 31640-2012 по этому поводу сказано следующее: «Расхождение результатов двух параллельных определений, полученными в условиях повторяемости, может превышать предел повторяемости r не более одного раза из двадцати». Последнее означает, что 95% указанных расхождений укладывается в данный предел.

Теперь снова обратимся к Протоколу. Результат измерения содержания СВ в нем представлен значением 45,5%. Выполним расчет по формуле для предела повторяемости (r_abs), задавая значение содержание СВ из Протокола вместо (y) в формуле и по требованию ГОСТ 31640-2012, проведя округление результата вычислений до первого десятичного знака. Полученное значение предела повторяемости составит 1,5% абсолютных.

Что это означает на практике?

Например, если оператор в лаборатории выполнил 2 параллельных определения СВ для одного и того же образца ОСР, а результаты этих определений были: 44,8 и 46,2%, и разница результатов определений составляет т.о. 1,4%, то оператор может выполнить вычисление среднего значения определений, которое будет 45,5% и будет представлено в итоговом Протоколе в качестве результата измерения, т.к. норматив оперативного контроля результатов измерений у оператора (r_abs = 1,5%) не был превышен.

Однако, если бы результаты определений были бы другими: 44,3% и 46,7%, а разница в этом случае составила бы 2,4%, имело бы место значительное превышение предела повторяемости, равного 1,5%, хотя среднее значение было бы тем же – 45,5%!

В этом случае оператор НЕ ИМЕЕТ ПРАВА вычислять среднее и представлять его как результат измерений. Оператор должен снова повторить 2 определения, вычислить разницу и проверить: не превышен ли норматив оперативного контроля 1,5 %. Если не превышен, вычислить результат измерения как среднее из 2-х определений – 45,5%, или, в противном случае, все измерения прекращаются до выяснения причин превышения предела: неисправное оборудование, испорченные реактивы, не соблюдение стабильных условий при выполнении определений и т.д.

Воспроизводимость результатов измерений

• измерений, отражающее близость друг к другу результатов измерений (x1 и x2), выполненных в различных условиях (в различное время, в различных местах, разными методами и средствами). При выполнении измерений в различных лабораториях оценивается предел межлабораторной воспроизводимости (D) или межлабораторной прецизионности (R).

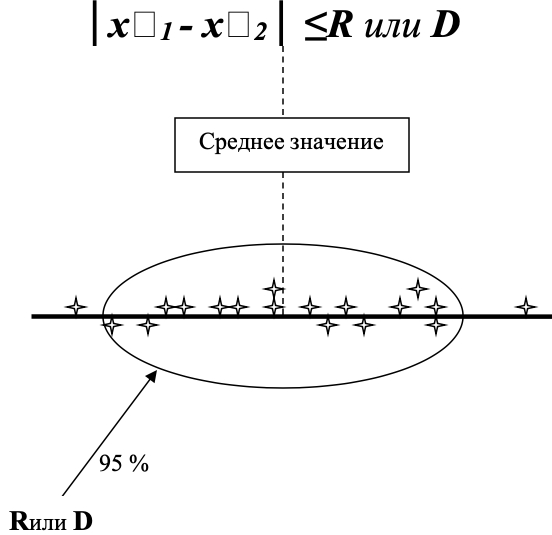
Предел воспроизводимости (межлабораторной прецизионности) характеризует разброс результатов измерений, например, у разных операторов при выполнении измерений в различных условиях или разброс результатов измерений одного и того же объекта в различных лабораториях.

При этом 95% результатов измерений укладывается в предел воспроизводимости (прецизионности).

Понятно, что R или D для одного и того же объекта измерения и метода всегда больше r или d.

Совершенно аналогично на основании формулы из Таблицы 1 и измеренного содержания СВ, указанного в Протоколе (у = 45,5%) можно оценить предел воспроизводимости (R), который в данном случае составит 2,9% (после округления).

Что это означает на практике?

Если один и тот же материал образца был отправлен на анализ в ДВЕ различные лаборатории, выполняющие измерения ОДНИМ и ТЕМ ЖЕ методом, но на разных комплектах оборудования, разными операторами и т.д., то мы получим два Протокола.

Рассмотрим теперь эти два Протокола из 2-х лабораторий. Пусть в первом был представлен результат измерения содержания СВ на уровне 45,5%, а во втором – 47,9%, соответственно.

Разность РИ составляет 2,4% и НЕ ПРЕВЫШАЕТ предел воспроизводимости (R = 2,9%), который рассчитан для среднего из 2-х РИ 46,7%. В таком случае наиболее достоверным будет среднее из 2-х РИ, т.е. 46,7%. Именно его надо использовать в дальнейшем как окончательный РИ.

Однако в случае, если в первом Протоколе было представлен результат измерения содержания СВ в ОСР, например, 42,3%, а во втором Протоколе – 45,5%. Разность РИ будет достигать 3,2%.

Как в таком случае оценить такие результаты: приемлемы ли они?

Если разность между РИ в условиях воспроизводимости составляет 3,2%, это ПРЕВЫШАЕТ предел воспроизводимости (R = 2,9%) — значит такие результаты не могут рассматриваться как удовлетворяющие условию воспроизводимости РИ и достоверные.

Как определить какой результат ближе к истинному?

Это требует привлечения метрологических знаний, выходящих за рамки предмета данной статьи. Но сделать это возможно с помощью специальных процедур контроля точности лабораторных измерений, описываемых, в частности в международном стандарте ГОСТ ИСО/МЭК 17025-2009 ОБЩИЕ ТРЕБОВАНИЯ К КОМПЕТЕНТНОСТИ ИСПЫТАТЕЛЬНЫХ И КАЛИБРОВОЧНЫХ ЛАБОРАТОРИЙ ISO/IEC 17025:2005.

Погрешность результата измерений

Погрешность выглядит как отклонение (в любую возможную сторону) результата измерений от опорного значения:

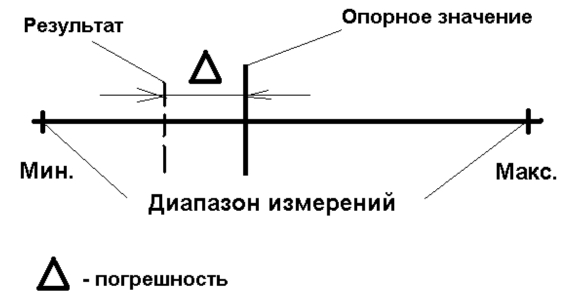
Но, поскольку отклонения результата измерений от опорного значения может быть как в минимальную (-), так и в максимальную (+) сторону, то в качестве метрологической характеристики в нормативных документах обычно приводят границы абсолютной или относительной погрешности при доверительной вероятности 95% (Р = 0,95) и тогда такую границу представляют в виде + , например, для абсолютной погрешности.

Для наглядности обратимся к Протоколу. В нем для РИ содержания СВ в ОСР (45,5%) указана погрешность +/-2% (а точнее — ее границы при доверительной вероятности 95%).

Как она была вычислена?

В формулу для оценки границ абсолютной погрешности РИ (см. Таблицу 1, раздел 3, ГОСТ 31640-2012) подставили значение РИ (у = 45,5%), и после округления получили границу погрешности: = +/-2%.

Что это означает на практике?

Среднее значение массовой доли СВ, согласно Протоколу, составляет 45,5%. Реальное (действительное) значение массовой доли сухого вещества в представленном образце корма № 55441/19 находится в границах от 43,5 до 47,5 % при доверительной вероятности (P = 0,95). Это означает, что на 100 повторных результатов измерений одного и того же образца 5 результатов из этой серии даже могут выйти за пределы указанных границ.

Как читать протокол лабораторных исследований с учетом знаний о метрологии

И только теперь, вооружившись необходимыми знаниями, мы может приступить снова к более полному рассмотрению и анализу данных Протокола.

Это, конечно, возможно только в том случае, если такой Протокол отвечает требованиям международного и национального стандарта ГОСТ ИСО/МЭК 17025-2009 ОБЩИЕ ТРЕБОВАНИЯ К КОМПЕТЕНТНОСТИ ИСПЫТАТЕЛЬНЫХ И КАЛИБРОВОЧНЫХ ЛАБОРАТОРИЙ ISO/IEC 17025:2005.

Наш Протокол отвечает этим требованиям.

Выводы из протокола:

1. Если обратиться к тексту нормативного документа ГОСТ 31640-2012 Корма. Методы определения содержания сухого вещества (можно найти в Интернете в свободном доступе), то можно в разделе 3 «Метрологические характеристики» найти формулы расчета границ абсолютной погрешности и убедиться, что погрешность измерения содержания сухого вещества в ОСР составляет 2%!

Таким образом, измеренное значение содержания может реально находится в границах от 43,5 и до 47,5%, а указанное в протоколе значение 45,5% НЕ ЯВЛЯЕТСЯ ТОЧНЫМ, но наиболее вероятным в серии повторных измерений.

Можно также вычислить предел межлабораторной прецизионности (R, %), и он составляет 2,9%. Это показывает насколько МОГУТ ОТЛИЧАТЬСЯ два результата для одного и того же образца, измеренного одним и тем же методом в 2-х разных лабораториях! И оба результата в этом случае надо оценивать как удовлетворяющие требованиям ГОСТ по точности.

1. Если аналогично рассмотреть второй нормативный документ из протокола ГОСТ 32044.1-2012 (ISO 5983-1:2005) КОРМА, КОМБИКОРМА, КОМБИКОРМОВОЕ СЫРЬЕ Определение массовой доли азота и вычисление массовой доли сырого протеина. Часть 1. Метод Къельдаля, то границы погрешностей для определения содержания сырого протеина составят (= +/- 1,2%, а предел межлабораторной прецизионности (R, %), составляет 1,8%.

Таким образом, для массовой доли сырого протеина в этом же образце среднее значение составляет 15,3%, а реальное значение этого показателя находится в пределах границ от 14,1 до 16,5% при доверительной вероятности (P = 0,95).

1. Все вышеуказанные результаты свидетельствуют, что даже самые лучшие мировые лаборатории, выполняющие измерения, не могут обеспечить абсолютную точность результатов своих измерений. И поэтому так важно учитывать погрешность при представлении результатов измерений для объективных оценок их качества. Сделать это возможно, если научиться правильно пользоваться нормативными документами на методы физико-химического анализа и не переоценивать их точности, а объективно воспринимать результаты измерений.

Общее заключение

Из всего вышеизложенного можно заключить:

• В науке и технике не существует абсолютно точных результатов измерений, всегда имеют место погрешности, которые надо правильно оценивать и адекватно воспринимать. Надо помнить: результат измерений носит вероятностный характер, а потому должен укладываться в допускаемые пределы отклонений от среднего.
• Граничные пределы отклонений для различных метрологических характеристик могут быть рассчитаны на основании нормативных документов на методы измерений (в частности, стандарты) или оценены на основании специального метрологического эксперимента – сравнения результатов измерений одних и тех же образцов в различных лабораториях. Допустимыми считаются отклонения, не превышающие граничные по абсолютной величине.
• Надо помнить, что наиболее вероятной оценкой результата измерения будет среднее значение из протоколов двух лабораторий, полученное в условиях воспроизводимости измерений.

Мы благодарим всех наших читателей, кто взял на себя труд дочитать до конца эту статью. В этой публикации мы постарались лишь в общих чертах затронуть подходы к восприятию и оценке результатов лабораторных физико-химических измерений. Если тема метрологии вызовет у нашей аудитории повышенный интерес, мы будем готовы продолжить цикл статей, посвященных проблемам метрологии и правилам организации работ по анализу образцов для обеспечения достоверности результатов их измерений.

С уважением, Владимир Шептун

---

Автор статьи: Владимир Шептун, к.х.н., методическая поддержка приложений и обслуживание клиентов компании Dinamica Generale S.p.A.в странах СНГ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ТЕХНИЧЕСКОМУ РЕГУЛИРОВАНИЮ И МЕТРОЛОГИИ
	РЕКОМЕНДАЦИИ ПО СТАНДАРТИЗАЦИИ	Р 50.1.060- 2006

Статистические
методы

РУКОВОДСТВО ПО ИСПОЛЬЗОВАНИЮ ОЦЕНОК ПОВТОРЯЕМОСТИ,
ВОСПРОИЗВОДИМОСТИ И ПРАВИЛЬНОСТИ ПРИ ОЦЕНКЕ НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЙ

Москва Стандартинформ 2007

Предисловие

Цели и принципы стандартизации в
Российской Федерации установлены Федеральным законом от 27 декабря 2002 г. № 184-ФЗ «О техническом
регулировании», а правила применения национальных стандартов Российской
Федерации – ГОСТ Р
1.0-2004 «Стандартизация в Российской Федерации. Основные положения»

Сведения о рекомендациях по
стандартизации

1
ПОДГОТОВЛЕНЫ Открытым акционерным обществом «Научно-исследовательский центр
контроля и диагностики технических систем» (ОАО НИЦ КД) и Техническим комитетом
по стандартизации ТК 125 «Статистические методы в управлении качеством
продукции» на основе собственного аутентичного перевода стандарта, указанного в
пункте 4

2
ВНЕСЕНЫ Управлением развития, информационного обеспечения и аккредитации
Федерального агентства по техническому регулированию и метрологии

3
УТВЕРЖДЕНЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Приказом Федерального агентства по техническому
регулированию и метрологии от 19 декабря 2006 г. № 319-ст 4

4 Настоящие рекомендации
являются идентичными по отношению к международному стандарту ИСО/ТУ 21748:2004
«Руководство по использованию оценок повторяемости, воспроизводимости и
правильности при оценке неопределенности измерений» (ISO/TS 21748:2004
«Guidance for the use of repeatability, reproducibility and trueness estimates
in measurement uncertainty estimation»).

Наименование настоящих
рекомендаций изменено относительно наименования указанного международного
стандарта для приведения в соответствие с ГОСТ
Р 1.5-2004 (подраздел 3.5).

При
применении настоящих рекомендаций рекомендуется использовать вместо ссылочных
международных стандартов соответствующие им национальные стандарты, сведения о
которых приведены в дополнительном приложении А

5 ВВЕДЕНЫ ВПЕРВЫЕ

Содержание

Введение:

Знание неопределенности,
связанной с результатами измерений, является важным для интерпретации
результатов. Без количественных оценок неопределенности невозможно решить,
превышают ли наблюдаемые отклонения результатов экспериментальную изменчивость,
соответствуют ли объекты испытаний установленным требованиям. Без информации о
неопределенности существует риск неверного толкования результатов, а
неправильные решения могут привести к ненужным расходам при производстве,
неправильным судебным выводам, неблагоприятным последствиям для здоровья или
неблагоприятным социальным последствиям.

Лаборатории, аккредитованные в
соответствии с ИСО/МЭК 17025:2005 «Общие требования к компетентности
испытательных и поверочных лабораторий», обязаны оценивать неопределенность
результатов измерений и испытаний и составлять соответствующий отчет.
Руководство GUM
( Guide to the expression of uncertainty in measurement ), изданное ИСО, основано на
принятом стандартном подходе. Однако оно относится к ситуации, когда известна модель
процесса измерений. Очень широкий диапазон стандартных методов испытаний может
быть подвергнут совместному исследованию в соответствии с ИСО 5725-2:1994,
Настоящие рекомендации устанавливают соответствующие методы оценки
неопределенности результатов измерений и испытаний, основанные на принципах GUM при анализе общих данных.

Общий подход, используемый в
настоящих рекомендациях, требует, чтобы:

– оценки повторяемости,
воспроизводимости и правильности метода, полученные при совместном исследовании
в соответствии с ИСО 5725-2:1994, могли быть получены по опубликованной
информации об использовании метода испытаний. Эти оценки позволяют получать
внутрилабораторные и межлабораторные составляющие неопределенности, а также
оценку неопределенности результатов, связанную с правильностью метода;

– лаборатория подтвердила на
основе проверок присущих ей смещения и прецизионности, что выполнение ею метода
испытаний совместимо с установленными требованиями к методу испытаний. Это
подтверждает, что опубликованные данные согласуются с результатами измерений и
испытаний, полученными лабораторией;

– любые влияния на результаты
измерений, которые не охвачены совместными исследованиями, были
идентифицированы, а отклонения, вызванные этими воздействиями, определены
количественно.

Оценку неопределенности
определяют объединением оценок дисперсии, полученных в соответствии с GUM .

Для контроля полного понимания
метода разброс результатов, полученных в совместном исследовании, часто полезно
сравнивать с оценками неопределенности измерений, полученными с использованием
процедур GUM . Такие сравнения будут более
эффективны при использовании последовательных оценок одного и того же
параметра, полученных на основе данных совместных исследований.

РЕКОМЕНДАЦИИ ПО СТАНДАРТИЗАЦИИ

Статистические методы РУКОВОДСТВО ПО ИСПОЛЬЗОВАНИЮ ОЦЕНОК ПОВТОРЯЕМОСТИ, ВОСПРОИЗВОДИМОСТИ И ПРАВИЛЬНОСТИ ПРИ ОЦЕНКЕ НЕОПРЕДЕЛЕННОСТИ ИЗМЕРЕНИЙ Statistical methods. Guidance for the use of repeatability, reproducibility and trueness estimates in measurement uncertainty estimation

Дата введения – 2007-06-01

1 Область применения

Настоящие рекомендации дают
руководство для:

– оценки неопределенности
измерений на основе данных, полученных в результате исследований, проводимых в
соответствии с ИСО 5725-2;

– сравнения результатов
совместного исследования с неопределенностью измерений, полученной с
использованием формальных принципов переноса неопределенности (см. раздел
14).

ИСО 5725-3 устанавливает
дополнительные модели для анализа промежуточной прецизионности. Однако, хотя
этот общий подход может быть применен к использованию расширенных моделей,
оценка неопределенности с использованием этих моделей не включена в настоящие
рекомендации.

Настоящие рекомендации применимы
во всех областях измерений и испытаний, когда должна быть определена
неопределенность результатов.

Настоящие рекомендации не
описывают применение данных повторяемости в отсутствие данных
воспроизводимости.

Настоящие рекомендации
предполагают, что признанные значимыми систематические воздействия устранены
или путем численной корректировки, включенной в метод измерений, или путем
анализа и устранения причины воздействий.

Настоящие рекомендации содержат
общее руководство. Представленный подход к оценке неопределенности применим для
многих целей, однако возможно применение других подходящих методов.

В общем случае информация,
приведенная в настоящих рекомендациях, относительно результатов, методов и
процессов измерений относится также к результатам, методам и процессам
испытаний.

2 Нормативные ссылки

В настоящем стандарте
использованы нормативные ссылки на следующие стандарты:

ИСО Руководство 33:2000
Использование стандартных образцов

ИСО/МЭК Руководство 43-1:1997 Проверка
компетентности путем межлабораторных сравнений. Часть 1. Разработка и
применение программ проверок компетентности лабораторий

ИСО 3534-1:1993 Статистика.
Словарь и условные обозначения. Часть 1. Вероятность и основные статистические
термины

ИСО 5725-1:1994 Точность
(правильность и прецизионность) методов и результатов измерений. Часть 1.
Основные положения и определения

ИСО 5725-2:1994 Точность
(правильность и прецизионность) методов и результатов измерений. Часть 2. Основной
метод определения повторяемости и воспроизводимости стандартного метода
измерений

ИСО 5725-3:1994 Точность
(правильность и прецизионность) методов и результатов измерений. Часть 3.
Промежуточные показатели прецизионности стандартного метода измерений

ИСО 5725-4:1994 Точность
(правильность и прецизионность) методов и результатов измерений. Часть 4.
Основные методы определения правильности стандартного метода измерений

ИСО 5725-5:1998 Точность
(правильность и прецизионность) методов и результатов измерений. Часть 5.
Альтернативные методы определения прецизионности стандартного метода измерений

ИСО 5725-6:1994 Точность
(правильность и прецизионность) методов и результатов измерений. Часть 6.
Использование значений точности на практике

ИСО/ТО 7871:1997 Контрольные
карты кумулятивных сумм. Руководство по управлению качеством и анализу данных с
помощью метода кумулятивных сумм

ИСО 8258:1991 Контрольные карты
Шухарта

ИСО 10576-1:2003 Руководство по
оценке соответствия установленным требованиям. Часть 1. Общие принципы

ИСО 11648-1:2003 Статистические
аспекты выборочного контроля нештучной продукции. Часть 1. Общие принципы

3 Термины и определения

В настоящем стандарте применены
термины по ИСО 5725-3, а также следующие термины с соответствующими определениями:

3.1 смещение ( bias ): Разность между математическим
ожиданием результатов наблюдений¹⁾ и принятым опорным значением.

Примечание – Смещение – общая
систематическая ошибка²⁾ в противоположность случайной ошибке. Может
быть один или более компонентов, образующих систематическую ошибку. Большее
систематическое смещение от принятого значения соответствует большему значению
смещения.

¹⁾
Применительно к настоящим рекомендациям под наблюдениями следует понимать
испытания и измерения.

²⁾ Применительно к измерениям под
ошибкой следует понимать «погрешность».

[ИСО 3534-1]

3.2 суммарная стандартная
неопределенность ( combined
standard uncertainty ) u (у) :
Стандартная неопределенность результата измерений, полученного через значения
нескольких других величин, равная положительному квадратному корню из суммы
членов, представляющих собой дисперсии или ковариации этих других величин,
взятых с весами, соответствующими степени влияния этих величин на результат
измерений.

( GUM [1])

3.3 коэффициент охвата ( coverage factor ) к: Числовой коэффициент, используемый
как множитель суммарной стандартной неопределенности при определении
расширенной неопределенности.

Примечание
– Коэффициент охвата к находится обычно в диапазоне от 2 до 3.

( GUM [1])

3.4 расширенная
неопределенность ( expanded
uncertainty ) U : Величина, определяемая интервалом
вокруг математического ожидания результатов измерений, охватывающим большую
долю распределения значений, которые обоснованно могут быть приписаны
измеряемой величине.

Примечания:

1 Эта доля может быть определена
через доверительную вероятность или уровень доверия интервала.

2 Чтобы связать
определенный уровень доверия с интервалом расширенной неопределенности,
необходимы предположения (в явной или неявной форме) о характере распределения
вероятностей результатов измерений и их суммарной стандартной неопределенности.
Уровень доверия, который соответствует этому интервалу, может соответствовать
действительности только в той степени, в какой могут быть справедливы
предположения.

3 Расширенную неопределенность называют
полной неопределенностью в рекомендациях [2] INC-1 (1980).

3.5 прецизионность ( precision ):
Близость между независимыми результатами наблюдений, полученными при
определенных принятых условиях.

Примечания:

1 Прецизионность зависит
от распределения случайных ошибок и не связана ни с истинным, ни с заданным
значениями.

2 Меру прецизионности
обычно выражают в терминах рассеяния и вычисляют как стандартное отклонение
результатов наблюдений. Малой прецизионности соответствует большое стандартное
отклонение.

3 Независимость результатов наблюдений
означает, что результаты получены таким образом, что отсутствует влияние
предыдущих результатов на том же самом или аналогичном объекте наблюдений.
Количественные меры прецизионности решающим образом зависят от принятых
условий. Условия повторяемости и условия воспроизводимости являются разными
степенями принятых условий.

[ИСО 3534-1]

3.6 повторяемость ( repeatability ): Прецизионность в условиях
повторяемости, то есть в условиях, когда независимые результаты наблюдений
получены одним методом на идентичных объектах наблюдений в одной лаборатории
одним и тем же оператором с использованием одного оборудования и за короткий
интервал времени.

[ИСО 3534-1]

3.7 стандартное отклонение
повторяемости ( repeatability
standard deviation ): Стандартное отклонение результатов
наблюдений, полученных в условиях повторяемости.

Примечания:

1 Это мера рассеяния
результатов наблюдений в условиях повторяемости.

2 Аналогично «дисперсию повторяемости» и
«коэффициент вариации повторяемости» надо определять как меры рассеяния
результатов наблюдений в условиях повторяемости.

[ИСО 3534-1]

3.8 воспроизводимость ( reproducibility ): Прецизионность в условиях
воспроизводимости, то есть в условиях, когда результаты наблюдений получены
одним методом на идентичных объектах наблюдений в различных лабораториях с
разными операторами с использованием различного оборудования.

Примечание
– Для обоснованного заявления воспроизводимости необходимые требования на
изменения условий. Воспроизводимость представляют количественно через дисперсию
результатов.

[ИСО 3534-1]

3.9 стандартное отклонение
воспроизводимости ( reproducibility
standard deviation ): Стандартное отклонение результатов
наблюдений, полученных в условиях воспроизводимости.

Примечания:

1 Это мера рассеяния
распределения результатов наблюдений в условиях воспроизводимости.

2 Аналогично «дисперсию воспроизводимости» и
«коэффициент вариации воспроизводимости» надо определять как меры рассеяния
результатов наблюдений в условиях воспроизводимости.

[ИСО 3534-1]

3.10 стандартная
неопределенность ( standard
uncertainty ) u (х _i ) :
Неопределенность результатов измерений, выраженная в виде стандартного
отклонения.

3.11 правильность ( trueness ): Близость среднего значения,
полученного на основании серии результатов наблюдений, к принятому опорному
значению.

Примечание
– Меру правильности обычно выражают в терминах смещения. Ссылка на правильность
как «точность среднего» не рекомендуется.

[ИСО 3534-1]

3.12 неопределенность
(измерения) ( uncertainty ):
Параметр, связанный с результатом измерений, характеризующий рассеяние
значений, которые обоснованно могут быть приписаны измеряемой величине.

Примечания:

1 Параметром может быть,
например, стандартное отклонение (или величина, кратная ему) или полуширина
интервала, имеющего установленный уровень доверия.

2 Неопределенность
измерений включает в себя в общем случае несколько составляющих. Некоторые из
этих составляющих могут быть оценены по статистическим распределениям
результатов серии измерений и охарактеризованы экспериментальным стандартным
отклонением. Другие составляющие, которые также могут быть охарактеризованы
стандартными отклонениями, оцениваются на основе предположений о распределении
вероятностей, основанных на экспериментальной или другой информации.

3 Понятно, что результат измерений является
лучшей оценкой измеряемой величины, а все составляющие неопределенности,
включая те, которые являются результатом систематических воздействий, таких как
поправки корректировки и эталоны, вносят свой вклад в рассеяние результатов.

( GUM [1])

3.13 бюджет
неопределенности ( uncertainty
budget ): Список источников
неопределенности с соответствующими им стандартными неопределенностями,
собранный для определения суммарной стандартной неопределенности результата
измерений.

Примечание
– Список часто включает в себя дополнительную информацию, такую как коэффициент
чувствительности (интенсивность изменения результатов в зависимости от величины
воздействия на результат), степени свободы для каждой стандартной
неопределенности и идентификацию средних, соответствующих каждой стандартной
неопределенности, в терминах оценок типа А или типа В.

4 Обозначения

a	– коэффициент, указывающий отрезок, отсекаемый прямой на оси абсцисс в эмпирической функции ;
B	– лабораторная составляющая смещения;
b	– коэффициент наклона прямой в эмпирической функции ;
c	– коэффициент в эмпирической функции ;
ci	– коэффициент чувствительности ;
d	– коэффициент показателя степени в эмпирической функции ;
e	– случайная погрешность результата измерений (остаточная ошибка);
er	– случайная погрешность результата измерений (остаточная ошибка) в условиях повторяемости;
k	– числовой коэффициент, используемый как множитель суммарной стандартной неопределенности u при определении расширенной неопределенности U ;
l	– количество лабораторий;
m	– среднее измеряемой величины;
N	– количество составляющих, используемых в вычислениях неопределенности;
n ′	– количество объединяемых составляющих при вычислении суммарной неопределенности в дополнение к совместно исследуемым данным;
nl	– количество повторений на одном уровне лабораторией l ;
nr	– количество повторений измерения;
p	– количество лабораторий;
Q	– количество объектов испытаний из большей (по количеству) партии;
q	– количество назначенных величин в соответствии с соглашением в процесс совместных исследований;
rij	– коэффициент корреляции xi и xj (изменяется от – 1 до + 1);
sb	– стандартное отклонение, представляющее межгрупповую составляющую дисперсии;
	– межгрупповая составляющая дисперсии;
sD	– оценочное или экспериментальное стандартное отклонение результатов наблюдений, полученных повторными измерениями на образце сравнения, используемом при контроле смещения;
si	– стандартное отклонение повторяемости c   степенями свободы;
sinh	– неопределенность, соответствующая неоднородности образца;
	– составляющая дисперсии, соответствующая неоднородности образца;
sL	– экспериментальное или оценочное межлабораторное стандартное отклонение;
	– скорректированная неопределенность, соответствующая В, когда вклад зависит от выходной переменной;
	– оцениваемая дисперсия В;
sr	– внутрилабораторное стандартное отклонение;
	– скорректированная оценка внутрилабораторного стандартного отклонения, когда вклад зависит от выходной переменной;
	– оцениваемая дисперсия er
sR	– оцениваемое стандартное отклонение воспроизводимости;
	– скорректированная оценка стандартного отклонения воспроизводимости;
	– скорректированное стандартное отклонение воспроизводимости, вычисленное по эмпирической модели, когда вклады зависят от выходной переменной;
sw	– внутрилабораторное стандартное отклонение, полученное из повторных измерений или других повторных исследований;
	– внутригрупповая составляющая дисперсии (часто внутрилабораторная составляющая дисперсии);
	– лабораторное стандартное отклонение разностей при сравнении обычного метода с точным методом;
xi	– i -е исходное значение при определении результата;
	– отклонение i -го исходного значения от номинального значения х;
xj	– j -е исходное значение при определении результата;
	– неопределенность, соответствующая δ, вызванная неопределенностью оценки δ, по измерениям исходного эталона или сравнения образца с сертифицированным значением ;
	– неопределенность, соответствующая сертифицированному значению
u ( y )	– суммарная стандартная неопределенность, соответствующая y ;
u ( Y )	– суммарная неопределенность для результата Y = f ( y 1 , y 2 ,…) ;
u 2 ( y )	– суммарная стандартная неопределенность, соответствующая у, выраженная через дисперсию3);
uinh	– неопределенность, соответствующая неоднородности выборки;
U	– расширенная неопределенность, равная стандартной неопределенности u , умноженной на k ;
U ( y )	– расширенная неопределенность у, когда U ( y ) = ku (у) ( k – коэффициент охвата);
yi	– результат испытаний i -го объекта точного метода при сравнении методов;
	– результат испытаний i -го объекта от обычного метода испытаний при сравнении методов;
y 0	– заданное значение для проверки квалификации;
Δ	– лабораторное смещение;
Δi	– оценка смещения i -й лаборатории, равная среднему лаборатории m , минус сертифицированное значение ;
	– среднее смещение лаборатории при сравнении обычного метода с фиксированным;
δ	– смещение, соответствующее используемому методу измерений;
	– оцененное или измеренное смещение;
μ	– неизвестное математическое ожидание результата4);
	– сертифицированное значение образца сравнения;
σ 0	– стандартное отклонение при проверке квалификации;
σ D	– истинное значение стандартного отклонения результатов, полученных повторными измерениями на образце сравнения, используемом для контроля смещения;
σ L	– межлабораторное стандартное отклонение; стандартное отклонение В;
	– дисперсия B ; межлабораторная дисперсия;
σ r	– внутрилабораторное стандартное отклонение; стандартное отклонение е r ;
	– дисперсия е r ; внутрилабораторная дисперсия;
σ w	– стандартное отклонение внутри группы;
σ w 0	– стандартное отклонение, требуемое для адекватной работы ИСО Руководство 33;
	– эффективная степень свободы для стандартного отклонения или неопределенности, соответствующей входному значению х i ;
	– число степеней свободы.

³⁾ В
соответствии с GUM [1] u²(у) – суммарная
дисперсия, соответствующая оценке y выходной величины.

⁴⁾ В
соответствии с ГОСТ
Р ИСО 5225.1 μ-истинное или принятое опорное значение
измеряемой величины.

5 Принципы

5.1 Отдельные результаты и свойства процесса
измерений

5.1.1 Неопределенность измерений
относят к отдельным результатам измерений. Повторяемость, воспроизводимость и
правильность, напротив, относят к выполнению процесса измерений или испытаний.
Для анализа в соответствии со всеми частями ИСО 5725 процесс измерений или
испытаний является единым методом измерений, используемым всеми лабораториями,
принимающими участие в исследовании. Следует заметить, что в настоящих
рекомендациях под методом измерений понимают единственную детальную процедуру
(как определено в Международном словаре основных и общих терминов в метрологии
( VIM ) [2] ). Неявно в настоящих рекомендациях предполагается, что
графики, отражающие выполнение процесса, полученные при исследовании метода,
соответствуют всем отдельным результатам измерений, полученным с помощью
процесса. Это предположение требует подтверждающих доказательств в виде данных
соответствующего контроля качества и уверенности в качестве процесса измерений
( раздел
7).

5.1.2 Ниже будет показано, что
дополнительно может потребоваться учитывать различия между отдельными объектами
испытаний. Однако в этом случае не нужно предпринимать индивидуальные и
детальные исследования неопределенности для каждого объекта испытаний при
наличии хорошо охарактеризованного и устойчивого процесса измерений.

5.2 Применение данных воспроизводимости

Применение данного документа
основано на двух принципах:

– стандартное отклонение
воспроизводимости, полученное при совместных исследованиях, является
правомерной основой для оценки неопределенности измерений (см. 2.1);

– воздействия, не наблюдаемые в
процессе совместных исследований, должны быть незначительными или явно
учитываться. Последний принцип является расширением основной модели,
используемой для совместных исследований (см. А.2.3).

5.3. Основные уравнения статистической
модели

5.3.1 Статистическая модель, на
которой основано данное руководство, сформулирована в виде уравнения:

,                                                          (1)

где у – наблюдаемый
результат, рассчитываемый по уравнению: y = f ( x ₁ , x ₂ ,…, x_n ) ;

μ – неизвестное математическое
ожидание;

δ –
смещение, присущее методу измерений;

B – лабораторная составляющая
смещения;

 – отклонение от
номинального значения х _i ;

c_i –
коэффициент чувствительности, равный δy / δx_i ;

е – остаточная ошибка.

Предполагается, что B и е подчиняются нормальному
распределению с нулевым средним и дисперсиями  и  соответственно. Эти предположения
формируют модель, используемую в ИСО 5725-2 для анализа совместных данных.

Так как наблюдаемые стандартные
отклонения смещения метода δ, лабораторные смещения B и остаточные ошибки е являются полными
мерами разброса в условиях совместного исследования, сумма  учитывает
воздействия, которые вызывают отклонения, не включенные в δ, В
или е, и, таким образом, эта сумма позволяет учесть влияние действий, которые
не выполнялись в ходе совместных исследований.

Примерами таких действий
являются следующие:

а)
подготовка объекта испытаний, выполняемая практически для каждого испытываемого
объекта, но выполненная до совместных исследований;

b )
влияние подвыборки в случае, когда объекты, подвергаемые совместному
исследованию, были гармонизированы до исследования. Предполагается, что  подчиняются
нормальному распределению с нулевым математическим ожиданием и дисперсией u ² ( x_i ) .

Пояснения для этой модели
приведены в приложении
А.

Примечание
– Ошибка обычно определяется как разность между установленным значением и
результатом измерений. В ( GUM [1] «ошибку» четко отличают
от «неопределенности» (разброса значений). При оценке неопределенности, однако,
важно характеризовать разброс значений, вызванный случайными воздействиями, и
включать его в модель. Для представленных целей это достигается включением
члена, характеризующего «ошибку» с нулевым математическим ожиданием, как в уравнении (1).

5.3.2 Учитывая модель,
описываемую уравнением (1), неопределенность u (у) , связанную с наблюдениями,
можно оценить, применяя уравнение:

,                                        (2)

где  – оценка дисперсии В;

 – оценка дисперсии
е;

 – неопределенность,
вызванная неопределенностью оценки δ, полученной на основе
измерений исходного эталона или образца сравнения с сертифицированным значением
;

u ( x_i ) –
неопределенность, связанная с .

Учитывая, что стандартное
отклонение воспроизводимости s_R ,
задаваемое равенством, , можно заменить на , уравнение (2) можно привести к уравнению

                                               (3)

5.4 Данные повторяемости

Данные повторяемости используют
в настоящих рекомендациях прежде всего для проверки прецизионности, которая в
соединении с другими тестами подтверждает, что конкретная лаборатория может
применять данные воспроизводимости математического ожидания и правильности при
оценке неопределенности. Данные повторяемости используют также при вычислении
составляющей воспроизводимости в неопределенности (см. 7.3 и 11).

6 Оценка неопределенности с использованием
оценок повторяемости, воспроизводимости и правильности

6.1 Процедура оценки неопределенности
измерений

Принципы, на которых основаны
настоящие рекомендации (см. 5.1), приводят к
следующей процедуре оценки неопределенности измерений:

а) получение оценок
повторяемости, воспроизводимости и правильности метода на основе опубликованной
информации о методе;

b )
проверка, не превышает ли лабораторное смещение, рассчитанное по измерениям на
основе данных, полученных в соответствии с перечислением а);

с) проверка, не превышает ли
прецизионность, полученная по текущим измерениям прецизионности, полученной на
основе оценок повторяемости и воспроизводимости в соответствии с перечислением
а);

d )
идентификация любых воздействий на измерение, которые не были учтены в процессе
исследований в соответствии с перечислением а), и определение количественной
оценки отклонения, которое может вызывать эти воздействия, учитывая коэффициент
чувствительности и неопределенности каждого воздействия;

е) объединение оценки
воспроизводимости (перечисление а)) с неопределенностью соответствующей
правильности (перечисления а) и b)) и результатами дополнительных воздействий
(перечисление d )) для
формирования оценки суммарной неопределенности, когда смещение и прецизионность
находятся под контролем в соответствии с перечислениями b ) и с).

Этапы этой процедуры описаны
более подробно в разделах 7- 11.

Примечание –
В рекомендациях предполагается, что в случае, когда смещение является
неконтролируемым, выполняют корректирующие действия, чтобы привести процесс в
управляющую зону.

6.2 Различия между фактической
прецизионностью и ее математическим ожиданием

Если фактическая прецизионность
отличается от математического ожидания прецизионности, полученного на основе
исследований в соответствии с перечислением а), соответствующие вклады в
неопределенность должны быть учтены. В 8.5
описаны регуляторы оценок воспроизводимости для общего случая, когда
прецизионность приближенно пропорциональна уровню отклика.

7 Установление соответствия данных выполнения
метода результатам измерений для конкретного процесса измерений

7.1 Общие положения

Результатами совместного
исследования являются s_R , s_r и, в
некоторых случаях, оценка смещения метода, которые формируют требования для
выполнения метода. При принятии метода для применения ожидается, что лаборатория
продемонстрирует, что она выполняет эти требования. В большинстве случаев это
достигается исследованиями, направленными на подтверждение контроля
повторяемости (см. 7.3)
и лабораторной составляющей смещения (см. 7.2), и постоянными проверками
выполнения метода (контроль и обеспечение качества (см. 7.4)).

7.2 Демонстрация контролируемости
лабораторной составляющей смещения

7.2.1 Общие требования

7.2.1.1 Лаборатория должна
продемонстрировать, что ее смещение при выполнении метода находится под
контролем, то есть лабораторная составляющая смещения не выходит за пределы
смещения, полученного из совместных исследований. В следующих описаниях
предполагается, что контроль смещения выполнен на материалах значениями,
близкими к объектам исследования при обычных испытаниях. В тех случаях, когда
материалы, используемые для проверки смещения, не имеют значений, близких к
материалам, исследуемым при обычных испытаниях, итоговые вклады в
неопределенность должны быть исправлены в соответствии с условиями 8.4 и 8.5.

7.2.1.2 В общем случае проверка
лабораторной составляющей смещения сводится к сравнению лабораторных
результатов с некоторыми эталонными значениями и представляет собой оценку В.
Уравнение (2) показывает, что неопределенность,
связанная с изменениями В, характеризуется s_L , непосредственно входящей в s_R . Однако, поскольку проверка
смещения имеет собственную неопределенность, неопределенность сравнения в
принципе увеличивает неопределенность результатов, получаемых при будущих
применениях метода. По этой причине важно гарантировать, что неопределенность,
связанная с проверкой смещения, мала по сравнению с s_R (в
идеале меньше, чем 0,2 s_R ) и,
следовательно, соответствующее увеличение неопределенности является
незначительным. В этом случае, если свидетельства чрезмерной лабораторной
составляющей смещения не обнаружены, уравнение (3)
применяют без изменений. Если неопределенность, связанная с проверкой смещения,
является большой, благоразумно увеличивать неопределенность, оцененную на
основе уравнения (3) (см. 3.13). Если на основе совместных исследований правильности
известно, что метод имеет незначительное смещение, известное смещение метода
следует учитывать при оценке лабораторного смещения, например, путем
исправления результатов на известное смещение метода.

7.2.2 Методы демонстрации контролируемости лабораторной
составляющей смещения.

7.2.2.1 Общие положения

Контролируемость смещения может
быть продемонстрирована одним из следующих методов. Последовательно одни и те
же общие критерии используются для всех тестов на смещение, приведенных в
настоящих рекомендациях, Допускается использовать более строгие тесты и
проверки.

7.2.2.2
Исследование образца сравнения или эталона стандартного метода измерений
Лаборатория l
должна исполнить n_l
повторных измерений на исходном эталоне в условиях повторяемости, чтобы
получить оценку смещения на этом веществе Δ _l ; (равную среднему лаборатории m минус стандартное значение ). При этом n_l , следует выбирать так, чтобы
неопределенность удовлетворяла неравенству . Следует заметить, что исходный эталон в общем случае не
является тем же эталоном, который использовали при оценке правильности метода.
Кроме того, Δ _l ,
вообще не равно В. Следуя Руководству ИСО/МЭК 33 (с соответствующим
изменением обозначений), процесс измерений выполняется адекватно, если:

.                                                                                 (4)

Заменив σ₀
на его приближение s_D
в
уравнении (4), получаем уравнение:

,                                                                             (5)

где n_l – количество повторений
лаборатории l ;

s_w – внутрилабораторное
стандартное отклонение, полученное на основе n_l повторений
или других исследований повторяемости;

s_L –
межлабораторное стандартное отклонение.

Соответствие критерию,
описываемому уравнением (4), является подтверждением того, что лабораторная
составляющая смещения B
находится в интервале значений, установленном при совместных исследованиях.
Следует обратить внимание на то, что образец сравнения или эталон используют
здесь для независимой проверки или в качестве контрольного вещества, а не для
калибровки.

Примечания:

1 Лаборатория может
применять более строгий критерий, чем уравнение (4),
используя коэффициент охвата менее 2 или выполняя альтернативный и более
чувствительный тест на смещение.

2 Эти процедуры предполагают, что
неопределенность, связанная с эталонным значением, мала по сравнению с σ _D.

7.2.2.3 Сравнения с заданным
методом испытаний, обладающим известной неопределенностью Лаборатория l должна проверить соответствующее
количество n_l
объектов испытаний, применяя заданный метод испытаний и метод, использованный
лабораторией, получив, таким образом, n_l пар  – результат
применения заданного метода к i -му
объекту, а  – значение,
полученное применением обычного метода испытаний для i -го объекта). Затем лаборатория должна
вычислять соответствующее среднее смещение , используя уравнение (6) и стандартное отклонение s ( Δ _y )
разностей:

                                                                 (6)

На практике значение n_l должно
быть выбрано так, чтобы неопределенность удовлетворяла неравенству . По аналогии с уравнениями (4)
и (5) процесс измерений удовлетворяет
требованиям, если . В этом случае уравнение (3)
используют без изменений.

Примечания:

1 Лаборатория может
выбирать более строгий критерий, чем уравнение (4),
используя коэффициент охвата менее 2 или выполняя альтернативный и более
чувствительный тест на смещение.

2 Эти процедуры предполагают, что
неопределенность, связанная с эталонным методом, мала по сравнению с σ₀.

7.2.2.4 Сравнение с другими лабораториями
при использовании того же метода

Если лаборатория l участвует в дополнительных совместных
исследованиях (например, при проверке квалификации в соответствии с ИСО/МЭК
Руководство 43-1), для которых она может оценивать смещение, эти данные можно
использовать для контроля смещения. Есть два возможных варианта:

а) при выполнении испытаний
используют эталон или образец сравнения с независимо назначенными значениями
неопределенности. Затем применяют процедуру 7.2.2.2
без изменений;

b )
проводят проверку соответствия q (≥1)
заданных значений у₁, у₂, …, у _q Лаборатории, чьи результаты
представлены значениями  следует рассчитать
свое среднее смещение  в соответствии с
уравнением (7) и стандартное отклонение s (Δ _y )
заданных значений.

.                                                                  (7)

Процесс измерений удовлетворяет
требованиям, если . В этом случае уравнение (3)
используют без изменений.

Примечания:

1 Эта процедура
предполагает, что заданные значения основаны на количестве результатов,
превышающем q, и
обладают незначительной неопределенностью.

2 В некоторых схемах
проверки квалификации все значения у _i, преобразуют в z-множество z_i = (у _i–у₀)/σ₀
вычитанием заданного значения у₀ и делением на
стандартное отклонение σ₀ (см. ИСО/МЭК Руководство 43-1). Если
стандартное отклонение метода менее или равно s_R, среднее z-множества лежит между  для назначенного
значения q. Это
является достаточным свидетельством контролируемости смещения.

7.2.3 Выявление существенной лабораторной
составляющей смещения

Как отмечено в разделе 1, настоящие рекомендации применимы
только в тех случаях, когда лабораторная составляющая смещения находится под
контролем. Если обнаружено чрезмерное смещение, предполагается, что будут
предприняты действия для приведения смещения в границы требуемого диапазона до
продолжения измерений. Такие действия обычно требуют проведения исследований и
устранения причины смещения.

7.3 Верификация повторяемости

7.3.1 Испытательная лаборатория
должна продемонстрировать, что ее повторяемость совместима со стандартным
отклонением повторяемости, полученным при совместных исследованиях.
Демонстрация достигается проведением анализа одного или более подходящих
испытываемых материалов для получения (объединяя результаты при необходимости)
стандартного отклонения повторяемости s_i v_i степенями свободы. Значения s_i необходимо сравнивать,
используя F -тест с 95 %-ным уровнем
доверия, со стандартным отклонением повторяемости s_r , полученным при совместных
исследованиях. На практике для получения v_i ≥
15 следует выполнять достаточно повторений.

7.3.2 Если s_i значительно больше s_r , лаборатория должна или
идентифицировать и устранять соответствующие причины, или использовать s_i вместо s_r во всех оценках
неопределенности, рассчитанных с использованием настоящих рекомендаций. Следует
обратить внимание, что это вызывает увеличение оценки стандартного отклонения
повторяемости s_r , так
как  будет заменено на  является
скорректированной оценкой стандартного отклонения воспроизводимости).

Наоборот, если s_i , значительно меньше s_r , лаборатория может также
использовать s_i ,
вместо s_r ,
получая меньшую оценку неопределенности.

Во всех исследованиях
прецизионности важно подтверждать, что данные свободны от неизвестных смещений,
и проверять постоянство стандартного отклонения s_w для различных объектов
испытаний. Если стандартное отклонение s_w непостоянно,
может быть полезно оценить прецизионность отдельно для каждого различного
класса объектов или построить общую модель (см. 8.5) для
этой зависимости.

Примечание
– Если требуется сравнение с заданным значением прецизионности, Руководство ИСО
33 более детально описывает соответствующий тест, основанный на . Здесь  соответствует
требуемому значению прецизионности.

7.4 Постоянная верификация

Кроме предварительной оценки
смещения и прецизионности, лаборатория должна принимать должные меры для
гарантии того, что процедура измерений остается в состоянии статистического
контроля. В частности, это включает следующее:

– соответствующий контроль
качества, включая регулярные проверки смещения и прецизионности. Для этих
проверок допускается использовать любые уместные устойчивые гомогенные объекты
испытаний или материалы. Настоятельно рекомендуется использование контрольных
карт (см. ИСО/ТО 7871 и ИСО 8258);

– меры по проверке качества,
включая использование соответственно обученного и квалифицированного персонала,
работающего в соответствующей системе качества.

8 Учет особенностей объекта испытаний

8.1 Общие положения

В совместных исследованиях или
оценке промежуточных показателей прецизионности в соответствии с ИСО 5725-2 и ИСО
5725-3 обычно проводят измерения на гомогенных материалах или объектах
небольшого количества типов. Это является обычной практикой для разделения
подготовленных материалов. Однако объекты испытаний могут изменяться в широком
диапазоне, что может требовать дополнительной обработки до испытаний. Например,
образцы для экологических испытаний часто поставляют высушенными и
гомогенизированными. Обычные образцы, как правило, являются влажными,
неоднородными и грубо разделенными. Соответственно необходимо исследовать и,
если необходимо, учитывать эти различия.

8.2 Отбор выборки

8.2.1 Процесс отбора выборки

Совместные исследования редко
включают в себя этап отбора выборки. Если метод, использованный внутри
лаборатории, включает в себя подвыборки или процедура оценивает свойство
большого объема материала по маленькому образцу, то влияние отбора выборки необходимо
исследовать. Может быть полезно обращаться к документации по отбору выборки,
например к ИСО 11648-1 или другим стандартам.

8.2.2 Негомогенность

Негомогенность обычно исследуют
экспериментально с применением дисперсионного анализа ( ANOVA )⁵⁾ к нескольким объектам
испытаний, для которых составляющая дисперсии , описывающая разброс между объектами, характеризует
негомогенность. Если после всех установленных действий по гомогенизации
испытываемые материалы признаны существенно неоднородными, эту оценку дисперсии
следует преобразовать непосредственно в стандартную неопределенность (то есть u_inx = s_inx ). В некоторых обстоятельствах, особенно
когда стандартное отклонение негомогенности найдено для выборки из Q объектов, взятой из партии, а средний
результат будет применим к другим объектам партии, вклад неопределенности
оценивают на основе предикционного интервала (то есть ). Можно также теоретически оценивать воздействие
негомогенности, используя знание процесса отбора выборки и предположений о
распределении, соответствующем выборке.

⁵⁾ Принятая в международной практике аббревиатура
для обозначения дисперсионного анализа ( Analysis of Variance).

8.3 Подготовка и предварительная обработка
выборки

В большинстве исследований
образцы являются гомогенными и могут быть дополнительно стабилизированы до
распределения. Могут потребоваться исследования, позволяющие учитывать
воздействия специфических процедур предварительной обработки внутри
лаборатории. Как правило, такие исследования устанавливают воздействие этой
процедуры на результаты измерений на исследуемых материалах с приблизительно или
точно установленными свойствами. Воздействием может быть изменение разброса или
систематических воздействий. Существенные изменения разброса следует устранять
прибавлением соответствующей составляющей к бюджету неопределенности
(предполагая, что воздействия увеличивают разброс). Если выявлены существенные
систематические воздействия, наиболее удобно устанавливать соответствующий
верхний предел. Следуя рекомендациям GUM
[1] , этот предел можно рассматривать как
границу прямоугольного или другого ограниченного симметричного распределения, а
оценку стандартной неопределенности можно задавать в виде полуширины области
изменений функции распределения, деленной на соответствующий коэффициент.

8.4 Изменение типа объекта испытаний

При необходимости следует
исследовать неопределенность, являющуюся результатом изменения типа или состава
объектов испытаний по сравнению с используемыми в совместных исследованиях. Как
правило, подобные воздействия должны быть предсказаны на основе установленных
воздействий, объемных свойств материала (которые дают оценку неопределенности,
полученную в соответствии с GUM
[1] ) или исследованы введением
систематических или случайных изменений типа или состава объектов испытаний
(см. приложение
В).

8.5 Изменение неопределенности в зависимости от
уровня отклика

8.5.1 Корректировка s_R

Обычно некоторые или большая
часть составляющих неопределенности измерений зависят от измеренного значения. ИСО
5725-2 рассматривает три простых случая, когда стандартное отклонение
воспроизводимости для положительной величины m приближенно описывается одной из
моделей

;                                                                                     (8)

;                                                                                (9)

,                                                                                    (10)

где  – откорректированная
оценка стандартного отклонения воспроизводимости, рассчитанная по приближенной
модели;

а, b , c и d – эмпирические коэффициенты,
полученные на основе пяти или большего количества различных объектов испытаний
с различными средними отклика m (а,
b и c являются положительными).

При использовании уравнений
(8)-(10) неопределенность должна основываться на оценке воспроизводимости,
рассчитанной с использованием соответствующей модели.

В условиях 7.3  должен учитывать член
s_r ,
отражающий вклад повторяемости. Для большинства целей имеет место простое
пропорциональное изменение .

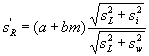,                                                              (11)

где  имеет то же самое
значение, как и в 7.3.

8.5.2 Изменение других вкладов в
неопределенность

В общем случае, если любая
составляющая неопределенности изменяется в соответствии с измеренным откликом предсказуемым
способом, соответствующая стандартная неопределенность у должна быть
откорректирована соответственно.

Примечание
– Если вклады в неопределенность прямо пропорциональны у, часто бывает
удобно выражать все существенные воздействия в терминах мультипликативных
воздействий на у, а всю неопределенность – в форме относительных
стандартных отклонений.

9 Дополнительные факторы

Раздел 8 рассматривает главные
факторы, которые обычно различаются в совместных исследованиях и обычных
испытаниях. Возможно, что в специфических случаях могут проявляться другие
воздействия. Это может быть вызвано тем, что контролируемые переменные случайно
или преднамеренно были постоянными в течение совместного исследования, или тем,
что полный диапазон условий, достижимых в обычной практике, не был охвачен при
совместных исследованиях.

Воздействия факторов, которые
считаются постоянными или которые изменяются недостаточно при совместных
исследованиях, следует оценивать отдельно либо в процессе экспериментального
изменения, либо в соответствии с прогнозом на основе теории. В тех случаях,
когда воздействия являются существенными, неопределенность, связанную с
соответствующими факторами, необходимо оценивать, регистрировать и объединять с
другими вкладами обычным способом (то есть суммировать в соответствии с уравнением (3)).

10 Общее выражение для суммарной стандартной
неопределенности

Уравнение
(3), при необходимости использовать скорректированную оценку  вместо , для учета факторов, рассматриваемых в разделе 8, приводит к общему
выражению (12) для оценки суммарной стандартной неопределенности u (у) соответствующему результату у.

.                                              (12)

Значение  подсчитывают в
соответствии с уравнением (13), см. также уравнение
(А.8).

,                                                   (13)

где p – количество лабораторий;

n – количество повторений в каждой
лаборатории.

Переменная u ( B ) не использована в уравнении
(12), потому что неопределенность s_L ,
соответствующая B , уже
включена в , Индекс i
охватывает
воздействия, идентифицированные в разделах 8 и 9 (индексы изменяются от 1 до ). Очевидно, что если воздействия и их неопределенности малы
по сравнению с s_R , то
ими можно пренебречь для большинства практических целей. Например,
неопределенность менее 0,2 s_R .
ведет к изменению менее чем на 0,02 s_R оценки полной неопределенности.

11 Бюджет неопределенности, основанный на
данных совместных исследований

Настоящие рекомендации
используют только одну приведенную в уравнении (3)
модель для описания результатов измерений или испытаний. Информацию,
подтверждающую справедливость модели, можно получать из различных источников,
но если неопределенность, соответствующая испытаниям, остается незначительной,
используют уравнение (3). Однако есть несколько
различных ситуаций, при которых уравнение (3)
немного изменяется. Например, если параметры воспроизводимости или
повторяемости зависят от отклика. Бюджет неопределенности, если
неопределенность совсем не зависит от отклика в исследуемом диапазоне, приведен
в таблице 1, а для случая, когда неопределенность зависит от отклика, – в
таблице 2.

Таблица 1 – Составляющие неопределенности, не
зависящие от отклика

Источник воздействия	Стандартная неопределенностьа, соответствующая у	Комментарий
δ		Используют, если смещение, выявленное при совместных исследованиях, устранено, а неопределенность является существенной
B	sL	См. таблицу 2
е r	sr	Если среднее, полученное по nr полных повторений метода b , применяют к объекту испытаний, неопределенность, соответствующая е r , принимает вид –
xi	ciu(xi)	См. Раздел 8 и приложение В
a Стандартная неопределенность измеряется в тех же единицах, что и у. b Метод может включать nr повторений всего метода и любые предусмотренные повторения.

Таблица 2 – Составляющие неопределенности, зависящие от отклика

Источник воздействия	Стандартная неопределенностьa, b , соответствующая у	Комментарий
δ		Используют, только если выявленное при совместном исследовании смещение устранено, а неопределенность является существенной. (Производную используют, чтобы охватить случаи, когда устранение смещения не сводится к простому сложению или вычитанию)
B		aL и bL – коэффициенты предполагаемой линейной зависимости между sL и средним откликом m , аналогичной уравнению (9). Эта форма применима, только если установлена зависимость sL от m . В противном случае используют комбинированную оценку, соответствующую В и е r таблицы 1
е		ar и br – коэффициенты предполагаемой линейной зависимости между sr и средним откликом m , аналогичной уравнению (9). Если среднее, полученное по nr полных повторений метода, применяют к объекту испытаний, неопределенность, соответствующая е r , принимает вид – . Эта форма применима, только если установлена зависимость sr от m . В противном случае используют объединенную оценку, соответствующую B и е r из таблицы 1
B, e		а и b – коэффициенты линейных отношений между sR и средним откликом m , как определено в уравнениях (9) и (10). Эту объединенную оценку следует использовать вместо отдельных оценок В и е r (см. таблицу 1), когда отдельные зависимости sL и sr от m не установлены
xi	ciu(xi)	См. Раздел 8 и приложение В
а Стандартную неопределенность измеряют в тех же единицах, что и у. b Предполагается простая линейная зависимость, соответствующая уравнению (9). с Метод может включать nr повторений всего метода и любые предусмотренные повторения.

12 Оценка неопределенности комбинированного
результата

12.1 Комбинированный результат
формируют из совокупности результатов различных испытаний, каждый из которых
охарактеризован совместными исследованиями. Например, вычисления по определению
состава мяса обычно объединяют определением содержания белка (рассчитанного
путем определения содержания азота), жира и влаги. При этом содержание каждого
вещества определяют соответствующим стандартным методом.

12.2 Неопределенность u ( y_i ) для
каждого результата у, может быть получена на основе принципов, приведенных
в настоящих рекомендациях, или непосредственно используя уравнения (1) или (2)
соответственно. Если величины у _i независимы, суммарную
неопределенность u ( Y ) для результата Y = f ( y ₁ , y ₂ ,…)
вычисляют по формуле:

.                                                                (14)

Если y_i не являются независимыми,
должны быть сделаны предположения относительно корреляции в соответствии с GUM [1] (также используют уравнение
(А.2)).

13 Представление информации о неопределенности

13.1 Общие положения

Неопределенность может быть
представлена в виде суммарной стандартной неопределенности u ( y ) или суммарной расширенной
неопределенности U ( y ) = ku ( y ) ( k – коэффициент охвата) (см. 13.2 и GUM [1] ). Может быть удобно представить неопределенность в
относительных величинах как коэффициент вариации или расширенную
неопределенность, выражаемые в процентах зарегистрированных результатов.

13.2 Выбор коэффициента охвата

13.2.1 Общие положения

При оценке суммарной расширенной
неопределенности применяют следующие исследования для выбора коэффициента
охвата k .

13.2.2 Уровень доверия

Для практических целей должно
быть указано значение суммарной расширенной неопределенности, соответствующее
уровню доверия 95 %. Однако выбор уровня доверия зависит от диапазона факторов,
таких как критичность и последствия применения неправильных результатов. Эти
факторы вместе с любыми рекомендациями или юридическими требованиями,
касающимися применения, должны быть рассмотрены при выборе k .

13.2.3 Степени свободы, соответствующие
оценке

13.2.3.1 Для большинства
практических целей, когда требуется 95 %-ный уровень доверия и число степеней
свободы в доминирующих составляющих неопределенности превышает 10 (>10),
выбор k = 2 обеспечивает достаточно
надежный охват вероятного диапазона значений. Однако есть обстоятельства, в
которых это приводит к существенной недооценке, особенно когда один или более
значимых членов уравнения (12) имеют число
степеней свободы менее 7.

13.2.3.2 Если один такой член u_i ( y ) с v_i ,- степенями свободы доминирует
[признаком является выполнение неравенства u_i ( y ) > 0,7 u ( y ) ], обычно достаточно взять в
качестве v_i
эффективные степени свободы v_eff ,
соответствующие u ( y ) .

13.2.3.3 Если несколько
существенных членов имеют приблизительно равную величину и степени свободы,
удовлетворяющие условию v_i
<<
10, для получения эффективных значений числа степеней свободы v_eff следует применять уравнение
Велча-Саттервейта (уравнение (15))

.                                                                    (15)

Значение k тогда выбирают из v_eff , используя значение квантиля
двустороннего распределения Стьюдента для требуемого уровня доверия и v_eff степеней свободы. Это наиболее
безопасно при округлении нецелых чисел v_eff до
ближайшего меньшего целого числа.

Примечание
– Во многих областях измерений и испытаний для нормального распределения
частота статистических выбросов является достаточно высокой, поэтому применение
высоких уровней доверия (>95 %) без хорошего знания распределения не
рекомендуется.

14 Сравнение данных выполнения метода и
неопределенности

14.1 Основные предположения

Оценка неопределенности измерений
в соответствии с настоящими рекомендациями обеспечивает стандартную
неопределенность, которая, хотя и основывается прежде всего на оценках
воспроизводимости или промежуточной прецизионности, отдает должное факторам,
которые не изменяются в процессе исследований, в которых эти оценки
прецизионности получены. В принципе итоговая стандартная неопределенность u ( y ) должна быть идентична
неопределенности, полученной на основе детальной математической модели процесса
измерений. Сравнение этих двух оценок, если это возможно, обеспечивает полезную
проверку качества оценки. Рекомендованная процедура описана в 14.2.

Процедура основана на двух
важных предположениях:

– во-первых, оценку стандартной
неопределенности u ( y ) с v_eff эффективными
степенями свободы обычно определяют в предположении о нормальном распределении
наблюдений (это означает, что ( n -1)( s ² /σ²)
подчиняется χ² распределению с ( n -1) степенями свободы), Это
предположение позволяет использовать F -критерий.
Однако, поскольку суммарная неопределенность может включать неопределенность,
связанную с величинами, описываемыми распределениями различной формы с
различными дисперсиями, результаты испытаний необходимо рассматривать как
индикатор, а уровень доверия следует выбирать с необходимой осторожностью;

– во-вторых, обычно
предполагают, что две оценки неопределенности, которые будут сравниваться,
полностью независимы. Это также маловероятно на практике, так как некоторые
факторы могут быть общими для обеих оценок. Более тонкие воздействия являются
предметом исследований для выявления влияния составляющей неопределенности,
соответствующей выполнению работ в разных лабораториях. Предполагается, что
приняты необходимые меры предосторожности, чтобы избежать этого воздействия.
Если значимые факторы являются общими для обеих оценок неопределенности,
очевидно, что оценки будут подобны значительно чаще, В этом случае, если
последовательные испытания не в состоянии выявлять существенные различия,
результаты не следует трактовать как свидетельство надежности модели измерений.

14.2 Процедура сравнения

Для сравнения двух оценок u ( y ) ₁ и u ( y ) ₂ ( u ( y ) ₁
является большей из них) с эффективными степенями свободы v ₁ и v ₂ соответственно,
используя уровень доверия α (например, для 95 %-ного уровня доверия
α = 0,05), необходимо выполнить следующие действия:

вычислить F = [ u (у) ₁ /и(у) ₂ ]²;

найти по таблицам или получить с
помощью программного обеспечения одностороннее верхнее критическое значение F_crit = F (α/2, v ₁ , v ₂ ). Если даны верхнее и нижнее значения,
выбирают верхнее значение, которое всегда больше 1;

если F > F_crit , то u ( y ) ₁
следует считать значительно больше, чем u ( y ) ₂ .

14.3 Причины различий

Существует много причин для существенного
различия между суммарными оценками неопределенности. Они включают в себя
следующее:

– подлинные различия в работе
лабораторий;

– неудачную модель, не
учитывающую влияние всех существенных воздействий на измерения;

– неверную оценку значимого вклада
в неопределенность.

Приложение А (справочное)
Подходы
к оценке неопределенности

А.1 Подход GUM

Руководство по оценке
неопределенности измерений ( GUM
[1] ), изданное ИСО, устанавливает
методологию оценки неопределенности измерений, связанную с результатом y в соответствии с моделью процесса
измерений. Методология GUM
базируется на рекомендациях Международной палаты мер и весов ( BIPM [3],
которые признают, что составляющие неопределенности можно оценивать либо на
основе статистического анализа серии наблюдений (оценка типа А), либо другими
средствами (оценка типа В), например, используя данные публикаций о
неопределенности образцов сравнения или эталонов или, при необходимости, мнения
специалистов. Отдельные составляющие выражают в виде стандартных отклонений и,
при необходимости, затем объединяют.

Выполнение рекомендаций В I РМ [3] в
GUM [1] начинается с модели измерений в виде
функции у = f ( x ₁ , х₂, … , х _N ), связывающей результат
измерений у со входными величинами х _i . Тогда в случае независимых
входных величин GUM дает
неопределенность u ( y ) в соответствии с уравнением
(А.1):

,                                                                 (А.1)

где с _i – коэффициент чувствительности,
оцениваемый в соответствии с уравнением с _i = dy / dx_i , (частная производная у
по х _i );

u ( x_i ) и u ( y ) – стандартные неопределенности,
то есть неопределенности измерений, выраженные в виде стандартных отклонений.

Если переменные не являются
независимыми, выражение для неопределенности является более сложным и
определяется уравнением:

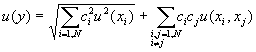,                                   ( A.2)

u ( x_i , x_j ) –
ковариация между x_i , x_j ;

c_i и c_j – коэффициенты
чувствительности, соответствующие уравнению (А.1). На практике часто ковариацию
выражают через коэффициент корреляции r_ij :

,                                                             (А.3)

где – .

В случаях, учитывающих
нелинейность модели измерений, уравнение (А.1)
расширяют, включая члены более высокого порядка. Эта ситуация более подробно
описана в GUM [1] . После вычисления комбинированной стандартной
неопределенности с использованием уравнений
(А.1)-(А.3) расширенную неопределенность определяют, умножая u ( y ) на коэффициент охвата k , который выбирают на основе числа
степеней свободы для u ( y ) . Более подробно это описано в разделе 13.

В подходе GUM существует неявное предположение, что
входные данные измерены или назначены. Если возникают воздействия, которые
могут быть не определены через измеримые величины (например, воздействие
оператора), удобно сформировать суммарную стандартную неопределенность u ( x_i ) ,
которая учитывает такие воздействия, или ввести дополнительные переменные в f (х₁, х₂,…,
х _N ).

Из-за
ориентации на входные величины этот подход иногда называют восходящим походом
оценки неопределенности.

Физическая интерпретация u ( y ) не является однозначной, так
как она может включать члены, полученные на основе экспертной оценки, и таким
образом u ( y ) лучше всего рассматривать как
функцию, характеризующую степень доверия. Однако можно получить более прямую
физическую интерпретацию, определив разброс результатов вычисления u ( y ) , который был бы получен, если
бы все входные переменные изменялись случайным образом в соответствии с принятым
для них распределением.

А.2 Принцип совместных
исследований

А.2.1
Основная модель

Планирование
эксперимента при совместных исследованиях, их организация и статистическая
обработка подробно описаны в ИСО 5725-1 – ИСО 5725-6. Самая простая модель,
лежащая в основе статистической обработки данных совместных исследований,
задается уравнением:

,                                                                            (А.4)

где m -математическое ожидание у;

В –
лабораторная составляющая смещения в условиях повторяемости и предположения о
нормальном распределении со средним 0 и стандартным отклонением σ _L ;

е _r – случайная ошибка в условиях
повторяемости и предположения о нормальном распределении со средним 0 и
стандартным отклонением σ _w .

Кроме того, предполагается, что В
и е _r ,
некоррелированы.

Применение уравнения (А.1) к этой простой модели с учетом того, что σ _w определяется через стандартное
отклонение повторяемости s_r ,
полученное при межлабораторном исследовании, приводит к уравнению (А.5) для
единственного результата у и уравнению (А.6) для суммарной стандартной
неопределенности результата u ( y ) :

  и ,                                                               (А.5)

.                                              (А.6)

По сравнению с ИСО 5725-2
уравнение (А.6) представляет собой лишь оценку стандартного отклонения
воспроизводимости s_R .

Так как этот подход
ориентируется на полное выполнение метода, его называют иногда нисходящим
подходом.

Следует
учитывать, что каждая лаборатория вычисляет свою оценку по уравнению у =
f ( x ₁ , х₂,…),
предполагая ее наилучшей оценкой измеряемой величины у для лаборатории.
Тогда, если у = f ( x ₁ , х₂,…) – общая
модель, используемая для описания поведения измерительной системы, то,
следовательно, при вычислении m
предполагается, что дисперсии, характеризующиеся оценками s_L и s_r , являются результатом изменения
величин х₁,…, х_n. Если предполагается,
что условия воспроизводимости обеспечиваются для случайной величины при всех
существенных воздействиях и применяется физическая интерпретация u ( y ) , приведенная выше, то из этого
следует, что u ( y ) в уравнении (А.6) является
оценкой u ( y ) , описанной уравнениями (А.1) или (А.2).

Первый принцип, на котором
основаны настоящие рекомендации, состоит в том, что стандартное отклонение
воспроизводимости, полученное в совместном исследовании, является основой для
оценки неопределенности измерений.

А.2.2 Включение данных
правильности

Правильность в общем случае
измеряется смещением относительно принятого опорного значения. В некоторых
совместных исследованиях правильность метода в конкретной системе измерений
(обычно СИ) исследуют путем анализа образца сравнения ( CRM ) или эталона единицы физической
величины с сертифицированным значением , выраженным в единицах этой системы (ИСО 5725-4). Итоговая
статистическая модель определяется уравнением:

,                                                                       (А.7)

где μ – эталонное
значение;

δ –
смещение метода.

Совместное исследование может
дать смещение  со стандартным
отклонением , рассчитанным в соответствии с уравнением:

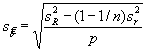,                                                              ( A.8)

где n – количество повторений в каждой
лаборатории;

р –
количество лабораторий.

Неопределенность , соответствующая этому смещению, задается уравнением:

,                                                                    (А.9)

где  – неопределенность,
соответствующая сертифицированному значению , используемому для оценки правильности при совместном
исследовании.

Если смещение, оцененное в процессе
испытаний, используют при вычислении результатов в лабораториях,
соответствующая ему неопределенность, если она не является незначительной,
должна включаться в бюджет неопределенности.

А.2.3 Другие
воздействия. Объединенная модель

На практике конечно s_R и  не обязательно
включают в себя все изменения, влияющие на результаты измерений. Отсутствие
некоторых важных факторов вызвано характером совместных исследований; некоторые
факторы могут отсутствовать или не оцениваться случайно или в соответствии с
планом эксперимента. Второй принцип, на котором основаны настоящие
рекомендации, состоит в том, что воздействия, не наблюдаемые в процессе
совместного исследования, или являются незначительными, или должны быть учтены.

Проще всего учесть эти
воздействия, рассматривая воздействие отклонений  от номинальных
значений х _i ,
необходимых для получения оценки у, и предполагая приближенную
линейность этих воздействий. Объединенная модель описывается уравнением:

.                                                           (А.10)

Суммирование ведется по всем
воздействиям, кроме представленных в B , δ, е.

Примеры включают в себя
воздействие отбора выборки, подготовки испытаний объекта и изменения состава
или типа отдельных объектов испытаний. В строгом смысле это линеаризованная
форма самой общей модели. При необходимости можно включать в нее члены более
высокого порядка или члены, учитывающие корреляцию, как описано в [1] .

Очевидно, что центрирование  не оказывает влияния
на u ( x_i ) , так
что , из чего следует, что для оценки неопределенности,
соответствующей у, можно использовать уравнение (А.10) и следующее
уравнение:

.                                       (А.11)

Суммирование ведется по воздействиям,
не учтенным в других членах уравнения.

Следует отметить, что при оценке
выполнения метода условия промежуточной прецизионности также могут быть описаны
уравнением (А.10), хотя число членов суммы соответственно будет больше,
поскольку по сравнению с условиями воспроизводимости в промежуточных условиях
меньшее количество переменных будет меняться случайным образом. В общем случае уравнение (А.10) можно применять к любым
условиям прецизионности, учитывая, что воздействия суммируются. В предельном
случае, когда s_r и s_L равны нулю, а неопределенность
общего смещения не определена, уравнение (А.11) становится идентичным уравнению (А.1).

Из этого следует два вывода:

– во-первых, необходимо
продемонстрировать, что количественные данные, доступные для совместного
исследования, согласуются с рассматриваемыми результатами испытаний;

– во-вторых, даже при
согласованности данных совместного исследования для определения реальной оценки
неопределенности с учетом дополнительных воздействий (х _i в уравнении (А.10)) могут быть необходимы дополнительные
исследования и предположения. При учете дополнительных воздействий
предполагается применение уравнения (А.1).

И, наконец, настоящие
рекомендации, утверждая, что надежную оценку неопределенности измерений можно
получать на основе анализа данных воспроизводимости и правильности, полученных
в соответствии с ИСО 5725-1 -ИСО 5725-6 ,
используют те же самые предположения, что и изложенные в перечисленных
стандартах:

а) если используются данные воспроизводимости,
предполагается, что все лаборатории подобны по выполнению работ. В частности,
их прецизионность повторяемости для данного объекта испытаний одинакова, а
лабораторная составляющая смещения В в уравнении
(А.10) соответствует тому же распределению, что и при совместных
исследованиях;

b )
испытываемые материалы, используемые в исследовании, являются гомогенными и
стабильными.

Следующие разделы включают
методологию проверки того, что дополнительные воздействия являются
незначительными, а если это не так, их неопределенности учтены в оценке
неопределенности результата.

А.3 Сопоставление подходов

Приведенные рассуждения
описывают два очевидно различных подхода к оценке неопределенности. Подход GUM [1] описывает неопределенность в виде дисперсии, полученной на
основе дисперсий соответствующих входных данных математической модели. Другой
подход использует факт, что если одни и те же воздействия заметно изменяются в
процессе исследования воспроизводимости, наблюдаемая дисперсия является оценкой
той же самой неопределенности. На практике значения неопределенности,
полученные на основе различных подходов, различны для разных целей, включая:

а) неполные математические
модели (то есть при наличии неизвестных воздействий);

b )
неполное или несущественное изменение всех воздействующих факторов в процессе
оценки воспроизводимости.

Сравнение двух различных оценок
безусловно полезно для оценки полноты модели измерений. Однако следует обратить
внимание, что наблюдаемую повторяемость или другую оценку прецизионности очень
часто рассматривают как отдельную составляющую неопределенности даже в подходе GUM [1] . Точно так же индивидуальные воздействия обычно проверяют
на их значимость или оценивают количественно до оценки воспроизводимости. На
практике для оценки неопределенности часто используют некоторые элементы обоих
подходов.

Когда оценка неопределенности
для интерпретации сопровождается результатами, важно, чтобы пробелы в каждом
подходе были заполнены. Возможности неполных моделей на практике обычно
дополняют консервативными оценками, позволяющими расширять ограничения для
неопределенности модели. В настоящих рекомендациях для устранения неадекватных
изменений входных воздействий рекомендуется определять оценки дополнительных
воздействий. Это является гибридным подходом, объединяя элементы и нисходящего,
и восходящего подходов.

Приложение В (справочное)
Экспериментальная
оценка неопределенности

B .1 Процедура оценки коэффициента
чувствительности

Если входные величины x_i могут
изменяться непрерывно по всему диапазону значений, рекомендуется исследовать
воздействие таких изменений. Простая процедура, предполагающая приблизительно
линейную зависимость результатов от x_i следующая:

а) выбирают подходящий диапазон
изменения переменной x_i ,
который должен быть ориентирован на лучшую оценку (или на значение, характерное
для указанного метода);

b )
выполняют всю процедуру измерений (или ту часть, которая касается x_i .) в каждом из пяти или более
уровней x_i
с
повторением при необходимости;

с) рассчитывают и изображают
линейную модель в соответствии с результатами, используя x_i в качестве абсциссы, а
результат измерений в качестве ординаты;

d )
коэффициентом чувствительности является наклон прямой, характеризуемый
коэффициентом c_i , в уравнениях (А.1) или (А.2).

Этот подход может дать различные
коэффициенты чувствительности для различных объектов испытаний. Это может быть
преимуществом во всесторонних исследованиях конкретного объекта или класса
объектов. Однако если коэффициент чувствительности должен быть применен к
большому диапазону различных ситуаций, важно проверять, чтобы различные объекты
вели себя аналогично.

B .2 Простая процедура оценки
неопределенности, вызванной случайным воздействием

Если входные величины x_j , являются дискретными и/или
неконтролируемыми, соответствующую неопределенность можно получать на основе
анализа экспериментов, в которых переменная изменяется случайным образом.
Например, тип почвы в экологических исследованиях может иметь непредсказуемое
воздействие на результаты анализа. Если случайные ошибки не зависят от уровня
исследуемой величины, можно исследовать дисперсию ошибки, являющейся
результатом таких изменений, используя серию объектов, для которых заданное
значение или доступно, или, если изменение известно, может быть выведено
теоретически.

Общая процедура включает в себя:

а) выполнение полного измерения
на представительном наборе объектов испытаний в условиях повторяемости,
используя равное количество повторений для каждого объекта;

b )
вычисление разности с заданным значением для каждого наблюдения;

с) проведение анализа
результатов (ранжированных по величине) в соответствие с ANOVA с использованием суммы квадратов для
формирования оценок внутригрупповой составляющей дисперсии  и межгрупповой
составляющей дисперсии . Стандартная неопределенность u_y ( x_i ) ,
являющаяся результатом изменения x_j ,
равна s_b .

Примечание
– Если различные объекты или классы объектов по-разному реагируют на
исследуемую величину (то есть существует взаимосвязь величины и класса
исследуемых объектов), взаимодействие увеличивает значение s_b. Детальное
исследование этой ситуации в настоящих рекомендациях не приводится.

Приложение С (справочное)
Примеры расчета неопределенности

С.1 Измерение содержания
монооксида углерода (СО) в отработавших газах автомобиля

С.1.1 Введение

До выпуска на рынок легковые автомобили должны проходить
испытания типа транспортного средства для проверки выполнения регулирующих
требований относительно количества монооксида углерода в отработавших газах.
Верхний предел составляет 2,2 г/км. Метод испытаний описан в Директиве ЕН
70/220 [4], где введены следующие требования:

– цикл двигателя задается как
функция скорости (км/ч), времени (с) и оборотов двигателя. Исследуемый автомобиль
помещают на специальные ролики для выполнения заданного количества циклов;

– измерительное оборудование –
газоанализатор на СО;

– контроль окружающей среды
проводят с использованием специальной камеры мониторинга загрязнений;

– персонал имеет специальную
подготовку.

Такие испытания на соответствие
можно выполнять в испытательной лаборатории предприятия по производству
автомобилей или в независимой испытательной лаборатории.

С.1.2 Данные совместных исследований

Перед принятием и использованием
такого метода испытаний необходимо оценивать факторы или источники, влияющие на
результаты метода испытаний (и, следовательно, на неопределенность результатов
испытаний). Такая оценка выполнялась по данным экспериментов, проводимых в
различных лабораториях. Для контроля метода испытаний межлабораторный
эксперимент проводился в соответствии с ИСО 5725-2. Цель межлабораторного
эксперимента состоит в том, чтобы оценить прецизионность метода испытаний при
применении его в данном наборе испытательных лабораторий. Оценка прецизионности
получена на основе данных, собранных в межлабораторном эксперименте со
статистическим анализом в соответствии с ИСО 5725-2. Исследование проводят так,
чтобы каждый участник выполнял все необходимые процессы измерений и учитывая
воздействующие факторы.

Было установлено, что
повторяемость лабораторий значимо не различается, а оценка стандартного
отклонения повторяемости метода испытаний равна 0,22 г/км. Оценка стандартного
отклонения воспроизводимости метода испытаний равна 0,28 г/км.

С.1.3 Контроль смещения

Оценка правильности (контроль
смещения по отношению к эталону) включает в себя методологические и технические
вопросы. Не существует «эталонного автомобиля» как образца сравнения.
Правильность следует контролировать при калибровке системы испытаний. Например,
калибровку анализатора СО можно выполнять с помощью эталонного газа, а
калибровку испытательного стенда можно выполнять для величин, таких как время,
длина, скорость и ускорение. Знание норм выбросов для различных скоростей и
наличие другой аналогичной информации подтверждают, что неопределенность,
связанная с этими калибровками, не дает существенных вкладов в
неопределенность, связанную с результатами измерений (то есть вся расчетная
неопределенность много меньше, чем стандартное отклонение воспроизводимости).
Смещение находится под контролем.

С.1.4 Прецизионность

Типовые дублированные
испытательные пробеги в лаборатории показали, что повторяемость приблизительно
составляет 0,20 г/км и находится в пределах диапазона повторяемости, найденного
при межлабораторном исследовании. Таким образом, прецизионность находится под
хорошим контролем.

С.1.5 Соответствие объектов
испытаний

Метод признают подходящим для
всех транспортных средств, относящихся к легковым автомобилям. Хотя большинство
транспортных средств признают соответствующими относительно легко и
неопределенность имеет тенденцию уменьшаться для более низких уровней выхлопов,
неопределенность важна на уровнях, близких к регулирующей границе. Поэтому было
решено использовать оценку неопределенности, близкую к регулирующей границе,
как корректную и несколько консервативную оценку неопределенности для более
низких уровней выделения СО. Необходимо заметить, если испытания транспортного
средства показывают выхлоп существенно больше установленной границы, может
оказаться необходимым проведение дополнительных исследований неопределенности,
если сравнения являются критичными. На практике, однако, такое транспортное
средство в любом случае нельзя предлагать для продажи без его модернизации.

С.1.6 Оценка неопределенности

Поскольку предшествующие исследования
установили должный контроль смещения и прецизионности в пределах испытательной
лаборатории, а также отсутствие воздействующих факторов, не учтенных при
совместных исследованиях, стандартное отклонение воспроизводимости,
используемое для оценки стандартного отклонения неопределенности, дает
расширенную неопределенность U
=
0,56 г/км ( k = 2).

Примечание
– Интерпретация неопределенности результатов в области проверки соответствия
рассмотрена в ИСО 10576-1.

С.2 Определение состава мяса

С.2.1 Введение

Для продукции из мяса необходимо
гарантировать, что состав мяса точно заявлен. Состав мяса определяют как
комбинацию содержания азота (преобразованного к общему белку) и жира.
Представленный пример показывает принцип объединения различных составляющих
неопределенности, каждая из которых непосредственно следует в основном из
оценок воспроизводимости, как описано в разделе 12.

С.2.2 Основные уравнения

Полный состав мяса W_meat определяют в соответствии с
уравнением:

,                                                                     (С.1)

где W_pro – общий
белок в мясе, выраженный в виде процента массы;

W_fat – общее содержание жира,
выраженное в виде процента массы.

Белок в мясе W_pro вычисляют
по формуле:

,                                                                     (С.2)

где f_N является фактором азота,
соответствующим материалу;

W _vN – полное
содержание азота в мясе.

В этом случае W _mN идентично общему содержанию
азота W_tN ,
определяемому в соответствии с анализом Кьельдаля.

С.2.3 Экспериментальные шаги при определении состава мяса

При определении состава мяса
применяют следующие экспериментальные шаги:

a )
определяют содержание жира W_fat ;

b )
определяют содержание азота W _mN по
Кьельдалю (среднее дублированных измерений);

с) вычисляют содержание
обезжиренного мяса W_pro и f_N (см.
уравнение (С.2));

d )
вычисляют общий состав мяса W_meat
(см.
уравнение (С.1)).

С.2.4 Составляющие неопределенности

Составляющие неопределенности
связаны с каждой из величин, перечисленных в С.2.3. Наиболее существенным
является W_pro
составляющий приближенно 90 % массы W_meat . Наибольшая неопределенность,
связанная с W_pro ,
является результатом:

а) неопределенности фактора f_N вследствие неполного знания
материала;

b )
отклонений метода в условиях воспроизводимости при повторении метода и при
точном выполнении метода в течение длительного времени;

с) неопределенности, связанной
со смещением метода;

d )
неопределенности содержания жира W_fat .

Примечание
– Неопределенности а), b)
и с) связаны с образцом, лабораторией и методом соответственно. Часто бывает
полезно грубо рассмотреть каждый из этих трех факторов при идентификации
неопределенности, а также неопределенность отдельных шагов в процедуре.

С.2.5 Оценка составляющих неопределенности

С.2.5.1 Неопределенность, соответствующая f_N

Неопределенность,
соответствующая f_N ,
может быть оценена по приведенному в публикациях диапазону значений. В [5] приведены результаты исследований содержания
азота в говядине, которые показывают четкое отличие между различными
источниками и кусками мяса. В [5] также даны
рекомендации по вычислению наблюдаемого стандартного отклонения для f_N =
0,052 и относительного стандартного отклонения 0,014 для большого диапазона
типов выборок.

Примечание
– Непосредственно применены данные содержания азота, определенные в [5], полученные с использованием метода Кьельдаля.

С.2.5.2 Неопределенность, соответствующая W_tN

Информация о двух совместных испытаниях [6], [7] позволяет получать оценку
неопределенности, вызванной плохой воспроизводимостью или ошибками выполнения
метода. Тщательное расследование условий испытаний показывает, во-первых, что
каждое исследование проводят по широкому диапазону типов выборки и с хорошим
репрезентативным набором компетентных лабораторий, а во-вторых, что стандартное
отклонение воспроизводимости s_R
хорошо коррелирует с уровнем азота. Для обоих испытаний наиболее подходящая
линейная функция задается уравнением s_R = 0,021 W_tN. То же самое исследование показывает, что
стандартное отклонение повторяемости пропорционально W_tN = 0,018 W_tN и межлабораторному члену s_L = 0,011 W_tN.

Метод таков, что каждое
измерение дублируют и определяют выборочное среднее. Член, соответствующий
повторяемости, который представляет собой оценку повторяемости единственного
результата, должен быть соответствующим образом приспособлен для учета
воздействия среднего двух результатов в лаборатории (см. комментарий,
относящийся к s_r в таблице
1). Неопределенность u ( W_tN ) ,
соответствующая содержанию азота, имеет вид:

.       (С.3)

Уравнение (С.3) дает лучшую
оценку неопределенности с W_tN , соответствующей
разумным изменениям при выполнении метода.

Воспроизводимость также
используют в качестве критерия оценки прецизионности отдельной лаборатории.
Метод устанавливает, что результаты должны быть отброшены, если данные попадают
вне 95 %-ного доверительного интервала (приблизительно равного ). Эта проверка гарантирует, что внутрилабораторная
прецизионность соответствует прецизионности совместного исследования.

Примечание
– Если эта проверка терпит неудачу чаще, чем в 5 % случаев, вероятно, что
прецизионность не находится под достаточным контролем и необходимы действия по
исправлению процедуры.

Необходимо также рассматривать
неопределенность, соответствующую W_tN и
являющуюся результатом воздействия неизвестного смещения метода. В отсутствии
надежных образцов сравнения сравнение с альтернативными методами, использующими
другие принципы, является установленным средством оценки смещения. Сравнение
метода Кьельдаля с методом анализа сжиганием для определения полного азота и
различных типов выборки установило различие 0,01 W_tN . Это удовлетворяет критерию 2 σ_D (см. ИСО Руководство 33, уравнение (4)), подтверждающему, что
неопределенность, связанная со смещением, адекватна значениям
воспроизводимости.

С.2.5.3 Неопределенность, соответствующая W_fat

Дополнительные данные совместных
испытаний для анализа жира [8] дают оценку
стандартного отклонения воспроизводимости 0,02 W_fat .
Анализ снова выполняют дважды, а результаты принимают только в случае, если
разность находится в соответствующих пределах повторяемости, гарантируя, что
лабораторная прецизионность находится под контролем. Предшествующая верификация
работы на подходящем образце сравнения для определения жира устанавливает, что
неопределенность, связанная со смещением, адекватна значениям
воспроизводимости.

С.2.6 Суммарная неопределенность

В таблице С.1 показаны
индивидуальные значения и неопределенность, подсчитанная с использованием этих
значений.

Таблица С.1 – Бюджет неопределенности для состава мяса

Количественный показатель	Значение xi
%	u(xi)	u(xi)/xi
Содержание жира Wfat	5,50	0,110	0,020
Содержание азота WmN	3,29	0,056	0,017
Фактор азота fN	3,65	0,052	0,014
Белок Wpro	90,1	90,1 × 0 ,022 = 1,98
Общий состав мяса Wmeat	95,6		0,021

Уровень
доверия в 95 % достигается умножением суммарной стандартной неопределенности на
коэффициент охвата k ,
равный 2, давая (при округлении до двух знаков после запятой) расширенную
неопределенность на состав мяса U = 4,0
%; то есть W_meat =
(95,6 ± 4,0) %.

Примечание
– Состав мяса может законно превышать 100 %-ный предел в некоторых видах
продукции.

Приложение D (справочное)
Сведения о соответствии ссылочных международных стандартов национальным
стандартам Российской Федерации

Таблица D.1

Обозначение ссылочного международного стандарта	Обозначение и наименование соответствующего национального стандарта
ИСО Руководство 33:2000	*
ИСО/МЭК Руководство 43-1:1997	*
ИСО 3534-1:1993	ГОСТ Р 50779.10-2000 (ИСО 3534-1:1993) Статистические методы. Вероятность и основы статистики. Термины и определения
ИСО 5725-1:1994	ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения
ИСО 5725-2:1994	ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
ИСО 5725-3:1994	ГОСТ Р ИСО 5725-3-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
ИСО 5725-4:1994	ГОСТ Р ИСО 5725-4-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений
ИСО 5725-5:1998	ГОСТ Р ИСО 5725-5-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
ИСО 5725-6:1994	ГОСТ Р ИСО 5725-6-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 6. Использование значений точности на практике
ИСО/ТО 7871:1997	ГОСТ Р 50779.45-2002 Статистические методы. Контрольные карты кумулятивных сумм. Основные положения
ИСО 8258:1991	ГОСТ Р 50779.42-1999 Статистические методы. Контрольные карты Шухарта
ИСО 10576-1:2003	ГОСТ Р ИСО 10576-1-2006 Статистические методы. Руководство по оценке соответствия установленным требованиям. Часть 1. Общие принципы
ИСО 11648-1	*
* Соответствующий национальный стандарт отсутствует. До его утверждения рекомендуется использовать перевод на русский язык данного международного стандарта. Перевод данного международного стандарта находится в Федеральном информационном фонде технических регламентов и стандартов.

Библиография

[1] Guide
to the expression of uncertainty in measurement (GUM) 1995

[2] ISO/IEC
VIM:1993 (International vocabulary of basic and general terms in metrology
(VIM))

[3]
Recommendation INC-1 (1998), BIPM

[4]
European Directive 70/220/EEC:1970 Measures to be taken against air pollution
by emissions from motor vehicles

[5]
Analytical Methods Committee. Analyst, 118 (1993), p. 1217

[6] Shure
B., Corrao P.A., Glover A., Malinowski A.J.J.AOAC Int., 65 (1982), p. 1339

[7]
King-Bring M., Sebranek J.G.J. Int., 76 (1993), p. 787

[8] Breese Jones D . Американский Проспект Министерства земледелия
№ 183 (август 1931)

Ключевые
слова : повторяемость, воспроизводимость, правильность,
прецизионность, смещение, дисперсия, суммарная неопределенность, бюджет
неопределенности

Смелость не всегда кричит. Иногда это тихий голос, который говорит в конце дня “Я попробую еще раз завтра”.

Индексы воспроизводимости процессов

Виктор Э. Кейн

(Компания Форд Мотор, отдел
трансмиссии и шасси, П. О. бокс 2097(7) Ливония, М1 48150)

Индексы воспроизводимости C_p, CPU, CPL, k и C_pk представляют параметры
процесса и тесно связаны с ними. Известно, что эти индексы образуют полную
систему показателей работы процесса и могут использоваться и с
двусторонними, и с односторонними допусками, и
с заданными номиналами, и без них. Многие японские предприятия в разных
отраслях промышленности постоянно применяют эти 5 индексов, и
автомобильная промышленность США тоже начала их применение во многих
областях. В статье рассматриваются различные применения этих индексов, а
также их связь со статистическими свойствами
выборок.

ВВЕДЕНИЕ

Количественное представление (квантификация) настройки процесса и его вариации
– основа для понимания качества изделий в любом производстве. Представим
себе ситуацию, когда среднее арифметическое процесса m и стандартное
отклонение s , неизвестны и оцениваются через `
х и s, соответственно. С
практической точки зрения ` х и s не безразмерные, а иногда
и неудобные статистические свертки, если учесть
сотни показателей на предприятии или у поставщиков. Во многих
ситуациях индексы воспроизводимости можно использовать для выяснения
соотношений между параметрами процесса m и s и инженерными требованиями,
которые могут включать в себя односторонние и двусторонние допуски с
заданными значениями (номиналами) или без них. Полученные в результате
индексы безразмерны и создают общий легко понятный язык для количественной
характеристики процесса.

Автомобильная промышленность в
настоящее время прилагает много усилий для
внедрения статистического управления процессами (СУП) на своих предприятиях и у поставщиков. Индексы воспроизводимости,
получаемые из СУП, нашли широкое применение не
только для оценки процесса, но и для принятия решений о закупках. В частности представляют
интерес индексы C_p и
C_pk, применяемые в Японии (Сулливан (1984, 1985 ), а с недавнего
времени в автомобильной промышленности США
(например, компанией Форд Мотор (1984). Эти индексы показывают соотношение между естественным допуском
(6s ), который принят в американской
литературе по контролю качества (см., Джуран и Грыня (1980,
р. 299) и инженерными допусками. Цель данной статьи – исследовать
возможные применены индексов воспроизводимости
в связи с их выборочными свойствами и методами оценивания. При обсуждении
постулируется, что выход процесса распределен приближенно нормально, а сам
процесс находится в статистически управляемом состоянии, Далее “крышечка”
^ будет обозначать оцениваемую величину.

ПОТЕНЦИАЛ
ПРОЦЕССА

Индекс
C_p.

Производственные процессы
проходят определенные этапы разработки прежде, чем начнется само
производство. Эти этапы “подтверждают” проверки на станках поставщика, пусконаладочные испытания станков и производственного оборудования и
предпусковые испытания всех режимов для выяснения того, способно ли
оборудование производить в ходе производства изделия, удовлетворяющие
требованиям . технических условий. Типичный
подход – выяснение того, попадает ли естественный допуск процесса (6s )
внутрь границ допуска. Альтернативная формулировка, применяемая в Японии
(Сулливан, 1984) – оценить индекс воспроизводимости C_p
Эти величины – просто разные способы соотношения допустимого разброса
процесса (допуск на изделие) и фактического разброса процесса
(естественный допуск), как показано на рис. 1, где ВГД- верхняя граница допуска, НГД -нижняя граница допуска, a NT –
естественный допуск. Показатель потенциала процесса
равен:

(1)

Рисунок 1. Соотношение параметров
С_р.

Величина C_p=1,0 указывает, что процесс
признается “воспроизводимым”, как показано на рис. 2. Вообще надо
оценивать стандартное отклонение процесса в формуле (1) для получения оценки воспроизводимости процесса
C_p^. Из-за выборочной вариации и ограничений
измерительного оборудования, обсуждаемых ниже, C_p^=1,0
обычно не используется как минимальное приемлемое значение.

Рисунок 2.   Распределение
отдельных деталей для воспроизводимого процесса
(Ср=1).

Рисунок 3.  Индексы Ср для
различных диапазонов распределения процесса

Процент допуска	100	75	50
Брак	0.27%	84 части на миллион	>0.1 части на миллион

Воспроизводимый процесс, в основе
которого лежит стабильное нормальное распределение, теоретически дает в
результате 0,27% изделий с параметрами,
выходящими за пределы допусков. Значение 1,0 было выбрано для демонстрации
связи C_p со стандартным шестисигмовым отклонением, используемым в
контрольных картах. Если процесс точно
воспроизводим, то:

(2)

где ВГУ – верхняя
граница управления;

НГУ-нижняя граница
управления;

n – объем выборки для подгруппы на
контрольной карте.

Соотношение в формуле (2)
указывает, что границы допуска, скорректированные на объем выборки, равны
контрольным границам для процесса с
C_p=1,0.

Первоначально
C_p использовалось для проведения сравнений
разного рода. На рис. 3 показано, как различные значения
C_p относятся к разбросу процесса с учетом ширины
допуска. Минимальное значение C_p=1,33 обычно применяется к
текущему процессу (см. Джуран, Грыня и Бингхем (1979
р. 9-22 ). Оно отражает очень низкую долю
брака (0,007%) и таким образом служит
ориентиром для эффективной стратегии предотвращения, производства бракованных изделий. Значение
C_p=1,33 часто используется для оценки качества
оборудования, так как долговременный статистический контроль обычно нельзя
организовать во время сертификационных
испытаний. Применение показателя 1,33 дает
некоторую гарантию, что по крайней мере сохранится C_p=1,0, если в процессе
производства возникнут, как подсказывает опыт, дополнительные источники
вариации. Следует заметить, что по-видимому
более естественно применять традиционный показатель:

Мотивация к применению
C_p вместо % от допуска (или “отношение
воспроизводимости” из работы Шарбонно и Вебстера,
1978) связана с естественным соотношением между потенциалом процесса,
количественно выраженным C_p, и работоспособностью
процесса, количественно выраженной показателем C_pk,
который описывается в следующих разделах. Существуют еще естественные обобщения показателя
C_p на односторонние допуски и многомерные
номиналы.

При изучении потенциала станка
часто не учитывается, управляем ли станок в статистическом смысле. Это явно
нецелесообразно, так как многие простые проблемы нельзя обнаружить, если не применяются стандартные контрольные карты,
даже при производстве мелких партий деталей (то есть при
N между 30 и 100). Слежение за ходом производства по контрольным картам – естественное средство выяснения проблем.
Однако невозможно определить, управляем ли станок статистически в течение длительного промежутка времени, если
работать с краткосрочным планом выборки.
Возникает вопрос: имеет ли исследование
краткосрочной воспроизводимости какое-либо значение для предсказания
долговременной работоспособности производства?
Если предположить, что нестабильный процесс будет иметь большее стандартное отклонение, чем такой же
стабильный, тог исследование потенциала краткосрочного процесса даст возможность
определить круг проблем. Как правило, о процессе судят по оцененной
воспроизводимости:

(3)

где
s – стандартное отклонение выборки,
вычисленное для объема N.

К сожалению, кратковременному
исследованию свойственны другие проблемы,
такие, как тщательно подготовленные заготовки,
новые инструменты, высококвалифицированные операторы и тому подобное, что
может сделать сертификационный процесс
отличным от типичных производственных операций. В общем, особые условия
краткосрочного сертификационного исследования сокращают изменчивость
относительно обычного производственного
процесса. Таким образом, эти исследования в основном служат для выполнения
более широкого круга проблем. Показатель C_p,
рассчитанный на основе краткосрочного исследования, главным образом
выявляет нижнюю границу изменчивости
(потенциал процесса), которую можно ожидать на начальной стадии
производства. Однако нет ничего невозможного в том, чтобы улучшить
начальный C_p в результате дальнейшего совершенствования
производства.

Обсуждение выборочных
ситуаций

Выборочную вариацию
C_p^ в (3) можно легко изучить, поскольку известно, как
применить хи-квадрат распределение выборочной
дисперсии (s²). Бурр (1976,
pp. 336-341) выводит кривую оперативной характеристики (ОХ) для проверки стандартного отклонения,
используя тот факт, что (N-l)s²/s
² имеет хи-квадрат распределение с (N-1) степенями
свободы. По аналогии можно рассчитать кривую ОХ для проверки
воспроизводимости процесса. Прежде всего следует отметить, что проверка
гипотезы (s ₀>0)

эквивалентна проверке
воспроизводимости процесса (c₀>0)

(4)

При использовании критической
области C_p^>с
функция мощности критерия (4) получается непосредственно из хи-квадрат
распределения выборочной дисперсии как:

(5)

где
– случайная величина с распределением хи-квадрат и с (N- 1)
степенями свободы. Удобно брать функцию мощности для C_p,
а не соответствующую функцию мощности для s ,
так как тогда не надо вводить поправку на различия в допусках процесса и
“нормализованную” воспроизводимость процесса можно изучать
непосредственно.

Пользуясь формулой (5), можно
вычислить кривую ОХ (C_p)=1-p
(C_p) и использовать ее для сравнения вариантов проверки.
Кривая ОХ позволяет понять порочность практики, когда пренебрегают
оценкой вариации выборки s ^ при оценивании воспроизводимости процесса.
Пусть мы хотим выяснить, воспроизводим ли процесс на уровне с₀=1,33 (то есть H₀: C_p?
1,33) при N=30 изделиям, а предел браковки (критическое значение) c=1,33.
Кривая ОХ (а) на рис. 4 показывает, что ОХ
(1,33)=0,40, а это значит, что вероятность ложного суждения о процессе как
о невоспроизводимом (принятие гипотезы H₀) равна 40%. Истинная воспроизводимость процесса должна
быть C_p=1,6 чтобы оставалось
всего 5% шансов для причисления процесса к невоспроизводимым при
критическом значении С=1,33.

Рисунок 4.  Кривая
оперативной характеристики для плана выборки, который отбрасывает гипотезу
о воспроизводимости процесса, если Ср<c, где а) N=30, c=1.33 и б) N=70,
c=1.46.

Отбор разумного критического
значения при проверке воспроизводимости требует назначения для значений
С_p приемлемого уровня качества (AQL, ПУК) и
неприемлемого уровня качества (RQL, НУК) (см. Бурр [1976, pp. 336-341]). Приемлемый уровень качества – это достаточно
высокая воспроизводимость процесса, так что мы будем принимать процесс с
воспроизводимостью выше, чем ПУК. НУК – это достаточно низкая
воспроизводимость, так что мы отбросим процессы с воспроизводимостью ниже,
чем НУК. Итак,

ПУК=C_p(высокая)>C_p(низкая)=НУК.

Исходя из формулы (5) a и b риски
будут:

Решая относительно
C_p(высокая)/C_p(низкая) и с получим:

где – Хи (100-ый процентиль хи-квадрат распределения с (N-1)
степенями свободы. В табл. 1 сведены значения для
C_p(высокая)/C_p(низкая) и
c/C_p(низкая) при разных объемах выборки и a =b равных
0,10 и 0,05. Критическое значение c и объем выборки N можно определить для любых
конкретных значений C_p(высокой) и
C_p(низкой). Например, если a =b =0,05,
C_p(высокая)=1,6 и C_p(низкая)=1,2, то
C_p(высокая)/C_p(низкая)=1,33, и из табл. 1: N=70 и c=(1,14)C_p(низкая)=1,37. Таким образом,
беря критическое значение 1,37 и объем выборки 70, получаем вероятность 5%
того, что процесс с C_p выше 1,6 будет признан
невоспроизводимым (принята H₀), и что процесс с
C_p ниже 1,2 будет признан воспроизводимым (отброшена
H₀).

Чтобы гарантировать, что любой
процесс с C_p ниже 1,33 (где ВГД-НГД=8s ) имеет
высокую вероятность быть признанным невоспроизводимым (а = 0,1), а процесс с Ср выше 1,66 (где ВГД-НГД=10s ) имеет высокую вероятность быть признанным
воспроизводимым (?=0,1), надо иметь C_p(высокая)/C_p(низкая)=1,25,
и из табл. 1: N=70 и c/C_p(низкая)=1,10, что
дает c=1,46. Кривая ОХ для
такого рода плана выборки – кривая (б) на рис.
4.

Этот пример показывает, что
практика использования N=30, имевшая место в прошлом в
автомобильной промышленности для сертификации станков, в целом
неадекватна. А практика использования минимального значения c=1,33,
принятая в настоящее время, может характеризовать невыборочные проблемы,
которые делают сертификационные испытания отличными от производства, но
минимальное значение 1,33 не может адекватно учесть выборочную
изменчивость. Возможно потребуются большее N и большее минимальное
значение C_p. Шарбонно и Бебстер (1978, р. 112) предлагают для нового
оборудования показатель воспроизводимости 1,5, не устанавливая, однако,
объема выборки.

Подход с использованием интервала
допуска

Альтернативный подход к
определению работоспособности процесса – построение интервала длиной
2Ks такого, что 100p процентов результатов процесса
покрывается данным интервалом с вероятностью g .
Это стандартный подход к воспроизводимости процесса – метод интервала
допуска. Интервалы допусков наряду с другими статистическими интервалами
обсуждаются Ханом (1970). Можно доказать, что индекс C_p
в формуле (4) допускает обобщение до:

(6)

где C_t^=C_p^, если
К=3. Если мы выберем N=70,
p=0,99, а g =0,95, то из
табл. 2 интервал допуска имеет длину 6,042s, то есть в сущности тот же самый, что и при
стандартном подходе. Однако для разных значений N, p и g будут разные
интервалы. Например, при N=30 и тех же
самых значениях p и g , как и раньше, К=3,35, так что
знаменатель в формуле (6) станет 6,7s. Таким образом, возрастающая
неопределенность для N=30 отражается в росте сомножителя при s в знаменателе формулы
(6).

РАБОТОСПОСОБНОСТЬ
ПРОЦЕССА

Очевидно, что индекс
C_p измеряет потенциал работоспособности процесса, так
как только разброс процесса соотносится с границами допуска; положение
среднего не учитывается. Можно получить любой процент бракованных деталей
при высоком C_p просто при расположении среднего значения
процесса достаточно близко к границе допуска. Таким образом, только
потенциал работоспособности процесса количественно оценивается с помощью
C_p, причем он достижим только для процессов, среднее
которых совпадает с серединой между пределами допусков.

Показатель C_pk
близок к индексу C_p, но использует среднее процесса и
может рассматриваться как показатель его работоспособности. Есть две
эквивалентные формы индекса C_pk. Первая формулировка
получается при рассмотрении верхней и нижней границ допуска в отдельности.
Вторая – использует отклонение среднего значения процесса от середины
между пределами допусков. Приведем оба вывода, так как каждый из них
по-разному освещает ситуацию.

Верхний и нижний показатели
воспроизводимости

Рассмотрим ситуацию с односторонним допуском, когда задан только один
предел. На рис. 5 показано распределение процесса относительно верхней границы
допуска. Соотношение фактического и допустимого размаха точно так же, как
и в (1), дает новый показатель CPU:

(7)

Индекс CPU был разработан
в Японии и применяется во многих японских компаниях. Для нижней границы
допуска совершенно аналогично формуле (7) имеем:

Рисунок 5. Соотношение параметров
CPU.

Оценки CPU и CPL обозначаются CPU и CPL и получаются при замене m и ? на
` х и s соответственно. Индексы
CPU (верхний C_p) и CPL (нижний
C_p) связаны с C_p
через:

и применяются для измерения
воспроизводимости процесса при наличии только одной границы допуска. Само
собой разумеется, что в случае с одной границей допуска CPU=1,0
означает половину бракованных деталей (0,136%) по сравнению с тем, что
дает C_p=1,0 в случае с
двусторонним допуском.

Индекс
C_pk

Так как CPU и CPL
используют настройку процесса, естественный показатель для двусторонних
допусков – это C_pk,
где:

Cpk = Min {CPU, CPL}
(8)

Рисунок 6. Соотношение параметров
Срк.

Таким образом, индекс C_pk использует нормированное
расстояние между средним процесса и ближайшей границей допуска. Несколько
другой подход – снижение величины C_p для процесса с
помощью коэффициента (1-k),
нормированного расстояния, на которое процесс удален от центра. Среднюю
точку диапазона допуска находим по формуле:

m = (BГД + НГД) /
2.

Расстояние между средним
значением процесса m , и оптимумом, средней
точкой т, равно m –m, когда мы предполагаем, что т? m ?
ВГД как показано на рис. 6.
Нормированное расстояние равно:

(9)

Знак к абсолютному значению
добавляется в том случае, когда НГД? m ? т. Оценка k
обозначается через k^ и получается при замене m на ` x в формуле (9).
Коэффициент k применяется в Японии как показатель, описывающий
величину, на которую процесс смещен от центра.
Индекс C_p, скорректированный на k в формуле (9)
равен:

Cpk = Cp (1-k) 
(10)

что алгебраически эквивалентно
(8). Так как 0? k? 1, то C_pk? C_p, в
предположении, что НГД? m ?
ВГД.

Рассмотрим искусственный пример,
пусть ВГД=20, НГД=8, s=2, `
х=16. Сначала заметим, что C_p=1,0,
так что процесс потенциально воспроизводим, если настроен на среднюю точку m=14. Однако, CPL=1,33, CPU=0,67, k=0,33, что дает в результате
C_pk=0,67. Приемлемый процесс потребует уменьшения s
и/или центрирования m .

НОМИНАЛЫ (ЦЕЛЕВЫЕ
ЗНАЧЕНИЯ)

Усилия по обеспечению качества
изделий проходят четыре фазы. На первой фазе надо просто “делать деталь,
как предписано”, причем проверка обычно используется для отбраковки по
принципу “годно – не годно”, чтобы
удостовериться, что все детали попали внутрь заданных на чертеже границ
допуска. Вторая фаза – применение контрольных карт для установления
стабильности процессов. Третья фаза –
минимизация изменчивости для достижения
однородности изделий. Идеи предупреждения
дефектов (то есть предотвращение брака в процессе изготовления) и
постоянное усовершенствование – часть этой фазы. Четвертая фаза –
реализация улучшенной воспроизводимости
процесса в более точной настройке средних на оптимальное значение
показателя качества изделия или более традиционно – в минимизации
затрат (то есть времени сборки). Последняя фаза не менее важна, чем
предшествующие. Инженеры-разработчики
концентрируются на вопросе “сколь многофункциональное изделие было бы лучше всего”
вместо того, чтобы выяснить, сколько характеристик надо учитывать, чтобы
изделие могло функционировать. Таким образом,
инженеры-производственники должны теперь добиваться требуемого
среднего (то есть целевого) значения, а также сохранять низкую
изменчивость, чтобы процесс оставался между
границами допуска.

Наиболее распространенное целевое
значение, которое применяется на сегодняшний
день, – середина между пределами допуска. Это значение часто выбирается
как целевое (номинал) для снижения затрат, так
как при этом минимизируется вероятность
производства бракованного изделия. Сегодня эксцентричные номиналы чаще всего применяются для
целенаправленного подбора размеров пар
деталей, чтобы облегчить сборку, или для целевого подбора таких размерных цепей на
операциях сборки, которые минимизировали бы трудности при проведении разборки. Джессуп
(1983) рассматривает применение функции потерь
Тагучи, которая ставит в соответствие
отклонение от выбранного целевого значения и
потери в деньгах. На рис. 7 показано
соотношение целевого значения (Т),
воспроизводимости процесса и затрат.

Рисунок 7. Воспроизводимость
процесса в случае использования целевых значений
(номиналов).

Есть множество способов распространения введенных
показателей воспроизводимости на случай
целевого значения (номинала). Следующее расширение использует аналогию
между фактическим и допустимым разбросами процесса, которая показана на
рис. 1. Показатель потенциала процесса связывает фактический
разброс процесса с допустимым. Из рис. 8 для ближайшего к ВГД значения Т
имеем:

В общем:

(11)

Показатель C_p в
формуле (11) – обобщение C_p из формулы (1), полученной
из отношения допустимого разброса процесса к фактическому. При T=m показатели
совпадают.

Рисунок 8. Соотношение параметров
Ср при использовании целевых значений.

Такую же аналогию можно применить
и к показателю k. Из рис. 9 для
ближайшего к ВГД значения T, имеем:

В общем:

(12)

где мы предполагаем, что m лежит
внутри границ допуска и 0? k? 1. Показатель k в формуле (12) – обобщение показателя k из формулы (9), они эквивалентны при
условии T=m . Таким образом индекс
C_pk в формуле (10) может применяться при замене
C_p и k соответственно на (11) и
(12):

Cpk =Min {CPU, CPL}.

где

Рисунок 9. Соотношение параметров
К при использовании целевых значений.

Обратите внимание, что
СPL=0, если |Т-m
|>T-НГД, и CPU=0, если |Т-m
|>ВГД-T. Эти показатели можно использовать при
односторонней границе допуска с целевым значением. Вышеприведенные
уравнения аналогичны (8) для C_pk и соответственно
CPL и CPU, при условии, что Т=m .

Простой пример иллюстрирует
применение этих индексов. Предположим, что ВГД=18, НГД=10, T=16, s
=0,67. Обратите внимание, что из формулы (11)
C_p=1,0. На рис. 10 представлены индексы
воспроизводимости для выбранных значений среднего.

Распределение	m	CPL	CPU	k	Cpk
	13	15	00	10	00
	14	20	00	10	00
	15	25	05	05	05
	16	30	10	00	10
	17	25	05	05	05

Рисунок 10.  Индексы
воспроизводимости процесса при целевом значении
T=16.

Заметьте, что из-за того, что
C_pk скорректировано на отклонении от Т, может быть воспроизводимость 0 и
не быть ни одной детали за пределами допуска.
Таким образом, отклонения в “длинную сторону” (то есть, туда,
где расстояние между Т и границей допуска максимально) от целевого значения Т влечет за собой
такое же уменьшение C_pk, что и отклонение в “короткую
сторону” (то есть туда, где расстояние между Т и границей допуска
минимально).

НЕДОСТАТКИ

Опыт показал, что в использовании
C_p и C_pk на традиционной основе
заложены потенциальные трудности. Эти недостатки в общем возникают из-за
пользователей, которые не имеют полного представления о статистических
принципах, а не из-за проблем, присущих самим индексам. Некоторые из этих
недостатков описываются ниже.

(1) Статистическая
управляемость – Существует тенденция к определению воспроизводимости
процесса до того, как сам процесс войдет в состояние статистической
управляемости. Воспроизводимость количественно характеризует обычную
вариацию и показывает, что можно ожидать от процесса в будущем. Наличие
конкретных причин вариации делает предсказания невозможными, а смысл
воспроизводимости неясным.

(2)
План выборки – Очевидно, что значения среднего размаха ` R,
часто используемого для оценки s , зависит от плана выборки. Таким
образом, можно доказать, что значение показателя воспроизводимости можно
легко менять простым изменением плана выборки. Ситуация покажется еще
более сложной, если учесть замечание, которое сделал У. Эдвардс Деминг инженеру, говорившему о своих достижениях
при введении процесса в состояние статистической управляемости. Деминг
заявил, что он мог бы любой процесс ввести в это состояние, причем просто
для выборки внутри подгрупп во времени. Это утверждение следует из
признания того факта, что число источников вариации растет с увеличением
интервала времени между выборками внутри подгруппы. Рассеивание выборок внутри подгрупп во времени будет
увеличивать ` R, расширяя контрольные пределы и, следовательно,
делая достижение статистически управляемого
состояния более вероятным. Однако увеличение ` R будет увеличивать
и оценку s , а значит уменьшать воспроизводимость процесса. И наоборот:
можно увеличить воспроизводимость процесса, используя выборки
последовательных деталей (то есть получая малый размах ` R), чтобы
получить минимум оценки s и максимум воспроизводимости. Однако в этом
случае труднее всего добиться статистической
управляемости, так как расстояние между контрольными пределами может стать
наименьшим. Таким образом, рассмотрение только статистической управляемости или только воспроизводимости процесса в отдельности не даст устойчивой
оценки работоспособности процесса – оба критерия надо рассматривать
совместно.

(3) Вычисления –
Иногда бывает трудно вычислять C_p и C_pk
непосредственно в цехе, где не все люди привыкли к математическим
формулам. Эту проблему можно рассматривать по-разному, но часто она
требует определенного обучения и (или) некоторой
автоматизации.

(4) Ненормальность –
Изменчивость результатов процесса может быть следствием ненормального
распределения показателя. Вероятно, есть смысл ожидать, что индексы
воспроизводимости в некоторой степени чувствительны к отклонениям от
нормальности. Для получения приближенной нормальности могут пригодиться
преобразования данных. Итак, можно определить процент бракованных деталей
как непосредственно, так и подобрав распределение. Этот процент можно
привести к эквивалентному индексу воспроизводимости для процесса, имеющего
нормальное
распределение.

(5) Износ инструмента – В
ситуации, когда изнашивается инструмент, первичный интерес представляет
оценка ` R по последовательному плану выборки. Технически `
R можно применять для оценки C_p, но
воспроизводимость обычно довольно высока. Работоспособность процесса
зависит от частоты смены инструмента. Это делает неудобным распространение
показателя C_pk в такой ситуации.

ПРИМЕНЕНИЯ

Цель любого индекса – удобная
свертка информации в наиболее подходящей форме. Статистики ` х и s
содержат большую часть информации о предполагаемом нормальном процессе и
самыми разными способами могут быть соотнесены с ВГД и НГД. Пять показателей воспроизводимости
C_p, CPU, CPL,
k и C_pk, приведенных
в табл. 3, составляют специальный “язык”, который понятен как в цехе, так и в конторе
управляющего. Некоторые области применения
описываются ниже, но в любом конкретном
приложении индексов надо учитывать описанные выше
недостатки.

Показатель	Уравнение оценивания	Применение
Ср		Потенциал процесса для двусторонних границ допуска
CPU		Работоспособность процесса относительно верхней границы допуска
CPL		Работоспособность процесса относительно нижней границы допуска
k		Отклонение среднего значения процесса от середины (m) между границами допуска
Cpk	Min {CPL, CPU} = Cp (1-k)	Работоспособность процесса для двусторонних границ допуска

(1) Предупреждение бракованной
продукции – Для различных типов испытаний станков и сертификации
процессов иногда бывает полезно и целесообразно установить норму
воспроизводимости. Типичная норма воспроизводимости – это C_pk=l,33, что делает появление брака маловероятным (см. Хоффнер, 1985) во многих ситуациях. Обратите
внимание: так как воспроизводимость обычно уже оценена, надо брать более
высокое критическое значение (с), чем предлагалось
ранее.

(2) Непрерывное
совершенствование – Внутри отдела или цеха часто бывает полезно
непрерывно следить за совершенствованием, что можно осуществить, наблюдая
за изменяющимися распределениями
воспроизводимостей процесса. Если, например, было 10% процессов с воспроизводимостями между 1 и 1,33
в данном месяце, а в следующем месяце некоторые из них имеют этот
показатель между 1,33 и 1,67, то усовершенствование произошло. За таким
сдвигом распределений легко осуществить мониторинг.

(3) Коммуникация – Применение
C_p и C_pk образует общий язык, который
не зависит от конкретных размеров и оценивает как потенциальную, так и
фактическую работоспособность производственных процессов.
Инженеры-разработчики и производственники получают возможность общения
друг с другом и выявления процессов с высокой воспроизводимостью.
Изменения в проекте могут способствовать сокращению затрат.
Производственники могут непосредственно общаться с поставщиками (см., например, Сулливан, 1984).

(4) Установление приоритетов
– Простая компьютерная распечатка процессов с неприемлемыми значениями
C_p или C_pk – помощница в установлении
приоритетов совершенствования процессов.

(5) Настройка или
изменчивость – Для любого показателя всегда имеет смысл сравнить
C_p и C_pk. Если C_pk
слишком мало, то надо выяснить для C_p, не слишком ли
велика изменчивость. Если C_p близко к
C_pk, то с настройкой процесса нет проблем. Индексы CPU, CPL и
k показывают, насколько близко среднее
подошло к границам допуска и насколько далеко оно от целевого
значения.

(6) Проверки – Для оценки
работоспособности систем применяются различные
типы проверок качества. Сравнение
воспроизводимостей внутренних с
воспроизводимостями, определенными в результате проверки, может помочь
выделить области, где возникают проблемы.

ВЫВОДЫ

Показатели воспроизводимости
могут применяться для эффективной свертки информации о процессе удобным
способом. Индексы C_p,
CPU, CPL, k и C_pk образуют группу
взаимодополняющих показателей, которые образуют удобную безразмерную
систему. Все эти показатели вместе определяют,
имеет ли процесс достаточно низкую изменчивость и удовлетворяет допускам процесса или есть проблема настройки. Они
могут применяться для односторонних и двусторонних пределов допуска и
могут обобщаться для работы с многомерными номиналами (показателями качества).

Вероятно, наибольшая ценность
этих показателей – в поддержке усилий, направленных на предотвращение
производства брака, а также в том, что дает метод мониторинга и
непрерывного совершенствования в широком диапазоне. Наконец, эти
показатели позволяют установить эффективный обмен информацией о потенциале
процесса и его работоспособности на языке, который легко
понимать.

REFERENCES

Burr, 1. R. (1976). Statistical Quality Control Methods Marcel Dekker, New York, New York. ;

Charbonneau, H. C. and Webster, G. L. (1978). Industrial Quality Control. Prentice Hall, Englewood Cliffs, New Jersey.

Ford Motor Company (1984).
Continuing Process Control and Process Capability lpmrovement. Ford Motor Company, Dearborn,
MI.

Hahn,
G. J. (1970). “Statistical Intervals for a
Normal Population Part 1. Tables. Examples and
Applications.” Journal of Quality
Technology 2, pp. 115-125.

Hotter, P. (1985). “Moving to Prevention: An
Industry in Transition.” Quality Progress 18, pp.
24-26.

Jessup, P. T. (1983).
“Process Capability, The Value of Improved Performance,” paper presented
at the ASQC Automotive Division Workshop
Seminar, November 2-4, Southfield,
Michigan.

Juran, J. M. and Gryna, F. M. (1980).
Quality Planning and Analysis McGraw-Hill, New York, New
York.

Juran, J. M. Gryna, F. M., and Bingham, R. S. (1979).
Quality Control Handbook. McGraw-Hill, New York, New
York.

Sullivan, L. P. (1984). “Reducing Variability: A New Approach to Quality.”
Quality Progress 17, pp. 16-21.

Sullivan, L. P. (1985).
“Letters.” Quality Progress 18, pp. 7-8. Key Words: Capability,
Target Value, Process Potential Process
Performance.

Опубликовано на https://www.spc-consulting.ru/

Также на сайте:
Инновационный метод как инструмент разработки и внедрения на предприятии системы менеджмента качества
Интегрированные системы менеджмента. что это такое?