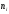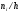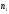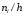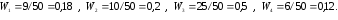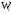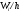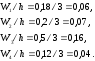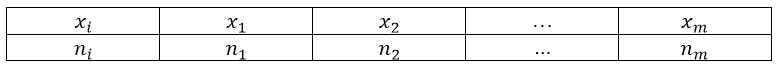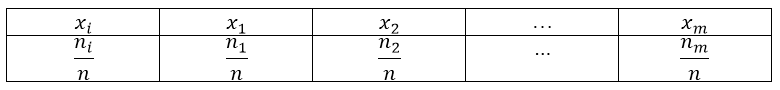Инструкции:
Используйте данный инструмент для построения графика частотных полигонов, чтобы построить частотный полигон на основе выборки, представленной в виде сгруппированных данных с классами и частотами. Введите эти классы и частоты в форму ниже:
Подробнее об этой программе frequency polygon graph maker
Идея группировки данных в большинстве случаев заключается в том, чтобы обобщить выборку, часто используя меры центральной тенденции, меры дисперсии и графики.
Одним из таких графиков, описывающих образец, является график
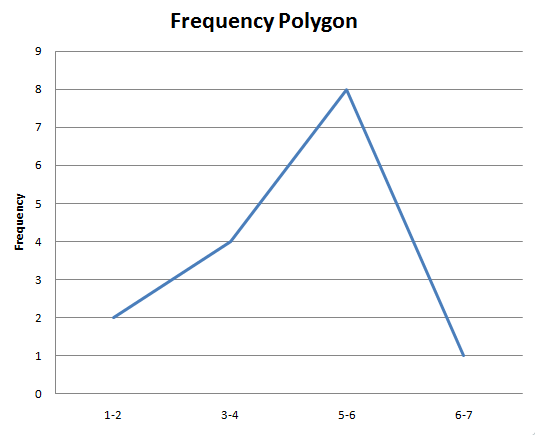
частотный многоугольник
, что позволяет получить быстрый снимок распределения значений в выборке.
Графически частотный многоугольник выглядит следующим образом:
Как на самом деле построить частотный многоугольник?
Построить частотный многоугольник на самом деле довольно просто:
Во-первых, необходимо иметь частотное распределение данных, либо в виде частоты отдельных значений, либо в виде классов.
Во-вторых, вы откладываете классы (или отдельные значения) на оси X, а их частоты – на оси Y, и наносите на график все соответствующие точки (X, Y).
В-третьих, соедините эти точки прямыми линиями, начиная от точек слева и заканчивая справа.
Это именно то, что делает для вас этот создатель частотных полигонов, а также большинство статистических программных пакетов (например, Excel).
Теперь, если вам нужно построить график многоугольника кумулятивной частоты, вам понадобится следующее
Составление Графика Огибающей
.
Настроив график, вы получите хорошее представление о том, как выглядит распределение, особенно если размер выборки достаточно велик. Действительно, например, если у вас достаточно большой объем выборки (скажем, n = 50) и у вас есть выборка, которая поступает из
популяция с нормальным распределением
то частотный многоугольник должен выглядеть достаточно колоколообразно.
Другие составители графиков описательной статистики
Построители графиков действительно важны в момент получения быстрого, но достаточно адекватного описания формы распределения случайной величины, которая попадает в выборку.
Возможно, вам будет интересно взглянуть на наши
Создатель Гистограмм
что, возможно, даст вам более точное представление о форме распределения. Вы также можете использовать
круговая диаграмма
или же
построитель графиков
, для соответствующего уровня измерения.
Построение полигона, гистограммы, кумуляты, огивы
Для наглядности строят различные графики статистического
распределения, и, в частности, полигон и гистограмму.
- Полигон
- Гистограмма
- Кумулята и огива
Полигон
Полигоном частот называют
ломаную, отрезки которой соединяют точки
. Для построения полигона частот на оси
абсцисс откладывают варианты
, а на оси ординат – соответствующие им
частоты
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки
. Для построения полигона относительных
частот на оси абсцисс откладывают варианты
, а на оси ординат – соответствующие им
относительные частоты (частости)
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 1
Построить полигон частот и
полигон относительных частот (частостей):
Решение
Вычислим относительные
частоты (частости):
Полигон частот
Полигон относительных частот
В случае интервального ряда для
построения полигона в качестве
берутся середины интервалов.
Гистограмма
В случае интервального
статистического распределения целесообразно построить гистограмму.
Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною
, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам. При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты
. Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.
В случае построения
гистограммы относительных частот (гистограммы частостей)
высоты в случае равных интегралов должны быть пропорциональны относительной
частоте
, а в случае неравных интервалов высота
равна плотности относительной частоты
.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 2
Построить гистограмму
частот и относительных частот (частостей)
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму
частот (случай неравных интервалов).
Решение
Вычислим плотности
частоты:
Гистограмма частот
Кроме этой задачи на другой странице сайта есть
пример построения полигона и гистограммы на одном графике для интервального вариационного ряда
Кумулята и огива
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Если при графическом
изображении вариационного ряда в виде кумуляты оси
поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той
лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения
признака — на оси ординат.
Пример 4
Построить кумулятивную
кривую:
Решение
Вычислим накопленные
частоты:
Кумулятивная кривая
Постройка полигона и гистограммы частот
Содержание:
- Что такое полигон и гистограмма частот
- Как построить полигон частот
- Как построить гистограмму частот
- Чему равна площадь гистограммы частот
- Примеры создания полигона и гистограммы в задачах
Что такое полигон и гистограмма частот
Для наглядного представления ряда распределения используют полигон и гистограмму частот.
Определение
Полигон частот – это ломаная, соединяющая точки (x1, n1), (x2, n2),…, (xk, nk), где xi – это варианты или наблюдаемые значения, а ni – частота вариантов.
Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x1, W1), (x2, W2),…, (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(W_i=frac{n_i}n)
где n – это объем выборки.
Гистограмму используют в случае непрерывного признака.
Определение
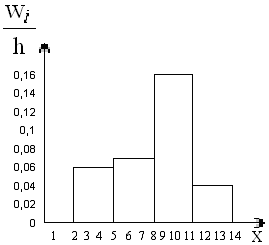
Гистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат Wi.
Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение Wi/h.
Как построить полигон частот
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие xi частоты ni. Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Пример
Полигон частот для выборки со следующими значениями:
xi 92, 94, 95, 96, 97, 98.
ni 1, 2, 2, 3, 1, 1.
Как построить гистограмму частот
Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты ni/h.
Пример гистограммы частот при частичном интервале h, равном 3.
Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.
Плотность частоты ni/h: 3,3; 8,3.
Чему равна площадь гистограммы частот
Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:
(frac{n_ih}h=n_i)
Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.
Примеры создания полигона и гистограммы в задачах
Задача 1
Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.
Нужно построить полигон частот по этим данным.
Решение
На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:
Задача 2
По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:
Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.
Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.
Всего в контрольной работе было 25 вопросов.
Необходимо построить гистограмму по этому ряду распределения.
Решение
Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.
Для
наглядности строят различные графики
статистического распределения, в
частности, полигон и гистограмму.
Определение.
Полигоном
частот называют ломаную, отрезки которой
соединяют точки (x1,
n1),
(x2,
n2),
…, (xk,
nk).
Для
построения полигона частот на оси
абсцисс откладывают варианты xi,
а на оси ординат – соответствующие им
частоты ni.
Точки (xi,
ni)
соединяют отрезками прямых и получают
полигон частот.
Определение.
Полигоном
относительных частот
называют ломаную, отрезки которой
соединяют точки (x1,
w1),
(x2,
w2),
…, (xk,
wk).
Для
построения полигона частот на оси
абсцисс откладывают варианты xi,
а на оси ординат wi.
Точки (xi,
wi)
соединяют отрезками прямых и получают
полигон относительных частот.
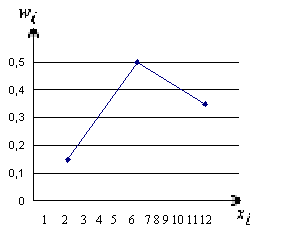
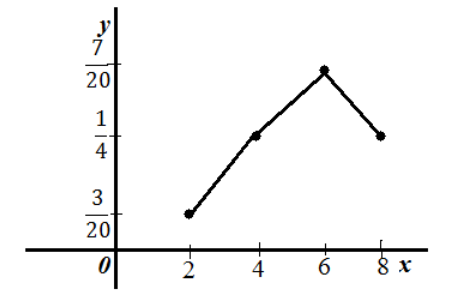
На
рисунке изображен полигон относительных
частот следующего распределения:
|
x |
1,5 |
3,5 |
5,5 |
7,5 |
|
w |
0,1 |
0,2 |
0,4 |
0,3 |
Рис.
6. Полигон относительных частот.
В
случае непрерывного признака целесообразно
строить гистограмму, для чего интервал,
в котором заключены все наблюдаемые
значения признака, разбивают на несколько
частичных интервалов длинной h
и находят для каждого частичного
интервала ni
–
сумму частот вариант, попавших в i-ый
интервал.
Определение.
Гистограммой
частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною h,
а высоты равны отношению
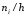
Рис.
7. Гистограмма частот.
Для
построения гистограммы частот на оси
абсцисс откладывают частичные интервалы,
а над ними проводят отрезки, параллельные
оси абсцисс, на расстоянии
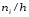
Площадь
i-го
частичного прямоугольника равна
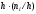
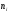
интервала; следовательно, площадь
гистограммы частот равна сумме всех
частот, то есть объему выборки n.
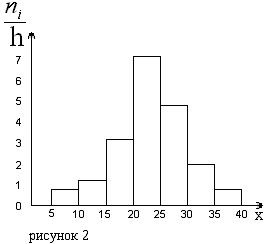
На
рисунке 2 изображена гистограмма частот
распределения объема n=100,
приведенного в таблице 1.
|
Частичный
длиною |
Сумма |
Плотность |
|
5 |
4 |
0,8 |
|
10 |
6 |
1,2 |
|
15 |
16 |
3,2 |
|
20 |
36 |
7,2 |
|
25 |
24 |
4,8 |
|
30 |
10 |
2,0 |
|
34 |
4 |
0,8 |
Определение.
Гистограммой
относительных частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длинною h,
а высоты равны отношению
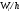
Для
построения гистограммы относительных
частот на оси абсцисс откладывают
частичные интервалы, а над ними проводят
отрезки, параллельные оси абсцисс на
расстоянии
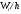
Площадьi-го
частичного прямоугольника равна
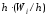
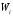
попавших вi-й
интервал. Следовательно, площадь
гистограммы относительных частот равна
сумме всех относительных частот, то
есть единице.
Примеры.
-
В
результате выборки получена следующая
таблица распределения частот.
|
|
2 |
6 |
12 |
|
|
3 |
10 |
7 |
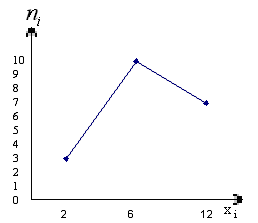
Построить
полигоны частот и относительных частот
распределения.
Для
начала построим полигон частот.
Рис.
8. Полигон частот.
Чтобы
построить полигон относительных частот
найдем относительные частоты, для чего
разделим частоты на объем выборки n.
n
=
3
+
10
+
7
=
20.
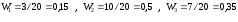
Получаем
|
|
2 |
6 |
12 |
|
|
0,15 |
0,50 |
0,35 |
Построим
полигон относительных частот.
Рис.
9. Полигон относительных частот.
2.
Построить гистограммы частот и
относительных частот распределения.
Найдем
плотность частоты
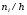
|
Частичный
длиною |
Сумма |
Плотность |
|
2 |
9 |
3 |
|
5 |
10 |
3,3 |
|
8 |
25 |
8,3 |
|
11 |
6 |
2 |
Построим
гистограмму частот.
Рис.
10. Гистограмма частот.
Чтобы
построить гистограмму относительных
частот, нужно найти относительные
частоты. Для этого найдем объем выборки
n.
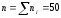
Теперь
найдем относительные частоты
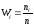
Получим:
|
Частичный |
Сумма |
Плотность |
|
2 |
0,18 |
0,06 |
|
5 |
0,2 |
0,07 |
|
8 |
0,5 |
0,16 |
|
11 |
0,12 |
0,04 |
Плотности
частот
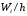
= 3.
Построим
гистограмму относительных частот.
Рис.11.
Гистограмма относительных частот.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Полигон частот и гистограмма частот
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Полигон частот
Пусть нам дан ряд распределения, записанный с помощью таблицы:
Рисунок 1.
Определение 1
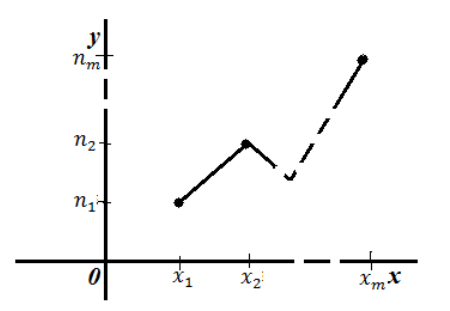
Полигон частот — ломанная, которая соединяет точки $(x_m,n_m)$ ($m=1,2,dots ,m)$.
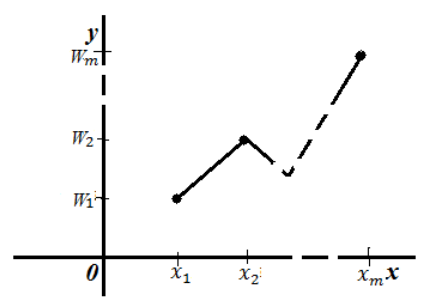
То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие частоты. Полученные точки соединяют ломанной:
Рисунок 2. Полигон частот.
Помимо обычной частоты существует еще понятие относительной частоты.
Получаем следующую таблицу распределения относительных частот:
Рисунок 3.
Определение 2
Полигон относительных частот — ломанная, которая соединяет точки $(x_m,W_m)$ ($m=1,2,dots ,m)$.
То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие относительные частоты. Полученные точки соединяют ломанной:
Рисунок 4. Полигон относительных частот.
Гистограмма частот
Помимо понятия полинома для непрерывных значений существует понятие гистограммы.
Определение 3
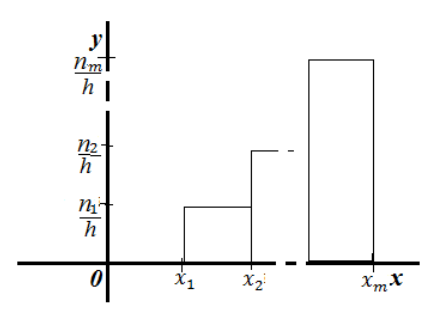
Гистограмма частот — ступенчатая фигура, состоящая из прямоугольников с основанием — частичными интервалами длины $h$ и высотами $frac{n_i}{h}$:
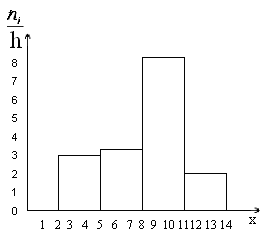
Рисунок 5. Гистограмма частот.
«Полигон частот и гистограмма частот» 👇
Заметим, что площадь одного такого прямоугольника $frac{n_ih}{h}=n_i$. Следовательно, площадь всей фигуры равна $sum{n_i}=n$, то есть равна объему выборки.
Определение 4
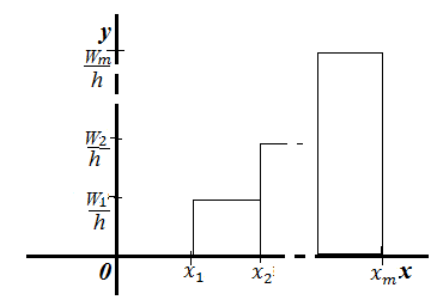
Гистограмма относительных частот — ступенчатая фигура, состоящая из прямоугольников с основанием — частичными интервалами длины $h$ и высотами $frac{W_i}{h}$:
Рисунок 6. Гистограмма относительных частот.
Заметим, что площадь одного такого прямоугольника $frac{W_ih}{h}=W_i$. Следовательно, площадь всей фигуры равна $sum{W_i}=W=1$.
Примеры задачи на построение полигона и гистограммы
Пример 1
Пусть распределение частот имеет вид:
Рисунок 7.
Построить полигон относительных частот.
Решение.
Построим сначала ряд распределения относительных частот по формуле $W_i=frac{n_i}{n}$
Рисунок 8.
Получим следующий полигон относительных частот.
Рисунок 9.
Пример 2
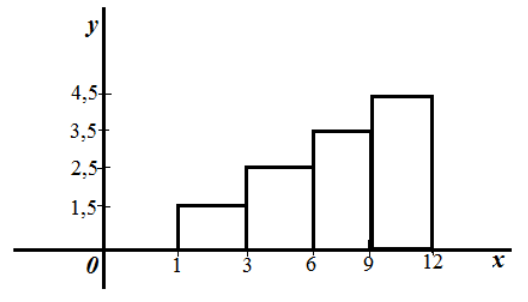
Дан ряд непрерывного распределения частот:
Рисунок 10.
Решение.
Очевидно, что данном случае длина частичного интервала $h=2.$ Найдем высоты прямоугольников каждой точки разбиения.
При $x=1$: $frac{3}{2}=1,5$.
При $x=3$: $frac{5}{2}=2,5.$
При $x=6$: $frac{7}{2}=3,5.$
При $x=9$: $frac{9}{2}=4,5.$
Получаем следующую гистограмму частот:
Рисунок 11.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 25.02.2023