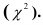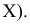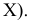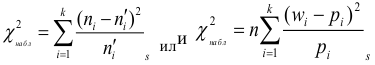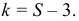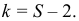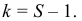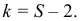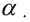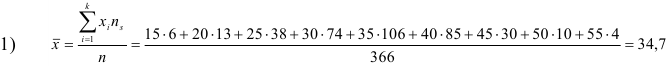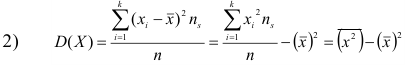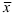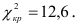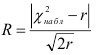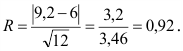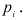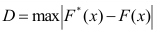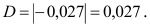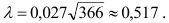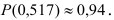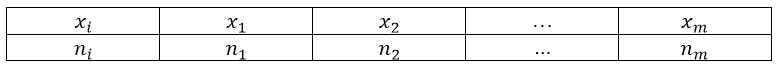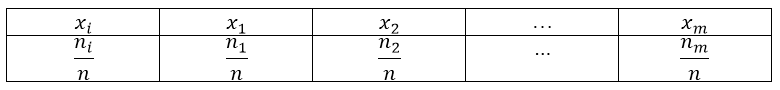Для
наглядности строят различные графики
статистического распределения, в
частности, полигон и гистограмму.
Определение.
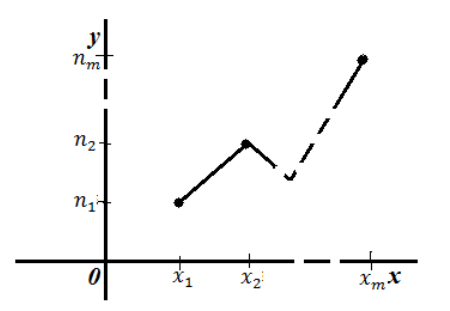
Полигоном
частот называют ломаную, отрезки которой
соединяют точки (x1,
n1),
(x2,
n2),
…, (xk,
nk).
Для
построения полигона частот на оси
абсцисс откладывают варианты xi,
а на оси ординат – соответствующие им
частоты ni.
Точки (xi,
ni)
соединяют отрезками прямых и получают
полигон частот.
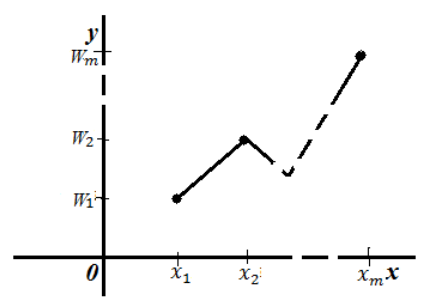
Определение.
Полигоном
относительных частот
называют ломаную, отрезки которой
соединяют точки (x1,
w1),
(x2,
w2),
…, (xk,
wk).
Для
построения полигона частот на оси
абсцисс откладывают варианты xi,
а на оси ординат wi.
Точки (xi,
wi)
соединяют отрезками прямых и получают
полигон относительных частот.
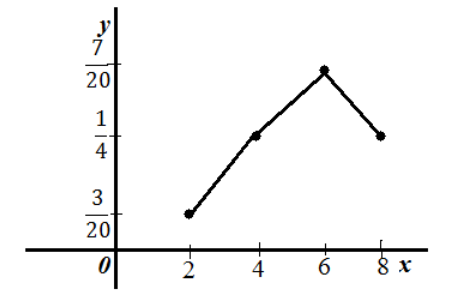
На
рисунке изображен полигон относительных
частот следующего распределения:
|
x |
1,5 |
3,5 |
5,5 |
7,5 |
|
w |
0,1 |
0,2 |
0,4 |
0,3 |
Рис.
6. Полигон относительных частот.
В
случае непрерывного признака целесообразно
строить гистограмму, для чего интервал,
в котором заключены все наблюдаемые
значения признака, разбивают на несколько
частичных интервалов длинной h
и находят для каждого частичного
интервала ni
–
сумму частот вариант, попавших в i-ый
интервал.
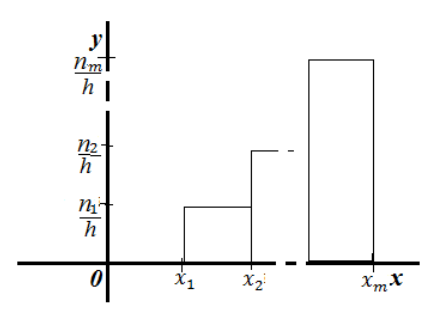
Определение.
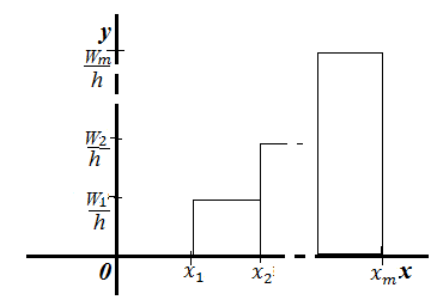
Гистограммой
частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною h,
а высоты равны отношению
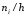
Рис.
7. Гистограмма частот.
Для
построения гистограммы частот на оси
абсцисс откладывают частичные интервалы,
а над ними проводят отрезки, параллельные
оси абсцисс, на расстоянии
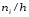
Площадь
i-го
частичного прямоугольника равна
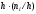
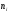
интервала; следовательно, площадь
гистограммы частот равна сумме всех
частот, то есть объему выборки n.
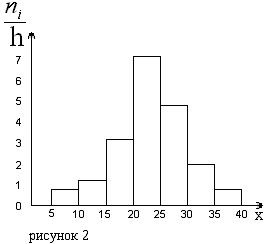
На
рисунке 2 изображена гистограмма частот
распределения объема n=100,
приведенного в таблице 1.
|
Частичный
длиною |
Сумма |
Плотность |
|
5 |
4 |
0,8 |
|
10 |
6 |
1,2 |
|
15 |
16 |
3,2 |
|
20 |
36 |
7,2 |
|
25 |
24 |
4,8 |
|
30 |
10 |
2,0 |
|
34 |
4 |
0,8 |
Определение.
Гистограммой
относительных частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длинною h,
а высоты равны отношению
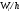
Для
построения гистограммы относительных
частот на оси абсцисс откладывают
частичные интервалы, а над ними проводят
отрезки, параллельные оси абсцисс на
расстоянии
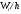
Площадьi-го
частичного прямоугольника равна
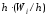
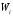
попавших вi-й
интервал. Следовательно, площадь
гистограммы относительных частот равна
сумме всех относительных частот, то
есть единице.
Примеры.
-
В
результате выборки получена следующая
таблица распределения частот.
|
|
2 |
6 |
12 |
|
|
3 |
10 |
7 |
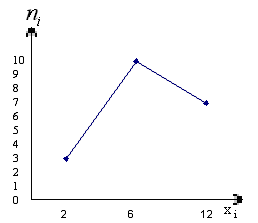
Построить
полигоны частот и относительных частот
распределения.
Для
начала построим полигон частот.
Рис.
8. Полигон частот.
Чтобы
построить полигон относительных частот
найдем относительные частоты, для чего
разделим частоты на объем выборки n.
n
=
3
+
10
+
7
=
20.
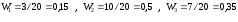
Получаем
|
|
2 |
6 |
12 |
|
|
0,15 |
0,50 |
0,35 |
Построим
полигон относительных частот.
Рис.
9. Полигон относительных частот.
2.
Построить гистограммы частот и
относительных частот распределения.
Найдем
плотность частоты
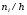
|
Частичный
длиною |
Сумма |
Плотность |
|
2 |
9 |
3 |
|
5 |
10 |
3,3 |
|
8 |
25 |
8,3 |
|
11 |
6 |
2 |
Построим
гистограмму частот.
Рис.
10. Гистограмма частот.
Чтобы
построить гистограмму относительных
частот, нужно найти относительные
частоты. Для этого найдем объем выборки
n.
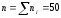
Теперь
найдем относительные частоты
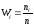
Получим:
|
Частичный |
Сумма |
Плотность |
|
2 |
0,18 |
0,06 |
|
5 |
0,2 |
0,07 |
|
8 |
0,5 |
0,16 |
|
11 |
0,12 |
0,04 |
Плотности
частот
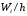
= 3.
Построим
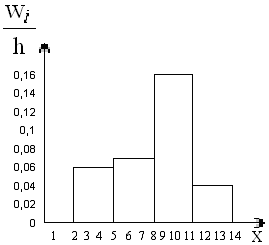
гистограмму относительных частот.
Рис.11.
Гистограмма относительных частот.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Предмет математической статистики (МС) – любой объект, изучаемый с количественной стороны в целях более точной оценки его качественного состояния.
При этом имеются в виду групповые объекты, т.е. явления массовые, в сфере которых проявляют свое действие статистические законы.
Единица наблюдения – составной элемент или член группового объекта.
Статистическая совокупность – множество относительно однородных, но индивидуально различимых единиц, объединенных для совместного (группового) изучения. Например, недопустимо изучать показатели изменчивости человеческого организма, объединяя в одну совокупность людей разного возраста и пола.
Статистический комплекс слагается из разнородных групп, каждая из которых состоит из однородных элементов, для совместного (комплексного) изучения. Вопрос о форме объединения экспериментатор решает сам в зависимости от объекта и цели исследования.
Признак – свойство, проявлением которого один предмет отличается от другого.
Пример:
Исследуется признак
Характерное свойство признаков – варьирование величины признака в определенных пределах. Эти колебания величины одного и того же признака, наблюдаемые в массе однородных элементов статистической совокупности, называются вариациями, а отдельные числовые значения варьирующего признака называются вариантами.
Признаки делятся на качественные (атрибутивные) и количественные.
Качественные признаки не поддаются непосредственному измерению и учитываются по наличию их свойств у отдельных членов изучаемой группы.
Пример:
Признак
Количественные признаки поддаются непосредственному измерению или счету. Их делят на мерные и счетные.
Мерные признаки варьируют непрерывно, их величина может принимать в определенных пределах (от – до) любые числовые значения. Аналог мерного признака в теории вероятностей есть непрерывная случайная величина.
Счетные признаки варьируют прерывисто (дискретно), их числовые значения часто выражаются целыми числами (число зерен в колосьях и т.п.).
Аналогом счетного признака в теории вероятности является дискретная случайная величина.
Признаки обозначаем так же, как случайные величины: 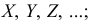
Признаки варьируют под влиянием различных, в том числе и случайных причин. Наряду с естественным варьированием на величине признака сказываются и ошибки, неизбежно возникающие при измерении изучаемых объектов.
Погрешность или ошибка – разница между результатами измерений и действительно существующими значениями измеряемого признака.
Технические ошибки – связаны с неточностью измерительных приборов и инструментов.
Личные ошибки возникают из-за личных качеств исследователя, его навыков и мастерства.
Случайные ошибки возникают из-за целого ряда других, не поддающихся регулированию и неустранимых причин.
Технические + личные ошибки = систематические ошибки. Их можно преодолеть соответствующими методами.
Случайные ошибки, как независимые от воли человека, остаются и сказываются на результатах наблюдений. Следовательно, варьирование признака складывается из естественной изменчивости признака и ошибок измерений.
При измерении количественного признака и при вычислении его характеристик применяются два вида округления:
- – округление с недостатком: если за последней сохраняемой цифрой следуют цифры 0, 1,2, 4, то они отбрасываются. Например, точность измерения
т.е. последняя сохраняемая цифра – вторая после запятой. Тогда
- – округление с избытком: если за последней сохраняемой цифрой следуют цифры 5, 6, 7, 8, 9, то последняя сохраняемая цифра увеличивается на единицу. Например,
Наблюдения над объектами могут охватывать все члены изучаемой совокупности без единого исключения или ограничиваться обследованием лишь некоторой части данной совокупности.
В первом случае наблюдения полные или сплошные, во втором – частичные или выборочные.
Полное обследование совокупности позволяет получить исчерпывающую информацию об объекте, но требует больших затрат времени, труда, ресурсов и в некоторых случаях невозможно или нецелесообразно. Например, чтобы определить всхожесть партии семян, нецелесообразно высеивать всю партию. Невозможно учесть всех обитателей фитопланктона для небольшого водоема и т.п.
Определение. Генеральной совокупностью называется вся совокупность объектов для изучения.
Выборкой или выборочной совокупностью называется отобранная тем или иным способом часть генеральной совокупности.
Количество членов генеральной совокупности обозначается 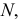
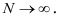
Чтобы выборка наиболее полно отображала структуру генеральной совокупности, необходимо, чтобы она была представительной (репрезентативной), т.е. для каждого элемента генеральной совокупности должна быть одинаковая возможность (вероятность) попасть в выборку, т.е. выборка должна быть случайной.
Отбор в выборку может быть повторный, если учтенная единица возвращается в генеральную совокупность и может попасть в выборку повторно.
Бесповторный отбор – учтенная единица не возвращается в генеральную совокупность, т.е. каждая отобранная единица регистрируется только один раз.
Таким образом, повторный отбор не влияет на состав генеральной совокупности и вероятность каждой единицы попасть в выборку не меняется. При бесповторном отборе вероятность единиц генеральной совокупности попасть в выборку изменяется, т.к. предшествующий отбор влияет на результаты последующего и на состав генеральной совокупности.
Идеальный случайный выбор производится по методу жеребьевки или лотереи, а также с помощью «случайных чисел». Существуют типический, серийный, механический и другие разновидности отборов.
Типический отбор используют тогда, когда генеральная совокупность расчленяется на отдельные типические группы. В таких случаях из каждой группы случайным образом отбирают одинаковое или пропорциональное число единиц. Затем вычисляют групповые характеристики, объединяемые далее в общую характеристику генеральной совокупности.
Серийный отбор используют, когда генеральная совокупность делится на серии обычно по территориальному принципу. Например, из 30 групп подростков намечено исследовать выборочно 6 групп, т.е. работают не с отдельными единицами, а с целыми сериями относительно однородных единиц.
Механический отбор используется, когда генеральную совокупность разбивают на несколько равных частей или групп. Затем из каждой группы отбирают по одной единице. Например, при исследовании посева ржи на урожайность намечено отобрать 100 растений, следовательно, поле должно быть разделено на 100 равных частей, из каждой части отбирается одна единица.
Отбор будет также механическим если из генеральной совокупности в выборку попадет каждая десятая, сотая и т.д. единица.
Систематизация наблюдений
Процесс систематизации результатов массовых наблюдений, объединения их в относительно однородные группы по некоторому признаку 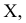
Наиболее распространенная форма группировки – статистические таблицы.
Особая форма группировки – статистические ряды, видное место среди них занимают вариационные ряды.
Определение. Вариационным рядом или рядом распределения называется двойной ряд чисел, показывающий как числовые значения признака (варианты) связаны с их повторяемостью в данной статистической совокупности.
Пример:
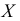
Число 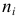
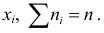
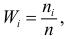
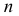
Ранжированный вариационный ряд выстроен по возрастанию или убыванию членов ряда.
В примере имеем ранжированный вариационный ряд вида:
Вариационные ряды есть безынтервальные, если признак дискретный, и интервальные, если признак непрерывный. Если признак варьирует дискретно, но в широких границах, то по данным наблюдений можно построить интервальный вариационный ряд. Будем рассматривать равноинтервальные ряды. Если признак варьирует непрерывно, то из интервального ряда можно построить безынтервальный ряд, т.е. разделение на ряды (безынтервальные и интервальные) по типу признака (дискретный или непрерывный) не однозначное.
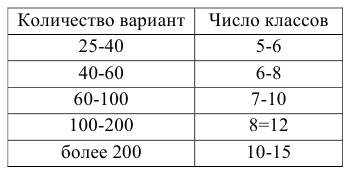
Для получения хорошо обозримого вариационного ряда и обеспечения достаточной точности вычисляемых по нему числовых характеристик следует разбить вариацию признака (в пределах от 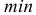
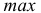
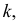
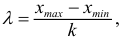
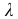
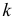
Существует формула Стерджеса 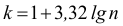
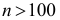
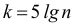
Техника построения вариационного ряда:
- Найдем
- Вычислим
- Значение
должно попасть примерно в середину первого классового интервала, поэтому нижняя граница
первого классового интервала будет
Прибавив к
число
получим верхнюю границу первого классового интервала, затем найдем верхнюю границу второго классового интервала и т.д. до тех пор, пока не получим интервал, в который попадет
- Верхние границы интервалов уменьшаем на величину
равную точности, принятой при измерении признака, для того, чтобы избежать момента, когда варианта совпадает с границей.
- Подсчитаем количество вариант
попавших в каждый интервал.
Пример:
Наблюдается признак 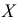
Выборка имеет вид: 8, 10, 6, 10, 8, 5, 11, 7, 10, 6, 9, 7, 8, 7, 9, 11, 8, 9, 10, 8, 7, 8, 11, 8, 7, 10, 8, 8, 5, 11, 8, 10, 12, 7, 5, 7, 9, 7, 10, 5, 8, 9, 7, 12, 8, 9, 6, 7, 8, 7, 11, 8, 6, 7,9, 10,6, 6,6,7,8, 10, И, 12.
Если 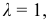
Полученный вариационный ряд выражает зависимость между отдельными вариантами и частотой (повторяемостью) вариант.
Пример:
Наблюдается признак 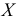
Выборка имеет вид:
1) Лимиты выборки:
Классовые интервалы:
4) Уменьшаем верхние границы интервалов на величину точности, принятой при измерении, т.е. на величину 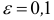
Итак, интервальный вариационный ряд имеет вид:
Соответствующий безынтервальный ряд, построенный по интервальным данным, будет иметь вид:
где 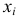
Графики вариационных рядов
Более наглядное изображение закономерности варьирования количественного признака – график вариационного ряда.
Полигон распределения
Полигон распределения (или многоугольник распределения) строится для безынтервального ряда: по оси 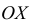
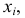
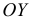
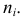
Гистограмма распределения частот
Гистограмма распределения частот 
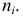
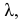
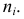
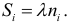
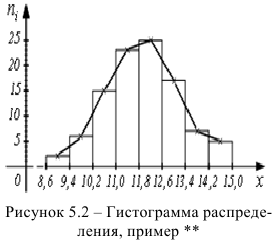
Пример:
Гистограмма данного распределения изображена на рис. 5.2. Если на приведенной гистограмме верхнее основание клетки поделить пополам точкой, соединить полученные точки ломаной, то получим вариационную кривую.
Аналогично можно построить гистограмму относительных частот 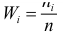
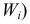
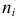
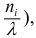
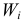
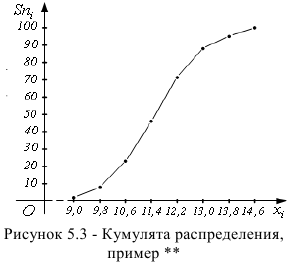
Кумулята
Кумулята (или график накопленных частот 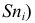
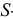
По оси 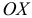
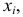
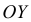
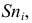
Пример:
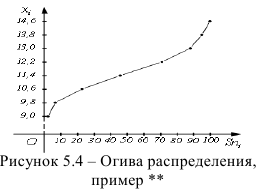
Огива
По оси 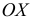
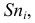
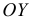
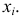
Пример:
Огива данного распределения приведена на рис. 5.4. Огива служит для сравнения вариационных рядов с разным количеством наблюдений.
Эмпирическая функция распределения
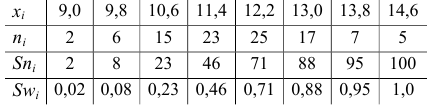
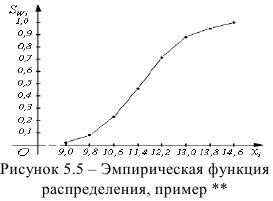
Эмпирическая функция распределения 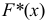
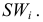
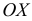
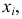
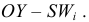
Пример:
Эмпирическая функция данного распределения приведена на рис. 5.5.
Аналогом 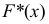
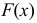
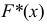
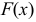
Основные характеристики варьирующих признаков
Средние величины:
Средние величины обладают способностью характеризовать целую группу однородных единиц одним (средним) числом. Например, средний рост, средняя продуктивность, средняя успеваемость и т.п.
Значение средних заключается в их свойстве аккумулировать или уравновешивать все индивидуальные отклонения, в результате чего проявляется то наиболее устойчивое и типичное, что характеризует качественное своеобразие варьирующего объекта, позволяет отличать один групповой объект от другого.
Средние величины могут характеризовать только однородную совокупность вариант, в противном случае средняя величина фиктивная. Средняя величина -это абстрактная величина, т.к. в действительности не существует, а иногда и не может существовать, но очень подходит для сравнения признаков.
При вычислении средних величин не обязательно группировать исходные данные в вариационный ряд.
Средняя арифметическая
Средняя арифметическая 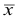
В случае, если выборка не сгруппированная, то 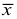
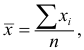
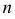
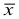
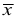
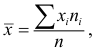
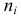
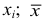
Свойства
1) если каждую варианту 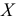
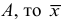
2) Если каждую варианту 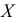
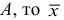
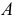
Средняя квадратическая
Средняя квадратическая 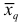
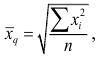
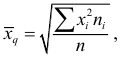
Пример:
Измерение диаметров нефтяных пятен при загрязнении водоема дало следующие результаты: 15, 20, 10, 25, 30 м.
Требуется определить средний диаметр нефтяного пятна. Применим формулу
Средняя арифметическая диаметров 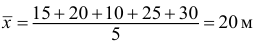
площадь всех пяти пятен равна 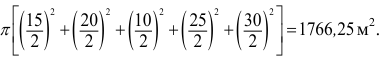
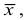
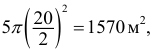
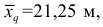
Средняя кубическая
Средняя кубическая 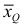
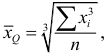
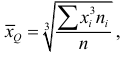
Средняя кубическая 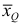
Средняя гармоническая
Средняя гармоническая 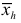
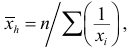
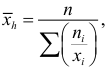
Пример:
Пять рабочих в течение одного часа (60 мин.) изготовили: первый – 10 деталей, второй – 20, третий – 25, четвертый – 30, пятый – 20. Всего за один час изготовлено 105 деталей. Средние количества деталей за один час 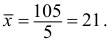
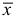
С помощью 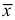
Найдем количество минут, затраченное на одну деталь каждым рабочим:
Найдем среднее время, затраченное на одну деталь одним рабочим:
Количество деталей в среднем изготовленных за час будет:
Аналогичный результат получим, если используем формулу среднего гармонического:
Следовательно, в случае усреднения меняющихся производительностей ил скоростей надо применять
Показатели вариации
Лимиты и размах выборки:
Простейшими показателями вариации (показателями разнообразия) являются лимиты: 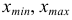
Пример:
Признаки 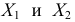
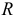
Среднее линейное отклонение
Среднее линейное отклонение 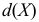
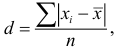
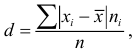
В условиях предыдущего примера линейные отклонения признаков:
Отсюда
Следовательно, признак 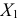
Дисперсия
Дисперсия 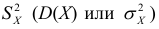
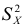
Расчетная формула дисперсии:
Таким образом, 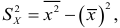
квадрата величины минус квадрат среднего арифметического.
Аналог в теории вероятностей – дисперсия 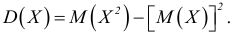
Свойства дисперсии:
1) если каждую варианту 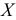
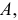
Следовательно, можно вычислять не только по 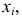
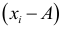
2) Если каждую варианту 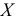
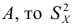
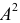
Следовательно, при наличии в совокупности многозначных вариант их можно сократить на некоторое постоянное число 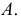
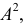
Свойства 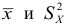
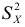
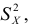
При 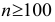
Пример:
Пусть признак 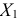
Обозначим сумму квадратов отклонений значений признака от центра 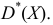
Дисперсия выборочная
Дисперсия исправленная
Пусть признак 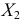
Дисперсия выборочная
Дисперсия исправленная
Среднее квадратическое отклонение
Среднее квадратическое отклонение (СКО) более удобная характеристика, чем дисперсия, т.к. выражается в тех же единицах, что 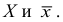
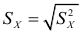
В условиях предыдущего примера
При одинаковых лимитах и размахе дисперсия и СКО не одинаковы. На их величине сказался различный характер варьирования признака.
Поправка Шеппарда.
При создании безынтервального вариационного ряда из интервального ряда частоты 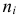
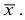
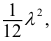
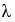
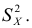
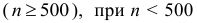
Пример:
Введем поправку Шеппарда:
Анализируя результат, приходим к выводу, что в этом примере данную поправку можно не использовать.
Коэффициент вариации
Дисперсия 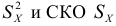
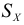
2) средние сравниваемых групп незначительно отличаются друг от друга. Если указанные условия не выполняются и необходимо сравнить разнообразие разных признаков или одинаковых при значительном различии средних, то СКО непосредственно не может быть использовано. В этих случаях используют не абсолютные, а относительные показатели вариации.
Коэффициент вариации 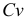
Примеры:
1) Сравнить два варьирующих признака. Для первого признака среднее 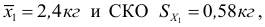
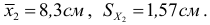
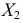
Следовательно, сильнее варьирует признак
2) Средняя длина зеркального карпа в одном садке 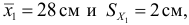
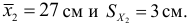
втором садке разнообразия больше и рыбы менее стандартны.
Отметим, варьирование признака 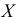
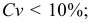
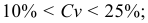
Структурные средние
На величину средней арифметической 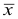
Медиана
Медиана 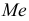
Если число вариант небольшое, то данные ранжируют и при нечетном 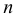
В данном случае медиана
Если число вариант четное, то медиана равна полусумме его центральных членов. Например,
В этом случае медиана
Если имеем вариационный интервальный ряд, то медиану находим по формуле
Вначале находим класс или интервал, к которому принадлежит медиана 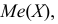
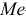
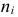
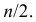
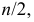
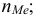
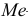
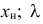
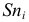
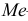
Пример:
Если из интервального вариационного ряда сформирован безынтервальный вариационный ряд, то медиану находим по формуле
где 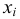
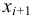
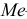
Пример:
Пример:
По предыдущей формуле:
Мода
Мода 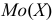
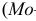
Если ряд безынтервальный, то 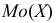
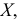
Если ряд интервальный, то моду находим по формуле
где 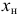
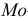
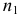
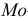
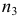
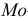
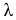
Пример:
Квантили
Квантили – значения признака 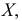
Квартили – три значения признака 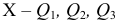
Децили – девять значений делят ряд на десять равных частей.
Перцентили – 99 значений делят ряд на 100 равных частей. Обозначают перцентили
Точечные и интервальные оценки генеральных параметров
Числовые показатели, характеризующие генеральную совокупность, называются генеральными показателями. Например, математическое ожидание генеральной совокупности 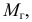
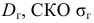
Числовые показатели, характеризующие выборку, называются выборочными характеристиками или статистиками. Например, 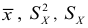
Выборочные характеристики – это величины случайные, варьирующие около своих генеральных параметров и являющиеся их приближенными оценками.
Пусть исследуется количественный признак 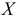
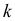
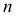
По каждой выборке подсчитаем некоторую статистику 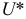
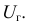
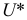
В большинстве случаев средние характеристики имеют нормальный закон распределения.
Определение. Характеристики, вычисленные одним числом, называются точечными оценками генеральных параметров.
Такие оценки должны удовлетворять условиям:
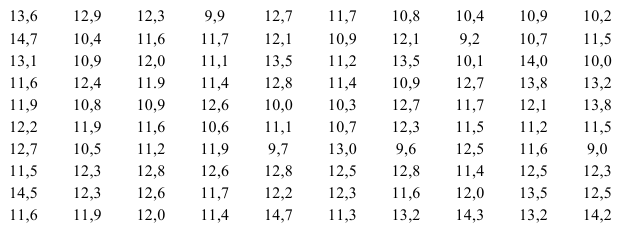
- состоятельность, т.е. оценка
стремится по вероятности к оцениваемому параметру
- эффективность, т.е. оценка
должна иметь наименьшую дисперсию по сравнению с другими аналогичными оценками. Например, для трех показателей, описывающих положение центра нормального распределения признака
– наиболее эффективной будет оценка
наименее эффективной –
Для дисперсий этих оценок характерно неравенство
- несмещенность оценки, т.е. математическое ожидание ее выборочного распределения совпадает со значением генерального параметра:
При соблюдении этого условия оценка не содержит систематических ошибок в сторону занижения или завышения.
Доказано, что наилучшими оценками для генеральных параметров 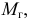
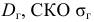
При выборке малого объема точечная оценка параметра может значительно отличаться от генерального значения. В таких случаях используют интервальные оценки. Интервальная оценка определяется двумя числами – границами интервала; такая оценка позволяет установить точность и надежность оценки.
Пусть по данным выборки подсчитана статистика 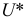
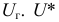
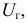
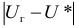
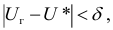
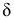
Так как работаем со статистическим материалом (массовыми однородными объектами), то категорически утверждать, что оценка 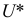
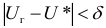
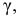
Определение. Доверительной вероятностью или надежностью называется вероятность
На практике наиболее часто задают надежность 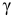
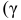
Противоположная вероятность 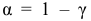
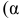
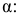
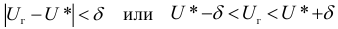
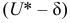
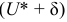
Говорим, что доверительный интервал заключает в себе 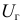
Для любой выборочной характеристики по соответствующей методике можно найти доверительный интервал с надежностью
Например, пусть количественный признак 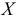
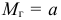
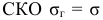
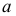
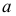
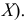
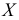
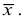
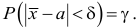
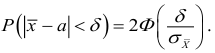
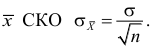
Обозначим 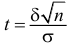
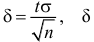
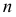
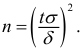
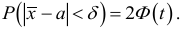
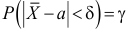
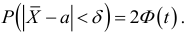
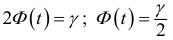
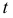
Таким образом, интервал 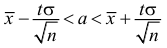
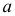
Пример:
Количественный признак 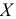
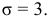
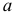
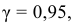
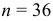
Точность оценки
Доверительный интервал:
Надежность 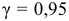
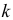
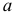
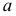
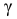
Рассмотрим случай, когда СКО 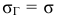
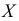
Случайная величина 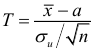
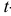
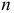
Дифференциальная функция этого распределения (плотность вероятности) обозначается 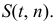
Доверительный интервал:
Величина 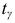
Пример:
Количественный признак 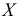
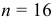
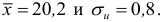
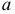
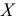
При 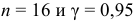
Замечание. Можно доказать, что при 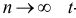
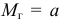
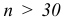
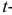
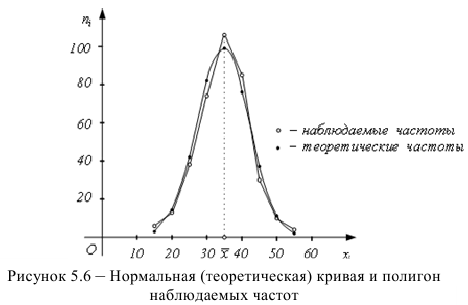
Построение нормальной кривой по опытным данным
Пусть признак 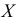
Если 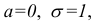
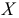
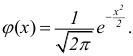
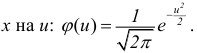
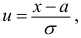
Сравниваем (5.1) и (5.2), получим:
Если параметры 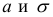
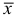
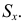
Пусть имеем безынтервальный вариационный ряд, где 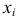
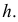
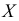
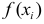
Величина 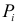
наблюдений выборки объемом 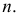
Один из способов построения нормальной кривой по данным наблюдений следующий:
1) поданным наблюдений вычислим параметры
2) найдем выравнивающие (теоретические) частоты по формуле
где 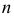
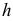
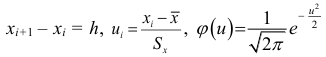
3) строим точки 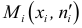
Пример:
Пусть статистическое распределение признака 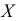
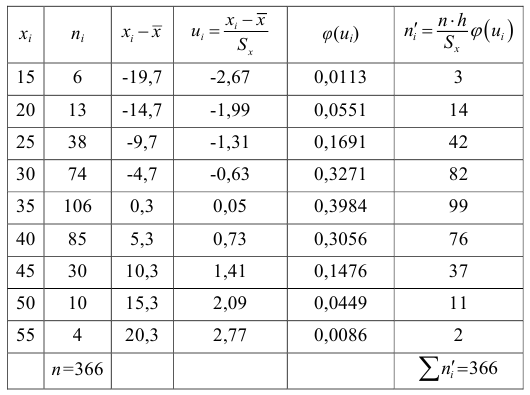
Найдем выравнивающие (теоретические) частоты 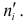
На рис.5.6 построены нормальная (теоретическая) кривая и полигон наблюдаемых частот. Сравнение графиков показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.
Статистическая гипотеза
Статистическая проверка гипотез является вторым после статистического оценивания параметров распределения и в то же время важнейшим разделом математической статистики.
Методы математической статистики позволяют проверить предположения о законе распределения некоторой случайной величины (генеральной совокупности), о значениях параметров этого закона (например 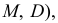
Пусть по некоторым данным имеются основания выдвинуть предположения о законе распределения или о параметре закона распределения случайной величины (или генеральной совокупности, на множестве объектов которой определена эта случайная величина). Задача заключается в том, чтобы подтвердить или опровергнуть это предположение, используя выборочные (экспериментальные) данные.
Проверить статистическую гипотезу – это значит проверить, согласуются ли данные, полученные из выборки с этой гипотезой. Проверка осуществляется с помощью статистического критерия.
Определение 1. Статистический критерий – правило, устанавливающее условия, по которым статистическая гипотеза принимается или отвергается.
Этот критерий называют еще критерием согласия (имеется в виду согласие принятой гипотезы с результатами, полученными из выборки).
Определение 2. Статистический критерий – это случайная величина 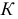
Гипотезу, выдвинутую для проверки ее согласия с выборочными данными, называют нулевой гипотезой и обозначают 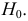
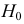
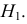
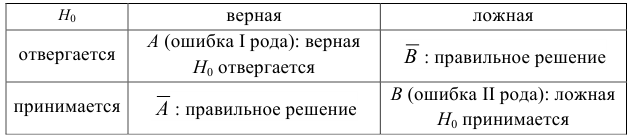
При проверке статистических гипотез можно допустить ошибку двух видов. Относительно гипотезы 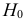
Определение. Уровнем значимости 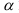
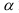
Чем меньше уровень значимости 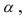
Тогда вероятность события 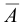
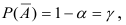
Определение. Критической областью 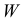
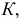
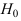
Критическая область 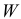
- вероятность попадания
при условии справедливости
была равна
при минимальном
- вероятность попадания
если справедлива
должна быть такой, что вероятность ошибки II рода, т.е.
должна быть минимальной. Вероятность не допуска ошибки II рода
называется мощностью критерия
эта величина должна быть максимальной.
- единственный способ одновременного уменьшения вероятностей ошибок I и II рода состоит в увеличении объема выборки.
Критерии согласия
Обычно эмпирические 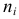
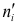
Возникает необходимость установить критерий (правило), который позволит судить, является ли расхождение между 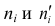
Если расхождение случайно, то говорим, что данные выборки согласуются с гипотезой о распределении генеральной совокупности и, следовательно, гипотезу можно принять. Если же расхождение значимо, то гипотезу следует отвергнуть.
Критерий согласия (критерий соответствия) – критерий, который позволяет судить о том, что расхождение эмпирического и теоретического распределений случайно или значимо (принимать гипотезу или отвергать).
Критерий «хи-квадрат» Пирсона
Критерий «хи-квадрат» Пирсона
Пусть количественный признак 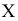
Выдвигается нулевая гипотеза 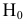
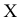
Вычисляется статистическая характеристика:
Критерий 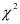
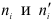
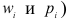
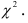
Величина 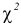
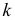
Число степеней свободы 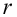
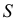
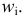
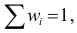
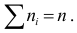
Если подбираем теоретическое распределение с тем условием, чтобы совпадали теоретическое и статистическое средние, то 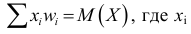
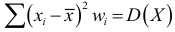
В случае, если признак 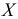
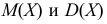
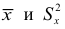
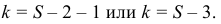
Если проверяем равномерный закон распределения, то его параметры 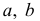
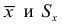
В случае закона Пуассона параметр 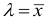
Если проверяем биномиальный закон распределения, то 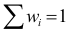
Если закон показательный, то его параметр 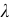
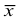
Вычисляем число степеней свободы 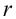
Итак, при проверке гипотезы о нормальном распределении 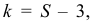
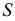
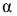
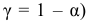
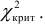
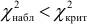
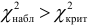
При использовании критерия «хи-квадрат» необходимо интервалы с числом 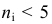
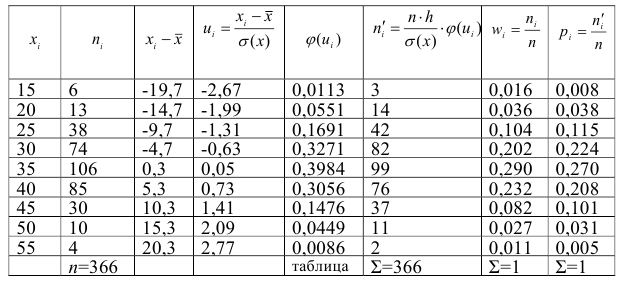
Пример:
Пусть количественный признак 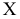
Такое задание признака 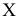
вариационному ряду вычислим основные числовые характеристики:
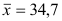
У нас 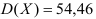
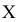
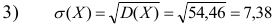
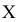
Выдвигаем нулевую гипотезу 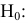
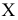
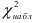
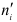
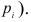
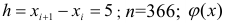
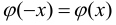
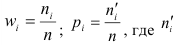
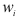
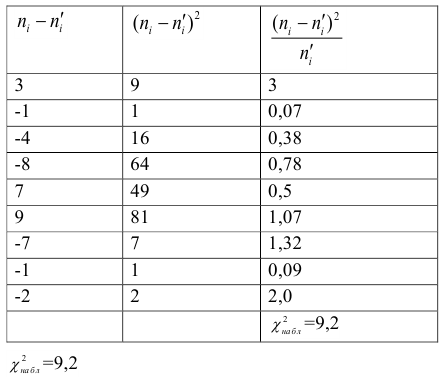
Приведем расчетную таблицу.
Сравниваем графы 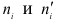
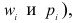
Вычисляем 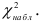
Вычисляем число степеней свободы 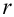
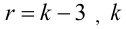
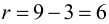
Задаем уровень значимости 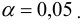
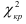
Вывод: 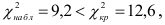
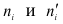
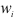
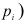
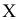
Критерий Романовского
Найдем величину (число)
В примере
Если 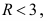
У нас: 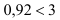
Если 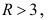
Критерий Колмогорова.
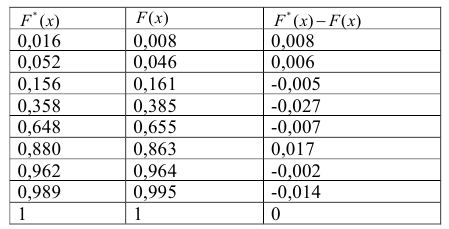
Этот критерий в расчетную таблицу требует еще три графы.
Графа 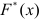
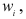
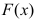
Найдем величину
В примере
Вычислим 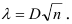
По таблице 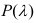
Вывод. Если 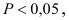
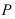
В примере: 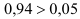
- Комбинаторика – правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Теоремы сложения и умножения вероятностей
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция – определение и вычисление
- Элементы теории ошибок
Постройка полигона и гистограммы частот
Содержание:
- Что такое полигон и гистограмма частот
- Как построить полигон частот
- Как построить гистограмму частот
- Чему равна площадь гистограммы частот
- Примеры создания полигона и гистограммы в задачах
Что такое полигон и гистограмма частот
Для наглядного представления ряда распределения используют полигон и гистограмму частот.
Определение
Полигон частот – это ломаная, соединяющая точки (x1, n1), (x2, n2),…, (xk, nk), где xi – это варианты или наблюдаемые значения, а ni – частота вариантов.
Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x1, W1), (x2, W2),…, (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(W_i=frac{n_i}n)
где n – это объем выборки.
Гистограмму используют в случае непрерывного признака.
Определение
Гистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат Wi.
Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение Wi/h.
Как построить полигон частот
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие xi частоты ni. Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Пример
Полигон частот для выборки со следующими значениями:
xi 92, 94, 95, 96, 97, 98.
ni 1, 2, 2, 3, 1, 1.
Как построить гистограмму частот
Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты ni/h.
Пример гистограммы частот при частичном интервале h, равном 3.
Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.
Плотность частоты ni/h: 3,3; 8,3.
Чему равна площадь гистограммы частот
Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:
(frac{n_ih}h=n_i)
Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.
Примеры создания полигона и гистограммы в задачах
Задача 1
Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.
Нужно построить полигон частот по этим данным.
Решение
На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:
Задача 2
По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:
Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.
Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.
Всего в контрольной работе было 25 вопросов.
Необходимо построить гистограмму по этому ряду распределения.
Решение
Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.
Интервальный вариационный ряд и его характеристики
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Общий вид интервального вариационного ряда
| Интервалы, (left.left[a_{i-1},a_iright.right)) | (left.left[a_{0},a_1right.right)) | (left.left[a_{1},a_2right.right)) | … | (left.left[a_{k-1},a_kright.right)) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k – число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).
Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg 100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала (left.left[a_{i-1},a_iright.right)) – это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) – середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
| (f_i) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| (S_i) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:
Построим кумуляту и эмпирическую функцию распределения:
Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$
п.3. Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) – соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).
Например:
Для распределения учеников по росту получаем:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
Для распределения учеников по росту получаем:
| $x_i$ | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
| (x_i^2w_i) – результат | 852,64 | 1660,12 | 2886,84 | 9826 | 10455,72 | 2767,68 | 1129,08 | 29578,08 |
$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$
п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.
Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
п.6. Алгоритм исследования интервального вариационного ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
| (f_i) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| (x_i) | 20 | 24 | 28 | 32 | 36 | ∑ |
| (f_i) | 1 | 7 | 12 | 6 | 4 | 30 |
| (w_i) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| (S_i) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | – |
| (x_iw_i) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| (x_i^2w_i) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.
5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).
Полигон частот и гистограмма частот
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Полигон частот
Пусть нам дан ряд распределения, записанный с помощью таблицы:
Рисунок 1.
Определение 1
Полигон частот — ломанная, которая соединяет точки $(x_m,n_m)$ ($m=1,2,dots ,m)$.
То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие частоты. Полученные точки соединяют ломанной:
Рисунок 2. Полигон частот.
Помимо обычной частоты существует еще понятие относительной частоты.
Получаем следующую таблицу распределения относительных частот:
Рисунок 3.
Определение 2
Полигон относительных частот — ломанная, которая соединяет точки $(x_m,W_m)$ ($m=1,2,dots ,m)$.
То есть, для построения полигона частот необходимо на оси абсцисс откладывают значения вариант, а по оси ординат соответствующие относительные частоты. Полученные точки соединяют ломанной:
Рисунок 4. Полигон относительных частот.
Гистограмма частот
Помимо понятия полинома для непрерывных значений существует понятие гистограммы.
Определение 3
Гистограмма частот — ступенчатая фигура, состоящая из прямоугольников с основанием — частичными интервалами длины $h$ и высотами $frac{n_i}{h}$:
Рисунок 5. Гистограмма частот.
«Полигон частот и гистограмма частот» 👇
Заметим, что площадь одного такого прямоугольника $frac{n_ih}{h}=n_i$. Следовательно, площадь всей фигуры равна $sum{n_i}=n$, то есть равна объему выборки.
Определение 4
Гистограмма относительных частот — ступенчатая фигура, состоящая из прямоугольников с основанием — частичными интервалами длины $h$ и высотами $frac{W_i}{h}$:
Рисунок 6. Гистограмма относительных частот.
Заметим, что площадь одного такого прямоугольника $frac{W_ih}{h}=W_i$. Следовательно, площадь всей фигуры равна $sum{W_i}=W=1$.
Примеры задачи на построение полигона и гистограммы
Пример 1
Пусть распределение частот имеет вид:
Рисунок 7.
Построить полигон относительных частот.
Решение.
Построим сначала ряд распределения относительных частот по формуле $W_i=frac{n_i}{n}$
Рисунок 8.
Получим следующий полигон относительных частот.
Рисунок 9.
Пример 2
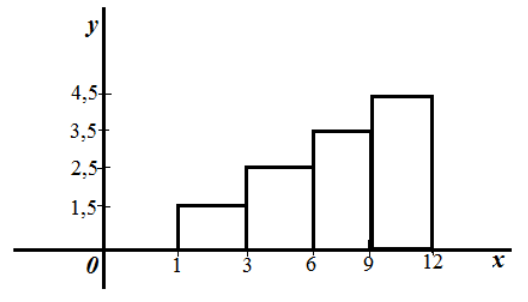
Дан ряд непрерывного распределения частот:
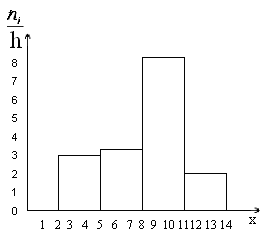
Рисунок 10.
Решение.
Очевидно, что данном случае длина частичного интервала $h=2.$ Найдем высоты прямоугольников каждой точки разбиения.
При $x=1$: $frac{3}{2}=1,5$.
При $x=3$: $frac{5}{2}=2,5.$
При $x=6$: $frac{7}{2}=3,5.$
При $x=9$: $frac{9}{2}=4,5.$
Получаем следующую гистограмму частот:
Рисунок 11.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 25.02.2023

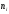
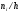
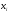
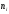
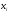
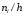
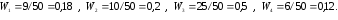
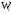
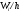
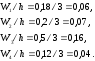
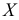
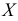
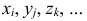
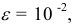 т.е. последняя сохраняемая цифра – вторая после запятой. Тогда
т.е. последняя сохраняемая цифра – вторая после запятой. Тогда 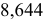
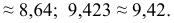
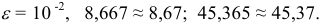
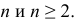
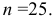

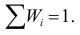

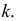
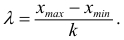
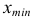 должно попасть примерно в середину первого классового интервала, поэтому нижняя граница
должно попасть примерно в середину первого классового интервала, поэтому нижняя граница 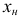 первого классового интервала будет
первого классового интервала будет 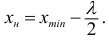 Прибавив к
Прибавив к 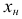 число
число 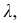 получим верхнюю границу первого классового интервала, затем найдем верхнюю границу второго классового интервала и т.д. до тех пор, пока не получим интервал, в который попадет
получим верхнюю границу первого классового интервала, затем найдем верхнюю границу второго классового интервала и т.д. до тех пор, пока не получим интервал, в который попадет 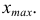
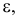 равную точности, принятой при измерении признака, для того, чтобы избежать момента, когда варианта совпадает с границей.
равную точности, принятой при измерении признака, для того, чтобы избежать момента, когда варианта совпадает с границей.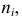 попавших в каждый интервал.
попавших в каждый интервал.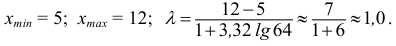

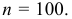
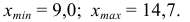
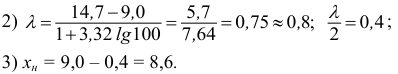
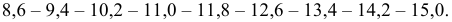
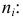

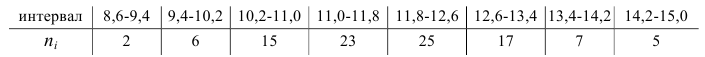


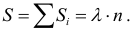
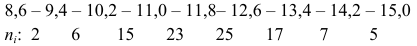
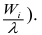


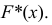
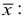
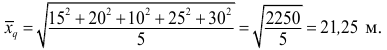
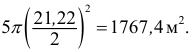
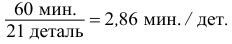
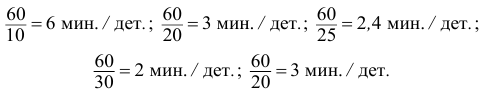
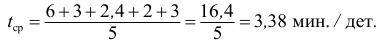
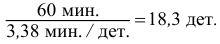
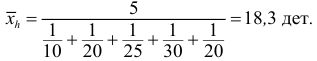
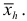
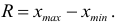
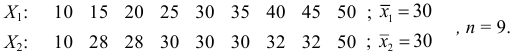
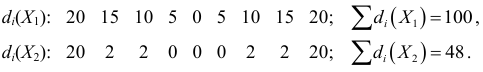
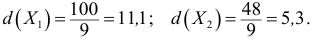
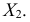
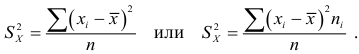
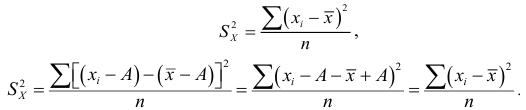
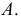
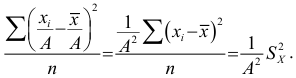
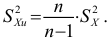
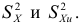
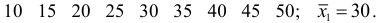
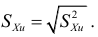
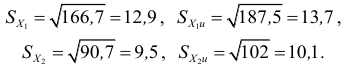
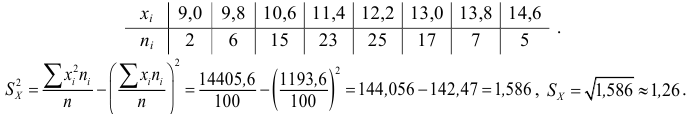
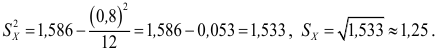
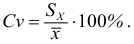
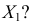
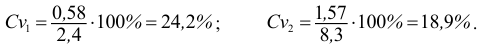
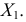
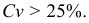
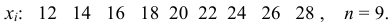
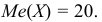
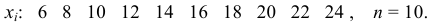
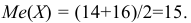
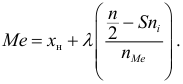
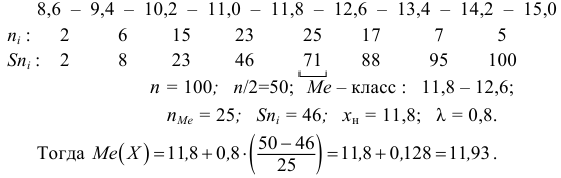
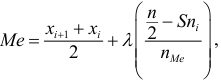
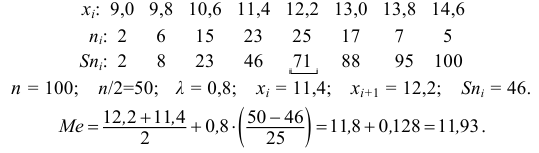
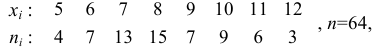
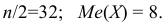
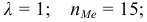
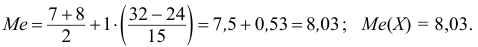
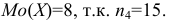
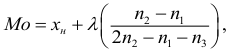
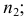
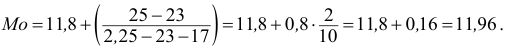
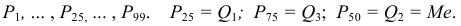
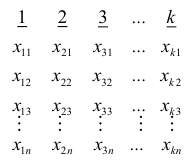
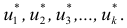
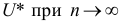 стремится по вероятности к оцениваемому параметру
стремится по вероятности к оцениваемому параметру 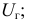
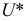 должна иметь наименьшую дисперсию по сравнению с другими аналогичными оценками. Например, для трех показателей, описывающих положение центра нормального распределения признака
должна иметь наименьшую дисперсию по сравнению с другими аналогичными оценками. Например, для трех показателей, описывающих положение центра нормального распределения признака 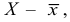
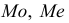 – наиболее эффективной будет оценка
– наиболее эффективной будет оценка 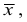 наименее эффективной –
наименее эффективной – 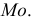 Для дисперсий этих оценок характерно неравенство
Для дисперсий этих оценок характерно неравенство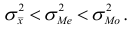
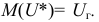 При соблюдении этого условия оценка не содержит систематических ошибок в сторону занижения или завышения.
При соблюдении этого условия оценка не содержит систематических ошибок в сторону занижения или завышения.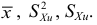
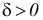
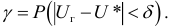
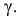
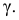
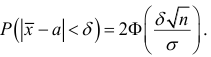
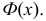
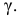
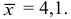
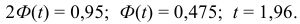
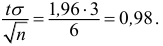
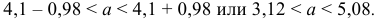
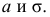
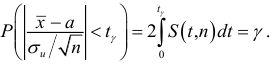
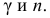
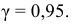
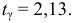
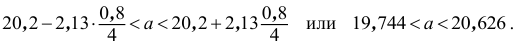
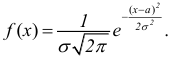
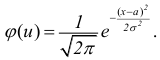
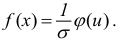
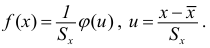
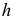
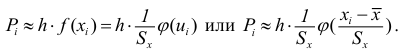
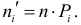
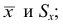
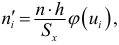
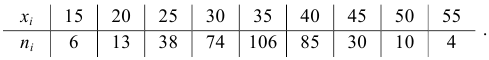
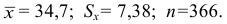
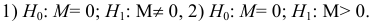
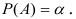
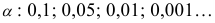
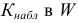 при условии справедливости
при условии справедливости 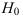 была равна
была равна 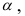 при минимальном
при минимальном 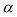
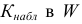 если справедлива
если справедлива 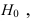 должна быть такой, что вероятность ошибки II рода, т.е.
должна быть такой, что вероятность ошибки II рода, т.е. 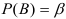 должна быть минимальной. Вероятность не допуска ошибки II рода
должна быть минимальной. Вероятность не допуска ошибки II рода 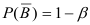 называется мощностью критерия
называется мощностью критерия 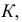 эта величина должна быть максимальной.
эта величина должна быть максимальной.