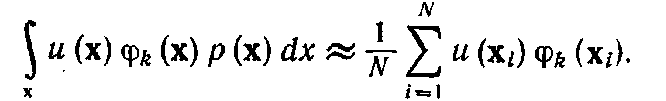Как найти полиномы лежандра - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 декабря 2021 года; проверки требуют 2 правки.

Многочлены Лежандра
Общая информация
Формула	$P_{n}(z)={frac {1}{2^{n}n!}}{frac {d^{n}}{dz^{n}}}(z^{2}-1)^{n}$
Скалярное произведение	${displaystyle (f,;g)=int limits _{-1}^{1}{f(x)g(x),dx}}$
Область определения
Дополнительные характеристики
Дифференциальное уравнение	$(1-z^{2}){frac {{mathrm d}^{2}u}{{mathrm d}z^{2}}}-2z{frac {{mathrm d}u}{{mathrm d}z}}+n(n+1)u=0$
Норма	${displaystyle \|P_{n}(x)\|={sqrt {frac {2}{2n+1}}}}$
Названы в честь	Лежандр, Адриен Мари

Многочлен Лежа́ндра — многочлен, который в наименьшей степени отклоняется от нуля в смысле среднего квадратического.
Образует ортогональную систему многочленов на отрезке [-1,;1] в пространстве $L^{2}$ .
Многочлены Лежандра могут быть получены из многочленов ${1,;x,;x^{2},;x^{3},;ldots }$ ортогонализацией Грама ― Шмидта.

Названы по имени французского математика Адриен Мари Лежандра.

Определение[править | править код]

Полиномы Лежандра и присоединённые функции Лежандра первого и второго рода[править | править код]

Рассмотрим дифференциальное уравнение вида

$(1-z^{2}){frac {{mathrm d}^{2}u}{{mathrm d}z^{2}}}-2z{frac {{mathrm d}u}{{mathrm d}z}}+n(n+1)u=0,$

(1)

где — комплексная переменная. Решения этого уравнения при целых имеют вид многочленов, называемых многочленами Лежандра. Полином Лежандра степени можно представить через формулу Родрига в виде^[1]

${displaystyle P_{n}(z)={frac {1}{2^{n}n!}}{frac {d^{n}}{dz^{n}}}(z^{2}-1)^{n}.}$

Часто вместо записывают косинус полярного угла:

${displaystyle P_{n}(cos theta )={frac {1}{2^{n}n!}}{frac {d^{n}}{d(cos theta )^{n}}}(cos ^{2}theta -1)^{n}.}$

Уравнение (1) можно получить из частного случая гипергеометрического уравнения, называемого уравнением Лежандра

$(1-z^{2}){frac {{mathrm d}^{2}u}{{mathrm d}z^{2}}}-2z{frac {{mathrm d}u}{{mathrm d}z}}+left[nu (nu +1)-{frac {mu ^{2}}{1-z^{2}}}right]u=0,$

(2)

где , — произвольные комплексные постоянные. Интерес представляют его решения, являющиеся однозначными и регулярными при |z|<1 (в частности, при действительных ) или когда действительная часть числа больше единицы. Его решения называют присоединёнными функциями Лежандра или сферическими функциями (гармониками). Подстановка вида $w=(z^{2}-1)^{{mu /2}}$ в (2) даёт уравнение Гаусса, решение которого в области |1-z|<2 принимает вид

${displaystyle w=P_{nu }^{mu }(z)={frac {1}{Gamma (1-mu )}}left({frac {z+1}{z-1}}right)^{mu /2}Fleft(-nu ,;nu +1;;1-mu ;;{frac {1}{2}}-{frac {z}{2}}right),}$

где — гипергеометрическая функция. Подстановка $w=z^{2}$ в (2) приводит к решению вида

${displaystyle w=Q_{nu }^{mu }(z)=e^{mu ipi }2^{-nu -1}{sqrt {pi }}{frac {Gamma (nu +mu +1)}{Gamma (nu +3/2)}}z^{-nu -mu -1}(z^{2}-1)^{mu /2}Fleft({frac {nu }{2}}+{frac {mu }{2}}+1,;{frac {nu }{2}}+{frac {mu }{2}}+{frac {1}{2}};;nu +{frac {3}{2}};;z^{-2}right),}$

определённым на |z|>1 . Функции $P_{nu }^{mu }(z)$ и $Q_{nu }^{mu }(z)$ называют функциями Лежандра первого и второго рода.^[2]

Справедливы соотношения^[3]

$P_{nu }^{mu }(z)=P_{{-nu -1}}^{mu }(z)$

$Q_{nu }^{mu }(z)sin pi (nu +mu )-Q_{{-nu -1}}^{mu }(z)sin pi (nu -mu )=pi e^{{imu pi }}cos(nu pi )P_{nu }^{mu }(z).$

Выражение через суммы[править | править код]

Многочлены Лежандра также определяются по следующей формуле:

${displaystyle P_{n}(x)={frac {1}{2^{n}}}sum _{k=0}^{E(n/2)}(-1)^{k}{binom {n}{k}}{binom {2n-2k}{n}}x^{n-2k}.}$

Рекуррентная формула[править | править код]

Они также могут быть вычислены по рекуррентной формуле (при )^[4]:

${displaystyle P_{n+1}(x)={frac {2n+1}{n+1}}xP_{n}(x)-{frac {n}{n+1}}P_{n-1}(x),}$

(3)

причём первые две функции имеют вид

${displaystyle P_{0}(x)=1,}$

${displaystyle P_{1}(x)=x.}$

Производная полинома Лежандра[править | править код]

Вычисляется по формуле^[5]

${displaystyle P'_{n}(x)={frac {n}{1-x^{2}}}[P_{n-1}(x)-xP_{n}(x)].}$

(4)

Корни полинома Лежандра[править | править код]

Вычисляются итеративно по методу Ньютона^[5]:

${displaystyle x_{i}^{(k+1)}=x_{i}^{(k)}-{frac {P_{n}(x_{i}^{(k)})}{P'_{n}(x_{i}^{(k)})}},}$

причём начальное приближение для -го корня () берётся по формуле^[5]

${displaystyle x_{i}^{(0)}=cos {frac {pi (4i-1)}{4n+2}}.}$

Значение полинома можно вычислять, используя рекуррентную формулу для конкретного значения x.
Производную также можно вычислять для конкретного значения x, используя формулу для производной.

Формулы с разложениями[править | править код]

Многочлены Лежандра также определяются следующими разложениями:

${displaystyle (1-2tx+t^{2})^{-{frac {1}{2}}}=sum _{n=0}^{infty }P_{n}(x)t^{n}}$

для ${displaystyle |t|<min left|xpm {sqrt {x^{2}-1}}right|,}$

${displaystyle (1-2tx+t^{2})^{-{frac {1}{2}}}=sum _{n=0}^{infty }P_{n}(x){frac {1}{t^{n+1}}}}$

для ${displaystyle |t|>max left|xpm {sqrt {x^{2}-1}}right|.}$

Следовательно,

${displaystyle P_{n}(x)={frac {(2n)!}{2^{n}(n!)^{2}}}left[x^{n}-{frac {n(n-1)}{2(2n-1)}}x^{n-2}+{frac {n(n-1)(n-2)(n-3)}{2cdot 4(2n-1)(2n-3)}}x^{n-4}-ldots right].}$

Присоединённые многочлены Лежандра[править | править код]

Присоединённые многочлены Лежандра определяются по формуле

${displaystyle P_{n}^{m}(x)=(1-x^{2})^{m/2}{frac {d^{m}}{dx^{m}}}P_{n}(x),}$

которую также можно представить в виде

${displaystyle P_{n}^{m}(cos theta )=sin ^{m}theta {frac {d^{m}}{d(cos theta )^{m}}}P_{n}(cos theta ).}$

При m=0 функция $P_{n}^{m}$ совпадает с $P_{n}$ .

Нормировка по правилу Шмидта[править | править код]

Нормированные по правилу Шмидта полиномы Лежандра выглядят следующим образом^[6]:

${displaystyle SP_{n}^{0}(x)=P_{n}^{0}(x),}$

${displaystyle SP_{n}^{m}(x)=(-1)^{m}left({frac {2(n-m)!}{(n+m)!}}right)^{1/2}P_{n}^{m}(x).}$

Сдвинутые многочлены Лежандра[править | править код]

Сдвинутые многочлены Лежандра определяются как ${displaystyle {tilde {P_{n}}}(x)=P_{n}(2x-1)}$ , где сдвигающая функция (это аффинное преобразование) выбрана так, чтобы однозначно отображать интервал ортогональности многочленов на интервал , в котором уже ортогональны сдвинутые многочлены ${tilde {P_{n}}}(x)$ :

${displaystyle int nolimits _{0}^{1}{tilde {P_{m}}}(x){tilde {P_{n}}}(x),dx={frac {1}{2n+1}}delta _{mn}.}$

Явное выражение для смещённых многочленов Лежандра задаётся как

${displaystyle {tilde {P_{n}}}(x)=(-1)^{n}sum _{k=0}^{n}{binom {n}{k}}{binom {n+k}{k}}(-x)^{k}.}$

Аналогом формулы Родрига для смещенных многочленов Лежандра является

${displaystyle {tilde {P_{n}}}(x)={frac {1}{n!}}{frac {d^{n}}{dx^{n}}}left[(x^{2}-x)^{n}right].}$

Выражения для некоторых первых сдвинутых многочленов Лежандра:

n	${tilde {P_{n}}}(x)$
0
1
2	${displaystyle 6x^{2}-6x+1}$
3	${displaystyle 20x^{3}-30x^{2}+12x-1}$
4	${displaystyle 70x^{4}-140x^{3}+90x^{2}-20x+1}$

Матрица функции многочлена Лежандра[править | править код]

${displaystyle {begin{pmatrix}0&0&-2&0&0&vdots &0&vdots &0\0&2&0&-6&0&vdots &0&vdots &vdots \0&0&6&0&-12&vdots &0&vdots &vdots \0&0&0&12&0&vdots &0&vdots &vdots \0&0&0&0&20&vdots &0&vdots &vdots \dots &dots &dots &dots &dots &ddots &vdots &dots &vdots \0&0&0&0&0&dots &k(k+1)&dots &vdots \dots &dots &dots &dots &dots &dots &dots &ddots &vdots \0&0&0&0&0&dots &0&dots &n(n+1)\end{pmatrix}}}$

Эта матрица является верхнетреугольной. Её определитель равен нулю, а собственные значения равны , где .

Примеры[править | править код]

Первые 6 многочленов Лежандра

Первые многочлены Лежандра в явном виде:

${displaystyle P_{0}(x)=1,}$

${displaystyle P_{1}(x)=x,}$

${displaystyle P_{2}(x)={frac {1}{2}}(3x^{2}-1),}$

${displaystyle P_{3}(x)={frac {1}{2}}(5x^{3}-3x),}$

${displaystyle P_{4}(x)={frac {1}{8}}(35x^{4}-30x^{2}+3),}$

${displaystyle P_{5}(x)={frac {1}{8}}(63x^{5}-70x^{3}+15x),}$

${displaystyle P_{6}(x)={frac {1}{16}}(231x^{6}-315x^{4}+105x^{2}-5),}$

${displaystyle P_{7}(x)={frac {1}{16}}(429x^{7}-693x^{5}+315x^{3}-35x),}$

${displaystyle P_{8}(x)={frac {1}{128}}(6435x^{8}-12,012x^{6}+6930x^{4}-1260x^{2}+35),}$

${displaystyle P_{9}(x)={frac {1}{128}}(12,155x^{9}-25,740x^{7}+18,018x^{5}-4620x^{3}+315x),}$

${displaystyle P_{10}(x)={frac {1}{256}}(46,189x^{10}-109,395x^{8}+90,090x^{6}-30,030x^{4}+3465x^{2}-63),}$

${displaystyle P_{11}(x)={frac {1}{256}}(88,179x^{11}-230,945x^{9}+218,790x^{7}-90,090x^{5}+15,015x^{3}-693x),}$

${displaystyle P_{12}(x)={frac {1}{1024}}(676,039x^{12}-1,939,938x^{10}+2,078,505x^{8}-1,021,020x^{6}+225,225x^{4}-18,018x^{2}+231),}$

${displaystyle P_{13}(x)={frac {1}{1024}}(1,300,075x^{13}-4,056,234x^{11}+4,849,845x^{9}-2,771,340x^{7}+765,765x^{5}-90,090x^{3}+3003x),}$

${displaystyle P_{14}(x)={frac {1}{2048}}(5,014,575x^{14}-16,900,975x^{12}+22,309,287x^{10}-14,549,535x^{8}+4,849,845x^{6}-765,765x^{4}+45,045x^{2}-429),}$

${displaystyle P_{15}(x)={frac {1}{2048}}(9,694,845x^{15}-35,102,025x^{13}+50,702,925x^{11}-37,182,145x^{9}+14,549,535x^{7}-2,909,907x^{5}+255,255x^{3}-6435x),}$

${displaystyle P_{16}(x)={frac {1}{32768}}(300540195x^{16}-1163381400x^{14}+1825305300x^{12}-1487285800x^{10}+669278610x^{8}-162954792x^{6}+19399380x^{4}-875160x^{2}+6435),}$

${displaystyle P_{17}(x)={frac {1}{32768}}(583,401,555x^{17}-2,404,321,560x^{15}+4,071,834,900x^{13}-3,650,610,600x^{11}+1,859,107,250x^{9}-535,422,888x^{7}+81,477,396x^{5}-5,542,680x^{3}+109,395x).}$

Поскольку ${displaystyle P_{n}(1)=1}$ , то

${displaystyle P_{n}(x)={frac {lambda _{0}+lambda _{1}x+lambda _{2}x^{2}+ldots +lambda _{n}x^{n}}{lambda _{0}+lambda _{1}+ldots +lambda _{n}}}={frac {sum limits _{i=0}^{n}lambda _{i}x^{i}}{sum limits _{i=0}^{n}lambda _{i}}}.}$

Свойства[править | править код]

При

уравнение принимает вид

${displaystyle P'_{n+1}(x)=xP'_{n}(x)+(n+1)P_{n}(x).}$

где $delta _{{kl}}$

— символ Кронекера.

Ряды многочленов Лежандра[править | править код]

Разложение липшицевой функции в ряд многочленов Лежандра[править | править код]

Липшицевая функция является функцией со свойством

{displaystyle |f(x)-f(y)|leqslant L|x-y|}

, где

Эта функция разлагается в ряд многочленов Лежандра.

Пусть — пространство непрерывных отображений на отрезке , , и .

Пусть

${displaystyle c_{n}(f)=int limits _{-1}^{1}f(x){tilde {P}}_{n}(x),dx,}$

тогда ${displaystyle c_{n}(f)}$ удовлетворяет следующему условию:

${displaystyle lim _{nto infty }c_{n}(f)=0.}$

Пусть ${displaystyle S_{n}f=sum _{k=0}^{n}c_{k}(f){tilde {P}}_{k}}$ и ${displaystyle S_{n}f}$ удовлетворяет следующим условиям:

${displaystyle forall xin Iquad S_{n}f(x)=int limits _{-1}^{1}K_{n}(x,;y)f(y),dy}$ , где ${displaystyle K_{n}(x,;y)={frac {n+1}{2}}{frac {P_{n+1}(x)P_{n}(y)-P_{n+1}(y)P_{n}(x)}{x-y}};}$
${displaystyle S_{n}f(x)-f(x)=int limits _{-1}^{1}K_{n}(x,;y){big (}f(y)-f(x){big )},dy;}$
${displaystyle forall xin [-1,1]quad lim _{nto infty }S_{n}f(x)=f(x).}$

Липшицеву функцию можно записать следующим образом:

${displaystyle f=sum _{n=0}^{infty }c_{n}(f){tilde {P}}_{n}.}$

Разложение голоморфной функции[править | править код]

Всякая функция , голоморфная внутри эллипса с фокусами −1 и +1, может быть представлена в виде ряда:

${displaystyle f(x)=sum _{n=0}^{infty }lambda _{n}P_{n}(x).}$

Теорема сложения[править | править код]

Для величин, удовлетворяющих условиям ${displaystyle 0leqslant psi _{1}<pi }$ , ${displaystyle 0leqslant psi _{2}<pi }$ , $psi _{1}+psi _{2}<pi$ , varphi — действительное число, можно записать теорему сложения для полиномов Лежандра первого рода:^[7]

${displaystyle P_{k}(cos psi _{1}cos psi _{2}+sin psi _{1}sin psi _{2}cos varphi )=P_{k}(cos psi _{1})P_{k}(cos psi _{2})+2sum limits _{m=1}^{infty }(-1)^{m}P_{k}^{-m}(cos psi _{1})P_{k}^{m}(cos psi _{2})cos mvarphi ,}$

или, в альтернативной форме через гамма-функцию:

${displaystyle P_{k}(cos psi _{1}cos psi _{2}+sin psi _{1}sin psi _{2}cos varphi )=P_{k}(cos psi _{1})P_{k}(cos psi _{2})+2sum limits _{m=1}^{infty }{frac {Gamma (k-m+1)}{Gamma (k+m+1)}}P_{k}^{m}(cos psi _{1})P_{k}^{m}(cos psi _{2})cos mvarphi .}$

Для полиномов Лежандра второго рода теорема сложения выглядит как^[8]

${displaystyle Q_{k}(cos psi _{1}cos psi _{2}+sin psi _{1}sin psi _{2}cos varphi )=P_{k}(cos psi _{1})Q_{k}(cos psi _{2})+2sum limits _{m=1}^{infty }(-1)^{m}P_{k}^{-m}(cos psi _{1})Q_{k}^{m}(cos psi _{2})cos mvarphi }$

при условиях ${displaystyle 0leqslant psi _{1}<pi /2}$ , ${displaystyle 0leqslant psi _{2}<pi }$ , $psi _{1}+psi _{2}<pi$ , varphi .

Функции Лежандра[править | править код]

Многочлены Лежандра (вместе с присоединёнными функциями Лежандра $P_{{n,;m}}(x)$ ) естественно возникают в теории потенциала.

Шаровые функции — это функции (в сферических координатах ) вида (с точностью до константы)

${displaystyle r^{n}P_{n}^{m}(cos theta )cos mvarphi }$

и ${displaystyle r^{n}P_{n}^{m}(cos theta )sin mvarphi ,}$

где $P_{n}^{m}$ — присоединённые многочлены Лежандра.
Они также представимы в виде ${displaystyle r^{n}Y_{nm}}$ , где ${displaystyle Y_{nm}}$ — сферические функции.

Шаровые функции удовлетворяют уравнению Лапласа всюду в $mathbb {R} ^{3}$ .

Примечания[править | править код]

↑ Градштейн, Рыжик, 1963, с. 1039.
↑ Бейтмен, Эрдейи, Т. 1, 1973, с. 126—127.
↑ Бейтмен, Эрдейи, Т. 1, 1973, с. 140.
↑ Цимринг, 1988, с. 196.
↑ ¹ ² ³ Цимринг, 1988, с. 197.
↑ John W. Eaton, David Bateman, Søren Hauberg, Rik Wehbring. GNU Octave. — Edition 4 for Octave version 4.4.1. — 2018. — С. 530—531.
↑ Градштейн, Рыжик, 1963, с. 1027.
↑ Градштейн, Рыжик, 1963, с. 1028.

Литература[править | править код]

Бейтмен Г., Эрдейи А. Высшие трансцендентные функции = Higher Transcendental Functions / Пер. Н. Я. Виленкина. — Изд. 2-е,. — М.: Наука, 1973. — Т. 1. — 296 с. — 14 000 экз.
Владимиров В. С., Жаринов В. В. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5.
Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. — Изд. 4-е, перераб. — М.: Государственное издательство физико-математической литературы, 1963. — 19 000 экз.
Кампе де Ферье Ж., Кемпбелл Р., Петьо Г., Фогель Т. Функции математической физики. — М.: Физматлит, 1963.
Никольский С. М. Квадратурные формулы. — М.: Наука, 1988.
Цимринг Ш. Е. Специальные функции и определенные интегралы. Алгоритмы. Программы для микрокалькуляторов: Справочник. — М.: Радио и связь, 1988.

Ссылки[править | править код]

Legendre Polynomials — University of Rochester, 2010.

Источник

The first six Legendre polynomials

In mathematics, Legendre polynomials, named after Adrien-Marie Legendre (1782), are a system of complete and orthogonal polynomials with a vast number of mathematical properties and numerous applications. They can be defined in many ways, and the various definitions highlight different aspects as well as suggest generalizations and connections to different mathematical structures and physical and numerical applications.

Closely related to the Legendre polynomials are associated Legendre polynomials, Legendre functions, Legendre functions of the second kind, and associated Legendre functions.

Definition by construction as an orthogonal system[edit]

In this approach, the polynomials are defined as an orthogonal system with respect to the weight function w(x)=1 over the interval . That is, P_n(x) is a polynomial of degree , such that

${displaystyle int _{-1}^{1}P_{m}(x)P_{n}(x),dx=0quad {text{if }}nneq m.}$

With the additional standardization condition ${displaystyle P_{n}(1)=1}$ , all the polynomials can be uniquely determined. We then start the construction process: ${displaystyle P_{0}(x)=1}$ is the only correctly standardized polynomial of degree 0. $P_{1}(x)$ must be orthogonal to $P_{0}$ , leading to ${displaystyle P_{1}(x)=x}$ , and $P_{2}(x)$ is determined by demanding orthogonality to $P_{0}$ and $P_{1}$ , and so on. $P_{n}$ is fixed by demanding orthogonality to all P_m with m < n . This gives conditions, which, along with the standardization ${displaystyle P_{n}(1)=1}$ fixes all coefficients in ${displaystyle P_{n}(x)}$ . With work, all the coefficients of every polynomial can be systematically determined, leading to the explicit representation in powers of given below.

This definition of the $P_{n}$ ‘s is the simplest one. It does not appeal to the theory of differential equations. Second, the completeness of the polynomials follows immediately from the completeness of the powers 1, ${displaystyle x,x^{2},x^{3},ldots }$ . Finally, by defining them via orthogonality with respect to the most obvious weight function on a finite interval, it sets up the Legendre polynomials as one of the three classical orthogonal polynomial systems. The other two are the Laguerre polynomials, which are orthogonal over the half line , and the Hermite polynomials, orthogonal over the full line , with weight functions that are the most natural analytic functions that ensure convergence of all integrals.

Definition via generating function[edit]

The Legendre polynomials can also be defined as the coefficients in a formal expansion in powers of of the generating function^[1]

${displaystyle {frac {1}{sqrt {1-2xt+t^{2}}}}=sum _{n=0}^{infty }P_{n}(x)t^{n},.}$

(2)

The coefficient of $t^{n}$ is a polynomial in of degree with . Expanding up to ${displaystyle t^{1}}$ gives

${displaystyle P_{0}(x)=1,,quad P_{1}(x)=x.}$

Expansion to higher orders gets increasingly cumbersome, but is possible to do systematically, and again leads to one of the explicit forms given below.

It is possible to obtain the higher $P_{n}$ ‘s without resorting to direct expansion of the Taylor series, however. Equation 2 is differentiated with respect to t on both sides and rearranged to obtain

${displaystyle {frac {x-t}{sqrt {1-2xt+t^{2}}}}=left(1-2xt+t^{2}right)sum _{n=1}^{infty }nP_{n}(x)t^{n-1},.}$

Replacing the quotient of the square root with its definition in Eq. 2, and equating the coefficients of powers of t in the resulting expansion gives Bonnet’s recursion formula

${displaystyle (n+1)P_{n+1}(x)=(2n+1)xP_{n}(x)-nP_{n-1}(x),.}$

This relation, along with the first two polynomials P₀ and P₁, allows all the rest to be generated recursively.

The generating function approach is directly connected to the multipole expansion in electrostatics, as explained below, and is how the polynomials were first defined by Legendre in 1782.

Definition via differential equation[edit]

A third definition is in terms of solutions to Legendre’s differential equation:

${displaystyle (1-x^{2})P_{n}''(x)-2xP_{n}'(x)+n(n+1)P_{n}(x)=0.}$

(1)

This differential equation has regular singular points at x = ±1 so if a solution is sought using the standard Frobenius or power series method, a series about the origin will only converge for |x| < 1 in general. When n is an integer, the solution P_n(x) that is regular at x = 1 is also regular at x = −1, and the series for this solution terminates (i.e. it is a polynomial). The orthogonality and completeness of these solutions is best seen from the viewpoint of Sturm–Liouville theory. We rewrite the differential equation as an eigenvalue problem,

${displaystyle {frac {d}{dx}}left(left(1-x^{2}right){frac {d}{dx}}right)P(x)=-lambda P(x),,}$

with the eigenvalue lambda in lieu of . If we demand that the solution be regular at
x=pm 1 , the differential operator on the left is Hermitian. The eigenvalues are found to be of the form
n(n + 1), with and the eigenfunctions are the P_n(x) . The orthogonality and completeness of this set of solutions follows at once from the larger framework of Sturm–Liouville theory.

The differential equation admits another, non-polynomial solution, the Legendre functions of the second kind $Q_{n}$ .
A two-parameter generalization of (Eq. 1) is called Legendre’s general differential equation, solved by the Associated Legendre polynomials. Legendre functions are solutions of Legendre’s differential equation (generalized or not) with non-integer parameters.

In physical settings, Legendre’s differential equation arises naturally whenever one solves Laplace’s equation (and related partial differential equations) by separation of variables in spherical coordinates. From this standpoint, the eigenfunctions of the angular part of the Laplacian operator are the spherical harmonics, of which the Legendre polynomials are (up to a multiplicative constant) the subset that is left invariant by rotations about the polar axis. The polynomials appear as $P_{n}(cos theta )$ where theta is the polar angle. This approach to the Legendre polynomials provides a deep connection to rotational symmetry. Many of their properties which are found laboriously through the methods of analysis — for example the addition theorem — are more easily found using the methods of symmetry and group theory, and acquire profound physical and geometrical meaning.

Orthogonality and completeness[edit]

The standardization ${displaystyle P_{n}(1)=1}$ fixes the normalization of the Legendre polynomials (with respect to the L² norm on the interval −1 ≤ x ≤ 1). Since they are also orthogonal with respect to the same norm, the two statements^{[clarification needed]} can be combined into the single equation,

${displaystyle int _{-1}^{1}P_{m}(x)P_{n}(x),dx={frac {2}{2n+1}}delta _{mn},}$

(where δ_mn denotes the Kronecker delta, equal to 1 if m = n and to 0 otherwise).
This normalization is most readily found by employing Rodrigues’ formula, given below.

That the polynomials are complete means the following. Given any piecewise continuous function f(x) with finitely many discontinuities in the interval [−1, 1], the sequence of sums

${displaystyle f_{n}(x)=sum _{ell =0}^{n}a_{ell }P_{ell }(x)}$

converges in the mean to f(x) as , provided we take

${displaystyle a_{ell }={frac {2ell +1}{2}}int _{-1}^{1}f(x)P_{ell }(x),dx.}$

This completeness property underlies all the expansions discussed in this article, and is often stated in the form

${displaystyle sum _{ell =0}^{infty }{frac {2ell +1}{2}}P_{ell }(x)P_{ell }(y)=delta (x-y),}$

with −1 ≤ x ≤ 1 and −1 ≤ y ≤ 1.

Rodrigues’ formula and other explicit formulas[edit]

An especially compact expression for the Legendre polynomials is given by Rodrigues’ formula:

${displaystyle P_{n}(x)={frac {1}{2^{n}n!}}{frac {d^{n}}{dx^{n}}}(x^{2}-1)^{n},.}$

This formula enables derivation of a large number of properties of the $P_{n}$ ‘s. Among these are explicit representations such as

${displaystyle {begin{aligned}P_{n}(x)&={frac {1}{2^{n}}}sum _{k=0}^{n}{binom {n}{k}}^{2}(x-1)^{n-k}(x+1)^{k},\P_{n}(x)&=sum _{k=0}^{n}{binom {n}{k}}{binom {n+k}{k}}left({frac {x-1}{2}}right)^{k},\P_{n}(x)&={frac {1}{2^{n}}}sum _{k=0}^{leftlfloor {frac {n}{2}}rightrfloor }(-1)^{k}{binom {n}{k}}{binom {2n-2k}{n}}x^{n-2k},\P_{n}(x)&=2^{n}sum _{k=0}^{n}x^{k}{binom {n}{k}}{binom {frac {n+k-1}{2}}{n}}.end{aligned}}}$

In the third representation, ⌊n/2⌋ stands for the largest integer less than or equal to n/2. The last representation, which is also immediate from the recursion formula, expresses the Legendre polynomials by simple monomials and involves the generalized form of the binomial coefficient.

The first few Legendre polynomials are:


0
1
2	${textstyle {tfrac {1}{2}}left(3x^{2}-1right)}$
3	${textstyle {tfrac {1}{2}}left(5x^{3}-3xright)}$
4	${textstyle {tfrac {1}{8}}left(35x^{4}-30x^{2}+3right)}$
5	${textstyle {tfrac {1}{8}}left(63x^{5}-70x^{3}+15xright)}$
6	${textstyle {tfrac {1}{16}}left(231x^{6}-315x^{4}+105x^{2}-5right)}$
7	${textstyle {tfrac {1}{16}}left(429x^{7}-693x^{5}+315x^{3}-35xright)}$
8	${textstyle {tfrac {1}{128}}left(6435x^{8}-12012x^{6}+6930x^{4}-1260x^{2}+35right)}$
9	${textstyle {tfrac {1}{128}}left(12155x^{9}-25740x^{7}+18018x^{5}-4620x^{3}+315xright)}$
10	${textstyle {tfrac {1}{256}}left(46189x^{10}-109395x^{8}+90090x^{6}-30030x^{4}+3465x^{2}-63right)}$

The graphs of these polynomials (up to n = 5) are shown below:

Applications of Legendre polynomials[edit]

Expanding a 1/r potential[edit]

The Legendre polynomials were first introduced in 1782 by Adrien-Marie Legendre^[2] as the coefficients in the expansion of the Newtonian potential

${displaystyle {frac {1}{left|mathbf {x} -mathbf {x} 'right|}}={frac {1}{sqrt {r^{2}+{r'}^{2}-2r{r'}cos gamma }}}=sum _{ell =0}^{infty }{frac {{r'}^{ell }}{r^{ell +1}}}P_{ell }(cos gamma ),}$

where r and r′ are the lengths of the vectors x and x′ respectively and γ is the angle between those two vectors. The series converges when r > r′. The expression gives the gravitational potential associated to a point mass or the Coulomb potential associated to a point charge. The expansion using Legendre polynomials might be useful, for instance, when integrating this expression over a continuous mass or charge distribution.

Legendre polynomials occur in the solution of Laplace’s equation of the static potential, ∇² Φ(x) = 0, in a charge-free region of space, using the method of separation of variables, where the boundary conditions have axial symmetry (no dependence on an azimuthal angle). Where ẑ is the axis of symmetry and θ is the angle between the position of the observer and the ẑ axis (the zenith angle), the solution for the potential will be

${displaystyle Phi (r,theta )=sum _{ell =0}^{infty }left(A_{ell }r^{ell }+B_{ell }r^{-(ell +1)}right)P_{ell }(cos theta ),.}$

A_l and B_l are to be determined according to the boundary condition of each problem.^[3]

They also appear when solving the Schrödinger equation in three dimensions for a central force.

Legendre polynomials in multipole expansions[edit]

Legendre polynomials are also useful in expanding functions of the form (this is the same as before, written a little differently):

${displaystyle {frac {1}{sqrt {1+eta ^{2}-2eta x}}}=sum _{k=0}^{infty }eta ^{k}P_{k}(x),}$

which arise naturally in multipole expansions. The left-hand side of the equation is the generating function for the Legendre polynomials.

As an example, the electric potential Φ(r,θ) (in spherical coordinates) due to a point charge located on the z-axis at z = a (see diagram right) varies as

${displaystyle Phi (r,theta )propto {frac {1}{R}}={frac {1}{sqrt {r^{2}+a^{2}-2arcos theta }}}.}$

If the radius r of the observation point P is greater than a, the potential may be expanded in the Legendre polynomials

${displaystyle Phi (r,theta )propto {frac {1}{r}}sum _{k=0}^{infty }left({frac {a}{r}}right)^{k}P_{k}(cos theta ),}$

where we have defined η = a/r < 1 and x = cos θ. This expansion is used to develop the normal multipole expansion.

Conversely, if the radius r of the observation point P is smaller than a, the potential may still be expanded in the Legendre polynomials as above, but with a and r exchanged. This expansion is the basis of interior multipole expansion.

Legendre polynomials in trigonometry[edit]

The trigonometric functions cos nθ, also denoted as the Chebyshev polynomials T_n(cos θ) ≡ cos nθ, can also be multipole expanded by the Legendre polynomials P_n(cos θ). The first several orders are as follows:

${displaystyle {begin{aligned}T_{0}(cos theta )&=1&&=P_{0}(cos theta ),\[4pt]T_{1}(cos theta )&=cos theta &&=P_{1}(cos theta ),\[4pt]T_{2}(cos theta )&=cos 2theta &&={tfrac {1}{3}}{bigl (}4P_{2}(cos theta )-P_{0}(cos theta ){bigr )},\[4pt]T_{3}(cos theta )&=cos 3theta &&={tfrac {1}{5}}{bigl (}8P_{3}(cos theta )-3P_{1}(cos theta ){bigr )},\[4pt]T_{4}(cos theta )&=cos 4theta &&={tfrac {1}{105}}{bigl (}192P_{4}(cos theta )-80P_{2}(cos theta )-7P_{0}(cos theta ){bigr )},\[4pt]T_{5}(cos theta )&=cos 5theta &&={tfrac {1}{63}}{bigl (}128P_{5}(cos theta )-56P_{3}(cos theta )-9P_{1}(cos theta ){bigr )},\[4pt]T_{6}(cos theta )&=cos 6theta &&={tfrac {1}{1155}}{bigl (}2560P_{6}(cos theta )-1152P_{4}(cos theta )-220P_{2}(cos theta )-33P_{0}(cos theta ){bigr )}.end{aligned}}}$

Another property is the expression for sin (n + 1)θ, which is

${displaystyle {frac {sin(n+1)theta }{sin theta }}=sum _{ell =0}^{n}P_{ell }(cos theta )P_{n-ell }(cos theta ).}$

Legendre polynomials in recurrent neural networks[edit]

A recurrent neural network that contains a d-dimensional memory vector, ${displaystyle mathbf {m} in mathbb {R} ^{d}}$ , can be optimized such that its neural activities obey the linear time-invariant system given by the following state-space representation:

${displaystyle {begin{aligned}A&=left[aright]_{ij}in mathbb {R} ^{dtimes d}{text{,}}quad &&a_{ij}=left(2i+1right){begin{cases}-1&i<j\(-1)^{i-j+1}&igeq jend{cases}},\B&=left[bright]_{i}in mathbb {R} ^{dtimes 1}{text{,}}quad &&b_{i}=(2i+1)(-1)^{i}.end{aligned}}}$

In this case, the sliding window of across the past theta units of time is best approximated by a linear combination of the first shifted Legendre polynomials, weighted together by the elements of at time :

${displaystyle u(t-theta ')approx sum _{ell =0}^{d-1}{widetilde {P}}_{ell }left({frac {theta '}{theta }}right),m_{ell }(t),quad 0leq theta 'leq theta .}$

When combined with deep learning methods, these networks can be trained to outperform long short-term memory units and related architectures, while using fewer computational resources.^[4]

Additional properties of Legendre polynomials[edit]

Legendre polynomials have definite parity. That is, they are even or odd,^[5] according to

${displaystyle P_{n}(-x)=(-1)^{n}P_{n}(x),.}$

Another useful property is

${displaystyle int _{-1}^{1}P_{n}(x),dx=0{text{ for }}ngeq 1,}$

which follows from considering the orthogonality relation with ${displaystyle P_{0}(x)=1}$ . It is convenient when a Legendre series ${textstyle sum _{i}a_{i}P_{i}}$ is used to approximate a function or experimental data: the average of the series over the interval [−1, 1] is simply given by the leading expansion coefficient $a_{0}$ .

Since the differential equation and the orthogonality property are independent of scaling, the Legendre polynomials’ definitions are “standardized” (sometimes called “normalization”, but the actual norm is not 1) by being scaled so that

${displaystyle P_{n}(1)=1,.}$

The derivative at the end point is given by

${displaystyle P_{n}'(1)={frac {n(n+1)}{2}},.}$

The Askey–Gasper inequality for Legendre polynomials reads

${displaystyle sum _{j=0}^{n}P_{j}(x)geq 0quad {text{for }}quad xgeq -1,.}$

The Legendre polynomials of a scalar product of unit vectors can be expanded with spherical harmonics using

${displaystyle P_{ell }left(rcdot r'right)={frac {4pi }{2ell +1}}sum _{m=-ell }^{ell }Y_{ell m}(theta ,varphi )Y_{ell m}^{*}(theta ',varphi '),,}$

where the unit vectors r and r′ have spherical coordinates (θ, φ) and (θ′, φ′), respectively.

Recurrence relations[edit]

As discussed above, the Legendre polynomials obey the three-term recurrence relation known as Bonnet’s recursion formula given by

${displaystyle (n+1)P_{n+1}(x)=(2n+1)xP_{n}(x)-nP_{n-1}(x)}$

and

${displaystyle {frac {x^{2}-1}{n}}{frac {d}{dx}}P_{n}(x)=xP_{n}(x)-P_{n-1}(x)}$

or, with the alternative expression, which also holds at the endpoints

${displaystyle {frac {d}{dx}}P_{n+1}(x)=(n+1)P_{n}(x)+x{frac {d}{dx}}P_{n}(x),.}$

Useful for the integration of Legendre polynomials is

${displaystyle (2n+1)P_{n}(x)={frac {d}{dx}}{bigl (}P_{n+1}(x)-P_{n-1}(x){bigr )},.}$

From the above one can see also that

${displaystyle {frac {d}{dx}}P_{n+1}(x)=(2n+1)P_{n}(x)+{bigl (}2(n-2)+1{bigr )}P_{n-2}(x)+{bigl (}2(n-4)+1{bigr )}P_{n-4}(x)+cdots }$

or equivalently

${displaystyle {frac {d}{dx}}P_{n+1}(x)={frac {2P_{n}(x)}{left|P_{n}right|^{2}}}+{frac {2P_{n-2}(x)}{left|P_{n-2}right|^{2}}}+cdots }$

where ‖P_n‖ is the norm over the interval −1 ≤ x ≤ 1

${displaystyle |P_{n}|={sqrt {int _{-1}^{1}{bigl (}P_{n}(x){bigr )}^{2},dx}}={sqrt {frac {2}{2n+1}}},.}$

Asymptotics[edit]

Asymptotically, for , the Legendre polynomials can be written as ^[6]

${displaystyle {begin{aligned}P_{ell }(cos theta )&={sqrt {frac {theta }{sin theta }}},J_{0}((ell +1/2)theta )+{mathcal {O}}left(ell ^{-1}right)\&={frac {2}{sqrt {2pi ell sin theta }}}cos left(left(ell +{tfrac {1}{2}}right)theta -{frac {pi }{4}}right)+{mathcal {O}}left(ell ^{-3/2}right),quad theta in (0,pi ),end{aligned}}}$

and for arguments of magnitude greater than 1^[7]

${displaystyle {begin{aligned}P_{ell }left(cosh xi right)&={sqrt {frac {xi }{sinh xi }}}I_{0}left(left(ell +{frac {1}{2}}right)xi right)left(1+{mathcal {O}}left(ell ^{-1}right)right),,\P_{ell }left({frac {1}{sqrt {1-e^{2}}}}right)&={frac {1}{sqrt {2pi ell e}}}{frac {(1+e)^{frac {ell +1}{2}}}{(1-e)^{frac {ell }{2}}}}+{mathcal {O}}left(ell ^{-1}right)end{aligned}}}$

where J₀ and I₀ are Bessel functions.

Zeros[edit]

All zeros of P_n(x) are real, distinct from each other, and lie in the interval (-1,1) . Furthermore, if we regard them as dividing the interval [-1,1] into n+1 subintervals, each subinterval will contain exactly one zero of $P_{n+1}$ . This is known as the interlacing property. Because of the parity property it is evident that if $x_{k}$ is a zero of P_n(x) , so is ${displaystyle -x_{k}}$ . These zeros play an important role in numerical integration based on Gaussian quadrature. The specific quadrature based on the $P_{n}$ ‘s is known as Gauss-Legendre quadrature.

From this property and the facts that ${displaystyle P_{n}(pm 1)neq 0}$ , it follows that ${displaystyle P_{n}(x)}$ has n-1 local minima and maxima in . Equivalently, ${displaystyle dP_{n}(x)/dx}$ has zeros in .

Pointwise evaluations[edit]

The parity and normalization implicate the values at the boundaries to be

${displaystyle P_{n}(1)=1,,quad P_{n}(-1)=(-1)^{n}}$

At the origin x=0 one can show that the values are given by

${displaystyle P_{2n}(0)={frac {(-1)^{n}}{4^{n}}}{binom {2n}{n}}={frac {(-1)^{n}}{2^{2n}}}{frac {(2n)!}{left(n!right)^{2}}}}$

${displaystyle P_{2n+1}(0)=0}$

Legendre polynomials with transformed argument[edit]

Shifted Legendre polynomials[edit]

The shifted Legendre polynomials are defined as

${displaystyle {widetilde {P}}_{n}(x)=P_{n}(2x-1),.}$

Here the “shifting” function x ↦ 2x − 1 is an affine transformation that bijectively maps the interval [0, 1] to the interval [−1, 1], implying that the polynomials P̃_n(x) are orthogonal on [0, 1]:

${displaystyle int _{0}^{1}{widetilde {P}}_{m}(x){widetilde {P}}_{n}(x),dx={frac {1}{2n+1}}delta _{mn},.}$

An explicit expression for the shifted Legendre polynomials is given by

${displaystyle {widetilde {P}}_{n}(x)=(-1)^{n}sum _{k=0}^{n}{binom {n}{k}}{binom {n+k}{k}}(-x)^{k},.}$

The analogue of Rodrigues’ formula for the shifted Legendre polynomials is

${displaystyle {widetilde {P}}_{n}(x)={frac {1}{n!}}{frac {d^{n}}{dx^{n}}}left(x^{2}-xright)^{n},.}$

The first few shifted Legendre polynomials are:

	${displaystyle {widetilde {P}}_{n}(x)}$
0
1
2	$6x^{2}-6x+1$
3	$20x^{3}-30x^{2}+12x-1$
4	$70x^{4}-140x^{3}+90x^{2}-20x+1$
5	${displaystyle 252x^{5}-630x^{4}+560x^{3}-210x^{2}+30x-1}$

Legendre rational functions[edit]

The Legendre rational functions are a sequence of orthogonal functions on [0, ∞). They are obtained by composing the Cayley transform with Legendre polynomials.

A rational Legendre function of degree n is defined as:

${displaystyle R_{n}(x)={frac {sqrt {2}}{x+1}},P_{n}left({frac {x-1}{x+1}}right),.}$

They are eigenfunctions of the singular Sturm–Liouville problem:

${displaystyle (x+1)partial _{x}(xpartial _{x}((x+1)v(x)))+lambda v(x)=0}$

with eigenvalues

${displaystyle lambda _{n}=n(n+1),.}$

Notes[edit]

^ Arfken & Weber 2005, p.743
^ Legendre, A.-M. (1785) [1782]. “Recherches sur l’attraction des sphéroïdes homogènes” (PDF). Mémoires de Mathématiques et de Physique, présentés à l’Académie Royale des Sciences, par divers savans, et lus dans ses Assemblées (in French). Vol. X. Paris. pp. 411–435. Archived from the original (PDF) on 2009-09-20.
^ Jackson, J. D. (1999). Classical Electrodynamics (3rd ed.). Wiley & Sons. p. 103. ISBN 978-0-471-30932-1.
^ Voelker, Aaron R.; Kajić, Ivana; Eliasmith, Chris (2019). Legendre Memory Units: Continuous-Time Representation in Recurrent Neural Networks (PDF). Advances in Neural Information Processing Systems.
^ Arfken & Weber 2005, p.753
^ Szegő, Gábor (1975). Orthogonal polynomials (4th ed.). Providence: American Mathematical Society. pp. 194 (Theorem 8.21.2). ISBN 0821810235. OCLC 1683237.
^ “DLMF: 14.15 Uniform Asymptotic Approximations”.

References[edit]

Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. “Chapter 8”. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. pp. 332, 773. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253. See also chapter 22.
Arfken, George B.; Weber, Hans J. (2005). Mathematical Methods for Physicists. Elsevier Academic Press. ISBN 0-12-059876-0.
Bayin, S. S. (2006). Mathematical Methods in Science and Engineering. Wiley. ch. 2. ISBN 978-0-470-04142-0.
Belousov, S. L. (1962). Tables of Normalized Associated Legendre Polynomials. Mathematical Tables. Vol. 18. Pergamon Press. ISBN 978-0-08-009723-7.
Courant, Richard; Hilbert, David (1953). Methods of Mathematical Physics. Vol. 1. New York, NY: Interscience. ISBN 978-0-471-50447-4.
Dunster, T. M. (2010), “Legendre and Related Functions”, in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248
El Attar, Refaat (2009). Legendre Polynomials and Functions. CreateSpace. ISBN 978-1-4414-9012-4.
Koornwinder, Tom H.; Wong, Roderick S. C.; Koekoek, Roelof; Swarttouw, René F. (2010), “Orthogonal Polynomials”, in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0-521-19225-5, MR 2723248

External links[edit]

A quick informal derivation of the Legendre polynomial in the context of the quantum mechanics of hydrogen
“Legendre polynomials”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Wolfram MathWorld entry on Legendre polynomials
Dr James B. Calvert’s article on Legendre polynomials from his personal collection of mathematics
The Legendre Polynomials by Carlyle E. Moore
Legendre Polynomials from Hyperphysics

Источник

Макеты страниц

В уравнении для обычно переходят от переменной к переменной Тогда уравнение принимает вид

Это уравнение называется обобщенным уравнением Лежандра, а его решения — присоединенными функциями Лежандра. Прежде чем анализировать уравнение (3.9), найдем решение в виде степенного ряда для обыкновенного дифференциального уравнения Лежандра, соответствующего

Для того чтобы искомое решение имело физический смысл электростатического потенциала, оно должно быть однозначно, конечно и непрерывно в интервале. Будем искать решение в виде ряда

где а — пока не определенный параметр. Подставляя это разложение в (3.10), получаем ряд

В этом разложении коэффициенты перед всеми степенями должны в отдельности обращаться в нуль. Для отсюда следует, что:

Для остальных j получаем соотношение

Как легко видеть, оба соотношения (3.13) эквивалентны, и достаточно считать, что лишь один из коэффициентов отличен от нуля. Считая мы получаем для а два значения: Из (3.14) следует, что разложение в ряд содержит только четные степени (при или только нечетные степени (при

Можно показать, что оба полученных ряда (соответствующие ) обладают следующими свойствами:

а) ряд сходится при при всех значениях

б) ряд расходится при если только он не обрывается.

Поскольку мы ищем решение, которое конечно при так же как и при необходимо потребовать, чтобы ряд обрывался. Так как а и j — целые неотрицательные числа или нуль, то из рекуррентной формулы (3.14) следует, что ряд обрывается лишь в том случае, когда I равно нулю или положительному целому числу. Но и в этом случае лишь один из двух рядов будет конечен при Если I четно, то конечен ряд для если нечетно, то конечен ряд для В обоих случаях старший: член пропорционален следующий 2 и т. д. до при четном или до при нечетном Эти многочлены принято нормировать так, чтобы при они обращались в единицу. Они называются полиномами Лежандра порядка Приведем несколько первых полиномов Лежандра:

Исходя из формул (3.11) и (3.14), полиномы Лежандра, представляемые в виде разложения по степеням можно преобразовать к весьма компактному виду, известному под названием формулы Родрига:

Эта формула может быть получена и другим, более изящным путем, в частности с помощью -кратного интегрирования уравнения (3.10).

Полиномы Лежандра образуют полную систему функций, ортогональных на интервале . Для доказательства ортогональности

можно использовать непосредственно дифференциальное уравнение (3.10). Напишем дифференциальное уравнение для умножим его на и проинтегрируем по интервалу

Интегрируя первый член по частям, находим

Вычитая из (3.18) такое же равенство с заменой I на и наоборот, приходим к условию ортогональности

При входящий в (3.19) интеграл должен быть равен нулю, а при он будет конечным. Чтобы вычислить значение этого интеграла, нужно воспользоваться явным представлением полиномов Лежандра, например формулой Родрига. При этом интеграл принимает вид

Интегрируя l раз по частям, получаем

В результате -кратного дифференцирования величины получим константу так что

(3.20)

Легко показать, что интеграл в (3.20) равен следовательно, условие ортогональности можно записать так:

а ортонормированные функции (см. гл. 2, § 9) имеют вид

Поскольку полиномы Лежандра образуют полную систему ортогональных функций, любая функция может быть разложена в ряд по полиномам Лежандра на

Фиг. 3.2.

Это разложение имеет вид

где

Рассмотрим для примера функцию, изображенную на фиг. 3.2:

В этом случае

Поскольку при нечетных полином нечетен относительно а при четных четен, отличны от нудя только коэффициенты с нечетным Таким образом, для нечетных имеем

Вычисляя последний интеграл с помощью формулы Родрига, найдем

где Таким образом, ряд для имеет вид

Полиномы Лежандра различного порядка связаны определенными рекуррентными соотношениями, которые оказываются весьма полезными при вычислении интегралов, нахождении полиномов высокого порядка по полиномам низкого порядка и т. п. Из формулы Родрига легко вывести соотношение

Комбинируя это соотношение с дифференциальным уравнением (3.10), можно получить целый ряд рекуррентных формул, например:

Для иллюстрации применения этих рекуррентных соотношений вычислим интеграл

Из первой формулы (3.29) найдем выражение для Подставляя его в (3.30), приведем интеграл к виду

Из условия ортогональности (3.21) следует, что интеграл отличен от нуля лишь при и равен при этом

Правые части в (3.31) фактически одинаковы, отличаясь лишь заменой I на Аналогично можно показать, что

где предполагается, что

Источник

Общая информация
Многочлены Лежандра
Формула	$P_{n}(z)={frac {1}{2^{n}n!}}{frac {d^{n}}{dz^{n}}}(z^{2}-1)^{n}$
Скалярное произведение	${displaystyle (f,;g)=int limits _{-1}^{1}{f(x)g(x),dx}}$
Область определения
Дополнительные характеристики
Дифференциальное уравнение	$(1-z^{2}){frac {{mathrm d}^{2}u}{{mathrm d}z^{2}}}-2z{frac {{mathrm d}u}{{mathrm d}z}}+n(n+1)u=0$
Норма	$\|\|P_{n}(x)\|\|={sqrt {{frac {2}{2n+1}}}}$
Названы в честь	Лежандр, Адриен Мари

Названы по имени французского математика Адриен Мари Лежандра.

Содержание

1 Определение
- 1.1 Полиномы Лежандра и присоединённые функции Лежандра первого и второго рода
- 1.2 Выражение через суммы
- 1.3 Рекуррентная формула
- 1.4 Производная полинома Лежандра
- 1.5 Корни полинома Лежандра
- 1.6 Формулы с разложениями
- 1.7 Присоединённые многочлены Лежандра
  - 1.7.1 Нормировка по правилу Шмидта
- 1.8 Сдвинутые многочлены Лежандра
2 Матрица функции многочлена Лежандра
3 Примеры
4 Свойства
5 Ряды многочленов Лежандра
- 5.1 Разложение липшицевой функции в ряд многочленов Лежандра
- 5.2 Разложение голоморфной функции
- 5.3 Теорема сложения
6 Функции Лежандра
7 Примечания
8 Литература
9 Ссылки

Определение

Полиномы Лежандра и присоединённые функции Лежандра первого и второго рода

Рассмотрим дифференциальное уравнение вида

$(1-z^{2}){frac {{mathrm d}^{2}u}{{mathrm d}z^{2}}}-2z{frac {{mathrm d}u}{{mathrm d}z}}+n(n+1)u=0,$

(УравнПолЛеж)

${displaystyle P_{n}(z)={frac {1}{2^{n}n!}}{frac {d^{n}}{dz^{n}}}(z^{2}-1)^{n}.}$

Часто вместо записывают косинус полярного угла:

${displaystyle P_{n}(cos theta )={frac {1}{2^{n}n!}}{frac {d^{n}}{d(cos theta )^{n}}}(cos ^{2}theta -1)^{n}.}$

Уравнение (УравнПолЛеж) можно получить из частного случая гипергеометрического уравнения, называемого уравнением Лежандра

$(1-z^{2}){frac {{mathrm d}^{2}u}{{mathrm d}z^{2}}}-2z{frac {{mathrm d}u}{{mathrm d}z}}+left[nu (nu +1)-{frac {mu ^{2}}{1-z^{2}}}right]u=0,$

(УравнЛеж)

где , — произвольные комплексные постоянные. Интерес представляют его решения, являющиеся однозначными и регулярными при |z|<1 (в частности, при действительных ) или когда действительная часть числа больше единицы. Его решения называют присоединёнными функциями Лежандра или шаровыми функциями. Подстановка вида $w=(z^{2}-1)^{{mu /2}}$ в (УравнЛеж) даёт уравнение Гаусса, решение которого в области |1-z|<2 принимает вид

${displaystyle w=P_{nu }^{mu }(z)={frac {1}{Gamma (1-mu )}}left({frac {z+1}{z-1}}right)^{mu /2}Fleft(-nu ,;nu +1;;1-mu ;;{frac {1}{2}}-{frac {z}{2}}right),}$

где — гипергеометрическая функция. Подстановка $w=z^{2}$ в (УравнЛеж) приводит к решению вида

определённым на |z|>1 . Функции $P_{nu }^{mu }(z)$ и $Q_{nu }^{mu }(z)$ называют функциями Лежандра первого и второго рода.^[2]

Справедливы соотношения^[3]

$P_{nu }^{mu }(z)=P_{{-nu -1}}^{mu }(z)$

$Q_{nu }^{mu }(z)sin pi (nu +mu )-Q_{{-nu -1}}^{mu }(z)sin pi (nu -mu )=pi e^{{imu pi }}cos(nu pi )P_{nu }^{mu }(z).$

Выражение через суммы

Многочлены Лежандра также определяются по следующим формулам:

$P_{n}(x)={frac {1}{2^{n}}}sum _{{k=0}}^{{E(n/2)}}(-1)^{k}{binom {n}{k}}{binom {2n-2k}{n}}x^{{n-2k}};$

$P_{n}(x)={frac {1}{2^{n}}}sum _{{k=0}}^{n}{binom {n}{k}}^{2}(x-1)^{{n-k}}(x+1)^{{k}};$

$P_{n}(x)={frac {(x+1)^{n}}{2^{n}}}sum _{{k=0}}^{n}(-1)^{k}{binom {n}{k}}^{2}left({frac {x-1}{x+1}}right)^{k}$

, если

$P_{n}(x)={frac {(x-1)^{n}}{2^{n}}}sum _{{k=0}}^{n}(-1)^{k}{binom {n}{k}}^{2}left({frac {x+1}{x-1}}right)^{k}$

, если

Рекуррентная формула

Они также могут быть вычислены по рекуррентной формуле (при n 1)^[4]:

$P_{n+1}(x)=frac{2n+1}{n+1}xP_n(x)-frac{n}{n+1}P_{n-1}(x),$

(РекуррЛеж)

причем первые две функции имеют вид

Производная полинома Лежандра

Вычисляется по формуле^[5]:

$P'_{{n}}(x)={frac {n}{1-x^{2}}}[P_{{n-1}}(x)-xP_{n}(x)].$

(ПроизвЛеж)

Корни полинома Лежандра

Вычисляются итеративно по методу Ньютона^[5]:

${displaystyle x_{i}^{(k+1)}=x_{i}^{(k)}-{frac {P_{n}(x_{i}^{(k)})}{P'_{n}(x_{i}^{(k)})}},}$

причем начальное приближение для -го корня () берется по формуле^[5]

${displaystyle x_{i}^{(0)}=cos[pi (4i-1)/(4n+2)].}$

Значение полинома можно вычислять используя рекуррентную формулу для конкретного значения x.
Производную также можно вычислять для конкретного значения x, используя формулу для производной.

Формулы с разложениями

Многочлены Лежандра также определяются следующими разложениями:

для ${displaystyle |t|<min |xpm {sqrt {x^{2}-1}}|colon }$

$(1-2tx+t^2)^{- frac{1}{2}}=sum_{n=0}^infty P_n(x)t^n,$

и для ${displaystyle |t|>max |xpm {sqrt {x^{2}-1}}|colon }$

$(1-2tx+t^2)^{- frac{1}{2}}=sum_{n=0}^infty P_n(x)frac{1}{t^{n+1}}.$

Следовательно,
${displaystyle P_{n}(x)={frac {(2n)!}{2^{n}(n!)^{2}}}[x^{n}-{frac {n(n-1)}{2(2n-1)}}x^{n-2}+{frac {n(n-1)(n-2)(n-3)}{2cdot 4(2n-1)(2n-3)}}x^{n-4}-ldots ].}$

Присоединённые многочлены Лежандра

Присоединённые многочлены Лежандра определяются по формуле:

$P_{n}^{m}(x)=(1-x^{2})^{{m/2}}{frac {d^{m}}{dx^{m}}}P_{n}(x),$

которую также можно представить в виде:

$P_{n}^{m}(cos theta )=sin ^{m}theta {frac {d^{m}}{d(cos theta )^{m}}}P_{n}(cos theta ).$

При m=0 функция $P_{n}^{m}$ совпадает с $P_{n}$ .

Нормировка по правилу Шмидта

Нормированные по правилу Шмидта полиномы Лежандра выглядят следующим образом^[6]:

${displaystyle SP_{n}^{0}(x)=P_{n}^{0}(x);}$

${displaystyle SP_{n}^{m}(x)=(-1)^{n}left({frac {2(n-m)!}{(n+m)!}}right)^{1/2}P_{n}^{m}(x).}$

Сдвинутые многочлены Лежандра

Сдвинутые многочлены Лежандра определяются как ${tilde {P_{n}}}(x)=P_{n}(2x-1)$ , где сдвигающая функция (это аффинное преобразование) — выбрана так чтобы однозначно отображать интервал ортогональности многочленов на интервал в котором уже ортогональны сдвинутые многочлены ${tilde {P_{n}}}(x)$ :

${displaystyle int nolimits _{0}^{1}{tilde {P_{m}}}(x){tilde {P_{n}}}(x),dx={frac {1}{2n+1}}delta _{mn}.}$

Явное выражение для смещённых многочленов Лежандра задаётся как:

${tilde {P_{n}}}(x)=(-1)^{n}sum _{{k=0}}^{n}{n choose k}{n+k choose k}(-x)^{k}.$

Аналогом формулы Родрига для смещенных многочленов Лежандра является:

${displaystyle {tilde {P_{n}}}(x)={frac {1}{n!}}{frac {d^{n}}{dx^{n}}}left[(x^{2}-x)^{n}right].}$

Выражения для некоторых первых сдвинутых многочленов Лежандра:

n	${tilde {P_{n}}}(x)$
0
1
2	$6x^{2}-6x+1$
3	$20x^{3}-30x^{2}+12x-1$
4	$70x^{4}-140x^{3}+90x^{2}-20x+1$

Матрица функции многочлена Лежандра

${begin{pmatrix}0&0&-2&0&0&vdots &0&vdots &0\0&2&0&-6&0&vdots &0&vdots &vdots \0&0&6&0&-12&vdots &0&vdots &vdots \0&0&0&12&0&vdots &0&vdots &vdots \0&0&0&0&20&vdots &0&vdots &vdots \dots &dots &dots &dots &dots &ddots &vdots &dots &vdots \0&0&0&0&0&dots &k(k+1)&dots &vdots \dots &dots &dots &dots &dots &dots &dots &ddots &vdots \0&0&0&0&0&dots &0&dots &n(n+1)\end{pmatrix}}$

Эта матрица является верхнетреугольной. Её определитель равен нулю, а собственные значения равны k(k+1) , где .

Примеры

Первые 6 многочленов Лежандра.

Первые многочлены Лежандра равны:

${displaystyle P_{0}(x)=1;}$
${displaystyle P_{1}(x)=x;}$
$P_{2}(x)={frac {1}{2}}(3x^{2}-1);$
$P_{3}(x)={frac {1}{2}}(5x^{3}-3x);$
$P_{4}(x)={frac {1}{8}}(35x^{4}-30x^{2}+3);$
$P_{5}(x)={frac {1}{8}}(63x^{5}-70x^{3}+15x);$
$P_{6}(x)={frac {1}{16}}(231x^{6}-315x^{4}+105x^{2}-5);$
$P_{7}(x)={frac {1}{16}}(429x^{7}-693x^{5}+315x^{3}-35x);$
$P_{8}(x)={frac {1}{128}}(6435x^{8}-12012x^{6}+6930x^{4}-1260x^{2}+35);$
$P_{9}(x)={frac {1}{128}}(12155x^{9}-25740x^{7}+18018x^{5}-4620x^{3}+315x);$
${displaystyle P_{10}(x)={frac {1}{256}}(46189x^{10}-109395x^{8}+90090x^{6}-30030x^{4}+3465x^{2}-63);}$
${displaystyle P_{11}(x)={frac {1}{256}}(88179x^{11}-230945x^{9}+218790x^{7}-90090x^{5}+15015x^{3}-693x);}$
${displaystyle P_{12}(x)={frac {1}{1024}}(676039x^{12}-1939938x^{10}+2078505x^{8}-1021020x^{6}+225225x^{4}-18018x^{2}+231);}$
${displaystyle P_{13}(x)={frac {1}{1024}}(1300075x^{13}-4056234x^{11}+4849845x^{9}-2771340x^{7}+765765x^{5}-90090x^{3}+3003x);}$
${displaystyle P_{14}(x)={frac {1}{2048}}(5014575x^{14}-16900975x^{12}+22309287x^{10}-14549535x^{8}+4849845x^{6}-765765x^{4}+45045x^{2}-429);}$
${displaystyle P_{15}(x)={frac {1}{2048}}(9694845x^{15}-35102025x^{13}+50702925x^{11}-37182145x^{9}+14549535x^{7}-2909907x^{5}+255255x^{3}-6435x);}$
${displaystyle P_{16}(x)={frac {1}{32768}}(300540195x^{16}-1163381400x^{14}+1825305300x^{12}-1487285800x^{10}+669278610x^{8}-162954792x^{6}+19399380x^{4}-875160x^{2}+6435);}$
${displaystyle P_{17}(x)={frac {1}{32768}}(583401555x^{17}-2404321560x^{15}+4071834900x^{13}-3650610600x^{11}+1859107250x^{9}-535422888x^{7}+81477396x^{5}-5542680x^{3}+109395x).}$

Поскольку ${displaystyle P_{n}(1)=1}$ , то

$P_{n}(x)={frac {1}{lambda _{0}+lambda _{1}+ldots +lambda _{n}}}(lambda _{0}+lambda _{1}x+lambda _{2}x^{2}+ldots +lambda _{n}x^{n})={frac {sum limits _{{i=0}}^{n}lambda _{i}x^{i}}{sum limits _{{i=0}}^{n}lambda _{i}}}.$

Свойства

${displaystyle U'_{n+1}(x)-2(n+1)xU_{n}(x)=0;}$
${displaystyle (x^{2}-1)U'_{n}(x)-2nxU_{n}(x)=0.}$

Присоединённые многочлены Лежандра являются решениями дифференциального уравнения

${frac {d}{dx}}left[(1-x^{2}){frac {d}{dx}}P_{n}(x)right]-{frac {m^{2}}{(1-x^{2})}}P_{n}(x)+n(n+1)P_{n}(x)=0.$

При

уравнение принимает вид

${displaystyle P'_{n+1}(x)=xP'_{n}(x)+(n+1)P_{n}(x).}$

Производящая функция для многочленов Лежандра равна:

$sum _{{n=0}}^{infty }P_{n}(z)x^{n}={frac {1}{{sqrt {1-2xz+x^{2}}}}}.$

Условие ортогональности этих полиномов на отрезке :

$int limits _{{-1}}^{1}P_{k}(x)P_{l}(x),dx={frac {2}{2k+1}}delta _{{kl}},$

где $delta _{{kl}}$ — символ Кронекера.

$||P_{n}||={sqrt {int limits _{{-1}}^{1}P_{n}^{2}(x),dx}}={sqrt {{frac {2}{2n+1}}}}.$

Нормированная функция многочленов Лежандра связана с нормой $P_{n}$ следующим соотношением:

${tilde P}_{n}(x)={frac {P_{n}(x)}{||P_{n}||}}={sqrt {{frac {2n+1}{2}}}}P_{n}(x).$

$P_{n}^{m}(-x)=(-1)^{{m+n}}P_{n}^{m}(x).$

${displaystyle P_{2n}}$ — четная функция;
${displaystyle P_{2n+1}}$ — нечетная функция.

Ряды многочленов Лежандра

Разложение липшицевой функции в ряд многочленов Лежандра

Липшицевая функция является функцией со свойством:

, где

Эта функция разлагается в ряд многочленов Лежандра.

Пусть — пространство непрерывных отображений на отрезке , и .

Пусть

$c_{n}(f)=int limits _{{-1}}^{1}f(x){tilde P}_{n}(x),dx,$

тогда ${displaystyle c_{n}(f)}$ удовлетворяет следующему условию:

$lim _{{nto infty }}c_{n}(f)=0.$

Пусть $S_{n}f=sum _{{k=0}}^{n}c_{k}(f){tilde P}_{k}$ и ${displaystyle S_{n}f}$ удовлетворяет следующим условиям:

$forall xin I,;S_{n}f(x)=int limits _{{-1}}^{1}K_{n}(x,;y)f(y),dy$ , где $K_{n}(x,;y)={frac {n+1}{2}}{frac {P_{{n+1}}(x)P_{n}(y)-P_{{n+1}}(y)P_{n}(x)}{x-y}};$
$S_{n}f(x)-f(x)=int limits _{{-1}}^{1}K_{n}(x,;y)(f(y)-f(x)),dy;$
$forall xin [-1,1],;lim _{{nto infty }}S_{n}f(x)=f(x).$

Липшецевую функцию можно записать следующим образом:

$f=sum _{{n=0}}^{infty }c_{n}(f){tilde P}_{n}.$

Разложение голоморфной функции

Всякая функция , голоморфная внутри эллипса с фокусами −1 и +1, может быть представлена в виде ряда:

$f(x)=sum _{{n=0}}^{infty }lambda _{n}P_{n}(x)$

Теорема сложения

или, в альтернативной форме через гамма-функцию:

Для полиномов Лежандра второго рода теорема сложения выглядит как^[8]

при условиях ${displaystyle 0leqslant psi _{1}<pi /2}$ , ${displaystyle 0leqslant psi _{2}<pi }$ , $psi _{1}+psi _{2}<pi$ , varphi .

Функции Лежандра

Шаровые функции — это функции (в сферических координатах ) вида (с точностью до константы)

$r^{n}P_{n}^{m}(cos theta )cos mvarphi$

и $r^{n}P_{n}^{m}(cos theta )sin mvarphi ,$

где $P_{n}^{m}$ — присоединённые многочлены Лежандра;

а точнее вида $r^{n}Y_{{nm}}$ , где $Y_{{nm}}$ — сферические функции.

Шаровые функции удовлетворяют уравнению Лапласа всюду в $mathbb {R} ^{3}$ .

Примечания

↑ Градштейн, Рыжик, 1963, с. 1039.
↑ Бейтмен, Эрдейи, Т. 1, 1973, с. 126—127.
↑ Бейтмен, Эрдейи, Т. 1, 1973, с. 140.
↑ Цимринг, 1988, с. 196.
↑ ¹ ² ³ Цимринг, 1988, с. 197.
↑ John W. Eaton, David Bateman, Søren Hauberg, Rik Wehbring. GNU Octave. — 2011. — С. 455—456.
↑ Градштейн, Рыжик, 1963, с. 1027.
↑ Градштейн, Рыжик, 1963, с. 1028.

Литература

Бейтмен Г., Эрдейи А. Высшие трансцендентные функции = Higher Transcendental Functions / Пер. Н. Я. Виленкина. — Изд. 2-е,. — М.: Наука, 1973. — Т. 1. — 296 с. — 14 000 экз.
Владимиров В. С., Жаринов В. В. Уравнения математической физики. — М.: Физматлит, 2004. — ISBN 5-9221-0310-5.
Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. — Изд. 4-е, перераб. — М.: Государственное издательство физико-математической литературы, 1963. — 19 000 экз.
Кампе де Ферье Ж., Кемпбелл Р., Петьо Г., Фогель Т. Функции математической физики. — М.: Физматлит, 1963.
Никольский С. М. Квадратурные формулы. — М.: Наука, 1988.
Цимринг Ш. Е. Специальные функции и определенные интегралы. Алгоритмы. Программы для микрокалькуляторов: Справочник. — М.: Радио и связь, 1988.

Ссылки

Legendre Polynomials — University of Rochester, 2010.

Источник

Многочлены Лежандра

Ортогональные
полиномиальные функции Лежандра

можно получить,
воспользовавшись следующим рекуррентным
соотношением:

(2.7.14)

где

Эти функции ортогональны в интервале

Приведем несколько
первых многочленов Лежандра:

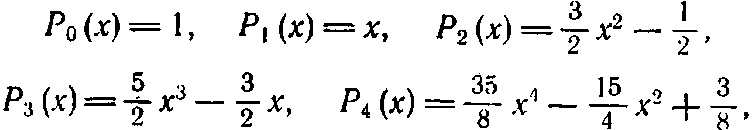
где функции

_и

заданы,
а функции

_,

и
получены
по формуле (2.7.14).
Эти функции ортогональны относительно
весовой функции

и(х)=
1.

Многочлены Лагерра

Для получения
многочленов Лагерра можно воспользоваться
рекуррентным соотношением

где

и

.
Эти
многочлены ортогональны

относительно
весовой функции

в
интервале

Приведем несколько
первых многочленов Лагерра:

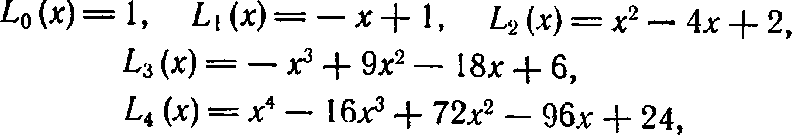
где функции

заданы,
а остальные получены по формуле
(2.7.16).

Многочлены Эрмита

Для получения
многочленов Эрмита используется
рекуррентное соотношение

(2.7.18)

где

Эти
функции ортогональны относи-

тельно
весовой функции

причем
интервал

ортогональности
составляет

это
обстоятельство

делает
использование таких функций чрезвычайно
удобным, поскольку
освобождает нас от забот относительно
диапазона изменения переменных.

Приведем несколько
первых многочленов Эрмита:

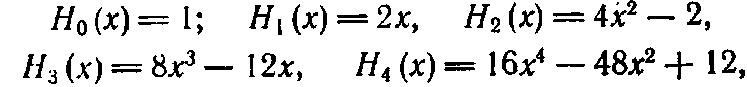
где функции

заданы, а
остальные определяются

по формуле (2.7.18).

2.4 Аппроксимация плотностей распределения функциями

Постановка задачи

Пусть

—
оценка плотности распределения

при-

чем, как и раньше,
под
подразумевается

.

Необходимо найти
такую оценку, которая обеспечила бы
минимизацию среднеквадратичной
ошибки (интегрального квадратичного
показателя качества), определяемой как

(4.6.47)

где
—
весовая функция.

Воспользуемся
разложением оценки

в
ряд

где
—коэффициенты,
подлежащие определению, а

—

множество заданных
базисных функций.

Подстановка
(4.6.48) в соотношение (4.6.47) дает

(4.6.49)

Требуется найти
такие коэффициенты

которые
обеспечат

минимизацию
интеграла вероятности ошибки R.
Необходимое
условие минимальности интеграла
вероятности ошибки R
заключается
в том, что

(
4.6.50)

Взяв частную
производную, получим

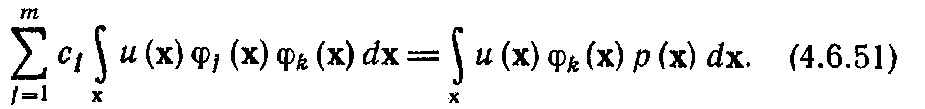
Взглянув на правую
часть уравнения (4.6.51),
нетрудно убедиться
в том, что она по определению равна
математическому ожиданию
функции
.
В соответствии с нашим предыдущим
анализом математическое ожидание можно
аппроксимировать выборочным средним,
т. е.

(4.6.52)

Подстановка этой
аппроксимирующей оценки в уравнение
(4.6.51)
дает

(4.6.53)

Если базисные
функции

выбраны
таким образом, что

они
ортогональны весовой функции

,
то из определения

ортогональности
следует

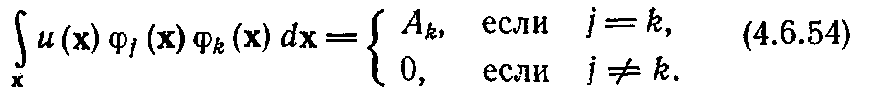
Подстановка
(4.6.54) в уравнение (4.6.53) приводит к
следующему
соотношению, позволяющему вычислить
искомые коэффициенты:

Если базисные
функции
ортонормированны,
то

для всех
Кроме того,
поскольку члены

не зависят
от

и, следовательно,
для всех коэффициентов одинаковы, то
их можно исключить из аппроксимирующего
выражения без всякого ущерба для
классификационной мощности коэффициентов.
В таком случае

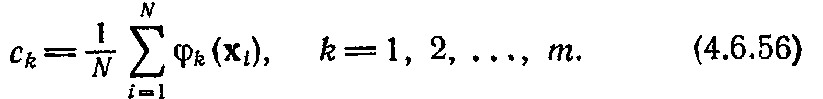
После того как
коэффициенты определены, с помощью
формулы (4.6.48) формируется оценка
плотности распределения

Для того чтобы
применение выражений (4.6.48) и (4.6.55) или
(4.6.56) приводило к успеху, необходимо
иметь в виду два существенных
обстоятельства. Во-первых, следует
полностью отдавать себе отчет в том,
что качество аппроксимации с помощью
выбранной системы базисных функций
зависит от числа m
членов разложения. Поскольку, по всей
вероятности, вид плотности распределения

нам
не известен, оценить

качество
аппроксимации

при
помощи непосредственного

сравнения
невозможно. С другой стороны, так как
оценка

отыскивается для
того, чтобы построить байесовский
классификатор, то заботиться следует
только о качестве распознавания,
доступном этому классификатору. Последнее
можно установить непосредственно в
эксперименте с обучающей выборкой. Если
при
некоторой оценке

качество
классификации оказывается
неудовлетворительным, следует попробовать
увеличить число
базисных функций и посмотреть, приводит
ли улучшение качества
оценки

к улучшению
качества классификатора.

Эту процедуру
можно продолжать вплоть до наступления
«насыщения» (когда введение
дополнительных членов не производит
никакого либо очень малый эффект) или
до тех пор, пока число членов не начнет
превосходить допустимую величину.

Вторым важным
моментом является выбор базисных
функций. Так, например, если плотность
распределения

имеет
синусоидальный
характер, а для разложения оценки
использован
степенной ряд, то очевидно, что число
членов будет значительно больше, чем
при выборе синусоидальных базисных
функций.
Естественно, при отсутствии априорных
сведений о
характере плотности распределения

базисные
функции в первую очередь должны выбираться
исходя из простоты реализации. Все,
что можно было бы сказать об общих
правилах выбора базисных функций,
сводится к тому, что при выполнении
условия линейной независимости и
некоторых других не очень жестких
ограничений на вид плотности распределения

можно
доказать сходимость

при

и

.
Отметим, что ортогональность является
частным случаем линейной независимости.

Пример.

Дана обучающая
выборка

(см.
Рис.1)

Известно, что
образы

,
а образы

Рис. 1

Требуется по
обучающей выборке построить оценки
плотностей распределения.

Плотности можно
аппроксимировать, применив выражения
вида:

Базисные функции

считаются ортогональными в области
определения образов. Поскольку наши
образы

,
будем использовать многочлены Лежандра,
так как областью их ортогональности
является интервал

.