Как найти полное сопротивление фазы тока

Полное сопротивление цепи переменного тока

В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.

Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.

Введем понятие полного сопротивления цепи переменному току – Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока

На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.

Рисунок 1. Классификация цепей переменного тока.

Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.

Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.

Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.

В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения U_L (напряжение на индуктивном сопротивлении) и напряжения U_R (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.

Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью.        а) – схема цепи; б) – сдвиг фаз тока и напряжения; в) – треугольник напряжений; д) – треугольник сопротивлений.

Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов U_L и U_R. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор U_AB является гипотенузой прямоугольного треугольника.

Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.

По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.

Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z²) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.

                                      (1)

Извлекая квадратный корень из обеих частей этого равенства, получим,

                                       (2)

 Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений

Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.

Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.

В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.

Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью.                                                а) – схема цепи; б) – треугольник сопротивлений.

Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.

Для данного случая:

(3)

 В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.

Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) – схема цепи; б) – треугольник сопротивлений.

Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.

                           (4)

Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (X_L или X_C преобладает).

После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.

                                     (5)

Или

                         (6)

Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.

Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.

Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.

Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.

Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) – параллельное соединение R и L; б) – параллельное соединение R и C.

Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z

Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.

                       (7)

Приводя к общему знаменателю подкоренное выражение, получим:

  (8)

 откуда:

                              (9)

Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.

Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.

Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:

                             (10)

 Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.

В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).

Рисунок 6. Эквивалентная схема колебательного контура.

Формула полного сопротивления для этого случая будет:

                   (11)

 Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:

 (12)

 В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие

                                     (13)

 При соблюдении этого условия полное сопротивление колебательного контура будет равно:

                                     (14)

 где L—индуктивность катушки в Гн;

С—емкость конденсатора в Ф;

R—активное сопротивление катушки в Ом.

Была ли эта статья полезной?

Для расчетов напряжений и токов через элементы электрической цепи нужно знать их общее сопротивление. Источники энергии делятся на два типа:

• постоянного тока (батарейки, выпрямители, аккумуляторы), электродвижущая сила (ЭДС) которых не изменяется во времени;
• переменного тока (бытовые и промышленные сети), ЭДС которых изменяется по синусоидальному закону с определенной частотой.

Активные и реактивные сопротивления

Сопротивление нагрузки бывает активным и реактивным. Активное сопротивление (R) не зависит от частоты сети. Это означает, что ток в нем изменяется синхронно с напряжением. Это то сопротивление, которое мы измеряем мультиметром или тестером.

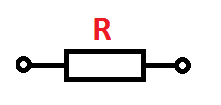Обозначение активного сопротивления

Реактивное сопротивление делится на два вида:

— индуктивное (трансформаторы, дроссели);

Обозначение индуктивного сопротивления

— емкостное ( конденсаторы).

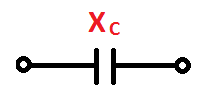Обозначение емкостного сопротивления

Отличительная черта реактивной нагрузки – наличие опережения или отставания тока от напряжения. В емкостной нагрузке ток опережает напряжение, а в индуктивной – отстает от него.

Физически это выглядит так: если разряженный конденсатор подключить к источнику постоянного тока, то в момент включения ток через него максимальный, а напряжение – минимальное. Со временем ток уменьшается, а напряжение — возрастает, пока конденсатор не зарядится.

Если подключить конденсатор к источнику переменного тока, то он будет постоянно перезаряжаться с частотой сети, а ток — увеличиваться раньше, чем напряжение.

Физические величины в формулах

Обозначение	Единица измерения	Наименование
С	Фарада (Ф)	емкость
ѡ	1/с	угловая частота
f	Герц (Гц)	частота
L	Генри (Гн)	индуктивность

Полное сопротивление электрической цепи переменного тока

В сети переменного тока нет нагрузки только активной или только реактивной. Нагревательный элемент помимо активного содержит индуктивное сопротивление, в электродвигателе индуктивное сопротивление преобладает над активным.

Величину полного сопротивления, учитывающего все активные и реактивные составляющие электрической цепи, подсчитывают по формуле:

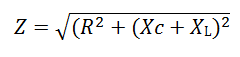
Расчет эквивалентного сопротивления элементов цепи

К одному источнику питания может быть подключено несколько сопротивлений. Для вычисления тока нагрузки источника подсчитывают эквивалентное сопротивление нагрузки. В зависимости от соединения элементов между собой, используются два способа.

Последовательное соединение сопротивлений.

В этом случае их величины складываются:

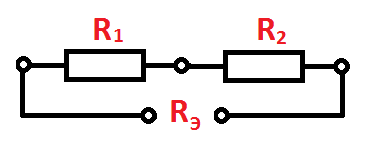Последовательное соединение двух сопротивлений

Чем больше сопротивлений соединено последовательно, тем больше эквивалентное сопротивление этой цепи. Бытовой пример: если контакт в штепсельной вилке ухудшится, это равносильно подключению последовательно с нагрузкой дополнительного сопротивления. Эквивалентное сопротивление нагрузки вырастет, а ток через нее – уменьшится.

1. Параллельное соединение сопротивлений.
2. Формула расчета выглядит намного сложнее:
3. 
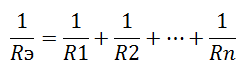
4. Случай применения этой формулы для двух параллельно соединенных сопротивлений:
5. Случай для соединения n одинаковых сопротивлений R:

Чем больше сопротивлений соединить параллельно, тем итоговое сопротивление цепи меньше. Это мы наблюдаем и в повседневной жизни: чем больше к сети подключить потребителей, тем меньше эквивалентное сопротивление и больше ток нагрузки.

Таким образом, расчет полного сопротивления электрической цепи происходит поэтапно:

1. Рисуется схема замещения цепи, содержащая активные и реактивные сопротивления.
2. Рассчитываются эквивалентные сопротивления отдельно для активной, индуктивной и емкостной составляющих нагрузки.
3. Рассчитывается полное сопротивление электрической цепи
4. Рассчитываются токи и напряжения в цепи источника питания.

Источник: http://electric-tolk.ru/polnoe-soprotivlenie-elektricheskoj-cepi/

Соединение элементов в цепи переменного напряжения и тока

Всем доброго времени суток! В прошлой статье я рассказал о воздействии переменного напряжения на элементы цепи (сопротивление, индуктивность и ёмкость) и воздействие этих элементов на напряжение, ток и мощность. В данной статье я расскажу о последовательном и параллельном соединении элементов цепи и воздействии на такие цепи переменного напряжения и тока.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

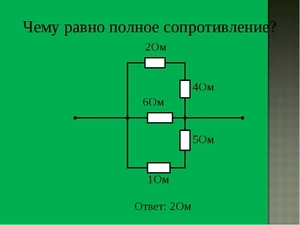
Последовательное соединение элементов цепи при переменном напряжении

Начнём с последовательного соединения сопротивления R, индуктивности L и ёмкости C и рассмотрим воздействие на неё переменного напряжения с частотой ω.

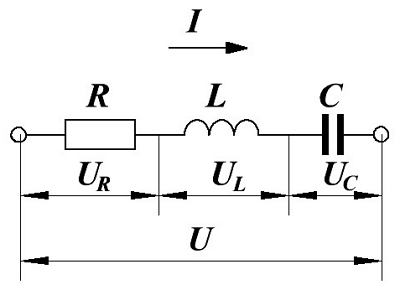
В данной цепи входное переменное напряжение U в соответствии со вторым законом Кирхгофа будет равно алгебраической сумме переменных напряжений на отдельных элементах

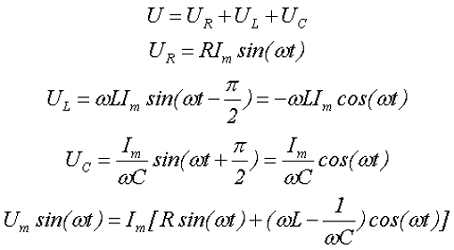
• где UR, UL, UC – напряжение на элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
• Im­ – амплитудное значение переменного тока.
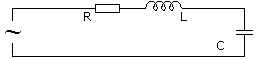
• Графическое изображение напряжений и токов на последовательно соединённых элементах цепи представлено ниже

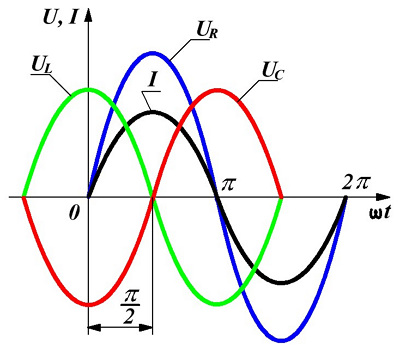
Итоговое выражение является тригонометрической формой записи второго закона Кирхгофа для мгновенных напряжений и его можно переписать в виде

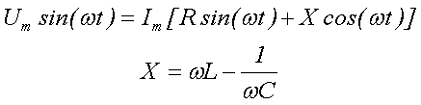
1. где R – активное сопротивление,
2. Х – реактивное сопротивление.
3. Значение активного сопротивления R всегда только положительно, а реактивное сопротивление Х может принимать, как положительное значение Х > 0, тогда оно имеет индуктивный характер, так и отрицательное значение X < 0, в этом случае реактивное сопротивление имеет ёмкостный характер.
4. В случае же нулевого значения реактивного сопротивления, имеет место резонанс напряжений

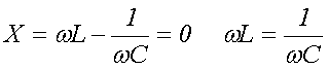
В этом случае сопротивление цепи представлено только активной нагрузкой R, а следовательно сдвиг фаз между напряжением и током будет нулевым.

При расчётах нас интересует не столько ток и напряжение на отдельных элементах, сколько ток и напряжение всей цепи. Для этого продолжим преобразовывать напряжение

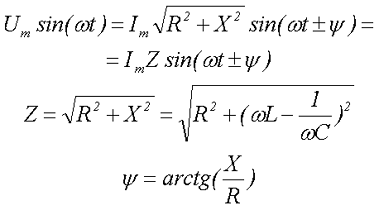
• где Z – полное сопротивление цепи,
• ψ – разность фаз между напряжением и током.
• Таким образом, амплитудное значение напряжения Um и амплитудное значение тока Im связаны между собой следующим соотношением

1. где Um­ – амплитудное значение переменного напряжения,
2. Im­ – амплитудное значение переменного тока,
3. Z – полное сопротивление цепи.

Параллельное соединение элементов цепи при переменном напряжении

Теперь рассмотрим параллельное соединение элементов цепи (сопротивления, индуктивности и ёмкости) и прохождение по ним переменного тока.

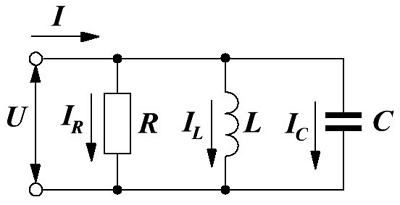
Подадим на вход такой цепи переменное напряжение U, тогда электрический ток в цепи I, в соответствии с первым законом Кирхгофа, будет равняться алгебраической суммы токов проходящей через элементы цепи

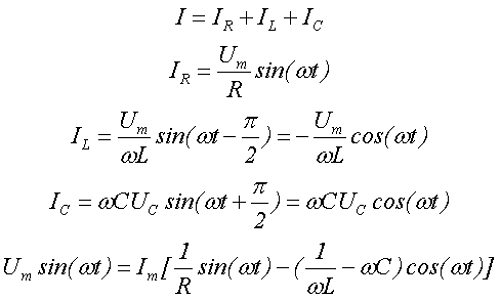
• IR, IL, IC – токи в элементах цепи, сопротивлении R, индуктивности L и ёмкости С, соответственно,
• Um­ – амплитудное значение переменного тока.
• Графическое изображение напряжений и токов в параллельно соединённых элементах цепи представлено ниже

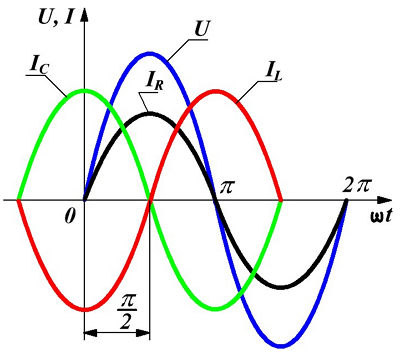
1. Аналогично второму закону Кирхгофа, для первого закона также существует тригонометрическая форма записи, которая соответствует получившемуся выражению. Выполним ещё одно преобразование данного выражения
2. где g – активная проводимость, b – реактивная проводимость.

Как видно из формулы, реактивная проводимость может быть положительной b > 0, тогда она имеет индуктивный характер, а может быть отрицательной b < 0, тогда реактивная проводимость имеет ёмкостный характер. А активная проводимость может быть только положительной.

• Отдельный случай представляет собой реактивная проводимость равная нулю, то есть в этом случае проводимость индуктивности и ёмкости одинаковы
• Такой случай называется резонансом токов, в этом случае общая проводимость будет определяться только активной проводимостью, а сдвиг фаз между напряжением и током в цепи будет нулевым.
• Определим зависимость между напряжением и силой тока в параллельной цепи
• где y – полная проводимость,
• ψ – разность фаз между напряжением и током в цепи.
• Тогда зависимость между напряжением и током в цепи с параллельно соединёнными элементами будет иметь вид
• где Um­ – амплитудное значение переменного напряжения,
• Im­ – амплитудное значение переменного тока,
• y – полная проводимость цепи.

Чему равна мощность в цепи при синусоидальном напряжении?

1. Мощность является основной энергетической характеристикой, поэтому рассмотрим мощность в цепи переменного напряжения.

   Мгновенная мощность в цепи будет равна

2. Как видно из получившегося выражения, мгновенная мощность состоит из постоянной составляющей UIcos(φ) и переменной составляющей UIcos(2ωt – φ), изменяющейся с удвоенной частотой по сравнению с частотой напряжения (тока).
3. Теперь определим среднее значение мощности за период или активную мощность, которая будет равна
4. где U – действующее значение переменного напряжения,
5. I – действующее значение переменного тока,
6. cos(φ) – коэффициент мощности.
7. Таким образом, активная мощность в цепи переменного напряжения (тока), равна произведению действующих значений напряжения и тока на коэффициент мощности.

При разработке и проектировании цепей переменного напряжения стараются сделать коэффициент мощности как можно больше, в идеале должен быть равен единице cos(φ) = 1. При небольших значениях данного коэффициента для создания в цепи необходимой мощности Р необходимо повышать величину напряжения U (тока I).

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Источник: https://www.electronicsblog.ru/silovaya-elektronika/soedinenie-elementov-v-cepi-peremennogo-napryazheniya-i-toka.html

Полное сопротивление: общие сведения, зависимость от других величин и формулы расчета

Все вещества по проводимости электрического тока (ЭТ) делятся на проводники, полупроводники и диэлектрики. Проводниками являются элементы, хорошо проводящие ЭТ. Это обусловлено наличием свободных электронов (СЭ). Полупроводники — особая группа веществ, проводимость которых зависит от внешних факторов, например, от температуры, освещенности и т. д. Диэлектриками являются все вещества, которые не проводят ЭТ из-за отсутствия или недостаточного количества СЭ. Для протекания тока по веществу требуется наличие СЭ, количество которых зависит от электронной конфигурации.

Электронная конфигурация какого-либо элемента берется из таблицы Менделеева. Ток оказывает на проводник тепловое действие, так как происходит взаимодействие СЭ с кристаллической решеткой (КР).Они замедляются, но с течением времени под действием электромагнитного поля снова ускоряются, после чего процесс взаимодействия повторяется много раз.

Процесс взаимодействия свободных заряженных частиц с КР вещества называется электрическим сопротивлением проводника. Обозначается сопротивление или электропроводимость буквой R, единицей измерения этой величины является Ом.

Зависимость электропроводимости

R зависит от внешних факторов окружающей среды, электрических величин, а также характерных особенностей проводника. Эти зависимости используются при расчетах схем и изготовлении радиодеталей. Существует несколько способов нахождения R, а иногда они комбинируются для получения эффективности и точности вычислений.

Электрические величины

К электрическим величинам, от которых зависит величина R, относятся I, U, электродвижущая сила (ЕДС обозначается е) и тип тока. R в электрических цепях рассчитывается по закону Ома для определенного участка цепи: I, протекающая в заданном участке электрической цепи, прямо пропорциональна U на этом участке и обратно пропорциональна R выбранного участка цепи. В виде формулы его можно записать следующим образом: I = U / R.

Исходя из следствия этого закона, можно получить сопротивление участка цепи: R = U / I.

Если требуется произвести расчет R на всем участке цепи, то нужно воспользоваться формулой (следствием из закона Ома для полной цепи) с учетом внутреннего R источника питания: R = (e / I) — R внутреннее.

Величина электрической проводимости рассчитывается не только при помощи законов Ома, но и с использованием геометрических параметров проводника и температуры. Кроме того, необходимо учитывать и тип тока (постоянный или переменный).

Геометрические параметры и тип вещества

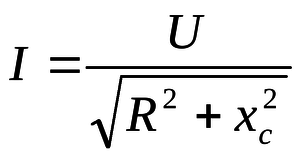
Зависимость от материала выражается коэффициентом, обозначающимся p. Он характеризует показатель удельного R проводника. Его значение берется из таблицы (при температуре +20 °C). Величина, обратная p, называется удельной проводимостью и обозначается σ. Взаимосвязь σ и p можно выразить формулой p = 1 / σ.

Кроме того, от площади поперечного сечения (S) также зависит R проводника.

Эта зависимость обусловлена тем, что при маленьком сечении плотность потока Э протекает через проводник и взаимодействие с КР становится более частым. Площадь поперечного сечения достаточно просто вычислить.

Для этого необходимо воспользоваться некоторым алгоритмом, если проводник (П) представляет собой провод цилиндрической формы:

1. Измерение диаметра проводника при помощи штангенциркуля (ШЦ).
2. Нахождение S при помощи формулы S = 3,1416 * sqr (d) / 4.

П может из себя представлять многожильный провод, поэтому для точного расчета необходимо найти S одной жилы, воспользовавшись алгоритмом нахождения для цилиндрической формы П, а затем результат умножить на количество жил.

Кроме того, бывают провода в форме квадрата и прямоугольника, но они встречаются редко. Для этого нужно выполнить следующие вычисления:

1. Для квадратной формы нужно замерить ШЦ одну из сторон и возвести ее в квадрат: S = sqr(a).
2. Для прямоугольной формы следует измерить две противолежащие стороны при помощи ШЦ, а затем произвести расчет по формуле S = a * b.

Из этих алгоритмов нахождения S можно сделать универсальный (абстрактный алгоритм). Он подходит для нахождения или расчетов величин, независимо от формы П при его разрезе, выполненном строго перпендикулярно относительно П. Алгоритм имеет следующий вид:

1. Визуально определить геометрическую фигуру при разрезе П.
2. Найти в справочнике формулу S.
3. Произвести измерения при помощи ШЦ необходимых величин.
4. Подставить в формулу и вычислить S.

Еще одной величиной является длина П, при увеличении которой R увеличивается. На основании этих величин можно вывести следующую формулу зависимости от типа вещества, длины (L) и S проводника: R = p * L / S.

Однако это значение R можно определить при температуре +20 °C. Для получения более точных расчетов нужно рассмотреть зависимость от температуры.

Температура проводника

Научно подтвержденным является факт, что p зависит от температуры. Это утверждение можно доказать практическим путем. Для проведения опыта необходимы следующие элементы, изображенные на схеме: спираль из нихрома (используется в нагревательных элементах), соединительные медные провода, источник питания, амперметр (для измерения I), вольтметр (измеряет U) и реостат.

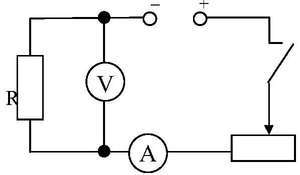
На схеме нагревательный элемент изображен в виде резистора. При его включении следует внимательно наблюдать за показаниями амперметра. Спираль начинает нагреваться, и показания амперметра уменьшаются по мере нагревания.

Согласно закону Ома для участка цепи необходимо сделать вывод, что при росте R ток уменьшается (обратно пропорциональная зависимость). Следовательно, значение R зависит от температуры.

При нагревании происходит увеличение ионов в КР нихромовой спирали и Э начинают чаще сталкиваться с ними.

В формуле R = p * L / S можно методом исключения найти показатель, зависящий от температуры. Последняя не оказывает влияния на длину П.

По формуле вычисления S зависимость также не прослеживается, поскольку геометрия П не зависит от температуры. Остается p, который зависит от температуры.

В физике существует формула зависимости p = p0 * [1 + a * (t — 20)]. Буква а является температурным коэффициентом:

• для металлов а > 0;
• для электролитов a < 0.

В этом случае происходит увеличение p. Процесс является обратимым, поэтому часть дефектов уменьшается (рекристаллический отжиг). Если на металл действуют силы растяжения или сжатия, то эта деформация является упругой.

Величина p уменьшается под действием силы сжатия, при которой происходит резкое уменьшение тепловых колебаний (ТК), а Э легче двигаются.

Но под действием силы растяжения происходит прямо пропорциональное увеличение p, при котором амплитуда ТК увеличивается.

Конечную формулу можно записать в виде R = p0 * [1 + a * (t — 20)] * L / S. Однако этот вариант нахождения R был рассмотрен в цепях с постоянным I, а под действием переменного I появляются новые величины, влияющие на расчеты.

Цепь переменного тока

Закон Ома применяется только для цепей постоянного тока. Для переменного U он изменен и, следовательно, существуют другие формулы нахождения R. Сопротивление в цепях с переменным I (ПТ) бывает:

• активным;
• индуктивным;
• емкостным;
• полным.

Активное сопротивление свидетельствует о том, что в цепи присутствует резистор или любая другая неемкостная или неиндуктивная нагрузка. Для его расчета необходимо произвести измерение значений амплитуд Um и Im.

При помощи приборов можно получить только действующие значения этих величин. Амплитудные значения рассчитываются по формулам Um = Ud * sqrt(2) и Im = Id * sqrt(2). Для определения активного сопротивления (обозначается R) нужно воспользоваться формулой Iм = Uм / R.

Из неё можно получить R = Ud * sqrt(2) / Im = Id * sqrt(2).

Если в цепи переменного I (ЦПТ) присутствуют катушка индуктивности, дроссель, контур и т. д., то появляется индуктивное R, которое обозначается Xl. Для расчета необходимо воспользоваться формулой Xl = w * L, предварительно измеряв частоту ПТ и рассчитав индуктивность.

Величина циклической частоты находится по формуле, для которой нужно измерять частоту ПТ (f): w = 2 * 3,1416 * f. Последняя измеряется при помощи осциллографа или частотомера. Для расчета индуктивности катушки необходимо воспользоваться справочником по физике или онлайн-калькулятором.

При наличии в ЦПТ емкости (конденсатора) возникает емкостное R, которое обозначается Xc. При протекании постоянного U конденсатор не пропускает I, а в ЦПТ он пропускает I и обладает емкостью (C) и Xc. Рассчитывается это значение по формуле Xc = 1 / (w * C), где:

• w — циклическая частота, которая рассчитывается аналогично вычислению Xl;
• C — емкость конденсатора, указанная на корпусе или измеренная соответствующим прибором.

Полное сопротивление цепи обозначается Z и представляет собой сумму всей нагрузки ЦПТ (активного, индуктивного и емкостного сопротивления). Для расчета нужно воспользоваться формулой полного сопротивления: Z = sqrt [sqr(R) + sqr (Xc — Xl)]. В ЦПТ величина Z зависит от:

• геометрии П;
• типа вещества, из которого сделан П;
• температуры;
• деформации различного вида;
• электрических показателей I, U, f, L, C и R.

Закон Ома для участка цепи принимает следующий вид: I = U / Z. Необязательно рассчитывать электропроводимость П, так как для этих целей существуют омметры. Расчет Xl и Xс следует производить самостоятельно.

Измерение сопротивления

Для измерения R необходимо обесточить участок или радиокомпонент и проследить за разрядкой цепей, где присутствуют конденсаторы. Перед проведением измерений нужно выставить необходимый режим на приборе и закоротить щупы для проверки прибора на исправность. Некоторые модели снабжены функцией звукового сигнала. После теста прибора следует приступить к измерениям.

Для нахождения точной величины Z проводника необходимо учитывать все величины, от которых оно зависит.

Вычисление Z позволяет точно рассчитать электрическую схему какого-либо устройства для избегания трудоемких измерений.

Измерить омметром можно только величину активного сопротивления, а Xl и Xc следует рассчитывать самостоятельно. Однако при помощи онлайн-калькуляторов сделать это не составит особого труда.

Источник: https://220v.guru/fizicheskie-ponyatiya-i-pribory/moschnost/soprotivlenie/raschet-polnogo-soprotivleniya-cepi-pod-deystviem-peremennogo-toka.html

Электрический импеданс

Импеданс (impedance) – комплексное, полное сопротивление переменному току электрической цепи с активным и реактивным сопротивлением.

Импеданс и общий сдвиг фаз для синусоидального тока можно рассчитать исходя из последовательного или параллельного соединения элементов цепи.

Последовательное соединение

При последовательном соединении, согласно Закону Ома для переменного тока, во всех элементах цепи ток будет общим I = U/Z, а значения напряжений на каждом элементе определятся пропорционально его сопротивлению:
на выводах резистора UR = IR; на выводах конденсатора UC = IXC; на выводах катушки UL = IXL.

Векторы индуктивной и ёмкостной составляющих напряжения направлены в противоположные стороны.
С учётом отрицательного ёмкостного сдвига, общее напряжение на реактивных элементах UX = UL — UC . Пропорционально напряжению, получим общее реактивное сопротивление X = XL — XC . Векторы напряжений на активной и реактивной составляющей импеданса имеют угол сдвига фаз 90 градусов.

U , UR и UX представим в виде прямоугольного треугольника напряжений с углом сдвига фаз φ.

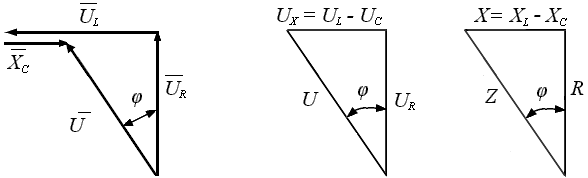
Тогда получим соотношение, согласно Теореме Пифагора, U ² = UR² + UX² .
Следовательно, с учётом пропорциональности элементов R, L, C значениям напряжений на их выводах, определим импеданс, который будет равен квадратному корню из суммы квадратов активного и реактивного сопротивлений цепи.

XL = ωL = 2πfL — реактивное сопротивление индуктивности. XC = 1/(ωC) = 1/(2πfC) — реактивное сопротивление ёмкости.

Угол сдвига фаз φ и его дополнение до 90° δ
определятся тригонометрическими функциями из треугольника сопротивлений с катетами R, X и гипотенузой Z, как показано на рисунке:

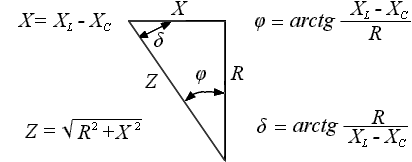
• Обычно, для облегчения расчётов, импеданс представляют в виде комплексного числа,
  где действительной его частью является активное сопротивление, а мнимой — реактивное.
  Для последовательного соединения импеданс можно записать в комплексном виде следующим образом:
• Z = R + jX
• Тогда в тригонометрической интерпретации модулем этого числа будет импеданс, а аргументом — угол φ.
  В соответствии с формулой Эйлера, запишем показательную форму комплексного импеданса:
• Z = |Z|ejargZ = Zejφ
• Отсюда активная составляющая импеданса R = Zcosφ
  Реактивная составляющая X = Zsinφ.

Параллельное соединение

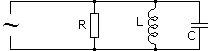
1. Для вычисления импеданса при параллельном соединении активных и реактивных сопротивлений будем исходить из суммы обратных им величин — проводимостей y = 1/Z, G = 1/R, b = 1/X.
2. y = 1/Z = √(G2 + b2)
3. Сдвиг фаз в этом случае будет определён треугольником сопротивлений следующим образом:

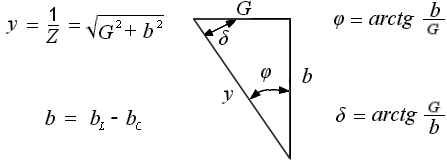
• Комплексную проводимость, как величину, обратную комплексному импедансу, запишем в алгебраической форме:
• Y = G — jb
• Либо в показательной форме:
• Y = |Y|e -jφ = ye -jφ

Здесь: Y — комплексная проводимость.
G — активная проводимость.
b — реактивная проводимость.
y — общая проводимость цепи, равная модулю комплексной проводимости.
e — константа, основание натурального логарифма.
j — мнимая единица. φ — угол сдвига фаз.

Онлайн-калькулятор расчёта импеданса и угла сдвига фаз

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Последовательное соединениеZ = √(R²+(XL-Xc)²)

Параллельное соединениеZ = 1/√(1/R²+(1/XL-1/Xc)²)

Похожие страницы с расчётами:

Реактивное сопротивление. Расчёт.

Частота резонанса колебательного контура LC. Расчёт.
Реактивная мощность и компенсация. Расчёт.

Замечания и предложения принимаются и приветствуются!

Источник: https://tel-spb.ru/impedance/

Расчет импеданса в параллельном соединении элементов цепи

Любая электрическая цепь включает в себя ряд элементов, среди которых встречаются активные и реактивные составляющие. При параллельном соединении активного, емкостного и индуктивного элемента схема выглядит таким образом:

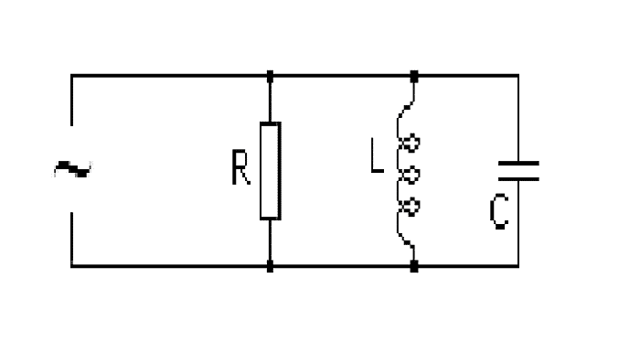Рис. 1. Параллельное соединение элементов электрической цепи

В зависимости от конкретной ситуации тот или иной элемент может исключаться из цепи, меняя тем самым характер нагрузки. Для геометрического определения суммарного значения всех сопротивлений производится сложение векторов. В зависимости от типа реактивной нагрузки результирующий вектор импеданса будет смещаться в положительный или отрицательный квадрант.

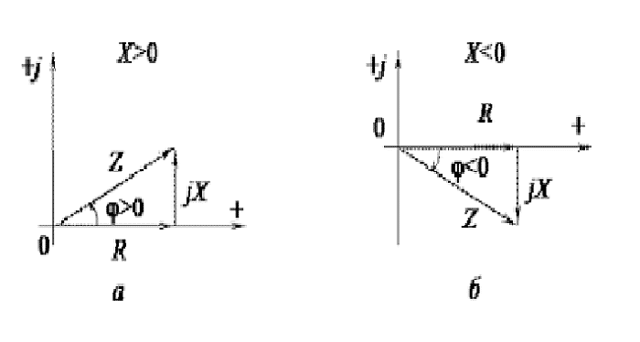Рис. 2. Векторное сложение сопротивления

Для вычисления полного сопротивления Z составляется уравнение согласно теоремы пифагора. Только сложению подлежит не сопротивление, а проводимость цепи. Из-за чего уравнение для определения сопротивления можно будет выразить по следующей формуле:

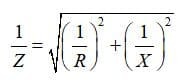
Где Z – комплексное сопротивление участка,  R – активное сопротивление участка, X – реактивное сопротивление участка.

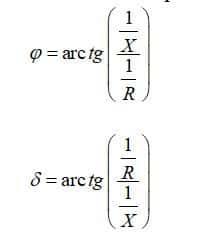
В связи с большим количеством расчетов, применяемых формул и необходимостью использования тригонометрических функций определение импеданса в параллельной цепи является достаточно сложной задачей, особенно, если делать это вручную. Но, при использовании онлайн калькулятора для расчета комплексного сопротивления достаточно ввести частоту, емкость конденсатора, индуктивность катушки и омическое сопротивление резистора. А все расчеты система произведет самостоятельно.

Источник: https://www.asutpp.ru/kalkulyator-rascheta-impedansa-v-parallelnom-soedinenii-elementov-tsepi.html

Полное сопротивление

Главная > Теория > Полное сопротивление

К любому базовому элементу схемы можно применить математическое описание, используя ток, напряжение и сопротивление. И если для постоянного тока эти зависимости просты, то математические выражения для систем переменного тока должны учитывать синусоидальный характер параметров цепи.

Разные элементы схемы переменного тока

Что такое импеданс

Полное сопротивление цепи переменного тока, или импеданс, обозначаемый Z, является отражением меняющегося во времени значения тока. Импеданс представляет собой векторную (двумерную) величину, состоящую из двух независимых скалярных одномерных значений: активного и реактивного сопротивления.

Активное сопротивление

Активная часть импеданса, обозначенная R, является мерой степени, с которой материал противостоит движению электронов между его атомами. Чем легче атомы высвобождают или принимают электроны, чем ниже сопротивление, которое выражается в положительном действительном числе ом.

Важно! Активное сопротивление неизменно при переменном и постоянном токе.

Примеры материалов с низким сопротивлением: медь, серебро, золото. Высокоомные вещества называются изоляторами, или диэлектриками, и включают в свой перечень слюду, стекло, полиэтилен и др. Материалы с промежуточным уровнем сопротивления – полупроводники, к примеру, арсенид галлия, кремний, германий.

При активной нагрузке ток и напряжение являются синфазными, то есть одновременно достигают пиковых значений и падают до нуля. Они меняются по закону:

• I(t) = Im x sin (ωt + θ);
• U(t) = R x Um x sin (ωt + θ), где:
• Im и Um – максимальные амплитуды тока и напряжения,
• ω – угловая частота,
• θ – угол сдвига фаз между ними, который будет равен 0.

На векторной диаграмме синфазный эффект представляется как наложение друг на друга векторов I и U вдоль одной оси.

Активная нагрузка на переменном токе

• При использовании резисторов в цепях синусоидального тока слово «импеданс» и символ Z используются для обозначения его сопротивления:
• R = Z.
• Импеданс может быть представлен также комплексным числом, так как он зависит от частоты схемы. Но в случае чисто резистивной нагрузки реактивная часть всегда будет равна 0:
• Z = R + j0 = R.
• Практические расчеты можно также выполнять по формуле:
• Z = Um/Im.

Реактивное сопротивление

Реактивная часть, обозначенная Х, – выражение степени, с которой электронный компонент схемы хранит или высвобождает энергию, когда ток и напряжение колеблются при каждом цикле. Х выражается в мнимом числе Ом.

Энергия может храниться и выделяться в двух видах:

1. Магнитного поля. Тогда реактивное сопротивление является индуктивным (+jXL);
2. Электрического поля. При этом реактивное сопротивление будет емкостным (-jXC).

Индуктивная нагрузка

Противодействие переменному току в цепи с катушкой зависит не только от ее индуктивности, но и от частоты токового сигнала. С ростом частоты увеличивается индуктивное сопротивление.

Чистой индуктивности в природе нет. Все электрические катушки, реле и трансформаторы имеют определенное активное сопротивление, обусловленное удельным сопротивлением медного провода. Тогда можно рассматривать индуктивную катушку как последовательное сопротивление R и XL.

Индуктивная нагрузка на переменном токе

1. Когда две и более индуктивных катушки соединены последовательно, или одиночная катушка также соединяется с резисторными элементами, то общее сопротивление резисторов:
2. R = R1+ R2 + R3 + …,
3. а общее значение:
4. XL = XL1 + XL2 + XL3 + …
5. Комплексное сопротивление цепи с катушкой принимает вид:
6. Z = R + jXL.

Мнимый показатель j показывает, что сигналы тока и напряжения сдвинуты по фазе на 90 градусов. Знак «+»  указывает на отставание тока на этот угол.

Фактические расчеты ведутся по формуле:

XL = 2π x f x L, где:

• f – токовая частота (Гц),
• L – значение индуктивности.

• Так как угловая частота ω = 2π x f, то XL = ω x L.
• Результирующая векторная диаграмма – прямоугольный треугольник, в котором катетами являются R и XL, а гипотенуза и будет полным сопротивлением Z.
• Исходя из соотношения сторон треугольника:
• Z² = R² + XL² и Z = √ (R² + XL²).

Емкостная нагрузка

Конденсаторы хранят энергию на проводящих пластинах в виде электрозаряда. На постоянном токе они могут удерживать этот заряд неограниченное количество времени (для чистого конденсатора). Чистых конденсаторных элементов не существует, они всегда имеют определенное внутреннее сопротивление, и появляется ток утечки.

При переменном синусоидальном сигнале конденсатор сначала заряжается в одном направлении, а в другой полупериод меняет полярность на противоположную. Таким образом, во времени заряд меняется, а энергия выделяется в цепь.

Емкостная нагрузка на переменном токе

1. Выражение для комплексного емкостного сопротивления:
2. Z = R – jXC,
3. где j со знаком «минус» указывает на опережение током напряжения на 90 градусов.
4. XC вычисляют по формуле:
5. XC = 1/(2π x f x C) = 1/ω x С.

Важно! Каждый конденсаторный элемент можно представлять в виде активного сопротивления R, соединенного последовательно с чистой емкостью С.

Формулой полного сопротивления электроцепи с емкостью будет:

Z = √ (R² + XС²).

Важно! Когда резисторы и конденсаторы последовательно соединены в одной и той же схеме, общий импеданс на векторной диаграмме имеет фазовый угол между 0 и 90 градусами, в зависимости от значения используемых компонентов.

• При наличии в одной схеме конденсатора и индуктивной катушки реактивная часть импедансов рассчитывается как:
• Z = XL – XC.
• Соответственно, выражение для полного импеданса:
• Z = √ (R² + (XL – XС)²).

Параллельные схемы RLC более сложны для анализа. Для вычисления импеданса значения активной и реактивной части сопротивления преобразуются в обратную величину – проводимость.

1. Комплексная проводимость равна Y = 1/Z = g – jb, где:

• g = R/(R² + X²),
• b = X/(R² + X²).

1. Численное значение импеданса в параллельной цепи:

Z = 1/√(1/R² + (1/XL² – 1/XС²).

Для практических расчетов можно воспользоваться калькуляторами в онлайн режиме, где просто вводятся параметры элементов схемы, в зависимости от вида их соединения.

Видео

Сопротивление тока: формула

Источник: https://jelectro.ru/teoriya/polnoe-soprotivlenie.html

2.5. Сопротивления в цепи переменного тока

В цепях
переменного тока выделяют следующие
виды сопротивлений.

Активное.
Активным называют сопротивление
резистора. Условное обозначение

Единицей
измерения сопротивления является Ом.
Сопротивление резистора не зависит от
частоты.

Реактивное.
В разделе реактивные выделяют три вида
сопротивлений: индуктивное xL и емкостное
хс и собственно реактивное. Для
индуктивного сопротивления выше была
получена формула XL = ωL.
Единицей измерения индуктивного
сопротивления также является Ом. Величина
xL линейно зависит от частоты.

Для
емкостного сопротивления выше была
получена формула XC = 1 / ωC.
Единицей измерения емкостного
сопротивления является Ом. Величина хс
зависит от частоты по обратно-пропорциональному
закону. Просто реактивным сопротивлением
цепи называют величину X = XL — XC.

Полное
сопротивление.
Полным сопротивлением цепи называют
величину

(2.28)

• Из этого
  соотношения следует, что сопротивления
  Z, R и X образуют треугольник: Z – гипотенуза,
  R и X – катеты. Для удобства в этом
  треугольнике рассматривают угол φ,
  который определяют уравнением
• (2.29)
• φ
  = arctg((XL — XC)
  / R),
• и называют
  углом сдвига фаз. С учетом него можно
  дать дополнительные связи
• (2.30)
• R
  = Z cos φ,
• (2.31)
• X
  = Z sin φ.

2.6. Мощности в цепях переменного тока

По аналогии
с мощностью в цепях постоянного тока
P = U I, в цепях переменного тока
рассматривают мгновенную мощность
p = u i. Для упрощения рассмотрим
мгновенную мощность в каждом из элементов
R, L и С отдельно.

Элемент r (резистор)

1. Зададим
   напряжение и ток в виде соотношений
2. u(t)
   = Um
   sin(ωt
   + ψu),
3. i(t)
   = Im
   sin(ωt
   + ψi).
4. Известно,
   что для резистора ψu
   = ψi,
   тогда для р получим
5. (2.

   32)

6. p(t)
   = u(t) i(t) = Um
   Im
   sin2(ωt
   + ψi).

Из
уравнения (2.32) видно, что мгновенная
мощность всегда больше нуля и изменяется
во времени.

В таких случаях принять
рассматривать среднюю за период Т
мощность

(2.33)

• Если
  записать Um
  и Im
  через действующие значения U и I: ,,
  то получим
• (2.34)
• P = U I.

По форме
уравнение (2.34) совпадает с мощностью на
постоянном токе. Величину Р равную
произведению действующих значений тока
и напряжения называют активной мощностью.
Единицей ее измерения является Ватт
(Вт).

Элемент l (индуктивность)

Известно,
что в индуктивности соотношение фаз
ψu = ψi + 90°.
Для мгновенной мощности имеет

(2.35)

Усредняя
уравнение (2.35) по времени за период Т
получим

1. Для
   количественной оценки мощности в
   индуктивности используют величину QL
   равную максимальному значению рL
2. (2.36)
3. QL
   = (Um
   Im)
   / 2

и называют
ее реактивной (индуктивной) мощностью.
Единицей ее измерения выбрали ВАр
(вольт-ампер реактивный). Уравнение
(2.36) можно записать через действующие
значения U и I и используя формулу
UL = I XL получим

(2.37)

QL = I2 XL.

Элемент с (ёмкость)

Известно,
что в емкости соотношение фаз ψu = ψi — 90°.
Для мгновенной мощности получаем

pC(t)
= u(t) I(t) = (Um
Im)
/ 2 · sin(2ωt).

Среднее
значение за период здесь также равно
нулю. По аналогии с уравнением (2.36) вводят
величину QC = I2 XC,
которую называют реактивной (емкостной)
мощностью. Единицей ее измерения также
является ВАр.

• Если в
  цепи присутствуют элементы R, L и С, то
  активная и реактивная мощности
  определяются уравнениями
• (2.37)
• P
  = U I cos φ,
• (2.38)
• Q = QL — QC,
• (2.39)
• Q
  = U I sin φ,
• где
  φ
  – угол
  сдвига
  фаз.
• Вводят
  понятие полной мощности цепи
• (2.40)

С учетом
уравнений (2.37) и (2.39), (2.40) можно записать
в виде

1. (2.41)
2. S = U I.
3. Единицей
   измерения полной мощности является ВА
   – вольт-ампер.

Источник: https://studfile.net/preview/6219684/page:4/

Активное сопротивление в цепи переменного тока

На векторных диаграммах можно показать, что ток и напряже­ние совпадают по фазе (рис. 52,а) или э. д.с. сдвинуты по фазе на некоторый угол (рис. 52,6). Условно принято считать, что векторы перемещаются в направлении против движения часовой стрелки.

Если векторы имеют различную длину, следовательно, их дейст­вующие значения разные (см. рис. 52, б).

• § 52. АКТИВНОЕ СОПРОТИВЛЕНИЕ В ЦЕПИ ПЕРЕМЕННОГО ТОКА
• Сопротивление, включенное в цепь переменного тока, в котором происходит превращение электрической энергии в полезную рабо­ту или в тепловую энергию, называется активным сопротивлением.
• К активным сопротивлениям при промышленной частоте (50 гц) относятся, например, электрические лампы накаливания и электро­нагревательные устройства.

Рассмотрим цепь переменного тока (рис. 53), в которую вклю­чено активное сопротивление. В такой цепи под действием перемен­ного напряжения протекает переменный ток. Изменение тока в Цепи, согласно закону Ома, зависит только от изменения напряже­ния, подключенного к ее зажимам.

Когда напряжение равно нулю, ток в цепи также равен нулю. По мере увеличения напряжения ток в Цепи возрастает и при максимальном значении напряжения ток становится наибольшим. При уменьшении напряжения ток убывает.

Когда напряжение изменяет свое направление, ток также изменяет свое направление и т. д.

Из сказанного следует, что в цепи переменного тока с актив­ным сопротивлением по мере изменения по величине и направлению напряжения одновременно пропорционально меняются величина и Направление тока. Это значит, что ток и напряжение совпадают по фазе.

Построим векторную диаграмму действующих величин тока и  напряжения для цепи с активным сопротивлением. Для этого отлов жим в выбранном масштабе по горизонтали вектор напряжения  Чтобы на векторной диаграмме показать, что напряжение и ток в  цепи совпадают по фазе (=0), откладываем вектор тока I по направлению вектора напряжения.

1. Сила тока в такой цепи определяется по закону Ома:
2. В этой цепи среднее значение мощности, потребляемой активным сопротивлением, выражается произведением действующих значения тока и напряжения.

Пример.  К  цепи  переменного  тока  с  активным  сопротивлением  r=55 ом  подключен генератор, максимальное значение напряжения которого Um=310,2 в.

Определить:

показание вольтметра, подключенного к зажимам генератора; показание амперметра, включенного в цепь; среднее значение мощности, потребляемой сопротивлением.

 Решение. Известно,  что  электроизмерительные  приборы,  включенные в цепь переменного тока, измеряют действующие  значения.  Поэтому  показание  вольтметра, измеряющего напряжение,

Показание амперметра, измеряющего действующее значение тока,

Среднее  значение  активной  мощности,  потребляемой  сопротивлением,  Р=220х4 = 880 вт или Р=I2r=42×55=16×55=880 вт.

§ 53. ИНДУКТИВНОСТЬ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

Прохождение электрического тока по проводнику или катушки сопровождается появлением магнитного поля. Рассмотрим электрическую цепь переменного тока (рис. 54,а), в которую включена катушка индуктивности, имеющая небольшое количество витком проволоки сравнительно большого сечения, активное сопротивления которой можно считать практически равным нулю.

Под действием э. д. с. генератора в цепи протекает переменный ток, возбуждающий переменный магнитный поток. Этот поток пересекает «собственные» витки катушки и в ней возникает электродвижущая сила самоиндукции

•    (55)
• где L — индуктивность катушки,
• — скорость изменения тока в ней.

Электродвижущая сила самоиндукции, согласно правилу Лен­ца, всегда противодействует причине, вызывающей ее. Так как э. д. с. самоиндукции всегда противодействует изменениям переменного тока, вызываемым э. д.с. генератора, то она препятствует прохож­дению переменного тока. При расчетах это учитывается по индук­тивному  сопротивлению,  которое  обозначается ХL  и  измеряется

в омах. Таким образом, индуктивное сопротивление катушки ХL зависит от величины э. д. с. самоиндукции, а следовательно, оно, как и э. д. с. самоиндукции, зависит от скорости изменения тока в ка­тушке (от частоты ) и от индуктивности катушки L:

1. где XL, — индуктивное сопротивление, ом,
2. ώ — угловая частота переменного тока, рад/сек,
3. L — индуктивность катушки, гн.
4.  Так как угловая частота переменного тока  , то индуктив­ное сопротивление

где, f—-частота переменного тока, гц.

Пример. Катушка,  обладающая  индуктивностью  L=0,5 гн,  присоединена к источнику переменного тока, частота которого f=50 гц. Определить:

• 1)  индуктивное сопротивление катушки при частоте f=50 гц;
• 2)  индуктивное сопротивление этой катушки переменному току, частота ко­торого f=800 гц.
• Решение. Индуктивное сопротивление переменному току при f=50 гц

При частоте тока f=800 гц

Приведенный пример показывает, что индуктивное сопротивление катушки повышается с увеличением частоты переменного тока,  протекающего по ней. По мере уменьшения частоты тока индуктивное сопротивление убывает.

Для постоянного тока, когда ток в катушке не изменяется и магнитный поток не пересекает ее витки,  э. д. с. самоиндукции не возникает, индуктивное сопротивлений катушки ХL равно нулю.

Катушка индуктивности для постоянного тока представляет собой лишь сопротивление

Выясним, как изменяется э. д. с. самоиндукции, когда по катушке индуктивности протекает переменный ток.

Известно, что при неизменной индуктивности катушки э. д. с. самоиндукции зависит от скорости изменения силы тока и она всегда направлена навстречу причине, вызвавшей ее.

На графике (рис. 54, в) переменный ток показан в виде синусоиды (сплошная линия). В первую четверть периода сила тока возрастает от нулевого до максимального значения. Электродвижущая сила самоиндукции ес, согласно правилу Ленца, препятствует увеличению тока в цепи.

Поэтому на графике (пунктирной линией) показано, что ес в это время имеет отрицательное значение. Во вторую четверть периода сила тока в катушке убывает до нуля. В это время э. д.с. самоиндукции изменяет свое направление и увеличивается препятствуя убыванию силы тока.

В третью четверть периода том изменяет свое направление и постепенно увеличивается до максимального значения; э. д. с. самоиндукции имеет положительное значение и далее, когда сила тока убывает, э. д. с.

самоиндукции опять меняет свое направление и вновь препятствует уменьшению силы  тока в цепи.

Источник: http://fiziku5.ru/uchebnye-materialy-po-fizike/aktivnoe-soprotivlenie-v-cepi-peremennogo-toka

Расчет сопротивления фаз

Реактивное
сопротивления фазы

.

Полное
сопротивление фазы и его аргумент

,
.

Расчет
линейных (фазных) токов

Линейные
токи находятся по уравнениям

,

где

;;;;

,

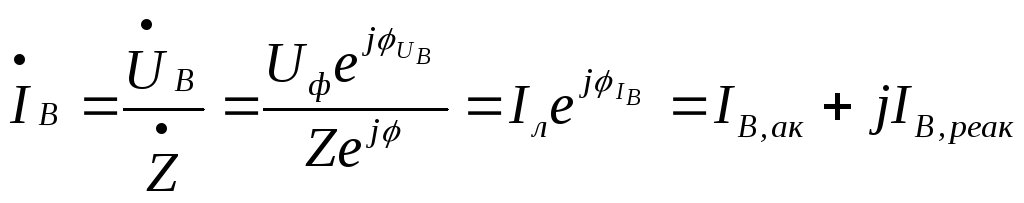где
;;;

,

где
;;.

Примерная
векторная диаграмма токов и напряжений
показана на рис.1.2.

Рис.
1.2. Векторная диаграмма токов и напряжений

Расчет
активных мощностей фаз и всей трехфазной
цепи

При
симметричной нагрузке активная мощность
в каждой фазе определятся уравнением
,
суммарная мощность сети.

Для
проверки правильности расчетов
целесообразно рассчитать суммарную
мощность, выделяемую в резисторах фаз

.

Задача 2. Исследование четырехпроводных трехфазных цепей при несимметричной нагрузке

1.
По базе данных (табл.2.1) для своего
варианта определить параметры
электрической цепи (рис. 2.1), питающей
от трехфазной сети синусоидального
тока.

Рис.
2.1

2.
Рассчитать фазные и линейные напряжения
и их аргументы.

3.
Рассчитать сопротивления фаз.

4.
Рассчитать линейные (фазные) токи и
построить векторную диаграмму токов и
напряжений.

5.
Рассчитать активные мощности фаз и в
целом всей трехфазной цепи.

6.
Исследовать влияние параметра, индекс
которого указан в столбце 17 табл. 2.1, на
токи ветвей и потребляемые мощности.
Построить графики
и,

Исходные данные трехфазной цепи по вариантам

Таблица2.1.

Номер варианта	Модули и аргументы фазных ЭДС	Сопротивления резисторов	Индекс изменяемого параметра
В	град	В	град	В	град	Ом
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
1	220	0	220	-120	220	120	20	20	10	5	20	0	5	0	20	6
2	220	0	220	-120	220	120	19	28.5	14	14	19	28.5	28	42	21	4
3	220	0	220	-120	220	120	18	27	13	13	18	27	27	40	19.5	7
4	220	0	220	-120	220	120	17	25.5	12	12	17	25.5	25	38	18	6
5	220	0	220	-120	220	120	16	24	11	11	16	24	24	36	16.5	5
6	220	0	220	-120	220	120	15	22.5	12	12	15	22.5	22	33	18	4
7	220	0	220	-120	220	120	14	21	13	13	14	21	21	31	19.5	3
8	220	0	220	-120	220	120	13	19.5	14	14	13	19.5	19	29	21	3
9	220	0	220	-120	220	120	12	18	15	15	12	18	18	27	22.5	2
10	220	0	220	-120	220	120	11	16.5	16	16	11	16.5	16	24	24	5
11	220	0	220	-120	220	120	12	18	17	17	12	18	18	27	25.5	6
12	220	0	220	-120	220	120	13	19.5	18	18	13	19.5	19	29	27	7
13	220	0	220	-120	220	120	14	21	19	19	14	21	21	31	28.5	8
14	220	0	220	-120	220	120	15	22.5	20	20	15	22.5	22	33	30	9
15	220	0	220	-120	220	120	16	24	21	21	16	24	24	36	31.5	2
16	220	0	220	-120	220	120	17	25.5	22	22	17	25.5	25	38	33	3
17	220	0	220	-120	220	120	18	27	16	16	18	27	27	40	24	4
18	220	0	220	-120	220	120	19	28.5	17	17	19	28.5	28	42	25.5	5
19	220	0	220	-120	220	120	20	30	18	18	20	30	30	45	27	6
20	220	0	220	-120	220	120	21	31.5	19	19	21	31.5	31	47	28.5	7
21	220	0	220	-120	220	120	22	33	20	20	22	33	33	49	30	8
22	220	0	220	-120	220	120	23	34.5	21	21	23	34.5	34	51	31.5	9
23	220	0	220	-120	220	120	24	36	22	22	24	36	36	54	33	8
24	220	0	220	-120	220	120	25	37.5	23	23	25	37.5	37	56	34.5	3
25	220	0	220	-120	220	120	24	36	24	24	24	36	36	54	36	5
26	220	0	220	-120	220	120	23	34.5	25	25	23	34.5	34	51	37.5	6
27	220	0	220	-120	220	120	22	33	24	24	22	33	33	49	36	7
28	220	0	220	-120	220	120	21	31.5	18	18	21	31.5	31	47	27	8
29	220	0	220	-120	220	120	20	30	19	19	20	30	30	45	28.5	2
30	220	0	220	-120	220	120	19	28.5	20	20	19	28.5	28	42	30	3
31	220	0	220	-120	220	120	18	27	21	21	18	27	27	40	31.5	5
32	220	0	220	-120	220	120	17	25.5	22	22	17	25.5	25	38	33	7
33	220	0	220	-120	220	120	16	24	23	23	16	24	24	36	34.5	9
34	220	0	220	-120	220	120	15	22.5	24	24	15	22.5	22	33	36	6
35	220	0	220	-120	220	120	16	24	25	25	16	24	24	36	37.5	7
36	220	0	220	-120	220	120	17	25.5	24	24	17	25.5	25	38	36	5
37	220	0	220	-120	220	120	18	27	23	23	18	27	27	40	34.5	3
38	220	0	220	-120	220	120	19	28.5	22	22	19	28.5	28	42	33	2
39	220	0	220	-120	220	120	20	30	21	21	20	30	30	45	31.5	4
40	220	0	220	-120	220	120	21	31.5	20	20	21	31.5	31	47	30	6
41	220	0	220	-120	220	120	22	33	19	19	22	33	33	49	28.5	8
42	220	0	220	-120	220	120	23	34.5	18	18	23	34.5	34	51	27	9
43	220	0	220	-120	220	120	24	36	24	24	24	36	36	54	36	3
44	220	0	220	-120	220	120	23	34.5	23	23	23	34.5	34	51	34.5	2
45	220	0	220	-120	220	120	22	33	22	22	22	33	33	49	33	5
46	220	0	220	-120	220	120	21	31.5	21	21	21	31.5	31	47	31.5	6
47	220	0	220	-120	220	120	20	30	20	20	20	30	30	45	30	7
48	220	0	220	-120	220	120	19	28.5	19	19	19	28.5	28	42	28.5	8
49	220	0	220	-120	220	120	18	27	18	18	18	27	27	40	27	9
50	220	0	220	-120	220	120	17	25.5	17	17	17	25.5	25	38	25.5	3

Расчет
фазных и линейных напряжений и их
аргументов

Фазные
напряжения на нагрузке находятся по
уравнениям

;
;,

где
;;;;;;.

Линейные
напряжения определяются уравнениями

где
;

;

;

при
;
при;

где
;

;

;

при
;
при;

где
;

;

;

при
;
при;.

Расчет
линейных (фазных) токов

Линейные
токи находятся по уравнениям

,

где

;;;;

,

где;;;;

,

где
;;;.

Ток
нулевого провода

,

где
;;

при
;
при;.

Примерная
векторная диаграмма токов и напряжений
приведена на рис.2.2.

Рис.
2.2. Векторная диаграмма токов и напряжений

Расчет
активных мощностей фаз и всей трехфазной
цепи

Активная
мощность в фазах определятся уравнениями
,;.

Суммарная
мощность трехфазной сети

.

Для
проверки правильности расчетов
целесообразно рассчитать суммарную
мощность, выделяемую в резисторах фаз

.

Исследование
влияния заданного параметра на токи
ветвей и потребляемые мощности

Исследования
провести с помощью программы Exsel
кр_3_2.xls.
Программа позволяет выполняет расчеты,
аналогичные ранее проведенным, для 23
значений заданного параметра.

Сопротивление
параметра изменяется от
до

.
Для построения графиков программа
формирует соответствующие таблицы и
строит требуемые графики.

Программу
Exsel
кр_3_2.xls
можно
получить на кафедре. На кафедре также
можно получить образец оформления
контрольной работы в виде файла Отчет
_3.doc/

Соседние файлы в папке Кон раб_3

• #

  11.02.201537.38 Кб66Exsel_3_1.xls

• #

  11.02.2015140.8 Кб55Exsel_3_2.xls

• #

  11.02.2015254.46 Кб51Exsel_3_3.xls

• #

  11.02.201588.06 Кб45Exsel_3_4.xls

• #
• #
• #