Так как в схеме есть нейтральный провод,
то напряжение на фазах нагрузки равно
соответствующему фазному напряжению
источника питания (обмотки генератора
считаем соединенными звездой, а
сопротивлением нейтрального провода
пренебрегаем):

Рисунок 9 – Схема
трёхфазной цепи при соединении
потребителей звездой
![]() ,
,
![]() ,
,
![]() ;
;
в численном
виде:
![]()
Определим реактивные сопротивления, принимая частоту сети переменного тока равной 50 Гц, а угловую частоту
ω = 2πf
=
2 ∙ 3,14 ∙ 50
= 314 1/с .
Реактивное
индуктивное
сопротивление
xL3 =
ω L3 = 314 ∙ 31,8 ∙ 10–3 = 10 Ом.
Реактивное
емкостное
сопротивление
xС2 =1/(ω С2) = 1/(314 ∙ 159 ∙ 10–6) = 20 Ом.
В общем случае
полное сопротивление
каждой из
фаз в комплексной форме определяют с
помощью выражения, которое использовалось
в однофазных цепях,
![]() .
.
Применяем эту формулу для нашего
конкретного случая и получаем полные
сопротивления фаз в следующем виде:
![]()
Комплексные
сопротивления фаз различны, следовательно,
нагрузка несимметричная.
Токи в линейных проводах (фазные токи
нагрузки) определяем с помощью закона
Ома:
![]()
![]()
![]()
Ток в нейтральном проводе находим по
первому закону Кирхгофа
![]()
Полные
мощности фаз:
![]()
![]()
![]()
Так как вещественная часть полной
мощности есть активная мощность цепи,
а мнимая часть – реактивная, то,
просуммировав отдельно вещественные,
а затем мнимые части мощностей трех
фаз, определяем трехфазную активную и
реактивную мощности.
Активная трехфазная мощность
![]()
Реактивная трехфазная мощность
![]()
Полная мощность
![]()
Активная трехфазная мощность нагрузки
может быть определена суммой активных
мощностей потребителей каждой из фаз
![]()
Относительная ошибка вычислений для
активной мощности
![]()
Реактивная трехфазная мощность нагрузки
также определяется суммой реактивных
мощностей потребителей каждой из фаз
Суммарная реактивная мощность всех потребителей
![]()
Относительная
ошибка вычислений для активной мощности
![]()
Ошибка
менее одного процента допускается.
Таким образом, баланс активных и
реактивных мощностей соблюдается,
значит токи определены правильно.
Векторную диаграмму размещаем на
комплексной плоскости с осями +1 и + j,
рисунок 3.21. Выбираем масштаб векторов
тока равным 10 А/деление, а векторов
напряжения – 40 В/деление. Строим
векторы фазных напряжений, а затем
векторы токов. Длина вектора соответствует
в масштабе модулю показательной формы
соответствующего выражения тока или
напряжения, а угол, под которым этот
вектор строится к вещественной оси,
равен аргументу комплексного значения
величины.
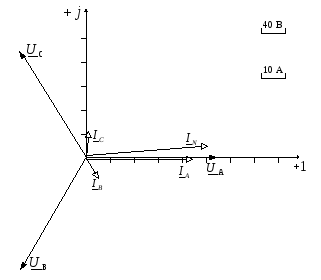
Рисунок 10
– Векторная диаграмма при соединении
потребителей
звездой с нейтральным проводом
2. Расчёт трёхфазной цепи при соединении потребителей треугольником.
Нарисуем
схему трёхфазной цепи, причем элементы
из фазы A,
B,
C
соединения потребителей
звездой подключим соответственно между
точками ab,
bc,
ca
при
соединении потребителей треугольником
(рисунок
11).
В
комплексной форме записи линейные
напряжения на нагрузке:
![]()
![]()
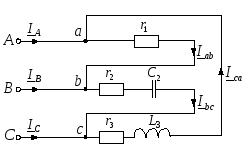
Рисунок
11 – Схема трёхфазной цепи при соединении
потребителей
треугольником
Сопротивления фаз
нагрузки в комплексной форме:
![]()
Фазные токи
определяем по закону Ома:
![]()
![]()
![]()
Для определения линейных токов используем
первый закон Кирхгофа для точек a,в,cсхемы (рисунок
11)
![]() А,
А,
![]() А,
А,
![]() А.
А.
Полные комплексные мощности
![]()
![]()
![]()
Трехфазная активная мощность
![]() Вт.
Вт.
Трехфазная
реактивная мощность
![]()
Трехфазная полная
мощность
![]()
Векторную диаграмму
токов для нагрузки, соединенной
треугольником,строим в масштабе
на комплексной плоскости относительно
осей +1 и + j
(рисунок12).На
векторной диаграмме линейные токи
получены на основании первого закона
Кирхгофа, путем вычитания одного вектора
фазного тока из соответствующего
другого.

Рисунок 12
– Векторная диаграмма токов
для
нагрузки, соединённой
треугольником
ЗАДАЧА
1
РАСЧЕТ ЛИНЕЙНОЙ
ЭЛЕКТРИЧЕСКОЙ
ЦЕПИ
ПОСТОЯННОГО
ТОКА
Для цепи, изображенной
на рисунке 13,
известны ЭДС Е1,
Е2
и внутренние сопротивления r01,
r02
источников
питания, а также сопротивления r1–r6.
Необходимо:
1.
Составить систему уравнений для
определения токов путем непосредственного
применения законов Кирхгофа. Решать
эту систему уравнений не следует.
2.
Определить токи ветвей методом контурных
токов.
3.
Составить баланс мощностей.
4.
Построить потенциальную диаграмму для
контура, включающего две ЭДС.
Значения параметров
элементов цепи приведены в таблице 1.
Теоретический материал и пример расчета
даны во втором разделе пособия, а также
в учебниках [1 – 4, 10].
Таблица
1
– Числовые
значения исходных данных к задаче № 3
-
Вариант
E1
E2
r01
r02
r1
r2
r3
r4
r5
r6
B
Ом
1
2
3
4
5
6
7
8
9
0
27
12
127
127
36
220
127
220
127
36
12
127
110
12
127
36
220
380
36
220
0,1
0,3
0,1
0,4
0,5
0,3
0,6
0,5
0,7
1,8
0,8
0,6
1,0
1,2
0,7
0,8
1,2
1,5
1,2
2,8
5
3
9
4
6
6
7
9
5
9
3
8
4
7
3
8
4
3
3
6
7
5
5
2
9
3
1
6
7
3
6
3
5
2
3
6
2
5
5
8
3
4
6
4
5
4
5
3
8
6
7
5
7
5
3
6
8
8
9
3
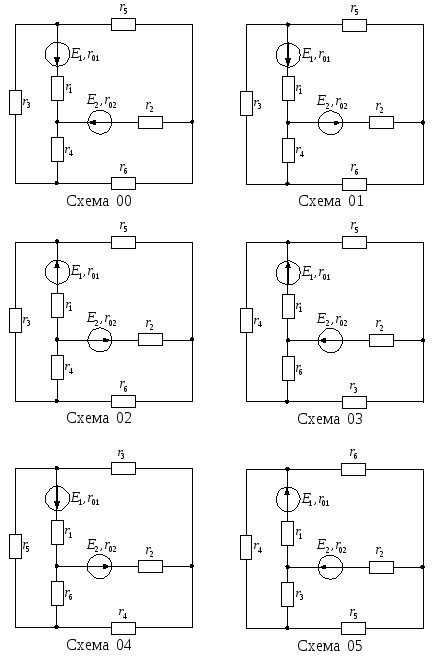
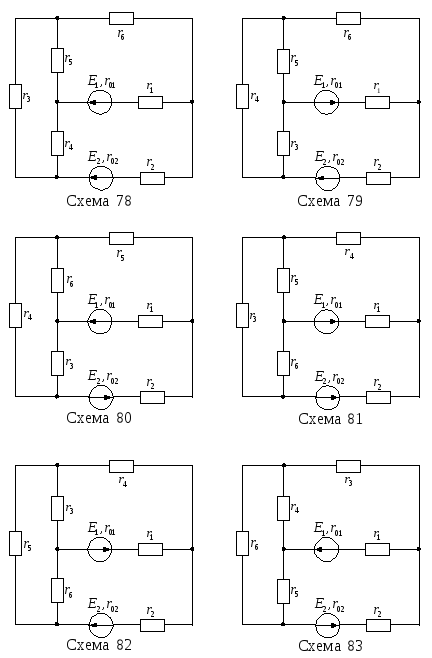
Рисунок 13
– Варианты электрических цепей к задаче
№ 1
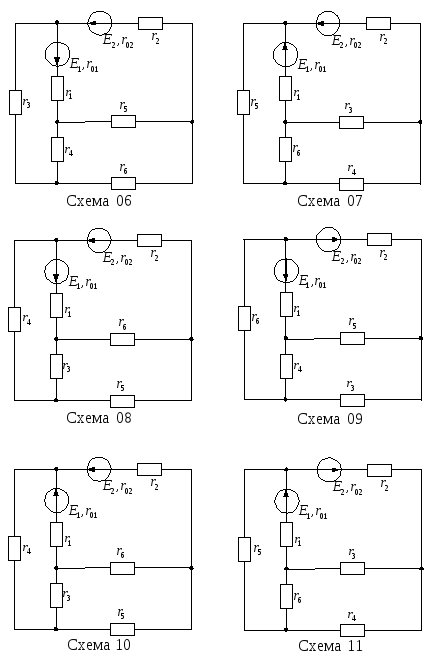
Продолжение рисунка
13

Продолжение рисунка
13

Продолжение рисунка
13
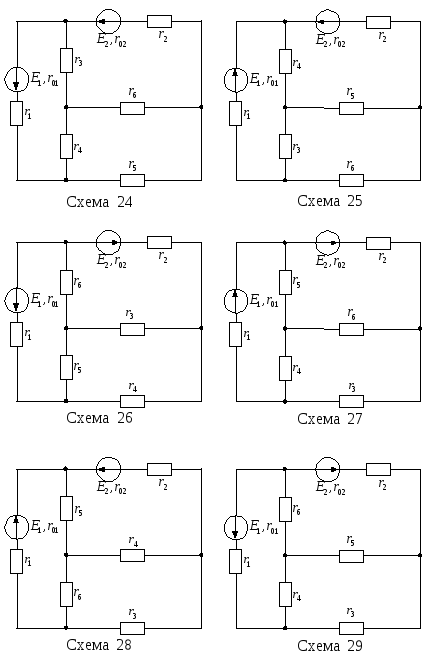
Продолжение рисунка
13
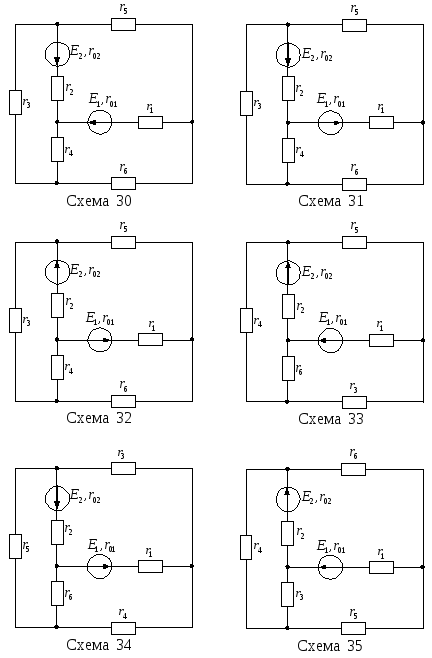
Продолжение рисунка
13

Продолжение рисунка
13

Продолжение рисунка
13

Продолжение рисунка
13

Продолжение рисунка
13
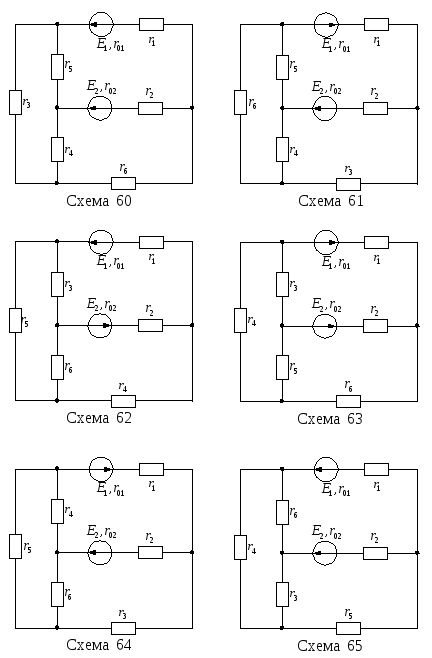
Продолжение рисунка
13

Продолжение рисунка
13
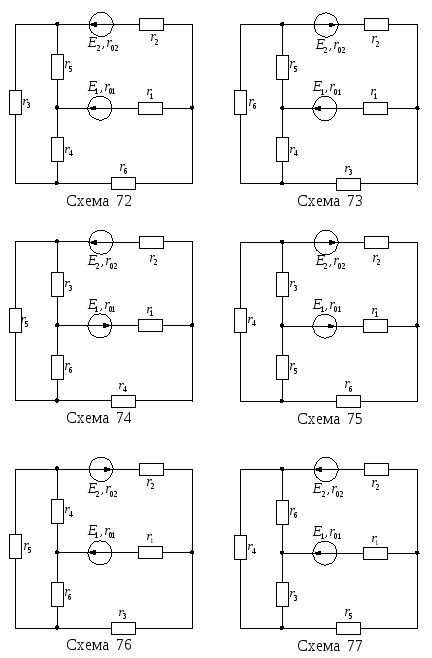
Продолжение рисунка
13
Продолжение рисунка
13
 Продолжение рисунка
Продолжение рисунка
13
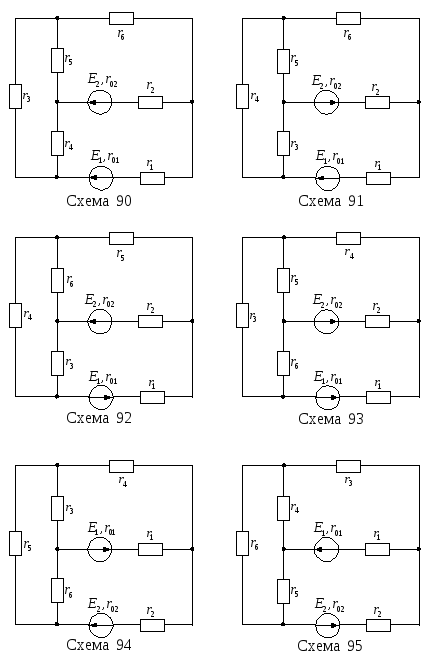
Продолжение рисунка
13

Продолжение рисунка
13
Соседние файлы в папке Методы с условиями
- #
- #
Содержание
- Определяем полные сопротивления отдельных ветвей. 2 страница
- 1. Расчет трехфазной цепи при соединении потребителей звездой.
- Определим реактивные сопротивления, принимая частоту сети переменного тока равной 50 Гц, а угловую частоту
- Активная трехфазная мощность
- Реактивная трехфазная мощность
- Полная мощность
- Суммарная реактивная мощность всех потребителей
- 2. Расчёт трёхфазной цепи при соединении потребителей треугольником.
Определяем полные сопротивления отдельных ветвей. 2 страница
В трехфазную четырехпроводную сеть включили звездой разные по характеру сопротивления. Значения сопротивлений и линейное напряжение приведены в таблице 4. Начертить схему цепи, определить полные сопротивления фаз, фазные токи, активную, реактивную и полную мощность отдельных фаз и всей цепи. Начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить графически числовое значение тока в нулевом проводе.
Указания к выполнению задачи №3.1:
Для решения данной задачи требуются знания учебного материала по теме «Трехфазные электрические цепи переменного тока», представление об особенностях соединения источников и потребителей, соотношениях между линейными и фазными напряжениями и токами при соединении в звезду, умения строить векторные диаграммы при симметричной и несимметричной нагрузках, а также в аварийных режимах. Данные для своего варианта взять из таблицы 4.
 ПРИМЕР:
ПРИМЕР:
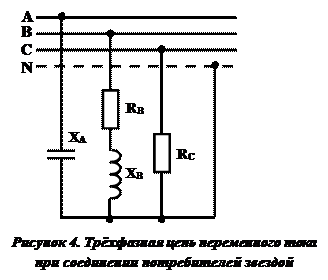
В трёхфазную четырёхпроводную сеть с частотой f = 50 Гц включили звездой несимметричную нагрузку:
— в фазу А – конденсатор с ёмкостным сопротивлением XC = 10 Ом;
— в фазу В – активное сопротивление R = 8 Ом и индуктивное XL= 6 Ом;
— в фазу С – активное сопротивление R = 5 Ом.
Линейное напряжение сети Uном = 380 В.
Определить полные сопротивления фаз, фазные напряжения и токи; начертить в масштабе векторную диаграмму цепи и найти графически ток в нулевом проводе; определить активную, реактивную и полную мощности, потребляемые цепью.
1. Определяем полное сопротивление каждой фазы:
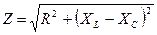 ;
;
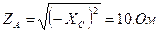 ;
; 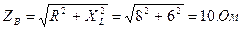 ;
; 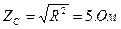 .
.
2. Определяем фазные напряжения: 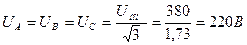
3. Находим фазные токи:
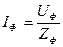 , тогда
, тогда 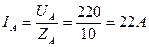 ;
; 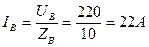 ;
; 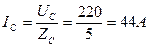 .
.
4. Построение векторной диаграммы:
Выбор масштаба: по напряжению: mU = 100 В/см; по току: mI = 10 A/см.
Первыми строят вектора фазных напряжений UA, UB, UC, располагая их под углом 120 о друг относительно друга (рисунок 5). Вектор IA опережает вектор UA на угол 90 о (т.к. на реактивной емкостной нагрузке напряжение отстаёт от тока по фазе на 90 о ); вектор IВ отстаёт от вектора UВ на угол φВ, который определяется из выражения 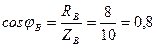 φВ = 36 о 50 ′ . Вектор IС совпадает с вектором напряжения UС (т.к. в фазе С содержится чисто активная нагрузка, а вектора напряжения и тока в этом случае имеют одинаковое направление). Ток в нулевом проводе равен геометрической сумме фазных токов.
φВ = 36 о 50 ′ . Вектор IС совпадает с вектором напряжения UС (т.к. в фазе С содержится чисто активная нагрузка, а вектора напряжения и тока в этом случае имеют одинаковое направление). Ток в нулевом проводе равен геометрической сумме фазных токов.
 Измерим длину вектора тока в нулевом проводе IО: lI »6,8см.
Измерим длину вектора тока в нулевом проводе IО: lI »6,8см.
Тогда 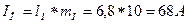 .
.
5. Определяем мощности, потребляемые цепью:
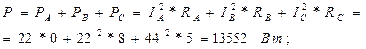
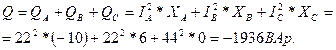
Знак минус показывает, что в цепи преобладает ёмкость.
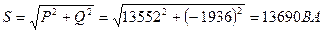 .
.
Задача 3.2
В трехфазную трехпроводную сеть включили треугольником разные по характеру сопротивления. Значения сопротивлений и линейное напряжение приведены в таблице 4. Начертить схему цепи, определить полные сопротивления фаз, фазные токи, активную, реактивную и полную мощность отдельных фаз и всей цепи. Начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить графически числовые значения линейных токов.
Указания к выполнению задачи №3.2:
Для решения данной задачи требуются знания учебного материала по теме «Трехфазные электрические цепи переменного тока», представление об особенностях соединения источников и потребителей, соотношениях между линейными и фазными напряжениями и токами при соединении в треугольник, умения строить векторные диаграммы при симметричной и несимметричной нагрузках, а также в аварийных режимах. Данные для своего варианта взять из таблицы 4.
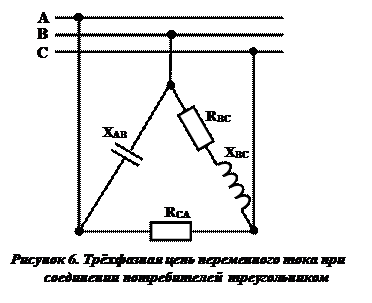
В трёхфазную сеть с частотой f = 50 Гц включили треугольником несимметричную нагрузку (рис.6):
— в фазу АВ – конденсатор с ёмкостным сопротивлением XC = 10 Ом;
— в фазу ВС – катушку с активным R = 4Ом и индуктивным сопротивлением XL= 3 Ом;
— в фазу СА – активное сопротивление R=10 Ом.
Линейное напряжение сети Uном = 220 В.
1. Определяем полное сопротивление каждой фазы:
 ;
;
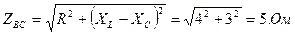 ;
;
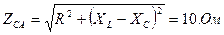
2. Определяем фазные токи и углы сдвига фаз:
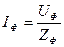 ,
,
тогда 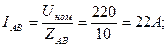 φАВ = -90 о ;
φАВ = -90 о ;
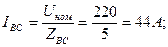
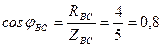 откуда угол φВС = 36 о 50 ′ ;
откуда угол φВС = 36 о 50 ′ ;
 φСА = 0;
φСА = 0;

3. Построение векторной диаграммы: Выбор масштаба по напряжению: mU = 80В/см; по току: mI = 10 A/см.
Вектора фазных напряжений UAВ, UBС, UCА располагают под углом 120 о друг относительно друга (рисунок 7). Под углом φАВ = —90 о к вектору напряжения UAB откладываем вектор тока IAB (т.к. в фазе чисто емкостная нагрузка); в фазе ВС вектор тока IBС должен отставать от вектора напряжения UBС на угол φВС = 36 о 50 ′ , а в фазе СА вектор тока IСА совпадает с вектором напряжения UСА (т.к. в фазе СА содержится чисто активная нагрузка, а вектора напряжения и тока в этом случае имеют одинаковое направление).
Строим векторы линейных токов на основании уравнений:

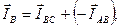
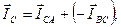
Измерив длины векторов линейных токов, находим их значения, пользуясь масштабом
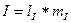 :
: 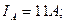
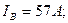
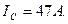
4. Определяем мощности, потребляемые цепью:
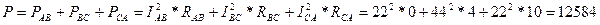 Вт;
Вт;
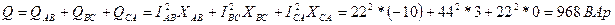 .
.
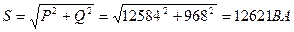 .
.
| вариант | Фаза А | Фаза В | Фаза С | UЛ, В | вариант | Фаза АВ | Фаза ВС | Фаза СА | UЛ, В | ||||||||
| R,Ом | XL ,Ом | XC,Ом | R,Ом | XL,Ом | XC,Ом | R,Ом | XL,Ом | XC,Ом | R,Ом | XL ,Ом | XC,Ом | R,Ом | XL,Ом | XC,Ом | R,Ом | XL,Ом | XC,Ом |
| 12,7 | 25,4 | ||||||||||||||||
| 12,7 | 25,4 | ||||||||||||||||
| 12,7 | 80,5 | ||||||||||||||||
| 82,7 | |||||||||||||||||
| 62,8 | |||||||||||||||||
| 80,5 | 12,7 | 25,4 | |||||||||||||||
| 40,5 | 80,5 | ||||||||||||||||
| 5,5 | 6,3 | ||||||||||||||||
| 82,7 | |||||||||||||||||
| 25,4 | 12,7 | ||||||||||||||||
| 25,4 | 12,7 | ||||||||||||||||
| 6,35 | 12,7 | ||||||||||||||||
| 12,7 | |||||||||||||||||
| 6,35 | 12,7 | ||||||||||||||||
| 12,7 | |||||||||||||||||
| 12,7 | |||||||||||||||||
| 12,7 | |||||||||||||||||
| 82,7 | |||||||||||||||||
| 2,5 | 4,6 | 7,5 | 82,7 | ||||||||||||||
| 80,5 | |||||||||||||||||
| 37,5 | 34,5 | 20,2 | 2,5 | 4,6 | 7,5 | ||||||||||||
| 25,4 | 12,7 | ||||||||||||||||
| 80,5 | |||||||||||||||||
| 25,4 | 12,7 | ||||||||||||||||
| 5,5 | 6,3 | ||||||||||||||||
| 17,3 | 17,3 | 17,3 | |||||||||||||||
| 80,5 | |||||||||||||||||
| 80,5 | 7,5 | 2,5 | 4,6 | ||||||||||||||
| 82,7 | |||||||||||||||||
| 2,5 | 4,6 | 7,5 | |||||||||||||||
| 28,3 | 17,3 | 17,3 | |||||||||||||||
| 80,5 | |||||||||||||||||
| 25,4 | 24,7 | 12,7 | |||||||||||||||
| 12,7 | 25,4 | ||||||||||||||||
| 2,5 | 4,6 | 7,5 |
Задача 4
Для питания пониженным напряжением частотой 50 Гц установлен трехфазный трансформатор номинальной мощностью SНОМ, к которому подключена нагрузка с полной мощностью S2, активной Р2, при коэффициенте мощности соsφ2. и коэффициенте нагрузки КН. Номинальные напряжения обмоток UНОМ1 и UНОМ2; номинальные токи в обмотках IНОМ1 и IНОМ2, токи в обмотках при фактической нагрузке I1 и I2, ЭДС в обмотках трансформатора Е1 и Е2. Коэффициент трансформации равен К. Число витков обмоток w1 и w2. Магнитный поток в магнитопроводе ФМ. Магнитные потери РМ=РХ, электрические потери РЭ=РК. КПД трансформатора при номинальной нагрузке ηНОМ, при действительной нагрузке η, максимальное значение КПД ηМ. Используя данные трансформатора, приведенные в таблице 5, и исходные данные, приведенные в таблице 7, определить все неизвестные величины. Ответить на вопрос из таблицы 6 в соответствии со своим вариантом.
Указания к выполнению задачи №4:
Для решения данной задачи необходимо знать устройство, принцип действия и соотношения между электрическими величинами трехфазных трансформаторов. Основными параметрами трансформаторов являются:
1. Номинальная мощность SНОМ. Это полная мощность (в кВА), которую трансформатор, установленный на открытом воздухе, может непрерывно отдавать в течение срока службы (20-25 лет) при номинальном напряжении и при максимальной и среднегодовой температуре окружающего воздуха соответственно 40 и 5 о С.
Поделиться с друзьями:
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
studopedia.su — Студопедия (2013 — 2023) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление
Генерация страницы за: 0.007 сек. —>
Источник
1. Расчет трехфазной цепи при соединении потребителей звездой.
Так как в схеме есть нейтральный провод, то напряжение на фазах нагрузки равно соответствующему фазному напряжению источника питания (обмотки генератора считаем соединенными звездой, а сопротивлением нейтрального провода пренебрегаем):

Рисунок 9 – Схема трёхфазной цепи при соединении потребителей звездой
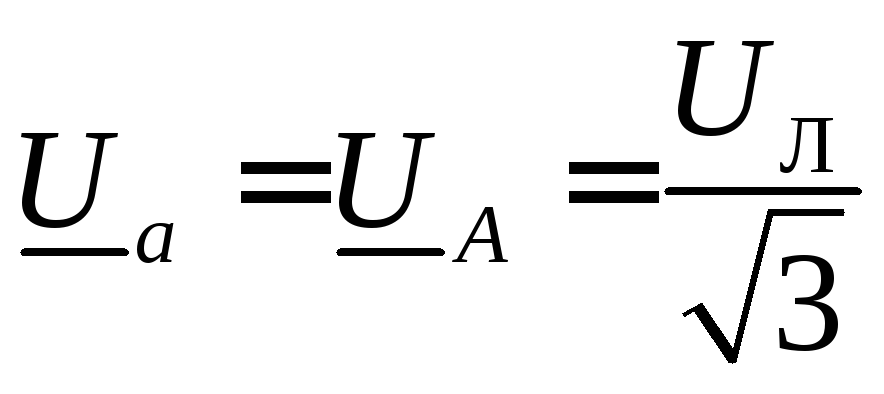 ,
, 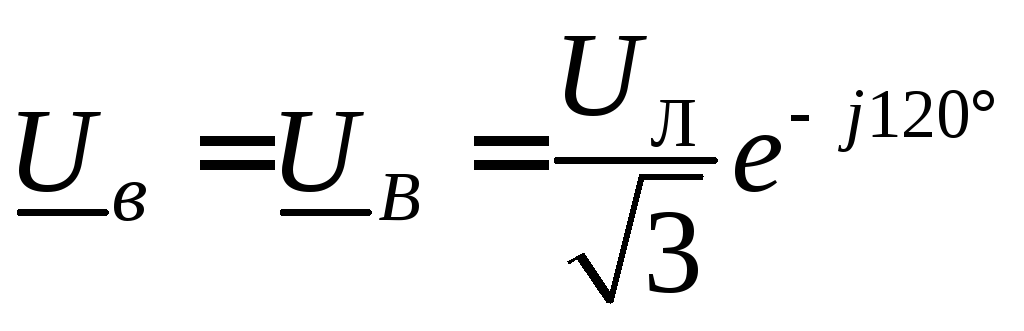 ,
, 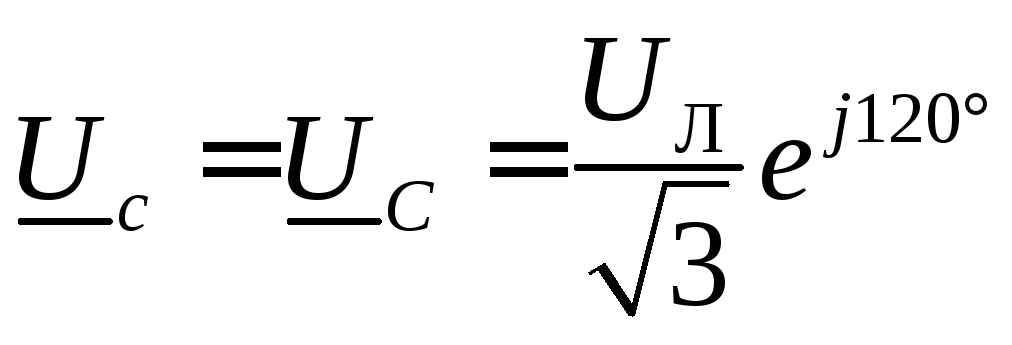 ;
;
в численном виде:

Определим реактивные сопротивления, принимая частоту сети переменного тока равной 50 Гц, а угловую частоту
ω = 2πf = 2 ∙ 3,14 ∙ 50 = 314 1/с .
Реактивное индуктивное сопротивление
Реактивное емкостное сопротивление
В общем случае полное сопротивление каждой из фаз в комплексной форме определяют с помощью выражения, которое использовалось в однофазных цепях,
 .
.
Применяем эту формулу для нашего конкретного случая и получаем полные сопротивления фаз в следующем виде:

Комплексные сопротивления фаз различны, следовательно, нагрузка несимметричная.
Токи в линейных проводах (фазные токи нагрузки) определяем с помощью закона Ома:
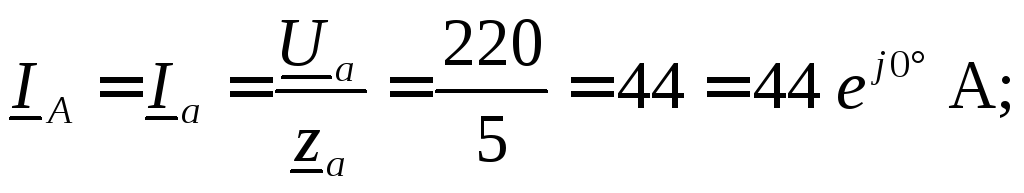
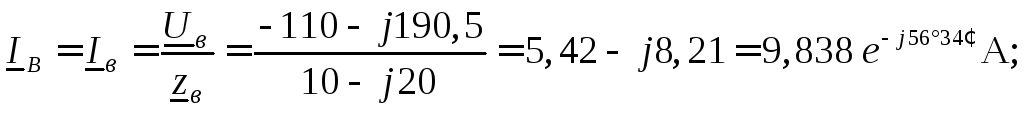
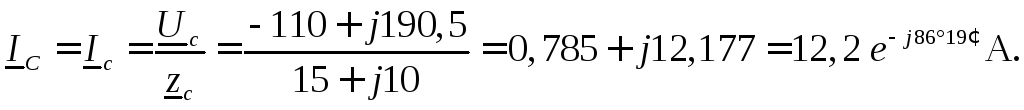
Ток в нейтральном проводе находим по первому закону Кирхгофа
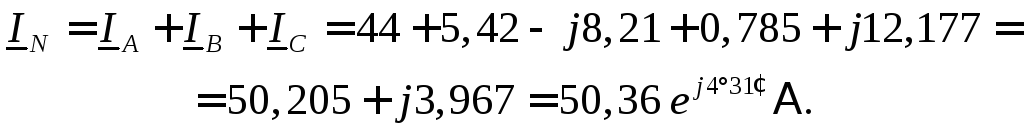
Полные мощности фаз:
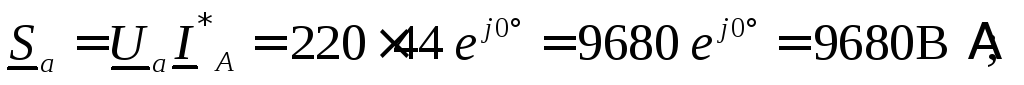
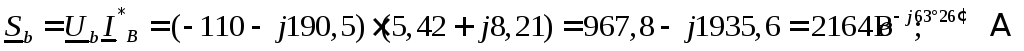
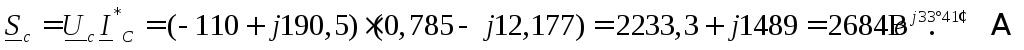
Так как вещественная часть полной мощности есть активная мощность цепи, а мнимая часть – реактивная, то, просуммировав отдельно вещественные, а затем мнимые части мощностей трех фаз, определяем трехфазную активную и реактивную мощности.
Активная трехфазная мощность

Реактивная трехфазная мощность

Полная мощность

Активная трехфазная мощность нагрузки может быть определена суммой активных мощностей потребителей каждой из фаз

Относительная ошибка вычислений для активной мощности

Реактивная трехфазная мощность нагрузки также определяется суммой реактивных мощностей потребителей каждой из фаз
Суммарная реактивная мощность всех потребителей

Относительная ошибка вычислений для активной мощности

Ошибка менее одного процента допускается. Таким образом, баланс активных и реактивных мощностей соблюдается, значит токи определены правильно.
Векторную диаграмму размещаем на комплексной плоскости с осями +1 и + j, рисунок 3.21. Выбираем масштаб векторов тока равным 10 А/деление, а векторов напряжения – 40 В/деление. Строим векторы фазных напряжений, а затем векторы токов. Длина вектора соответствует в масштабе модулю показательной формы соответствующего выражения тока или напряжения, а угол, под которым этот вектор строится к вещественной оси, равен аргументу комплексного значения величины.

Рисунок 10 – Векторная диаграмма при соединении
потребителей звездой с нейтральным проводом
2. Расчёт трёхфазной цепи при соединении потребителей треугольником.
Нарисуем схему трёхфазной цепи, причем элементы из фазы A, B, C соединения потребителей звездой подключим соответственно между точками ab, bc, ca при соединении потребителей треугольником (рисунок 11).
В комплексной форме записи линейные напряжения на нагрузке:
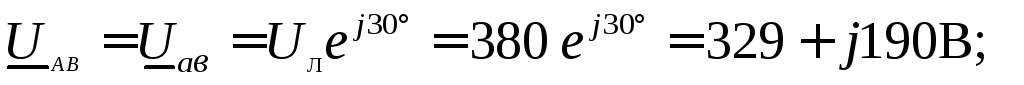
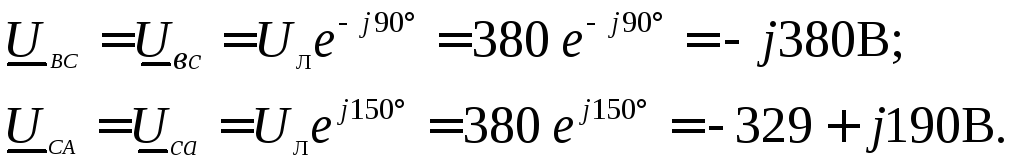

Рисунок 11 – Схема трёхфазной цепи при соединении потребителей
Сопротивления фаз нагрузки в комплексной форме:
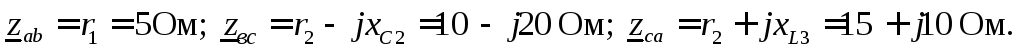
Фазные токи определяем по закону Ома:

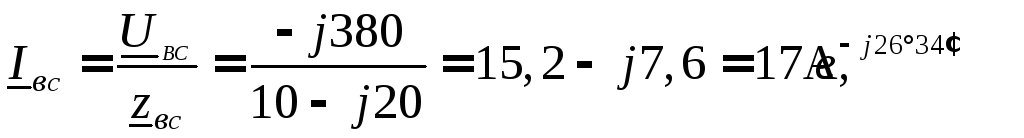
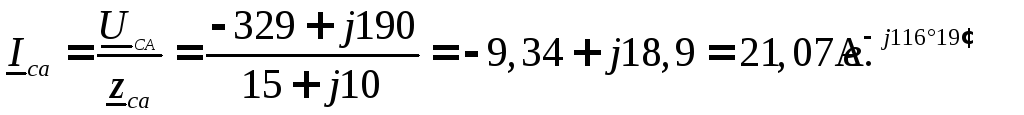
Для определения линейных токов используем первый закон Кирхгофа для точек a,в,cсхемы (рисунок 11)
 А,
А,
 А,
А,
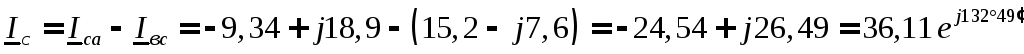 А.
А.
Полные комплексные мощности
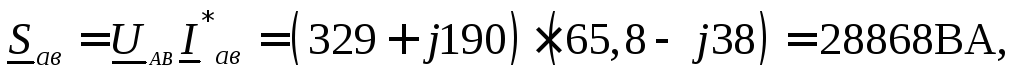
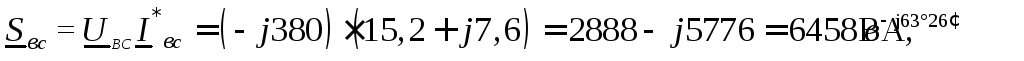

Трехфазная активная мощность
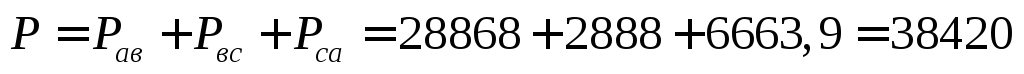 Вт.
Вт.
Трехфазная реактивная мощность
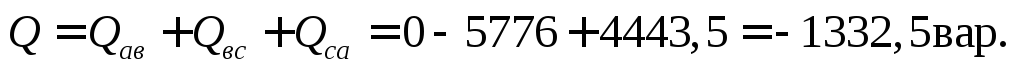
Трехфазная полная мощность
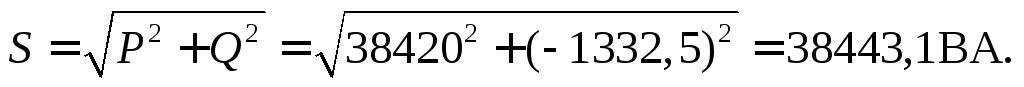
Векторную диаграмму токов для нагрузки, соединенной треугольником,строим в масштабе на комплексной плоскости относительно осей +1 и + j (рисунок12).На векторной диаграмме линейные токи получены на основании первого закона Кирхгофа, путем вычитания одного вектора фазного тока из соответствующего другого.
Источник
Что такое полное сопротивление цепи и как его правильно найти
Содержание
- 1 Виды электрических сопротивлений
- 2 Определение эквивалентного сопротивления
- 3 Как определяется ПС при последовательном соединении емкостей и индуктивностей
- 4 Определение ПС при использовании параллельного соединения элементов
- 5 Видео по теме
Для начала нужно понять, что такое электрическое сопротивление. Это физическая величина, которая отражает противодействие движению электротока по схеме или же внутри проводника. Данная величина взаимосвязана с электронапряжением и силой электротока, что отражено в законе Ома, названном так по имени немецкого физика.

Формулировка закона Ома
Виды электрических сопротивлений
Известно о двух видах электронапряжения — постоянном и переменном. В электроцепи постоянного тока присутствует исключительно активное электросопротивление. Таким является любое электросопротивление, поглощающее энергию. В этом случае найти полное сопротивление поможет формулировка закона Ома.
В электроцепях с переменным напряжением есть реактивное электросопротивление, то есть такое, которое энергию не поглощает. Оно делится на емкостное и индуктивное. В реальности не существует электроцепей только с каким-либо одним видом электросопротивления. Наряду с резисторами в них используются емкости и катушки индуктивности. Поэтому в электротехнике вводится такое понятие, как полное сопротивление цепи, представляющееся в виде векторной суммы всех электросопротивлений, присутствующих в данной цепи.

Классификация электроцепей переменного электротока
Величина реактивного электросопротивления зависит от частоты параметров используемой электросети. Формула, с помощью которой можно определить емкостное электросопротивление, выглядит так:

Определение емкостного сопротивления
Здесь ω — угловая частота. Она связана с частотой электросети f и определяется по формуле:

Значение угловой частоты
Индуктивное электросопротивление находим с помощью такого выражения:

Определение индуктивного электросопротивления
В формулах для определения емкостного и индуктивного электросопротивления используются определенные физические величины. Их обозначение и единицы измерения приводятся в таблице ниже. Само электросопротивление измеряется в омах.

Таблица физических величин
Чтобы вычислить полное сопротивление цепи Z, учитывающее все имеющиеся активные и реактивные составляющие, следует воспользоваться формулой:

Вычисление импеданса
Определение эквивалентного сопротивления
В электросхеме может быть использовано несколько нагрузок одного вида, соединенных между собой последовательно или параллельно. В первом случае их электросопротивления складываются. Поэтому эквивалентное сопротивление будет тем больше, чем больше элементов соединено последовательно.

Электроцепь с последовательно соединенными активными проводниками
Если используется параллельное соединение проводников, расчет полного сопротивления цепи выполняется несколько иначе:

Определение эквивалентного электросопротивления при параллельном соединении
В данном случае эквивалентное сопротивление с увеличением количества используемых нагрузок будет уменьшаться. Такое явление можно наблюдать в повседневной жизни: чем больше к электросети подключено потребителей, тем меньшим будет значение эквивалентного электросопротивления и большим электроток нагрузки.
Как определяется ПС при последовательном соединении емкостей и индуктивностей
При наличии реактивной нагрузки в электроцепи будет наблюдаться опережение или отставание электротока от электронапряжения. При подключении индуктивной нагрузки электроток отстает от электронапряжения, а емкостной, наоборот, опережает. То есть, при подключении конденсатора к источнику переменного электротока он будет постоянно перезаряжаться с частотой, соответствующей частоте электросети. Электроток при этом будет увеличиваться раньше, чем электронапряжение. При подключении индуктивного контура наблюдается обратный результат.

Графическое изображение электрических величин при последовательно соединенных элементах электроцепи
Рассмотрим схему с использованием последовательно соединенных резистора и индуктивности.

Электросхема с использованием резистора и индуктивности соединенных последовательно
Для этого участка цепи результирующее электронапряжение в точках А и В можно определить достаточно простым способом — геометрическим сложением векторов UL и UR. Как видно из рисунка, результирующий вектор UАВ — это гипотенуза треугольника. Следовательно, чтобы рассчитать ее, можно применить теорему Пифагора:
![]()
Определение результирующего электронапряжения
Если исходить из формулировки закона Ома, то электронапряжение — это произведение электросопротивления и силы электротока. Поскольку последний параметр во всех точках электроцепи имеет одинаковое значение, то квадрат ПС — это сумма квадратов электросопротивлений, называемых активными и реактивным:

Сумма квадратов электросопротивлений
Следовательно, полное сопротивление приведенной цепи Z определяется выражением:

Определение ПС
Кроме расчетов для определения ПС в цепи можно использовать еще и геометрический способ, являющийся построением треугольника, представленного на рисунке 11д. Его катеты — это активное и реактивное электросопротивление для участка цепи. Понятно, что стороны треугольника следует откладывать в одном масштабе.
Полное сопротивление цепи в рассматриваемом случае не будет исключительно активным или реактивным. В него входят обе составляющие. По этой причине угол сдвига по фазе между электротоком и электронапряжением может меняться от 0 до 90 градусов. К какому из этих предельных значений будет приближена величина φ, зависит от вида преобладающего электросопротивления. Если индуктивная составляющая превышает активную, φ стремится к 90 градусам, а преобладающая активная составляющая уменьшает его до нуля.
Теперь рассмотрим электроцепь с присутствующими в ней резистором и конденсатором, соединенными последовательно. Полное сопротивление цепи и в данном случае можно определить, используя построение треугольника.

Электросхема с последовательно соединенными резистором и конденсатором
Как можно увидеть из рисунка, треугольник сопротивлений, построенный для активно-емкостного участка цепи, развернут в другую сторону. Это связано с тем, что электроток в емкости опережает электронапряжение (в активно-индуктивной ветви электроток отстает от электронапряжения). Полное электрическое сопротивление цепи Z в данном случае будет равно:

Определение импеданса при использовании резистора и конденсатора в электроцепи
Если же в электроцепи присутствуют все виды электросопротивлений, то сначала следует найти реактивную составляющую, а потом уже и значение ПС или импеданса.

Электросхема с использованием разных видов электросопротивлений
Общее реактивное электросопротивление для данного участка цепи — это разница между индуктивной и емкостной составляющими, поскольку они по своему характеру являются противоположными друг другу.

Расчет общего реактивного электросопротивления
Полное сопротивление электрической цепи при наличии индуктивной и емкостной составляющей определяется по формуле:

Определение ПС при наличии индуктивности и емкости в электроцепи
Треугольник электросопротивлений при наличии индуктивной и емкостной составляющей показан на рисунке.
Немаловажно понимать, что если одно из электросопротивлений (емкостное или индуктивное) больше другого более, чем в десять раз, то составляющую с наименьшим значением можно оставить без внимания.
Определение ПС при использовании параллельного соединения элементов
На рисунке ниже изображены графики электронапряжений и электротоков, присутствующих на нагрузках при параллельном соединении.

Графики электронапряжений и электротоков при параллельном соединении элементов электроцепи
Чтобы определить полное электрическое сопротивление цепи, включающей резистор и индуктивность или резистор и емкость, соединенные параллельно, необходимо в первую очередь найти проводимость каждой параллельной линии, затем общую проводимость этой цепи между точками А и В. На последнем этапе вычисляется ПС между А и В.

Пример электросхемы с параллельно соединенными элементами
Вычисляемое значение проводимости активного участка цепи равняется 1/R, индуктивного — 1/ ωL. Формула для определения полной проводимости выглядит так:

Полная проводимость участка электроцепи
Приводя к общему знаменателю выражение под знаком корня, получаем следующее выражение:

Формула после преобразования
Отсюда находим формулу для определения ПС для участка цепи с параллельно соединенными резистором и индуктивностью:

Определение ПС при параллельно соединенных элементах
Формула для вычисления ПС при использовании параллельного соединения резистора и емкости имеет такой вид:

Определение ПС при параллельном соединении резистора и емкости
В радиотехнике чаще всего используется параллельное соединение конденсатора и катушки индуктивности, например, в колебательном контуре. Поскольку катушка имеет и индуктивное, и активное сопротивление, то в индуктивную ветвь включается еще резистор.

Схема колебательного контура
Для определения ПС следует воспользоваться формулой:

Определение ПС колебательного контура
Учитывая то, что активное электросопротивление катушки значительно меньше индуктивного, формулу можно представить так:

Формула для расчета ПС колебательного контура
Значение индуктивности и емкости для колебательного контура принято выбирать так, чтобы соблюдалось условие:

Условие для колебательного контура
В данном случае для определения ПС колебательного контура получаем очень простую формулу:

Упрощенная формула для расчета ПС колебательного контура
С целью облегчения расчетов импеданса используют комплексные числа. Действительную часть такого числа представляет активное электросопротивление, а мнимую — реактивное.
Для последовательно соединенных радиоэлементов ПС в комплексном виде можно представить так:

Определение комплексного ПС
В тригонометрической интерпретации модулем комплексного числа является ПС, а аргументом — угол φ.

Треугольник сопротивлений
Следовательно, активную и реактивную составляющие ПС можно найти по формулам:

Определение составляющих ПС
При вычислении ПС или импеданса для параллельно соединенных элементов используют сумму проводимостей — величин, обратных электросопротивлениям.

Треугольник проводимостей
Комплексная проводимость является величиной, обратной комплексному электросопротивлению. Алгебраически она выражается так:

Определение комплексной проводимости
Вычисление импеданса является достаточно сложной задачей, поскольку используется большое количество формул, тригонометрических функций. Поэтому с целью облегчения расчетов можно воспользоваться онлайн калькулятором. Чтобы получить результат, понадобится лишь ввести значение частоты электротока, емкость конденсатора, индуктивность катушки, сопротивление резистора.
Видео по теме
Полное сопротивление цепи переменного тока
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току – Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.

Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.

Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) – схема цепи; б) – сдвиг фаз тока и напряжения; в) – треугольник напряжений; д) – треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.

По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z2) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
 (1)
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
 (2)
(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.

Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) – схема цепи; б) – треугольник сопротивлений.
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:
 (3)
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.

Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) – схема цепи; б) – треугольник сопротивлений.
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
 (4)
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
 (5)
(5)
Или
 (6)
(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.

Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) – параллельное соединение R и L; б) – параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
 (7)
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
 (8)
(8)
откуда:
 (9)
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
 (10)
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).

Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
 (11)
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
 (12)
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
 (13)
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
 (14)
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Загрузить PDF
Загрузить PDF
Полное сопротивление, или импеданс, характеризует сопротивление цепи переменному электрическому току. Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток. Импеданс можно рассчитать при помощи простой формулы.
Формулы
- Полное сопротивление Z = R или XLили XC (если присутствует что-то одно)
- Полное сопротивление (последовательное соединение) Z = √(R2 + X2) (если присутствуют R и один тип X)
- Полное сопротивление (последовательное соединение) Z = √(R2 + (|XL – XC|)2) (если присутствуют R, XL, XC)
- Полное сопротивление (любое соединение) = R + jX (j — мнимое число √(-1))
- Сопротивление R = I / ΔV
- Индуктивное сопротивление XL = 2πƒL = ωL
- Емкостное сопротивление XC = 1 / 2πƒL = 1 / ωL
-

1
Импеданс обозначается символом Z и измеряется в омах (Ом). Вы можете измерить импеданс электрической цепи или отдельного элемента. Импеданс характеризует сопротивление цепи переменному электрическому току. Есть два типа сопротивления, которые вносят вклад в импеданс:[1]
- Активное сопротивление (R) зависит от материала и формы элемента. Наибольшим активным сопротивлением обладают резисторы, но и другие элементы цепи обладают небольшим активным сопротивлением.
- Реактивное сопротивление (X) зависит от величины электромагнитного поля. Наибольшим реактивным сопротивлением обладают катушки индуктивности и конденсаторы.
-

2
Сопротивление — это фундаментальная физическая величина, описываемая законом Ома: ΔV = I * R.[2]
Эта формула позволит вам вычислить любую из трех величин, если вы знаете две другие. Например, чтобы вычислить сопротивление, перепишите формулу так: R = I / ΔV. Вы также можете измерить сопротивление при помощи мультиметра.- ΔV — это напряжение (разность потенциалов), измеряемое в вольтах (В).
- I — сила тока, измеряемая в амперах (А).
- R — это сопротивление, измеряемое в омах (Ом).
-

3
Реактивное сопротивление имеет место только в цепях переменного тока. Как и активное сопротивление, реактивное сопротивление измеряется в омах (Ом). Есть два типа реактивного сопротивления:
- Индуктивным сопротивлением XC обладают катушки индуктивности, создающие магнитное поле, которое препятствует изменению направления тока в цепи.[3]
Чем быстрее меняется направление тока, тем больше индуктивное сопротивление. - Емкостным сопротивлением XC обладают конденсаторы, которые накапливают электрический заряд. При изменении направления тока в цепи конденсатор неоднократно обнуляет и накапливает электрический заряд. Чем дольше конденсатор заряжается, тем больше емкостное сопротивление.[4]
Поэтому чем быстрее меняется направление тока, тем меньше емкостное сопротивление.
- Индуктивным сопротивлением XC обладают катушки индуктивности, создающие магнитное поле, которое препятствует изменению направления тока в цепи.[3]
-

4
Вычислите индуктивное сопротивление. Это сопротивление прямо пропорционально быстроте изменения направления тока, то есть частоты тока. Эта частота обозначается символом ƒ и измеряется в герцах (Гц). Формула для расчета индуктивного сопротивления: XL = 2πƒL, где L — индуктивность, измеряемая в генри (Гн).[5]
- Индуктивность L зависит от количества витков в катушке индуктивности.[6]
Также вы можете измерить индуктивность. - Если вы знакомы с единичной окружностью, то представьте, что один цикл переменного тока равен одному полному вращению этой окружности (на 2π радиан). Если умножить это значение на ƒ, которая измеряется в герцах (единиц в секунду), вы получите результат, измеряемый в радианах в секунду. Это единица измерения угловой скорости, которая обозначается через ω. Вы можете переписать формулу для вычисления индуктивного сопротивления так: XL=ωL[7]
- Индуктивность L зависит от количества витков в катушке индуктивности.[6]
-

5
Вычислите емкостное сопротивление. Это сопротивление обратно пропорционально быстроте изменения направления тока, то есть частоты тока. Формула для вычисления емкостного сопротивления: XC = 1 / 2πƒC.[8]
С — это емкость конденсатора, измеряемая в фарадах (Ф).- Вы можете измерить электрическую емкость.
- Эту формулу можно переписать так: XC = 1 / ωL (объяснения см. выше).
Реклама
-

1
Если цепь состоит исключительно из резисторов, то импеданс вычисляется следующим образом. Сначала измерьте сопротивление каждого резистора или посмотрите значения сопротивления на схеме цепи.[9]
- Если резисторы соединены последовательно, то полное сопротивление R = R1 + R2 + R3…
- Если резисторы соединены параллельно, то полное сопротивление R = 1 / R1 + 1 / R2 + 1 / R3 …
-

2
Сложите одинаковые реактивные сопротивления. Если в цепи присутствуют исключительно катушки индуктивности или исключительно конденсаторы, то полное сопротивление равно сумме реактивных сопротивлений. Вычислите его следующим образом:[10]
- Последовательное соединение катушек: Xtotal = XL1 + XL2 + …
- Последовательное соединение конденсаторов: Ctotal = XC1 + XC2 + …
- Параллельное соединение катушек: Xtotal = 1 / (1/XL1 + 1/XL2 …)
- Параллельное соединение конденсаторов: Ctotal = 1 / (1/XC1 + 1/XC2 …)
-

3
Вычтите индуктивные и емкостные сопротивления, чтобы получить общее реактивное сопротивление. Так как при возрастании одного типа сопротивления другое уменьшается, то они, как правило, компенсируют друг друга. Чтобы найти общее реактивное сопротивление, вычтите меньшее сопротивление из большего.[11]
- Или воспользуйтесь формулой: Xtotal = |XC – XL|
-

4
Вычислите импеданс по активному и реактивному сопротивлениям в последовательной цепи. Нельзя просто сложить эти величины, так как они меняются с течением времени, но достигают максимальных значений в разное время.[12]
Поэтому воспользуйтесь формулой:Z = √(R2 + X2).[13]
- Вычисления по этой формуле включают в себя использование векторов, но вы можете воспользоваться теоремой Пифагора, представив R и X в качестве катетов прямоугольного треугольника, а сопротивление Z — как гипотенузу.[14]
[15]
- Вычисления по этой формуле включают в себя использование векторов, но вы можете воспользоваться теоремой Пифагора, представив R и X в качестве катетов прямоугольного треугольника, а сопротивление Z — как гипотенузу.[14]
-

5
Вычислите импеданс по активному и реактивному сопротивлениям в параллельной цепи. В этом случае используются комплексные числа (это единственный способ вычислить полное сопротивление в параллельной цепи, в которой есть как активное, так и реактивное сопротивление).
- Z = R + jX, где j — мнимая единица: √(-1). Используйте j вместо i, чтобы не перепутать мнимую единицу (j) с силой тока (I).
- Складывать эти числа нельзя. Например, полное сопротивление может быть представлено так: 60 Ом + j120 Ом.
- Если у вас есть две последовательные цепи, то вы можете отдельно сложить натуральные числа и отдельно — комплексные. Например, если Z1 = 60 Ом + j120 Ом, а к этой цепи последовательно подключен резистор с Z2 = 20Ω, то Ztotal = 80Ω + j120Ω.
Реклама
Советы
- Общее сопротивление (активное и реактивное сопротивления) также может быть выражено через мнимое число.
Реклама
Об этой статье
Эту страницу просматривали 168 436 раз.
