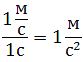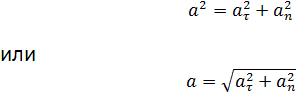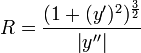Как найти полное ускорение формула

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).

Среднее ускорение

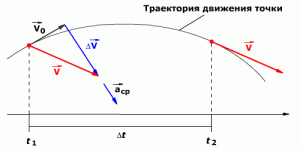
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с², то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

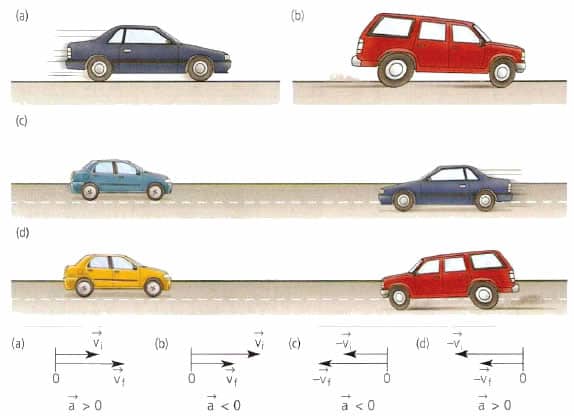
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

v2 > v1

а направление вектора ускорения совпадает с вектором скорости 

Если скорость тела по модулю уменьшается, то есть

v2 < v1

то направление вектора ускорения противоположно направлению вектора скорости  Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.

Рис. 1.9. Мгновенное ускорение.

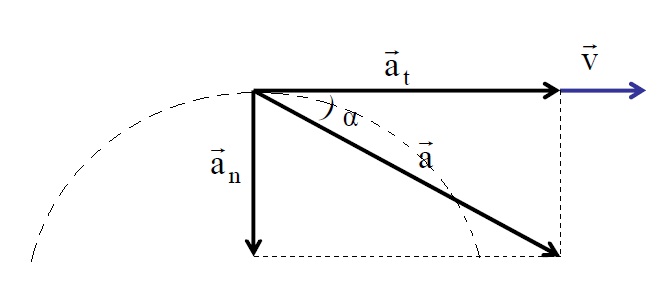
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное ускорение

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения  (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

Направление полного ускорения также определяется правилом сложения векторов:

Полное ускорение

Полное
ускорение при
криволинейном движении складывается
из тангенциального и нормального
ускорений по правилу
сложения векторов и
определяется формулой:

(согласно
теореме Пифагора для прямоугольно
прямоугольника).

Направление
полного ускорения также определяется правилом
сложения векторов:

• =

  _τ
  +

  _n

Кривизна траектории.

Траекто́рия
материа́льной то́чки  — линия в
трёхмерном пространстве,
представляющая собой множество точек,
в которых находилась, находится или
будет находиться материальная
точка при
своём перемещении в пространстве.
Существенно, что понятие о траектории
имеет физический смысл даже при отсутствии
какого-либо по ней движения. Кроме того,
и при наличии движущегося по ней объекта,
траектория сама по себе не может ничего
дать в отношении причин движения, то
есть о действующих силах.

формула
радиуса кривизны

Вращательное движение

Враща́тельное
движе́ние —
вид механического
движения.
При вращательном движении
абсолютно твёрдого тела его точки
описывают окружности, расположенные в
параллельных плоскостях.
Центры всех окружностей лежат при этом
на одной прямой, перпендикулярной к
плоскостям окружностей и называемой осью
вращения.
Ось вращения может располагаться внутри
тела и за его пределами. Ось вращения
в данной системе отсчёта может быть как
подвижной, так и неподвижной. Например,
в системе отсчёта, связанной с Землёй,
ось вращения ротора генератора на
электростанции неподвижна.

Вращательное
движение тела
в зависимости от времени t характеризуют угловые
величины:
φ (угол поворота в радианах), ω (угловая
скорость в рад/сек) и ε (угловое ускорение
в рад/сек²).

Закон
вращательного движения тела выражается
уравнением φ
= f (t).

Радиус вектор

Ра́диус-ве́ктор (обычно
обозначается 
 или
просто 
 )
— вектор,
задающий положения точки в пространстве относительно
некоторой заранее фиксированной точки,
называемой началом координат.

Для
произвольной точки в пространстве,
радиус-вектор — это вектор, идущий из
начала координат в эту точку.

Длина
радиус-вектора,
или его модуль, определяет расстояние,
на котором точка находится от начала
координат, а стрелка указывает направление
на эту точку пространства.

На
плоскости углом радиус-вектора называется
угол, на который радиус-вектор повёрнут
относительно оси
абсцисс в
направлении против часовой стрелки.

Угловая скорость, ускорение

Углова́я
ско́рость — векторная физическая
величина, характеризующая скорость
вращения тела. Вектор угловой скорости
по величине равен углу поворота
тела в единицу времени:

,

а
направлен по оси
вращения согласно правилу
буравчика,
то есть, в ту сторону, в которую ввинчивался
бы буравчик с
правой резьбой, если бы вращался в ту
же сторону. Единица
измерения угловой
скорости, принятая в
системах СИ и СГС) — радианы в секунду.

Углово́е
ускоре́ние — псевдовекторная физическая
величина,
характеризующая быстроту изменения угловой
скорости твёрдого
тела.

При вращении тела
вокруг неподвижной оси,
угловое ускорение по модулю равно:

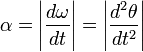
Вектор углового
ускорения α направлен
вдоль оси вращения (в сторону 
 при
ускоренном вращении и противоположно 
 —
при замедленном).

При
вращении вокруг неподвижной точки
вектор углового ускорения определяется
как первая производная от вектора
угловой скорости ω по
времени^[2],
то есть

,

и
направлен по касательной
к годографу вектора 
 в
соответствующей его точке.

Существует
связь между тангенциальным и
угловым ускорениями:

,

где R — радиус
кривизны траектории
точки в
данный момент времени. Итак, угловое
ускорение равно второй производной от
угла поворота по времени или первой
производной от угловой скорости по
времени. Угловое ускорение измеряется
в рад/сек² .

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В кинематике для однозначного определения характеристик движения тела в любой точке траектории необходимо знать его скорость и ускорение. Зависимость от времени этих величин предоставляет всю необходимую информацию для вычисления пройденного телом пути. Рассмотрим подробнее в статье, что такое ускорение тангенциальное и нормальное ускорение.

В физике

Прежде чем рассматривать для механического движения ускорение нормальное и тангенциальное ускорение, познакомимся с самим физическим понятием. Определение ускорения является достаточно простым. В физике под ним понимают характеристику изменения скорости. Последняя является векторной величиной, определяющей быстроту изменения координат движущегося объекта в пространстве. Скорость измеряется в метрах в секунду (расстояние, пройденное за единицу времени). Если ее обозначить символом v¯, тогда математическое определение ускорения a¯ будет выглядеть так:

a¯ = dv¯/dt

Это равенство определяет так называемое полное мгновенное ускорение. Мгновенным оно называется потому, что характеризует изменение скорости лишь в данный момент времени.

Если движение является равноускоренным, то есть в течение длительного времени ускорение не меняет своего модуля и направления, тогда можно записать следующую формулу для его определения:

a¯ = Δv¯/Δt

Где Δt>>dt. Величина a¯ здесь называется средним ускорением, которое в общем случае отличается от мгновенного.

Ускорение измеряется в системе СИ в метрах в квадратную секунду (м/с²).

Траектория движения и компоненты полного ускорения

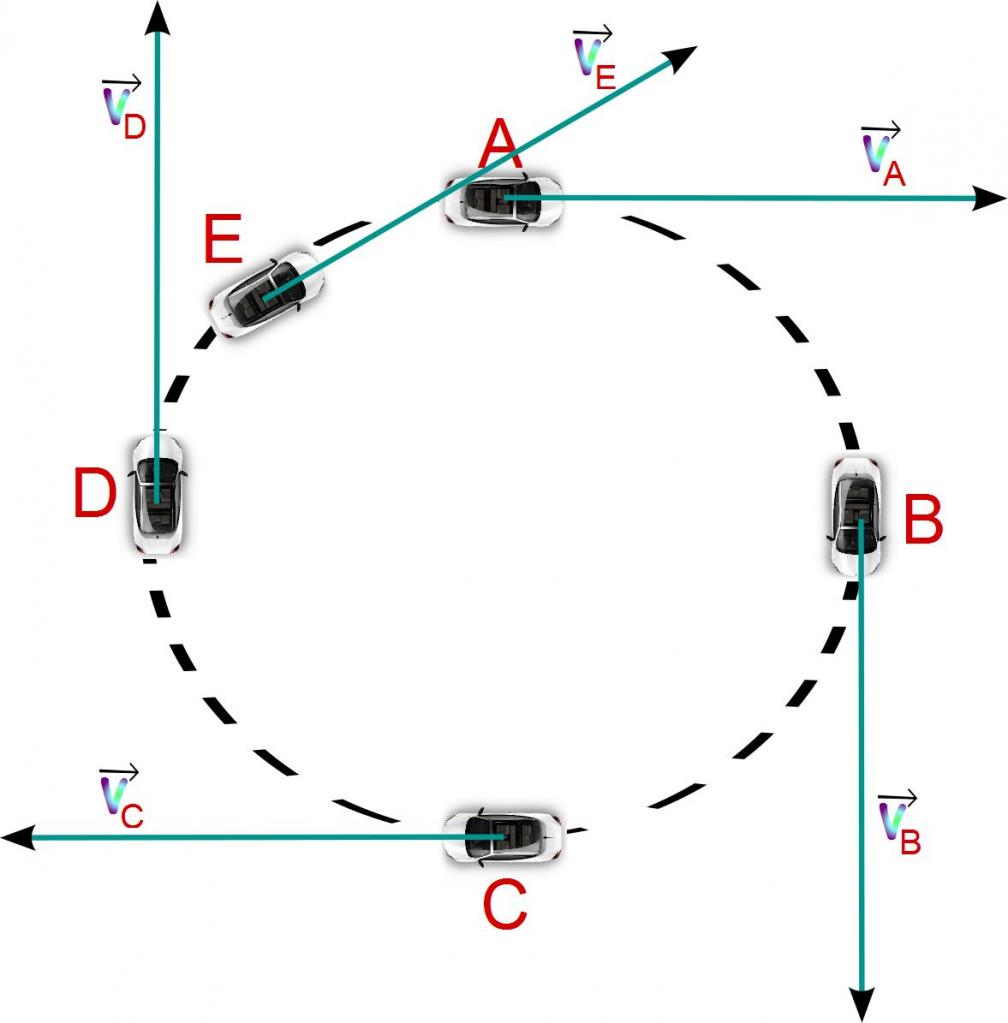
Чаще всего тела в природе движутся по кривым траекториям. Примерами такого перемещения являются: вращение по своим орбитам планет, параболическое падение камня на землю, поворот автомобиля. В случае криволинейной траектории в любой момент времени скорость направлена по касательной к рассматриваемой точке траектории. Как при этом направлено ускорение?

Чтобы ответить на поставленный выше вопрос, запишем скорость тела в следующей форме:

v¯ = v*u_t¯

Здесь u_t¯ – вектор скорости единичный, индекс t означает, что он направлен по касательной к траектории (тангенциальная компонента). Символом v обозначен модуль скорости v¯.

Теперь, следуя определению ускорения, можно провести дифференцирование скорости по времени, имеем:

a¯ = dv¯/dt = dv/dt*u_t¯ + v*d(u_t¯)/dt

Таким образом, полное ускорение a¯ представляет собой векторную сумму двух компонент. Первое и второе слагаемое называются нормальным и тангенциальным ускорением точки. Подробнее рассмотрим каждую из этих компонент.

Ускорение тангенциальное

Запишем еще раз формулу для этой компоненты полного ускорения:

a_t¯ = dv/dt*u_t¯

Это выражение позволяет описать свойства величины a_t¯:

• Она направлена точно так же, как и сама скорость или противоположно ей, то есть по касательной к траектории. Об этом свидетельствует элементарный вектор u_t¯.
• Она характеризует изменение скорости по абсолютной величине, что отражает множитель dv/dt.

Эти свойства позволяют сделать важный вывод: для прямолинейного движения полное и тангенциальное ускорения – это одна и та же величина. В случае криволинейного перемещения полное ускорение всегда больше по модулю, чем тангенциальное. Когда рассматривают физические задачи на прямолинейное равноускоренное движение, то ведут речь именно об этой компоненте ускорения.

Ускорение нормальное

Рассматривая тему скорости, ускорения тангенциального и ускорения нормального, дадим характеристику последней величине. Запишем формулу для нее:

a_n¯ = v*d(u_t¯)/dt = v*d(u_t¯)/dL*dL/dt

Чтобы записать явно правую часть равенства, воспользуемся следующими соотношениями:

dL/dt = v;

d(u_t¯)/dL = 1/r

Здесь dL – это пройденный телом путь за промежуток времени dt, r – радиус кривизны траектории. Первое выражение соответствует определению скорости, второе равенство следует из геометрических соображений. Пользуясь этими формулами, получаем конечное выражение для нормального ускорения:

a_n¯ = v²/r

То есть величина a_n¯ не зависит от изменения скорости, как тангенциальная компонента, а определяется исключительно ее модулем. Нормальное ускорение вдоль нормали к данному участку траектории направлено, то есть к центру кривизны. Например, во время движения по окружности вектор a_n¯ направлен к ее центру, поэтому нормальное ускорение называют часто центростремительным.

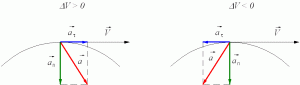
Если за изменение абсолютной величины скорости ответственно ускорение тангенциальное, то нормальная компонента ответственна за изменение вектора скорости, то есть она определяет траекторию перемещения тела.

Ускорение полное, нормальное и тангенциальное

Разобравшись с понятием ускорения и с его компонентами, приведем теперь формулу, которая позволяет определить полное ускорение. Поскольку рассмотренные компоненты направлены под углом 90 ^o друг к другу, то для определения абсолютной величины их векторной суммы можно использовать теорему Пифагора. Формула для полного ускорения имеет вид:

a = √(a_t² + a_n²)

Направление величины a¯ можно определить по отношению к вектору любой из компонент. Например, угол между a¯ и a_n¯ вычисляется так:

θ = arctg(a_t/a_n)

Учитывая приведенную выше формулу для модуля a¯, можно сделать вывод: при равномерном движении по окружности полное ускорение совпадает с центростремительным.

Решение задачи

Пусть тело движется по окружности радиусом 1 метр. Известно, что его скорость изменяется по следующему закону:

v = 2*t² + 3*t

Необходимо определить ускорение тангенциальное и нормальное ускорение в момент t = 4 секунды.

Для тангенциального имеем:

a_t = dv/dt = 4*t + 3 = 19 м/с²

Для того чтобы найти модуль ускорения нормального, сначала следует вычислить значение скорости в заданный момент времени. Имеем:

v = 2*4² + 3*4 = 44 м/с

Теперь можно воспользоваться формулой для a_n:

a_n = v²/r = 44²/1 = 1936 м/с²

Таким образом, мы определили все величины, которые требовалось найти для решения задачи.

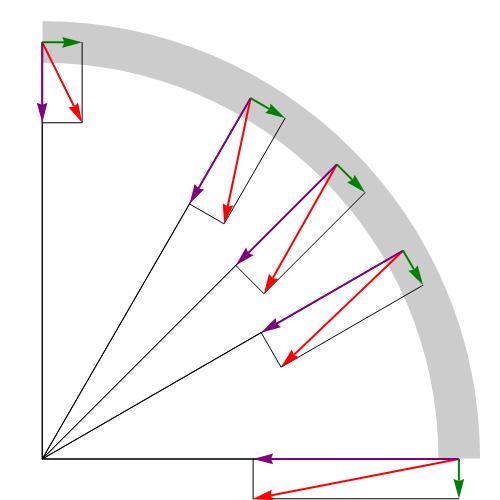
4.1. Движение по окружности с постоянной скоростью.

Движение по окружности — простейший вид криволинейного движения.

4.1.1. Криволинейное движение — движение, траекторий которого является кривая линия.

Для движения по окружности с постоянной скоростью:

1) траектория движения — окружность;

2) вектор скорости направлен по касательной к окружности;

3) вектор скорости постоянно меняет свое направление;

4) за изменение направления скорости отвечает ускорение, называемое центростремительным (или нормальным) ускорением;

5) центростремительное ускорение меняет только направление вектора скорости, при этом модуль скорости остается неизменным;

6) центростремительное ускорение направлено к центру окружности, по которой происходит движение (центростремительное ускорение всегда перпендикулярно вектору скорости).

4.1.2. Период (T) — время одного полного оборота по окружности.

Это величина постоянная, так как длина окружности постоянная и скорость движения постоянна

4.1.3 Частота  — число полных оборотов за 1 с.

По сути, частота отвечает на вопрос: как быстро вращается тело?

4.1.4. Линейная скорость — показывает, какой путь проходит тело за 1 с (это та же самая скорость, о которой говорилось в предыдущих темах)

где R — радиус окружности.

4.1.5. Угловая скорость показывает, на какой угол поворачивается тело за 1 с.

где  — угол, на который повернулось тело за время

4.1.6. Центростремительное ускорение

Напомним, что центростремительное ускорение отвечает только за поворот вектора скорости. При этом, так как скорость постоянная величина, то значение ускорения тоже постоянно.

4.1.7. Закон изменения угла поворота

Это полный аналог закона движения при постоянной скорости :

Роль координаты x играет угол роль начальной координаты играет скорость  — угловая скорость И с формулой следует работать так же, как ранее работали с формулой закона равномерного движения.

4.2. Движение по окружности с постоянным ускорением.

4.2.1. Тангенциальное ускорение

Центростремительное ускорение отвечает за изменение направления вектора скорости, но если еще меняется и модуль скорости, то необходимо ввести величину отвечающую за это — тангенциальное ускорение

Из вида формулы ясно, что  — это обычное ускорение, о котором говорилось раньше. Если то справедливы формулы равноускоренного движения:

где S — путь, который проходит тело по окружности.

Итак, еще раз подчеркнем, отвечает за изменение модуля скорости.

4.2.2. Угловое ускорение

Мы ввели аналог скорости для движения по окружности — угловая скорость. Естественно будет ввести и аналог ускорения — угловое ускорение

Угловое ускорение связано с тангенциальным ускорением:

Из формулы видно, что если тангенциальное ускорение постоянно, то и угловое ускорение будет постоянно. Тогда можем записать:

Формула является полным аналогом закона равнопеременного движения, поэтому работать с этой формулой мы уже умеем.

4.2.3. Полное ускорение

Центростремительное (или нормальное) и тангенциальное ускорения не являются самостоятельными. На самом деле, это проекции полного ускорения на нормальную (направлена по радиусу окружности, то есть перпендикулярно скорости) и тангенциальную (направлена по касательной к окружности в сторону, куда направлен вектор скорости) оси. Поэтому

Нормальная и тангенциальные оси всегда перпендикулярны, следовательно, абсолютно всегда модуль полного ускорения можно найти по формуле:

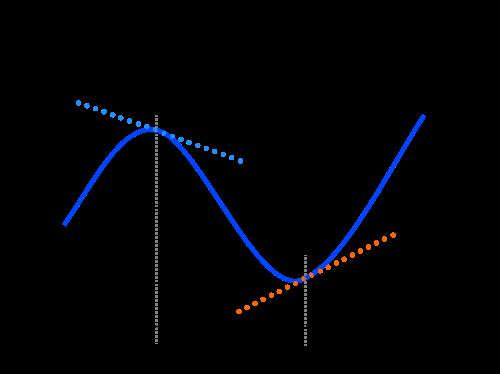
4.4. Движение по криволинейной траектории.

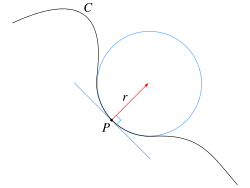
Движение по окружности является частным видом криволинейного движения. В общем случае, когда траектория представляет собой произвольную кривую (см. рис.), всю траекторию можно разбить на участки: AB и DE — прямолинейные участки, для которых справедливы все формулы движения по прямой; а для каждой участка, который нельзя рассмотреть как прямую, строим касательную окружность (окружность, которая касается траектории только в этой точке) — в точках C и D. Радиус касательной окружности называется радиусом кривизны. В каждой точке траектории радиус кривизны имеет свое значение.

Формула для нахождения радиуса кривизны :

где  — нормальное ускорение в данной точке (проекция полного ускорения на ось, перпендикулярную вектору скорости).