Как найти полное ускорение колеса

Пример решения задачи по определению величины и направления скорости и полного ускорения точки колеса, для момента времени, когда угол будет равен заданному значению.

Задача

Кривошип ОА, вращаясь вокруг оси, перпендикулярной плоскости чертежа и проходящей через точку О, приводит в движение колесо II, которое катится без скольжения по неподвижному колесу I.

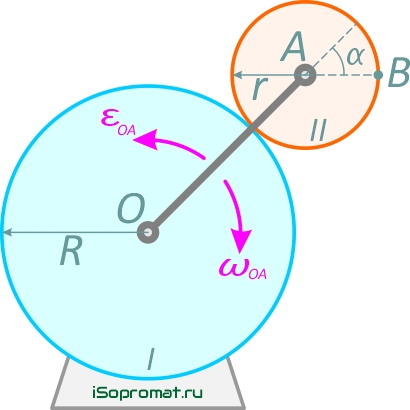
Рис. 2

Найти скорость и ускорение точки В колеса II, для момента времени, когда угол α=45°,
если R=40 см, r=20 см, ω_OA=4 с^-1, ε_OA=2 с^-2 (рис. 2).

Другие примеры решений >
Помощь с решением задач >

Решение

Теория по теме

Колесо II движется в плоскости чертежа, т.е. совершает плоскопараллельное движение.

По условию, колесо I неподвижно, значит, точка соприкосновения колес является МЦС для колеса II.

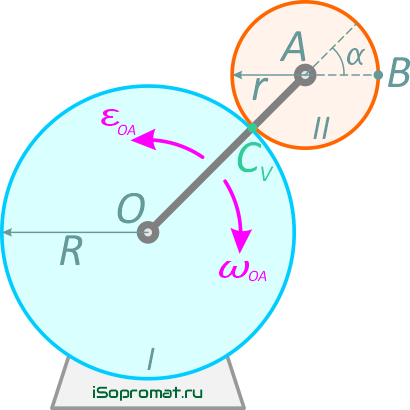
Рис. 2.10

Обозначим ее как C_V (эта точка не принадлежит кривошипу ОА). Скорость точки В определяется выражением

и направлена перпендикулярно отрезку ВС_V, в сторону вращения колеса II (рис. 2.11)

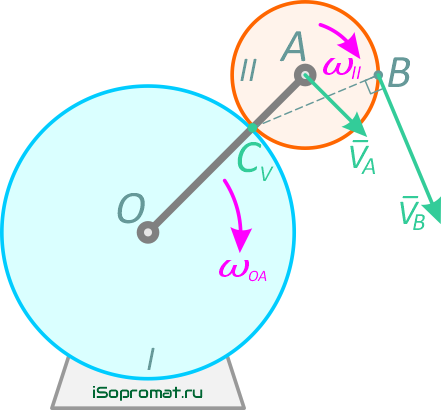
Рис. 2.11

Для определения угловой скорости ω_II запишем выражение для скорости точки А.

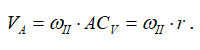
С другой стороны, точка А принадлежит кривошипу ОА. Скорость точки А, принадлежащей кривошипу, определяется выражением

и направлена ⊥ОА в сторону вращения кривошипа ОА. Из этих рассуждений следует:

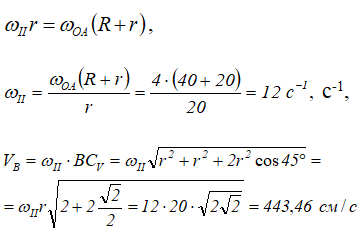
Найдем скорость точки В, используя теорему о скоростях точек плоской фигуры. Для этого примем точку А за полюс.

Тогда

Величина и направление скорости точки А определяются из условий движения кривошипа ОА.
V_A=ω_OA×OA
и вектор V_A⊥ОА и направлен в сторону вращения кривошипа (рис. 2.12).

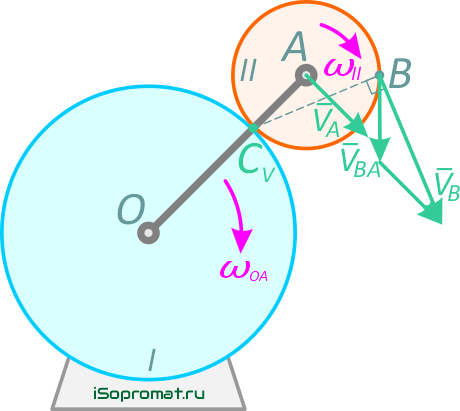
Рис. 2.12

Скорость V_BA — это скорость точки В во вращательном движении вокруг полюса А.

Величина скорости
V_BA=ω_II×r=12×20=240 см/с
и этот вектор направлен ⊥ отрезку АВ в сторону вращения колеса II.

Чтобы сложить V_A и V_BA, перенесем вектор V_A в конец вектора V_BA. Соединяя начало вектора V_BA с концом вектора V_A, получим вектор V_B. Из построения:

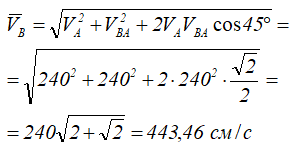
Определим ускорение точки В.

Согласно теореме об ускорении точки плоской фигуры, ускорение точки В можно определить из выражения

где a_A — ускорение точки А, принятой за полюс;

a_BA — ускорение точки В во вращательном движении, вокруг полюса А.

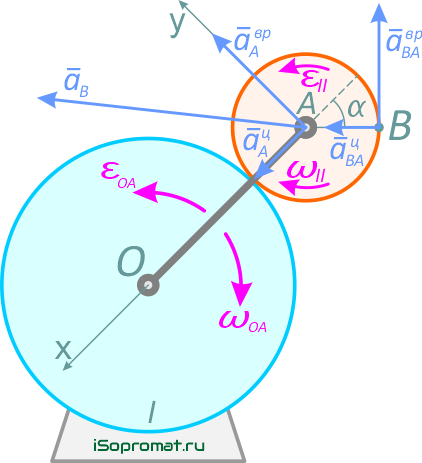
Рис. 2.13

Точка А – принадлежит колесу II и кривошипу ОА, движение которого известно, тогда

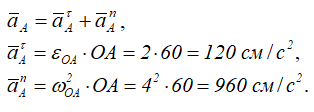
Ускорение a_BA (ускорение во вращательном движении) состоит из двух слагаемых:

где

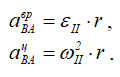
Найдем ε_II по определению:

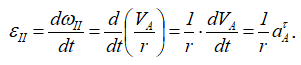
Подставляя числовые значения, получим

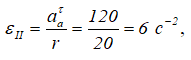
тогда

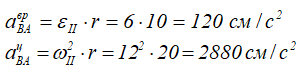
Ускорение точки В найдем, спроецировав все векторы уравнения

на выбранные оси координат ОХ и OY.

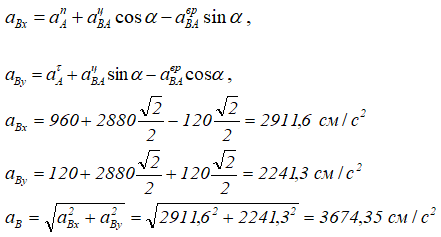
Углы, которые составляют вектор ускорения a_B с осями ОХ и OY, определим через направляющие косинусы.

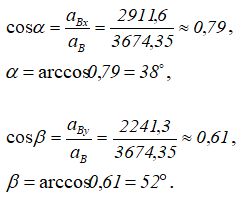
Скорость и ускорение точки В колеса II, для момента времени, когда угол α=45° найдены.

Другие примеры решения задач >

Рассмотрим
твердое тело, которое враща­ется
вокруг неподвижной оси. Тогда от­дельные
точки этого тела будут описывать
окружности разных радиусов, центры
ко­торых лежат на оси вращения. Пусть
не­которая точка движется по окружности
радиуса R
(рис.6).
Ее положение через промежуток времени
t
зададим
углом .
Элементарные (бесконечно малые) углы
поворота рассматривают как векторы.
Мо­дуль вектора d
равен
углу поворота, а его направление совпадает
с направле­нием поступательного
движения острия винта, головка которого
вращается в на­правлении движения
точки по окружности, т. е. подчиняется
правилу
правого, винта (рис.6).
Векторы, направления которых связываются
с направлением вращения, называются
псевдовекторами
или
акси­альными
векторами. Эти
векторы не имеют определенных точек
приложения: они мо­гут откладываться
из любой точки оси вращения.

Угловой
скоростью называется
вектор­ная величина, равная первой
производной угла поворота тела по
времени:

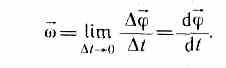
Вектор
«в направлен вдоль оси вращения по
правилу правого винта, т. е. так же, как
и вектор d
(рис. 7). Размерность угловой скорости
dim=T^-1,
a .
ее единица — радиан в секунду (рад/с).

Линейная скорость
точки (см. рис. 6)

В векторном виде
формулу для линейной скорости можно
написать как вектор­ное произведение:

При
этом модуль векторного произведе­ния,
по определению, равен

,
а
направление совпадает с
направлением
поступательного движения правого винта
при его вращении от 
к R.

Если
=const,
то
вращение равномер­ное и его можно
характеризовать перио­дом
вращения Т
—
временем, за которое точка совершает
один полный оборот, т. е. поворачивается
на угол 2.
Так как промежутку времени t=T
соответствует =2,
то =
2/Т,
откуда

Число
полных оборотов, совершаемых телом при
равномерном его движении по окружности,
в единицу времени называет­ся частотой
вращения:

Угловым
ускорением называется
век­торная величина, равная первой
производ­ной угловой скорости по
времени:

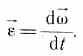
При вращении тела
вокруг неподвижной оси вектор углового
ускорения направлен вдоль оси вращения
в сторону вектора элементарного
приращения угловой ско­рости. При
ускоренном движении вектор

13

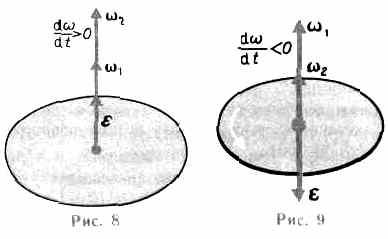
 сонаправлен
вектору 
(рис.8),
при замедленном.— противонаправлен
ему (рис. 9).

Тангенциальная
составляющая ускорения

Нормальная
составляющая ускорения

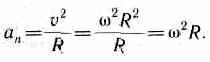
Таким
образом, связь между линейны­ми (длина
пути s,
пройденного
точкой по дуге окружности радиуса R,
линейная
ско­рость v,
тангенциальное
ускорение а_,
нор­мальное ускорение а_n)
и угловыми величи­нами (угол поворота
,
угловая скорость (о, угловое ускорение
)
выражается сле­дующими формулами:

В
случае равнопеременного движения точки
по окружности (=const)

где
₀
— начальная угловая скорость.

Контрольные
вопросы

• Что
называется материальной точкой? Почему
в механике вводят такую модель?

• Что
такое система отсчета?

• Что
такое вектор перемещения? Всегда ли
модуль вектора перемещения равен отрезку
пути,

пройденному точкой?

• Какое
движение называется поступательным?
вращательным?

• Дать
определения векторов средней скорости
и среднего ускорения, мгновенной
скорости

и мгновенного
ускорения. Каковы их направления?

• Что
характеризует тангенциальная
составляющая ускорения? нормальная
составляющая

ускорения? Каковы
их модули?

• Возможны
ли движения, при которых отсутствует
нормальное ускорение? тангенциальное

ускорение? Приведите
примеры.

• Что
называется угловой скоростью? угловым
ускорением? Как определяются их
направления?

• Какова
связь между линейными и угловыми
величинами?

Задачи

1.1.
Зависимость
пройденного телом пути от времени
задается уравнением s
= A+Вt+Сt²+Dt³
(С
= 0,1 м/с²,
D
= 0,03 м/с³).
Определить: 1) через какое время после
начала движения ускорение а тела будет
равно 2 м/с²;
2) среднее ускорение <а>
тела за этот промежуток времени. [ 1) 10
с; 2) 1,1 м/с²]

1.2.
Пренебрегая сопротивлением воздуха,
определить угол, под которым тело брошено
к гори­зонту, если максимальная высота
подъема тела равна 1/4 дальности его
полета. [45°]

1.3.
Колесо
радиуса R
=
0,1 м вращается так, что зависимость
угловой скорости от времени задается
уравнением 
= 2At+5Вt⁴
(A=2
рад/с²
и B=1
рад/с⁵).
Определить полное ускорение точек обода
колеса через t=1
с после начала вращения и число оборотов,
сделан­ных колесом за это время. [а =
8,5 м/с²;
N
= 0,48]

14

1.4.
Нормальное ускорение точки, движущейся
по окружности радиуса r=4
м,
задается уравнением а_n=А+-Bt+Ct²
(A=1
м/с²,
В=6
м/с³,
С=3
м/с⁴).
Определить: 1) тангенциальное ускорение
точки; 2) путь, пройденный точкой за время
t₁=5
с после начала движения; 3) полное
ускорение для момента времени t₂=1
с. [ 1) 6 м/с²;
2) 85 м; 3) 6,32 м/с²]

1.5.
Частота
вращения колеса при равнозамедленном
движении за t=1
мин
уменьшилась от 300 до 180 мин^-1.
Определить: 1) угловое ускорение колеса;
2) число полных оборотов, сделанных
колесом за это время. [1)
0,21 рад/с²;
2) 360]

1.6.
Диск
радиусом R=10
см вращается вокруг неподвижной оси
так, что зависимость угла поворота
радиуса диска от времени задается
уравнением =A+Bt+Ct²+Dt³
(B
= l рад/с,
С=1
рад/с²,
D=l
рад/с³).
Определить для точек на ободе колеса к
концу второй секунды после начала
движения: 1) тангенциальное ускорение
а_;
2) нормальное ускорение а_n;
3) полное ускорение а. [ 1) 0,14 м/с²;
2) 28,9 м/с²;
3) 28,9 м/с²]

Соседние файлы в папке Трофимова

• #
• #
• #
• #
• #
• #

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---

---

---

---

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Связь со вторым законом Ньютона

Как вывести формулу центростремительного ускорения

Движение по циклоиде*

iSopromat.ru

Пример решения задачи по определению величины и направления скорости и полного ускорения точки колеса, для момента времени, когда угол будет равен заданному значению.

Задача

Кривошип ОА, вращаясь вокруг оси, перпендикулярной плоскости чертежа и проходящей через точку О, приводит в движение колесо II, которое катится без скольжения по неподвижному колесу I.

Решение

Колесо II движется в плоскости чертежа, т.е. совершает плоскопараллельное движение.

По условию, колесо I неподвижно, значит, точка соприкосновения колес является МЦС для колеса II. Обозначим ее как C_V (эта точка не принадлежит кривошипу ОА). Скорость точки В определяется выражением

и направлена перпендикулярно отрезку ВС_V, в сторону вращения колеса II (рис. 2.11)

Для определения угловой скорости ω_II запишем выражение для скорости точки А.

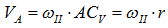
С другой стороны, точка А принадлежит кривошипу ОА. Скорость точки А, принадлежащей кривошипу, определяется выражением

и направлена ⊥ОА в сторону вращения кривошипа ОА. Из этих рассуждений следует:

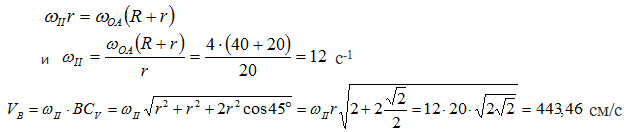
Найдем скорость точки В, используя теорему о скоростях точек плоской фигуры. Для этого примем точку А за полюс.

Тогда
V_B=V_A+V_BA (векторно).
Величина и направление скорости точки А определяются из условий движения кривошипа ОА.
V_A=ω_OA×OA
и вектор V_A⊥ОА и направлен в сторону вращения кривошипа (рис. 2.12).

Скорость V_BA — это скорость точки В во вращательном движении вокруг полюса А.

Величина скорости
V_BA=ω_II×r=12×20=240 см/с
и этот вектор направлен ⊥ отрезку АВ в сторону вращения колеса II.

Чтобы сложить V_A и V_BA, перенесем вектор V_A в конец вектора V_BA. Соединяя начало вектора V_BA с концом вектора V_A, получим вектор V_B. Из построения:

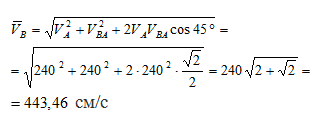
Согласно теореме об ускорении точки плоской фигуры, ускорение точки В можно определить из выражения

где a_A — ускорение точки А, принятой за полюс;

a_BA — ускорение точки В во вращательном движении, вокруг полюса А.

Точка А – принадлежит колесу II и кривошипу ОА, движение которого известно, тогда

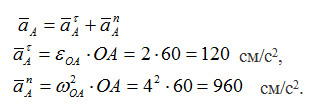
Ускорение a_BA (ускорение во вращательном движении) состоит из двух слагаемых:

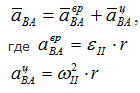
Найдем ε_II по определению:

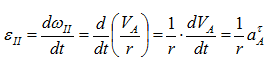
Подставляя числовые значения, получим

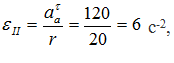
Ускорение точки В найдем, спроецировав все векторы уравнения

на выбранные оси координат ОХ и OY.

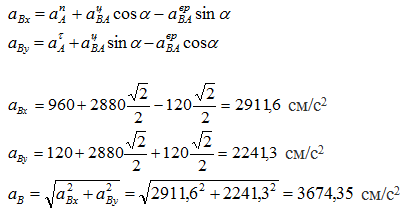
Углы, которые составляют вектор ускорения a_B с осями ОХ и OY, определим через направляющие косинусы.

Источник

Решения задач по теме: «Движение тела по окружности»

Урок №________ Дата_________ Класс_9______ Учитель Физики Османова Л.М .

Тема урока: Решения задач по теме: «Движение тела по окружности»

Цели урока: закрепить представление о криволинейном движении, основных характеристик частоты, периода, центростремительного ускорения и центростремительной силы.

Повторить виды механического движения. Закрепить понятия: движение по окружности, центростремительное ускорение, период, частота.

Развивать умения применять теоретические знания для решения конкретных задач, развивать культуру логического мышления, развивать интерес к предмету; познавательную деятельность при постановке и проведении эксперимента.

Формировать мировоззрение в процессе изучения физики и аргументировать свои выводы, воспитывать самостоятельность, аккуратность.

Воспитание коммуникативной и информационной культуры учащихся.

Форма работы: фронтальная, индивидуальная, групповая.

Тип урока: повторение и обобщение знаний, умений решать задачи по теме.

Вид урока: комбинированный с элементами исследования

Мотивация к учебной деятельности

« Незнающие пусть научатся, знающие – вспомнят еще раз

II . Актуализация опорных знаний.

Изменение положения тела в пространстве с течением времени. (Движение)

Физическая векторная величина, измеряемая в метрах. (Перемещение)

Физическая векторная величина, характеризующая быстроту движения. (Скорость)

Основная единица измерения длины в физике. (Метр)

Физическая величина, единицами измерения которой служат год, сутки, час. (Время)

Длина траектории . (Путь)

Единицы измерения ускорения (м/с 2 )

(Проведение диктанта с последующей проверкой, самооценка работ учениками) Работа в паре.
Тема урока : Решения задач по теме: «Движение тела по окружности»

Учитель. Что характеризует движение тела по окружности

Решение у доски задачи с подробным объяснением

Колесо делает 120 оборотов за 2 минуты. Какова частота вращения колеса и период вращения?

Точильный круг радиусом 10 см делает один оборот за 0,2 с. Найдите скорость точек, наиболее удаленных от оси вращения.

Автомобиль движется по закруглению дороги радиусом 100 м. Чему равно центростремительное ускорение автомобиля, если он движется со скоростью 54 км/ч?

Какова скорость движения автомобиля, если его колеса радиусом 30 см делают 600 оборотов в минуту?

Подведение итогов урока. Выставление оценок.

З адача 1 C какой скоростью велосипедист проходит закругление с радиусом 25 метров, если центростремительная скорость его движения равна 4 м/с?

Задача 2 Колесо радиусом 40 см делает один оборот за 0,4 секунды. Найти скорость точек на ободе колеса.

Задача 3 Колесо велосипедиста имеет радиус 40 см. С какой скоростью едет велосипедист, если колесо делает 4 оборота в секунду? Чему равен период вращения колеса?

Задача 4 С какой скоростью велосипедист должен проходить середину выпуклого моста радиусом 22,5 метра, чтобы его центростремительное ускорение было бы равно ускорению свободного падения?

Задача 5 Чему равно центростремительное ускорение тела, движущегося по окружности радиус ом 50 см при частоте вращения 5 оборотов в секунду?

задача1. Колесо радиусом 80 см делает один оборот за 0,8 секунды. Найти скорость точек на ободе колеса.

Задача 2 Скорость точек экватора Солнца при его вращении вокруг своей оси равно 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек его экватора.

Задача 3 Какова скорость движения автомобиля, если его колесо радиусом 30 см делает 500 оборотов в минуту?

Задача 4 Чему равна центростремительная сила и центростремительное ускорение, действующие на пращу массой 800 г, вращающуюся на веревке длиной 60 сантиметров равномерно со скоростью 2 м/с?

Задача 5 Период обращения космического корабля вокруг Земли равен 90 минутам. Высота подъема корабля над поверхностью Земли составляет 300 км, радиус Земли равен 6400 км. Определить скорость корабля.

9кл.Самостоятельная работа по теме : «Движение тела по окружности»

Задача 1 C какой скоростью велосипедист проходит закругление с радиусом 25 метров, если центростремительная скорость его движения равна 4 м/с?

Задача 2 Колесо радиусом 40 см делает один оборот за 0,4 секунды. Найти скорость точек на ободе колеса.

Задача 3 Колесо велосипедиста имеет радиус 40 см. С какой скоростью едет велосипедист, если колесо делает 4 оборота в секунду? Чему равен период вращения колеса?

Задача 4 С какой скоростью велосипедист должен проходить середину выпуклого моста радиусом 22,5 метра, чтобы его центростремительное ускорение было бы равно ускорению свободного падения?

Задача 5 Чему равно центростремительное ускорение тела, движущегося по окружности радиусом 50 см при частоте вращения 5 оборотов в секунду?

9 кл. Самостоятельная работа по теме : «Движение тела по окружности»

задача1. Колесо радиусом 80 см делает один оборот за 0,8 секунды. Найти скорость точек на ободе колеса.

Задача 2 Скорость точек экватора Солнца при его вращении вокруг своей оси равно 2 км/с. Найти период вращения Солнца вокруг своей оси и центростремительное ускорение точек его экватора.

Задача 3 Какова скорость движения автомобиля, если его колесо радиусом 30 см делает 500 оборотов в минуту?

Задача 4 Чему равна центростремительная сила и центростремительное ускорение, действующие на пращу массой 800 г, вращающуюся на веревке длиной 60 сантиметров равномерно со скоростью 2 м/с?

Задача 5 Период обращения космического корабля вокруг Земли равен 90 минутам. Высота подъема корабля над поверхностью Земли составляет 300 км, радиус Земли равен 6400 км. Определить скорость корабля.

Источник