6.
Криволинейное
движение. Угловое перемещение, угловые
скорость и ускорение тела. Путь и
перемещение при криволинейном движении
тела.
Криволинейное
движение –
это движение, траектория которого
представляет собой кривую линию
(например, окружность, эллипс, гиперболу,
параболу). Примером криволинейного
движения является движение планет,
конца стрелки часов по циферблату и
т.д. В общем случае скорость
при криволинейном движении изменяется
по величине и по направлению.
Криволинейное
движение материальной точки считается
равномерным движением, если
модульскорости постоянен
(например, равномерное движение по
окружности), и равноускоренным, если
модуль и направление скорости изменяется
(например, движение тела, брошенного
под углом к горизонту).
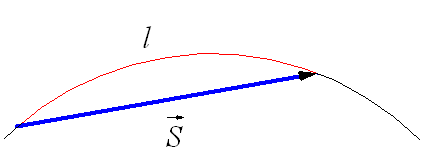
Рис.
1.19. Траектория и вектор перемещения при
криволинейном движении.
При
движении по криволинейной траектории вектор
перемещения ![]() направлен
направлен
по хорде (рис. 1.19), аl –
длина траектории.
Мгновенная скорость движения тела (то
есть скорость тела в данной точке
траектории) направлена по касательной
в той точке траектории, где в данный
момент находится движущееся тело (рис.
1.20).
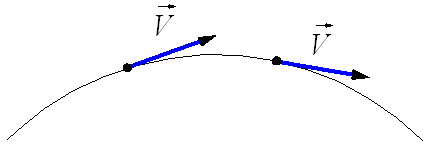
Рис.
1.20. Мгновенная скорость при криволинейном
движении.
Криволинейное
движение – это всегда ускоренное
движение. То есть ускорение
при криволинейном движении присутствует
всегда, даже если модуль скорости не
изменяется, а изменяется только
направление скорости. Изменение величины
скорости за единицу времени –
это тангенциальное
ускорение:
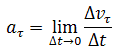
или
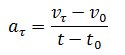
Где vτ,
v0 –
величины скоростей в момент времени t0 +
Δt и t0 соответственно.
Тангенциальное
ускорение в
данной точке траектории по направлению
совпадает с направлением скорости
движения тела или противоположно ему.
Нормальное
ускорение –
это изменение скорости по направлению
за единицу времени:
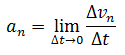
Нормальное
ускорение направлено
по радиусу кривизны траектории (к оси
вращения). Нормальное ускорение
перпендикулярно направлению скорости.
Центростремительное
ускорение –
это нормальное ускорение при равномерном
движении по окружности.
Полное
ускорение при равнопеременном
криволинейном движении тела равно:
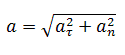
Движение
тела по криволинейной траектории можно
приближённо представить как движение
по дугам некоторых окружностей (рис.
1.21).
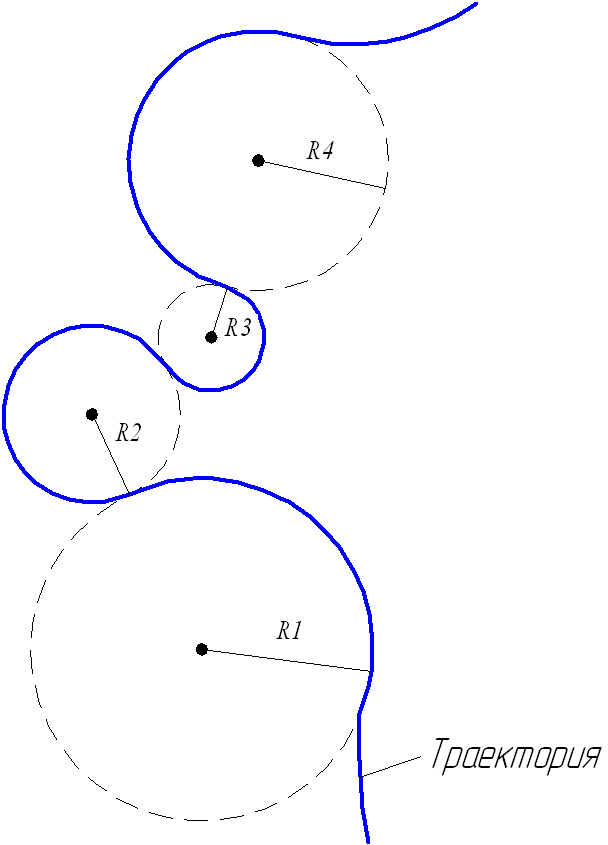
Рис.
1.21. Движение тела при криволинейном
движении.
ИЛИ
Криволинейное
движение
Криволинейные
движения –
движения, траектории которых представляют
собой не прямые, а кривые линии. По
криволинейным траекториям движутся
планеты, воды рек.
Криволинейное
движение – это всегда движение с
ускорением, даже если по модулю скорость
постоянна. Криволинейное движение с
постоянным ускорением всегда происходит
в той плоскости, в которой находятся
векторы ускорения и начальные скорости
точки. В случае криволинейного движения
с постоянным ускорением в
плоскости xOy проекции vxи vy ее
скорости на оси Ox и Oy и
координаты x и y точки
в любой момент времениt определяется
по формулам
![]()
![]()
![]()
![]()
![]()
Частным
случаем криволинейного движения –
является движение по окружности. Движение
по окружности, даже равномерное, всегда
есть движение ускоренное: модуль скорости
все время направлен по касательной к
траектории, постоянно меняет направление,
поэтому движение по окружности всегда
происходит с центростремительным
ускорением ![]() где r –
где r –
радиус окружности.
Вектор
ускорения при движении по окружности
направлен к центру окружности и
перпендикулярно вектору скорости.
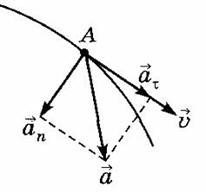
При
криволинейном движении ускорение можно
представить как сумму нормальной ![]() и
и
тангенциальной ![]() составляющих:
составляющих:
![]() ,
,
![]() –
–
нормальное (центростремительное)
ускорение, направлено к центру кривизны
траектории и характеризует изменение
скорости по направлению:
![]()
v
– мгновенное
значение скорости, r –
радиус кривизна траектории в данной
точке.
![]() –
–
тангенциальное (касательное) ускорение,
направлено по касательной к траектории
и характеризует изменение скорости по
модулю.
Полное
ускорение, с которым движется материальная
точка, равно:
![]() .
.
Кроме
центростремительного ускорения,
важнейшими характеристиками
равномерного движения по окружности
являются период и частота обращения.
Период
обращения—
это время, за которое тело совершается
один оборот.
Обозначается
период буквой Т (с)
и определяется по формуле:
![]()
где t —
время обращения, п —
число оборотов, совершенных за это
время.
Частота
обращения—
это величина, численно равная числу
оборотов, совершенных за единицу времени.
Обозначается
частота греческой буквой ![]() (ню)
(ню)
и находится по формуле:
![]()
Измеряется
частота в 1/с.
Период
и частота — величины взаимно обратные:
![]()
Если
тело, двигаясь по окружности со
скоростью v, делает
один оборот, то пройденный этим телом
путь можно найти, умножив скорость v на
время одного оборота:
l
= vT. С
другой стороны, этот путь равен длине
окружности 2πr.
Поэтому
vT
= 2πr,
![]()
![]()
где w (с-1) – угловая
скорость.
При
неизменной частоте обращения
центростремительное ускорение прямо
пропорционально расстоянию от движущейся
частицы до центра вращения.
Угловая
скорость (w)
– величина, равная отношению угла
поворота радиуса, на котором находится
вращающаяся точка, к промежутку времени,
за который произошел этот поворот:
![]() .
.
Связь
между линейной и угловой скоростями:
v=
wr.
Движение
тела можно считать известным лишь тогда,
когда известно, как движется каждая его
точка. Самое простое движение твердых
тел – поступательное. Поступательным называется
движение твердого тела, при котором
любая прямая, проведенная в этом теле,
перемещается параллельно самой себе.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Криволинейное движение – это движение, траектория которого представляет собой кривую линию (например, окружность, эллипс, гиперболу, параболу). Примером криволинейного движения является движение планет, конца стрелки часов по циферблату и т.д. В общем случае скорость при криволинейном движении изменяется по величине и по направлению.
Криволинейное движение материальной точки считается равномерным движением, если модуль скорости постоянен (например, равномерное движение по окружности), и равноускоренным, если модуль и направление скорости изменяется (например, движение тела, брошенного под углом к горизонту).
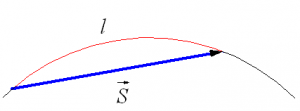
Рис. 1.19. Траектория и вектор перемещения при криволинейном движении.
При движении по криволинейной траектории вектор перемещения![]() направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).
направлен по хорде (рис. 1.19), а l – длина траектории. Мгновенная скорость движения тела (то есть скорость тела в данной точке траектории) направлена по касательной в той точке траектории, где в данный момент находится движущееся тело (рис. 1.20).
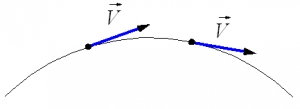
Рис. 1.20. Мгновенная скорость при криволинейном движении.
Криволинейное движение – это всегда ускоренное движение. То есть ускорение при криволинейном движении присутствует всегда, даже если модуль скорости не изменяется, а изменяется только направление скорости. Изменение величины скорости за единицу времени – это тангенциальное ускорение:
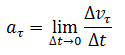
или
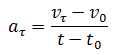
Где vτ, v0 – величины скоростей в момент времени t0 + Δt и t0соответственно.
Тангенциальное ускорение в данной точке траектории по направлению совпадает с направлением скорости движения тела или противоположно ему.
Нормальное ускорение — это изменение скорости по направлению за единицу времени:
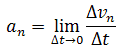
Нормальное ускорение направлено по радиусу кривизны траектории (к оси вращения). Нормальное ускорение перпендикулярно направлению скорости.
Центростремительное ускорение – это нормальное ускорение при равномерном движении по окружности.
Полное ускорение при равнопеременном криволинейном движении тела равно:
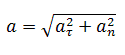
Движение тела по криволинейной траектории можно приближённо представить как движение по дугам некоторых окружностей (рис. 1.21).
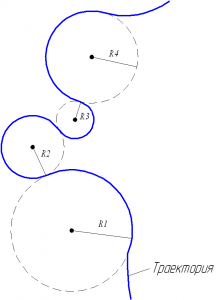
Рис. 1.21. Движение тела при криволинейном движении.
Рассматривая криволинейное движение тела, мы увидим, что его скорость в разные моменты различна. Даже в том случае, когда модуль скорости не меняется, все же имеет место изменение направления скорости. В общем случае меняются и модуль и направление скорости.
Таким образом, при криволинейном движении скорость непрерывно изменяется, так что это движение происходит с ускорением. Для определения этого ускорения (по модулю и направлению) требуется найти изменение скорости как вектора, т. е. найти приращение модуля скорости и изменение ее направления.
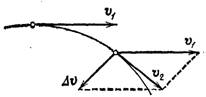
Рис. 49. Изменение скорости при криволинейном движении
Пусть, например, точка, двигаясь криволинейно (рис. 49), имела в некоторый момент скорость
![]()
а через малый промежуток времени — скорость
![]()
. Приращение скорости есть разность между векторами
![]()
и
![]()
. Так как эти векторы имеют различное направление, то нужно взять их векторную разность. Приращение скорости выразится вектором
![]()
, изображаемым стороной параллелограмма с диагональю
![]()
и другой стороной
![]()
. Ускорением
![]()
называется отношение приращения скорости к промежутку времени
![]()
, за который это приращение произошло. Значит, ускорение
![]()
По направлению
![]()
совпадает с вектором
![]()
.
Выбирая
![]()
достаточно малым, придем к понятию мгновенного ускорения (ср. § 16); при произвольном
![]()
вектор
![]()
будет представлять среднее ускорение за промежуток времени
![]()
.
Направление ускорения при криволинейном движении не совпадает с направлением скорости, в то время как для прямолинейного движения эти направления совпадают (или противоположны). Чтобы найти направление ускорения при криволинейном движении, достаточно сопоставить направления скоростей в двух близких точках траектории. Так как скорости направлены по касательным к траектории, то по виду самой траектории можно сделать заключение, в какую сторону от траектории направлено ускорение. Действительно, так как разность скоростей
![]()
в двух близких точках траектории всегда направлена в ту сторону, куда искривляется траектория, то, значит, и ускорение всегда направлено в сторону вогнутости траектории. Например, когда шарик катится по изогнутому желобу (рис. 50), его ускорение на участках
![]()
и
![]()
направлено так, как показывают стрелки, причем это не зависит от того, катится шарик от
![]()
к
![]()
или в обратном направлении.

Рис. 50. Ускорения при криволинейном движении всегда направлены в сторону вогнутости траектории
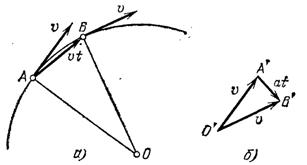
Рис. 51. К выводу формулы для центростремительного ускорения
Рассмотрим равномерное движение точки по криволинейной траектории. Мы уже знаем, что это — ускоренное движение. Найдем ускорение. Для этого достаточно рассмотреть ускорение для частного случая равномерного движения по окружности. Возьмем два близких положения
![]()
и
![]()
движущейся точки, разделенных малым промежутком времени
![]()
(рис. 51, а). Скорости движущейся точки в
![]()
и
![]()
равны по модулю, но различны по направлению. Найдем разность этих скоростей, пользуясь правилом треугольника (рис. 51, б). Треугольники
![]()
и
![]()
подобны, как равнобедренные треугольники с равными углами при вершине. Длину стороны
![]()
, изображающей приращение скорости за промежуток времени
![]()
, можно положить равной
![]()
, где
![]()
— модуль искомого ускорения. Сходственная ей сторона
![]()
есть хорда дуги
![]()
; вследствие малости дуги длина ее хорды может быть приближенно принята равной длине дуги, т.е.
![]()
. Далее,
![]()
;
![]()
, где
![]()
— радиус траектории. Из подобия треугольников следует, что отношения сходственных сторон в них равны:
![]()
откуда находим модуль искомого ускорения:
![]()
(27.1)
Направление ускорения перпендикулярно к хорде
![]()
. Для достаточно малых промежутков времени можно считать, что касательная к дуге практически совпадает с ее хордой. Значит, ускорение можно считать направленным перпендикулярно (нормально) к касательной к траектории, т. е. по радиусу к центру окружности. Поэтому такое ускорение называют нормальным или центростремительным ускорением.
Если траектория — не окружность, а произвольная кривая линия, то в формуле (27.1) следует взять радиус окружности, ближе всего подходящей к кривой в данной точке. Направление нормального ускорения и в этом случае будет перпендикулярно к касательной к траектории в данной точке. Если при криволинейном движении ускорение постоянно по модулю и направлению, его можно найти как отношение приращения скорости к промежутку времени, за который это приращение произошло, каков бы ни был этот промежуток времени. Значит, в этом случае ускорение можно найти по формуле
![]()
(27.2)
аналогичной формуле (17.1) для прямолинейного движения с постоянным ускорением. Здесь
![]()
— скорость тела в начальный момент, a
![]()
— скорость в момент времени
![]()
.
Общие сведения
В физике даётся вполне однозначное определение движению. Под ним понимают изменение положения физической точки в пространстве по отношению с другими объектами. Считается, что любое тело состоит из совокупности точек, перемещающихся одинаково по отношению друг к другу. Поэтому любой объект принято обозначать в виде элементарной точки.
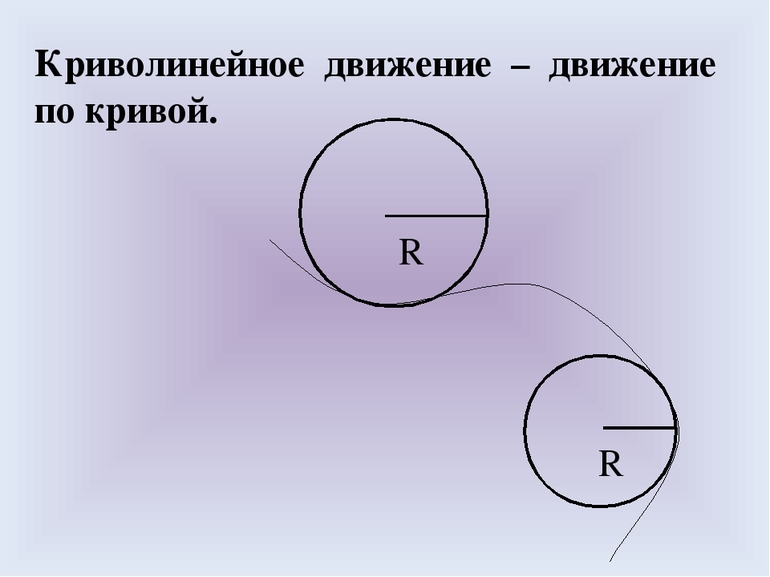
Кинематика не изучает, почему движение таково, а рассматривает только путь перемещения. С точки зрения физики, криволинейное движение — это путь, пройденный материальной точкой по кривой траектории. Если же траектория прямая, то изменение положения называется прямолинейным.
Криволинейное движение — это всегда ускоренное перемещение. Оно может быть:
- Равномерным. В этом случае скорость перемещения по модулю остаётся постоянной на всём прошедшем расстоянии. Например, движение по окружности.
- Равноускоренным. Признаком такого движения является изменение скорости и направления. Например, брошенное тело под углом.
Основной характеристикой понятия является вектор перемещения. Обозначается он латинской буквой S со стрелочкой вверху. Направлен он всегда по хорде. Кроме вектора, передвижение по кривой линии определяется тангенциальным и нормальным ускорением.
В первом случае характеристика обозначает изменение величины скорости в единицу времени: at = lim Δv / Δt, где: v — начальная скорость в момент времени t0 + Δt. Тангенциальное ускорение может как совпадать по направлению со скоростью, так и быть ей противоположной.
Нормальным ускорением называют характеристику, перпендикулярную направлению скорости: an = V2 / r, где: r — радиус окружности. Оно всегда совпадает с радиусом кривизны пути. Подвидом такого ускорения является центростремительная сила. Проявляется она при равномерном перемещении по окружности.
Таким образом, если движение является криволинейным, то вектора скорости и ускорения не лежат на одной прямой. Из простых примеров криволинейного движения можно выделить: течение воды в реке, перелёт на самолёте, катание на колесе обозрения.
Центростремительное ускорение
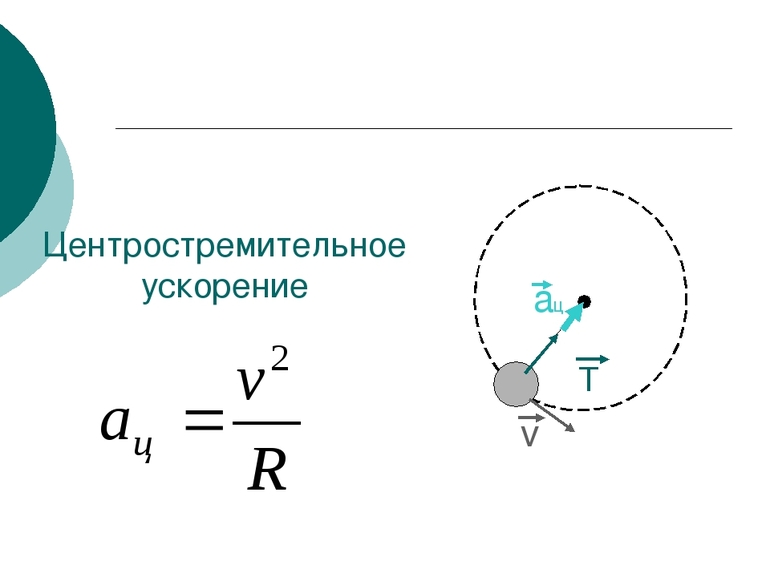
Если движение равномерное, но происходит оно по кривой, всё равно будет фиксироваться ускорение точки. Это происходит из-за того, что ускорение определяется как изменение скорости к промежутку времени. Поэтому если точка движется равномерно, то это значит, что модуль скорости остаётся одинаковым, но направление вектора изменяется. То есть будет справедливо записать: v = v0, но v ≠ v0. Можно сделать вывод, что изменение скорости существует, если Δv ≠ 0, при этом ускорение тоже не равно нулю: a ≠ 0.
Рассмотрим самый простой вид криволинейного перемещения. Существует история, что ещё во времена Аристотеля древние греки считали окружность идеальной линией. Из-за этого исторического факта астрономам приходилось объяснять движение планет, как комбинацию перемещений космических тел по окружности.
Можно представить тело, изменяющее своё положение по окружности. Траектория перемещения в декартовой системе координат будет выглядеть в виде полусферы. Пусть за её центр будет принята точка O. Тело движется равномерно. В какой-то момент времени его скорость будет V0. Её вектор направлен по касательной и совпадает по направлению с перемещением тела. Через некоторое время объект переместится в другую точку. Его скорость по-прежнему останется направленной по касательной, при этом модуль не изменится. То есть V = V0, но вектора их неравны: V ≠ V0.

Пусть стоит задача — найти равномерное движение по окружности. Иными словами, определить направление вектора и вычислить его модуль. В первую очередь необходимо узнать, куда же направлен вектор ускорения. Чтобы ответить на этот вопрос, нужно опираться на исходную формулу: a = Δv / Δt. Отсюда можно сделать вывод, что куда будет направлен вектор V, туда будет направлено и ускорение a.
Для наглядности можно построить вектор изменения скорости частицы, движущейся по рассматриваемой траектории. Чтобы построить график, описывающий ситуацию, нужно перенести V0 параллельно вектору V к его началу. Соединив два свободных конца перпендикуляром, получится треугольник. По правилу вычитания векторов можно получить вектор изменения скорости: Δv = V — V0. Направлен он будет сверху вниз.
Так как V0 направлен по касательной перпендикулярно радиусу, при этом угол треугольника при основании стремится к нулю, можно утверждать, что Δv перпендикулярен V. Значит, и вектор ускорения перпендикулярен V. Отсюда следует, что вектор ускорения направлен к центру окружности, поэтому его и называют центростремительным ускорением.
Движение по произвольной кривой
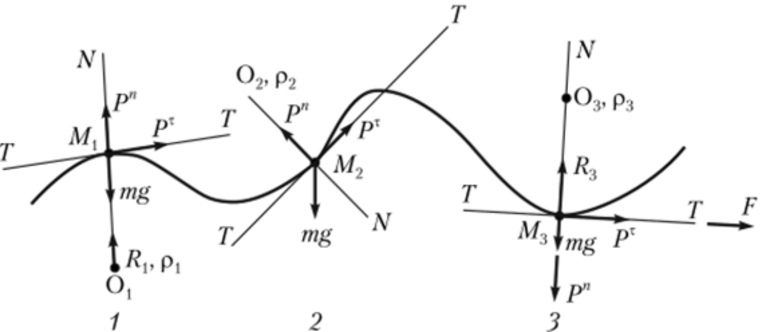
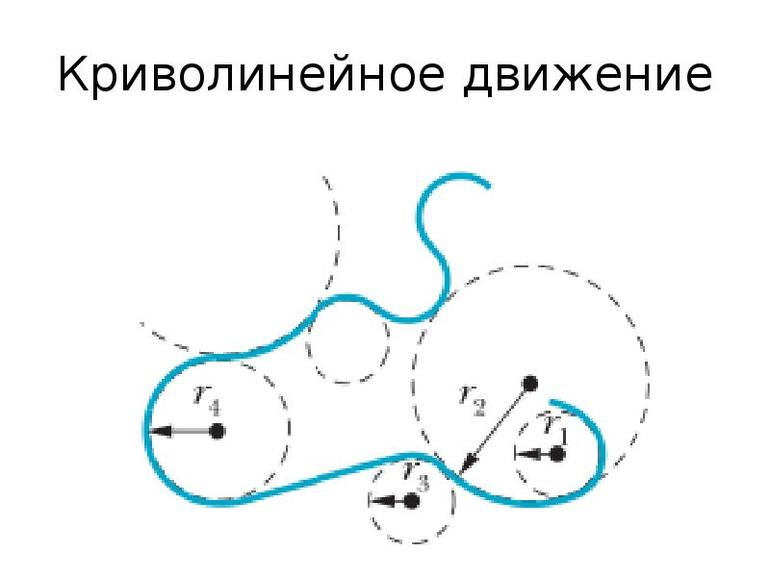
Рассмотрим простейший случай равномерного перемещения. Можно представить ситуацию, что если руль автомобиля держать неподвижно, то он будет ехать по прямой или по окружности. В реальной ситуации при езде всё время приходится поворачивать руль автомобиля, то есть в каждый момент времени происходит перемещение по окружности. При этом с каждым поворотом колеса управления радиус окружности изменяется. В данный момент времени он всегда совпадает с траекторией движения и называется радиусом кривизны траектории.
На графике движения можно отметить несколько точек. В одной из них скорость будет равняться V1. Немного дальше пройденное расстояние изменится, но скорость останется той же. Поменяется и направление V2. Через определённое время скорость будет равняться V3. Это движение равномерное.
Относительно точки V1 можно построить касающуюся её окружность с центром r1. По аналогии движения за рулём, это то же самое, что в рассматриваемой точке зафиксировать поворот управления на постоянный угол. Для V2 центр радиуса находится в точке r2, а V3 в r3.
В любом из этих трёх случаев происходит движение по окружности. То есть криволинейное движение произвольной формы — это перемещение по окружности любого радиуса. Если же радиус изменяется, то в любой момент меняется и центростремительное ускорение. Но при этом направление всегда совпадает с радиусом. Самое большое ускорение будет в том месте, где радиус самый маленький, и наоборот. Таким образом можно утверждать, что всякий раз ускорение будет перпендикулярно скорости при равномерном движении.
Кроме центростремительного ускорения, важными характеристиками, описывающими движение, являются следующие величины:
- Период. Показывает, за сколько времени точка совершит один оборот: T = t /n. Где t — время, за которое происходит определённое число оборотов, равное n.
- Частота. Определяет, сколько оборотов совершенно за единицу времени: λ = n / t.
- Угловая скорость. Является отношением угла поворота радиуса ко времени, за который произошёл поворот: W = φ / Δt = 2 * p / T = V / r.
Это основные формулы для криволинейного движения, использующиеся при решении задач. Кроме того, в заданиях используется связь между линейной и угловой скоростями: v = w * r, а также формула полного ускорения: a = at + an.
Решение простых задач
Виды движения изучаются на уроках физики в седьмом классе средней школы. На них ученикам объясняют понятия поступательного и равномерного движения, даются необходимые уравнения. Решение задач на уроках необходимо для закрепления пройденного материала и реального понимания ситуаций, при которых используются знания о видах перемещения.
Вот некоторые типы заданий, часто встречающиеся в различных вариантах у учащихся при сдаче ими тестов или написании контрольных работ:

- Линейная скорость точек рабочей поверхности наждачного круга диаметром 300 мм не должна превышать 35 метров в секунду. Допустима ли посадка круга на вал электродвигателя, совершающего обращение со скоростью 1400 оборотов в минуту? Согласно условию, необходимо найти, как связаны между собой V1 c Vmax. То есть линейную скорость и частоту вращения. Для расчёта необходимо использовать формулу связи скоростей: v = w * r. Так как поверхность абразива плоская, то радиус его будет равняться: r = d / 2. Подставив все исходные данные, можно записать: v = 2 * p * n / 2 = p * n * d = 3,14 * 1400 * 1/60с * 0,3 м = 22 м/с. Следовательно, из полученного значения можно сделать вывод, что посадка допустима.
- Какова линейная скорость точек земной поверхности на широте 46,50 при суточном вращении? Радиус Земли принять равным 6400 км. Другими словами, нужно выяснить линейную скорость. Широта рассчитывается вдоль меридиана и, по сути, это угол, измеряемый между двумя точками. Одна из них находится на экваторе, а другая — в указанном месте. Между радиусами, проведёнными из этих точек, угол составляет φ. Решить поставленную задачу можно, используя формулы: v = w * r и w = 2 * p / T. Следует учесть, что радиус, соответствующий 46,50, будет меньше радиуса Земли. Для того чтобы найти нужное значение, необходимо построить виртуальный треугольник и, используя тригонометрические формулы, записать, что cos φ = r / R. Учитывая, что направлена мгновенная скорость при криволинейном движении к центру, формула будет иметь вид: V = (2 * p / T) * R * cos φ = (6,28 * 6400 * 103 * cos 46,50) / 24 * 3,600 c = 465 * 0,69 м/с = 320 м/с.
Таким образом решать задачи на нахождение различных параметров при криволинейном движении без учёта его вызвавшей причины несложно. При этом следует правильно определить тип движения и знать основные формулы.
Пример сложного уровня
В большей мере такого уровня задачи являются поучительными, так как они используются для реальных случаев. Например, при расчётах работы различных технических установок. Вот одна из них.
Пусть движение от шкива один к шкиву четыре передаётся при помощи двух временных передач. Найти частоту вращения в оборотах в минуту и угловую скорость шкива четыре, если шкив один делает 1200 об/мин, а радиусы шкивов: R1 — 8 см, R2 — 32 см, R3 — 11 см, R4 — 55 см, при этом они жёстко укреплены на одном валу. Передающие ремни принять идеальными.

Для решения этой задачи нужно вначале определить направление вращения. Из условия задачи следует, что первый шкив будет вращаться в другую сторону по сравнению с остальными тремя. Для того чтобы найти угловую скорость последнего ролика, нужно будет последовательно определить параметры предшествующих ему шкивов.
Линейная скорость точек движения на ролике первого и второго шкива одинакова. Это следует из того, что ремни идеальные, не проскакивают и не растягиваются. Таким образом будет справедливо записать: V1 = V2. Так как w1 * r1 = w2 * r2, можно составить отношение: r1 / r2 = w1 / w2 или r1 / r2 = 2 * p * n2 / 2 * p * n1. То есть отношение примет вид: r1 / r2 = n2 / n1.
Так как третий шкив закреплён жёстко на валу со вторым, то образованную систему можно считать одним твёрдым телом. Применительно к нему можно говорить об общей угловой скорости или одинаковой частоте вращения. Получается, что n3 = n2. Тогда можно записать: n3 = n1 = r1 / r2.
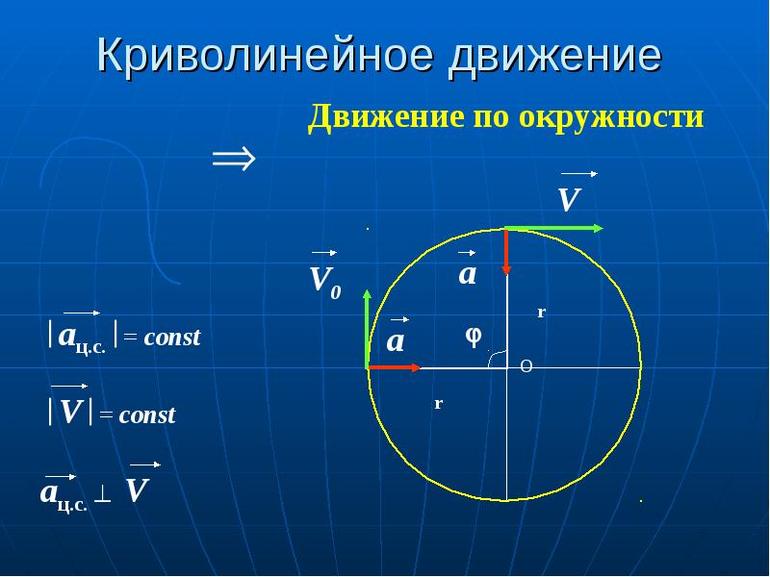
На следующем шаге необходимо определить линейную скорость на четвёртом ролике. Из условия известно, что V3 = V4, так как их соединение идеальное. Это значит, что можно связать скорости третьего и четвёртого шкива с частотами: V4 = 2 *p * n4 * r4; V3 = 2 * p * n3. Из полученного равенства нужно выразить n4. Оно будет равняться: n4 = n3 * r3 / r4. В эту формулу необходимо подставить n3 и получить итоговую формулу: n4 = n1 * (r1 * r3) / (r2 * r4).
Теперь нужно подставить исходные данные и выполнить расчёт. При этом переходить в систему СИ нет необходимости: n1 = 1200 об/мин * (8 * 11) / (32 * 55) = 1200 * 1 / 20 об/мин = 60 об/мин. Для того чтобы найти угловую скорость, частоту необходимо умножить на 2p. При этом учесть, что угловая скорость измеряется в радианах в секунду. Поэтому w4 = 2 * p * n4 = 6, 28 * 1 = 6,28 рад/сек. Интересной особенностью является то, что частота вращения первого шкива в двадцать раз больше четвёртого. Задача решена.
Ускорение, теория и онлайн калькуляторы
Ускорение
Определение ускорения
Определение
Ускорение ($overline{a}$) – это векторная физическая величина, показывающая как быстро изменяется скорость тела ($overline{v}$).
Мгновенное ускорение (ускорение в определенный момент времени) – это величина равная:
[overline{a}={mathop{lim }_{Delta tto 0} frac{Delta overline{v}}{Delta t} }=frac{doverline{v}}{dt}=dot{v}left(tright)left(1right).]
Средним ускорением ($leftlangle arightrangle $) за промежуток времени $Delta t=t_2-t_1$ называют физическую величину, равную отношению изменения скорости ($Delta v=v_2-v_1$) в единицу времени:
[leftlangle arightrangle =frac{Delta v}{Delta t}left(2right).]
Единицей измерения ускорения в Международной системе единиц (СИ) является метр на секунду в квадрате:
[left[aright]=frac{м}{с^2}.]
Направление вектора ускорения зависит от характера движения тела.
Ускорение при прямолинейном движении
Если материальная точка движется прямолинейно, то вектор ускорения направлен вдоль той же прямой, что и вектор скорости. Изменяется только величина скорости.
Переменное движение называют ускоренным, если скорость материальной точки постоянно увеличивается по модулю. При этом $a>0$, векторы ускорения и скорости сонаправлены.
Если скорость по модулю убывает, то движение называют замедленным ($a<0;; overline{a}uparrow downarrow overline{v}$).
Движение материальной точки называют равнопеременным, если движение происходит с постоянным ускорением ($overline{a}=const$). При равнопеременном движении мгновенная скорость ($overline{v}$) и ускорение материальной точки связаны выражением:
[overline{v}={overline{v}}_0+overline{a}t left(3right),]
где ${overline{v}}_0$ – скорость тела в начальный момент времени.
Ускорение материальной точки при криволинейном движении
При произвольном движении полное ускорение предпочтительно разложить на две компоненты: по направлению скорости (тангенциальная составляющая ускорения) и перпендикулярную составляющую к скорости (центростремительное) ускорение.
Тангенциальная (касательная) компонента ускорения направлена вдоль прямой параллельной вектору мгновенной скорости материальной точки (по касательной к траектории движения), обозначается она обычно как $a_{tau }$, равна:
[{overline{a}}_{tau }=frac{dv}{dt}{overline{e}}_{tau }left(4right),]
где ${overline{e}}_{tau }$ – единичный вектор, касательный к траектории движения.
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. При ускоренном движении материальной точки касательное ускорение направлено по скорости.
Нормальное ускорение (обозначается как ${overline{a}}_n$) перпендикулярно вектору скорости, направлено к центру кривизны траектории. Оно характеризует быстроту изменения направления вектора скорости. Величина нормального ускорения определяется как:
[a_n=frac{v^2}{R}={omega }^2Rleft(5right),]
где $R$ – радиус кривизны траектории движения материальной точки в рассматриваемой точке.
Полное ускорение ($overline{a}$) материальной точки равно:
[overline{a}={overline{a}}_{tau }+{overline{a}}_nleft(6right).]
Модуль полного ускорения точки при криволинейном движении находят как:
[a=sqrt{a^2_{tau }+a^2_n}left(7right).]
Полное ускорение имеет направление по секущей в сторону вогнутости траектории.
Примеры задач с решением
Пример 1
Задание. По значениям, которые принимают нормальное и тангенциальное ускорения можно делать вывод о виде движения, которое совершает материальная точка. Определите, какое движение совершается точкой, если:
1) $a_n=0,$
2) $a_{tau }=0; a_n=0,$
3) $a_{tau }=0; a_nne 0,$
4) $a_{tau }=0; a_n=const.$
Решение. 1)В том случае, если $a_n=0$, то скорость может изменяться только по величине, следовательно, движение прямолинейное.
2) Если $a_{tau }=0;; a_n=0,$ направление скорости не изменяется ($a_n=0$), постоянна скорость и по модулю ($a_{tau }=0$), значит, мы имеем дело с равномерным и прямолинейным движением.
3) Если $a_{tau }=0;; a_nne 0$, то движение будет криволинейным, так как изменяется направление скорости ($a_nne 0$), но со скоростью постоянной по величине.
4) При $a_{tau }=0;; a_n=const$ – точка движется по окружности равномерно.
Пример 2
Задание. На рис.1 дан график зависимости ускорения материальной точки от времени при прямолинейном движении. В какой точке графика скорость максимальна? Начальная скорость равна нулю.
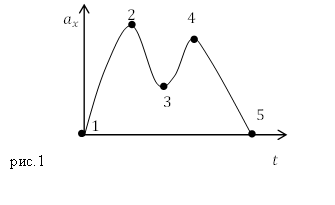
Решение. При прямолинейном движении (допустим по оси X) ускорение и скорость связаны соотношением:
[a_x=frac{dv_x}{dt}left(2.1right),]
следовательно, скорость найдем как:
[v_x=intlimits^{t_2}_{t_1}{a_xdt}left(2.2right).]
Из геометрического смысла интеграла, помним, что интеграл равен площади криволинейной трапеции, которая ограничена функцией, стоящей под интегралом (у нас $a_x$), осью времени (в нашем случае) и прямыми $t=t_1$ (время начала движения) и $t=t_k left(где t_k -конечное врямя движенияright). $ Максимальной площадь трапеции будет в точке 5. Следовательно, ускорение максимально в точке 5.
Ответ. Точка 5
Читать дальше: частота колебаний.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
