I. Механика
Тестирование онлайн
Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.
Период и частота
Период вращения T – это время, за которое тело совершает один оборот.
Частота вращение – это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.
Используя предыдущие формулы, можно вывести следующие соотношения
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.
Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.
Вращение Земли
Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.
Связь со вторым законом Ньютона
Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.
Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой
Как вывести формулу центростремительного ускорения
Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна vA и vB соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.
Разница векторов есть . Так как , получим
Движение по циклоиде*
В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.
Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.
Мгновенная скорость определяется по формуле
Определить полное ускорение точки (29 ноября 2009)
Механика. Молекулярная физика. Термодинамика. Б. А. Фёдоров.
- версия для печати
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Комментарии
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Начальная скорость точки равна нулю, поэтому изменение ее скорости:
Средняя скорость точки равна:
С другой стороны, vcp = (v − vo) / 2 = (1/2) v.
Тогда Δt = 2пR / v.
Нормальное ускорение равно:
Полное ускорение точки:
Подставляя числовые данные, получим:
- Войдите или зарегистрируйтесь, чтобы отправлять комментарии
Можно было найти скорость в конечной точке через
Движение по окружности
Движение по окружности – простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆ φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
Если угол поворота мал, то ∆ l ≈ ∆ s .
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω , то есть скорости изменения угла поворота.
Определение. Угловая скорость
Угловая скорость в данной точке траектории – предел отношения углового перемещения ∆ φ к промежутку времени ∆ t , за которое оно произошло. ∆ t → 0 .
ω = ∆ φ ∆ t , ∆ t → 0 .
Единица измерения угловой скорости – радиан в секунду ( р а д с ).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
a n = ∆ v → ∆ t , ∆ t → 0
Модуль центростремительного ускорения можно вычислить по формуле:
a n = v 2 R = ω 2 R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v → за малый промежуток времени ∆ t . ∆ v → = v B → – v A → .
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a → = ∆ v → ∆ t , ∆ t → 0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что O A A B = B C C D .
Если значение угла ∆ φ мало, расстояние A B = ∆ s ≈ v · ∆ t . Принимая во внимание, что O A = R и C D = ∆ v для рассмотренных выше подобных треугольников получим:
R v ∆ t = v ∆ v или ∆ v ∆ t = v 2 R
При ∆ φ → 0 , направление вектора ∆ v → = v B → – v A → приближается к направлению на центр окружности. Принимая, что ∆ t → 0 , получаем:
a → = a n → = ∆ v → ∆ t ; ∆ t → 0 ; a n → = v 2 R .
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
Здесь R → – радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов – нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
a τ = ∆ v τ ∆ t ; ∆ t → 0
Здесь ∆ v τ = v 2 – v 1 – изменение модуля скорости за промежуток ∆ t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие v x и v y .
Если движение равномерное, величины v x и v y а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T = 2 π R v = 2 π ω
[spoiler title=”источники:”]
http://www.afportal.ru/physics/together/583
http://zaochnik.com/spravochnik/fizika/kinematika/dvizhenie-po-okruzhnosti/
[/spoiler]
Пример решения задачи по определению нормального, касательного и модуля полного ускорения точки, а также, угла с вектором скорости, точки, движущейся по окружности заданного радиуса и известному закону заданному уравнением.
Задача
Точка движется по окружности радиуса R=4 м, закон ее движения определяется уравнением s=4,5t3 (s в метрах, t в секундах).
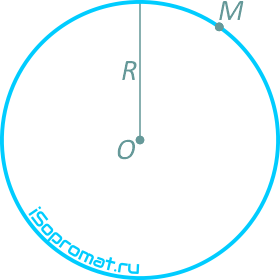
Рисунок 1.6
Определить модуль полного ускорения и угол φ его с вектором скорости в тот момент t1, когда скорость будет равна 6 м/с (рисунок 1.6).
Другие примеры решений >
Помощь с решением задач >
Решение
Дифференцируя s по времени, находим модуль вектора скорости точки
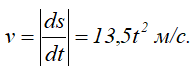
Другие видео
Скорость точки направлена по касательной к траектории (окружности), т.е. перпендикулярно линии радиуса.
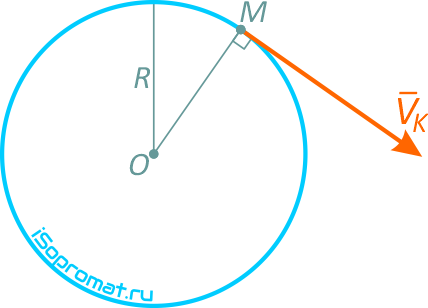
Подставляя в предыдущее выражение значение скорости, получим 6=13,5t12, откуда находим
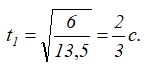
Касательное ускорение для любого момента времени равно
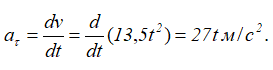
При t=t1=2/3 с
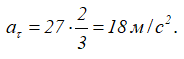
Так как для окружности радиус кривизны ρ=R, то нормальное ускорение для любого момента времени равно
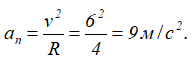
Модуль вектора полного ускорения точки равен
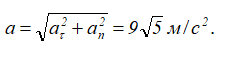
Направление нормального, касательного и полного ускорений точки
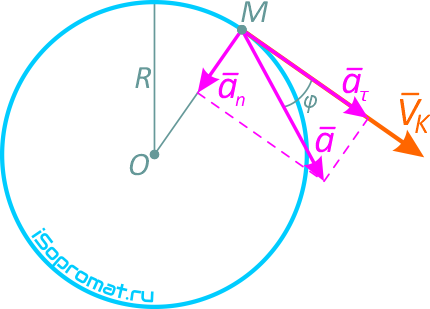
Угол между вектором полного ускорения и вектором скорости определим следующим образом:
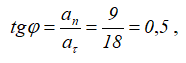
отсюда
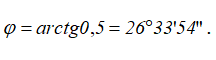
Другие примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Решение задач и лекции по технической механике, теормеху и сопромату
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Движение по окружности
Криволинейное движение — механическое движение, траектория которого — кривые линии с произвольным ускорением и произвольной скоростью.
Угловая скорость — величина, характеризующая скорость вращения материальной точки вокруг центра вращения. [omega=dfracvarphi t=dfrac{2pi}{t}]
Период обращения — это время одного полного оборота.
Частота обращения — величина, обратная периоду. Частота показывает, сколько полных оборотов совершает материальная точка за секунду. [nu=dfrac1T]
Тангенциальное ускорение — компонента ускорения, направленная по касательной к траектории движения.
Нормальное (центростремительное) ускорение — компонента ускорения, характеризующая быстроту изменения направления вектора скорости для траектории с кривизной, направленное к центру кривизны траектории. [a_text{цс}=dfrac{v^2}{r}]
Полное ускорение тела, движущегося по окружности равно векторной сумме тангенциального и нормального ускорений. [overrightarrow a_text{полн}=overrightarrow a_text{тан}+overrightarrow a_text{цс}]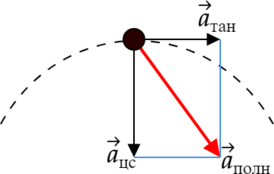 
Шарик движется по окружности радиусом (R_1 = 2) м со скоростью ( upsilon_1 = 3) м/с. Во сколько раз изменится его центростремительное ускорение, если радиус его окружности уменьшить в (n = 3) раза, а скорость увеличить в (k = 5) раз?
По определению центростремительное ускорение равно: [a_{text{ц1}} = frac{upsilon_1^2}{R_1} qquad (1)] [a_{text{ц2}} = frac{upsilon_2^2}{R_2} qquad (2)]
По условию задачи: [upsilon_2=kupsilon_1 qquad (3)] [R_2 = frac{R_1}{n} qquad (4)]
Подставляя (3), (4) и (1) в (2) получаем: [a_{text{ц2}} = dfrac{(kupsilon_1)^2}{dfrac{R_1}{n}} = nk^2frac{upsilon_1^2}{R_1} = nk^2a_{text{ц1}}] [frac{a_{text{ц2}}}{a_{text{ц1}}} = nk^2 = 3cdot5^2 = 75]
Ответ: 75
Тело движется по окружности радиусом (R=4) м. В какой момент времени центростремительное ускорение (a_text{цс} = 1 text{ м/с$^2$})?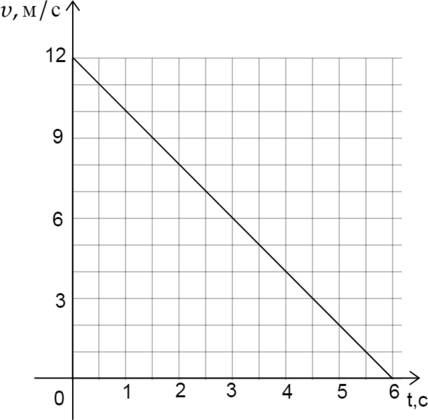 
При движении по окужности центростремительное ускорение можно найти по следующей формуле: [a_text{цс} = frac{upsilon^2}{R}] где (v) – скорость тела
Отсюда: [upsilon = sqrt{a_text{цс} cdot R} = sqrt{1 cdot 4} = 2text{ м/с }] По графику видно, что (upsilon = 2) м/с в момент времени (t=5) с.
Ответ: 5
Верхнюю точку моста радиусом 100 м автомобиль проходит со скоростью 20 м/с. Чему равно центростремительное ускорение автомобиля? (Ответ дайте в метрах в секунду в квадрате.)
Центростремительное ускорение (нормальное): (displaystyle a_{text{цс}}=frac{upsilon^2}R=frac{(20 text{ м/с})^2}{100 text{ м}}=4) м/с(^2)
Ответ: 4
Велосипедист едет по круговому треку и замедляется. На рисунке указано направление скорости велосипедиста. Под каким номером верно указано направление центростремительного ускорения? Тангенциального ускорения? Куда направлено полное ускорение? (В ответе укажите последовательность цифр, например: 153)
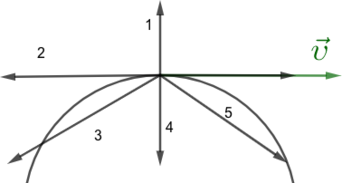
Нормальная составляющая ускорения (центростремительное ускорение) характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело.
Тангенциальная составляющая ускорения характеризует быстроту изменения величины (модуля) скорости. Тангенциальное ускорение всегда коллинеарно скорости:
1) Если тангенциальная составляющая ускорения сонаправлена со скоростью, то движение будет ускоренное
2) Если тангенциальная составляющая ускорения противонаправлена скорости, то движение будет замедленным
Полное ускорение – это сумма нормального и тангенциального: [vec{a}_{text{полн}}=vec{a}_{text{норм}}+vec{a}_{text{танг}}]
Центростремительное ускорение направлено к центру (4). Так как велосепидист замедляется, то тангенциальное направлено против скорости (2). Полное ускорение является суммой 2 и 4, следовательно полное ускорение под номером 3.
Ответ: 423
Тело равномерно движется по окружности. Угловая скорость тела равна (w=6,5) рад/с. За какое время (t) тело совершит 5,5 оборотов? Принять (pi=3,14). Ответ округлить до десятых.
Cпособ 1:
Найдем длину дуги окружности: [l=2pi r,] где (r) — радиус окружности.
Т.к. тело прошло эту длину 5,5 раз, оно прошло путь: [S=5,5l=11pi rquad(1)] Выразим формульно линейную скорость (v) и угловую скорость тела:
[begin{cases}
v=2pi rnu\
w=2pinu
end{cases}
Rightarrow
v=wrquad(2)]
Т.к. тело движется равномерно, (v=const). По закону равномерного движения: [S=vt] Подставим ((1)) и ((2)): [11pi r=wrt] Осталось выразить (t): [t=dfrac{11pi}{w}=dfrac{11cdot3,14}{6,5text{ рад/с}}approx5,3text{ c}]
Cпособ 2 :
Выразим формульно (w): [w=dfrac{Deltavarphi}{t},quad(1)] где (Deltavarphi) — угол поворота тела. [Deltavarphi=dfrac{S}{r},] где (S=5,5l=5,5cdot2pi r=11pi r) — путь, пройденный телом. [Deltavarphi=dfrac{11pi r}{r}=11piquad(2)] Подставим (2) в (1): [w=dfrac{11pi}{t}] Осталось выразить (t): [t=dfrac{11pi}{w}=dfrac{11cdot3,14}{6,5text{ рад/с}}approx5,3text{ c}]
Ответ: 5,3
Две материальные точки движутся по окружностям радиусами (R_1) и (R_2), причем (R_2 = 3R_1). Скорости тел равны. Чему равно отношение их центростремительных ускорений?
По определению центростремительное ускорение равно: [a_{text{ц1}} = frac{upsilon^2}{R_1}] [a_{text{ц2}} = frac{upsilon^2}{R_2}]
Тогда искомое отношение равно: [frac{a_{text{ц1}}}{a_{text{ц2}}} = frac{dfrac{upsilon^2}{R_1}}{dfrac{upsilon^2}{R_2}} = frac{R_2}{R_1} = frac{3R_1}{R_1} = 3]
Ответ: 3
Точечное тело равномерно движется по окужности радиусом (R=2) м. На рисунке изображён график зависимости угла поворота (varphi) от времени (t). Найдите значение линейной скорости тела в интервале времени (3pi<t<5pi).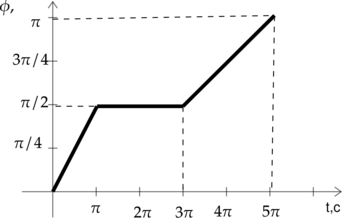 
Линейная скорость тела, движущегося по окружности: [upsilon = omega cdot R qquad (1)] где (omega) – угловая скорость.
Угловая скорость: [omega = frac{Deltavarphi}{Delta t} qquad (2)] Подставив (2) в (1), получим: [upsilon = frac{Deltavarphi}{Delta t} cdot R] [upsilon = frac{dfrac{pi}{2}}{2pi} cdot 2 =0,5 text{ м/с}]
Ответ: 0,5
УСТАЛ? Просто отдохни
Движение по окружности – простейший случай криволинейного движения тела. Когда тело движется вокруг некоторой точки, наряду с вектором перемещения удобно ввести угловое перемещение ∆φ (угол поворота относительно центра окружности), измеряемое в радианах.
Зная угловое перемещение, можно вычислить длину дуги окружности (путь), которую прошло тело.
∆l=R∆φ
Если угол поворота мал, то ∆l≈∆s.
Проиллюстрируем сказанное:
Угловая скорость
При криволинейном движении вводится понятие угловой скорости ω, то есть скорости изменения угла поворота.
Угловая скорость в данной точке траектории – предел отношения углового перемещения ∆φ к промежутку времени ∆t, за которое оно произошло. ∆t→0.
ω=∆φ∆t, ∆t→0.
Единица измерения угловой скорости – радиан в секунду (радс).
Существует связь между угловой и линейной скоростями тела при движении по окружности. Формула для нахождения угловой скорости:
ω=vR
Нормальное ускорение
При равномерном движении по окружности, скорости v и ω остаются неизменными. Меняется только направление вектора линейной скорости.
При этом равномерное движение по окружности на тело действует центростремительное, или нормальное ускорение, направленное по радиусу окружности к ее центру.
an=∆v→∆t, ∆t→0
Модуль центростремительного ускорения можно вычислить по формуле:
an=v2R=ω2R
Докажем эти соотношения.
Рассмотрим, как изменяется вектор v→ за малый промежуток времени ∆t. ∆v→=vB→-vA→.
В точках А и В вектор скорости направлен по касательной к окружности, при этом модули скоростей в обеих точках одинаковы.
По определению ускорения:
a→=∆v→∆t, ∆t→0
Взглянем на рисунок:
Треугольники OAB и BCD подобны. Из этого следует, что OAAB=BCCD.
Если значение угла ∆φ мало, расстояние AB=∆s≈v·∆t. Принимая во внимание, что OA=R и CD=∆v для рассмотренных выше подобных треугольников получим:
Rv∆t=v∆v или ∆v∆t=v2R
При ∆φ→0, направление вектора ∆v→=vB→-vA→ приближается к направлению на центр окружности. Принимая, что ∆t→0, получаем:
a→=an→=∆v→∆t; ∆t→0; an→=v2R.
При равномерном движении по окружности модуль ускорения остается постоянным, а направление вектора изменяется со временем, сохраняя ориентацию на центр окружности. Именно поэтому это ускорение называется центростремительным: вектор в любой момент времени направлен к центру окружности.
Запись центростремительного ускорения в векторной форме выглядит следующим образом:
an→=-ω2R→.
Здесь R→ – радиус вектор точки на окружности с началом в ее центре.
Тангенциальное ускорение
В общем случае ускорение при движении по окружности состоит из двух компонентов – нормальное, и тангенциальное.
Рассмотрим случай, когда тело движется по окружности неравномерно. Введем понятие тангенциального (касательного) ускорения. Его направление совпадает с направлением линейной скорости тела и в каждой точке окружности направлено по касательной к ней.
aτ=∆vτ∆t; ∆t→0
Здесь ∆vτ=v2-v1 – изменение модуля скорости за промежуток ∆t
Направление полного ускорения определяется векторной суммой нормального и тангенциального ускорений.
Движение по окружности в плоскости можно описывать при помощи двух координат: x и y. В каждый момент времени скорость тела можно разложить на составляющие vx и vy.
Если движение равномерное, величины vx и vy а также соответствующие координаты будут изменяться во времени по гармоническому закону с периодом T=2πRv=2πω
При произвольном
криволинейном движении вектор скорости
может изменяться как по величине, так
и по направлению. В этом случае существует
ускорение, характеризующее быстроту
изменения скорости по величине, и
ускорение, характеризующее быстроту
изменения скорости по направлению.
Рассмотрим три
частных случая.
При движении по
прямолинейной траектории
–
орт скорости
остается постоянным, т.е.
=сonst,
поэтому
.
Если
0,
то ускорение направлено так же, как и
скорость. Если
0,
направление ускорения противоположно
направлению скорости. Модуль ускорения
равен
.
При равномерном
движении по окружности =сonst,
изменяется
(рис.1.6,а),
поэтому:
.
(1.4)
Найдем производную
орта скорости
.
s
R
О
а)
б)
Рис.1.6
Из рис.1.6 видно,
что за время t
орт скорости поворачивается на угол
и получает приращение
.
По определению
.
При
и
.
Тогда
,
– еди-ничный вектор, имеющий такое же
направление, как и
.
При произвольном
переходе единичный вектор
превращается в
-орт
нормали к траектории в той точке, в
которой частица была в моментt.
Таким образом,
.
(1.5)
Подставив (1.5) в
(1.4), получим
– нормальное уско-рение.
При равномерном
движении по окружности ускорение
направлено по нормали к скорости. Поэтому
называют его нормальным ускорением и
в обозначении ставят индекс n.
При неравномерном
движении частицы по криволинейной
траектории оба множителя в формуле
изменяются со временем. Применив правило
дифференцирования произведения функций,
найдем выражение для ускорения
.
Видно, что в общем
случае ускорение распадается на два
слагаемых. Одно из них
коллинеарно скорости и, следовательно,
направлено по касательной к траектории.
Поэтому его называют тангенциальным
(т.е. касательным) ускорением и обозначают
.
Второе слагаемое
совпадает с
,
т.е. определяется формулой
и является нормальным ускорением. Первое
слагаемое характеризует быстроту
изменения модуля скорости, второе
быстроту изменения направления скорости.
Составляющие
и
перпендикулярны друг другу (рис.1.7).
Поэтому квадрат модуля ускорения равен
сумме квадратов модулей составляющих
.
|
Рис.1.7 |
Отсюда
|
будет равно
.1.4. Движение точки по окружности. Угловая скорость. Угловое ускорение
При вращении
твердого тела все его точки движутся
по окружности, центры которых лежат на
единой прямой, называемой осью вращения.
Окружности, по которым движутся точки
тела, лежат в плоскости, перпендикулярной
к этой оси.
Радиус-вектор
каждой точки – есть вектор, проведенный
из центра окружности в данную точку. Он
поворачивается за время t
на один и тот же угол .
Векторная величина
называется угловой скоростью, гдеt
– время, за
которое совершается поворот на угол
.
Из определения видно, что вращение точки
по окружности описывается угловой
скоростью
.
|
Вектор |
М1 Рис.1.8 |
направлен вдоль оси, вокруг которой
М2ра угловой скорости.
При равномерном
вращении угловая скорость
,
а угол поворота
.
Единицей угловой
скорости в системе СИ является радиан
в секунду
.
Угловая скорость
– есть величина постоянная, она указывает,
на какой угол поворачивается тело за
единицу времени. В этом случае она
называется круговой или циклической
частотой.
Равномерное
движение можно охарактеризовать также
периодом обращения. Периодом называется
время, за которое тело делает один
оборот, т.е. поворачивается на угол 2.
Поскольку за время, равное Т совершается
угол поворота 2,
то
;
.
Число оборотов за
единицу времени (частоту) обозначим
и выразим период и циклическую частоту
через эту величину
;
;
.
Угол поворота за
время t
можно записать через частоту
и полное
число оборотов
N
;
.
При неравномерном
вращении величина
изменяется со временем и за промежуток
времени t
получает приращение .
Величина,
характеризующая изменение вектора
угловой скорости со временем, называется
угловым ускорением
.
Таким образом,
изменение угловой скорости по времени
характеризуется угловым ускорением
,
которое определяется как производная
угловой скорости по времени
.
Единица измерения
углового ускорения
.
При неподвижной оси вращения векторы
и
коллинеарны и направлены вдоль оси
вращения. Если угловая скорость
увеличивается
,
то векторы
и
одинаково направлены, если угловая
скорость уменьшается
,
то векторы
и
противоположно направлены.
При неравномерном
вращении для угла поворота, угловой
скорости и ускорения справедливо
соотношение
,
где
0
– начальная угловая скорость.
Найдем соотношение
между
(рис.1.9).
|
М1 R s М2 Рис.1.9 |
Пусть за малый
Величина |
.
– называ-ется линейной скоростью точки.
Подставляя значение
s
из предыдущего равенства, получим
,
т.е. линейная
скорость точки прямо пропорциональна
радиусу и угловой скорости
.
(1.6)
Выясним соотношение
между
и
.
Нормальное ускорение точек прямо
пропорционально квадрату линейной
скорости и обратно пропорционально
радиусу
.
(1.7)
Подставляя в
уравнение (1.7) уравнение (1.6), получим
следующее выражение для нормального
ускорения:
.
Модуль тангенциального
ускорения равен модулю первой производной
от линейной скорости
.
(1.8)
Подставляя (1.6) в
уравнение (1.8) найдем, что
.
Но так как
,
то
.
Для нахождения соотношения между
векторами
и
сделаем чертеж (рис.1.10). Пусть тело
вращается вокруг осиz
с угловой скоростью
.
Выберем точку О на оси и проведем
радиус-вектор
из этой точки к точке С. Из треугольника
ОАС видно, что
.
Умножим обе части равенства на
и получим cледующее выражение:
.
Так как
– модуль скорости,
– модуль векторного произведения
,
то
.
Откуда следует,
что вектор скорости равен векторному
произведению вектора угловой скорости
на радиус-вектор
:
.
(1.9)
Формуле (1.9) можно
придать иной вид. Для этого представим
|
A C
O Рис.1.10 |
радиус-вектор
Векторы |
z
и умножим это равенство векторно на
:
.
и
,
.
(1.10)
Выведем соотношение
для тангенциального и углового ускорения.
По определению тангенциальное ускорение
есть первая производная от вектора
скорости по времени (1.8). Подставляя
(1.10) в (1.8), получим
,
т. е.
.
