Полная механическая энергия тела равна сумме его кинетической и потенциальной энергии.
Полную механическую энергию рассматривают в тех случаях, когда действует закон сохранения энергии и она остаётся постоянной.
Если на движение тела не оказывают влияния внешние силы, например, нет взаимодействия с другими телами, нет силы трения или силы сопротивления движению, тогда полная механическая энергия тела остаётся неизменной во времени.
Eпот+Eкин=const
Разумеется, что в повседневной жизни не существует идеальной ситуации, в которой тело полностью сохраняло бы свою энергию, так как любое тело вокруг нас взаимодействует хотя бы с молекулами воздуха и сталкивается с сопротивлением воздуха. Но, если сила сопротивления очень мала и движение рассматривается в относительно коротком промежутке времени, тогда такую ситуацию можно приближённо считать теоретически идеальной.
Закон сохранения полной механической энергии обычно применяют при рассмотрении свободного падения тела, при его вертикальном подбрасывании или в случае колебаний тела.
Пример:
При вертикальном подбрасывании тела его полная механическая энергия не меняется, а кинетическая энергия тела переходит в потенциальную и наоборот.
Преобразование энергии отображено на рисунке и в таблице.
|
Точка нахождения тела |
Потенциальная энергия |
Кинетическая энергия |
Полная механическая энергия |
|
3) Самая верхняя (h = max) |
Eпот
= m⋅g⋅h (max) |
Eкин
= 0 |
Eполная
= m⋅g⋅h |
|
2) Средняя (h = средняя) |
Eпот
= m⋅g⋅h |
Eкин
= m⋅v22 |
Eполная
= m⋅v22 + m⋅g⋅h |
|
1) Самая нижняя (h = 0) |
Eпот
= 0 |
Eкин
= m⋅v22 (max) |
Eполная
= m⋅v22 |
Исходя из того, что в начале движения величина кинетической энергии тела одинакова с величиной его потенциальной энергии в верхней точке траектории движения, для расчётов могут быть использованы ещё две формулы.
Если известна максимальная высота, на которую поднимается тело, тогда можно определить максимальную скорость движения по формуле:
Если известна максимальная скорость движения тела, тогда можно определить максимальную высоту, на которую поднимается тело, брошенное вверх, по такой формуле:
Чтобы отобразить преобразование энергии графически, можно использовать имитацию «Энергия в скейт-парке», в которой человек, катающийся на роликовой доске (скейтер) перемещается по рампе. Чтобы изобразить идеальный случай, предполагается, что не происходит потерь энергии в связи с трением. На рисунке показана рампа со скейтером, и далее на графике показана зависимость механической энергии от места положения скейтера на траектории.
На графике синей пунктирной линией показано изменение потенциальной энергии. В средней точке рампы потенциальная энергия равна (нулю). Зелёной пунктирной линией показано изменение кинетической энергии. В верхних точках рампы кинетическая энергия равна (нулю). Жёлто-зелёная линия изображает полную механическую энергию — сумму потенциальной и кинетической — в каждый момент движения и в каждой точке траектории. Как видно, она остаётся (неизменной) во всё время движения. Частота точек характеризует скорость движения — чем дальше точки расположены друг от друга, тем больше скорость движения.
На графике видно, что значение потенциальной энергии в начальной точке совпадает со значением кинетической энергии в середине рампы.
В реальной ситуации всегда происходят потери энергии, так как часть энергии выделяется в виде тепла под влиянием сил трения и сопротивления.
Поэтому для того, чтобы автомобиль двигался с равномерной и неизменной скоростью, необходимо постоянно подводить дополнительную энергию, которая компенсировала бы энергетические потери.
Полная механическая энергия
Энергия тела — физическая величина, которая показывает работу, совершаемую рассматриваемым телом в течение любого, в том числе неограниченного периода времени.
Объект, который совершает положительную работу, расходует частично энергию. В случае, когда положительную работу совершают над телом, его энергия возрастает. Если рассматривается отрицательная работа, то эффект будет противоположным. Таким образом, энергия выражается через физическую величину, характеризующую способность тела или системы взаимодействующих объектов совершать работу. Единицей измерения энергии в СИ является Джоуль (Дж).
Кинетическая энергия — это энергия тел, находящихся в движении.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В качестве движущихся тел рассматриваются не только перемещающиеся тела, но и объекты, которые вращаются. Кинетическая энергия возрастает по мере увеличения массы тела и скорости, с которой оно движется, то есть перемещается, либо вращается в пространстве. Кинетическая энергия определяется телом, по отношению к которому проводят измерения скорости рассматриваемого объекта. Для расчета кинетической энергии Ек тела, масса которого составляет m, движущегося со скоростью v, используют следующую формулу:
Потенциальная энергия — энергия тел или их частей, которые взаимодействуют друг с другом.
Потенциальная энергия тел отличается в зависимости от силы, которая на них воздействует:
- сила тяжести;
- сила упругости;
- архимедова сила.
Любая потенциальная энергия определяется силой взаимодействия и расстоянием между взаимодействующими телами или их частями. Для расчета потенциальной энергии выбирают какой-то условный нулевой уровень. В качестве примера потенциальной энергии можно рассмотреть энергию, которой будет обладать груз, поднятый на определенную высоту над поверхностью Земли, или сжатая пружина. Потенциальная энергия рассчитывается по формуле:
Энергия может трансформироваться из одного вида в другой. Так кинетическая энергия объекта может преобразоваться в его потенциальную энергию, и наоборот.
Механическая энергия тела — это сумма его кинетической и потенциальной энергий.
Механическая энергия любого тела определяется несколькими факторами:
- Объект, относительно которого выполняют измерение скорости рассматриваемого тела.
- Условные нулевые уровни, присущие всем разновидностям имеющихся у тела потенциальных энергий.
Данная величина является одной из основных характеристик тела. С помощью механической энергии определяют способность тела или системы объектов совершать работу по причине изменений скорости тела, либо взаимного положения тел, находящихся во взаимодействии.
Закон изменения и сохранения полной механической энергии
Закон сохранения и превращения энергии: энергия не может возникать ниоткуда, либо исчезать бесследно. Можно лишь наблюдать переход одного вида энергии в другой, либо от одного тела к другому.
Закон сохранения механической энергии: когда тела системы испытывают на себе воздействие силы тяжести или силы упругости, сумма кинетической и потенциальной энергии не будет изменяться, таким образом, механическая энергия сохраняется.
Изменение механической энергии системы тел определяется, как сумма работы внешних по отношению к системе тел и работы внутренних сил трения и сопротивления. Формула для расчета имеет следующий вид:
В случае замкнутой системы тел ее полная механическая энергия будет изменена только в том случае, когда совершается работа внутренних диссипативных сил системы таких, как сила трения:
Aвнешн = 0, то ΔW = Адиссип
Когда рассматривают консервативную систему тел, то есть при отсутствии сил трения и сопротивления, полная механическая энергия системы тел изменяется при работе внешних, относительно системы тел, сил:
Чему равна полная энергия, как изменяется по времени
Полная механическая энергия тела определяется суммой его кинетической и потенциальной энергии. Определение полной механической энергии справедливо в случае действия закона сохранения энергии, и ее постоянном значении.
В ситуации, когда тело движется без влияния внешних сил, включая отсутствие взаимодействия с другими телами, силы трения и силы сопротивления, полная механическая энергия тела не меняется со временем. С помощью формулы это утверждение можно записать следующим образом:
В реальном мире нельзя смоделировать таких идеальных ситуаций, в условиях которых объект полностью сохраняет свою энергию. Причиной этому является постоянное взаимодействие тела с другими телами, к примеру с молекулами воздуха или сопротивлением воздуха.
В случаях, когда сила сопротивления минимальна, и поступательное или другое движение наблюдают в относительно короткое время, подобную систему можно принять за теоретически идеальную. Как правило, закон сохранения полной механической энергии справедлив для тела, совершающего свободное падение, при вертикальном подбрасывании объекта или в случае колебательного движения тела такого, как маятник.
К примеру, во время вертикального подбрасывания тела наблюдают сохранение его полной механической энергии. Кинетическая энергия объекта при этом трансформируется в потенциальную, и наоборот. Амплитуда изменений энергий представлена на графике.
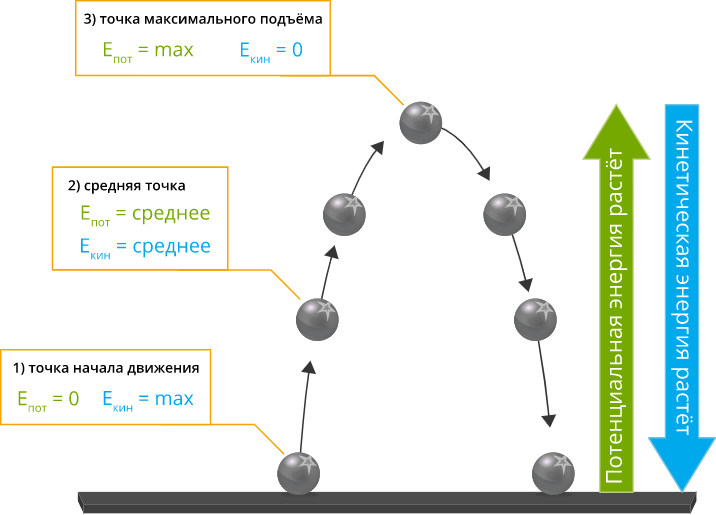
В зависимости от точки нахождения тела энергия будет рассчитываться следующим образом:
- самая верхняя точка при (h = max) , (Eпот = mgh) , (Eкин = 0) , (Eполная = mgh) ;
- средняя точка при (h = средняя) , (Eпот = mgh) , (Eкин = mv2/2) , (Eполная = mgh + mv2/2) ;
- самая нижняя точка при (h = 0) , (Eпот = 0) , (Eкин = mv2/2) , (Eполная = mv2/2) .
В начале пути тело обладает кинетической энергией, которая будет равна его потенциальной энергии в верхней точке траектории движения. Исходя из этого, можно использовать еще несколько полезных формул. При известном значении максимальной высоты, на которую поднимется тело, максимальная скорость движения будет определена следующим образом:
При известном значении максимальной скорости, с которой движется тело, можно рассчитать максимальную высоту подъема тела, брошенного вверх. Формула будет иметь такой вид:
Механическая энергия
Энергия – скалярная величина. Любую энергию в системе СИ измеряют в Джоулях.
В механике рассматривают два вида энергии тел – кинетическую энергию и потенциальную энергию.
Сумма кинетической и потенциальной энергии называется полной механической энергией
Кинетическая энергия
Кинетическая энергия – это энергия движения. Любое тело, находящееся в движении, обладает кинетической энергией.
В русском языке есть глагол «кинуть». Бросим (кинем) камень – он будет находиться в движении, то есть, будет обладать кинетической энергией.
Когда тело изменяет свою скорость, изменяется его кинетическая энергия.
Скорость увеличивается – кинетическая энергия тоже растет, скорость падает – кинетическая энергия уменьшается.
Если тело покоится, кинетической энергии нет. Математики в таком случае запишут: (E_=0 ).
Рассмотрим тело, движущееся по поверхности с какой-либо скоростью (рис 1а).
Зная массу и скорость тела, можно рассчитать его кинетическую энергию с помощью формулы:
( E_ left( textright) ) – кинетическая энергия;
( m left( textright) ) – масса тела;
( v left( frac>right) ) – cскорость, с которой тело движется.
Потенциальная энергия
Любое тело, поднятое над поверхностью, обладает потенциальной возможностью упасть и совершить работу. Например, потенциальная энергия поднятого над гвоздем молотка переходит в работу по забиванию гвоздя в доску.
Физики говорят: поднятое на высоту тело обладает потенциальной энергией.
Примечание: Потенциальная энергия возникает у тела из-за притяжения Земли.
Вообще, потенциальная энергия – это энергия взаимодействия (притяжения, или отталкивания). В нашем примере – энергия притяжения тела и Земли.
Если тело изменит высоту, на которой оно находится, будет изменяться его потенциальная энергия.
Тело опускается вниз – потенциальная энергия уменьшается.
Тело поднимается выше – потенциальная энергия растет.
Когда тело находится на поверхности земли, потенциальной энергии у него нет (E_
=0).
Рассмотрим тело, находящееся на какой-либо высоте над поверхностью земли (рис 1б).
Можно рассчитать потенциальную энергию тела, зная его массу и высоту тела над поверхностью земли, с помощью формулы:
[ large boxed = m cdot g cdot h>]
( E_
left( textright) ) – потенциальная энергия;
( m left( textright) ) – масса тела;
( h left( textright) ) – высота, на которую тело подняли над поверхностью земли.
Полная механическая энергия тела
Если сложить кинетическую энергию тела с его потенциальной энергией в какой-либо момент времени, мы получим полную механическую энергию, которой тело обладало в этот момент времени.
Летящий в небе самолет (рис. 3) одновременно будет обладать и кинетической энергией – он движется, и потенциальной энергией – он находится на высоте.
Любая энергия – это скаляр (просто число). Значит, энергия направления не имеет и ее можно складывать алгебраически.
( E_
left( textright) ) – потенциальная энергия тела;
( E_ left( textright) ) – кинетическая энергия, которой обладает тело;
( E_> left( textright) ) – полная механическая энергия этого тела;
Закон сохранения механической энергии

Если мы погуглим определение слова «Энергия», то скорее всего найдем что-то про формы взаимодействия материи. Это верно, но совершенно непонятно.
Поэтому давайте условимся здесь и сейчас, что энергия — это запас, который пойдет на совершение работы.
Энергия бывает разных видов: механическая, электрическая, внутренняя, гравитационная и так далее. Измеряется она в Джоулях (Дж) и чаще всего обозначается буквой E.
Механическая энергия
Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.
Она представляет собой совокупность кинетической и потенциальной энергии. Кинетическая энергия — это энергия действия. Потенциальная — ожидания действия.
Представьте, что вы взяли в руки канцелярскую резинку, растянули ее и отпустили. Из растянутого положения резинка просто «полетит», как только вы ей позволите это сделать. В этом процессе в момент натяжения резинка обладает потенциальной энергией, а в момент полета — кинетической.
Еще один примерчик: лыжник скатывается с горы. В самом начале — на вершине — у него максимальная потенциальная энергия, потому что он в режиме ожидания действия (ждущий режим ), а внизу горы он уже явно двигается, а не ждет, когда с ним это случится — получается, внизу горы кинетическая энергия.
Кинетическая энергия
Еще разок: кинетическая энергия — это энергия действия. Величина, которая очевиднее всего характеризует действие — это скорость. Соответственно, в формуле кинетической энергии точно должна присутствовать скорость.
Кинетическая энергия
Ек — кинетическая энергия [Дж]
m — масса тела [кг]
Чем быстрее движется тело, тем больше его кинетическая энергия. И наоборот — чем медленнее, тем меньше кинетическая энергия.
Задачка раз
Определить кинетическую энергию собаченьки массой 10 кг, если она бежала за мячом с постоянной скоростью 2 м/с.
Решение:
Формула кинетической энергии
Ответ: кинетическая энергия пёсы равна 20 Дж.
Задачка два
Найти скорость бегущего по опушке гнома, если его масса равна 20 кг, а его кинетическая энергия — 40 Дж
Решение:
Формула кинетической энергии
Ответ: гном бежал со скоростью 2 м/с.
Онлайн-уроки физики в Skysmart не менее увлекательны, чем наши статьи!
Потенциальная энергия
В отличие от кинетической энергии, потенциальная чаще всего тем меньше, чем скорость больше. Потенциальная энергия — это энергия ожидания действия.
Например, потенциальная энергия у сжатой пружины будет очень велика, потому что такая конструкция может привести к действию, а следовательно — к увеличению кинетической энергии. То же самое происходит, если тело поднять на высоту. Чем выше мы поднимаем тело, тем больше его потенциальная энергия.
Потенциальная энергия деформированной пружины
Еп — потенциальная энергия [Дж]
k — жесткость [Н/м]
x — удлинение пружины [м]
Потенциальная энергия в поле тяжести
Еп = mgh
Еп — потенциальная энергия [Дж]
m — масса тела [кг]
g — ускорение свободного падения [м/с 2 ]
На планете Земля g ≃ 9,8 м/с 2
Задачка раз
Найти потенциальную энергию рака массой 0,1 кг, который свистит на горе высотой 2500 метров. Ускорение свободного падения считать равным 9,8 м/с 2 .
Решение:
Формула потенциальной энергии Еп = mgh
Eп = 0,1 · 9,8 · 2500 = 2450 Дж
Ответ: потенциальная энергия рака, свистящего на горе, равна 2450 Дж.
Задачка два
Найти высоту горки, с которой собирается скатиться лыжник массой 65 кг, если его потенциальная энергия равна 637 кДж. Ускорение свободного падения считать равным 9,8 м/с 2 .
Решение:
Формула потенциальной энергии Еп = mgh
Переведем 637 кДж в Джоули.
637 кДж = 637000 Дж
Ответ: высота горы равна 1000 метров.
Задачка три
Два шара разной массы подняты на разную высоту относительно поверхности стола (см. рисунок). Сравните значения потенциальной энергии шаров E1 и E2. Считать, что потенциальная энергия отсчитывается от уровня крышки стола.

Решение:
Потенциальная энергия вычисляется по формуле: E = mgh
По условию задачи
Таким образом, получим, что
Закон сохранения энергии
В физике и правда ничего не исчезает бесследно. Чтобы это как-то выразить, используют законы сохранения. В случае с энергией — Закон сохранения энергии.
Закон сохранения энергии
Полная механическая энергия замкнутой системы остается постоянной.
Полная механическая энергия — это сумма кинетической и потенциальной энергий. Математически этот закон описывается так:
Закон сохранения энергии
Еполн. мех. — полная механическая энергия системы [Дж]
Еп — потенциальная энергия [Дж]
Ек — кинетическая энергия [Дж]
const — постоянная величина
Задачка раз
Мяч бросают вертикально вверх с поверхности Земли. Сопротивление воздуха пренебрежимо мало. Как изменится высота подъёма мяча при увеличении начальной скорости мяча в 2 раза?
Решение:
Должен выполняться закон сохранения энергии:
В начальный момент времени высота равна нулю, значит Еп = 0. В этот же момент времени Ек максимальна.
В конечный момент времени все наоборот — кинетическая энергия равна нулю, так как мяч уже не может лететь выше, а вот потенциальная максимальна, так как мяч докинули до максимальной высоты.
Это можно описать соотношением:
Разделим на массу левую и правую часть
Из соотношения видно, что высота прямо пропорциональна квадрату начальной скорости, значит при увеличении начальной скорости мяча в два раза, высота должна увеличиться в 4 раза.
Ответ: высота увеличится в 4 раза
Задачка два
Тело массой m, брошенное с поверхности земли вертикально вверх с начальной скоростью v0, поднялось на максимальную высоту h0. Сопротивление воздуха пренебрежимо мало. Чему будет равна полная механическая энергия тела на некоторой промежуточной высоте h?
Решение
По закону сохранения энергии полная механическая энергия изолированной системы остаётся постоянной. В максимальной точке подъёма скорость тела равна нулю, а значит, оно будет обладать исключительно потенциальной энергией Емех = Еп = mgh0.
Таким образом, на некоторой промежуточной высоте h, тело будет обладать и кинетической и потенциальной энергией, но их сумма будет иметь значение Емех = mgh0.
Задачка три
Мяч массой 100 г бросили вертикально вверх с поверхности земли с начальной скоростью 6 м/с. На какой высоте относительно земли мяч имел скорость 2 м/с? Сопротивлением воздуха пренебречь.
Решение:
Переведем массу из граммов в килограммы:
m = 100 г = 0,1 кг
У поверхности земли полная механическая энергия мяча равна его кинетической энергии:
На высоте h потенциальная энергия мяча есть разность полной механической энергии и кинетической энергии:
Ответ: мяч имел скорость 2 м/с на высоте 1,6 м
Переход механической энергии во внутреннюю
Внутренняя энергия — это сумма кинетической энергии хаотичного теплового движения молекул и потенциальной энергии их взаимодействия. То есть та энергия, которая запасена у тела за счет его собственных параметров.
Часто механическая энергия переходит во внутреннюю. Происходит этот процесс путем совершения механической работы над телом. Например, если сгибать и разгибать проволоку — она будет нагреваться.
Или если кинуть мяч в стену, часть энергии при ударе перейдет во внутреннюю.
Задачка
Какая часть начальной кинетической энергии мяча при ударе о стену перейдет во внутреннюю, если полная механическая энергия вначале в два раза больше, чем в конце?
Решение:
В самом начале у мяча есть только кинетическая энергия, то есть Емех = Ек.
В конце механическая энергия равна половине начальной, то есть Емех/2 = Ек/2
Часть энергии уходит во внутреннюю, значит Еполн = Емех/2 + Евнутр
Ответ: во внутреннюю перейдет половина начальной кинетической энергии
Закон сохранения энергии в тепловых процессах
Чтобы закон сохранения энергии для тепловых процессов был сформулирован, было сделано два важных шага. Сначала французский математик и физик Жан Батист Фурье установил один из основных законов теплопроводности. А потом Сади Карно определил, что тепловую энергию можно превратить в механическую.
Вот что сформулировал Фурье:
При переходе теплоты от более горячего тела к более холодному температуры тел постепенно выравниваются и становятся едиными для обоих тел — наступает состояние термодинамического равновесия.
Таким образом, первым важным открытием было открытие того факта, что все протекающие без участия внешних сил тепловые процессы необратимы.
Дальше Карно установил, что тепловую энергию, которой обладает нагретое тело, непосредственно невозможно превратить в механическую энергию для производства работы. Это можно сделать, только если часть тепловой энергии тела с большей температурой передать другому телу с меньшей температурой и, следовательно, нагреть его до более высокой температуры.
Закон сохранения энергии в тепловых процессах
При теплообмене двух или нескольких тел абсолютное количество теплоты, которое отдано более нагретым телом, равно количеству теплоты, которое получено менее нагретым телом.
Математически его можно описать так:
Уравнение теплового баланса
Qотд — отданное системой количество теплоты [Дж]
Qпол — полученное системой количество теплоты [Дж]
Данное равенство называется уравнением теплового баланса. В реальных опытах обычно получается, что отданное более нагретым телом количество теплоты больше количества теплоты, полученного менее нагретым телом:
Это объясняется тем, что некоторое количество теплоты при теплообмене передаётся окружающему воздуху, а ещё часть — сосуду, в котором происходит теплообмен.
Чтобы разобраться в задачках, читайте нашу статью про агрегатные состояния вещества.
Задачка раз
Сколько граммов спирта нужно сжечь в спиртовке, чтобы нагреть на ней воду массой 580 г на 80 °С, если учесть, что на нагревание пошло 20% затраченной энергии.
Удельная теплота сгорания спирта 2,9 · 107 Дж/кг, удельная теплоёмкость воды 4200 Дж/(кг · °С).
Решение:
При нагревании тело получает количество теплоты
где c — удельная теплоемкость вещества
При сгорании тела выделяется энергия
где q — удельная теплота сгорания топлива
По условию задачи нам известно, что на нагревание воды пошло 20% энергии, полученной при горении спирта.
Ответ: масса сгоревшего топлива равна 33,6 г.
Задачка два
Какое минимальное количество теплоты необходимо для превращения в воду 500 г льда, взятого при температуре −10 °С? Потерями энергии на нагревание окружающего воздуха пренебречь. Удельная теплоемкость льда равна 2100 Дж/кг · ℃, удельная теплота плавления льда равна 3,3 · 10 5 Дж/кг.
Решение:
Для нагревания льда до температуры плавления необходимо:
Qнагрев = 2100 · 0,5 · (10 − 0) = 10 500 Дж
Для превращения льда в воду:
Qпл = 3,3 · 10 5 · 0,5 = 165 000 Дж
Таким образом, для превращения необходимо затратить:
Q = Qнагрев + Qпл = 10 500 + 165 000 = 175 500 Дж = 175,5 кДж
Ответ: чтобы превратить 0,5 кг льда в воду при заданных условиях необходимо 175,5 кДж тепла.
Одним из фундаментальных правил, существующих в природе, является закон сохранения механической энергии. Формула, описывающая его, справедлива лишь для замкнутой системы тел. Что интересно открытие явления приписывают не физикам, а корабельному доктору из Германии Юлию Майеру изложившему идею о сохранении и превращении силы. Но только через несколько лет выдвинутая им теория была подтверждённая учёными Джеймсом Джоулем и Германом Гельмгольцем.
Оглавление:
- Общие сведения
- Потенциальная и кинетическая работа
- Полная энергия
- Содержание и применение закона

Общие сведения
Пожалуй, материя — это главное понятие в физике. Она определяется множеством содержимого пространства-времени, модели создающую теоретически-физическую конструкцию. По сути, это вещество, не зависящее от сознания человека. Мерой взаимодействия материи является энергия. Это скалярная физическая величина, с помощью которой ещё описывают и всевозможные формы движения.
С фундаментальной точки зрения, энергия характеризуется двумя явлениями:
- импульсом;
- моментом.
Впервые слово «энергия» встречается в трудах Аристотеля. Под ним он понимал деятельность человека. Происходит термин от греческого ἐνέργεια, что означает «действие». В 1686 году немецкий философ Лейбниц заимствовал слово для характеристики «живой силы». С помощью этого термина учёный обозначал произведение массы тела на квадрат его скорости. В современной интерпретации — это удвоенная кинетическая работа. Лейбниц считал, что любой объект обладает энергией, которая тратится при движении из-за снижения скорости. При этом утраченная часть переходит к атомам.

Англичанин Томас Юнг первым предложил использовать слово «энергия» для описания процессов связанных с движением и взаимодействием тел. Через двадцать лет Гаспар-Гюстав Кориолис установил связь между термином и работой. Дальнейшее осмысливание меры материи позволило разделить её на кинетическую и потенциальную.
Много лет среди учёных велись дискуссии, чем же является энергия — субстанцией или величиной. Развитие механики требовало введение новых понятий и формул, описывающих различные открытые явления. Так появились законы термодинамики, энтропии, понятия чёрного тела. Наука об изучении энергии разделилась на множество областей. Но в итоге учёные пришли к выводу, что это не субстанция, существующая сама по себе, а лишь мера её измерения.

Как оказалось, все виды механической энергии представляют собой величину, характеризующуюся направлением движения. Тело может обладать одновременно различными типами энергии: электрической, термической, химической, внутриядерной. Было установлено, что в первом приближении энергию можно разделить на внутреннюю и внешнюю. К последней стали относить все те явления, которые происходят при перемещении тела. При этом главным открытием в механике стал закон сохранения полной механической энергии полученный, как следствие из утверждений Ньютона.
Потенциальная и кинетическая работа
Энергия — это величина, описывающая возможность чего-либо совершать механическую работу. То есть она характеризует результат действия силы. Численно работу можно определить, как произведение модулей силы (меры воздействия) и перемещения на косинус угла между ними: A = F * S * cos (a). В качестве единиц измерения энергии принят джоуль. Один [Дж] равен работе, совершаемой для переноса материальной точки при приложении силы в один ньютон на расстояние в один метр.
Механическую энергию разделяют на два типа:
- потенциальную (ПЭ);
- кинетическую (КЭ).
Разобраться в чём между ними отличие проще всего, рассмотрев пример. Кинетическая работа связана с движением. Например, бегун, летящий самолёт, падающий камень. Другими словами, чтобы тело изменило своё положение нужно затратить силу, величина которой характеризуется энергией.
То есть любой объект имеющее массу и скорость обладает такой величиной. Однако этот параметр не является абсолютным. Он зависит от выбранной системы отсчёта.
Человек сидящий на стуле относительно Земли находится в покое. Так как он недвижим, то он не совершает никакой работы. Но утверждать, что его кинетическая энергия равняется нулю нельзя. Если наблюдать за ним с другой планеты или скажем космического корабля, то относительно их человек находится в движении. Это связано с тем, что Земля вращается вокруг Солнца. Следовательно, он обладает какой-то величиной КЭ.
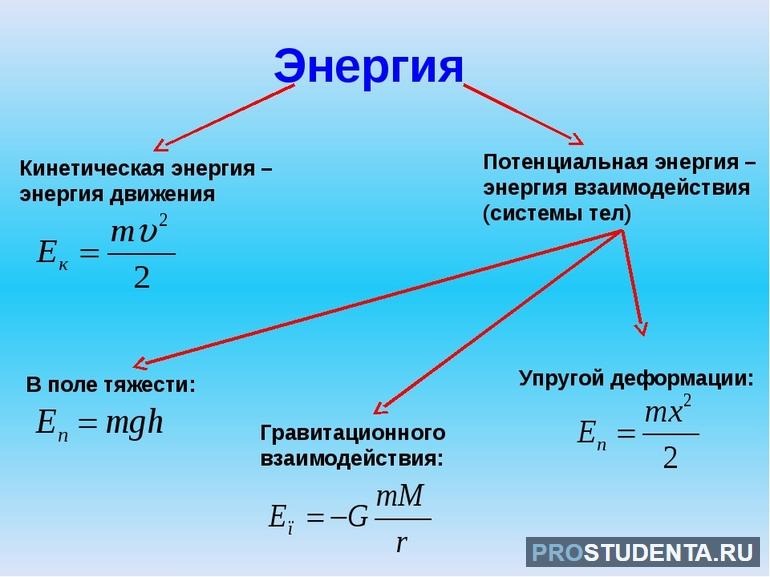
Теперь можно представить, что в дверь позвонили и человек пошёл её открывать. Уже и относительно планеты он обладает КЭ. Причём чем тяжелее человек и быстрее скорость его движения, тем её величина больше. Определить энергию тела при его движении можно по следующей формуле: E = m * V2 / 2.
Значение же ПЭ определяется расположением тел и характером взаимодействия между ними. Иными словами, она зависит от положения объекта. Например, камень, лежащий на столе, обладает нулевым значением по отношению к поверхности. Но в то же время относительно Земли камень будет иметь уже какое-то другое значение. На Земле ПЭ обусловлена гравитацией и равняется работе силы притяжения затрачиваемой на изменение положения тела по отношению к нулевому уровню. Найти её можно по формуле: W = m * g * h, где h — высота нахождения объекта над относительным уровнем сравниваемого с ним тела.
Полная энергия

Можно сказать, что тело, находящееся в движении или покое одновременно обладает как потенциальной, так и кинетической энергиями. Но при этом выполняется разная работа. В качестве яркого примера можно привести маятник. Движение груза происходит из-за возникновения механических колебаний. Совершаются они под действием сил тяжести, упругости и трения. При колебаниях происходит постоянное превращение энергии из одного вида в другой.
Пусть система отсчёта будет выбрана так, что в положении равновесия ПЭ будет равняться нулю. Для того чтобы маятник вышел из этого состояния необходимо приложить силу, заставляющую подвешенное тело, переместиться на высоту h. Тогда, можно сказать, что у маятника появится скорость V. Другими словами, возникнет КЭ. Выполненная работа заставит отклониться тело до какого-то максимального значения. Причём в этом положении скорость движения станет равной нулю. Так как высота определяет ПЭ, то в точке максимального отклонения она будет наибольшей.
Из-за действия силы тяжести маятник, достигнув наибольшей точки отклонения, начнёт возвратное движение. У тела вновь появится скорость, которая достигнет своего наибольшего значения в точке равновесия. Значит, в этом положении КЭ станет максимальным.
Другими словами, в процессе работы маятника происходит постоянное изменение энергии. Из потенциальной она превращается в кинетическую и наоборот. Причём это изменение происходит симметрично — на какую величину первая возрастает, на такую же уменьшается вторая. В крайних точках отклонения полная энергия будет состоять из суммы значений потенциальной и кинетической. Из сказанного следует, что полная механическая энергия маятника для любой точки траектории его движения будет оставаться постоянной величиной.

Таким образом, можно сформулировать определение полной энергии: значение работы для изолированной системы равняется сумме энергий движения и гравитационной, и является постоянной: Ep = E + W. Исходя из такой формулировки можно утверждать, что E для замкнутой системы остаётся неизменной. Это правило получило название закон полной механической энергии.
Но идеальных систем не бывает. При движении всегда возникает сила трения. Поэтому этот закон можно переписать так: A = W — E, где A — работа сил трения.
Содержание и применение закона
Главное следствие из закона сохранения мех. энергии (ЗСЭ) формулируется так: для описания независимой системы может быть использована скалярная физическая величина, характеризующая параметры системы и способная не изменяться с течением времени.
Пусть есть тело, которое двигается из точки один в точку два. E полное для любого момента времени будет определяться суммой ПЭ и КЭ. Тогда справедливо записать: E1 + W1 = E2 + W2, где:
- E 1, E 1 — соответственно КЭ в начальный и конечный момент времени;
- W1, W2 — значения ПЭ в первой и второй точке.

При движении тела происходит изменение как КЭ, так и ПЭ. Причём часть одной переходит в другую, поэтому равенство сохраняется. Если пренебречь сопротивлением среды и трением, то механические энергии будут равны друг другу в любой момент времени. Вернее, наибольшее значение ПЭ в состоянии один равняется максимальной КЭ тела в положении два.
Кратко закон можно записать в виде равенства: E = E + W = mgh + (mV2 / 2) = const. Как показали опыты, если на систему не оказывается постороннее влияние, то постоянное значение суммы будет оставаться одинаковым сколь угодное количество времени. Но в реальных системах энергия не остаётся постоянной. Но её потери не исчезают бесследно, а переходят в иной вид. Например, КЭ за счёт сил трения превращается в тепловую, то есть во внутреннюю. Это и есть суть закона.
Раскрыть смысл правила можно формулой, имеющей вид: Δ E + Δ W = A + Q, где:
- Δ E — величина, показывающая изменение механической энергии;
- Δ W — параметр показывающий как поменялось внутреннее состояние;
- A — работа сторонних сил;
- Q — количество выделившегося тепла.

Таким образом, при любых физических взаимодействиях E ниоткуда не возникает и никуда не исчезает, а только переходит из одной формы состояния в другую. Как оказалось, полностью превратить КЭ в тепловую невозможно. Телу всегда принадлежит внутренняя и внешняя энергия.
С помощью открытого закона стало возможным решать различные задачи, связанные с механическим движением. Например, выяснить какое количество тепла может получиться при том или ином процессе, рассчитать мощность источника электричества, определить степень деформации и необходимую силу для выполнения нужного действия.
При этом открытый закон применим не только для решения задач, но и позволяет в будущем открыть новые явления.
Как найти механическую энергию
Механическая энергия бывает двух видов: кинетическая и потенциальная. Их сумма носит название полной механической энергии. Механическая энергия Е дает характеристику взаимодействия тел. Она является функцией взаимного расположения и скоростей.

Инструкция
Чтобы найти полную механическую энергию, выполните следующие действия. Определите кинетическую энергию. Определите потенциальную энергию. Сложите полученные результаты.
Кинетическая энергия – это энергия, которой обладает механическая система, и которая зависит от скоростей движения ее различных точек. Различают кинетическую энергию вращательного или поступательного движения. Единица измерения энергии в системе СИ — Джоуль. Чтобы найти кинетическую энергию, нужно воспользоваться формулой: Ex= mv²/2, где: Ek – кинетическая энергия, (дж); m – масса тела (кГ); v–скорость (м/с).
Кинетическая энергия рассматриваемого тела, которое движется со скоростью υ, показывает, какую работу, чтобы придать телу эту скорость, должна выполнить сила, воздействующая на тело, находящееся в покое. Чтобы определить потенциальную энергию, воспользуйтесь формулой: Ep = mgh, где: Ep – потенциальная энергия, (дж); g — ускорение свободного падения (м2); m– масса тела (кГ); h — высота центра масс тела над выбранным произвольно уровнем (м). Потенциальная энергия – это характеристика взаимодействия двух или больше тел или тела и какого-либо поля. Каждая физическая система в идеале стремится к положению с наименьшей или нулевой потенциальной энергией.
Если кинетическую энергию можно определить для отдельно взятого тела, то потенциальная энергия характеризует два или более тела или само положение тела по отношению к внешнему полю. Кинетическая энергия характеризуется скоростью; потенциальная — взаиморасположением тел. Зная массу тела, скорость его движения, а также высоту центра масс, несложно будет произвести вышеперечисленные расчеты и вычислить составляющие, из которых складывается полная энергия отдельно взятого тела.
Видео по теме
Источники:
- Основные энергетические понятия
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Полная
механическая энергия
Полная
механическая энергия – сумма кинетической
и потенциальной энергии тела.
Полная
механическая энергия:
–
характеризует движение и взаимодействие
тел; и
–
является функцией скоростей и взаимного
расположения тел.
![]()
Закон
сохранения механической энергии
Механическая
энергия консервативной механической
системы сохраняется во времени. Проще
говоря, при отсутствии диссипативных
сил (например, сил трения) механическая
энергия не возникает из ничего и не
может никуда исчезнуть.
Для
замкнутой системы физических тел,
например, справедливо равенство
Ek1 +
Ep1 =
Ek2 +
Ep2,
где Ek1,
Ep1 —
кинетическая и потенциальная энергии
системы какого-либо взаимодействия,Ek2,
Ep2 —
соответствующие энергии после.
Закон
сохранения энергии —
это интегральный
закон.
Это значит, что он складывается из
действия дифференциальных законов и
является свойством их совокупного
действия.
Формулировка закона сохранения механической энергии.
Полная
механическая энергия,
т.е. сумма потенциальной и кинетической
энергии тела, остается постоянной, если
действуют только силы упругости и
тяготения и отсутствуют силы трения.
12)Вращательное движение твердого тела. Момент инерции материальной точки и твердого тела относительно неподвижной оси. Кинетическая энергия вращающегося твердого тела. Теорема Штейнера.
Враща́тельное
движе́ние —
вид механического
движения.
При вращательном движении
абсолютно твёрдого тела его точки
описывают окружности, расположенные в
параллельных плоскостях.
Центры всех окружностей лежат при этом
на одной прямой, перпендикулярной к
плоскостям окружностей и называемой осью
вращения.
Ось вращения может располагаться внутри
тела и за его пределами. Ось вращения
в данной системе отсчёта может быть как
подвижной, так и неподвижной. Например,
в системе отсчёта, связанной с Землёй,
ось вращения ротора генератора на
электростанции неподвижна.
При
равномерном вращении (T оборотов в
секунду),
-
Частота
вращения —
число оборотов тела в единицу времени.
![]()
,
-
Период вращения —
время одного полного оборота. Период
вращения T и
его частота ν связаны
соотношением T =
1 / ν.
-
Линейная
скорость точки,
находящейся на расстоянии R от оси
вращения
![]()
,
-
Угловая
скорость вращения
тела
![]()
.
-
Момент
инерции механической
системы относительно
неподвижной оси a («осевой
момент инерции») — физическая
величина Ja,
равная сумме произведений масс
всех nматериальных
точек системы
на квадраты их расстояний до оси:
![]()
,
где: mi —
масса i-й
точки, ri —
расстояние от i-й
точки до оси.
Осевой момент
инерции тела Ja является
мерой инертности тела во вращательном
движении вокруг оси a подобно
тому, как масса тела
является мерой его инертности
в поступательном
движении.
-
Кинетическая
энергия вращательного движения
![]()
где Iz — момент
инерции тела
относительно оси вращения. ω — угловая
скорость.
Теоре́ма
Гю́йгенса — Ште́йнера,
или просто теорема
Штейнера (названа
по имени швейцарского математика Якоба
Штейнера и
голландского математика, физика и
астронома Христиана
Гюйгенса): момент
инерции тела J относительно
произвольной оси равен сумме момента
инерции этого тела JC относительно
параллельной ей оси, проходящей через
центр масс тела, и произведения массы
тела m на
квадрат расстояния d между
осями:
![]()
где
JC —
известный момент инерции относительно
оси, проходящей через центр масс тела,
J —
искомый момент инерции относительно
параллельной оси,
m —
масса тела,
d —
расстояние между указанными осями.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
