Как найти полную механическую энергию пружины

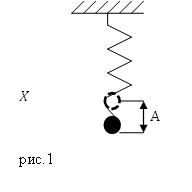
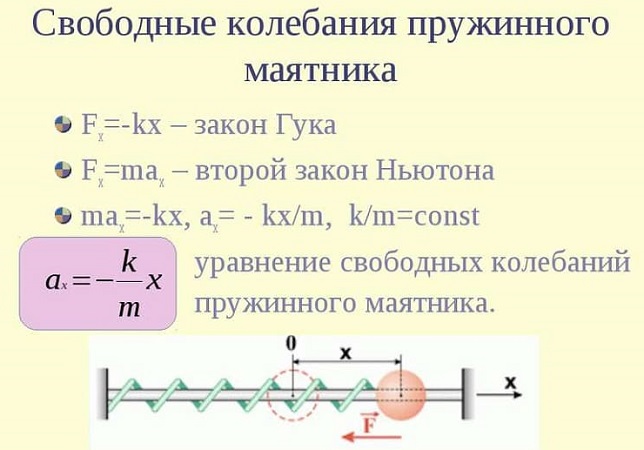
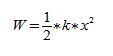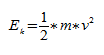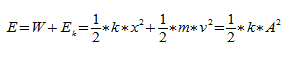Рассмотрим процесс превращения энергии при колебательном движении идеального горизонтального пружинного маятника (рис. (1)).

Рис. (1). Колебания горизонтального пружинного маятника

Будем считать, что в системе сил трения и сил сопротивления нет.

Когда эта система находится в равновесии и никакого колебания не происходит, скорость тела равна нулю и отсутствует деформация пружины (рис. (2)) В этом случае энергии у данного маятника нет.

Рис. (2). Положение пружинного маятника в равновесии

Когда тело выводится из положения равновесия, например пружина сжимается на некоторую величину (рис. (3)) телу сообщается некоторый запас потенциальной энергии:

Рис. (3). Положение пружинного маятника при сжатой пружине

Если теперь отпустить груз, не удерживать его, то он начнёт своё движение к положению равновесия, пружина начнёт выпрямляться, и деформация пружины будет уменьшаться (рис. (4)) Следовательно, будет уменьшаться и её потенциальная энергия.

Скорость же тела будет увеличиваться, и по закону сохранения энергии потенциальная энергия пружины будет превращаться в кинетическую энергию движения тела:

Рис. (4). Движение груза к положению равновесия

В момент прохождения те­лом положения равновесия (рис. (5)) его по­тенциальная энергия равна нулю, а кинетическая будет максимальна.

Рис.(5). Прохождение грузом положения равновесия

Потом вступает в действие явление инерции. Тело, которое обладает некоторой массой, по инерции проходит точку равновесия (рис. (6)). Скорость тела начинает уменьшаться, а деформация, удлинение пружины, увеличивается. Следовательно, кине­тическая энергия тела убывает, а потенциальная, наоборот, возрастает.

Рис. (6). Положение пружинного маятника при удлинении пружины

В точке максимального отклонения тела его кинетическая энергия равна нулю, а потенциальная — максимальна (рис. (7)).

Рис. (7). Положение пружинного маятника в точке максимального отклонения тела

Таким образом, при колебаниях периодически проис­ходит переход потенциальной энергии в кинетическую и обрат­но.

Рис. (8). Колебания вертикального пружинного маятника

Если для вертикального пружинного маятника выбрать систему отсчёта таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю, то всё описанное выше для горизонтального маятника можно применить для данного маятника.

Рассмотрим процесс превращения энергии при колебательном движении идеального горизонтального пружинного маятника.

Будем считать, что в системе сил трения и сил сопротивления нет. Когда эта система находится в равновесии, и никакого колебания не происходит, скорость тела равна нулю, и отсутствует деформация пружины. В этом случае энергии у данного маятника нет.

Выводя тело из положения равновесия, например, сжимая пружину на некоторую величину, ему сообщается некоторый запас потенциальной энергии: Eпkx22.

Если теперь отпустить груз, не удерживать его, то он начнет свое движение к положению равновесия, пружина начнет выпрямляться и деформация пружины будет уменьшаться. Следовательно, будет уменьшатся и ее потенциальная энергия. Скорость же тела будет увеличиваться, и по закону сохранения энергии потенциальная энергия пружины будет превращаться в кинетическую энергию движения тела:

Eкmv

.

В момент прохождения те­лом положения равновесия его по­тенциальная энергия равна нулю, а кинетическая будет максимальна.

Потом вступает в действие явление инерции. Тело, которое обладает некоторой массой, по инерции проходит точку равновесия. Скорость тела начинает уменьшаться, а деформация, удлинение пружины, увеличивается. Следовательно, кине­тическая энергия тела убывает, а потенциальная наоборот, возрастает.

В точке максимального отклонения тела его кинетическая энергия равна нулю, а потенциальная — максимальна.

Таким образом, при колебаниях периодически проис­ходит переход потенциальной энергии в кинетическую и обрат­но. Обрати внимание!

Полная механическая энергия пружинного маятника в каждой точке его траектории постоянна и равна сум­ме его кинетической и потенци­альной энергий: Emv22kx22.

Если для вертикального пружинного маятника выбрать систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю, то все описанное выше для горизонтального маятника можно применить для данного маятника. Источники:

ОпределениеПружинным маятником называют систему, которая состоит из упругой пружины, к которой прикреплен груз.

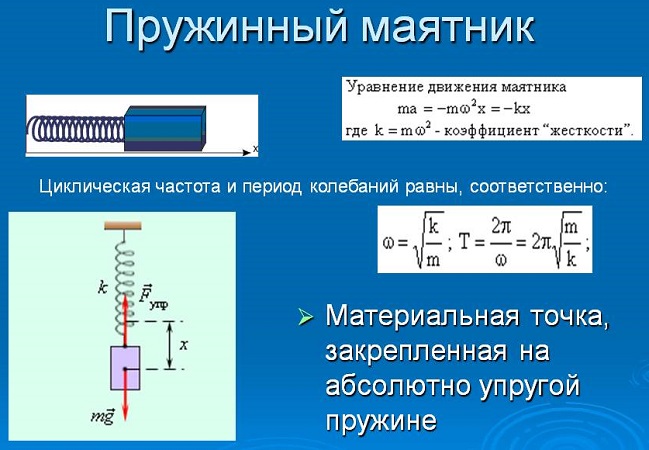
Допустим, что масса груза равна $m$, коэффициент упругости пружины $k$. Масса пружины в таком маятнике обычно не учитывается. Если рассматривать вертикальные движения груза (рис.1), то он движется под действием силы тяжести и силы упругости, если систему вывели из состояния равновесия и предоставили самой себе.

Уравнения колебаний пружинного маятника

Пружинный маятник, совершающий свободные колебания является примером гармонического осциллятора. Допустим, что маятник совершает колебания вдоль оси X. Если колебания малые, выполняется закон Гука, то уравнение движения груза имеет вид: [ddot{x}+{omega }^2_0x=0left(1right),] где ${щu}^2_0=frac{k}{m}$ – циклическая частота колебаний пружинного маятника. Решением уравнения (1) является функция:

[x=A{cos left({omega }_0t+varphi right)=A{sin left({omega }_0t+{varphi }_1right) } }left(2right),] где ${omega }_0=sqrt{frac{k}{m}}>0$- циклическая частота колебаний маятника, $A$ – амплитуда колебаний; ${(omega }_0t+varphi )$ – фаза колебаний; $varphi $ и ${varphi }_1$ – начальные фазы колебаний. В экспоненциальном виде колебания пружинного маятника можно записать как:

[Re tilde{x}=Releft(Acdot exp left(ileft({omega }_0t+varphi right)right)right)left(3right).].

[custom_ads_shortcode1]

Формулы периода и частоты колебаний пружинного маятника

Если в упругих колебаниях выполняется закон Гука, то период колебаний пружинного маятника вычисляют при помощи формулы: [T=2pi sqrt{frac{m}{k}}left(4right).] Так как частота колебаний ($nu $) – величина обратная к периоду, то:

[nu =frac{1}{T}=frac{1}{2pi }sqrt{frac{k}{m}}left(5right).].

[custom_ads_shortcode2]

Формулы амплитуды и начальной фазы пружинного маятника

Зная уравнение колебаний пружинного маятника (1 или 2) и начальные условия можно полностью описать гармонические колебания пружинного маятника. Начальные условия определяют амплитуда ($A$) и начальная фаза колебаний ($varphi $). Амплитуду можно найти как:

None [tg varphi =-frac{v_0}{x_0{omega }_0}left(7right),] где $v_0$ – скорость груза при $t=0 c$, когда координата груза равна $x_0$.

[custom_ads_shortcode3]

Энергия колебаний пружинного маятника

При одномерном движении пружинного маятника между двумя точками его движения существует только один путь, следовательно, выполняется условие потенциальности силы (любую силу можно считать потенциальной, если она зависит только от координат). Так как силы, действующие на пружинный маятник потенциальны, то можно говорить о потенциальной энергии.

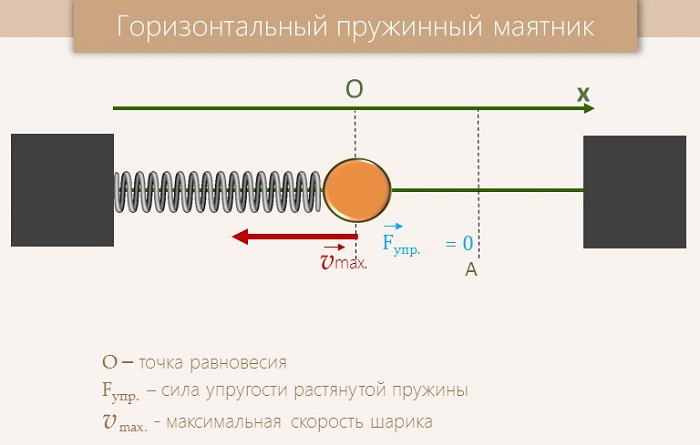
Пусть пружинный маятник совершает колебания в горизонтальной плоскости (рис. 2). За ноль потенциальной энергии маятника примем положение его равновесия, где поместим начало координат.

Силы трения не учитываем. Используя формулу, связывающую потенциальную силу и потенциальную энергию для одномерного случая:

None [E_p=frac{kx^2}{2}=frac{m{{omega }_0}^2x^2}{2}left(9right).] Закон сохранения энергии для пружинного маятника запишем как:

[frac{m{dot{x}}^2}{2}+frac{m{{omega }_0}^2x^2}{2}=const left(10right),] где $dot{x}=v$ – скорость движения груза; $E_k=frac{m{dot{x}}^2}{2}$ – кинетическая энергия маятника. Из формулы (10) можно сделать следующие выводы:

• Максимальная кинетическая энергия маятника равна его максимальной потенциальной энергии.
• Средняя кинетическая энергия по времени осциллятора равна его средней по времени потенциальной энергии.

[custom_ads_shortcode1]

Примеры задач с решением

Пример 1Задание. Маленький шарик, массой $m=0,36$ кг прикреплен к горизонтальной пружине, коэффициент упругости которой равен $k=1600 frac{Н}{м}$. Каково было начальное смещение шарика от положения равновесия ($x_0$), если он при колебаниях проходит его со скоростью $v=1 frac{м}{с}$?

Решение. Сделаем рисунок.

По закону сохранения механической энергии (так как считаем, что сил трения нет), запишем:

[E_{pmax}=E_{kmax }left(1.1right),] где $E_{pmax}$ – потенциальная энергия шарика при его максимальном смещении от положения равновесия; $E_{kmax }$ – кинетическая энергия шарика, в момент прохождения положения равновесия. [E_{kmax }=frac{mv^2}{2}left(1.2right).] Потенциальная энергия равна:

None [frac{mv^2}{2}=frac{k{x_0}^2}{2}left(1.4right).] Из (1.4) выразим искомую величину:

[x_0=vsqrt{frac{m}{k}}.] Вычислим начальное (максимальное) смещение груза от положения равновесия:

[x_0=1cdot sqrt{frac{0,36}{1600}}=1,5 cdot {10}^{-3}(м).] Ответ. $x_0=1,5$ ммПример 2Задание. Пружинный маятник совершает колебания по закону: $x=A{cos left(omega tright), } $где $A$ и $omega $ – постоянные величины. Когда возвращающая сила в первый раз достигает величины $F_0,$ потенциальная энергия груза равна $E_{p0}$. В какой момент времени это произойдет?

Решение. Возвращающей силой для пружинного маятника является сила упругости, равная:

None [E_p=frac{kx^2}{2}=frac{kA^2{{cos }^2 left(omega tright) }}{2}left(2.2right).] В момент времени, который следует найти $F=F_0$; $E_p=E_{p0}$, значит:

[frac{E_{p0}}{F_0}=-frac{A}{2}{cos left(omega tright) }to t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }.] Ответ. $t=frac{1}{omega } arc{cos left(-frac{2E_{p0}}{AF_0}right) }$Читать дальше: формулы равноускоренного прямолинейного движения.

Модель иллюстрирует превращения энергии при гармонических колебаниях тела под действием силы упругости, потенциальная энергия которой пропорциональна квадрату смещения тела из положения равновесия: где A > 0 – коэффициент пропорциональности. В случае колебаний груза на пружине: где k – жесткость пружины. Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия.

Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению:

F (t) = ma (t) = –mω2x (t).

В этом соотношении ω – круговая частота гармонических колебаний. Таким свойством обладает упругая сила в пределах применимости закона Гука: Fупр = –kxСилы любой другой физической природы, удовлетворяющие этому условию, называются квазиупругими.

При свободных механических колебаниях кинетическая и потенциальная энергии изменяются периодически. При максимальном отклонении тела от положения равновесия его скорость, а следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на горизонтально расположенной пружине потенциальная энергия – это энергия упругих деформаций пружины. Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией. Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и т. д.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот. Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной.

None

Графически показано соотношение между потенциальной и кинетической энергиями при колебаниях в любой момент времени. Обратите внимание, что в отсутствие затухания полная энергия колебательной системы остается неизменной, потенциальная энергия достигает максимума при максимальном отклонении тела от положения равновесия, а кинетическая энергия принимает максимальное значение при прохождении тела через положение равновесия.

Полная механическая энергия характеризует движение и взаимодействие тел, следовательно, зависит от скоростей и взаимного расположения тел. Полная механическая энергия замкнутой механической системы равна сумме кинетической и потенциальной энергии тел этой системы:

[custom_ads_shortcode2]

Закон сохранения энергии

Закон сохранения энергии – фундаментальный закон природы. В ньютоновской механике закон сохранения энергии формулируется следующим образом:

• Полная механическая энергия изолированной (замкнутой) системы тел остаётся постоянной.

Другими словами:

• Энергия не возникает из ничего и не исчезает никуда, она может только переходить из одной формы в другую.

Классическими примерами этого утверждения являются: пружинный маятник и маятник на нити (с пренебрежимо малым затуханием). В случае пружинного маятника в процессе колебаний потенциальная энергия деформированной пружины (имеющая максимум в крайних положениях груза) переходит в кинетическую энергию груза (достигающую максимума в момент прохождения грузом положения равновесия) и обратно. В случае маятника на нити потенциальная энергия груза переходит в кинетическую энергию и обратно.

[custom_ads_shortcode3]

2 Оборудование

2.1 Динамометр. 2.2 Штатив лабораторный.

2.3 Груз массой 100 г – 2шт. 2.4 Линейка измерительная.

2.5 Кусочек мягкой ткани или войлока.

[custom_ads_shortcode1]

3 Теоретическое обоснование

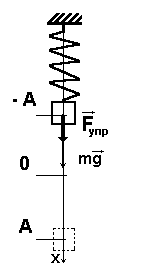
Схема экспериментальной установки приведена на рисунке 1.

Динамометр укреплен вертикально в лапке штатива. На штатив по­мещают кусочек мягкой ткани или войлока. При подвешивании к ди­намометру грузов растяжение пружины динамометра определяется положением указателя. При этом максимальное удлинение (или стати­ческое смещение) пружины хвозникает тогда, когда сила упругости пружины с жесткостью k уравновешивает силу тяжести груза массой т:

kx=mg,(1) где g = 9,81— ускорение свободного падения.

Следовательно,. (2) Статическое смещение характеризует новое положение равновесия О’ нижнего конца пружины (рис. 2).

Если груз оттянуть вниз на расстояние А от точки О’ и отпустить в точке 1, то возникают периодические колебания груза. В точках 1 и 2, называемых точками поворота, груз останавливается, изменяя на­правление движения на противоположное. Поэтому в этих точках ско­рость груза v = 0.

Максимальной скоростью v_maxгруз будет обладать в средней точ­ке О’. На колеблющийся груз действуют две силы: постоянная сила тяжести mg и переменная сила упругости kx. Потенциальная энергия тела в гравитационном поле в произвольной точке с координатой х равна mgx. Потенциальная энергия деформированного тела соответственно равна .

При этом за нуль отсчета потенциальной энергии для обеих сил принята точка х = 0, соответствующая положению указателя для не­растянутой пружины.

Полная механическая энергия груза в произвольной точке скла­дывается из его потенциальной и кинетической энергии. Пренебрегая силами трения, воспользуемся законом сохранения полной механиче­ской энергии.

Приравняем полную механическую энергию груза в точке 2 с коор­динатой -(х-А) и в точке О’ с координатой -х(3) Раскрывая скобки и проводя несложные преобразования, приведем формулу (3) к виду(4) Тогда модуль максимальной скорости грузов(5) Жесткость пружины можно найти, измерив статическое смещение х0Как следует из формулы (1),(6) Соответственно(7)

Источники:

• www.yaklass.ru
• www.webmath.ru
• files.school-collection.edu.ru
• studfiles.net

Полная энергия колебаний, теория и онлайн калькуляторы

Полная энергия колебаний

Энергия колебаний пружинного маятника

Рассмотрим превращения энергии, которые происходят при гармонических колебаниях в консервативной системе на примере пружинного маятника. Так как пружинный маятник мы считаем консервативной системой, то механическая энергия ее постоянна:

[E=E_k+E_p=const left(1right).]

Проверим справедливость выражения (1),) непосредственным суммированием выражений для кинетической и потенциальной энергии рассматриваемого маятника.

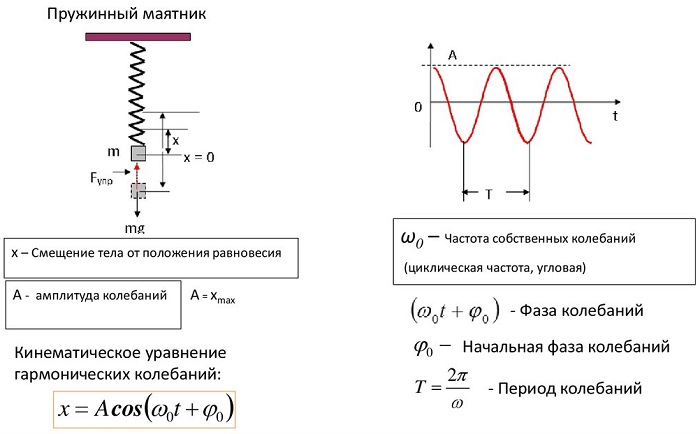
Уравнение колебаний маятника запишем в виде:

[x=A{cos left({omega }_0t+varphi right)(2) },]

где $x$ – смещение груза маятника по оси X. В таком случае изменение кинетической энергии груза, совершающего колебания на напружине равна:

[E_k=frac{m}{2}A^2{{omega }_0}^2{{sin}^2 left({omega }_0t+varphi right)left(3right). }]

Потенциальна энергия пружинного маятника равна: потенциальной энергии упругодеформированной пружины и потенциальной энергии груза в поле тяжести Земли:

[E_p=frac{kx^2}{2}=frac{k}{2}A^2{{cos}^2 left(щ_0t+цright) }left(4right).]

Суммируем правые части выражений (3) и (4), получим:

[E=frac{m}{2}A^2{щ_0}^2{{sin}^2 left(щ_0t+цright)+ }frac{k}{2}A^2{{cos}^2 left(щ_0t+цright) }=frac{k}{2}A^2=frac{1}{2}m{omega }^2_0A^2left(5right).]

где ${{omega }_0}^2=frac{k}{m}$.

Из формулы (5) мы видим, что неизменная суммарная энергия колебательной системы равна потенциальной ее энергии в точках максимального отклонения от положения равновесия (при $x=pm A$). Энергия $E$ равна кинетической энергии при прохождении грузом положения равновесия, скорость груза равна:

[v_x=pm {omega }_0Aleft(6right).]

В ходе взаимных превращений потенциальная и кинетическая энергии гармонически колеблются с одинаковой амплитудой, равной $frac{E}{2}$ находятся в противофазе друг с другом, частота их колебаний равна $2{omega }_0$.

[{E_k =frac{E}{2}left[1-{cos 2({omega }_0t+varphi ) }right]left(7right). }]

[E_p=frac{E}{2}left[1+{cos 2({omega }_0t+varphi ) }right]left(8right).]

И так, выражения (7) и (8) показывают, что кинетическая и потенциальная энергии колебательной системы совершают гармонические колебания вокруг их общего значения $frac{E}{2}$ с удвоенной частотой 2${omega }_0$, тогда как полная энергия системы остается постоянной. Она связана с амплитудой колебаний как:

[E=frac{k}{2}A^2.]

Энергия колебательных систем с одной степенью свободы

Все, что сказано для пружинного маятника можно применить , для любых механических колебаний систем с одной степенью свободы. Мгновенное положение такой системы можно определить, используя один параметр, который называют обобщенной координатой ($q$), например, угла поворота или смещения по оси координат. При этом величина $dot{q}=frac{dq}{dt}$ называется обобщённой скоростью.

Потенциальная энергия в таких обозначениях примет вид:

[E_p=frac{alpha q^2}{2}left(9right),]

кинетическая энергия:

[E_p=frac{beta {dot{q}}^2}{2}left(10right),]

где $alpha , beta $ – параметры системы. Полная энергия системы в нашем случае равна:

[E=frac{alpha q^2}{2}+frac{beta {dot{q}}^2}{2}=const left(11right),]

обобщенная координата совершает гармонические колебания с частотой:

[{omega }_0=sqrt{frac{alpha }{beta }}left(12right).]

Примеры задач на полную энергию колебаний

Читать дальше: понятие силы.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Пружинный маятник – колебательная система, которая состоит из тела, подвешенного к пружине. Эта система способна к совершению свободных колебаний.

Подобные системы довольно широко распространены за счет своей функциональной гибкости. Механизмы на основе таких маятников часто используются как элементы средств автоматики. 

В том числе они нашли применение в контактных взрывателях различных боеприпасов, в качестве акселерометров в контурах управления ракет. Так же они активно используются в предохранительных клапанах, устанавливаемых в трубопроводах.

Что такое пружинный маятник

Пружинным маятником в физике называют систему, совершающую колебательные движения под действием силы упругости. 

Приняты следующие обозначения:

• m – масса тела;

• k – коэффициент жесткости пружины.

Общий вид маятника:

Особенностями пружинных маятников являются:

1. Сочетание тела и пружины. Массой пружины обычно в расчетах пренебрегают. Роль тела могут играть различные объекты. На них оказывают действие внешние силы. Груз может крепиться разными способами. Витки пружины, которыми она начинается и заканчивается, изготавливают с учетом повышенной нагрузки;

2. У любой пружины есть исходное положение, предел сжатия и растяжения. При максимальном сжатии зазора между витками нет. Когда она максимально растянута, возникает необратимая деформация;

3. Полная механическая энергия появляется с началом процесса обратимого деформирования. В этот момент на объект не оказывает действие сила упругости;

4. Колебательные движения происходят под влиянием силы упругости. Масштаб влияния определяется несколькими причинами (тип сплава, расположение витков и т. д.). Так как может происходить и сжатие и растяжение, можно сделать вывод, что сила упругости действует в двух противоположных направлениях;

5. От массы тела, величины и направления прикладываемой силы зависит скорость в плоскости его перемещения. Например, если подвесить груз к пружине и, растянув её, отпустить, то груз будет перемещаться в двух плоскостях: вертикально и горизонтально.

Виды пружинных маятников

Существует два типа данной системы:

1. Вертикальный маятник – на тело довольно сильно влияет сила тяжести. Это влияние обуславливает увеличение инерционных движений, которые совершает тело в исходной точке.

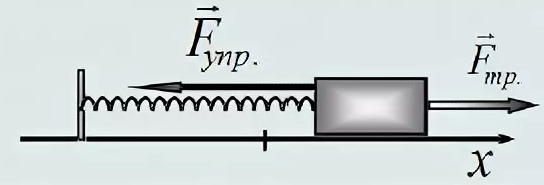
2. Горизонтальный – в таком варианте при движении на груз начинает действовать сила трения, возникающая по причине того, что груз лежит на поверхности.

Сила упругости в пружинном маятнике

До начала деформирования пружина находится в равновесном состоянии. Прикладываемое усилие может как растягивать, так и сжимать её. 

Применяя к пружинному маятнику закон сохранения энергии, мы можем рассчитать силу упругости в нем. Упругость прямо пропорциональна расстоянию, на которое сместился груз.

Расчёт силы упругости может быть проведен таким образом:

F_упр = – k*x

где k — коэффициент жесткости пружины (Нм),

x – смещение (м).

Уравнения колебаний пружинного маятника

Свободные колебания пружинного маятника описываются с помощью гармонического закона. 

Если допустить вероятность того, что колебания идут вдоль оси Х, и при этом выполняется закон Гука, то уравнение примет вид:

F(t) = ma(t) = – mw2x(t),

где w – радиальная частота гармонического колебания.

Для проведения расчета колебаний, учитывая все вероятности, применяют следующие формулы:

Период и частота свободных колебаний пружинного маятника

При разработке проектов всегда определяется период колебаний и их частота. Для их измерения используются известные в физике формулы.

Изменение циклической частоты покажет формула, приведенная на рисунке:

Факторы, от которых зависит частота:

1. Коэффициент упругости. На этот коэффициент влияет количество витков, их диаметр, расстояние между ними, длина пружины, жесткость используемого сплава и т. д.

2. Масса груза. От этого фактора зависит возникающая инерция и скорость перемещения.

Амплитуда и начальная фаза пружинного маятника

Учитывая начальные условия и рассчитав уравнение колебаний, можем точно описать колебания пружинного маятника. 

В качестве начальных условий используются: амплитуда (А) и начальная фаза колебаний (ϕ).

Энергия пружинного маятника

При рассмотрении колебания тел учитывают, что груз движется прямолинейно. Полная механическая энергия тела в каждой точке траектории является константой и равняется сумме его потенциальной энергии и кинетической энергии.

Потенциальная энергия:

Кинетическая энергия:

Полная энергия:

Расчет имеет особенности. При его проведении нужно учитывать несколько условий:

1. Колебания проходят в двух плоскостях: вертикальной и горизонтальной.

2. В качестве равновесного положения выбирается ноль потенциальной энергии. Находясь в этом положении пружина сохраняет свою форму.

3. Влияние силы трения при расчете не учитывают.

Дифференциальное уравнение гармонических колебаний пружинного маятника 

Отметим, что пружинный маятник — это обобщенное определение. Скорость движения груза (тела) напрямую зависит от комплекса условий, в том числе приложенного к нему усилия.