Как найти полную мощность в электротехнике

Классическая электродинамика
Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

Единицей измерения в Международной системе единиц (СИ) является ватт (русское обозначение: Вт, международное: W).

Мгновенная электрическая мощность[править | править код]

Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки в точку , к величине пробного заряда. То есть можно сказать, что электрическое напряжение численно равно работе по переносу единичного заряда из точки в точку . Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу или над ним будет совершена работа, численно равная электрическому напряжению, действующему на участке цепи. Умножив напряжение на количество единичных зарядов, мы, таким образом, получаем работу, которую совершает электрическое поле по перемещению этих зарядов от начала участка цепи до его конца.
Мощность, по определению — это работа в единицу времени.

Введём обозначения:

 — напряжение на участке (принимаем его постоянным на интервале );

 — количество зарядов, прошедших от к за время ;

 — работа, совершённая зарядом при движении по участку ;

 — мощность.

Записывая вышеприведённые рассуждения, получаем:

Для единичного заряда на участке :

Для всех зарядов:

Поскольку ток есть электрический заряд, протекающий по проводнику в единицу времени, то есть по определению, в результате получаем:

Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:

Если участок цепи содержит резистор c электрическим сопротивлением , то:

Дифференциальные выражения для электрической мощности[править | править код]

Мощность, выделяемая в единице объёма, равна:

где:

 — напряжённость электрического поля;

 — плотность тока.

Отрицательное значение скалярного произведения (векторы и противонаправлены или образуют тупой угол) означает, что в данной точке электрическая мощность не рассеивается, а генерируется за счёт работы сторонних сил.

В случае изотропной среды в линейном приближении:

где  — удельная проводимость, величина, обратная удельному сопротивлению.

В случае наличия анизотропии (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла) в линейном приближении:

где  — тензор проводимости.

Мощность постоянного тока[править | править код]

Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:

Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:

где  — электрическое сопротивление.

Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:

где  — ЭДС.

Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность прибавляется к поглощаемой или вычитается из отдаваемой.

Мощность переменного тока[править | править код]

В цепях переменного тока формула для мощности постоянного тока может быть применена лишь для расчёта мгновенной мощности, которая сильно изменяется во времени и для большинства простых практических расчётов не слишком полезна непосредственно. Прямой расчёт среднего значения мощности требует интегрирования по времени. Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.

Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.

Активная мощность[править | править код]

Единица измерения в СИ — ватт^[1].

Среднее за период значение мгновенной мощности называется активной электрической мощностью или электрической мощностью:

В цепях однофазного синусоидального тока , где и  — среднеквадратичные значения напряжения и тока,  — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи или её проводимость по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью активная связана соотношением .

В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отражённой мощностью.

Реактивная мощность[править | править код]

Единица измерения, по предложению Международной электротехнической комиссии, – вар (вольт-ампер реактивный); (русское обозначение: вар; международное: var). В терминах единиц СИ, как отмечено в 9-ом издании Брошюры СИ, вар когерентен произведению вольт-ампер. В Российской Федерации эта единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения в области «электротехника»^[1][2]:

Вар определяется как реактивная мощность цепи с синусоидальным переменным током при действующих значениях напряжения 1 В и тока 1 А, если сдвиг фазы между током и напряжением ^[3].

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения и тока , умноженному на синус угла сдвига фаз между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью и активной мощностью соотношением:

Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.

Необходимо отметить, что величина для значений от 0 до плюс 90° является положительной величиной. Величина для значений от 0 до −90° является отрицательной величиной. В соответствии с формулой , реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии, возвращаемой от индуктивной и ёмкостной нагрузки в источник переменного напряжения.

Полная мощность[править | править код]

Единица измерения — В·А, вольт-ампер (русское обозначение: В·А; международное: V·A). В Российской Федерации эта единица допущена к использованию в качестве внесистемной единицы без ограничения срока с областью применения «электротехника»^[1][2].

Полная мощность — величина, равная произведению действующих значений периодического электрического тока в цепи и напряжения на её зажимах связана с активной и реактивной мощностями соотношением:

где:

 — активная мощность;

 — реактивная мощность (при индуктивной нагрузке , а при ёмкостной ).

Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:

Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.

Комплексная мощность[править | править код]

Мощность, аналогично импедансу, можно записать в комплексном виде:

где:

 — комплексное напряжение;

 — комплексный ток;

 — импеданс;

 — оператор комплексного сопряжения.

Модуль комплексной мощности равен полной мощности Действительная часть равна активной мощности а мнимая  — реактивной мощности с корректным знаком в зависимости от характера нагрузки.

Измерения[править | править код]

• Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра, амперметра и фазометра.
• Для измерения коэффициента реактивной мощности применяют фазометры
• Государственный эталон мощности — ГЭТ 153—2012 Государственный первичный эталон единицы электрической мощности в диапазоне частот от 1 до 2500 Гц. Институт-хранитель: ВНИИМ

Потребление мощности некоторыми электроприборами[править | править код]

Значения потребляемой электрической мощности некоторых потребителей

Электрический прибор	Мощность,Вт
Лампочка фонарика	1
Сетевой роутер, хаб	10…20
Системный блок ПК	100…1700
Системный блок сервера	200…1500
Монитор для ПК ЭЛТ	15…200
Монитор для ПК ЖК	2…40
Лампа люминесцентная бытовая	5…30
Лампа накаливания бытовая	25…150
Холодильник бытовой	15…700
Электропылесос	100… 3000
Электрический утюг	300…2 000
Стиральная машина	350…2 000
Электрическая плитка	1000…2000
Сварочный аппарат бытовой	1000…5500
Двигатель лифта невысокого дома	3 000…15 000
Двигатель трамвая	45 000…75 000
Двигатель электровоза	650 000
Электродвигатель шахтной подъёмной машины	1 000 000…5 000 000
Электродвигатель прокатного стана	6 000 000…32 000 000

Выходная мощность[править | править код]

Измеряется как долговременная (RMS^[en]), так и кратковременная (PMO, PMPO) мощности, способные отдавать усилителями мощности.

также см.: КПД

См. также[править | править код]

• Ваттметр
• Электрический ток
• Коэффициент мощности
• Список параметров напряжения и силы электрического тока
• Закон Ома
• КПД

Примечания[править | править код]

Литература[править | править код]

• ГОСТ 8.417-2002 Единицы величин.
• ПР 50.2.102-2009 Положение о единицах величин, допускаемых к применению в Российской Федерации.
• Л. А. Бессонов . Теоретические основы электротехники. Электрические цепи: учебник

для бакалавров. — 12-е изд., испр. и доп. — М.: Юрайт, 2016. — 702 с. — (Бакалавр. Углубленный курс). — 1000 экз. — ISBN 978-5-9916-3210-2.

• Гольдштейн Е. И., Сулайманов А. О., Гурин Т. С. Мощностные характеристики электрических цепей при несинусоидальных токах и напряжениях. ТПУ, — Томск, 2009, Деп. в ВИНИТИ, 06.04.09, № 193 — 2009. — 146 с.

Ссылки[править | править код]

• Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. ToeHelp.Ru. Дата обращения: 7 марта 2022.
• Для чего нужна компенсация реактивной мощности. Школа для электрика (2010). Дата обращения: 7 марта 2022.
• . ред. Д. Макаров : Как рассчитать мощность электрического тока? Заметки электрика. ASUTPP. Дата обращения: 7 марта 2022.

( 2 оценки, среднее 5 из 5 )

Активная, реактивная и полная (кажущаяся) мощности

Простое объяснение с формулами

Активная мощность (P)

Другими словами активную мощность можно назвать: фактическая, настоящая, полезная, реальная мощность. В цепи постоянного тока мощность, питающая нагрузку постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, то есть

P = V I

потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением. Другими словами, в цепи постоянного тока нет никакого коэффициента мощности.

Но при синусоидальных сигналах, то есть в цепях переменного тока, ситуация сложнее из-за наличия разности фаз между током и напряжением. Поэтому среднее значение мощности (активная мощность), которая в действительности питает нагрузку, определяется как:

P = V I Cosθ

В цепи переменного тока, если она чисто активная (резистивная), формула для мощности та же самая, что и для постоянного тока: P = V I.

Формулы для активной мощности

P = V I – в цепях постоянного тока

P = V I cosθ – в однофазных цепях переменного тока

P = √3 V_L I_L cosθ – в трёхфазных цепях переменного тока

P = 3 V_Ph I_Ph cosθ

P = √ (S² – Q²) или

P =√ (ВА² – вар²) или

Активная мощность = √ (Полная мощность² – Реактивная мощность²) или

кВт = √ (кВА² – квар²)

Реактивная мощность (Q)

Также её мощно было бы назвать бесполезной или безваттной мощностью.

Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, известна как реактивная (Q).

Реактивной называется мощность, которая потребляется и затем возвращается нагрузкой из-за её реактивных свойств. Единицей измерения активной мощности является ватт, 1 Вт = 1 В х 1 А. Энергия реактивной мощности сначала накапливается, а затем высвобождается в виде магнитного поля или электрического поля в случае, соответственно, индуктивности или конденсатора.

Реактивная мощность определяется, как

Q = V I sinθ

и может быть положительной (+Ve) для индуктивной нагрузки и отрицательной (-Ve) для емкостной нагрузки.

Единицей измерения реактивной мощности является вольт-ампер реактивный (вар): 1 вар = 1 В х 1 А. Проще говоря, единица реактивной мощности определяет величину магнитного или электрического поля, произведённого 1 В х 1 А.

Формулы для реактивной мощности

Q = V I sinθ

Реактивная мощность = √ (Полная мощность² – Активная мощность²)

вар =√ (ВА² – P²)

квар = √ (кВА² – кВт²)

Полная мощность (S)

Полная мощность – это произведение напряжения и тока при игнорировании фазового угла между ними. Вся мощность в сети переменного тока (рассеиваемая и поглощаемая/возвращаемая) является полной.

Комбинация реактивной и активной мощностей называется полной мощностью. Произведение действующего значения напряжения на действующее значение тока в цепи переменного тока называется полной мощностью.

Она является произведением значений напряжения и тока без учёта фазового угла. Единицей измерения полной мощности (S) является ВА, 1 ВА = 1 В х 1 А. Если цепь чисто активная, полная мощность равна активной мощности, а в индуктивной или ёмкостной схеме (при наличии реактивного сопротивления) полная мощность больше активной мощности.

Формула для полной мощности

S = V I

Полная мощность = √ (Активная мощность² + Реактивная мощность²)

kVA = √(kW² + kVAR²)

Следует заметить, что:

• резистор потребляет активную мощность и отдаёт её в форме тепла и света.
• индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля.
• конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля.

Все эти величины тригонометрически соотносятся друг с другом, как показано на рисунке:

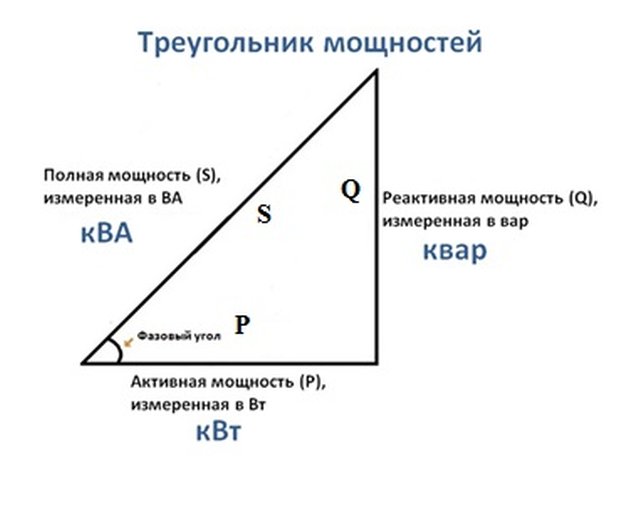
Что такое активная, реактивная и полная мощность — простое объяснение

В цепях постоянного тока не разделяют мощность на разные составляющие, такие как активная и реактивная, поэтому используют простое выражение P=U*I. Но с переменным током дело обстоит иначе. В этой статье мы рассмотрим, что такое активная, реактивная и полная мощность электрической цепи.

Определение

Нагрузка электрической цепи определяет, какой ток через неё проходит. Если ток постоянный, то эквивалентом нагрузки в большинстве случаев можно определить резистор определённого сопротивления. Тогда мощность рассчитывают по одной из формул:

P=U*I

P=I2*R

P=U2/R

По этой же формуле определяется полная мощность в цепи переменного тока.

Нагрузку разделяют на два основных типа:

• Активную – это резистивная нагрузка, типа – ТЭНов, ламп накаливания и подобного.
• Реактивную – она бывает индуктивной (двигатели, катушки пускателей, соленоиды) и емкостной (конденсаторные установки и прочее).

Последняя бывает только при переменном токе, например, в цепи синусоидального тока, именно такой есть у вас в розетках. В чем разница между активной и реактивной энергией мы расскажем далее простым языком, чтобы информация стала понятной для начинающих электриков.

Смысл реактивной нагрузки

В электрической цепи с реактивной нагрузки фаза тока и фаза напряжения не совпадают во времени. В зависимости от характера подключенного оборудования напряжение либо опережает ток (в индуктивности), либо отстаёт от него (в ёмкости).

Для описания вопросов используют векторные диаграммы. Здесь одинаковое направление вектора напряжения и тока указывает на совпадение фаз. А если вектора изображены под некоторым углом, то это и есть опережение или отставание фазы соответствующего вектора (напряжения или тока).

Давайте рассмотрим каждый из них.

В индуктивности напряжение всегда опережает ток. «Расстояние» между фазами измеряется в градусах, что наглядно иллюстрируется на векторных диаграммах. Угол между векторами обозначается греческой буквой «Фи».

В ёмкости ситуация противоположна – ток опережает напряжение, потому что индуктивность заряжаясь потребляет большой ток, который уменьшается по мере заряда. Хотя чаще говорят, что напряжение отстаёт от тока.

Если сказать кратко и понятно, то эти сдвиги можно объяснить законами коммутации, согласно которым в ёмкости напряжение не может изменится мгновенно, а в индуктивности – ток.

Треугольник мощностей и косинус Фи

Если взять всю цепь, проанализировать её состав, фазы токов и напряжений, затем построить векторную диаграмму. После этого изобразить активную по горизонтальной оси, а реактивную – по вертикальной и соединить результирующим вектором концы этих векторов – получится треугольник мощностей.

Он выражает отношение активной и реактивной мощности, а вектор, соединяющий концы двух предыдущих векторов – будет выражать полную мощность. Всё это звучит слишком сухо и запутано, поэтому посмотрите на рисунок ниже:

Буквой P – обозначена активная мощность, Q – реактивная, S – полная.

Формула полной мощности имеет вид:

Самые внимательные читатели наверняка заметили подобие формулы теореме Пифагора.

Единицы измерения:

• P – Вт, кВт (Ватты);
• Q – ВАр, кВАр (Вольт-амперы реактивные);
• S – ВА (Вольт-амперы);

Расчёты

Для вычисления полной мощности используют формулу в комплексной форме. Например, для генератора расчет имеет вид:

А для потребителя:

Но применим знания на практике и разберемся как рассчитать потребляемую мощность. Как известно мы, обычные потребители, оплачиваем только за потребление активной составляющей электроэнергии:

P=S*cosФ

Здесь мы видим, новую величину cosФ. Это коэффициент мощности, где Ф – это угол между активной и полной составляющей из треугольника. Тогда:

cosФ=P/S

В свою очередь реактивная мощность рассчитывается по формуле:

Q = U*I*sinФ

Для закрепления информации, ознакомьтесь с видео лекцией:

Всё вышесказанное справедливо и для трёхфазной цепи, отличаться будут только формулы.

Ответы на популярные вопросы

Полная, активная и реактивная мощности являются важной темой в электричестве для любого электрика. В качестве заключения мы сделали подборку из 4 часто задаваемых вопросов на этот счёт.

• Какую работу выполняет реактивная мощность?

Ответ: полезной работы не выполняет, но нагрузкой на линии является полная мощность, в том числе с учетом реактивной составляющей. Поэтому чтобы снизить общую нагрузку с ней борются или говоря грамотным языком компенсируют.

— В этих целях используют установки для компенсации реактива. Это могут быть конденсаторные установки или синхронные компенсаторы (синхронные электродвигатели). Подробнее мы рассматривали этот вопрос в статье: https://samelectrik.ru/kompensaciya-reaktivnoj-moshhnosti.html

• Из-за каких потребителей возникает реактив?

— Это в первую очередь электродвигатели – самый многочисленный вид электрооборудования на предприятиях.

• Чем вредит большое потребление реактивной энергии?

— Кроме нагрузки на линии электропередач следует учитывать, что предприятия оплачивает полную мощность, а физические лица – только активную. Это приводит к повышенной сумме оплаты за электроэнергию.

На видео предоставлено простое объяснение понятий реактивной, активной и полной мощностей:

На этом мы и заканчиваем рассмотрение данного вопроса. Надеемся, теперь вам стало понятно, что такое активная, реактивная и полная мощность, какие между ними отличия и как определяется каждая величина.

Материалы по теме:

Источник: https://samelectrik.ru/chto-takoe-aktivnaya-reaktivnaya-i-polnaya-moshhnost.html

Активная реактивная и полная мощность

Содержание:

В электротехнике среди множества определений довольно часто используются такие понятия, как активная, реактивная и полная мощность. Эти параметры напрямую связаны с током и напряжением в замкнутой электрической цепи, когда включены какие-либо потребители.

Для проведения вычислений применяются различные формулы, среди которых основной является произведение напряжения и силы тока. Прежде всего это касается постоянного напряжения. Однако в цепях переменного тока мощность разделяется на несколько составляющих, отмеченных выше.

Вычисление каждой из них также осуществляется с помощью формул, благодаря которым можно получить точные результаты.

Формулы активной, реактивной и полной мощности

Основной составляющей считается активная мощность. Она представляет собой величину, характеризующую процесс преобразования электрической энергии в другие виды энергии.

То есть по-другому является скоростью, с какой потребляется электроэнергия. Именно это значение отображается на электросчетчике и оплачивается потребителями.

Вычисление активной мощности выполняется по формуле: P = U x I x cosф.

В отличие от активной, которая относится к той энергии, которая непосредственно потребляется электроприборами и преобразуется в другие виды энергии – тепловую, световую, механическую и т.д., реактивная мощность является своеобразным невидимым помощником.

Расчеты реактивной мощности производятся по формуле: Q = U x I x sinф.

Полной мощностью является величина, состоящая из активной и реактивной составляющих. Именно она обеспечивает потребителям необходимое количество электроэнергии и поддерживает их в рабочем состоянии. Для ее расчетов применяется формула: S = .

Как найти активную, реактивную и полную мощность

Активная мощность относится к энергии, которая необратимо расходуется источником за единицу времени для выполнения потребителем какой-либо полезной работы. В процессе потребления, как уже было отмечено, она преобразуется в другие виды энергии.

В цепи переменного тока значение активной мощности определяется, как средний показатель мгновенной мощности за установленный период времени.

Следовательно, среднее значение за этот период будет зависеть от угла сдвига фаз между током и напряжением и не будет равной нулю, при условии присутствия на данном участке цепи активного сопротивления.

Последний фактор и определяет название активной мощности. Именно через активное сопротивление электроэнергия необратимо преобразуется в другие виды энергии.

При выполнении расчетов электрических цепей широко используется понятие реактивной мощности. С ее участием происходят такие процессы, как обмен энергией между источниками и реактивными элементами цепи. Данный параметр численно будет равен амплитуде, которой обладает переменная составляющая мгновенной мощности цепи.

В отличие от активной мощности, измеряемой в ваттах, реактивная мощность измеряется в вар – вольт-амперах реактивных.

Итоговое значение реактивной мощности в разветвленных электрических цепях представляет собой алгебраическую сумму таких же мощностей у каждого элемента цепи с учетом их индивидуальных характеристик.

Основной составляющей полной мощности является максимально возможная активная мощность при заранее известных токе и напряжении. При этом, cosф равен 1, когда отсутствует сдвиг фаз между током и напряжением. В состав полной мощности входит и реактивная составляющая, что хорошо видно из формулы, представленной выше. Единицей измерения данного параметра служит вольт-ампер (ВА).

Источник: https://electric-220.ru/news/aktivnaja_reaktivnaja_i_polnaja_moshhnost/2017-01-14-1156

Активная мощность: формула, как определить — Asutpp

Мощностные характеристики установки или сети являются основными для большинства известных электрических приборов. Активная мощность (проходящая, потребляема) характеризует часть полной мощности, которая передается за определенный период частоты переменного тока.

Определение

Активная и реактивная мощность может быть только у переменного тока, т. к. характеристики сети (силы тока и напряжения) у постоянного всегда равны.

Единица измерений активной мощности  Ватт, в то время, как реактивной – реактивный вольтампер и килоВАР (кВАР).

Стоит отметить, что как полная, так и активная характеристики могут измеряться в кВт и кВА, это зависит от параметров конкретного устройства и сети. В промышленных цепях чаще всего измеряется в килоВаттах.

Соотношение энергий

Прибор	Мощность бытовых приборов, Вт/час
Зарядное устройство	2
Люминесцентная лампа ДРЛ	От 50
Акустическая система	30
Электрический чайник	1500
Стиральной машины	2500
Полуавтоматический инвертор	3500
Мойка высокого давления	3500

Исходя из всего, сказанного выше, активная мощность – это положительная характеристика конкретной электрической цепи, которая является одним из основных параметров для выбора электрических приборов и контроля расхода электричества.

Генерация активной составляющей

Обозначение реактивной составляющей:

Это  номинальная величина, которая характеризует нагрузки в электрических устройствах при помощи колебаний ЭМП и потери при работе прибора. Иными словами, передаваемая энергия переходит на определенный реактивный преобразователь (это конденсатор, диодный мост и т. д.) и проявляется только в том случае, если система включает в себя эту составляющую.

Расчет

Для выяснения показателя активной мощности, необходимо знать полную мощность, для её вычисления используется следующая формула:

S = U I, где U – это напряжение сети, а I – это сила тока сети.

Этот же расчет выполняется при вычислении уровня передачи энергии катушки при симметричном подключении. Схема имеет следующий вид:

Схема симметричной нагрузки

Расчет активной мощности учитывает угол сдвига фаз или коэффициент (cos φ), тогда:

S = U * I * cos φ.

Очень важным фактором является то, что эта электрическая величина может быть как положительной, так и отрицательной. Это зависит от того, какие характеристики имеет cos φ.

Если у синусоидального тока угол сдвига фаз находится в пределах от 0 до 90 градусов, то активная мощность положительная, если от 0 до -90 – то отрицательная.

Правило действительно только для синхронного (синусоидального) тока (применяемого для работы асинхронного двигателя, станочного оборудования).

Также одной из характерных особенностей этой характеристики является то, что в трехфазной цепи (к примеру, трансформатора или генератора), на выходе активный показатель полностью вырабатывается.

Расчет трехфазной сети

Максимальная и активная обозначается P, реактивная мощность – Q.

Из-за того, что реактивная обуславливается движением и энергией магнитного поля, её формула (с учетом угла сдвига фаз) имеет следующий вид:

QL = ULI = I2xL

Из-за того, что реактивная и активная характеристики связаны с полной мощностью, их соотношение (баланс) имеет следующий вид:

S = √P2 + Q2, и все это равняется U*I .

Но если ток проходит непосредственно по реактивному сопротивлению. То потерь в сети не возникает. Это обуславливает индуктивная индуктивная составляющая – С и сопротивление – L. Эти показатели рассчитываются по формулам:

Сопротивление индуктивности: xL = ωL = 2πfL,

Сопротивление емкости: хc = 1/(ωC) = 1/(2πfC).

Для определения соотношения активной и реактивной мощности используется специальный коэффициент. Это очень важный параметр, по которому можно определить, какая часть энергии используется не по назначению или «теряется» при работе устройства.

При наличии в сети активной реактивной составляющей обязательно должен рассчитываться коэффициент мощности.

Эта величина не имеет единиц измерения, она характеризует конкретного потребителя тока, если электрическая система содержит реактивные элементы.

С помощью этого показателя становится понятным, в каком направлении и как сдвигается энергия относительно напряжения сети. Для этого понадобится диаграмма треугольников напряжений:

Диаграмма треугольников напряжений

К примеру, при наличии конденсатора формула коэффициента имеет следующий вид:

cos φ = r/z = P/S

Для получения максимально точных результатов рекомендуется не округлять полученные данные.

Компенсация

Учитывая, что при резонансе токов реактивная мощность равняется 0:

Q = QL – QC = ULI – UCI

Для того чтобы улучшить качество работы определенного устройства применяются специальные приборы, минимизирующие воздействие потерь на сеть. В частности, это ИБП. В данном приборе не нуждаются электрические потребители со встроенным аккумулятором (к примеру, ноутбуки или портативные устройства), но для большинства остальных источник бесперебойного питания является необходимым.

При установке такого источника можно не только установить негативные последствия потерь, но и уменьшить траты на оплату электричества. Специалисты доказали, что в среднем, ИБП поможет экономить от 20 % до 50 %. Почему это происходит:

1. Значительно уменьшается нагрузка силовых трансформаторов;
2. Провода меньше нагреваются, это не только положительно влияет на их работу, но и повышает безопасность;
3. У сигнальных и радиоустройств уменьшаются помехи;
4. На порядок уменьшаются гармоники в электрической сети.

В некоторых случаях специалисты используют не полноценные ИБП, а специальные компенсирующие конденсаторы. Они подходят для бытового использования, доступны и продаются в каждом электротехническом магазине. Для расчета планируемой и полученной экономии можно использовать все вышеперечисленные формулы.

Источник: https://www.asutpp.ru/aktivnaya-moshhnost-cepi-peremennogo-toka.html

Что такое полная, активная и реактивная мощность?

ЧТО ТАКОЕ ПОЛНАЯ, АКТИВНАЯ И РЕАКТИВНАЯ МОЩНОСТЬ? ОТ СЛОЖНОГО К ПРОСТОМУ.

В повседневной жизни практически каждый сталкивается с понятием «электрическая мощность», «потребляемая мощность» или «сколько эта штука «кушает» электричества».

В данной подборке мы раскроем понятие электрической мощности переменного тока для технически подкованных специалистов и покажем на картинке электрическую мощность в виде «сколько эта штука кушает электричества» для людей с гуманитарным складом ума :-).

Мы раскрываем наиболее практичное и применимое понятие электрической мощности и намеренно уходим от описания дифференциальных выражений электрической мощности.

ЧТО ТАКОЕ МОЩНОСТЬ ПЕРЕМЕННОГО ТОКА?

Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.

Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел.

Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.

Активная мощность (Real Power)

Среднее за период Τ  значение мгновенной мощности называется активной  мощностью, и

выражается формулой:  

В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.

Реактивная мощность (Reactive Power)

Единица измерения — вольт-ампер реактивный (русское обозначение: вар, кВАР; международное: var).

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними:

Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.

Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до минус 90° является отрицательной величиной. В соответствии с формулой    

Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например,асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

 Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора.

Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.

 Мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока.

Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например,асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

 Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора.

Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

 Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения

Полная мощность (Apparent Power)

Единица полной электрической мощности — вольт-ампер (русское обозначение: В·А, ВА, кВА-кило-вольт-ампер; международное: V·A, kVA).

Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: ; соотношение полной мощности с активной и реактивной мощностями выражается в следующем виде:     где P — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q›0, а при ёмкостной Q‹0).Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:

Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.

Визуально и интуитивно-понятно все вышеперечисленные формульные и текстовые описания полной, реактивной и активной мощностей передает следующий рисунок 🙂 

Специалисты компании НТС-групп (ТМ Электрокапризам-НЕТ) имеют огромный опыт подбора специализированного оборудования для построения систем обеспечения жизненно важных объектов бесперебойным электропитанием.

Мы умеем максимально качественно учитывать множество электрических и эксплуатационных параметров, которые позволяют выбрать экономически обоснованный вариант построения системы бесперебойного электропитанияс применением стабилизаторов напряжения, топливных электростанций, источников бесперебойного питания и др. сопутствующего оборудования.

© Материал подготовлен специалистами компании НТС-групп (ТМ Электрокапризам-НЕТ) с использованием информации из открытых источников, в т.ч. из свободной энциклопедии ВикипедиЯ https://ru.wikipedia.org  

Источник: http://electrokaprizam.net/content/35-chto-takoe-kva-kwt-kvar

Реактивная мощность

Главная > Теория > Реактивная мощность

Главная цель при передаче электроэнергии – повышение эффективности работы сетей. Следовательно, необходимо уменьшение потерь. Основной причиной потерь является реактивная мощность, компенсация которой значительно повышает качество электроэнергии.

Батареи статических конденсаторов

Реактивная мощность вызывает ненужный нагрев проводов, перегружаются электроподстанции. Трансформаторная мощность и кабельные сечения вынужденно подвергаются завышениям, сетевое напряжение снижается.

Понятие о реактивной мощности

Для выяснения, что же такое реактивная мощность, надо определить другие возможные виды мощности. При существовании в контуре активной нагрузки (резистора) происходит потребление исключительно активной мощности, полностью расходуемой на энергопреобразование. Значит, можно сформулировать, что такое активная мощность, – та, при которой ток совершает эффективную работу.

На постоянном токе происходит потребление исключительно активной мощности, рассчитываемой соответственно формуле:

P = U x I.

Измеряется в ваттах (Вт).

В электроцепях с переменным током при наличии активной и реактивной нагрузки мощностной показатель суммируется из двух составных частей: активной и реактивной мощности.

Реактивная нагрузка бывает двух видов:

1. Емкостная (конденсаторы). Характеризуется фазовым опережением тока по сравнению с напряжением;
2. Индуктивная (катушки). Характеризуется фазовым отставанием тока по отношению к напряжению.

Емкостная и индуктивная нагрузка

Если рассмотреть контур с переменным током и подсоединенной активной нагрузкой (обогреватели, чайники, лампочки с накаливающейся спиралью), ток и напряжение будут синфазными, а полная мощность, взятая в определенную временную отсечку, вычисляется путем перемножения показателей напряжения и тока.

Однако когда схема содержит реактивные компоненты, показатели напряжения и тока не будут синфазными, а будут различаться на определенную величину, определяемую углом сдвига «φ».

Пользуясь простым языком, говорится, что реактивная нагрузка возвращает столько энергии в электроцепь, сколько потребляет. В результате получится, что для активной мощности потребления показатель будет нулевой.

Реактивная мощность – часть энергии, которая позволяет устанавливать электромагнитные поля, требуемые оборудованием переменного тока.

Расчет реактивной мощности ведется по формуле:

Q = U x I x sin φ.

В качестве единицы измерения реактивной мощности служит ВАр (вольтампер реактивный).

Выражение для активной мощности:

P = U x I x cos φ.

Треугольник мощностей

Мощность электрического тока

Взаимосвязь активной, реактивной и полной мощности для синусоидального тока переменных значений представляется геометрически тремя сторонами прямоугольного треугольника, называемого треугольником мощностей.

Электроцепи переменного тока потребляют две разновидности энергии: активную мощность и реактивную.

Кроме того, значение активной мощности никогда не является отрицательным, тогда как для реактивной энергии возможна либо положительная величина (при индуктивной нагрузке), либо отрицательная (при емкостной нагрузке).

Важно! Из треугольника мощностей видно, что всегда полезно снизить реактивную составляющую, чтобы повысить эффективность системы.

Чтобы была рассчитана полная мощность, необходимо знать разность фаз между синусоидальными значениям U и I.

Коэффициент мощности

Пользуясь геометрически представленной векторной картиной, можно найти отношение сторон треугольника, соответствующих полезной и полной мощности, что будет равно косинусу фи или мощностному коэффициенту:

cos φ = P/S.

Данный коэффициент находит эффективность работы сети.

Количество потребляемых ватт – то же самое, что и количество потребляемых вольтампер при мощностном коэффициенте, равном 1 или 100%.

Важно! Полная мощность тем ближе к показателю активной, чем больше cos φ, или чем меньше угол сдвига синусоидальных величин тока и напряжения.

Если, к примеру, имеется катушка, для которой:

• Р = 80 Вт;
• Q = 130 ВАр;
• тогда S = 152,6 BA как среднеквадратичный показатель;
• cos φ = P/S = 0,52 или 52%

Можно сказать, что катушка требует 130 ВАр полной мощности для выполнения полезной работы 80 Вт.

Коррекция cos φ

В чем измеряется мощность

Для коррекции cos φ применяется тот факт, что при емкостной и индуктивной нагрузке вектора реактивной энергии располагаются в противофазе. Так как большинство нагрузок является индуктивными, подключив емкость, можно добиться увеличения cos φ.

Принцип компенсации реактивной мощности

Главные потребители реактивной энергии:

1. Трансформаторы. Представляют собой обмотки, имеющие индуктивную связь и посредством магнитных полей преобразуюшие токи и напряжения. Эти аппараты являются основным элементом электросетей, передающих электроэнергию. Особенно увеличиваются потери при работе на холостом ходу и при низкой нагрузке. Широко используются трансформаторы в производстве и в быту;
2. Индукционные печи, в которых расплавляются металлы путем создания в них вихревых токов;
3. Асинхронные двигатели. Крупнейший потребитель реактивной энергии. Вращающий момент в них создается посредством переменного магнитного поля статора;
4. Преобразователи электроэнергии, такие как силовые выпрямители, используемые для питания контактной сети железнодорожного транспорта и другие.

Конденсаторные батареи подсоединяются на электроподстанциях для того, чтобы контролировать напряжение в пределах установленных уровней.

Нагрузка меняется в течение дня с утренними и вечерними пиками, а также на протяжении недели, снижаясь в выходные, что изменяет показатели напряжения.

Подключением и отключением конденсаторов варьируется его уровень. Это делается от руки и с помощью автоматики.

Как и где измеряют cos φ

Реактивная мощность проверяется по изменению cos φ специальным прибором – фазометром. Его шкала проградуирована в количественных значениях cos φ от нуля до единицы в индуктивном и емкостном секторе. Полностью скомпенсировать негативное влияние индуктивности не удастся, но возможно приближение к желаемому показателю – 0,95 в индуктивной зоне.

https://www.youtube.com/watch?v=MdbG1f-SIC4

Фазометры применяются при работе с установками, способными повлиять на режим работы электросети через регулирование cos φ.

1. Так как при финансовых расчетах за потребленную энергию учитывается и ее реактивная составляющая, то на производствах устанавливаются автоматические компенсаторы на конденсаторах, емкость которых может меняться. В сетях, как правило, используются статические конденсаторы;
2. При регулировании cos φ у синхронных генераторов путем изменения возбуждающего тока необходимо его отслеживать визуально в ручных рабочих режимах;
3. Синхронные компенсаторы, представляющие собой синхронные двигатели, работающие без нагрузки, в режиме перевозбуждения выдают в сеть энергию, которая компенсирует индуктивную составляющую. Для регулирования возбуждающего тока наблюдают за показаниями cos φ по фазометру.

Коррекция коэффициента мощности – одна из эффективнейших инвестиций для сокращения затрат на электроэнергию. Одновременно улучшается качество получаемой энергии.

Видео

Источник: https://elquanta.ru/teoriya/reaktivnaya-moshhnost.html

Активная и реактивная мощность. За что платим и работа

Активная и реактивная мощность — потребители электрической энергии на то и потребители, чтобы эту энергию потреблять.

Потребителя интересует та энергия, потребление которой идет ему на пользу, эту энергию можно назвать полезной, но в электротехнике ее принято называть активной.

Это энергия, которая идет на нагрев помещений, готовку пищи, выработку холода, и превращаемая в механическую энергию (работа электродрелей, перфораторов, электронасосов и пр.).

В понятиях активная и реактивная мощность сталкиваются противоречивые интересы потребителей электрической энергии и ее поставщиков.

Потребителю выгодно платить только за потребленную им полезную электроэнергию, поставщику выгодно получать оплату за сумму активной и реактивной электроэнергии.

Можно ли совместить эти кажущиеся противоречивыми требования? Да, если свести количество реактивной электроэнергии к нулю. Рассмотрим, возможно ли подобное, и насколько можно приблизиться к идеалу.

Активная и реактивная мощность

Активная мощность

Существуют потребители электроэнергии, у которых полная и активная мощности совпадают. Это потребители, у которых нагрузка представлена активными сопротивлениями (резисторами). Среди бытовых электроприборов примерами подобной нагрузки являются лампы накаливания, электроплиты, жарочные шкафы и духовки, обогреватели, утюги, паяльники и пр.

Указанная у этих приборов в паспорте, одновременно является активная и реактивная мощность .

Это тот случай, когда мощность нагрузки можно определить по известной из школьного курса физики формуле, перемножив ток нагрузки на напряжение в сети.

Ток измеряется в амперах (А), напряжение в вольтах (В), мощность в ваттах (Вт). Конфорка электрической плиты в сети с напряжением 220 В при токе в 4,5 А потребляет мощность 4,5 х 220 = 990 (Вт).

Реактивная мощность

Иногда, проходя по улице, можно увидеть, что стекла балконов покрыты изнутри блестящей тонкой пленкой. Эта пленка изъята из бракованных электрических конденсаторов, устанавливаемых с определенными целями на питающих мощных потребителей электрической энергии распределительных подстанциях. Конденсатор – типичный потребитель реактивной мощности.

В отличие от потребителей активной мощности, где главным элементом конструкции является некий проводящий электричество материал (вольфрамовый проводник в лампах накаливания, нихромовая спираль в электроплитке и т.п.). В конденсаторе главный элемент – не проводящий электрический ток диэлектрик (тонкая полимерная пленка или пропитанная маслом бумага).

Реактивная емкостная мощность

Красивые блестящие пленки, что вы видели на балконе – это обкладки конденсатора из токопроводящего тонкого материала. Конденсатор замечателен тем, что он может накапливать электрическую энергию, а затем отдавать ее – своеобразный такой аккумулятор.

Если включить конденсатор в сеть постоянного тока, он зарядится кратковременным импульсом тока, а затем ток через него протекать не будет. Вернуть конденсатор в исходное состояние можно, отключив его от источника напряжения и подключив к его обкладкам нагрузку.

Некоторое время через нагрузку будет течь электрический ток, и идеальный конденсатор отдает в нагрузку ровно столько электрической энергии, сколько он получил при зарядке.

Подключенная к выводам конденсатора лампочка может на короткое время вспыхнуть, электрический резистор нагреется, а неосторожного человека может «тряхнуть» или даже убить при достаточном напряжении на выводах и запасенном количестве электричества.

Интересная картина получается при подключении конденсатора к источнику переменного электрического напряжения.

Поскольку у источника переменного напряжения постоянно меняются полярность и мгновенное значение напряжения (в домашней электросети по закону, близкому к синусоидальному).

Конденсатор будет непрерывно заряжаться и разряжаться, через него будет непрерывно протекать переменный ток. Но этот ток не будет совпадать по фазе с напряжением источника переменного напряжения, а будет опережать его на 90°, т.е. на четверть периода.

Это приведет к тому, что суммарно половину периода переменного напряжения конденсатор потребляет энергию из сети, а половину периода отдает, при этом суммарная потребляемая активная электрическая мощность равна нулю. Но, поскольку через конденсатор течет значительный ток, который может быть измерен амперметром, принято говорить, что конденсатор – потребитель реактивной электрической мощности.

Вычисляется реактивная мощность как произведение тока на напряжение, но единица измерения уже не ватт, а вольт-ампер реактивный (ВАр).

Это означает, что конденсатор потребляет 0,3 х 220 = 66 (ВАр) реактивной мощности – сравнимо с мощностью средней лампы накаливания, но конденсатор, в отличие от лампы, при этом не светится и не нагревается.

Реактивная индуктивная мощность

Если в конденсаторе ток опережает напряжение, то существуют ли потребители, где ток отстает от напряжения? Да, и такие потребители, в отличие от емкостных потребителей, называются индуктивными, оставаясь при этом потребителями реактивной энергии. Типичная индуктивная электрическая нагрузка – катушка с определенным количеством витков хорошо проводящего провода, намотанного на замкнутый сердечник из специального магнитного материала.

На практике хорошим приближением чисто индуктивной нагрузки является работающий без нагрузки трансформатор (или стабилизатор напряжения с автотрансформатором). Хорошо сконструированный трансформатор на холостом ходу потребляет очень мало активной мощности, потребляя мощность в основном реактивную.

Реальные потребители электрической энергии и полная электрическая мощность

Из рассмотрения особенностей емкостной и индуктивной нагрузки возникает интересный вопрос – что произойдет, если емкостную и индуктивную нагрузку включить одновременно и параллельно.

Ввиду их противоположной реакции на приложенное напряжение, эти две реакции начнут компенсировать друг друга. Суммарная нагрузка окажется только емкостной или индуктивной, и в некотором идеальном случае удастся добиться полной компенсации.

Выглядеть это будет парадоксально – подключенные амперметры зафиксируют значительные (и равные!) токи через конденсатор и катушку индуктивности, и полное отсутствие тока в объединяющих их общей цепи.

Описанная картина несколько нарушается лишь тем, что не существует идеальных конденсаторов и катушек индуктивности, но подобная идеализация помогает понять суть происходящих процессов.

Вернемся к реальным потребителям электрической энергии. В быту мы пользуемся в основном потребителями чисто активной мощности (примеры приведены выше), и смешанной активно-индуктивной. Это электродрели, перфораторы, электродвигатели холодильников, стиральных машин и прочей бытовой техники.

Также к ним относятся электрические трансформаторы источников питания бытовой радиоэлектронной аппаратуры и стабилизаторов напряжения. В случае подобной смешанной нагрузки, помимо активной (полезной) мощности, нагрузка потребляет еще и реактивную мощность, в итоге полная мощность отказывается больше активной мощности.

Полная мощность измеряется в вольт-амперах (ВА), и всегда представляет собой произведение тока в нагрузке на напряжение на нагрузке.

Таинственный «косинус фи»

Отношение активной мощности к полной называется в электротехнике «косинусом фи». Обозначается cos φ. Это отношение называется также и коэффициентом мощности. Нетрудно видеть, что для случая чисто активной нагрузки, где полная мощность совпадает с активной, cos φ = 1. Для случаев чисто емкостной или индуктивной нагрузок, где нулю равна активная мощность, cos φ = 0.

В случае смешанной нагрузки значение коэффициента мощности заключается в пределах от 0 до 1. Для бытовой техники обычно в диапазоне 0,5-0,9. В среднем можно считать его равным 0,7, более точное значение указывается в паспорте электроприбора.

За что платим?

И, наконец, самый интересный вопрос – за какой вид энергии платит потребитель. Исходя из того, что реактивная составляющая суммарной энергии не приносит потребителю никакой пользы, при этом долю периода реактивная энергия потребляется, а долю отдается, платить за реактивную мощность незачем.

Но бес, как известно, кроется в деталях.

Поскольку смешанная нагрузка увеличивает ток в сети, возникают проблемы на электростанциях, где электроэнергия вырабатывается синхронными генераторами, а именно: индуктивная нагрузка «развозбуждает» генератор, и приведение его в прежнее состояние обходится в затраты уже реальной активной мощности на его «довозбуждение».

Таким образом, заставить потребителя платить за потребляемую реактивную индуктивную мощность вполне справедливо. Это побуждает потребителя компенсировать реактивную составляющую своей нагрузки, а, поскольку эта составляющая в основном индуктивная, компенсация заключается в подключении конденсаторов наперед рассчитанной емкости.

Потребитель находит возможность платить меньше

Если потребителем оплачивается отдельно потребляемая активная и реактивная мощность. Он готов идти на дополнительные затраты и устанавливать на своем предприятии батареи конденсаторов, включаемые строго по графику в зависимости от средней статистики потребления электроэнергии по часам суток.

Существует также возможность установки на предприятии специальных устройств (компенсаторов реактивной мощности), подключающих конденсаторы автоматически в зависимости от величины и характера потребляемой в данный момент мощности. Эти компенсаторы позволяют поднять значение коэффициента мощности с 0,6 до 0,97, т.е. практически до единицы.

Принято также, что если соотношение потребленной реактивной энергии и общей не превышает 0,15, то корпоративный потребитель от оплаты за реактивную энергию освобождается.

Бытовые однофазные счетчики электрической энергии учитывают лишь активную мощность электрической нагрузки, за нее и выставляется счет на оплату. Т.е.

в настоящее время даже не существует технической возможности выставить индивидуальному потребителю счет за потребленную реактивную мощность.

Особых стимулов компенсировать индуктивную составляющую нагрузки у потребителя нет, да это и сложно осуществить технически. Постоянно подключенные конденсаторы при отключении индуктивной нагрузки будут бесполезно нагружать подводящую электропроводку.

Другое дело, что производитель иногда устанавливает компенсационные конденсаторы на входе потребителей с индуктивной составляющей нагрузки. Эти конденсаторы, при правильном их подборе, несколько снизят потери энергии в подводящих проводах, при этом несколько повысив напряжение на подключенном электроприборе за счет уменьшения падения напряжения на подводящих проводах.

Но, что самое главное, компенсация реактивной энергии у каждого потребителя, от квартиры до огромного предприятия, снизит токи во всех линиях электропитания, от электростанции до квартирного щитка. За счет реактивной составляющей полного тока, что уменьшит потери энергии в линиях и повысит коэффициент полезного действия электросистем.

Похожие темы:

Источник: https://electrosam.ru/glavnaja/jelektrotehnika/aktivnaia-i-reaktivnaia-moshchnost/

Что такое активная, реактивная и полная мощность

В отличии от сетей постоянного тока, где мощность имеет выражение    и не изменяется во времени, в сетях переменного тока это не так.

Мощность в цепи переменного тока также есть переменной величиной. На любом участке цепи в любой момент времени t она определяется  как  произведение мгновенных значений напряжения и тока.

Рассмотрим, что представляет активная мощность

В цепи с чисто активным сопротивлением она равна:

Если принять  и  тогда выйдет:

Где 

Исходя из выражений выше — активная энергия состоит из двух частей — постоянной  и переменной  , которая меняется с двойной частотой. Среднее ее значение 

График Р(ωt)

Отличие реактивной мощности от активной

В цепи, где есть реактивное сопротивление (возьмем для примера индуктивное) значение мгновенной мощности равно:

Соответственно  и  в итоге получим:

Данное выражение показывает, что реактивная энергия содержит только переменную часть, которая изменяется с двойной частотой, а ее среднее значение равно нулю

График q(ωt)

Если ток и напряжение имеют синусоидальную форму и сеть содержит элементы типа R-L или R-C, то в таких сетях кроме преобразования энергии в активном элементе R вдобавок еще и изменяется энергия электрического и магнитного полей в реактивных элементах L и C.

В таком случае полная мощность сети будет равна сумме:

Что такое полная мощность на примере простой R-L цепи

Графики изменения мгновенных значений u,i:

Графики изменения мгновенных значений u,i:

φ — фазовый сдвиг между током и напряжением

Уравнение для S примет следующий вид 

Подставим вместо  и заменим амплитудные значения на действующие:

Значение S рассматривается как сумма двух величин , где

 и  — мгновенные активные и реактивные мощности на участках R-L.

Графики p,q,s:

Как видим из графика, наличие индуктивной составляющей повлекло за собой появление отрицательной части в полной мощности (заштрихованная часть графика), что снижает ее среднее значение. Это происходит из-за фазового сдвига, в какой-то момент времени ток и напряжение находятся в противофазе, поэтому появляется отрицательное значение S.

Итоговые выражения для действующих значений:

Активная составляющая сети выражается в ваттах (Вт), а реактивная в вольт-амперах реактивных (вар).

Полная мощность сети S, обусловлена номинальными данными генератора. Для генератора она обусловлена выражением:

Также энергию сети можно выразить через каждую составляющую отдельно:

Где S, P, Q – соответственно активное, реактивное и полное сопротивление сети. Они образуют треугольник мощностей:

Треугольник мощностей с преобладающей индуктивной нагрузкой

Если вспомнить теорему Пифагора, то из прямоугольного треугольника можно получить такое выражение:

Реактивная составляющая в треугольнике является положительной (QL), когда ток отстает от напряжения, и отрицательной (QC), когда опережает:

Треугольник мощностей с преобладающей емкостной нагрузкой

Для реактивной составляющей сети справедливо алгебраическое выражение:

Из чего следует что индуктивная и емкостная энергия взаимозаменяемы. То есть если вы хотите уменьшить влияние индуктивной части цепи, вам необходимо добавить емкость, и наоборот. Ниже пример данной схемы :

Схема компенсации реактивной составляющей

Векторная диаграмма показывает влияние конденсатора на cosφ. Как видно, что при включении конденсатора cosφ2> cosφ1 и  Iл

Источник: http://elenergi.ru/chto-takoe-aktivnaya-reaktivnaya-i-polnaya-moshhnost.html

Активная, реактивная и полная мощность: формула, измерение, в чём измеряются показатели

Мощность является важным фактором для оценки эффективности работы электрооборудования в сети энергосистемы. Использование её предельных значений может привести к перегрузкам сети, аварийным ситуациям и выходу оборудования из строя. Для того чтобы обезопасить себя от этих негативных последствий, необходимо понимать, что такое активная реактивная и полная мощность.

Мощность, которая фактически потребляется или используется в цепи переменного тока, называется активной, в кВт или МВт. Мощность, которая постоянно меняет направление и движется, как по направлению в цепи, так и реагирует сама на себя, называется реактивной, в киловольт (kVAR) или MVAR.

Очевидно, что мощность потребляется только при сопротивлении. Чистый индуктор и чистый конденсатор её не потребляют.

В чистом резистивном контуре ток находится в фазе с приложенным напряжением, тогда как в чистом индуктивном и ёмкостном контуре ток смещён на 90 градусов: если индуктивная нагрузка подключена в сеть, он теряет напряжение на 90 градусов. При подключении ёмкостной нагрузки происходит смещение тока на 90 градусов в обратную сторону.

В первом случае создаётся активная мощность, а во втором — реактивная.

Силовой треугольник

Полная мощность — это векторная сумма активной и реактивной мощности. Элементы полной мощности:

• Активная, P.
• Реактивная, Q.
• Полная, S.

Реактивная мощность не работает, она представлена как мнимая ось векторной диаграммы. Активная мощность работает и является реальной стороной треугольника.

Из этого принципа разложения мощностей понятно, в чём измеряется активная мощность. Единицей для всех видов мощности является ватт (W), но это обозначение обычно закрепляется за активной составляющей.

Полная мощность условно выражается в ВА .

Единица для Q составляющей выражается как var, что соответствует реактивному вольт-амперу. Она не передаёт никакой чистой энергии нагрузке, тем не менее она выполняет важную функцию в электрических сетях. Математическая связь между ними может быть представлена векторами или выражена с использованием комплексных чисел, S = P + j Q (где j — мнимая единица).

Расчёт энергии и мощности

Средняя мощность P в ваттах (W) равна энергии, потребляемой E в джоулях (J), делённой на период t в секундах (секундах): P (W) = E (J) / Δ t (s).

Когда ток и напряжение находятся на 180 градусов по фазе, PF отрицательный, нагрузка подаёт электроэнергию в источник (примером может служить дом с солнечными батареями на крыше, которые подают питание в энергосистему). Пример:

• P составляет 700 Вт, а фазовый угол составляет 45, 6;
• PF равен cos (45, 6) = 0, 700. Тогда S = 700 Вт / cos (45, 6) = 1000 В⋅А.

Отношение активной к полной мощности называется коэффициентом мощности (PF). Для двух систем, передающих такое же количество активной нагрузки, система с более низким PF будет иметь большие оборотные токи из-за электроэнергии, которая возвращается обратно.

Эти большие токи создают большие потери и снижают общую эффективность передачи. Схема с более низким PF будет иметь большую полную нагрузку и более высокие потери для одинакового количества активной нагрузки. PF = 1, 0, когда есть фазный ток.

Он равен нулю, когда ток приводит или отстаёт от напряжения на 90 градусов.

Например, PF =0,68 и означает, что только 68 процентов от общего объёма поставленного тока фактически выполняют работу, остальные 32 процента являются реактивными. Производители коммунальных услуг не берут с потребителей плату за её реактивные потери.

Однако если в источнике нагрузки клиента есть неэффективность, которая приводит к тому, что PF падает ниже определённого уровня, коммунальные услуги могут взимать плату с клиентов, чтобы покрыть увеличение использования топлива на электростанциях и ухудшение линейных показателей сети.

Характеристики полной S

Формула полной мощности зависит от активной и реактивной мощности и представлена как энергетический треугольник (Теорема Пифагора). S = (Q 2 + P 2) 1 / 2, где:

• S = полная (измерение в киловольт-ампер, кВА);
• Q = реактивная (реактивность на киловольтах, kVAR);
• P = активная (киловатт, кВт).

Она измеряется во вольт-амперах (В⋅А) и зависит от напряжения, умноженного на весь поступающий ток. Это векторная сумма P и Q составляющих, которая подсказывает, как найти полную мощность. Однофазная сеть: V (V) = I (A) x R (Ω).

P (W) = V (V) x I (A) = V 2 (V) / R (Ω) = I 2 (A) x R (Ω).

Трёхфазная сеть:

Напряжение V в вольтах (V) эквивалентно току I в амперах (A), умноженному на импеданс Z в омах (Ω):

V (V) = I (A) x Z (Ω) = (| I | x | Z |) ∠ ( θ I + θ Z ).

S (VA) = V (V) x I (A) = (| V | x | I |) ∠ ( θ V — θ I ).

Активная P

Это мощность, которая используется для работы, её активная часть, измеряемая во Вт и является силой, потребляемой электрическим сопротивлением системы. P (W) = V (V) x I (A) x cos φ

Реактивная Q

Она не используется для работы в сети. Q измеряется в вольт-амперах (VAR). Увеличение этих показателей приводит к уменьшению коэффициента мощности (PF). Q (VAR) = V (V) x I (A) x sin φ.

Коэффициент эффективности сетей

PF определяется размерами P и S, его вычисляют по теореме Пифагора. Рассматривается косинус угла между напряжением и током (несинусоидальный угол), фазовая диаграмма напряжения или тока от энергетического треугольника.

Коэффициент PF равен абсолютному значению косинуса комплексного энергетического фазового угла (φ): PF = | cosφ | Эффективность энергосистемы зависит от коэффициента PF и для повышения эффективности использования в энергосистеме необходимо его увеличивать.

Ёмкостные и индуктивные нагрузки

Сохранённая энергия в электрическом и магнитном полях в условиях нагрузки, например, от двигателя или конденсатора, вызывает смещение между напряжением и током.

Поскольку ток протекает через конденсатор, накапливание заряда вызывает возникновение противоположного напряжения на нём. Это напряжение увеличивается до некоторого максимума, продиктованного структурой конденсатора.

В сети с переменным током на конденсаторе постоянно меняется напряжение. Конденсаторы называются источником реактивных потерь и, таким образом, вызывают ведущий PF.

Индукционные машины являются одними из наиболее распространённых типов нагрузок в электроэнергетической системе. Эти машины используют индукторы или большие катушки проволоки для хранения энергии в виде магнитного поля.

Когда напряжение сначала проходит через катушку, индуктор сильно сопротивляется этому изменению тока и магнитного поля, что создает задержку времени с максимальным значением. Это приводит к тому, что ток отстаёт от напряжения по фазе.

Поскольку эти устройства оказывают противоположное воздействие на фазовый угол между напряжением и током, их можно использовать для отмены эффектов друг друга.

Обычно это принимает форму конденсаторных банков, используемых для противодействия запаздывающим PF, вызванным асинхронными двигателями.

Погашения реактивного влияния в электросетях

Активная реактивная и полная мощность определяет PF главный фактор для оценки эффективности использования электроэнергии в сети энергосистемы.

Если PF высокий, то, можно сказать, что более эффективно электроэнергия используется в энергосистеме. Поскольку PF плох или уменьшается, эффективность использования электроэнергии в энергосистеме снижается.

Низкий PF или снижение его обусловлены различными причинами. Для повышения PF существуют специальные способы коррекции.

Использование конденсаторов является наилучшим и эффективным способом повышения эффективности сети.

Метод, известный как реактивная компенсация, используется для уменьшения кажущегося потока мощности на нагрузку за счёт уменьшения реактивных потерь.

Например, для компенсации индуктивной нагрузки шунтирующий конденсатор устанавливается вблизи самой нагрузки. Это позволяет потреблять конденсатором всю Q и не передавать их по линиям передачи.

Эта практика экономит энергию, потому что она уменьшает количество энергии, которое требуется, для выполнения того же объёма работы. Кроме того, она позволяет использовать более эффективные конструкции линий электропередачи с использованием меньших проводников или меньшего количества проводников с разъёмами и оптимизировать конструкцию трансмиссионных вышек.

Предложенная система делит традиционный метод на управление напряжением и Q:

• управление напряжением для регулировки напряжения вторичной шины подстанций;
• регулирование Q для регулирования напряжения первичной шины.

В этой системе на подстанциях установлены два типа устройств для взаимодействия контроля напряжения и контроля Q.

Управление напряжением и реактивной мощностью

Это два аспекта одного воздействия, которые поддерживают надёжность и облегчают коммерческие транзакции в сетях передачи. На силовой системе переменного тока (AC) напряжение контролируется путём управления производством и поглощением Q. Существует три причины, по которым необходим такой вид управления:

1. Оборудование энергосистемы предназначено для работы в диапазоне напряжений, обычно в пределах ± 5% от номинального напряжения. При низком напряжении оборудование работает плохо, лампочки обеспечивают меньшую освещённость, асинхронные двигатели могут перегреваться и быть повреждёнными, а некоторые электронные устройства не будут работать вообще. Высокие напряжения могут повредить оборудование и сократить срок его службы.
2. Q потребляет ресурсы передачи и генерации. Чтобы максимизировать реальную мощность, которая может быть передана через перегруженный интерфейс передачи, потоки Q должны быть минимизированы. Аналогичным образом производство Q может ограничить реальную мощность генератора.
3. Движущая реактивность в передающей сети несёт реальные потери мощности. Для восполнения этих потерь должны компенсироваться мощность и энергия.

Система передачи является нелинейным потребителем Q в зависимости от загрузки системы.

При очень низкой нагрузке система генерирует Q, которая должна поглощаться, а при большой нагрузке система потребляет большое количество Q, которую необходимо заменить.

Требования к Q системы также зависят от конфигурации генерации и передачи. Следовательно, системные реактивные требования меняются во времени по мере изменения уровней нагрузки и моделей нагрузки и генерации.

Работа системы имеет три цели управления Q и напряжениями:

1. Она должна поддерживать достаточное напряжение во всей системе передачи и распределения как для текущих, так и для непредвиденных условий.
2. Обеспечить минимизацию перегрузки реальных потоков энергии.
3. Стремиться минимизировать реальные потери мощности.

Объёмная энергетическая система состоит из множества единиц оборудования, любая из которых может быть неисправна.

Таким образом, система предназначена для того, чтобы выдерживать выход из строя отдельного оборудования, продолжая работать в интересах потребителей.

Вот почему электрическая система требует реальных резервов мощности для реагирования на непредвиденные обстоятельства и поддержания резервов Q.

Источник: https://220v.guru/fizicheskie-ponyatiya-i-pribory/moschnost/izmerenie-aktivnoy-reaktivnoy-i-polnoy-moschnosti.html

Мощностные характеристики нагрузки можно точно задать одним единственным параметром (активная мощность в Вт) только для случая постоянного тока, так как в цепи постоянного тока существует единственный тип сопротивления – активное сопротивление.

Мощностные характеристики нагрузки для случая переменного тока невозможно точно задать одним единственным параметром, так как в цепи переменного тока существует два разных типа сопротивления – активное и реактивное. Поэтому только два параметра: активная мощность (это полезная мощность, отбираемая нагрузкой, в том числе и ИБП, из электросети и преобразуемая в энергию любого иного вида (механическую, тепловую, электрическую, электромагнитную и др.) и реактивная мощность ( это мощность или поток энергии, циркулирующий через реактивное сопротивление электрической цепи (емкостное или индуктивное).

Рассеяния энергии на реактивных элементах не происходит, так как полученная ими энергия от источника и энергия и возвращенная обратно в сеть в течение периода эквивалентны. Считается, что в большинстве случаев реактивная энергия (мощность), циркулирующая в электрической цепи, является паразитной и приводит к нежелательному разогреву проводников, а также к перегреву и ухудшению режимов работы прочих устройств сети, как генерирующих электричество, так и его потребителей.) точно характеризуют нагрузку.

Принцип действия активного и реактивного сопротивлений совершенно различный. Активное сопротивление – необратимо преобразует электрическую энергию в другие виды энергии (тепловую, световую и т.д.) – примеры: лампа накаливания, электронагреватель (параграф 39, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007). Реактивное сопротивление – попеременно накапливает энергию затем выдаёт её обратно в сеть – примеры: конденсатор, катушка индуктивности (параграф 40,41, Физика 11 класс В.А. Касьянов М.: Дрофа, 2007).

Дальше в любом учебнике по электротехнике Вы можете прочитать, что активная мощность (рассеиваемая на активном сопротивлении) измеряется в ваттах, а реактивная мощность (циркулирующая через реактивное сопротивление) измеряется в варах; так же для характеристики мощности нагрузки используют ещё два параметра: полную мощность и коэффициент мощности.
Все эти 4 параметра:

• Активная мощность: обозначение P, единица измерения: Ватт
• Реактивная мощность: обозначение Q, единица измерения: ВАр (Вольт Ампер реактивный)
• Полная мощность:обозначение S, единица измерения: ВА (Вольт Ампер)
• Коэффициент мощности: обозначение k или cosФ, единица измерения: безразмерная величина

Эти параметры связаны соотношениями:  S*S=P*P+Q*Q,   cosФ=k=P/S
Также cosФ называется коэффициентом мощности (Power Factor – PF)

Поэтому в электротехнике для характеристики мощности задаются любые два из этих параметров так как остальные могут быть найдены из этих двух.

То же самое и с источниками питания. Их мощность (нагрузочная способность) характеризуется одним параметром для источников питания постоянного тока – активная мощность (Вт), и двумя параметрами для ист. питания переменного тока. Обычно этими двумя параметрами являются полная мощность (ВА) и активная (Вт). См. например параметры ДГУ и ИБП.

Большинство офисной и бытовой техники, активные (реактивное сопротивление отсутствует или мало), поэтому их мощность указывается в Ваттах. В этом случае при расчёте нагрузки используется значение мощности ИБП в Ваттах. Если нагрузкой являются компьютеры с блоками питания (БП) без коррекции входного коэффициента мощности (APFC), лазерный принтер, холодильник, кондиционер, электромотор (например погружной насос или мотор в составе станка), люминисцентные балластные лампы и др. – при расчёте используются все вых. данные ибп: кВА, кВт, перегрузочные характеристики и др.

Нагрузочная способность ИБП и ДГУ нормирована на стандартную промышленную нагрузку (коэффициент мощности 0.8 с индуктивным характером). Например, ИБП 100 кВА / 80 кВт. Это означает, что устройство может питать активную нагрузку максимальной мощности 80 кВт, или смешанную (активно-реактивную) нагрузку максимальной мощности 100 кВА с индуктивным коэффициентом мощности 0.8. В стабилизаторах напряжения дело обстоит иначе.

Для стабилизатора напряжения коэффициент мощности нагрузки безразличен. Например, стабилизатор напряжения 100 кВА. Это означает, что устройство может питать активную нагрузку максимальной мощности 100 кВт, или любую другую (чисто активную, чисто реактивную, смешанную) мощностью 100 кВА или 100 кВАр с любым коэффициентом мощности емкостного или индуктивного характера. Обратите внимание, что это справедливо для линейной нагрузки (без высших гармоник тока). При больших гармонических искажениях тока нагрузки (высокий КНИ) выходная мощность стабилизатора снижается.