Как найти полную силу давления

По определению, давление – это сила, приходящаяся на единицу площади поверхности. Если речь идет о давлении некоторой силы на некоторую поверхность – то берут составляющую силы, направленную перпендикулярно поверхности, если говорят о давлении жидкостей и газов – то по закону Паскаля давление в этих средах передается во все стороны одинаково.

Давление измеряется в Паскалях –  [Па], [Па]=[Н/м]. Эта единица измерения является единицей СИ. Также давление (атмосферное) измеряют в мм рт. ст., а большие давления – в атмосферах или барах. Нормальное атмосферное давление – это давление величиной Па, или 760 мм рт.ст.

Галилео Галилей изобрел насос для полива и обнаружил, что столб воды в трубке никогда не поднимается выше 10 м, и не мог объяснить этот факт. Потом Торичелли, ученик Галилео, проводил опыты со ртутью, и ртуть поднималась в запаянной трубке на 760 мм. Торичелли доказал, что воздух имеет вес, и атмосфера, таким образом, давит на поверхность планеты с определенной силой. Это вызвано силой гравитации. Именно давление окружающего воздуха и заставляет ртуть из чашки подниматься вверх по трубке на определенную высоту. Высота этого столба зависит от плотности жидкости: чем она плотнее, тем столбик ниже.  Далее Блез Паскаль доказал, что, чем выше поднимаешься над поверхностью земли, тем меньше  атмосферное давление.

Отто фон Герике,  бургомистр Магдебурга, наглядно доказал существование атмосферного давления, поставив свой опыт с магдебургскими полушариями (под таким названием мы теперь их и знаем). Плотно прижав полушария друг к другу, он откачал воздух изнутри, и даже две восьмерки лошадей не смогли разъединить их.

Задача 1. Выразить давление 1 мм рт. ст. в единицах СИ.

---

Известно, что нормальное давление может быть выражено в мм рт.ст., и тогда оно равно 760 мм  рт.ст., или в Паскалях – единицах СИ, и тогда нормальным считают давление в Па.

Приравняем эти две величины: мм рт.ст Па, откуда мм рт.ст Па.

Задача 2.  Определить давление, которое оказывает шило на брусок, если оно действует с силой 100 Н и площадь его острия равна мм

---

Давление – это сила, приходящаяся на единицу площади: . Сила дана в единицах СИ – ньютонах, а площадь – нет, поэтому выразим площадь в квадратных метрах: в одном метре – 1000 мм, следовательно, в одном квадратном метре – мм, или мм. У нас площадь – всего четыре сотых мм, или из миллиона:

Теперь найдем давление:

Мы определили давление в Па, а давление, равное Па, еще называют одной атмосферой или баром. Тогда ответ этой задачи можно выразить еще в атмосферах (барах): , или 25000 атмосфер.

Задача 3. Цилиндрические сосуды уравновешены на весах. В сосуды наливают одинаковую массу воды. Нарушится ли равновесие весов? Одинаково ли будет давление воды на дно сосудов?

---

Так как весы были уравновешены, то после добавления на обе их чаши одинаковой массы они из равновесия не выйдут. Поскольку из картинки понятно, что сосуды разного диаметра, то понятно, что одна и та же масса воды, имеющая один и тот же объем, при разных диаметрах образует разной высоты слои в этих сосудах. То есть высота столба жидкости будет больше в узком сосуде, чем в широком. Так как давление воды прямо зависит от высоты столба , то в широком сосуде давление воды на дно меньше, чем в узком.

Задача 4. Рассчитать давление воды на самой большой глубине Тихого океана – 11035 м, на наибольшей глубине Азовского моря – 14 м. Принять плотность воды в Азовском море равной 1020 кг/м.  Атмосферное давление считать нормальным.

---

Давление в открытых сосудах (к ним можно отнести и моря с океанами) равно сумме атмосферного давления и давления столба жидкости. Таким образом, давление на самой большой глубине океана равно (с учетом плотности морской воды 1030 кг/м):

Это давление в Па, а в атмосферах – 1137,6 атм.

То есть каждые 10 метров водяного столба создают давление ровно в 1 атмосферу – вот почему в изобретенном Галилеем насосе вода не поднималась выше 10 метров, как он ни старался.

Давление в Азовском море:

Или 2,42 атмосферы.

Ответ: в океане Па, или 1137,6 атм, в Азовском море Па, или 2,42 атмосферы.

Задача 5. Определить высоту уровня воды в водонапорной башне, если манометр,  установленный у ее основания, показывает давление Па. Атмосферное давление считать нормальным.

---

Существенное отличие этой задачи от предыдущей в том, что башня – не открытый сосуд, то есть манометр будет показывать только давление столба жидкости. Отсюда, зная плотность воды, находим высоту столба:

Ответ: 22,4 метра

Задача 6. Желоб, до краев наполненный водой, имеет высоту см, ширину нижнего основания см и верхнего см. Определить силу давления воды на м длины боковой стенки. Атмосферное давление считать нормальным.

---

Так как желоб открыт, то давление будет складываться из атмосферного давления и давления столба жидкости. Причем на верхний край боковой стенки жидкость не давит совсем (глубина равна 0, или, что то же самое – высота столба), а на нижний край жидкость давит как раз полной высотой столба. Поэтому, для того чтобы рассчитать давление, при расчете возьмем среднее давление – то есть давление на половине глубины желоба.

Сила давления , рассчитаем давление и площадь боковой стенки:

см или 0,08 м, тогда

Наконец, определяем силу:

Ответ: 14400 Н

Задача 7. Шар перекрывает отверстие радиусом  в плоской стенке, разделяющей жидкости, давление которых  и . С какой силой жидкость прижимает шар к отверстию?

---

Силу, зная  давление, можно найти как произведение давления на площадь:  .

На шарик будут давить обе жидкости, но, поскольку их давления разные, то и давить они будут по-разному. Первая будет давить с силой , и  сила эта направлена вниз. Вторая будет давить с силой , и эта сила направлена уже вверх. Тогда суммарная сила давления на шарик будет: , направлена вниз.

Ответ: , направлена вниз.

Задача 8. Коническая пробка перекрывает сразу два отверстия в плоском сосуде, заполненном жидкостью с давлением . Радиусы отверстий  и . С какой силой  жидкость действует на пробку?

---

Аналогично предыдущей задаче, жидкость будет давить на пробку во всех направлениях, но давление на боковую поверхность «справа» будет компенсировать давление на боковую поверхность «слева», в результате чего различие будет только в давлении, которое оказывает жидкость на «верх» и «низ» пробки. На верхнее основание пробки – то есть на площадь пробки в отверстии – – жидкость будет давить вверх, пытаясь эту пробку вытолкнуть, с силой . На нижнее основание пробки – то есть на площадь пробки в отверстии – – жидкость будет давить вниз, пытаясь эту пробку втолкнуть поглубже, с силой . Суммарная сила давления жидкости на пробку – разность этих двух сил, и, так как верхнее основание пробки больше нижнего, то в итоге жидкость больше будет давить вверх, чем вниз: , направлена вверх.

Ответ: , направлена вверх.

Задача 8. Плоскодонная баржа получила пробоину в дне площадью см. С какой силой нужно давить на пластырь, которым закрывают отверстие, чтобы сдержать напор воды  на глубине м? Вес пластыря не учитывать.

---

Так как баржа, как и водонапорная башня – сосуд, закрытый сверху, то атмосферное давление не учитываем. Таким образом, вода будет давить  на пробоину с силой, равной произведению давления столба воды на глубине пробоины на площадь пробоины. Давление столба воды на такой глубине равно кПа, а сила, с которой надо будет удерживать пластырь, по  третьему закону Ньютона равна силе давления воды:

Ответ: 360 Н

Давление

Известно, что человеку удобнее ходить по глубокому снегу на лыжах, так как при этом он меньше проваливается под снег. А разрезать предметы удобнее остро отточенным ножом. Причина этого – давление. В первом случае мы стремимся уменьшить давление на снег, а во втором случае, мы стараемся максимально увеличить давление.

Формула давления твердого тела

Рассмотрим твердое тело, например, кирпич. Пусть он лежит на горизонтальной поверхности и давит на нее своим весом (рис. 1).

Рис. 1. Твердое тело опирается на поверхность площадью S и давит на нее своим весом mg

На рисунке символом S обозначена нижнее основание тела – это площадь, на которую тело опирается (давит). Сила, с которой тело давит на поверхность – это сила тяжести mg.

Давление, которое твердое тело оказывает на поверхность, можно рассчитать так:

[ large boxed{ P = frac{F_{perp}}{S} }]

Примечание: Эта формула подходит для расчета давления твердых тел. Существует еще одна формула, с помощью которой рассчитывают давление жидкостей.

​( P left( text{Па}right) )​ – давление;

( F_{perp} left(H right) )  – сила, которая давит (сила давления). Эта сила располагается под прямым углом к поверхности;

( S left( text{м}^{2}right) ) – площадь, на которую давит сила.

Иногда в условии задачи указывают площадь в квадратных сантиметрах, или других единицах, отличающихся от основных единиц, принятых в СИ. Чтобы правильно рассчитать давление, нужно уметь переводить площадь в квадратные метры.

В системе СИ давление измеряется в Паскалях.

[ large 1 text{Па} = frac{1 H}{1 text{м}^{2}} ]

Поэтому, перед решением задач, нужно давление переводить в Паскали, если в условии встретятся другие единицы измерения давления.

В некоторых школьных задачах просят найти не давление, а силу давления. Нужно уметь их различать.

Сила давления, как и любая сила, измеряется в Ньютонах. Именно она давит на поверхность.

А давление — это дробь, в числителе расположена сила, которая давит, а в знаменателе — площадь поверхности, на которую давят. Давление измеряют в Паскалях.

Примечание: Давление – это сила, деленная на площадь. Сила должна располагаться перпендикулярно поверхности (рис. 2а).

Когда сила не перпендикулярна поверхности

Силу раскладываем на проекции, если она направлена к поверхности не под прямым углом (рис. 2б). Выберем часть силы, расположенную перпендикулярно поверхности. Именно эту часть силы и нужно подставлять в формулу для расчета давления.

Рис. 2. Если сила, которая давит на поверхность, направлена не под прямым углом к поверхности, раскладываем силу на проекции и выбираем часть, которая располагается к поверхности перпендикулярно

Оценка статьи:

Загрузка…

Полная сила – давление

Cтраница 3

Если плоская стенка подвергается одностороннему давлению жидкости ( на несмоченной стороне стенки-атмосферное давление), то полная сила давления Р, воспринимаемая стенкой, и нормальная к ней ( фиг.
 [31]

Если плоская стенка подвергается одностороннему давлению жидкости ( на несмоченной стороне стенки – атмосферное давление), то полная сила давления Р, воспринимаемая стенкой, и нормальная к ней ( фиг.
 [32]

Понятно, что в простейших случаях ( см., например, рис. 5.8 а) интенсивность определяется простым делением полной силы давления на длину, площадь или объем участка ее приложения.
 [33]

Ширина трущихся поверхностей кулака назначается соответственно длине валика кулака, размеры которого находятся из расчета на удельное давление и изгиб от полной силы давления пара.
 [34]

Обозначим через р гидростатическое давление в одной какой-либо точке грани abed и будем считать его средним для всей грани. Тогда полная сила давления на эту грань с точностью до бесконечно малых высшего порядка определится выражением dPx pdydz, где dydz – площадь грани.
 [35]

На поверхность тела также действует главный вектор всех сил трения между частицами воздуха и этой поверхностью. Поэтому полная сила давления воздушного потока на тело будет равна геометрической сумме главных векторов динамических сил и сил трения. Если обтекаемая поверхность негладкая и движение потока плавное ( без срыва струи), то будет действовать только составляющая трения.
 [36]

Как следует из предыдущего изложения, полная сила избыточного гидростатического давления Р приложена в центре давления. Вектор полной силы давления Р должен проходить через точку пересечения ее горизонтальной и вертикальной составляющих под углом а. Центр давления для криволинейных поверхностей находится графоаналитическим путем.
 [37]

С такой же силой колечко давит на спираль в горизонтальном направлении. Таким образом, полная сила давления F колечка на спираль слагается из горизонтально.
 [38]

Так как силы давления действуют по нормали к стенке, а ось у параллельна стенке, то составляющая Ry силы R равна нулю. Таким образом, для определения полной силы давления R достаточно найти ее проекции Rx и Rz на оси х и г и сложить полученные составляющие по правилу параллелограмма.
 [39]

Выражение, стоящее в скобках, представляет собой гидростатическое давление в центре тяжести площади стенки. Поэтому последнее уравнение можно формулировать так: полная сила давления жидкости на плоскую стенку равна произведению площади стенки на гидростатическое давление в ее центре тяжести. В практике часто приходится иметь дело с открытыми сосудами, у которых давление на поверхности жидкости и со стороны несмоченной поверхности стенки будут одинаковы.
 [40]

На рис. 37 показана конструкция висячего клапана, предложенная автором. Для уменьшения коэффициента перекрытия в этом клапане резиновой прокладке передается не полная сила давления, а ее ничтожная часть.
 [41]

Если плоская стенка подвергается одностороннему давлению жидкости ( на несмоченной стороне стенки – атмосферное давление), то полная сила давления Р, воспринимаемая стенкой и нормальная к ней ( фиг.
 [42]

Если чайной ложкой привести во вращение воду в стакане, то после прекращения помешивания чаинки и песчинки, имеющиеся в ней, собираются в центре дна. Дело в том, что эти частицы тяжелее воды и опускаются на дно. Здесь их вращение замедляется благодаря силам трения о дно стакана, и под влиянием разности гидростатических давлений частицы перемещаются к центру дна. Вычислим теперь полную силу давления жидкости на дно сосуда.
 [43]

Если мы при определении силы полного гидростатического давления, действующего на плоские фигуры, по существу производим простое сложение параллельных сил, то при решении аналогичной задачи для криволинейных поверхностей приходится производить сложение сил гидростатического давления, имеющих различные направления. Это обстоятельство значительно усложняет задачу, требуя применения специальных расчетных приемов. Принцип, положенный в основу существующих решений, заключается в определении составляющих силы суммарного гидростатического давления по нескольким направлениям, не лежащим в одной плоскости, с последующим геометрическим сложением этих частных сил. Результат сложения дает величину полной силы давления жидкости на криволинейную поверхность как по величине, так и по направлению. Одновременно графическим путем находится и центр давления для криволинейной поверхности. Обычно достаточно брать два направления: вертикальное и горизонтальное.
 [44]

Описанный в § 1 главы IV принцип действия насоса с регулятором обусловливает некоторые особенности э нагружении его приводной части по сравнению с насосом без регулятора. В отличие от этого шток насоса с регулятором в начале хода сжимается силой, равной произведению давления нагнетания на площадь штока. Это объясняется тем, что давление с обеих сторон поршня приблизительно одинаково и равно давлению нагнетания. После посадки поршня регулятора давление во всасывающей полости становится равным давлению во всасывающем трубопроводе и шток сжимается ( нагнетание из бесштоковой полости) или растягивается ( нагнетание из штоковой полости) полной силой давления.
 [45]

Страницы:  

   1

   2

   3

Силу гидростатического давления на
криволинейную поверхность определяют
по формуле

где
—
составляющие силы избыточного давления
по соответствующим координатным осям.
В случае цилиндрической криволинейной
поверхности

где

и
— горизонтальная и вертикальная
составляющие силыР.

Горизонтальная составляющая избыточного
давления Р_х равна
си­ле давления на вертикальную проекцию
криволинейной поверхности

где р_м — манометрическое
давление на поверхности жидкости,

h_ц —
глубина погружения центра тяжести
вертикальной проекции криволинейной
поверхности;

—
площадь вертикальной проекции
криволинейной поверхности. Если
манометрическое давление на свободной
поверхности жид­кости равно нулю
(р_o= р_а), то

В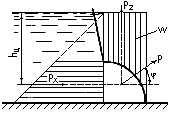ертикальная
составляющая
равна весу жидкости в объеме тела
давления. Тело давления располо­жено
между вертикальными плос­костями,
проходящими через край­ние образующие
цилиндрической по­верхности, самой
цилиндрической поверхностью и свободной
поверх­ностью жидкости или ее
продолже­нием.

Если давление на свободной поверхности
жидкости
,
то тело давления ограничивается сверху
пьезометрической плоскостью, удаленной
от свободной поверхности жидкости на
расстояние

Направление силы Р определяется
тангенсом угла:

Если криволинейная поверхность не
цилиндрическая, то горизон­тальную
составляющую Р_y
определяют аналогично силеР_х.

Примеры

2.28. Определить силу давления воды
на деталь, имеющую форму четверти
кругового цилиндра радиуса =0,5 м. Найти
угол,
под котором эта сила направлена к
горизонту. Расчет вести на единицу
ширины конструкции. Высота конструкции
Н=5 м.

Р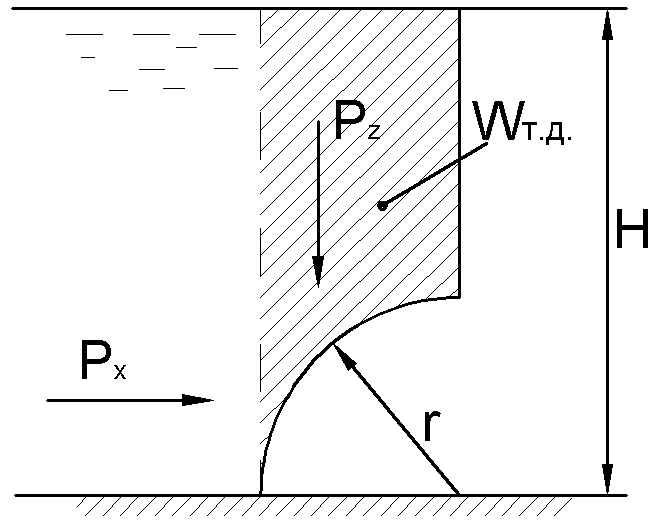ешение:

Найдем горизонтальную составляющую
силы гидростатического давления воды:

Р_x=,

где h_c=H-;
;

=
^Н.

Найдем
вертикальную составляющую:

P_z=.

Для чего
определим объем тела давления:

^Wт.д=м3.

^{Тогда
Pz
=H.}

Результирующая
сила найденных составляющих равна:

^Р
=3,31Н.

Угол между
линией действия этой силы и линией
горизонта равен:

Ответ:P= 3, 31
H;
.

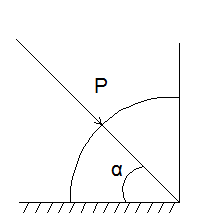
2.29. Определить величину Р и направление
угол α равнодействующей силы давления
на цилиндрический затвор плотины,
перекрывающий прямоугольное отверстиеh=D= 1,0 м и
ширинойb= 5,0 м. Глубина
воды слева -H₁= 3,4 м,
справа -H₂=D/2.

Решение: 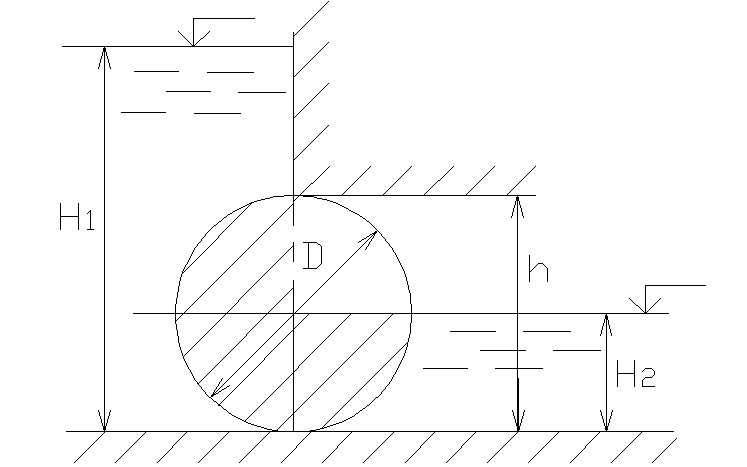Для
нахождения силы гидростатического
давления на цилиндр необходимо
использовать зависимость:

,

^{где
– горизонтальная
составляющая}

полной силы гидростатического
давления воды;

^{– вертикальная
составляющая}полной силы
гидростатического давления воды.

Направление равнодействующей силы
гидростатического давления воды найдем
по формуле:

Горизонтальная составляющая силы
давления воды:

– слева

– справа

Их равнодействующая величина равна
алгебраической сумме:

.

Вертикальная составляющая силы
давления на затвор равна весу воды в
объеме тела давления (на рисунке
заштриховано):

.

Результирующая сила гидростатического
давления на цилиндрический затвор
составит:

.

Направление этой силы, т.е. угол
наклона к горизонту составит:

.

^Ответ:

2.30.Определить силу суммарного
давления на торцовую плоскую стенку
цилиндрической цистерны диаметроми точку её приложения. Высота горловины.
Цистерна заполнена бензином до верха
горловины.

Решение. Сила суммарного давления
бензина на торцовую стенку цистерны
равна

где
–
плотность бензина (табл. П-3).

Точка приложения (центр давления) силы
суммарного давления расположена на
глубине (от верхней кромки горловины)

Ответ:

2.31.Определить силу суммарного
давления на секторный затвор и её
направление. Глубина воды перед затвором
Н=4м, длина затвораL=8м,
угол.

Решение.Горизонтальная составляющая
полной силы давления на секторный затвор
равна силе давления на вертикальную
проекцию затвора:

.

Вертикальную составляющую полной силы
давления на секторный затвор определяем
по формуле:

,

где W- объём тела давленияabcдлинойL;

–
площадь фигурыabc;

Найдем элементы
и площадь фигурыabc:

;

;

;

;

;

;

;

.

Равнодействующую сил давлений определяем
по формуле:

.

Направление этой силы определяется
углом
:

;.

Ответ: ;.

2.32.По стальному трубопроводу
диаметромподаётся вода под давлениемОпределить напряжение в стенке трубы,
если ее толщина.

Решение.Суммарная сила давления,
разрывающая трубу в продольном
направлении, равна гидростатическому
давлению, умноженному на площадь
вертикальной проекции криволинейной
стенки:

Разрыв происходит по двум продольным
сечениям стенки трубы. Напряжение,
возникающее в материале стенки, равно

Ответ: МПа

2.33.Определить силы, разрывающие
горизонтальную, наполненную бензином
цистерну длинойпо сечениями,
если диаметр цистерны,
а высота горловины.
Цистерна заполнена бензином плотностью=740кг/до верха горловины.

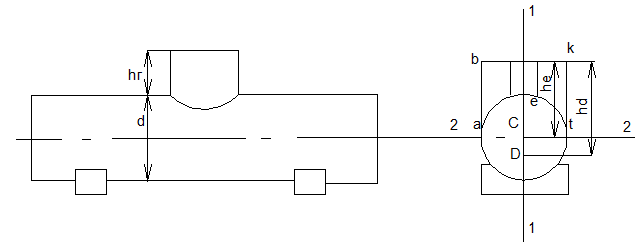
Решение.Сила, разрывающая цистерну
по сечению,
равна горизонтальной составляющей силы
давления воды на криволинейную стенкуили:

.

Силы, растягивающие цистерну по сечению
2-2, равны силам, действующим на криволинейные
стенки aetиaft. Эти силы также направлены противоположно
друг другу. Сила давления на криволинейную
стенкуaet

,

где W– объём телаabkt;

ω – площадь фигуры abktea;

.

Подставляя цифровые значения, находим:

.

Ответ: ;.

2.34. Для выпуска сточных вод в море
построен трубопровод диаметром,
уложенный по дну на глубине.
Определить силы, действующие на
трубопровод, когда он не заполнен.

Решение. Сила, действующая на
трубопровод сверху, определяется как
вертикальная составляющая суммарных
сил давления на криволинейную поверхность.
Она равна весу воды в объёме тела,
т.е. (надлины трубопровода)

где
–
плотность морской воды (табл. П-3).

Сила
,
действующая на трубопровод снизу, больше
силына величину веса воды в рассматриваемом
участке трубопровода, т.е.;
собственный вес трубыдолжен быть равендля того, чтобы исключить возможность
её всплывания.

Силы, действующие на трубопровод по
горизонтали, равны и направлены
противоположно друг другу .Каждая из
этих сил равна горизонтальной составляющей
сил давления воды на криволинейную
стенку, которая, в свою очередь, равна
силе суммарного давления воды на
вертикальную проекцию трубы, т.е. (на
длины трубопровода)

Ответ:
.

2.35.Определить силу гидростатического
давления воды на
ширины нижней криволинейной части
сооружения, если

Решение.

1) Горизонтальная составляющая силы
давления воды на криво­линейную часть
сооружения равна силе давления на
вертикальную проекцию этой поверхности

2) Вертикальная составляющая

равна весу жидкости в объеме тела
давле­ния. Обозначим площадь фигуры
через.
Тогда:

3) Суммарная сила давления воды на
криволинейную часть сооружения

4) Расстояние от свободной поверхности
воды до линии действия горизонталь­ной
составляющей Р_х.

5)
Вертикальная составляющая
проходит через центр тяжести фигуры.
Расстояниецентра тяжести фигурыот линии
равно стати­ческому моменту этой
фигурыотносительно линии,
деленному на площадь фигуры,
причем расстояние центра тяжести
четверти круга
от линии:

;

Сила
проходит через точку пересеченияc
линий действия горизонтальной и
вертикальной составляющих под угломк горизонту, причем

Заметим, что при круговой цилиндрической
поверхности сила
всегда проходит через центр круга.

Ответ:

2.36.Определить величину и направление
силы гидростатического давления воды
на
ширины вальцового затвора диаметром.

Решение.

1) Горизонтальная составляющая

2) Вертикальная составляющая

3) Суммарная сила давления

4) Составляющая Р_х проходит
на расстоянии у_дот свободной
поверхности:

составляющая
проходит на расстоянииот линии,
равном

5) Равнодействующая Р приложена в
точкеО под угломк горизонту и про­ходит через центр
круга, причем

Ответ: ;.

2.37. Определить силу гидростатического
давления воды на 1м ширины вальцового
затвора диаметромприи.

Решение.1) Горизонтальная составляющая
силы давления воды слева

справа

2) Вертикальная составляющая силы
давления воды, равная весу жидкости в
объеме тела давления (на рисунке
заштриховано):

где
– площадь фигуры,
для определения которой рассмотрим
треуголь­ник:

,

3) Суммарная сила давления

4) Угол наклона силы Рк горизонту
определяется по тангенсу угла
:

Ответ:

2.38. Определить силу давления воды
на
ширины затвора, перекрывающего канал
между двумя смежными камерами, если
глубина воды в левой камерев правой

Решение. 1) Горизонтальная составляющая
силы давления воды на затвор слева

справа

откуда

2) Вертикальная составляющая P_z
равна весу жидкости в объеме тела
давления (на рисунке заштриховано):

где d – длина
основания тела давления;

b= 1м– его
ширина. Для определениярассмотрим треугольникиАВОиАВС:

Угол

3) Суммарная сила давления на затвор

Сила Рпроходит через шарнирОпод угломк горизонту, причем

Ответ:

2.39.Цилиндр радиусоми длинойперекры­вает отверстие в дне резервуара
размерамисм.
Определить: силу давления воды на цилиндр
при.

Решение.1) Горизонтальная составляющая
силы давления воды на ци­линдр равна
нулю, так как и на его основания и на
продольные вертикальные проекции
действуют соответственно равные и
противоположно направленные силы.

2) Вертикальная составляющая равна весу
жидкости в объёме тела давления (на
рисунке заштриховано):

Из рисунка видно, что

.

Тогда площади сегментов s₁
иs₂определяются
по формулам

Ответ:

2.40. На горизонтальной плите установлен
стальной сосуд без дна в форме усеченного
конуса с толщиной стенкимм. Определить при каком уровне воды в
сосудеhон оторвется от
плиты, если известныD=2
м,d=0,5 м, Н=2 м.

Решение: Сосуд может оторваться от
плиты в том случае, если вертикальная
сила гидростатического давления воды
на

наклонные (конические) стенки сосуда
превысит силу веса самого сосуда.
Составим уравнение равновесия этих
сил:

G=_т.д.;

Где G=,

т/м³=8,5Н/м³;

S_бок=–
боковая поверхность конуса;

l-длина образующей:

^l=м,

тогда S_бок=м².

^{Вес сосуда равен
G=8,4Н.}

Тело давления –это заштрихованная
фигура, которая создает вертикальную
отрывающую силу F_z.

Запишем объем тела давления:

^Wт.д.=,
()

где r₁–является
неизвестной величиной. Выразим ее через
глубину воды в сосудеh.

Для этого cоставим
пропорцию для подобных треугольников
АВС и АМN:

АМ=х.

^{Тогда,
откуда х =}.

^{Тогда d1=2r1=D–}.

Теперь выразим радиус r₁:

^r1=.

Подставим значение r₁в уравнение ():

^Wт.д.=,

Раскрываем скобки, приведем подобные
элементы, получим:

=1,04h-0,4h²-0,15h³.

^{Учитывая, что}м³,

Окончательно получаем:

0,15h³-0,4h²+1,04h-0,5=0

Способом подстановок “h”
в это уравнение найдем значение:

h=0,58 м.

^{Проверка: 0,15};

0,6333-0,6350.

Ответ: h=0,58 м.

2.41. Определить силу натяжения троса,
удерживающего криволинейный затвор,
представляющий собой четверть кругового
цилиндра радиусаR=1 м,
перекрывающего канал прямоугольного
сечения ширинойb=3 м.
Глубина наполнения канала водойH=2
м.

Решение:Для определения силы
натяжения троса составим

уравнение моментов всех сил, действующих
на затвор, относительно

точки О:

;

ТR=P_zl_p+P_xl_b.

Для чего найдем составляющие Р_хи Р_z

силы гидростатического давления на
криволинейный

(цилиндрический) затвор:

Р_x==10⁴=
=H.

Точка приложения этой составляющей
находится на расстоянии l_bот оси шарнира 0:

L_b=l_д-(H-R),

L_д=l_c+;

l_b=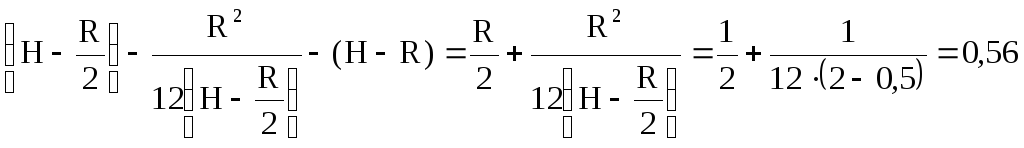м.

Составляющая P_zнаходится через объем тела давленияW_т.д.:

P_z=,

где W_т.д.=.

Тогда P_z=H.

Линия действия этой вертикальной
составляющей проходит через центр
тяжести фигуры 1-0-2-3-4. Расстояние l_р
центра тяжести фигуры 1-0-2-3-4 от линии
0-2 равно статическому моменту этой
фигурыSотносительно
линии 1-0-2, поделенному на площадь фигурыF(причем расстояние центра
тяжести четверти круга 1-0-4 от линии
1-0-2 равно е=0,4244R).

^м.

Тогда Т= H.

^{Ответ: Т=4,52Н.}

2.42. Найти величину и направление
силы гидростатического давления воды
на 1м ширины криволинейного затвора,
если известны

Решение:Результирующая
сила гидростатического давления равна.
Найдём составляющие этой силыи:

Найдём параметры затвора:

Тогда горизонтальная составляющая
равна :

Найдём вертикальную составляющую,
для чего вычислим объём тела давления:,

;;;.

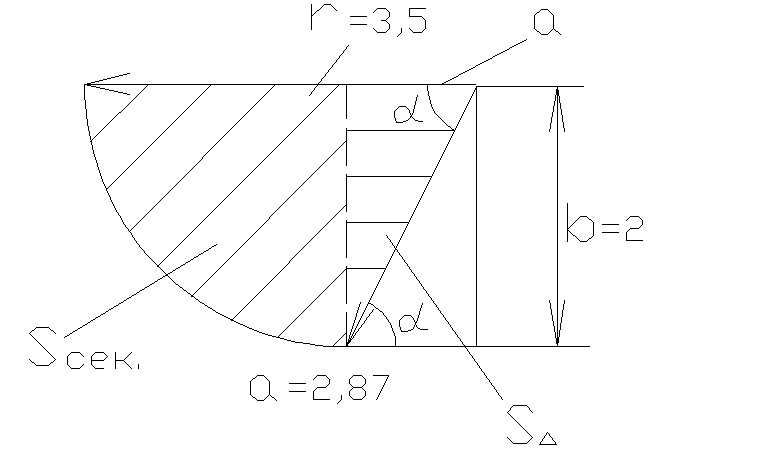
Найдём площадь треугольника:

S_∆.

Площадь сектора составит:

.

Площадь тела давления:

.

Тогда объём тела давления составит:

.

.

Полная сила гидростатического давления
на затвор составит:

,

а направление этой силы определяется
углом φ:

.

Ответ:
,.

2.43. Определить горизонтальнуюи вертикальнуюсоставляющие силы давления воды на
горизонтальный цилиндр диаметромd= 30 см, который вставлен чepeз
отверстие в наклонной стенке (α = 30º)
внутрь резервуара на расстоянииl= 0,8 м. Уровень воды над осью цилиндра Н
= 1,0 м.

Pешение:

Горизонтальная составляющая силы
давления на цилиндр определяется
так:

где–
заглубление центра тяжести

вертикальной проекции криволи-

нейной поверхности , т.е.

,

–
площадь вертикальной проекции цилиндра:

.

Тогда:

Вертикальная составляющая силы давления
воды на цилиндр равна:

гдеW– объём тела давления,
который найдём из геометрии.

Рассмотрим ∆ АВС и ∆ МСD.
Они равны,

так как АС = СМ =
;
ВС =CD=;

Поэтому объёмы будут равны:

Тогда объём тела давления определяется
так:

.

Либо объём тела давления найдём так.

Из ∆ АВС:

из ∆ МСD:

Тогда:

Найдём:

.

Окончательно:

Ответ:

2.44. В прямоугольном окне вертикальной
стенке установлен цилиндрический затвор
(270º) диаметромD= 100 см и
длинойb= 2,0 м. Определить
усилие Р на цапфы и момент М от воздействия
жидкости на затвор. Весом затвора
пренебречь. Напор над осью крепления Н
= 1,0 м.

Решение:

Так как затвор выполнен в виде цилиндра,

то для нахождения усилия на цапфы
используем

расчетные формулы для определения сил

гидростатического давления на
криволинейную поверхность:

где Р_х– горизонтальная составляющая
силы гидростатического давления,
определяется по формуле:

,

где h_C– заглубление центра тяжести вертикальной
проекции криволинейной поверхности
под уровень свободной поверхности (в
данном случае);

−
площадь вертикальной проекции
криволинейной поверхности:

.

Тогда

,

где

− удельный вес воды приt= 20ºС [1, табл. 1 Приложения].

P_Z–
вертикальная составляющая силы
гидростатического давления, которая
равна весу жидкости в объеме тела
давления ( тело давления показано на
расчетной схеме):

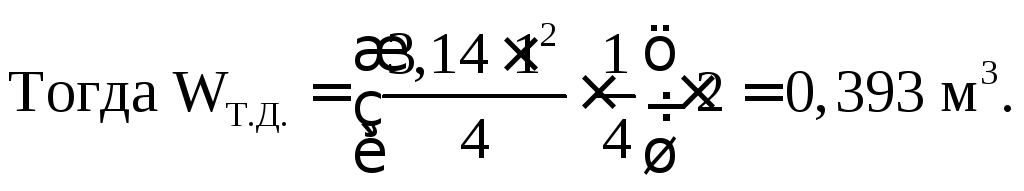
Полная сила гидростатического давления,

действующая на цапфы, расположенные
на

горизонтальной оси цилиндра, равна:

.

Направление этой силы определяется
тангенсом угла α:

.

Линия действия (приложения) силы Р
проходит через центр цилиндра (через
цапфы).

Найдем теперь момент от воздействия
жидкости на затвор – М.

Этот момент в общем случае состоит
из
– момента от горизонтальной
составляющей силы
;
–
момента от вертикальной составляющей
силы.

Момент от горизонтальной составляющей,
в свою очередь, состоит из двух моментов:
– от горизонтальной составляющей,
действующей на верхнюю (криволинейную
поверх- ность)

– от горизонтальной
составляющей, действующей на нижнюю
часть цилиндра.

Однако эти две горизонтальные
составляющие можно привести к одной со
своим плечом действия:

где

– момент инерции проекции,

Тогда

.

Таким образом, момент от горизонтальной
составляющей будет:

(вращает против часовой стрелки).

Момент от вертикальной составляющей
будет определяться силой
и плечом.

Сила
будет
равна выталкивающей силе (архимедовой)
численно равной весу жидкости (воды) в
объеме, вытесненной 1/4 объема цилиндра:

.

Составляющая
проходит на расстоянииот линииab(см. расчетную
схему).

Тогда момент от
равен:

(вращает по часовой стрелки).

Суммарный момент от воздействия жидкости
на затвор составит:

(вращает против часовой стрелки).

Ответ:
.

2.45. В шарообразном углублении радиусаналита вода весом.
В воду погружен шарик радиусом.
Каким должен быть вес шарика,
чтобы он плавал в положении, концентричном
углублению?

Решение:

Составим равенство объемов:

,

где
– объем воды в углублении;

– объем погруженной части

шарика в воду;

– суммарный объем воды и погруженной
части шарика.

Тогда
или.

Из рисунка следует, что
или.

Обозначим
.
Тогда уравнение примет вид:

или

,
где.

Тогда
.

Вычислим значения:

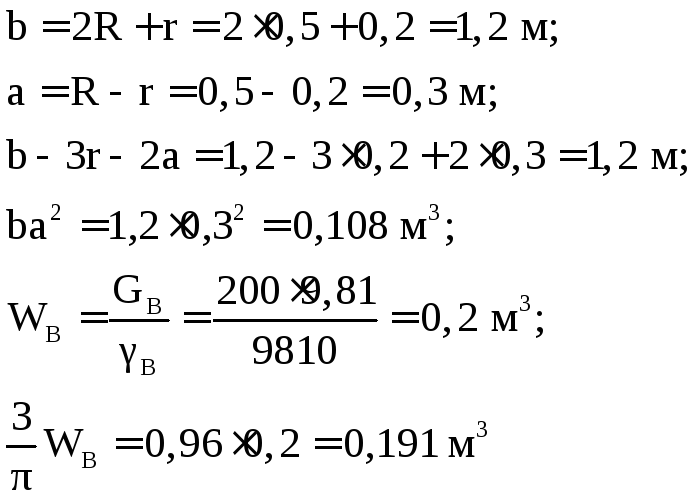
подставим в предыдущее уравнение
и запишем его относительно h:

Решение этого квадратного уравнения
будет h= 0,109 м.

Так как
,
то вес шарикаили

.

Ответ:

2.46.
Определить величину и направление
равнодействующей силы давления воды
на цилиндрический затвор плотины,
перекрывающий донное отверстие высотойh=D=1,2 м.
и ширинойb= 6 м. Глубина
воды слева Н₁= 3,8 м, справа Н₂=D/2.

Решение:Равнодействующая сила
давления воды на цилиндрический затвор
определяется так:

,

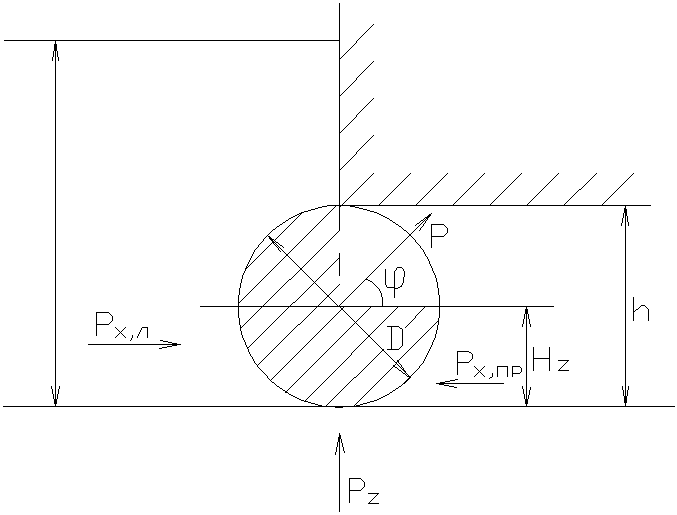
где P_Xгоризонтальная составляющая силы
давления воды;

P_Z–
вертикальная составляющая силы давления
воды.

Найдем горизонтальную составляющую P_X. Она складывается из силы давления
воды, действующей слеваP_Xли справаP_Xпр:

P_Xл= р_С.лω_{z л}
= γ(Н₁ +)Db.

Аналогично:

P_Xпр= р_с.пр ω_z
пр = γb.

Тогда равнодействующая горизонтальных
сил составит:

P_X
=P_Xл-P_Xпр
= γ(Н₁ +)Db– γb= γb[(H₁ −)D−];

P_X
= 998 ∙ 9,81 ∙ 6 ∙ [(3,8 −)
∙ 1,2 −]
= 215 кН.

Найдем вертикальную составляющую P_Z.
Она равна весу жидкости в объеме тела
давления ( на рисунке заштриховано):

P_Z
= γW= γb=γb(3/16)πD²;

P_Z
= 998 ∙ 9,81 ∙ 6 ∙ (3/16) ∙ 3,14 ∙ 1,2²=
49,8 кН.

Суммарная сила давления:

.

Угол наклона силы Pк
горизонту:

γ=arctg=arctg
=13º5′.

Ответ: P= 220,7 кН ; γ =
13º5′.

2.47. Стальной шарик радиусомR= 7 см закрывает отверстие диаметромD= 10 см в плоской стенке, удерживаясь
силой гидростатического давления.
Определить, при каком напоре водыhшарик оторвется от отверстия.

Решение:

Н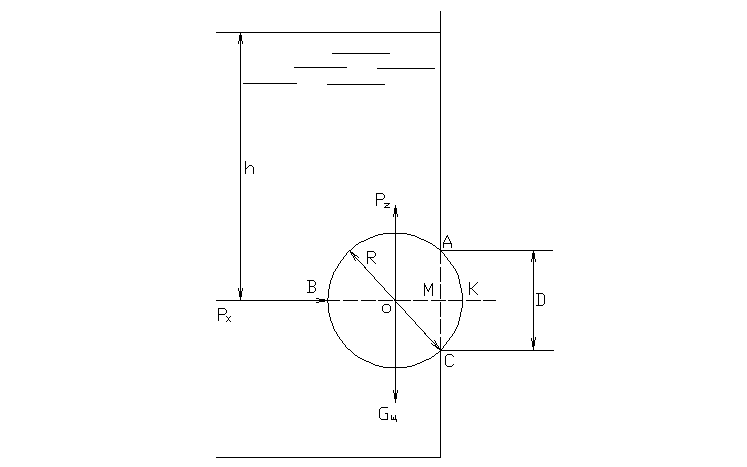айдём
вес шарика:Вертикальная составляющая силы
гидростатического давления воды на
шарик:

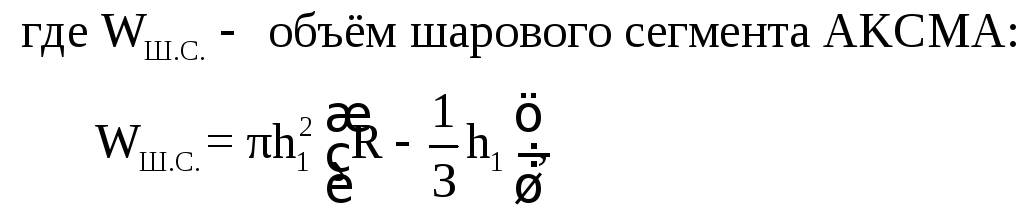
Вес шарика в воде будет на величину
меньше,
т.е.

Для сохранения равновесия необходимо
составить уравнение моментов сил
относительно точки C:

,

Тогда

откуда найдём

Ответ:

2.48. Определить величину и направление
действия силы на сегментный затвор
ширинойb3,0м,
радиусомR2,0м,
если известны углы,,.

Решение:

Сила давления жидкости на сегментный
затвор равна:

,

а её направление определяется углом
:

,

где
;

,

где
– объём тела давления, равный величине

Найдём эти величины из геометрии:

;;

;

;

;

=;

;;

;

;

;

,;

;

;

Тогда объём тела давления равняется

.

Найдём составляющие полной силы
гидростатического давления. Горизонтальная,
действующая слева, горизонтальная,
действующая справа

H;

H.

Их сумма равна H.

Вертикальна составляющаяH.

Полная сила гидростатического давления
на затвор составит

H=54,6кН.

tgоткуда.

Ответ:Р=54,6кН;.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #