Как найти полный дифференциал функции arcsin - Сайт, где вы сможете решить свои вопросы

Алекс Кравченко

Ученик

(162),
на голосовании

9 лет назад

Голосование за лучший ответ

Михаил Ужов

Эксперт пока не указал должность

9 лет назад

dz=(∂z/∂x)dx+(∂z/∂y)dy=(-1/(x²√(1-(y/x)²))dx+(1/(x√(1-(y/x)²))dy==(1/√(x²-y²))(-dx/x+dy).

Похожие вопросы

Источник

Сообщения без ответов | Активные темы | Избранное

	Полный дифференциал от арксинуса частного 22.11.2019, 22:34
29/08/19 38	Необходимо найти полный дифференциал от функции: $w=arcsinfrac{x}{y}$ . У меня получилось: $dw=frac{ydx-xdy}{ysqrt{y^2-x^2}}$ , а правильный ответ согласно учебнику: $dw=frac{ydx-xdy}{leftlvert yrightrvertsqrt{y^2-x^2}}$ . Не могу понять, как получается модуль в знаменателе.

Eule_A

Re: Полный дифференциал от арксинуса частного

22.11.2019, 22:41

Модератор

30/09/17
1237

У меня получилось:

А Вы промежуточных шагов не пропускайте. Аккуратно напишите производную арксинуса для начала. Можно здесь, можно для себя.

Gecko	Re: Полный дифференциал от арксинуса частного 22.11.2019, 23:01
29/08/19 38	$dw=frac{dx}{ysqrt{1-(frac{x}{y})^2}}-frac{xdy}{y^2sqrt{1-(frac{x}{y})^2}}=frac{ydx-xdy}{y^2sqrt{frac{y^2-x^2}{y^2}}}=frac{ydx-xdy}{ysqrt{y^2-x^2}}$

Eule_A

Re: Полный дифференциал от арксинуса частного

22.11.2019, 23:03

Модератор

30/09/17
1237

Gecko

Последний переход нужно ещё раз осмыслить.

Gecko	Re: Полный дифференциал от арксинуса частного 22.11.2019, 23:07
29/08/19 38	Конечно! Детская ошибка . Спасибо!

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Источник

Дифференциал функции

dy=f′(x)dx

Как видим, для нахождения дифференциала нужно умножить производную на dx. Это позволяет из таблицы формул для производных сразу записать соответствующую таблицу для дифференциалов.

Полный дифференциал для функции двух переменных: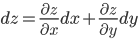

Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=d_xf(x,y,z)dx+d_yf(x,y,z)dy+d_zf(x,y,z)dz

Решение онлайн
Видеоинструкция
Также решают

Примеры

≡ x^2/(x+2)

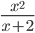
cos²(2x+π) ≡ (cos(2*x+pi))^2

≡ x+(x-1)^(2/3)

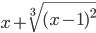
см. также Вычисление приближенно с помощью дифференциала

Определение. Функция y=f(x) называется дифференцируемой в точке x₀, если ее приращение в этой точке можно представить в виде ∆y=A∆x + α(∆x)∆x, где A – константа, а α(∆x) – бесконечно малая при ∆x → 0.

Требование дифференцируемости функции в точке эквивалентно существованию производной в этой точке, причем A=f’(x₀).

Пусть f(x) дифференцируема в точке x₀ и f ‘(x₀)≠0, тогда ∆y=f’(x₀)∆x + α∆x, где α= α(∆x) →0 при ∆x→0. Величина ∆y и каждое слагаемое правой части являются бесконечно малыми величинами при ∆x→0. Сравним их: 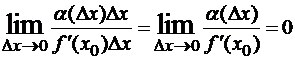, то есть α(∆x)∆x – бесконечно малая более высокого порядка, чем f’(x₀)∆x.

то есть ∆y~f’(x₀)∆x. Следовательно, f’(x₀)∆x представляет собой главную и вместе с тем линейную относительно ∆x часть приращения ∆y (линейная – значит содержащая ∆x в первой степени). Это слагаемое называют дифференциалом функции y=f(x) в точке x₀ и обозначают dy(x₀) или df(x₀). Итак, для произвольных значений x

dy=f′(x)∆x. (1)

Полагают dx=∆x, тогда

dy=f′(x)dx. (2)

Пример. Найти производные и дифференциалы данных функций.

а) y=4^tg2^x

Решение:

дифференциал:

б)

Решение:

дифференциал:

в) y=arcsin²(lnx)

Решение:

дифференциал:

г)

Решение:

=

дифференциал:

Пример. Для функции y=x³ найти выражение для ∆y и dy при некоторых значениях x и ∆x.

Решение. ∆y = (x+∆x)³ – x³ = x³ + 3x²∆x +3x∆x² + ∆x³ – x³ = 3x²∆x+3x∆x²+∆x³; dy=3x²∆x (взяли главную линейную относительно ∆x часть ∆y). В данном случае α(∆x)∆x = 3x∆x² + ∆x³.