Задана функция двух переменных z=x*arctg y . Найти полные дифференциалы функции первого и второго порядка в произвольной точке.
Полный дифференциал первого порядка функции определяется формулой [math]partial z = frac{{partial z}}{{partial x}}dx + frac{{partial z}}{{partial y}}dy[/math]. Найдём частные производные заданной функции:
[math]frac{{partial z}}{{partial x}} = {(x cdot arctg,y)’_x} = arctg,y[/math]
[math]frac{{partial z}}{{partial y}} = {(x cdot arctg,y)’_y} = frac{x}{{1 + {y^2}}}[/math]
Тогда полный дифференциал первого порядка заданной функции имеет вид:
[math]dz(x;y) = arctg,y,dx + frac{x}{{1 + {y^2}}}dy[/math]
Найдём частные производные второго порядка заданной функции:
[math]frac{{{partial ^2}z}}{{partial {x^2}}} = {(arctg,y)’_x} = 0[/math]
[math]frac{{{partial ^2}z}}{{partial {y^2}}} = {left( {frac{x}{{1 + {y^2}}}} right)^prime }_y = x cdot left( { – 2frac{y}{{{{(1 + {y^2})}^2}}}} right) = frac{{ – 2xy}}{{{{(1 + {y^2})}^2}}}[/math]
[math]frac{{{partial ^2}z}}{{partial xpartial y}} = {(arctg,y)’_y} = frac{1}{{1 + {y^2}}}[/math]
Полный дифференциал второго порядка заданной функции:
[math]{d^2}z(x;y) = 2left( {frac{1}{{1 + {y^2}}}} right)dxdy – left( {frac{{2xy}}{{{{(1 + {y^2})}^2}}}} right)d{y^2}[/math]
Подскажите пожалуйста, правильно ли решение. Спасибо…
Дифференциал функции
dy=f′(x)dx
Как видим, для нахождения дифференциала нужно умножить производную на dx. Это позволяет из таблицы формул для производных сразу записать соответствующую таблицу для дифференциалов.
Полный дифференциал для функции двух переменных: 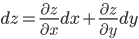
Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=dxf(x,y,z)dx+dyf(x,y,z)dy+dzf(x,y,z)dz
- Решение онлайн
- Видеоинструкция
- Также решают
Примеры
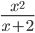 ≡ x^2/(x+2)
≡ x^2/(x+2)
cos2(2x+π) ≡ (cos(2*x+pi))^2
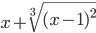 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)
см. также Вычисление приближенно с помощью дифференциала
Определение. Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение в этой точке можно представить в виде ∆y=A∆x + α(∆x)∆x, где A – константа, а α(∆x) – бесконечно малая при ∆x → 0.
Требование дифференцируемости функции в точке эквивалентно существованию производной в этой точке, причем A=f’(x0).
Пусть f(x) дифференцируема в точке x0 и f ‘(x0)≠0, тогда ∆y=f’(x0)∆x + α∆x, где α= α(∆x) →0 при ∆x→0. Величина ∆y и каждое слагаемое правой части являются бесконечно малыми величинами при ∆x→0. Сравним их: 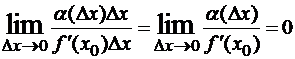 , то есть α(∆x)∆x – бесконечно малая более высокого порядка, чем f’(x0)∆x.
, то есть α(∆x)∆x – бесконечно малая более высокого порядка, чем f’(x0)∆x.
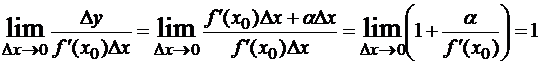
то есть ∆y~f’(x0)∆x. Следовательно, f’(x0)∆x представляет собой главную и вместе с тем линейную относительно ∆x часть приращения ∆y (линейная – значит содержащая ∆x в первой степени). Это слагаемое называют дифференциалом функции y=f(x) в точке x0 и обозначают dy(x0) или df(x0). Итак, для произвольных значений x
dy=f′(x)∆x. (1)
Полагают dx=∆x, тогда
dy=f′(x)dx. (2)
Пример. Найти производные и дифференциалы данных функций.
а) y=4tg2x
Решение:

дифференциал: 
б) 
Решение:

дифференциал: 
в) y=arcsin2(lnx)
Решение:

дифференциал: 
г) 
Решение:
 =
= 
дифференциал: 
Пример. Для функции y=x3 найти выражение для ∆y и dy при некоторых значениях x и ∆x.
Решение. ∆y = (x+∆x)3 – x3 = x3 + 3x2∆x +3x∆x2 + ∆x3 – x3 = 3x2∆x+3x∆x2+∆x3; dy=3x2∆x (взяли главную линейную относительно ∆x часть ∆y). В данном случае α(∆x)∆x = 3x∆x2 + ∆x3.
Дифференциалом
(первого порядка) функции
называется главная часть ее приращения,
линейная относительно приращения
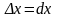
независимой переменной x.
Дифференциал функции равен произведению
ее производной
на
дифференциал независимой переменной
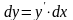
.
Отсюда
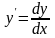
.
Если приращение
аргумента мало по абсолютной величине,
то дифференциал
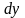
функции
и приращение
функции приближенно равны между собой
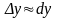
,
ибо по определению
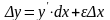
или
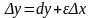
,
где
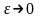
при
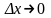
.
Иными словами, разность между приращением
и
дифференциалом
функции
есть бесконечно малая высшего порядка.
Поэтому при
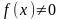
,
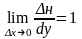
,
т.е. приращение функции и ее дифференциал
– эквивалентные бесконечно малые.
Следовательно,
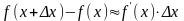
,
откуда имеем
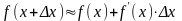
.
Последняя формула часто используется
в приближенных вычислениях, т.к. позволяет
по известному значению функции и ее
производной в точке x
найти приближенно значение функции в
точке
.
Пример
1 . Вычислить
приближенно arctg1,02,
заменяя приращение функции дифференциалом.
Решение.
Формула
применительно к данной функции f(x)=arctg
x
перепишем в виде:
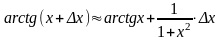
,
где
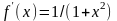
.
У нас
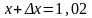
;x=1;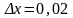
.
Подставляя эти значения, получим
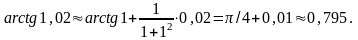
Пример2.
Найти
дифференциал dy.
y=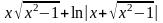
Решение. Имеем
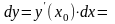
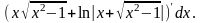
Находим
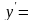
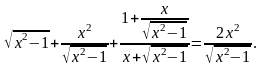
Следовательно,
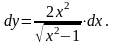
Ответ:
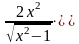
Логарифмическая производная
Логарифмической
производной
функции
называется производная от логарифма
этой функции, т.е.
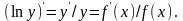
Применение
предварительного логарифмирования по
основанию e
функции иногда упрощает процесс
нахождения ее производной. Сначала надо
прологарифмировать данную функцию:
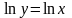
,
затем взять производные от обеих частей
равенства:
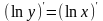
и
найти
из полученного уравнения. Пусть
требуется найти производную от
степенно-показательной функции
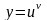
,
где
и
–
функции аргумента x
. Логарифмируя обе части исходного
равенства, получим
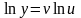
(по
свойству логарифма:
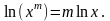
).
Дифференцируя последнее равенство по
х,
имеем
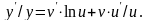
Умножая
обе части равенства на y
и заменяя затем y
через uv,
окончательно получаем
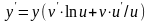
,
или после очевидных преобразований:

Пример
3. Найти
.
если
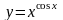
.
Решение.
Логарифмируя,
получим:
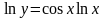
.
Дифференцируем обе части получим
равенства по х:
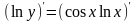
,
или
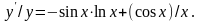
Отсюда
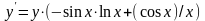
или

.
Замечание.
Во многих
случаях оказывается выгодным, прежде
чем дифференцировать заданную функцию,
взять ее логарифм, определить затем
производную от этого логарифма и по
производной от логарифма отыскать
производную от заданной функции. Это
так называемый прием логарифмического
дифференцирования. К
этому приему удобно прибегать при
дифференцировании: а) Произведения
нескольких функций; б) дроби, числитель
и знаменатель которой содержат
произведения; в) выражений, содержащих
корни из дробей. К нему прибегают всегда
при дифференцировании функции вида
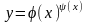
,
т.е. когда и основание степени, и показатель
степени есть функции от x
.
Дифференцирование
функций, заданных
параметрически
Пусть
функция y
аргумента x
задана при помощи параметрических
уравнений:
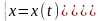
,
где t
параметр, причем каждому значению
соответствует только по одному значению
x
и y
. В механике эти уравнения называются
уравнениями движения точки, т.е. линия
которую описывает на плоскости движущаяся
точка. Например, функция, заданная
параметрически:
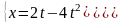
.
Представляет собой на плоскости прямую,
ибо исключив параметр t
из этих уравнений, получим y=x/2
. Однако, практически исключение параметра
t
из уравнений часто задача трудная,
порой просто неразрешимая. Если функций
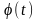
и
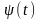
–
дифференцируемые и
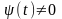
, то производная функции, заданной
параметрически, вычисляется по формуле:
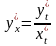
.
Или в других обозначениях
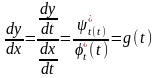
.
Вторую
производную от y
по x
находим, дифференцируяпоследнее
соотношение
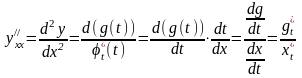
Найти
производную
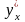
от функции, заданной параметрически.
Пример
4 .
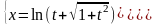
Решение.
Находим
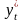
и

и полученные выражения подставляем в
формулу:
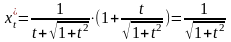
,
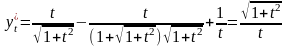
.
Получаем
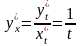
Ответ:
1/t.
Пример
5 .
Составить
уравнение касательной и нормали к кривой
в точке при t=0,
если

Решение.
Последовательно
находим: x0=2e0=2;
y0=e-0=1,

,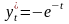
,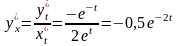
,
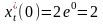
,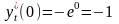
,
,M0(2,1).
Как
известно, если кривая задана в явном
виде y=f(x),
то уравнения касательной и нормали в
точке M0(x0,y0).
имеют соответственно вид:
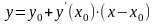
,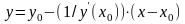
.
где
y0=f(x0),
(y0)
/=(f(x0))
/.
Поэтому, напишем уравнения касательной
и нормали к исходной кривой в точке
касания M0(2,1)
при t=0
соответственно: y=1-0,5(x-2)
, или y=-0,5x+2,
или x+2y-4=0
– уравнения касательной; y=1+(1/0,5)(x-2),
или
y=2x-3,
или 2x–y-3=0
– уравнения нормали.
Производные
высших порядков. Формула Лейбница
Производной второго
порядка функции y=f(x)
называется производная от ее производной

или
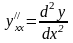
.
Механический
смысл второй производной:
если
истолковывается как скорость
некоторого
процесса, то
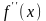
характеризует ускорение того же самого
процесса.
Аналогично
определяются производные третьего,
четвертого и других порядков:

=
,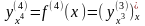
=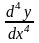
,…
Вообще,
производной n-го
порядка,
или n-ой
производной от функции называется
производная от ее (n-1)-го
порядка.
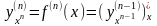
=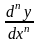
.
На практике, иногда удается найти закон,
для n-ой
производной. При
нахождении производной n-го
порядка от произведения двух функций
u(x)
и v(x)
можно применять формулу Лейбница:
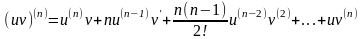
.где
биноминальные коэффициенты

,
,
причем
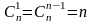
;
и т.д.
Пример
6.
Найти

для функции y=x6e3x.
Решение.
Применяем
формулу Лейбница, полагая u=x6,
v=e3x,
для случая n=5:
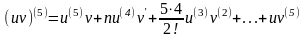
Находим
пять производных от каждого из
сомножителей :
u
/=6x5,
u //=30x4,
u (3)=120x3,
u(4)=360x2,
u(5)=720x,
v
/=3e3x,
v //=9e3x,
v (3)=33e3x,
v (4)=34e3x
v (5)=35e3x..
Подставляя
эти производные в формулу Лейбница,
получаем

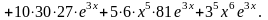
Правило
Лопиталя
При
раскрытие неопределенностей вида
и
можно
применять
правило Лопиталя. Используя теоремы о
дифференцируемых функциях (теорему
Коши) можно пределы вычислять так:
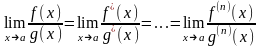
,
производные вычисляются до тех пор,
пока не исчезнет неопределенность.
Пример
1. Найти
предел
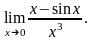
Решение.
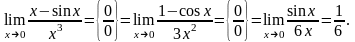
Пример
2.
Найти предел
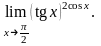
Решение.
Это –
неопределенность вида

.
Положим
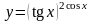
и прологарифмируем:
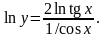

Таким
образом
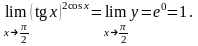
Замечание.
Теоремы о дифференцируемых функциях
Ролля, Лагранжа, Коши студентам надо
разобрать самостоятнльно.
Возрастание
и убывание, локальный
экстремум функции
Функция
называется возрастающей
на некотором интервале (рис.16.1), если
для любых значений
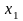
и
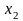
из этого интервала из неравенства
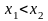
следует неравенство
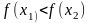
.
Если же из неравенства
следует нестрогое неравенство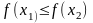
,
то функция называется неубывающей
на этом
интервале.
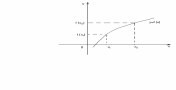
Рис.
16.1
Функция
называется убывающей
(рис.16.2) на
некотором интервале, если для любых х1
и х2
из этого
интервала и неравенства
следует неравенство
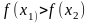
.
Если же из неравенства
следует нестрогое неравенство

,
то функция называется невозрастающей
на этом интервале.
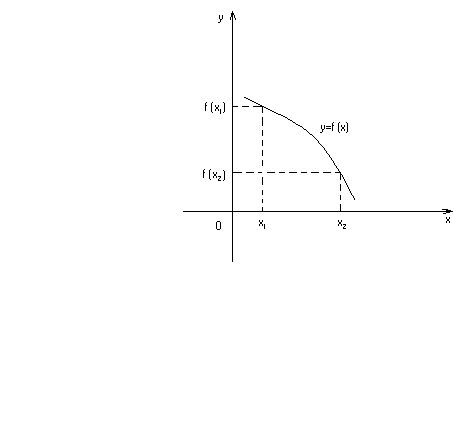
Рис.
16.2
Все
выше названные функции называются
монотонными.
Достаточное
условие возрастания (убывания) функции:
Если
функция
непрерывна на отрезке [a,b]
и ее производная
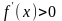
(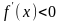
)
при

,
то функция
возрастает
(убывает)
на этом отрезке [a,b].
Говорят, что функция
имеет в точке
х1
максимум
(рис.16.3),
если значение функции
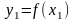
в этой точке больше всех других ее
значений во всех точках х,
достаточно
близких к
точке х1
и отличных
от нее, т.е.
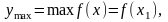
если
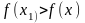
для всякой точки

из некоторой окрестности точки х1.
Говорят, что функция
имеет в точке
х2
минимум
(рис.16.3),
если значение функции
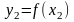
в этой точке меньше всех других ее
значений во всех точках х,
достаточно
близких к
точке х1
и отличных
от нее, т.е.
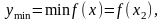
если
для всякой точки
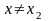
из некоторой окрестности точки x2.
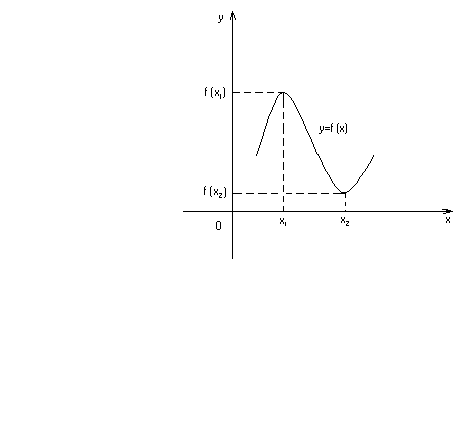
Рис.
16.3
Максимум
или минимум функции называется экстремумом
функции.
Точки в которых достигается экстремум,
называются точками
экстремума
(максимума
или минимума).
Необходимое
условие существования экстремума:
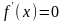
или
не существует
для
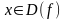
, т.е.
функция
может иметь экстремум только в тех
точках области определения, где
выполняются эти условия. Такие точки
называются
критическими
точками
1-го рода,
т.е. точки, только подозрительные на
экстремум.
Достаточные
условия
существования и отсутствия экстремума
непрерывной функции
:
Первое
правило.
Если
производная
меняет знак при переходе через критическую
точку x0
, то точка x0
является
точкой экстремума, причем:
а)
Функция имеет максимум
в точке
x0
,если для
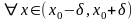
,
где
, имеет место
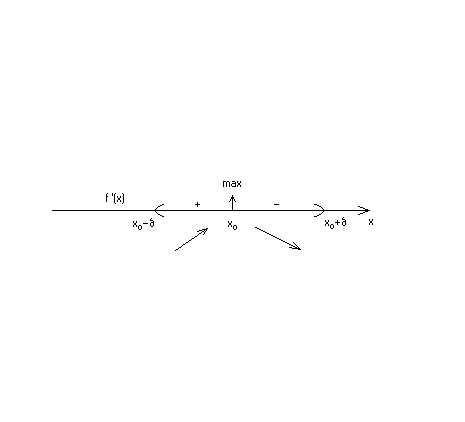
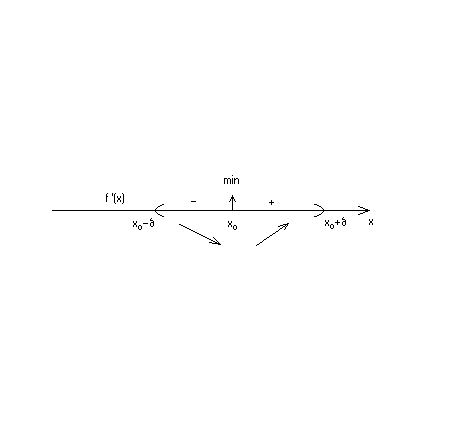
б)
Функция имеет минимум
в точке
x0
,если для
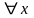
из

-окрестности
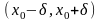
имеет место
Если
при переходе через критическую точку
x0
производная
не меняет знак, то экстремум нет в этой
точке:
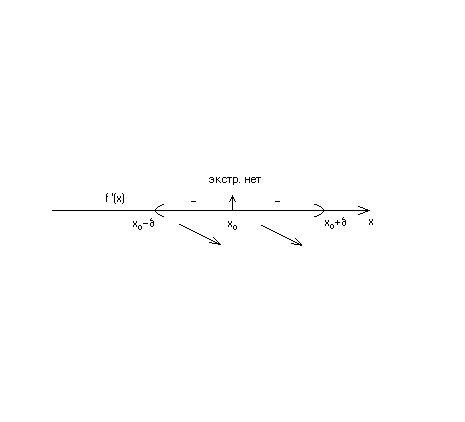
или

Второе
правило.
Если в
критической точке x0
первая производная
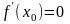
,
а вторая производная
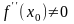
,
то точка x0
будет точкой экстремума, причем:
а)
если
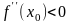
, то x0
– точка максимума;
б)
если
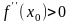
, то x0–
точка минимума.
Замечание.
В более
общем случае, когда первая из не равных
нулю в точке x0
производных функции
имеет порядок k:
Если
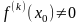
,
то если k
-четное, то точка x0
является точкой максимума при
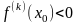
и точкой минимума при
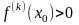
;
если же k
-нечетное, то точка x0
является точкой экстремума.
Пример
7.
Построить
графики функций с помощью производной
первого порядка.
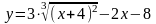
Решение.
1)
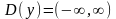
,
т.е.
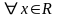
.
2)
Функция общего вида, т. к.

3)
Находим точки пересечения графика
функции к осям координат: а) с осью oy
, x=0 :
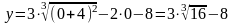
.
точка
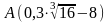
,
т.е. y(0)
-0,5.
б) с осью ox,
y=0:
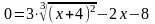
,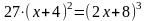
,
или
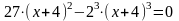
, откуда
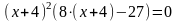
,
x1=-4
или x2=-5/8.
Итак имеем
точки В1(-4,0);
В2(-5/8;0).
4)
Находим интервалы знакопостоянства
функции.
y>0
,если
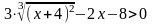
;
решаем это неравенство:
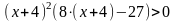
.
Знак y:
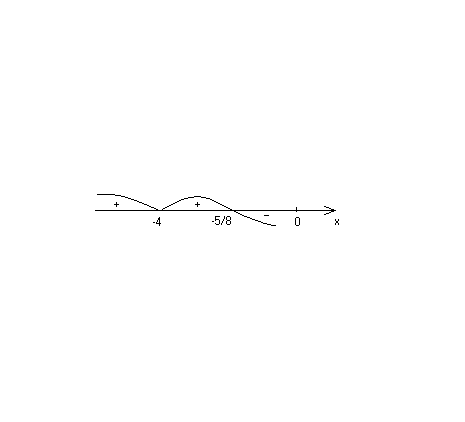
Откуда
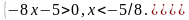
Значит, функция
y>0
при
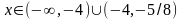
и y<0
при
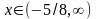
.
5)
Находим критические точки, интервала
возрастания и убывания функции, экстремум
функции
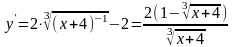
;
а)
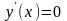
,
если
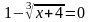
,
т.е. x=-3.
б)
не
существует при x=-4.
Получим
x=-3
, x=-4
– критические точки 1-го рода.
Знак
:
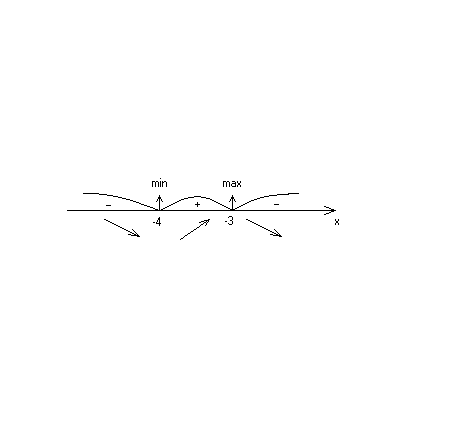
Имеем
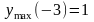
;
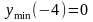
.
Составим
таблицу.
-

-4
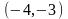
-3

y
/–
не
сущ.+
0
–
yy
убывает
0
возрастает
1
убывает
min
max
График
данной функции представлен на рис.16.4).
Так как при x=-4,
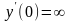
,
то минимум имеет характер точки
заострения.
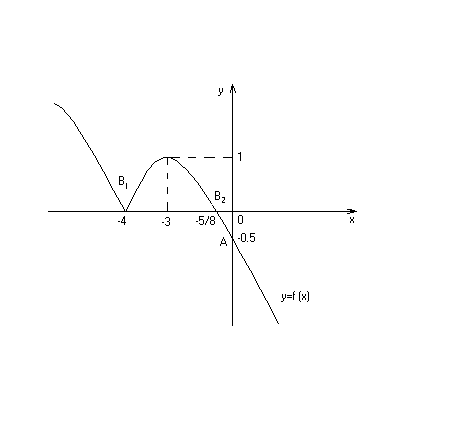
Рис.
16.4
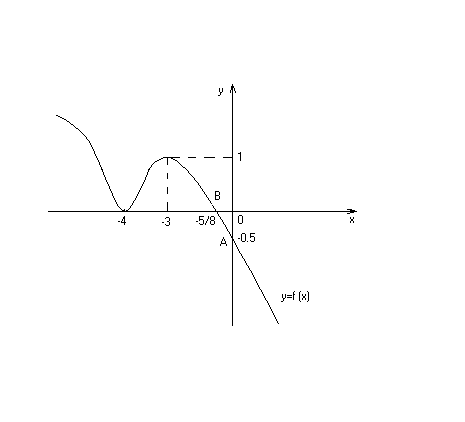
Рис.
16.5
На
основании проведенного по первой
производной исследования, можно было
представить график рассматриваемой
функции и таким, как на (рис. 16.5). Уточнение
графика функции по второй производной
позволит точнее изобразить участки
убывания и возрастания функции,
установить, что график не имеет точек
перегиба и всюду обращен выпуклостью
вверх.
Асимптоты
Если
кривая
какой-либо своей частью неограниченно
удаляется от начала координат, то эта
бесконечная ветвь кривой может иметь
асимптоту. Асимптотой
кривой
называется
прямая,
к которой
кривая неограниченно приближается или
с одной стороны (рис.16.6) или все время
пересекая ее (рис.16.7)
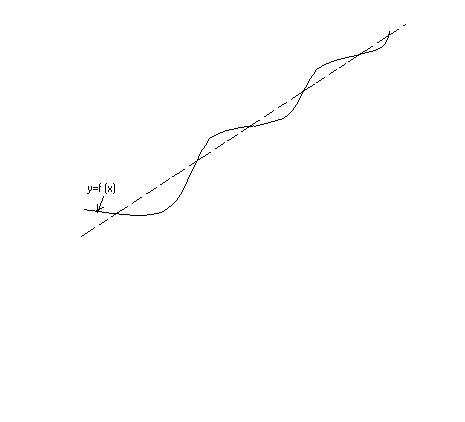
Рис.
16.6 Рис. 16.7
При
неограниченном удалении точки (x,y)
кривой от точки О(0,0).
Асимптоты бывают вертикальные,
горизонтальные и наклонные.
1.
Если существует число а
такое, что
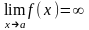
,
то прямая x=a
является вертикальной
асимптотой.
Вертикальные
асимптоты находят как точки разрыва
2-го рода функции.
2.Если
существует конечный предел функции
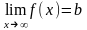
или
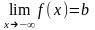
,
то прямая y=b
является горизонтальной
(правой или
левой) асимптотой.
3.Если
существуют конечные пределы
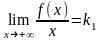
,
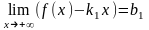
или
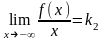
,
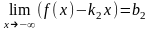
,
то прямая y=k1x+b1
есть
правая
наклонная
асимптота
кривой, а прямая y=k2x+b2
есть левая
наклонная
асимптоты.
Заметим, что частным случаем наклонной
асимптоты при k1,2
=0 и
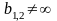
является горизонтальная асимптота.
График функции
не может иметь более одной правой и
более одной левой асимптоты (наклонной
или горизонтальной).
Направление
выпуклости кривой. Точки перегиба
Говорят,
что график дифференцируемой функции
обращен выпуклостью
вверх (вогнутостью вниз)
на интервале

,
если соответствующая дуга кривой
расположена ниже
касательной,
проведенной
в любой точке M(x,f(x))
этой дуги (рис.16.9)

Рис.
16.9
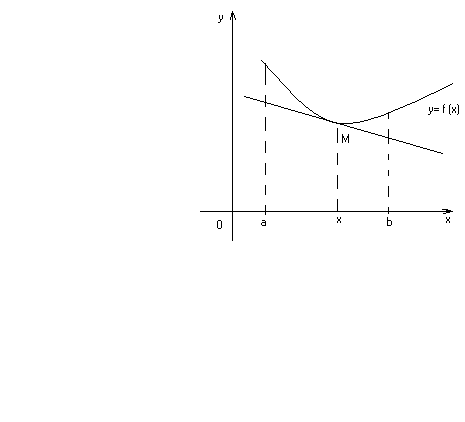
Рис.
16.10
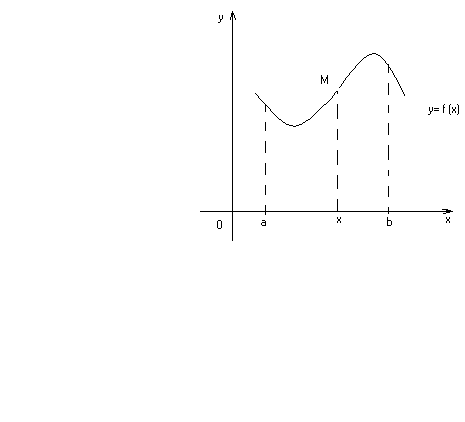
Рис.
16.11
Говорят,
что кривая графика функции обращена
выпуклостью
вниз (вогнутостью вверх)
на интервале
, чем соответствующая дуга кривой
расположена выше
касательной,
проведенной
в любой точке M(x,f(x))
этой дуги (рис.16,10).
Достаточное
условие
направления
выпуклости кривой
:
а)
если
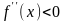
внутри интервала
,
то дуга кривой выпукла
вверх
(обозначают
)
на этом интервале.
б)
если

при x
,
то дуга кривой
выпукла
вниз
(обозначают
)на
этом интервале.
Таким
образом, для нахождения интервалов
выпуклости вверх (вниз) дуги кривой,
надо найти
и решить неравенство:
(
).
Точкой
перегиба
непрерывной
кривой
называется точка M0(x0,f(x0))
, при переходе через которую кривая
меняет направление выпуклости (рис.16,11).
Для
абсциссы x0
точки перегиба графика
вторая производная
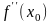
равна нулю или не существует.
Точки,
которых
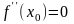
или
не существует, и при этом сама функция
в точке x=x0
определена, называются критическими
точками 2-го рода.
Правило:
Если вторая
производная
функции при переходе через критическую
точку 2-го рода меняет знак, то точка
M0(x0,f(x0))
, есть точка перегиба кривой графика
функции. Это есть достаточное
условие существования точки перегиба
кривой.
Пример
8 . Найти
интервалы выпуклости и точки перегиба
кривой

.
Решение.
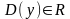
,
т.е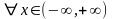
,
ибо x2+12>0.
Находим
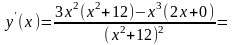

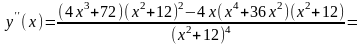
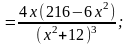
Находим
критические точки 2-го рода
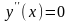
, если x=0
или
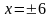
.
Других
критических точек 2-го рода нет, т.к.
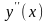
существует всюду в
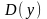
.
Знак
:
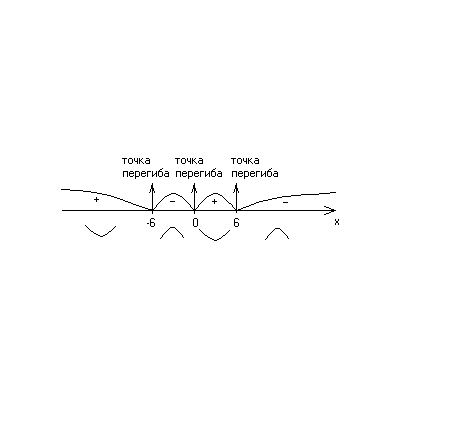
Таким
образом, на интервале

и
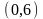
кривая выпукла вниз, на интервалах
(-6,0)
и
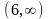
кривая выпукла вниз, на интервалах
(-6;0) и
– выпукла вверх; точки перегиба М1(0;0),
М2(-6;-9/2),
М3(6,9/2).
Заметим,
что
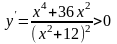
при
,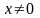
;
следовательно, функция возрастающая
всюду на
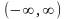
.
Кривая графика симметрична относительно
начала координат в силу нечетности
функции (рис. 16.12).
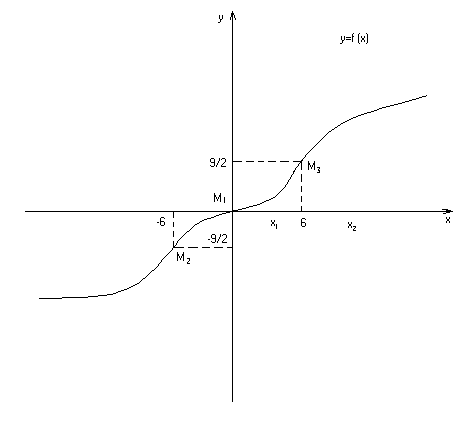
Рис.
16.12
Общая
схема полного исследованфункции и
построение графика функции
При
построении графика функции исследование
свойств функции можно проводить по
следующей схеме:
1.
Нахождение области определения функции;
нахождение точек разрыва функции и
установление их характера.
2.
Установление наличия периодичности и
симметрии относительно оси OY
или относительно начала координат по
четности или нечетности функции.
3.
Нахождение точек пересечения кривой с
координатными осями: с осью OY,
вычисляя f(0),
и с осью OX,
решая
уравнение f(x)=0
и вычислив тем самым, нули функции.
4.
Определение интервалов знакопостоянства
функции.
5.
Определение асимптот графика функции
и «поведение функции в бесконечности».
6.
Определение интервалов возрастания и
убывания функции, точек экстремума(максимума
и минимума). Вычисление значения
экстремумов.
7.
Нахождение точек перегиба, устанавливая
интервалы направления выпуклости (вверх
и вниз) кривой. Если исследуемая функция
четная или нечетная, достаточно
исследовать и построить ее график для
положительных значений аргумента из
области определения. Затем воспользоваться
симметрией. Полезно получаемые данные
сразу наносить на чертеж. Заметим, что
порядок исследования можно менять,
выбирая по целесообразности, исходя из
конкретных особенностей функции.
Пример
9.
Провести
полное исследование функций и построить
их графики.
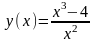
Решение
.
1)
Функция имеет смысл, если
;
следовательно,
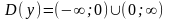
.Точка
x=0–
точка разрыва второго рода.
2)
Функция не является четной и нечетной,
так как
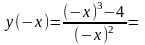

при
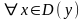
.
3)
Точек пересечения с осью ординат нет,
так как

.
Найдем нули функции: y=0
при

,
x3-4=0.
Значит ,
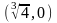
– точка пересечения с осью OX.
4)
Приравнивая знаменатель нулю, получаем
вертикальную асимптоту, ибо
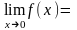
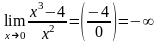
.
Ищем наклонные асимптоты. При
полуем: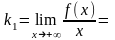
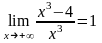
,
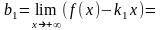

.
Следовательно,
правой асимптотой является прямая y=x.
Аналогично, при

имеем:
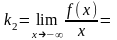
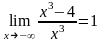
,

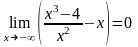
,
т.е.
y=x
является также левой наклонной
асимптотой.
5)
Определим интервалы знакопостоянства
функции. Функция y>0,
если
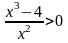
, или

,
где
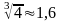
.
Знак y:
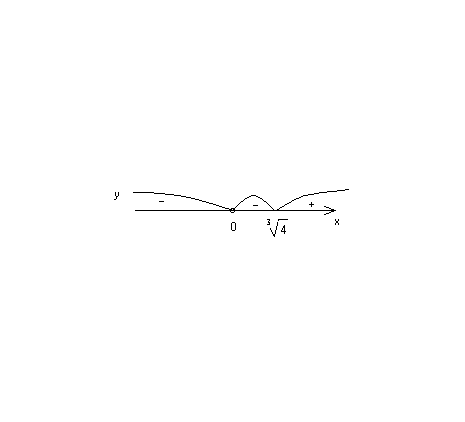
Следовательно,
график функции расположен выше оси OX
при
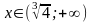
и ниже оси ОХ
при
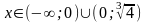
.
6)
Находим критические точки первого и
второго рода , т.е. точки, в которых
обращаются в нуль или не существуют
производные y
/
и y
//
данной функции. Имеем:
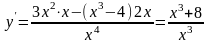
,
y
/=0
при
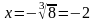
.
Следовательно,
x=-2
– критическая точка первого рода ,т.е.
точка , подозрительная на экстремум;
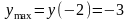

при
.
Критических
точек второго рода ,т.е. точек, подозрительных
на перегиб, нет, производные y
/
и y
//
не существуют еще только при x=0,
где не существует и сама функция y.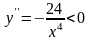
при
.
Следовательно, кривая графика выпукла
вверх всюду.
|
|
-2 |
|
0 |
|
|
|
|
|
y |
– |
-3 |
– |
– |
– |
0 |
+ |
|
y |
+ |
0 |
– |
+ |
+ |
+ |
|
|
y |
– |
-1,5 |
+ |
– |
– |
– |
– |
|
Вы- вод |
y возр. |
y max |
y убыв. |
y не |
y возр. |
0 |
y возр. |
Где
символ

обозначает выпуклость вверх кривой
график. По результатам исследования
строим график функции (рис.16.13).
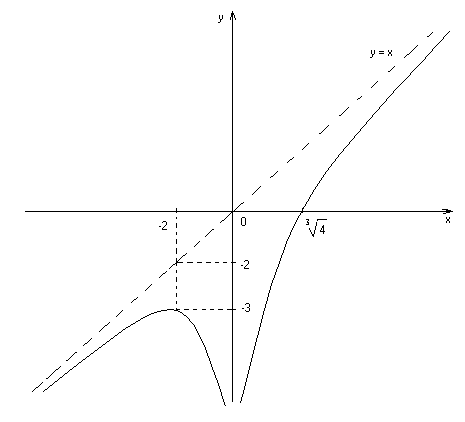
Рис.
16.13
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Дифференциал функции
- Геометрическое содержание дифференциала
- Применение дифференциала к приблизительным вычислениям
- Дифференциал функции и функция
- Дифференциал функции и его определение
- Геометрический смысл дифференциала
- Основные свойства дифференциала
- Свойство инвариантности формы дифференциала
- Применение дифференциалов при приближенных вычислениях
- Дифференциал функции с примерами
- Справочные сведения
- Определение производной
- Правила вычисления производных, связанные с арифметическими действиями над функциями
- Формулы для производных основных элементарных функций
Дифференциал функции
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х))
Понятие дифференциала функции:
С понятием производной тесно связано важное понятие математики — понятие дифференциала.
Пусть дана функция у = f(х), дифференцирования в точке х. Это означает, что существует 
Следовательно, справедливо соотношение:

Отсюда: 
Как видно, прирост функции складывается из двух слагаемых. Второе слагаемое  как произведение бесконечно малых величин, является бесконечно малым более высокого порядка, чем
как произведение бесконечно малых величин, является бесконечно малым более высокого порядка, чем  Значит, при малых
Значит, при малых  второе слагаемое менее важное, чем первое, и именно первое слагаемое составляет основную часть прироста функции (главную часть).
второе слагаемое менее важное, чем первое, и именно первое слагаемое составляет основную часть прироста функции (главную часть).
Дифференциалом функции у = f(х) в точках х называют главную часть прироста функции  и обозначают символом dy. По определению
и обозначают символом dy. По определению 
При  , получаем
, получаем  , или
, или  , то есть дифференциал аргумента равный его приросту. Тогда
, то есть дифференциал аргумента равный его приросту. Тогда

то есть дифференциал функции у = f(х) в точках х равен произведению производной в этой точке на дифференциал аргумента.
Отсюда,  и выражение, которое мы раньше обозначали одним символом, теперь можно рассматривать как дробь, равен отношению дифференциала функции к дифференциалу аргумента.
и выражение, которое мы раньше обозначали одним символом, теперь можно рассматривать как дробь, равен отношению дифференциала функции к дифференциалу аргумента.
Геометрическое содержание дифференциала
Рассмотрим график непрерывной функции у = f(х) (рис. 1).
Производная функции при  равна тангенсу угла наклона касательной к графику функции в точке
равна тангенсу угла наклона касательной к графику функции в точке  , то есть
, то есть


На рис. 1 видно, что касательная разбивает прирост функции KN на два отрезка: KP, который соответствует слагаемому  и PN, который равен слагаемому
и PN, который равен слагаемому  Если прирост аргумента стремится к нулю, то отрезок NP уменьшается значительно быстрее, чем отрезок PK. Следовательно, прирост ординаты касательной KP является главной частью прироста функции у = f (х). Из треугольника MPK находим:
Если прирост аргумента стремится к нулю, то отрезок NP уменьшается значительно быстрее, чем отрезок PK. Следовательно, прирост ординаты касательной KP является главной частью прироста функции у = f (х). Из треугольника MPK находим:

Потому, что  ;
;  , получаем
, получаем  .
.
Следовательно, дифференциал функции у = f (х) геометрически изображается приростом ординаты касательной, проведённой в точке  при заданных значениях
при заданных значениях  и
и  .
.
Пример 1. Найти дифференциал функции 
Решение: Находим производную данной функции:

Умножаем производную на дифференциал аргумента, получаем дифференциал функции:

Ответ: 
Пример 2. Найти дифференциал функции 
Решение: Сначала найдём производную данной функции:

Умножим производную на дифференциал аргумента, получаем дифференциал функции:

Ответ: 
Пример 3. Вычислить значение дифференциала функции 

Решение: Дифференциал вычислим согласно формулы 
Прежде чем использовать эту формулу, найдём производную функции и её значение при 

Отсюда, 
Ответ: 
Применение дифференциала к приблизительным вычислениям
Прирост функции и дифференциал функции отличаются один от другого на малую величину Если пренебречь этой малой величиной, то получим приближённое равенство:
Если пренебречь этой малой величиной, то получим приближённое равенство:

то есть при малых приростах аргумента  прирост функции можно заменить её дифференциалом.
прирост функции можно заменить её дифференциалом.
Учитывая, что  , получаем
, получаем  , откуда
, откуда

Эти приближённые равенства используются для приближённых вычислений, так как вычисление дифференциала функции значительно проще, чем вычисление её прироста.
Пример4. Вычислить приближённое значение прироста функции  при изменении аргумента от х = 2 до х = 2,001.
при изменении аргумента от х = 2 до х = 2,001.
Решение: Находим дифференциал аргумента  . Прирост аргумента малый, поэтому прирост
. Прирост аргумента малый, поэтому прирост  приближённо равен его дифференциалу
приближённо равен его дифференциалу  .
.
Дифференциал функции вычислим по формуле:  . Сначала найдём производную и её значение при х=2.
. Сначала найдём производную и её значение при х=2.


Точное значение прироста функции найдём по формуле:

Сравнив полученный результат с дифференциалом  , видим, что абсолютная погрешность равна 0,000001. Однако абсолютная погрешность не даёт достаточно полной характеристики точности подсчёта, поэтому вычисли м и относительную погрешность:
, видим, что абсолютная погрешность равна 0,000001. Однако абсолютная погрешность не даёт достаточно полной характеристики точности подсчёта, поэтому вычисли м и относительную погрешность:

Такая точность почти всегда достаточна для прикладных вычислений, поэтому вместо прироста функции находят её дифференциал.
Ответ: 
Пример 5. Вычислите приближённое значение функции 
Решение: Найдём дифференциал аргумента  . Прирост аргумента малый, поэтому для вычисления приближённого значения функции воспользуемся формулой:
. Прирост аргумента малый, поэтому для вычисления приближённого значения функции воспользуемся формулой:

Сначала найдём значение функции при х=2: 
Дифференциал находим по формуле:  , для этого найдём производную функции и её значение при х=2:
, для этого найдём производную функции и её значение при х=2:

Ответ: 
Пример 6. Найти приближённое значение  .
.
Решение: Нам необходимо найти приближённое значение функции  при х=16,06.
при х=16,06.
Найдём дифференциал аргумента: 
прирост аргумента малый, поэтому

Дифференциал находим по формуле:  , для этого сначала найдём производную функции и её значение при х=16.
, для этого сначала найдём производную функции и её значение при х=16.

Ответ: 
Пример 7. Найти приближённое значение 
Решение: Как и предыдущем примере, имеем 

Ответ:
Пример 8. Объём куба, ребро которого равно 4см., при нагревании увеличивается на 0,96см3. Как при этом увеличивается ребро куба?
Решение: Объём куба с ребром х вычисляется по формуле: V=х3. Поскольку 
Дифференциал функции вычисляется по формуле  , отсюда
, отсюда  . Прежде чем воспользоваться формулой найдём производную функции V и её значение при х=4:
. Прежде чем воспользоваться формулой найдём производную функции V и её значение при х=4: 
Теперь находим 
Ответ: Ребро куба увеличилось приблизительно на 0,02 см.
Дифференциал функции и функция
Дифференциал — главная часть прироста функции.


Дифференциал функции и его определение
Определение дифференциала
Если функция y = f (x) имеет в точке х производную, то  и приращение функции
и приращение функции  можно представить в виде
можно представить в виде
 , (4.3)
, (4.3)
где  — бесконечно малая величина, стремящаяся к нулю вместе с
— бесконечно малая величина, стремящаяся к нулю вместе с  .
.
В формуле (4.3) второе слагаемое  есть бесконечно малая более высшего порядка, чем
есть бесконечно малая более высшего порядка, чем , и поэтому главную часть суммы составляет первое слагаемое
, и поэтому главную часть суммы составляет первое слагаемое  , которое называется дифференциалом функции.
, которое называется дифференциалом функции.
Определение. Главная линейная часть приращения функции, равная произведению производной на приращение независимой переменной, называется дифференциалом функции f (x).
Обозначается дифференциал символом dy или df(x). Итак,
 (4.4)
(4.4)
Приращение  независимой переменной также обозначают так:
независимой переменной также обозначают так:  . Это объясняют тем, что для функции y = x дифференциал
. Это объясняют тем, что для функции y = x дифференциал  . Поэтому равенство (4.4) записывают dy = f ‘(x) dx.
. Поэтому равенство (4.4) записывают dy = f ‘(x) dx.
Пример 1. Найти дифференциал функции y = 1 + ln x.
Решение. 
Пример 2. Найти дифференциал функции  .
.
Решение. Вычислим сначала производную y’, использовав правило дифференцирования сложной функции
 Следовательно,
Следовательно,
Геометрический смысл дифференциала
Дифференциал функции имеет простое геометрическое толкование.
Пусть имеем график функции y = f (x). Возьмем на этой кривой точку М (х, у) и проведем в ней касательную к кривой.

Рис. 4.
Пусть  — угол наклона касательной с положительным направлением оси Оx. Тогда
— угол наклона касательной с положительным направлением оси Оx. Тогда  .
.
Дадим х некоторое приращение  . На рис. 4
. На рис. 4  . Тогда ордината точки М получит приращение
. Тогда ордината точки М получит приращение  , а ордината точки М, касательной — приращение СD. Учитывая, что ∠ DМС =
, а ордината точки М, касательной — приращение СD. Учитывая, что ∠ DМС =  , имеем СD = МС tg
, имеем СD = МС tg  ; или СD =
; или СD = .
.
С геометрической точки зрения дифференциал dy функции y = f (x) в данной точке есть приращение ординаты касательной к графику функции в этой точке, когда x получает приращение  .
.
Основные свойства дифференциала
1) Дифференциал постоянной равна нулю dc = 0.
2) Дифференциал алгебраической суммы функций равен алгебраической сумме дифференциалов этих функций  .
.
3) Дифференциал произведения двух функций равен сумме произведений каждой из функций на дифференциал второй функции 
4) Дифференциал частного находится по формуле
 .
.
Докажем свойство 3)


Свойство инвариантности формы дифференциала
Пусть дана сложная функция y = f (u), где  . Тогда
. Тогда  , а
, а 
Поскольку dy = d [f (x)] = f ‘(x) dx, то можем сделать вывод, если вместо независимой переменной х подставить произвольную функцию от х, то форма дифференциала не меняется. Это свойство носит название инвариантности формы дифференциала.
Применение дифференциалов при приближенных вычислениях
Дифференциалы используют при приближенных вычислениях значений функций, применяя примерное равенство  . В развернутом виде имеем:
. В развернутом виде имеем:

Откуда значение функции  .
.
Пример 1. Вычислить приближенно ln 1,02 с помощью дифференциала.
Решение. Число ln 1,02 является значением функции y = ln x при х = 1,02. Взяв  имеем
имеем 

Итак, ln 1,02 = ln 1 + 1⋅ 0,02 = 0,02.
Пример 2. Вычислить  .
.
Решение. Запишем  в виде
в виде 
Будем рассматривать данное число как значение функции  при
при 
Взяв  и учитывая, что
и учитывая, что  имеем
имеем
 и поэтому
и поэтому

Дифференциал функции с примерами
Дифференциалом функции  называется произведение ее производной на приращение независимой переменной:
называется произведение ее производной на приращение независимой переменной:  (2.23) В частности, при
(2.23) В частности, при  получаем
получаем  (2.24) т. е. дифференциал независимой переменной равен приращению этой переменной. Формулу (2.23) можно, следовательно, написать так
(2.24) т. е. дифференциал независимой переменной равен приращению этой переменной. Формулу (2.23) можно, следовательно, написать так  (2.25) откуда
(2.25) откуда  (2-26) dx Дифференциал функции
(2-26) dx Дифференциал функции  равен приращению
равен приращению  ординаты касательной
ординаты касательной  проведенной к графику этой функции в точке
проведенной к графику этой функции в точке  когда аргумент получает приращение
когда аргумент получает приращение  (рис. 2.1).
(рис. 2.1).

Из определения производной и дифференциала вытекает, что  где
где  т.е. дифференциал функции отличается от приращения на бесконечно малую высшего порядка, чем
т.е. дифференциал функции отличается от приращения на бесконечно малую высшего порядка, чем  Рис. 2.1 При малых
Рис. 2.1 При малых  справедлива приближенная формула
справедлива приближенная формула  (2.27) или
(2.27) или  (2.28) Если
(2.28) Если  дифференцируемые функции от
дифференцируемые функции от  постоянная, то верны следующие свойства дифференциалов:
постоянная, то верны следующие свойства дифференциалов:


По этой ссылке вы найдёте полный курс лекций по высшей математике:
Примеры с решением
Пример 1.
Найти дифференциал функции  Решение. По формуле (2.25) находим
Решение. По формуле (2.25) находим 
Пример 2.
Найти дифференциал функции  Решение. На основании формулы (2.25) получаем
Решение. На основании формулы (2.25) получаем 
Пример 3.
Найти дифференциал функции  Решение. В данном случае функция обозначена буквой
Решение. В данном случае функция обозначена буквой  аргумент буквой
аргумент буквой  Формула (2.25) перепишется так:
Формула (2.25) перепишется так:  На основании этой формулы находим
На основании этой формулы находим 
Пример 4.
Вычислить значение дифференциала функции  когда х изменяется от 1 до 1,1. Решение. Прежде всего находим общее выражение для дифференциала этой функции:
когда х изменяется от 1 до 1,1. Решение. Прежде всего находим общее выражение для дифференциала этой функции:  Подставляя значения
Подставляя значения  в последнюю формулу, получаем искомое значение дифференциала:
в последнюю формулу, получаем искомое значение дифференциала: 
Пример 5.
Заменяя приращение функции дифференциалом, приближенно найти  Решение. Формула (2.28) применительно к данной функции перепишется в виде arctg
Решение. Формула (2.28) применительно к данной функции перепишется в виде arctg  В нашем случае
В нашем случае  Подставляя эти значения в формулу, получим
Подставляя эти значения в формулу, получим  Следовательно,
Следовательно, 
Возможно вам будут полезны данные страницы:
Справочные сведения
Определение производной
Предел отношения  при
при  называется производной функции
называется производной функции  в точке
в точке  Этот предел обозначают одним из следующих символов:
Этот предел обозначают одним из следующих символов:  Таким образом,
Таким образом,  Если в каждой точке
Если в каждой точке  существует
существует  т. е. если производная
т. е. если производная  существует для всех
существует для всех  то функция
то функция  называется дифференцируемой на интервале
называется дифференцируемой на интервале 
Вычисление производной называют дифференцированием.
Правила вычисления производных, связанные с арифметическими действиями над функциями
Если функции 
 имеют производные в некоторой точке, то функция
имеют производные в некоторой точке, то функция  — постоянные) также имеет в этой точке производную, причем
— постоянные) также имеет в этой точке производную, причем  Если функции
Если функции  имеют производные в некоторой точке, то и функция
имеют производные в некоторой точке, то и функция  имеет производную в этой точке, причем
имеет производную в этой точке, причем  Если функции
Если функции  имеют производные в некоторой точке и
имеют производные в некоторой точке и  в ней, то функция
в ней, то функция  также имеет производную в этой точке, причем
также имеет производную в этой точке, причем 
Формулы для производных основных элементарных функций
1) Степенная функция:  Область существования производной функции
Область существования производной функции  может быть и шире. Например, если
может быть и шире. Например, если  то
то 
2) Показательная функция. Если  то
то  в частности,
в частности,  .
.
3) Логарифмическая функция. Если  то в частности,
то в частности, 
4) Тригонометрические функции: 
5) Обратные тригонометрические функции: 
6) Гиперболические функции: 
Дифференциал функции
Если приращение  функции
функции  в точке
в точке  представимо в виде
представимо в виде  (5) где
(5) где  не зависит от
не зависит от  то функция называется дифференцируемой в точке.
то функция называется дифференцируемой в точке.
Таким образом, если равенство (5) верно, то

Дифференциалом,  независимой переменной
независимой переменной  называется ее приращение
называется ее приращение  т. е. по определению полагают
т. е. по определению полагают  Для дифференцируемости функции в точке (т. е. для существования дифференциала) необходимо и достаточно, чтобы функция имела в этой точке конечную производную. Дифференциал функции
Для дифференцируемости функции в точке (т. е. для существования дифференциала) необходимо и достаточно, чтобы функция имела в этой точке конечную производную. Дифференциал функции  выражается через производную
выражается через производную  следующим образом:
следующим образом:  (6)
(6)
Эта формула позволяет вычислять дифференциалы функций, если известны их производные. Если функция  дифференцируема в каждой точке интервала
дифференцируема в каждой точке интервала  то,
то,  (7) для всех
(7) для всех  Равенство (5) может быть записано в виде
Равенство (5) может быть записано в виде  Если
Если  то для приближенного вычисления значения функции в точке
то для приближенного вычисления значения функции в точке  можно пользоваться формулой
можно пользоваться формулой  (8) так как абсолютная и относительная погрешности при таком приближении сколь угодно малы при достаточно малом Дж.
(8) так как абсолютная и относительная погрешности при таком приближении сколь угодно малы при достаточно малом Дж.
Примеры с решениями
Пример 1.
Вычислить производную функции

Пример 2.
Вычислить производную функции  в точке
в точке  А Функция
А Функция  является композицией двух функций:
является композицией двух функций:  Функция
Функция  в точке
в точке  имеет производную, причем
имеет производную, причем  Функция
Функция  в точке
в точке  также имеет производную, причем
также имеет производную, причем  По формуле (1) получаем
По формуле (1) получаем 


Лекции:
- Объемы подобных фигур
- Алгебра логики
- Эластичность функции
- Разностные уравнения
- Случайная вероятность
- Тригонометрические комплексные числа
- Непрерывность функции
- Теорема о разложении на множители
- Экстремум функции многих переменных
- Пределы в математике
Полный дифференциал функции
Как найти?
Постановка задачи
Найти полный дифференциал функции двух переменных $ z = f(x,y) $
План решения
Формула полного дифференциала функции записывается следующим образом:
$$ dz = f’_x (x,y) dx + f’_y (x,y) dy $$
- Находим первые частные производные функции $ z = f(x,y) $
- Подставляя полученные производные $ f’_x $ и $ f’_y $ в формулу, записываем ответ
Примеры решений
| Пример 1 |
| Найти полный дифференциал функции двух переменных $ z = 2x + 3y $ |
| Решение |
|
Находим частные производные первого порядка: $$ f’_x = 2 $$ $$ f’_y = 3 $$ Подставляем полученные выражения в формулу полного дифференциала и записываем ответ: $$ dz = 2dx + 3dy $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ dz = 2dx + 3dy $$ |
| Пример 2 |
| Найти полный дифференциал функции нескольких переменных $ u = xyz $ |
| Решение |
|
Так как функция состоит из трёх переменных, то в формуле полного дифференциала функции необходимо это учесть и добавить третье слагаемое $ f’_z dz $: $$ du = f’_x dx + f’_y dy + f’_z dz $$ Аналогично как и в случае функции двух переменных находим частные производные первого порядка: $$ u’_x = yz $$ $$ u’_y = xz $$ $$ u’_z = xy $$ Используя формулу записываем ответ: $$ du = yzdx + xzdy + xydz $$ |
| Ответ |
| $$ du = yzdx + xzdy + xydz $$ |
| Пример 3 |
| Вычислить значение полного дифференциала функции $ z = x^3+y^4 $, при $ x = 1 $, $ y = 2 $, $ dx = 0.03 $ и $ dy = -0.01 $ |
| Решение |
|
Берем частные производные первого порядка: $$ z’_x = 3x^2 $$ $$ z’_y = 4y^3 $$ Воспользовавшись формулой составляем полный дифференциал: $$ dz = 3x^2 dx + 4y^3 dy $$ Из условия задачи известны все переменные для вычисления значения дифференциала. Подставив их и вычислим значение: $$ dz = 3cdot 1^2 cdot 0.03 + 4 cdot 2^3 cdot (-0.01) = 0.09 – 0.32 = -0.23 $$ |
| Ответ |
| $$ dz = -0.23 $$ |