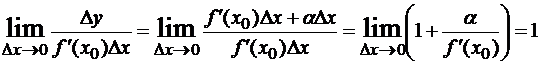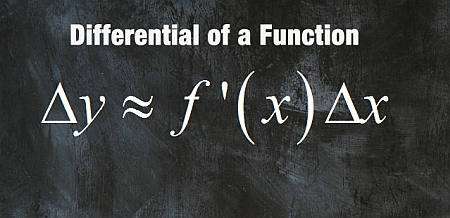Дифференциал функции
dy=f′(x)dx
Как видим, для нахождения дифференциала нужно умножить производную на dx. Это позволяет из таблицы формул для производных сразу записать соответствующую таблицу для дифференциалов.
Полный дифференциал для функции двух переменных: 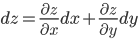
Полный дифференциал для функции трех переменных равен сумме частных дифференциалов: d f(x,y,z)=dxf(x,y,z)dx+dyf(x,y,z)dy+dzf(x,y,z)dz
- Решение онлайн
- Видеоинструкция
- Также решают
Примеры
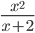
cos2(2x+π) ≡ (cos(2*x+pi))^2
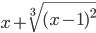
см. также Вычисление приближенно с помощью дифференциала
Определение. Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение в этой точке можно представить в виде ∆y=A∆x + α(∆x)∆x, где A – константа, а α(∆x) – бесконечно малая при ∆x → 0.
Требование дифференцируемости функции в точке эквивалентно существованию производной в этой точке, причем A=f’(x0).
Пусть f(x) дифференцируема в точке x0 и f ‘(x0)≠0, тогда ∆y=f’(x0)∆x + α∆x, где α= α(∆x) →0 при ∆x→0. Величина ∆y и каждое слагаемое правой части являются бесконечно малыми величинами при ∆x→0. Сравним их: 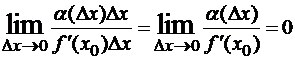
то есть ∆y~f’(x0)∆x. Следовательно, f’(x0)∆x представляет собой главную и вместе с тем линейную относительно ∆x часть приращения ∆y (линейная – значит содержащая ∆x в первой степени). Это слагаемое называют дифференциалом функции y=f(x) в точке x0 и обозначают dy(x0) или df(x0). Итак, для произвольных значений x
dy=f′(x)∆x. (1)
Полагают dx=∆x, тогда
dy=f′(x)dx. (2)
Пример. Найти производные и дифференциалы данных функций.
а) y=4tg2x
Решение:
дифференциал:
б)
Решение:
дифференциал:
в) y=arcsin2(lnx)
Решение:
дифференциал:
г)
Решение:

дифференциал: 
Пример. Для функции y=x3 найти выражение для ∆y и dy при некоторых значениях x и ∆x.
Решение. ∆y = (x+∆x)3 – x3 = x3 + 3x2∆x +3x∆x2 + ∆x3 – x3 = 3x2∆x+3x∆x2+∆x3; dy=3x2∆x (взяли главную линейную относительно ∆x часть ∆y). В данном случае α(∆x)∆x = 3x∆x2 + ∆x3.
Дифференциалом функции
называется главная (линейная по
) часть приращения функции. Чтобы понять данное определение, рассмотрим следующий рисунок.
На рисунке изображён график функции
и
касательной
к ней в точке
.
Дадим аргументу функции
некоторое приращение
,
тогда функция
также получит некоторое приращение
.
Величина
называется
дифференциалом функции
.
При этом, из графика следует, что
равно приращению ординаты касательной, проведённой в точке
к функции
.
Именно поэтому дифференциалом называют линейную часть приращения функции, т.е. приращение ординаты касательной.
Из рисунка следует, что угол наклона касательной
,
который она образует с положительным направлением оси
и
– равны. Кроме того, тангенс угла наклона касательной равен значению производной функции в точке касания:
Из треугольника
следует, что:
Таким образом, дифференциал функции выражается следующей формулой:
Рассмотрим ещё такой момент: из рисунка следует, что
, причем
. Причем, чем меньше
, тем меньший вклад в величину
вносит значение
. Т.е. при достаточно малых значениях
, можно считать, что
. Данное соотношение позволяет вычислять приближенное значение функции в точке
, если известно её значение в точке
.
Дифференциал высшего порядка (например порядка
) определяется как дифференциал от дифференциала
-ого порядка:
Например, дифференциал второго порядка вычисляется следующим образом:
Аналогичным образом получаем формулу для вычисления дифференциала
-ого порядка:
где
–
-ая производная функции
по переменной
.
Пару слов стоит сказать о вычислении дифференциала функции многих переменных, который в этом случае называется
полным дифференциалом. Полный дифференциал функции, зависящей от
-переменных
определяется по формуле:
Выражения для дифференциалов высших порядков функции многих переменных можно получить исходя из общей формулы:
В общем случае, для возведения суммы в
-ую степень необходимо воспользоваться формулой бинома Ньютона. Рассмотрим процесс получения формулы полного дифференциала второго порядка функции двух переменных:
Наш онлайн калькулятор способен вычислить дифференциалы разных порядков для любых функций одной или нескольких переменных с описанием подробного решения на русском языке.
Инструкции:
Используйте этот дифференциальный калькулятор, чтобы найти дифференциал функции, которую вы предоставляете, в заданной точке, которую вы предоставляете, показывая все шаги. Пожалуйста, введите функцию и точку в поле формы ниже.
Дифференциальный калькулятор
Этот калькулятор позволит вам вычислить дифференциал предоставляемой вами функции в указанную вами точку, показывая все этапы процесса.
Предоставляемая вами функция может быть любой допустимой дифференцируемой функцией, такой как f(x) = x^2 + 2x или f(x) = x^2*sin(x), просто упомянем два примера.
Затем, когда вы указали функцию и точку для дифференциального расчета, просто нажмите “Рассчитать”, чтобы просмотреть все этапы показанного процесса.
Идея
Дифференциал
находится вплотную с линией касательной и
Линейное Приближение
, так как дифференциал точно измеряет изменение y вдоль
Касательная линия
в заданной точке.
Что такое дифференциал?
В дифференциальном исчислении идея состоит в том, что производные дают вам информацию о мгновенной скорости изменения функции в данной точке.
Понятие дифференциала использует
скорость изменения
определяется производной в данной точке (x_0), чтобы аппроксимировать поведение функции ее
Касательная линия
.
Формула дифференциала основана на идее, что
[displaystyle Delta y approx f'(x_0) Delta x ]
где (Delta y = y – f(x_0)) и (Delta x = x – x_0). Для дифференциала (dy) определим
[displaystyle dy = f'(x_0) dx ]
Это (расплывчатое) определение основано на идее, что линейная аппроксимация и функция приближаются к одному и тому же поведению, когда (x) достаточно близко к (x_0).
Шаги для вычисления дифференциала
-
Шаг 1:
Определите функцию f(x) и точку x0, в которой вы хотите вычислить дифференциал -
Шаг 2:
Вычислите производную f'(x) и оцените ее в x0, чтобы получить f'(x0). Упростите его, если это необходимо -
Шаг 3:
Используйте формулу (displaystyle dy = f'(x_0) dx )
Иногда вы встретите дифференциал, записанный как (displaystyle Delta y = f'(x_0) Delta x = f'(x_0)(x-x_0) ), как форму указания на то, что вы будете использовать дифференциал для оценки изменений y, измеренных (Delta y).
Дифференциальный калькулятор dy
Используя
Дифференциальный калькулятор
может сэкономить ваше время в процессе расчета производной. Идея дифференциала всегда была странной в том смысле, что она кажется нечетко определенной.
Хотя существует способ формального определения дифференциалов и их операций (предмет, называемый дифференциальными формами), большинство математиков не видят причин для существования дифференциалов, поскольку они не предоставляют никакой новой информации, которую производная или приближение первого порядка не предоставлять.
Полная дифференциальная интерпретация
Наиболее распространенное применение и интерпретация дифференциала – это использование в его “конечном” выражении:
[displaystyle Delta y = f'(x_0) Delta x = f'(x_0)(x-x_0) ]
где вы хотите оценить изменение y, измеренное (Delta y), по изменению x, измеренному (Delta x), и производной в точке.
Иногда это (Delta y) называют
полная вариация
или же
полный дифференциал
.
Советы и рекомендации
Не забывайте, что дифференциал можно рассматривать как теоретическое определение (displaystyle dy = f'(x_0) dx ), которое указывает на бесконечно малую вариацию у, вызванную бесконечно малой вариацией х.
Его также можно использовать в его полной дифференциальной форме, в которой у вас есть
[displaystyle Delta y approx f'(x_0)(x-x_0)]
который сообщает вам приблизительное изменение y при изменении x (от (x_0) до (x)).
Центр всего алгебраического калькулятора начинается с мощности основных чисел дробей.
Пример: дифференциальный калькулятор
Рассмотрим функцию: (f(x) = x^2). Найдите его дифференциал в точке (x_0 = 1).
Отвечать:
В случае этого первого примера мы работаем с функцией (displaystyle f(x)=x^2), для которой нам нужно вычислить ее дифференциал в точке (x_0 = 1).
Функция уже упрощена, поэтому мы можем перейти непосредственно к вычислению ее производной:
( displaystyle frac{d}{dx}left(x^2right))
In this case we use the Power Rule for polynomial terms: (frac{d}{dx}left( x^2 right) = 2x)
( displaystyle = ,,)
(displaystyle 2x)
Дифференциал
: Формула для дифференциала функции (displaystyle f(x)=x^2) в точке (x_0 = 1):
[dy = f'(x_0)(x – x_0) ]
Мы определяем (displaystyle y_0 = f(x_0)), поэтому подстановка значения точки (x_0 = 1) в функцию приводит к:
[y_0 = f(x_0) = fleft(1right) = 1^2 = 1]
Также подстановка значения точки (x_0 = 1) в вычисленную производную приводит к:
[f'(x_0) = f’left(1right) = 2cdot 1 = 2 ]
Итак, теперь мы подставляем это значение в дифференциальную формулу, чтобы получить:
[dy = f'(x_0)(x – x_0) ][Rightarrow dy = 2left(x-1right) ][Rightarrow dy = 2x-2 ]
Вывод
: Следовательно, мы находим, что дифференциал для функции (displaystyle f(x)=x^2) в точке (x_0 = 1) равен:
[dy = 2x-2 ]
Пример: дифференциальный расчет
Для заданной функции: (f(x) = x^3 + 3x^2 – 2) найти дифференциал в точке (x_0 = 2).
Отвечать:
Теперь нам нужно найти дифференциал для функции (displaystyle f(x)=x^3+3x^2-2),
( displaystyle frac{d}{dx}left(x^3+3x^2-2right))
By linearity, we know (frac{d}{dx}left( x^3+3x^2-2 right) = frac{d}{dx}left(x^3right)+3 cdot frac{d}{dx}left(x^2right)-frac{d}{dx}left(2right)), so plugging that in:
( displaystyle = ,,)
(displaystyle frac{d}{dx}left(x^3right)+3 cdot frac{d}{dx}left(x^2right)-frac{d}{dx}left(2right))
Since the derivative of a constant is 0, we get that:
( displaystyle = ,,)
(displaystyle frac{d}{dx}left(x^3right)+3 cdot frac{d}{dx}left(x^2right))
Using the Power Rule for polynomial terms: (frac{d}{dx}left( x^2 right) = 2x) and (frac{d}{dx}left( x^3 right) = 3x^2)
( displaystyle = ,,)
(displaystyle 3x^2+3 cdot 2x)
( displaystyle = ,,)
(displaystyle 3x^2+3cdot 2x)
We reduce the integers that can be multiplied: (displaystyle 3times2 = 6)
( displaystyle = ,,)
(displaystyle 3x^2+6x)
Directly reorganizing/simplifying/expanding
( displaystyle = ,,)
(displaystyle 3left(x+2right)x)
Дифференциальный Расчет
: Мы используем следующую формулу для дифференциала, который нам нужно построить для данной функции (displaystyle f(x)=x^3+3x^2-2), в данной точке (x_0 = frac{1}{2}):
[dy = f'(x_0)(x – x_0) ]
Заметьте, что (displaystyle y_0 = f(x_0)), что означает, что вычисляя функцию в (x_0 = frac{1}{2}), мы находим:
[y_0 = f(x_0) = fleft(frac{1}{2}right) = left(frac{1}{2}right)^3+3left(frac{1}{2}right)^2-2 = -frac{9}{8}]
Тогда получим производную в точке (x_0 = frac{1}{2}):
[f'(x_0) = f’left(frac{1}{2}right) = 3left(frac{1}{2}right)^2+6cdot frac{1}{2} = frac{15}{4} ]
Следовательно, мы получаем следующее
[dy = f'(x_0)(x – x_0) ][Rightarrow dy = left(frac{15}{4}right)left(x-frac{1}{2}right) ][Rightarrow dy = frac{15}{4}x-frac{15}{8} ]
Вывод
: Окончательный вывод состоит в том, что искомый дифференциал определяется выражением:
[dy = frac{15}{4}x-frac{15}{8} ]
Дифференциальный пример
Нам дана функция: (f(x) = frac{sin(x)}{x}). Найдите его дифференциал в точке (x_0 = frac{pi}{2}).
Решение:
Предусмотрена следующая функция: (displaystyle f(x)=frac{sinleft(xright)}{x}), для которой нужно вычислить ее дифференциал в точке (x_0 = frac{pi}{2}).
Функция уже упрощена, поэтому мы можем перейти непосредственно к вычислению ее производной:
( displaystyle frac{d}{dx}left(frac{sinleft(xright)}{x}right))
Using the Quotient Rule: (frac{d}{dx}left( frac{sinleft(xright)}{x} right) = frac{x cdot frac{d}{dx}left(sinleft(xright)right)-sinleft(xright)cdot frac{d}{dx}left(xright)}{x^2})
( displaystyle = ,,)
(displaystyle frac{x cdot frac{d}{dx}left(sinleft(xright)right)-sinleft(xright)cdot frac{d}{dx}left(xright)}{x^2})
We already know that (frac{d}{dx}left(xright) = 1)
( displaystyle = ,,)
(displaystyle frac{x cdot frac{d}{dx}left(sinleft(xright)right)-sinleft(xright)}{x^2})
Directly differentiating: (frac{d}{dx}left( sinleft(xright) right) = cosleft(xright))
( displaystyle = ,,)
(displaystyle frac{x cdot cosleft(xright)-sinleft(xright)}{x^2})
So then after simplifying:
( displaystyle = ,,)
(displaystyle frac{xcosleft(xright)-sinleft(xright)}{x^2})
Расчет
: Теперь пришло время найти дифференциал, связанный с (displaystyle f(x)=frac{sinleft(xright)}{x}), для заданной точки (x_0 = frac{pi}{2}). Используемая формула:
[dy = f'(x_0)(x – x_0) ]
Подставляем значение точки (x_0 = frac{pi}{2}) в вычисленную производную, что приводит к:
[f'(x_0) = f’left(frac{pi}{2}right) = frac{cosleft(frac{pi{}}{2}right)}{frac{pi{}}{2}}-frac{sinleft(frac{pi{}}{2}right)}{left(frac{pi{}}{2}right)^2}
= -frac{4}{pi{}^2} ]
Поэтому, используя дифференциальную формулу:
[dy = f'(x_0)(x – x_0) ][Rightarrow dy = left(-frac{4}{pi{}^2}right)left(x-frac{1}{2}pi{}right) ][Rightarrow dy = frac{2}{pi{}}-frac{4x}{pi{}^2} ]
Вывод
: Соответствующий дифференциал:
[dy = frac{2}{pi{}}-frac{4x}{pi{}^2} ]
Другие калькуляторы дифференцирования
Поиск производных
без сомнения, является ключевым элементом исчисления. Производные предоставляют информацию, необходимую для понимания
скорость изменения
функций. поскольку они имеют тесную связь.
К счастью, поиск деривативов — это систематический процесс (не обязательно простой), если вы будете следовать определенным правилам.
правила дифференциации
. Чаще всего используются правила
Правило Продукта
,
Правило квоты
и
Правило цепи
.
Линейный или
приближения первого порядка
концептуально попытаться аппроксимировать функцию линией, по крайней мере локально, и может многое рассказать о поведении функции, близкой к определенной точке.
Дифференциальные уравнения по-шагам

Примеры дифференциальных уравнений
- Простейшие дифференциальные уравнения 1-порядка
-
y' + y = 0
-
y' - 5*y = 0
-
x*y' - 3 = 0
- Дифференциальные уравнения с разделяющимися переменными
-
(x-1)*y' + 2*x*y = 0
-
tan(y)*y' = sin(x)
- Линейные неоднородные дифференциальные уравнения 1-го порядка
-
y' + 7*y = sin(x)
- Линейные однородные дифференциальные уравнения 2-го порядка
-
3*y'' - 2*y' + 11y = 0
- Уравнения в полных дифференциалах
-
dx*(x^2 - y^2) - 2*dy*x*y = 0
- Решение дифференциального уравнения заменой
-
x^2*y' - y^2 = x^2
- Смена y(x) на x в уравнении
-
x^2*y' - y^2 = x^2
- Линейные дифференциальные уравнения 3-го порядка
-
y''' + 3*y'' + y' + 3y = 0
-
y''' + 2*y'' + y' = exp(-x)
-
y''' + 3*y'' + y' + 3y = sin(x) + 2
- Другие
-
-6*y - 5*y'' + y' + y''' + y'''' = x*cos(x) + sin(x)
Что умеет калькулятор дифференциальных уравнений?
- Детальное решение для:
- Обыкновенное дифференциальное уравнение
- Разделяемые переменные
- Уравнение Бернулли
- Уравнение в полных дифференциалах
- Дифференциальное уравнение первого порядка
- Дифференциальное уравнение второго порядка
- Дифференциальное уравнение третьего порядка
- Однородное дифференциальное уравнение
- Неоднородное дифференциальное уравнение
- Дифференциальные уравнения с заменой
- Система обыкновенных дифференциальных уравнений
- Строит графики множества решений
- Решает задачу Коши
- Классификация дифференциальных уравнений
- Примеры численных решений
Подробнее про Дифференциальные уравнения
.
Указанные выше примеры содержат также:
- модуль или абсолютное значение: absolute(x) или |x|
-
квадратные корни sqrt(x),
кубические корни cbrt(x) -
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x) - показательные функции и экспоненты exp(x)
-
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x) -
натуральные логарифмы ln(x),
десятичные логарифмы log(x) -
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x) -
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x) -
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x) -
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x) -
знак числа:
sign(x) -
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x) -
Факториал от x:
x! или factorial(x) - Гамма-функция gamma(x)
- Функция Ламберта LambertW(x)
-
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)
Правила ввода
Можно делать следующие операции
- 2*x
- – умножение
- 3/x
- – деление
- x^2
- – возведение в квадрат
- x^3
- – возведение в куб
- x^5
- – возведение в степень
- x + 7
- – сложение
- x – 6
- – вычитание
- Действительные числа
- вводить в виде 7.5, не 7,5
Постоянные
- pi
- – число Пи
- e
- – основание натурального логарифма
- i
- – комплексное число
- oo
- – символ бесконечности
Решение дифференциальных уравнений
Данный онлайн калькулятор позволяет вычислять дифференциальные уравнения практически любого типа и порядка: линейные дифференциальные уравнения, с разделяемыми или неразделяемыми переменными, уравнения Бернулли и т.д. При этом у вас есть возможность решать уравнения в общем виде или получить частное решение соответствующее введенным вами начальным (граничным) условиям.
По умолчанию в уравнении функция y является функцией от переменной x. Однако вы можете задать своё обозначение переменной, если напишете, например, y(t) в уравнении, то калькулятор автоматически распознает, что y есть функция от переменной t. С помощью калькулятора вы сможете решать дифференциальные уравнения любой сложности и вида: однородные и неоднородные, линейные или нелинейные, первого порядка или второго и более высоких порядков, уравнения с разделяющимися или не разделяющимися переменными и т.д. Решение диф. уравнения даётся в аналитическом виде, имеет подробное описание. Дифференциальные уравнения очень часто встречаются в физике и математике. Без их вычисления невозможно решать многие задачи (особенно в математической физике).
Одним из этапов решения дифференциальных уравнений является интегрирование функций. Есть стандартные методы решений дифференциальных уравнений. Необходимо привести уравнения к виду с разделяющимися переменными y и x и отдельно проинтегрировать разделенные функции. Чтобы это сделать иногда следует провести определенную замену.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»