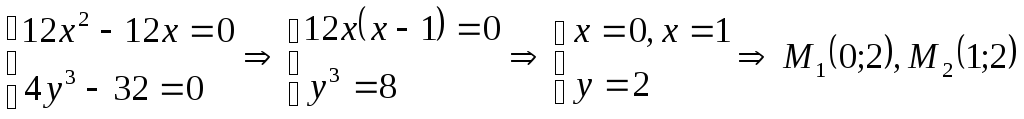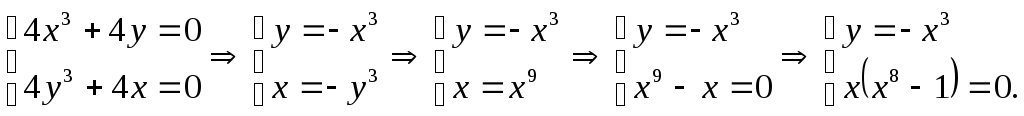Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву, химии, теормеху, сопромату и другим предметам можно здесь всего за 10 минут.
Полный дифференциал функции
Как найти?
Постановка задачи
Найти полный дифференциал функции двух переменных $ z = f(x,y) $
План решения
Формула полного дифференциала функции записывается следующим образом:
$$ dz = f’_x (x,y) dx + f’_y (x,y) dy $$
- Находим первые частные производные функции $ z = f(x,y) $
- Подставляя полученные производные $ f’_x $ и $ f’_y $ в формулу, записываем ответ
Примеры решений
| Пример 1 |
| Найти полный дифференциал функции двух переменных $ z = 2x + 3y $ |
| Решение |
|
Находим частные производные первого порядка: $$ f’_x = 2 $$ $$ f’_y = 3 $$ Подставляем полученные выражения в формулу полного дифференциала и записываем ответ: $$ dz = 2dx + 3dy $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ dz = 2dx + 3dy $$ |
| Пример 2 |
| Найти полный дифференциал функции нескольких переменных $ u = xyz $ |
| Решение |
|
Так как функция состоит из трёх переменных, то в формуле полного дифференциала функции необходимо это учесть и добавить третье слагаемое $ f’_z dz $: $$ du = f’_x dx + f’_y dy + f’_z dz $$ Аналогично как и в случае функции двух переменных находим частные производные первого порядка: $$ u’_x = yz $$ $$ u’_y = xz $$ $$ u’_z = xy $$ Используя формулу записываем ответ: $$ du = yzdx + xzdy + xydz $$ |
| Ответ |
| $$ du = yzdx + xzdy + xydz $$ |
| Пример 3 |
| Вычислить значение полного дифференциала функции $ z = x^3+y^4 $, при $ x = 1 $, $ y = 2 $, $ dx = 0.03 $ и $ dy = -0.01 $ |
| Решение |
|
Берем частные производные первого порядка: $$ z’_x = 3x^2 $$ $$ z’_y = 4y^3 $$ Воспользовавшись формулой составляем полный дифференциал: $$ dz = 3x^2 dx + 4y^3 dy $$ Из условия задачи известны все переменные для вычисления значения дифференциала. Подставив их и вычислим значение: $$ dz = 3cdot 1^2 cdot 0.03 + 4 cdot 2^3 cdot (-0.01) = 0.09 – 0.32 = -0.23 $$ |
| Ответ |
| $$ dz = -0.23 $$ |
IV.
ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
§
10. Основы дифференцирования функции
двух переменных
Частная производная
от функции
по переменной x
– это предел
.
Частная производная
от функции
по переменной y
– это предел
.
Соответствующие
обозначения:
и
,
или же
и
.
Производная
– это скорость изменения функции при
малом изменении переменной x,
когда переменная y
постоянна. Очевидно,
– новая функция.
При поиске
считаем, что y
– это число, выраженное буквой (параметр).
Тогда получаем функцию одной переменной
,
а производную от неё находим по правилам
дифференцирования функции одной
переменной.
Так же
– это скорость изменения функции при
малом изменении y
и постоянном x,
а при поиске
составляем функцию
и дифференцируем её как функцию одной
переменной.
Пример 1.
Частные производные от функции
:
;
.
Пример 2.
Найдём частные производные от функции
:
;
.
В 1-м случае вынесли
постоянный множитель
,
не зависящий от x,
а во 2-м случае – множитель
,
не зависящий от y.
Пример 3.
Для функции
найдём
;
.
Полный дифференциал
показывает, как примерно
изменится функция, если увеличить x
на величину
и одновременно
y
– на величину
(если
или
,
то речь об уменьшении x
или y).
Пример 4.
Найдём полный дифференциал функции
в общем виде и в точке
:
а)
– при
получается производная степенной
функции;
б)
– при
получается
производная показательной функции.
Таким образом, в
общем виде
,
или, если вынести общий множитель,
.
Чтобы найти полный
дифференциал в точке, подставив её
координаты
и
,
тогда
.
Смысл
результата.
Пусть надо найти, например, значение
функции
в точке
,
или, что то же самое, найти величину
.
Если взять точку
,
то
.
При переходе в точку N
изменение аргументов составило
и
(разность старых и новых координат).
Полный дифференциал
в точке M
(не в N!)
равен приращению
функции при переходе из точки
в
.
Поэтому
.
Более точно,
.
Пример 5. Найдём
для нескольких функций полные дифференциалы
в общем виде и в конкретной точке M:
а)
пусть
;
,
тогда
.
Дифференциал в
общем виде
;
в точке M
будет
.
б) пусть
даны
и
;
тогда
.
Дифференциал в
общем виде:
;
в точке:
;
в)
если даны
и
,
то
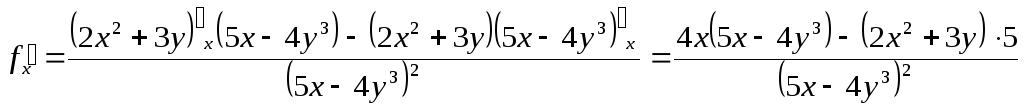
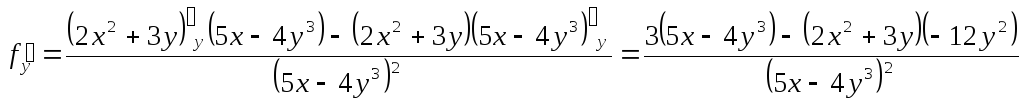
Упростим числители:
;
.
В полном дифференциале
вынесем общий множитель:
,
подставим координаты
точки:
,
или
.
Так, чтобы найти
,
считаем
,
затем
и
,
после чего
и соответственно
.
Пример 6.
При помощи полного дифференциала найдём
значение функции
при
(угол выражен в радианах).
Подберём точку
как можно ближе к
,
чтобы в ней легко вычислялось значение
.
Это точка
:
.
Частные производные
в общем виде:
,
,
а в точке
будет
,
и
.
Значит, около
точки
функция меняется примерно так же, как
меняется переменная x.
В нашем случае
.
Новое значение
функции
.
Более точное
значение
почти совпадает с приближённым. Отличие
вызвано тем, что
,
а не 1;
Ответ:
.
Пример 7.
При помощи полного дифференциала найдём
.
Представим это
число как значение функции
в точке
.
При этом
и
,
а для таких аргументов функцию
легко посчитать:
.
Итак,
,
,
,
.
Тогда
при
и
.
Для
частные производные
;
.
В точке M
и
,
тогда
(функция растёт в
2 раза быстрее, чем 2-й аргумент).
Итак,
.
Ответ:
(более точное значение равно
).
ЧП1.
Найдите частные производные для функций
1) а)
; б)
;
в)
; г)
;
2) а)
; б)
;
в)
; г)
;
3) а)
; б)
;
в)
; г)
;
4) а)
; б)
;
в)
; г)
;
5) а)
; б)
;
в)
; г)
;
6) ;
7) .
ЧП2.
Найдите полные дифференциалы функций
в указанной точке:
1) а)
; б)
;
в)
; г)
;
2) а)
; б)
;
в)
; г)
;
3) а)
; б)
;
в)
г)
.
ЧП3.
Найдите при помощи полного дифференциала
приближённые значения
1) а)
; б)
; в)
; г)
;
2) а)
; б)
; в)
; г)
;
3) а)
; б)
; в)
; г)
;
4) а)
; б)
; в)
; г)
.
Экстремум функции
двух переменных
Точка M
называется точкой минимума функции
,
если можно указать открытую область D
(часть плоскости xOy),
в которой значение
– наименьшее из всех. Более строго, M
– точка минимума, если существует D,
что
а)
(точка входит в эту область и не принадлежит
её границе);
б)
(в любой другой точке этой же области
значение функции меньше, чем в интересующей
нас точке).
При замене на
условие
получим определение точки максимума.
Например,
– точка минимума функции
,
поскольку в ней
,
а в любой другой точке
.
Схема поиска
точек экстремума для функции
1) Найдём
и
,
затем – точки
,
где обе производные равны 0;
2) найдём 2-е
производные
,
т.е. соответственно
;
3) координаты точки
подставим во 2-е производные. Получим
числа
;
4) если,
в точке
экстремума нет. Если
,
то смотрим, каков знак A:
если
,
то
– точка минимума,
если же
,
то
– точка максимума;
5) если в
оказалось, что
,
необходимы другие методы решения,
выходящие за рамки пособия (разложение
в ряд Тейлора);
6) таким же образом
3-й, 4-й и 5-й шаги выполняем для остальных
точек.
Пример 8.
Найдём экстремумы функции
.
1)
решаем систему
(уравнения решены
независимо, и подходят все сочетания
координат);
2) находим 2-е
производные
;
;
;
Проверяем точку
,
подставив
и
:
3)
;
;
;
4)
,
экстремума в
нет.
Проверяем точку
,
подставив
и
:
3)
;
;
;
4)
,
экстремум в
есть.
Поскольку
,
то данный экстремум – это минимум. Можно
найти его значение
.
Ответ:
минимум при
и
,
равный –50.
Пример 9.
Исследуем на экстремум функцию
.
1) Находим
решаем систему
Здесь
.
У 2-го уравнения
3 корня: –1, 0 и 1, но координаты зависимы:
если
,
то
,
если
,
то
,
если
,
то
.
Получаем 3 точки:
;
2) берём 2-е производные
;
;
;
проверяем точку
:
3)
;
;
;
4)
,
в
есть экстремум, а поскольку
,
то этот экстремум – минимум. Его значение
;
проверяем точку
:
3)
;
;
;
4)
,
экстремума в
нет.
Легко видеть, что
для точки
результаты те же, что и для
.
Ответ:
минимум, равный –2, при
и
,
а также при
и
.
Замечание 1.
Если в записи функции поменять все
знаки, точки минимума станут точками
максимума, и наоборот. При этом координаты
точек не изменятся. Так, из примера 9
следует, что для
получим максимум, равный 2, при
и
,
а также при
и
.
Если же к функции
добавить (или отнять) любое число,
изменится лишь значение экстремума, но
не его тип. Так, у функции
окажется максимум при
и
,
а также при
и
,
равный 2+50=52.
ЧП4.
Найдите точку экстремума функции
при указанных параметрах a,
b.
Найдите значение функции в этой точке
и определите тип экстремума:
а)
a
= 2; b
= 3; б)
a
= 3; b
= 2; в)
a
= 2; b
= 5; г)
a
= 5; b
= 4;
д)
a
= 6; b
= 1; е)
a
= 1; b
= 2; ж)
a
= 0; b
= 4; з)
a
= 3; b
= 0.
ЧП5.
Найдите точку экстремума функции
при указанных параметрах a,
b.
Найдите значение функции, определите
тип экстремума:
а)
a
= 2; b
= 3; б)
a
= 3; b
= 2; в)
a
= 2; b
= 5; г)
a
= 5; b
= 4;
д)
a
= 6; b
= 1; е)
a
= 1; b
= 2; ж)
a
= 0; b
= 4; з)
a
= 3; b
= 0.
Замечание
2. Функции
двух переменных ведут себя сложнее, чем
функции одной переменной. Так, при
решении задач на экстремум:
а) даже у непрерывных
функций могут быть несколько точек
максимума и ни одной точки минимума
(или наоборот);
б) все стационарные
точки могут оказаться седловыми
точками, из
которых функция растёт при изменении
x
и убывает при изменении y
(или наоборот). Тем самым у функции не
окажется ни максимума, ни минимума.
Замечание 3.
Приведённая схема исследования на
экстремум предполагает, что функция
дифференцируема в точках экстремума.
Однако это не обязательно. Так, функция
в точке
имеет максимум, но её производные в
данной точке обращаются в бесконечность.
Подобные случаи выходят за рамки пособия.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ирина Алексеевна Антоненко
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Если для каждой пары $(x,y)$ значений двух независимых переменных из некоторой области ставится в соответствие определенное значение $z$, то говорят, что $z$ является функцией двух переменных $(x,y)$. Обозначение: $z=f(x,y)$.
В отношении функции $z=f(x,y)$ рассмотрим понятия общего (полного) приращения функции и полного дифференциала.
Пусть дана функция $z=f(x,y)$двух независимых переменных $(x,y)$.
Если аргументу $x$ дать приращение $Delta x$, а аргументу $y$ — приращение $Delta y$, то получается полное приращение заданной функции $z=f(x,y)$. Обозначение:
Пример 1
Записать полное приращение заданной функции
[z=x+y.]
Решение:
По определению полного приращения некоторой функции найдем:
$Delta z=x+Delta x+y+Delta y$ – полное приращение функции $z=f(x,y)$.
Пример 2
Вычислить полное приращение заданной функции $z=xy$ в точке $(1;2)$ при $Delta x=0,1;, , Delta y=0,1$.
Решение:
По определению полного приращения некоторой функции найдем:
$Delta z=(x+Delta x)cdot (y+Delta y)$ – полное приращение функции $z=f(x,y)$.
Следовательно,
[Delta z=(1+0,1)cdot (2+0,1)=1,1cdot 2,1=2,31.]
Определение 2
Если для каждой тройки $(x,y,z)$ значений трех независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией трех переменных $(x,y,z)$ в данной области.
Обозначение: $w=f(x,y,z)$.
Определение 3
Если для каждой совокупности $(x,y,z,…,t)$ значений независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией переменных $(x,y,z,…,t)$ в данной области.
Обозначение: $w=f(x,y,z,…,t)$.
«Полное приращение и полный дифференциал» 👇
Для функции трех и более переменных, аналогично как для функции двух переменных определяются полное приращение:
Пример 3
Записать полное приращение заданной функции
[w=(x+y)cdot z.]
Решение:
По определению полного приращения некоторой функции найдем:
$Delta w=((x+Delta x)+(y+Delta y))cdot (z+Delta z)$ – полное приращение функции $w=f(x,y,z)$.
Пример 4
Вычислить полное приращение заданной функции $w=xyz$ в точке $(1;2;1)$ при $Delta x=0,1;, , Delta y=0,1;, , Delta z=0,1$.
Решение:
По определению полного приращения некоторой функции найдем:
$Delta w=(x+Delta x)cdot (y+Delta y)cdot (z+Delta z)$ – полное приращение функции $w=f(x,y,z)$.
Следовательно,
[Delta z=(1+0,1)cdot (2+0,1)cdot (1+0,1)=1,1cdot 2,1cdot 1,1=2,541.]
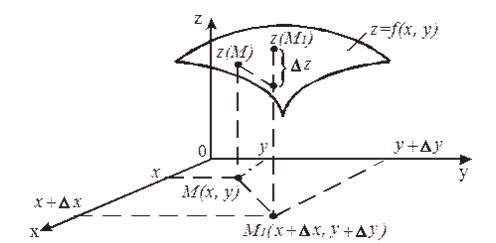
С геометрической точки зрения полное приращение функции $z=f(x,y)$ (по определению $Delta z=f(x+Delta x,y+Delta y)-f(x,y)$) равно приращению аппликаты графика функции $z=f(x,y)$ при переходе от точки $M(x,y)$ к точке $M_{1} (x+Delta x,y+Delta y)$ (рис. 1).
Рисунок 1.
Определение 4
Полный дифференциал заданной функции $z=f(x,y)$ является линейной частью приращения функции и записывается в виде
[dz=f’_{x} (x,y)cdot Delta x+f’_{y} (x,y)cdot Delta y.]
Пример 5
Записать полный дифференциал заданной функции
[z=x+2y.]
Решение:
Определим частные производные заданной функции:
[f’_{x} (x,y)=1,, , f’_{y} (x,y)=2.]
По определению полного дифференциала некоторой функции найдем:
[dz=1cdot Delta x+2cdot Delta y=Delta x+2cdot Delta y.]
Пример 6
Вычислить полный дифференциал заданной функции $z=xy$ в точке $(1;2)$ при $Delta x=0,1;, , Delta y=0,1$.
Решение:
Определим частные производные заданной функции:
[f’_{x} (x,y)=y,, , f’_{y} (x,y)=x.]
По определению полного дифференциала некоторой функции найдем:
[dz=ycdot Delta x+xcdot Delta y.]
Следовательно,
[dz|_{(1,2)} =2cdot 0,1+1cdot 0,1=0,2+0,1=0,3.]
Для функции трех и более переменных, аналогично как для функции двух переменных определяются полный дифференциал:
[dw=f’_{x} (x,y,z)cdot Delta x+f’_{y} (x,y,z)cdot Delta y+f’_{z} (x,y,z)cdot Delta z,] [dw=f’_{x} (x,y,z,…,t)cdot Delta x+f’_{y} (x,y,z,…,t)cdot Delta y+…+f’_{t} (x,y,z,…,t)cdot Delta t.]
Пример 7
Записать полный дифференциал заданной функции
[w=(x+y)cdot z.]
Решение:
Определим частные производные заданной функции:
[f’_{x} (x,y,z)=z,, , f’_{y} (x,y,z)=z,, , , f’_{z} (x,y,z)=x+y.]
По определению полного дифференциала некоторой функции найдем:
[dz=zcdot Delta x+zcdot Delta y+(x+y)cdot Delta z.]
Определение 5
Приращения независимых переменных, а именно, $Delta x,, , Delta y,, , Delta z,…,Delta t$ называют дифференциалами независимых переменных $x,y,z,…,t$. Обозначение: $dx,dy,dz,…,dt$.
В новых обозначениях выражения для полного дифференциала принимает следующий вид:
Замечание 1
Функция, имеющая непрерывные частные производные в заданной точке, является дифференцируемой в данной точке, при этом полный дифференциал функции в данной точке равен сумме произведений частных производных на дифференциалы независимых переменных соответственно.
Пример 8
Записать полный дифференциал заданной функции
[w=xcdot z.]
Решение:
Определим частные производные заданной функции:
[f’_{x} (x,y,z)=z,, , f’_{y} (x,y,z)=0,, , , f’_{z} (x,y,z)=x.]
По определению полного дифференциала некоторой функции найдем:
[dz=zcdot dx+0cdot dy+xcdot dz=zcdot dx+xcdot dz.]
Пример 9
Записать полный дифференциал заданной функции $z=xy$ в точке $(1;2)$.
Решение:
Определим частные производные заданной функции:
[f’_{x} (x,y)=y,, , f’_{y} (x,y)=x.]
По определению полного дифференциала некоторой функции найдем:
[dz=ycdot dx+xcdot dy.]
Запишем полный дифференциал в заданной точке:
[dz|_{(1,2)} =2cdot dx+1cdot dy=2dx+dy.]
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Полный дифференциал функции
Содержание:
- Дифференцируемость и полный дифференциал функции
- Примеры с решением
Дифференцируемость и полный дифференциал функции
Пусть функция 







Главная часть приращение функции 




Поэтому равенство (44.2) можно переписать в виде 
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Для функции двух переменных 


Число А называют пределом функции 












Для функции 



Возможно вам будут полезны данные страницы:
Частная производная функции 


где 





Если полное приращение функции 









Функция, обладающая непрерывными частными производными, имеет полный дифференциал, причем

Дифференциалы независимых переменных совпадают с их приращениями: 



Функцию, имеющую полный дифференциал, называют дифференцируемой.
Если функция дифференцируема в некоторой точке, то она и непрерывна в ней. Из формулы 



Примеры с решением
Пример 1.
Пусть 






Пример 2.
Найти производную функции: 1) 

Пример 3.
Найти полное приращение и полный дифференциал функции 
В соответствии с определением полное приращение 
Подставив в эту формулу значения


получим полное приращение данной функции в точке


Поскольку

то полный дифференциал данной функции выражается формулой 
Подставив в эту формулу соответствующие значения

получим значение полного дифференциала
Лекции:
- Прямые и плоскости в пространстве
- Нахождение рациональных корней
- Свойства прямоугольного треугольника
- Частное решение дифференциального уравнения
- Интегрирование иррациональных функций
- Интегральный признак сходимости ряда. Знакочередующиеся ряды
- Предел числовой последовательности
- Найти производную функции
- Исследовать функцию на непрерывность: пример решения
- Преобразование графиков функций
При выполнении некоторых расчётов в исследованиях, проектировании, анализе полученных опытных путём данных часто возникает необходимость предварительной прикидки результата, которую удобно выполнять, используя дифференциал функции.
Приближённые вычисления, выполненные с его помощью, могут дать новые направления дальнейшего изучения объектов и их разработок.
Понятие и геометрический смысл дифференциала
Пусть y = f (x) имеет производную не равную нулю.
Применяя свойства предела функции, получают равенство.
После умножения обеих частей на приращение аргумента Δx, образуется тождество:
в котором в правой части записано слагаемое, являющееся бесконечно малой одного порядка с Δx, далее идет слагаемое более высокого порядка.
Определение 1
Дифференциалом функции y = f (x) первого порядка называется главная часть её приращения f′(x)Δx, которую обозначают dy (или d(f(x)). Для наглядного представления и понимания определения рассматривается касательная к графику функции y = f(x) в точке x.
Когда значение переменной сдвигается по построенной прямой (получает приращение) на некоторую малую величину Δx, значение второй координаты точки тоже меняется.
Значит, дифференциал функции y = f(x) в точке x равен приращению ординаты касательной, когда её абсцисса меняется на величину Δx.
Определение 2
Дифференциал от дифференциала называется дифференциалом второго порядка. Таким же рекуррентным образом вводятся понятия дифференциалов более высоких порядков.
Формы записи дифференциала
Для нахождения дифференциала независимой переменной рассматривают функцию y = x, учитывая, что x’ = 1, а, следовательно:
- dx = Δx
Отсюда получается формула:
- dy = f'(x)dx
Для второго порядка вводится обозначение d2y.
Свойства дифференциала
Существующая таблица производных помогает выделить некоторые свойства дифференциалов, например, для суммы, произведения, частного получаются следующие правила:
Одним из важных свойств является инвариантность (неизменность) формы записи, независимо от того, является ли функция элементарной или композицией элементарных (сложной). Фактически:
Полный дифференциал функции
Математика не ограничивается множеством функций одного независимого аргумента. Рассматриваются зависимости от двух и более переменных.
Определения похожи, отличается вид главной части. Рассматриваются несколько слагаемых. Например, если z = f(x;y) то
Последнее равенство есть формула полного дифференциала. Для функции нескольких переменных сохраняется принцип построения.
Если рассматривают приращения только по одной переменной, то приходят к понятию частных дифференциалов.
Высшая математика позволяет находить приближённо общий корень системы уравнений, пользуясь дифференциальным исчислением, делать прикидку результатов, прогнозировать получаемое.
Источник: https://nauka.club/matematika/algebra/differentsial-funktsii.html
Дифференциальные уравнения в полных дифференциалах
Дифференциальным уравнением в полных дифференциалах называется уравнение вида:
- P(x,y)dx + Q(x,y)dy = 0, где левая часть является полным дифференциалом какой-либо функции двух переменных.
Обозначим неизвестную функцию двух переменных (её-то и требуется найти при решении уравнений в полных дифференциалах) через F и скоро вернёмся к ней. Первое, на что следует обратить внимание: в правой части уравнения обязательно должен быть нуль, а знак, соединяющий два члена в левой части, должен быть плюсом.
Второе — должно соблюдаться некоторое равенство, которое является подтверждением того, что данное дифференциальное уравнение является уравнением в полных дифференциалах.
Эта проверка является обязательной частью алгоритма решения уравнений в полных дифференциалах (он во втором параграфе этого урока), так процесс поиска функции F достаточно трудоёмкий и важно на начальном этапе убедиться в том, что мы не потратим время зря.
Итак, неизвестную функцию, которую требуется найти, обозначили через F. Сумма частных дифференциалов по всем независимым переменным даёт полный дифференциал. Следовательно, если уравнение является уравнением в полных дифференциалах, левая часть уравнения представляет собой сумму частных дифференциалов. Тогда по определению:
- dF = P(x,y)dx + Q(x,y)dy.
Вспоминаем формулу вычисления полного дифференциала функции двух переменных:
Решая два последних равенства, можем записать:
Первое равенство дифференцируем по переменной «игрек», второе — по переменной «икс»:
Так как, получим, что является условием того, что данное дифференциальное уравнение действительно представляет собой уравнение в полных дифференциалах.
Алгоритм решения дифференциальных уравнений в полных дифференциалах
Шаг 1. Убедиться, что уравнение является уравнением в полных дифференциалах. Для того, чтобы выражение было полным дифференциалом некоторой функции F(x, y), необходимо и достаточно, чтобы . Иными словами, нужно взять частную производную по x одного слагаемого в левой части выражения и частную производную по y другого слагаемого и, если эти производные равны, то уравнение является уравнением в полных дифференциалах.
Шаг 2. Записать систему уравнений из частных производных, составляющих функцию F:
Шаг 3. Проинтегрировать первое уравнение системы — по x (y остаётся константой и выносится за знак интеграла). Таким образом восстанавливаем функцию F:
, где — пока неизвестная функция от y.
Альтернативный вариант (если так интеграл найти проще) — проинтегрировать второе уравнение системы — по y (x остаётся константой и выносится за знак интеграла). Таким образом так же восстанавливается функция F:
, где — пока неизвестная функция от х.
Шаг 4. Результат шага 3 (найденный общий интеграл) продифференцировать по y (в альтернативном варианте — по x) и приравнять ко второму уравнению системы:
а в альтернативном варианте — к первому уравнению системы:
Из полученного уравнения определяем (в альтернативном варианте ).
Шаг 5. Результат шага 4 интегрировать и найти (в альтернативном варианте найти ).
Шаг 6. Результат шага 5 подставить в результат шага 3 — в восстановленную частным интегрированием функцию F. Произвольную постоянную C чаще записывают после знака равенства — в правой части уравнения. Таким образом получаем общее решение дифференциального уравнения в полных дифференциалах. Оно, как уже говорилось, имеет вид F(x, y) = C.
Источник: https://function-x.ru/differential_equations5.html