-
Дифференциалом
второго порядка функции
 называется дифференциал от дифференциала
называется дифференциал от дифференциала
первого порядка:
![]() .
.
Пример 4.
Для функции
![]() найти дифференциал второго порядка.
найти дифференциал второго порядка.
Найдем частные
производные первого и второго порядка:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;![]() ;
;
Дифференциал
второго порядка равен
![]() .
.
7. Градиент функции двух переменных
![]() .
.
Свойства градиента
-
Градиент показывает
направление
наибольшего
возрастания значений функции. -
Длина вектора
градиента равен максимальной
скорости
изменения функции в направлении
градиента. -
Для функции
 градиент
градиент
 перпендикулярен
перпендикулярен
линии уровня,
проходящей через точку
 .
.
Пример 5.
Дана функция
![]() .
.
Найти градиент![]() в точке
в точке![]() и построить его.
и построить его.
Найдем координаты
градиента – частные производные.
![]() .
.
В точке
![]() градиент
градиент
равен
![]() .
.
Начало вектора![]() в точке
в точке![]() ,
,
а конец – в точке![]() .
.
 5
5
![]()
1
0
2 4
![]()
Аналогично
определяется градиент функции трех
переменных
![]() :
:
![]()
Контрольные вопросы
-
Дайте определение
функции двух переменных
 .
. -
Что является
областью определения функции
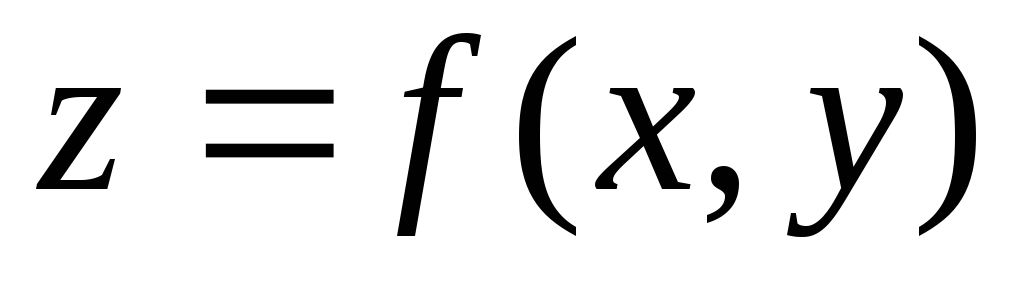 ?
? -
Что является
графиком функции двух переменных
 ?
? -
Графиком какой
функции двух переменных является
плоскость? -
Что называется
линией уровня функции
 ?
? -
Как расположены
линии уровня линейной функции
 ?
? -
Как расположены
линии уровня функции
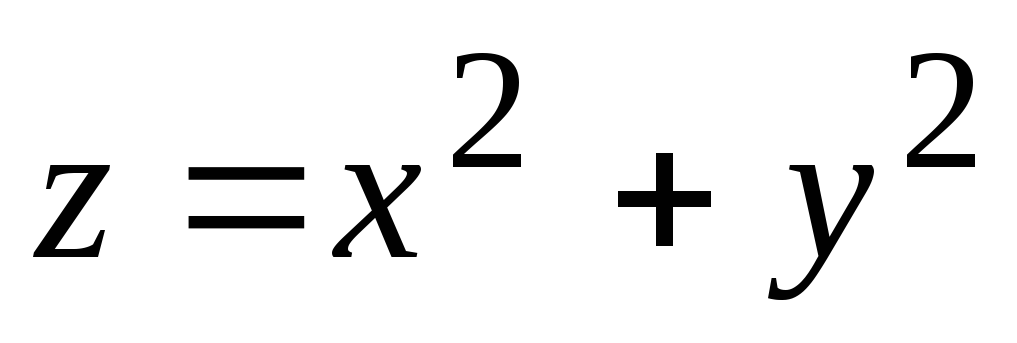 ?
? -
Запишите
частное приращение функции двух
переменных по переменной
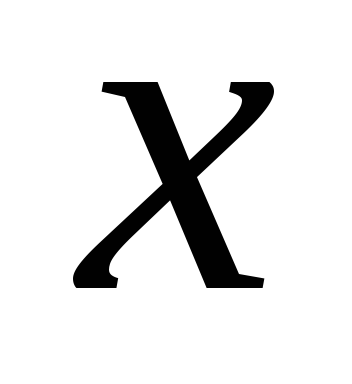 .
. -
Как
определяется частная производная
функции
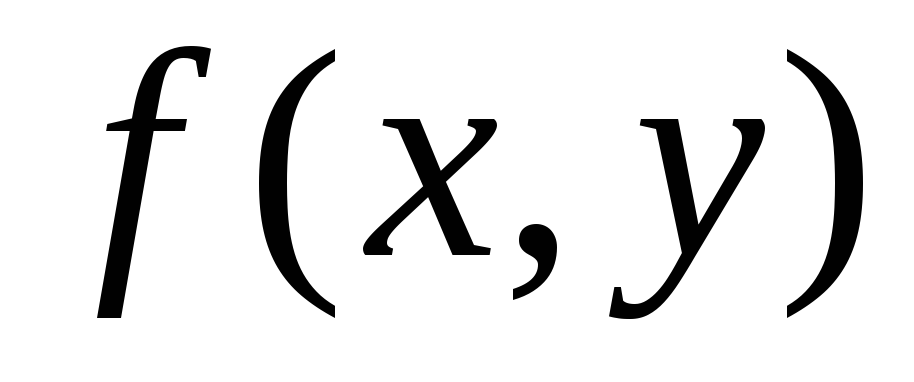 по переменной
по переменной ?
?
По переменной ?
? -
Как вычисляются
частные производные? -
Дайте
определение частных производных второго
порядка, третьего,
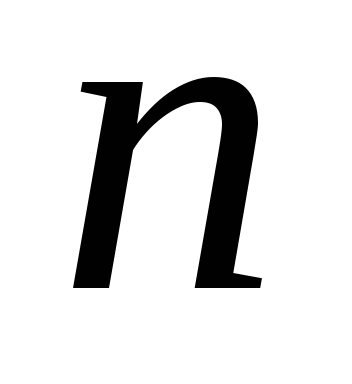 -го
-го
порядка функции .
. -
Что
означает символическая запись
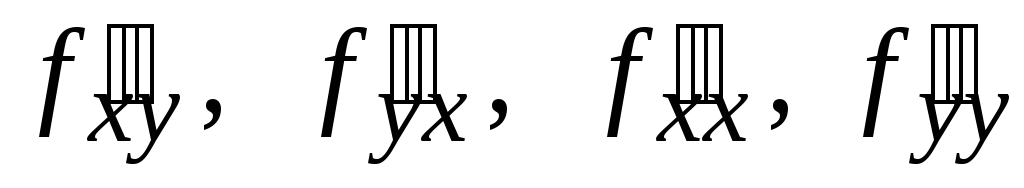 ?
? -
Сформулируйте
свойство смешанных частных производных
функций двух переменных. -
Запишите полное
приращение для функций двух переменных. -
Что называется
полным дифференциалом функции
 ?
? -
Как найти полный
дифференциал функции
 ?
? -
Запишите формулу
для нахождения дифференциала второго
порядка функции
 .
. -
Какова связь между
полным дифференциалом функции нескольких
переменных и ее полным приращением? -
Сформулируйте
свойства градиента. -
Как
расположен градиент функции
 относительно линий уровня?
относительно линий уровня?
Тема 2. Экстремум функции двух переменных
Содержание
-
Локальный
экстремум -
Условный
экстремум функции двух переменных
1. Локальный экстремум
-
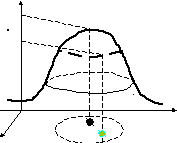
Максимумы и
минимумы функции называются экстремумами
функции.
![]()
![]()
![]()
![]()
![]()
![]()
На рисунке точка
![]() является точкой максимума функции.
является точкой максимума функции.
-
Точка
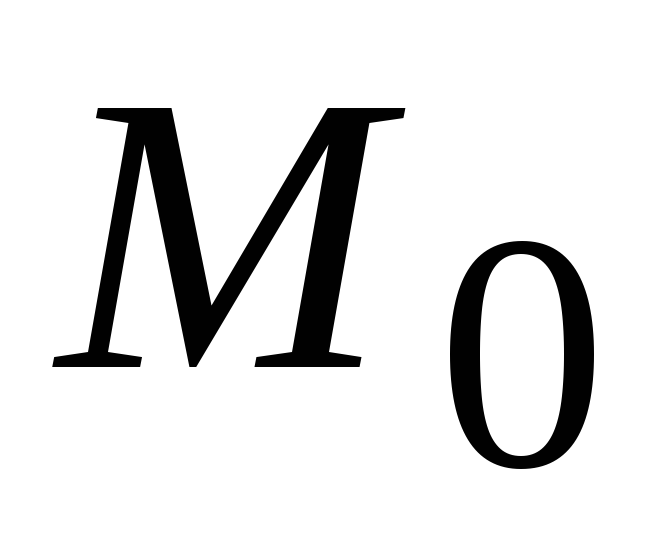 называетсястационарной
называетсястационарной
точкой функции
 ,
,
если она является внутренней
точкой
области определения функции и все
частные производные первого
порядка в
ней равны
нулю. -
Точка
 ,
,
в которой частные производные равны
нулю или не существуют, называетсякритической
точкой функции
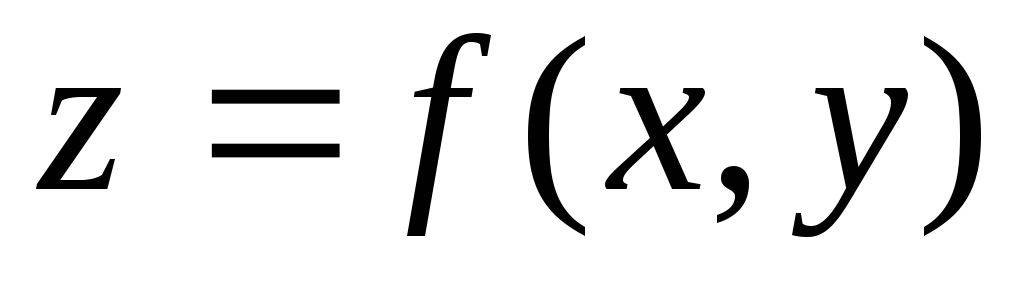 .
.
Таким образом,
точки экстремума следует искать среди
ее критических точек.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Дифференцируемость функции нескольких переменных:
Рассмотрим функцию 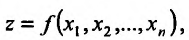
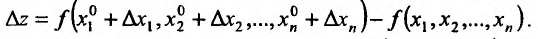
Определение 16.1.1. Функция 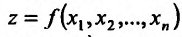 называется дифференцируемой в точке
называется дифференцируемой в точке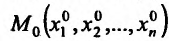 если ее полное приращение в этой точке может быть представлено в виде:
если ее полное приращение в этой точке может быть представлено в виде: 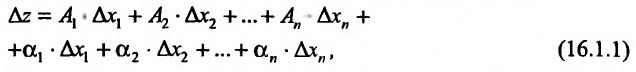
где 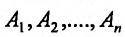 – постоянные величины, а
– постоянные величины, а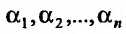 – бесконечно малые при
– бесконечно малые при 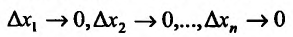 функции, равные нулю при
функции, равные нулю при 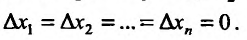
Равенство (16.1.1) называется условием дифференцирусмости функции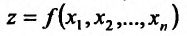 в точке
в точке 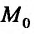 . Это условие можно записать и в следующем виде:
. Это условие можно записать и в следующем виде:
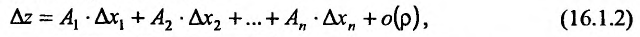
где 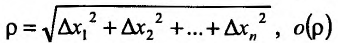 – бесконечно малая функция более высокого порядка малости по сравнению с
– бесконечно малая функция более высокого порядка малости по сравнению с 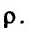 . Справедлива следующая теорема.
. Справедлива следующая теорема.
Теорема 16.1.1. Если функция 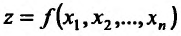 дифференцируема в точке
дифференцируема в точке 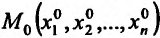 то в этой точке существуют частные производные по всем аргументам, причем
то в этой точке существуют частные производные по всем аргументам, причем 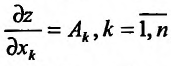 , где
, где 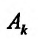 определяются из условия (16.1.1) или (16.1.2) дифференцируемости функции.
определяются из условия (16.1.1) или (16.1.2) дифференцируемости функции.
Доказательство. Пусть функция 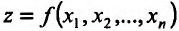 дифференцируема в точке
дифференцируема в точке 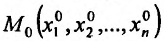 . Тогда выполняется равенство (16.1.2), из которого следует, что частное приращение
. Тогда выполняется равенство (16.1.2), из которого следует, что частное приращение 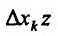 функции
функции 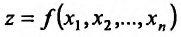 в этой точке равно
в этой точке равно 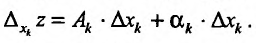 . Разделив все члены этого равенства на
. Разделив все члены этого равенства на 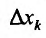 и, перейдя к пределу при
и, перейдя к пределу при 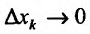 , последовательно получим:
, последовательно получим: 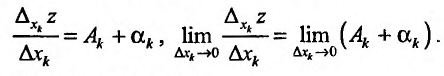
Откуда следует, что
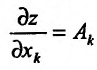 , так как
, так как 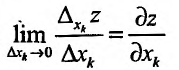
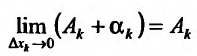 , так как
, так как 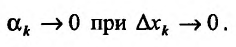
Теорема доказана.
Из доказанной теоремы следует, что условие дифференцируемости (16.1.2) можно записать в следующей форме:
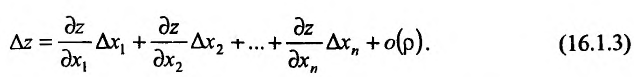
Так как коэффициенты 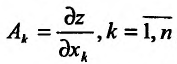 определяются единственным образом, то дифференцируемую функцию можно представить единственным образом в форме (16.1.1) или (16.1.2).
определяются единственным образом, то дифференцируемую функцию можно представить единственным образом в форме (16.1.1) или (16.1.2).
Кроме того, из дифференцируемое функции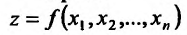 в точке
в точке 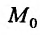 следует ее непрерывность в этой точке.
следует ее непрерывность в этой точке.
Сформулируем теперь достаточные условия дифференцируемости функции.
Теорема 16.1.2. Если функция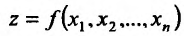 имеет частные производные по всем аргументам в некоторой окрестности точки
имеет частные производные по всем аргументам в некоторой окрестности точки 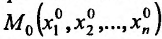 непрерывные в самой точке
непрерывные в самой точке  , то она дифференцируема в точке
, то она дифференцируема в точке 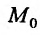
Доказательство. Для простоты доказательство приведем для функции z = f(x,y) двух переменных. Предположим, что функция z = f(x,y) имеет непрерывные частные производные в рассматриваемой точке 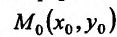 . Выразим полное приращение
. Выразим полное приращение 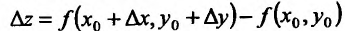 через частные производные. Для этого в правой части равенства прибавим и вычтем
через частные производные. Для этого в правой части равенства прибавим и вычтем 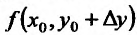 :
:
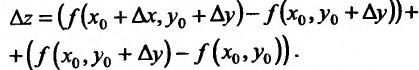
Выражение 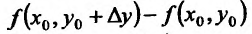 – приращение по у, a
– приращение по у, a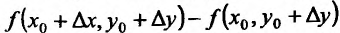 приращение по х. Применяя к каждому из приращений теорему Лагранжа (применить теорему Лагранжа можем, так как частные производные непрерывны в точке
приращение по х. Применяя к каждому из приращений теорему Лагранжа (применить теорему Лагранжа можем, так как частные производные непрерывны в точке 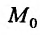 ), получим:
), получим:
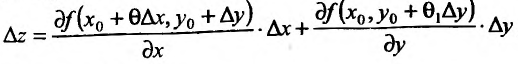
где 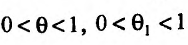
Так как частные производные, по предположению, непрерывны, то
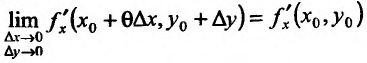
и
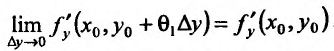
Тогда, используя представления, для функции, имеющей предел, получим.
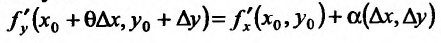
и
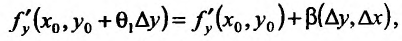
где 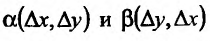 – бесконечно малые функции порядка малости выше по сравнению с
– бесконечно малые функции порядка малости выше по сравнению с 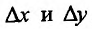 , и, следовательно,
, и, следовательно, 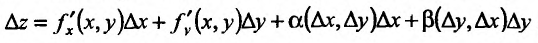
Приращение функции представлено в форме (16.1.2), значит, функция z = f(x,y) дифференцируема в точке 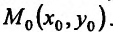 . Теорема доказана.
. Теорема доказана.
Дифференциал функции первого и высших порядков
Главную линейную относительно приращений аргументов часть приращения функции 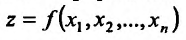 в точке
в точке
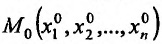 называют полным дифференциалом dz дифференцируемой функции:
называют полным дифференциалом dz дифференцируемой функции:
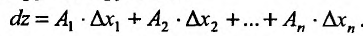
Используя (16.1.3), это равенство можно переписать в виде:
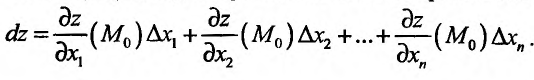
Под дифференциалом 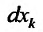 независимой переменной хк будем понимать число, равное приращению
независимой переменной хк будем понимать число, равное приращению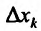 . Тогда полный дифференциал будет определяться равенством:
. Тогда полный дифференциал будет определяться равенством:
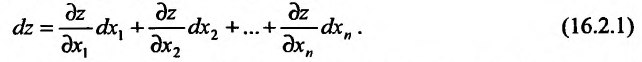
Формула (16.2.1) дифференциала функции 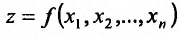 установлена для случая, когда аргументы
установлена для случая, когда аргументы 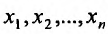 являются независимыми переменными. Эта же формула справедлива и в том случае, когда аргументы
являются независимыми переменными. Эта же формула справедлива и в том случае, когда аргументы 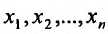 сами являются дифференцируемыми функциями некоторых новых аргументов
сами являются дифференцируемыми функциями некоторых новых аргументов 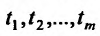 , которые можно считать независимыми. Это свойство первого дифференциала называют свойством инвариантности его формы.
, которые можно считать независимыми. Это свойство первого дифференциала называют свойством инвариантности его формы.
Для функции z = f(x,y) двух переменных дифференциал определяется по формуле:

Ясно, что если функция z = f(x,y) дифференцируема в точке, то она имеет единственный дифференциал, так как частные производные определяются однозначно.
Полный дифференциал применяется в приближенных вычислениях. Для этого формулу полного приращения 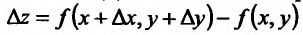 представим в виде:
представим в виде:
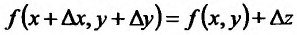
Из предыдущего ясно, что, с точностью до бесконечно малых высшего порядка относительно 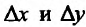 , можно написать равенство:
, можно написать равенство:
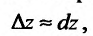 , где
, где 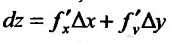 .
.
Поэтому
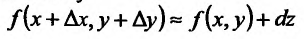
или 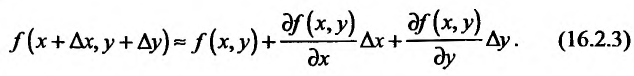
Формула (16.2.3) используется в приближенных вычислениях.
Пример:
Вычислить дифференциал функции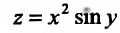
Решение:
Из рассуждений, приведенных выше, следует, что для вычисления дифференциала функции z = f(x,y), нужно вычислить частные производные и подставить их в формулу (46.2.2). Вычислив частные производные:
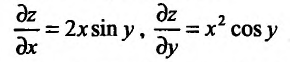
и подставив их в формулу полного дифференциала, получим:
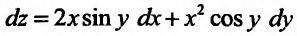
Пример:
Вычислить значение выражения
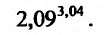
Решение:
Введем в рассмотрение функцию 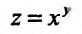 и выделим
и выделим 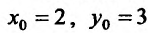 . Тогда
. Тогда 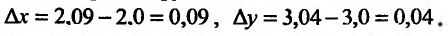 . Вычислим:
. Вычислим:
а) частные производные функции 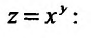
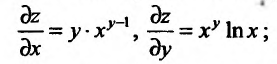
б) значения функции и частных производных в точке (2;3):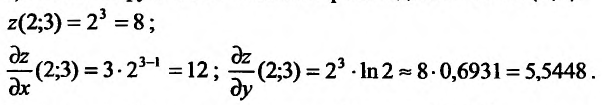
Подставив найденные значения в формулу (16.2.3), получим: 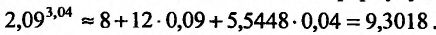 .
.
Предположим, что величина, стоящая в правой части (16.2.2), представляет собой функцию аргументов 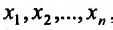 , дифференцируемую в данной точке
, дифференцируемую в данной точке 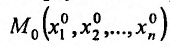 . Тогда сама функция
. Тогда сама функция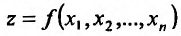 должна быть дважды дифференцируемой в точке
должна быть дважды дифференцируемой в точке 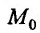 , а аргументы являлись независимыми переменными или два раза дифференцируемыми функциями некоторых независимых переменных
, а аргументы являлись независимыми переменными или два раза дифференцируемыми функциями некоторых независимых переменных 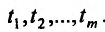 . При этих предположениях можно рассматривать дифференциал
. При этих предположениях можно рассматривать дифференциал
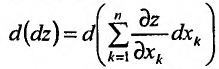
который называется вторым дифференциалом или дифференциалом второго порядка функции 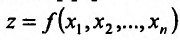 и обозначается
и обозначается 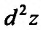 .
.
Дифференциал 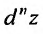 любого порядка п вводится по индукции, го есть
любого порядка п вводится по индукции, го есть
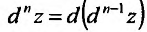
В случае, когда аргументы 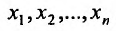 являются независимыми переменными, для дифференциала второго порядка справедливо представление:
являются независимыми переменными, для дифференциала второго порядка справедливо представление:
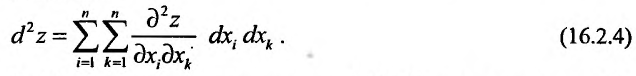
Дифференциал второго порядка (16.2.4) представляет собой симметричную (так как 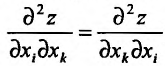 ) квадратичную форму от переменных
) квадратичную форму от переменных , коэффициенты которой равны соответствующим частным производным второго порядка функции
, коэффициенты которой равны соответствующим частным производным второго порядка функции  . В частности, дифференциал второго порядка функции z= f(x,y) определяется равенством:
. В частности, дифференциал второго порядка функции z= f(x,y) определяется равенством:
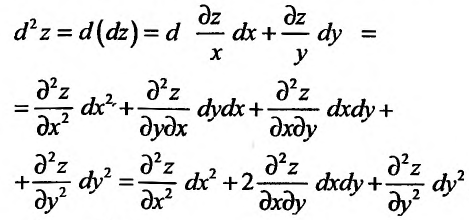
так как

Если аргументы 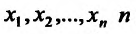 раз дифференцируемой функции
раз дифференцируемой функции 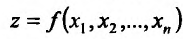 в точке
в точке 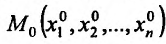 являются независимыми переменными, для дифференциала n-го порядка этой функции справедливо представление:
являются независимыми переменными, для дифференциала n-го порядка этой функции справедливо представление:
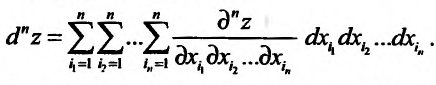
Другой вид имеют представления для второго и последующих дифференциалов функции 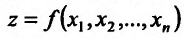 в случае, когда аргументы
в случае, когда аргументы 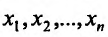 являются функциями переменных
являются функциями переменных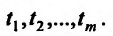
Пример:
Вычислить дифференциал второго порядка функции
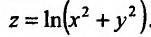
Решение:
Применим формулу (16.2.5) предварительно вычислив последовательно частные производные первого и второго порядков:
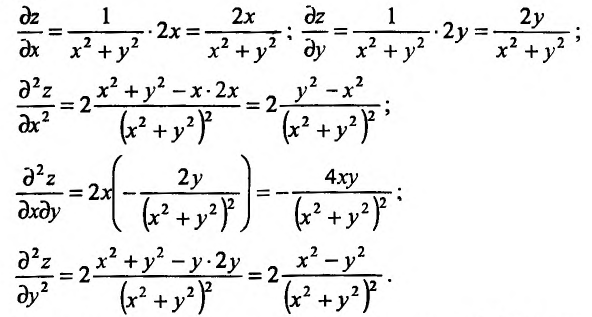
Подставив значения частных производных в (16.2.5), получим искомое выражение дифференциала второго порядка заданной функции:
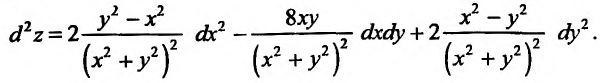
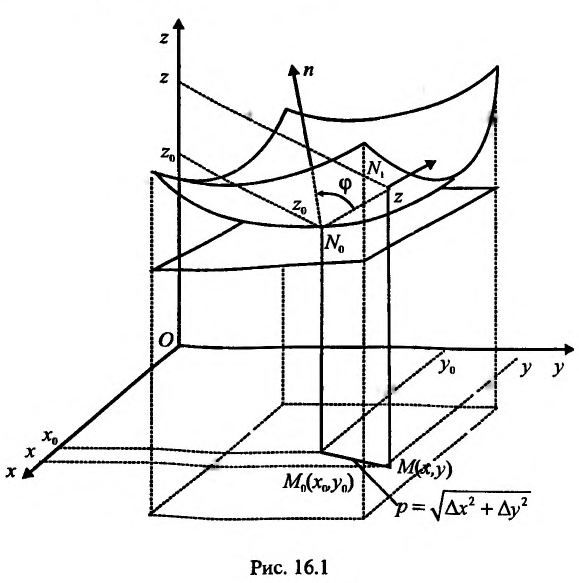
Геометрический смысл условия
Рассмотрим функцию двух переменных z= f(x,y) и предположим, что она дифференцируема в точке  . Тогда (16.1.2) можно записать в виде:
. Тогда (16.1.2) можно записать в виде:
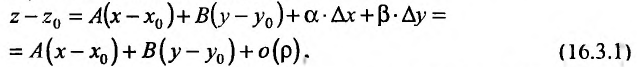
где А и В – постоянные величины, равные частным производным в точке 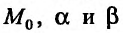 – бесконечно малые при
– бесконечно малые при 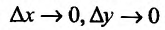 функции,
функции, 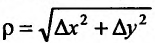 .
.
Из аналитической геометрии известно, что уравнение  определяет некоторую плоскость, проходящую через точку
определяет некоторую плоскость, проходящую через точку 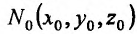 и имеющую нормальный вектор
и имеющую нормальный вектор 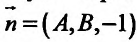 .
.
С геометрической точки зрения, графиком функции z = f(x,y) является поверхность в системе прямоугольных декартовых координат (x,y,z), проектирующаяся на плоскость Оху в область определения функции.
Назовем плоскость, проходящую через точку 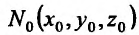 поверхности, касательной плоскостью в этой точке, если угол между этой плоскостью и секущей плоскостью, проходящей через точку
поверхности, касательной плоскостью в этой точке, если угол между этой плоскостью и секущей плоскостью, проходящей через точку 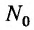 и любую другую точку
и любую другую точку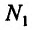 поверхности, стремятся к нулю, если точка
поверхности, стремятся к нулю, если точка 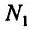 стремится к точке
стремится к точке 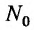 .
.
Очевидно, что плоскость (16.3.2) проходит через точку 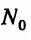 поверхности. Так как координаты вектора
поверхности. Так как координаты вектора 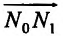 секущей плоскости равны
секущей плоскости равны 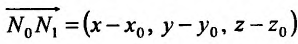 , то угол между векторами
, то угол между векторами  и
и  определяется по формуле:
определяется по формуле:
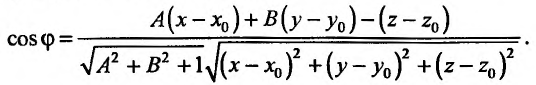
Из условия дифференцируемое™ (16.1.2) следует, что разность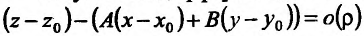 является величиной бесконечно малой, при
является величиной бесконечно малой, при 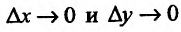 . Значит
. Значит 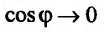 когда
когда 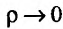 , то есть
, то есть 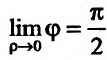 . Следовательно, плоскость
. Следовательно, плоскость 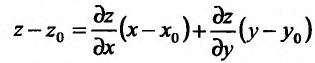 касательная к поверхности z = f(x,y).
касательная к поверхности z = f(x,y).
Таким образом, с геометрической точки зрения, дифференцируемость функции z = f(x,y) в точке 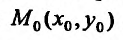 означает наличие касательной плоскости (16.3.3) к поверхности функции z = f(x,y) в точке
означает наличие касательной плоскости (16.3.3) к поверхности функции z = f(x,y) в точке  (см. рис. 16.1).
(см. рис. 16.1).
Производная по направлению
Рассмотрим функцию z=f(x,y), определенную в некоторой окрестности точки  и дифференцируемую в точке
и дифференцируемую в точке  , и всевозможные лучи, выходящие из точки М0. Направление каждого луча задается единичным вектором
, и всевозможные лучи, выходящие из точки М0. Направление каждого луча задается единичным вектором 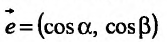 с направляющими косинусами, где
с направляющими косинусами, где 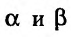 углы, которые составляет вектор
углы, которые составляет вектор 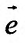 с осями координат Ох и Оу.
с осями координат Ох и Оу.
Фиксируем некоторый луч, выходящий из точки 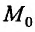 , выберем на нем произвольную точку М(х,у) и рассмотрим вектор
, выберем на нем произвольную точку М(х,у) и рассмотрим вектор 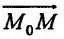 , обозначив его величину через l (см. рис. 16.2). Тогда координаты этого вектора
, обозначив его величину через l (см. рис. 16.2). Тогда координаты этого вектора 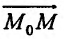 определяются его величиной l и направлением фиксированного луча, которое совпадает с направлением единичного вектора
определяются его величиной l и направлением фиксированного луча, которое совпадает с направлением единичного вектора 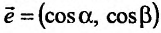 :
:
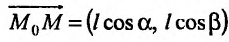
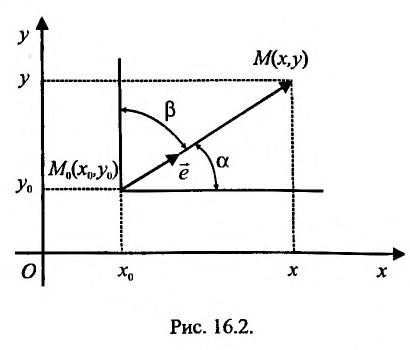
С другой стороны, координаты вектора 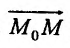 равны разностям координат конечной и начальной точек вектора:
равны разностям координат конечной и начальной точек вектора: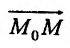
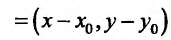 Сопоставляя два соотношения для координат вектора
Сопоставляя два соотношения для координат вектора 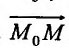 , получим равенства:
, получим равенства: 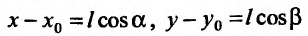 или
или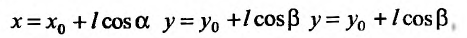 Подставив, значения координат х и у в функцию z = f(x,y), получим, что на луче, выходящем из точки
Подставив, значения координат х и у в функцию z = f(x,y), получим, что на луче, выходящем из точки 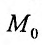 , направление которого определяется единичным вектором
, направление которого определяется единичным вектором 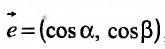 , функция z = f(x,y) представляет собой сложную функцию одной переменной l вида
, функция z = f(x,y) представляет собой сложную функцию одной переменной l вида 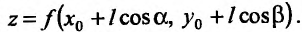 .
.
Определение 16.4.1. Производная сложной функции 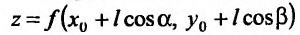 по переменной l, в точке 1 = 0, называется производной функции z = f(x,y) в точке
по переменной l, в точке 1 = 0, называется производной функции z = f(x,y) в точке  по направлению, определяемому единичным вектором
по направлению, определяемому единичным вектором 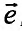 , и обозначаемой символом
, и обозначаемой символом 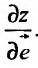 .
.
Так как вдоль луча 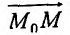 функция z = f{x.y) является функцией одной переменной l, то производную по направлению можно рассматривать как предел отношения прирашения функции z = f(x,y) к величине l вектора
функция z = f{x.y) является функцией одной переменной l, то производную по направлению можно рассматривать как предел отношения прирашения функции z = f(x,y) к величине l вектора 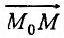 , когда эта величина стремиться к нулю:
, когда эта величина стремиться к нулю:
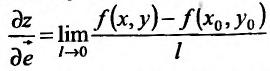
Из определения 16.4.1 получим формулу для вычисления производной по направлению, определяемому вектором 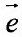
Пример №1
Вычислить производную функции 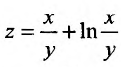 в точке
в точке 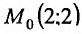 по направлению, определяемому вектором
по направлению, определяемому вектором 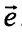 , который составляет с осью Ох угол равный 45°.
, который составляет с осью Ох угол равный 45°.
Решение:
Воспользуемся формулой (16.4.1) и вычислим частные производные заданной функции:
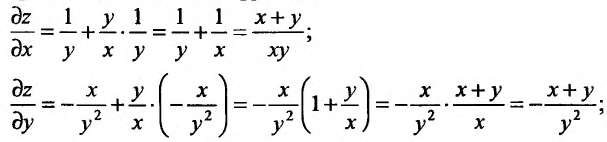
и их значения в точке 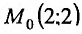 :
:
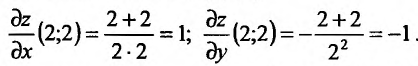
Подставив эти значения в формулу (16.4.1), получим:

Это означает, что заданная функция в указанном направлении является постоянной.
В практических приложениях особый интерес представляет вопрос о направлении быстрейшего возрастания функции в точке. С этой целью вводится понятие градиента дифференцируемой в данной точке  функции z = f(x,y).
функции z = f(x,y).
Определение 16.4.2. Градиентом функции z = f(x,y) в данной точке  называется вектор, имеющий своим началом эту точку, координатами которого являются частные производные этой функции в точке
называется вектор, имеющий своим началом эту точку, координатами которого являются частные производные этой функции в точке  .
.
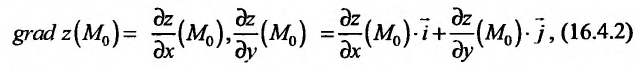
где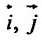 – единичные векторы координатных осей Ох и Оу.
– единичные векторы координатных осей Ох и Оу.
Воспользовавшись тем, что, скалярное произведение векторов равно сумме произведений одноименных координат этих векторов, выражение (16.4.1) для производной по направлению, определяемому вектором 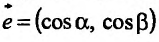 , можно рассматривать как скалярное произведение векторов
, можно рассматривать как скалярное произведение векторов 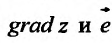 :
:

Скалярное произведение двух векторов равно произведению длин этих векторов на косинус угла между ними. Поэтому выражение (16.4.3) можно переписать в виде:
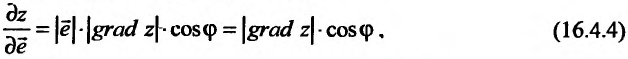
где 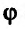 – угол между векторами
– угол между векторами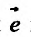 и
и 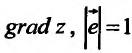 . Из равенства (16.4.4) следует теорема.
. Из равенства (16.4.4) следует теорема.
Теорема 16.4.1. Градиент функции z = f(x,y) в точке 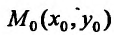 характеризует направление и величину максимального роста этой функции в точке
характеризует направление и величину максимального роста этой функции в точке 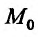 .
.
Действительно, производная 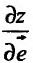 достигает максимального значения при
достигает максимального значения при 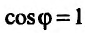 , то есть если
, то есть если 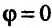 . Это означает, что направление вектора
. Это означает, что направление вектора 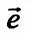 совпадает с направлением вектора
совпадает с направлением вектора 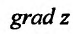 , причем производная
, причем производная 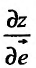 в этом направлении равна
в этом направлении равна 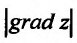 .
.
Очевидно, что направление противоположное градиенту, будет являться направлением быстрейшего убывания функции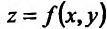 .
.
Пример №2
Найти направление быстрейшего возрастания функции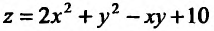 в точке
в точке 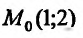 и вычислить значение производной в этом направлении.
и вычислить значение производной в этом направлении.
Решение:
Как доказано выше, направление и величину максимального роста функции определяет градиент этой функции. Поэтому вычислим частные производные этой функции: 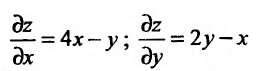 и их значения в точке
и их значения в точке 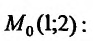
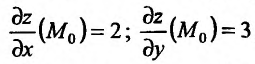 и подставим в выражение (16.4.2):
и подставим в выражение (16.4.2): 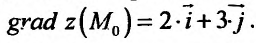
Следовательно, искомое направление составляет угол 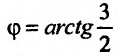 осью Ох. Производная по направлению, определяемая градиентом этой функции в данной точке, равна
осью Ох. Производная по направлению, определяемая градиентом этой функции в данной точке, равна 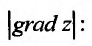
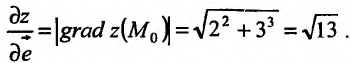
Выясним геометрический смысл вектора grad z. Для этого рассмотрим линии уровня функции z = f(x,y), понимая под этим термином те линии, на которых функция z = f(x,y) сохраняет постоянное значение, то есть удовлетворяет соотношению f(х,у)=с. Построим касательную к линии уровня, угловой коэффициент которой равен-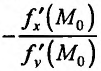 . Угловой коэффициент grad z в точке
. Угловой коэффициент grad z в точке 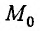 равен
равен 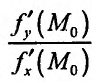 . Произведение угловых коэффициентов касательной и grad z равно — 1. Следовательно, вектор grad z в каждой точке линии уровня имеет направление перпендикулярное к
. Произведение угловых коэффициентов касательной и grad z равно — 1. Следовательно, вектор grad z в каждой точке линии уровня имеет направление перпендикулярное к 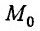 линии уровня.
линии уровня.
Аналогично определяется производная по направлению и градиент для дифференцируемой в данной точке 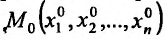 функции
функции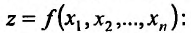
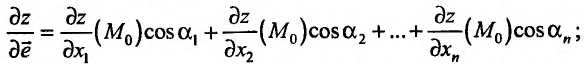
Производная по направлению, определяемому вектором 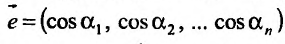 , также равна скалярному произведению вектора
, также равна скалярному произведению вектора 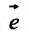 и grad z:
и grad z:
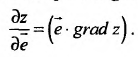
Определение экстремума функции двух переменных
Пусть функция n переменных 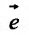 определена в некоторой окрестности точки
определена в некоторой окрестности точки 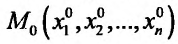 пространства
пространства 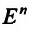 . Функция z = f(м) будет иметь в точке
. Функция z = f(м) будет иметь в точке 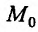 локальный максимум (минимум), если существует такая
локальный максимум (минимум), если существует такая 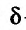 -окрестность точки
-окрестность точки 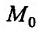 , что для всех точек М из этой окрестности значение
, что для всех точек М из этой окрестности значение 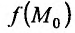 является наибольшим (наименьшим) среди всех значений
является наибольшим (наименьшим) среди всех значений 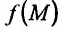 этой функции. Точки локального максимума или локального минимума называются точками экстремума.
этой функции. Точки локального максимума или локального минимума называются точками экстремума.
Рассмотрим функцию двух переменных z = f(x, у) и определим необходимые условия экстремума. Функция z = f(x,y) достигает максимума в точке 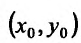 , если значение
, если значение 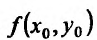 не меньше всех смежных значений функции, то есть
не меньше всех смежных значений функции, то есть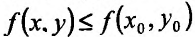 Для всех точек (х,у) из некоторой
Для всех точек (х,у) из некоторой 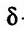 -окрестности точки
-окрестности точки 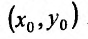 достаточно близких к точке и отличных от нее.
достаточно близких к точке и отличных от нее.
Функция z = f(x,y) достигает минимума в точке 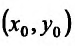 , если
, если 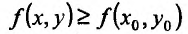 для всех (х,y) из некоторой
для всех (х,y) из некоторой  -окрестности точки
-окрестности точки 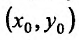 . Максимум и минимум функции называются экстремумами функции.
. Максимум и минимум функции называются экстремумами функции.
Итак, пусть точка 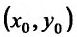 – является точкой локального максимума либо минимума, то есть точкой локального экстремума. Фиксируем у функции
– является точкой локального максимума либо минимума, то есть точкой локального экстремума. Фиксируем у функции 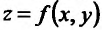 аргумент
аргумент 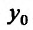 , то есть, положим
, то есть, положим 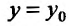 . Рассмотрим функцию
. Рассмотрим функцию 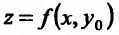 одной независимой переменной X. По предположению она должна достигать локального максимума при
одной независимой переменной X. По предположению она должна достигать локального максимума при 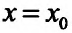 , и поэтому ее производная по X должна или превращаться в нуль или не существовать. Но производная функции
, и поэтому ее производная по X должна или превращаться в нуль или не существовать. Но производная функции 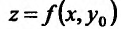 – это частная производная по X функции
– это частная производная по X функции 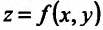 и, следовательно, она должна или равняться нулю или не существовать. Аналогичным рассуждением убедимся, что и производная функции
и, следовательно, она должна или равняться нулю или не существовать. Аналогичным рассуждением убедимся, что и производная функции 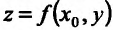 по у должна или обращаться в нуль или не существовать при
по у должна или обращаться в нуль или не существовать при 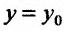 – Итак, мы приходим к следующей теореме.
– Итак, мы приходим к следующей теореме.
Теорема 17.1.1. Функция z = f(x,y) может достигать локального максимума либо минимума лишь при тех значениях х и у, при которых частные производные первого порядка 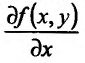 и
и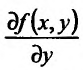 обращаются в нуль либо не существуют.
обращаются в нуль либо не существуют.
Аналогичное утверждение справедливо и для функции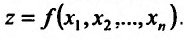
Если функция 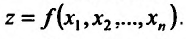 имеет в точке
имеет в точке 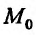 частные производные и точка
частные производные и точка 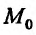 является точкой локального экстремума, то все частные производные первого порядка обращаются в нуль в точке
является точкой локального экстремума, то все частные производные первого порядка обращаются в нуль в точке 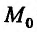 :
:
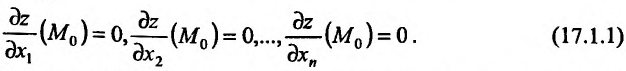
Равенства (17.1.1) являются лишь необходимыми и не являются достаточными условиями локального экстремума. Например, у функции z = ху частные производные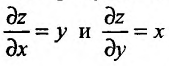 обращаются в нуль в точке
обращаются в нуль в точке 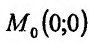 , но экстремума в этой точке функция z = xy не имеет, так как в как угодно малой
, но экстремума в этой точке функция z = xy не имеет, так как в как угодно малой 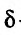 -окрестности этой точки функция принимает как положительные, так и отрицательные значения.
-окрестности этой точки функция принимает как положительные, так и отрицательные значения.
Точки, в которых обращаются в нуль все частные производные первого порядка функции z= f(x,y), называются стационарными точками.
Отметим, что если функция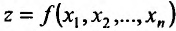 дифференцируема в точке
дифференцируема в точке 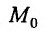 и имеет в этой точке локальный экстремум, то дифференциал dz этой функции в точке
и имеет в этой точке локальный экстремум, то дифференциал dz этой функции в точке 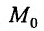 равен нулю:
равен нулю:
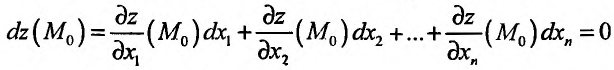
при любых 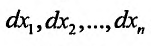
Пример №3
Исследовать функцию 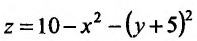 на экстремум.
на экстремум.
Решение:
Функция определена при 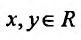 . Вычислим частные производные заданной функции
. Вычислим частные производные заданной функции 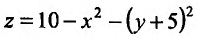 :
:
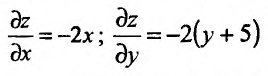
и приравняем их к нулю. Получим систему:
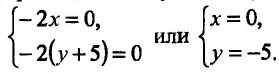
Итак, точка 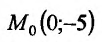 может быть точкой экстремума Наличие экстремума можно установить лишь с помощью достаточного условия.
может быть точкой экстремума Наличие экстремума можно установить лишь с помощью достаточного условия.
Достаточное условие экстремума
При формулировке достаточного условия локального экстремума функции n переменных 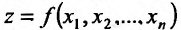 важную роль играет дифференциал второго порядка этой функции:
важную роль играет дифференциал второго порядка этой функции:

который представляет собой квадратичную форму относительно дифференциалов аргументов 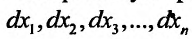 . Введем обозначение
. Введем обозначение
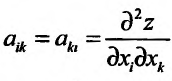 (в частности,
(в частности,
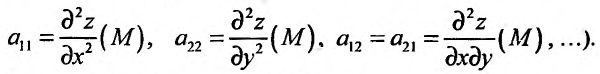
Тогда матрица квадратичной формы

может бьггь записана в виде:
где 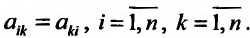 Используя критерий Сильвестра: «Для того, чтобы квадратичная форма (17.2.2) была положительно определенной (отрицательно определенной), необходимо и достаточно, чтобы все главные миноры матрицы (17.2.3) были положительные, то есть чтобы
Используя критерий Сильвестра: «Для того, чтобы квадратичная форма (17.2.2) была положительно определенной (отрицательно определенной), необходимо и достаточно, чтобы все главные миноры матрицы (17.2.3) были положительные, то есть чтобы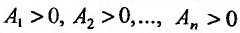 (чтобы знаки главных миноров матрицы (17.2.3) чередовались, то есть
(чтобы знаки главных миноров матрицы (17.2.3) чередовались, то есть 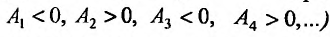 можно сформулировать достаточные условия экстремума функции двух переменных.
можно сформулировать достаточные условия экстремума функции двух переменных.
Теорема 17.2.1. Пусть функция двух переменных z = f(x,y) один раз дифференцируема в окрестности точки 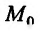 и два раза дифференцируема в самой точке
и два раза дифференцируема в самой точке 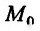 и пусть
и пусть 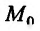 является стационарной точкой. Тогда, если в точке
является стационарной точкой. Тогда, если в точке 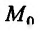 выполнено условие
выполнено условие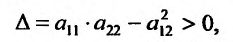 , то функция z = f(x, у) имеет в точке
, то функция z = f(x, у) имеет в точке 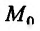 локальный экстремум (максимум при
локальный экстремум (максимум при 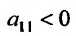 и минимум при
и минимум при 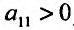 ). Если же в точке
). Если же в точке 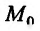
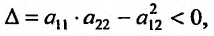 , то функция z = f(x, у) не имеет в этой точке локального экстремума. Случай
, то функция z = f(x, у) не имеет в этой точке локального экстремума. Случай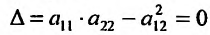 требует дополнительного исследования.
требует дополнительного исследования.
Справедливость первой части теоремы вытекает из критерия Сильвестра, так как главные миноры матрицы (17.2.3) квадратичной формы равны
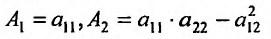 и если
и если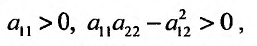
то дифференциал второго порядка является положительно определенной квадратичной формой, а если
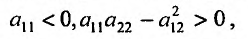 то отрицательно определенной квадратичной формой.
то отрицательно определенной квадратичной формой.
Знак разности 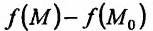 определяется дифференциалом второго порядка, что следует из формулы Тейлора:
определяется дифференциалом второго порядка, что следует из формулы Тейлора:
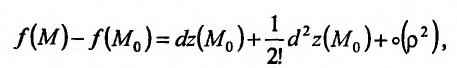
где 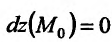 . Тогда если
. Тогда если 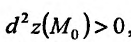 , то разность
, то разность 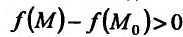 , и тогда
, и тогда 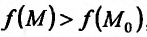 , следовательно, точка
, следовательно, точка 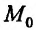 является точкой минимума. Если же
является точкой минимума. Если же 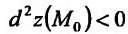 , то
, то 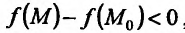 и тогда
и тогда 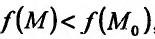 , следовательно, точка
, следовательно, точка 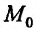 является точкой максимума. Если же в точке
является точкой максимума. Если же в точке 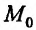
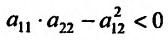 , то дифференциал второго порядка
, то дифференциал второго порядка 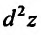 представляет собой знакопеременную квадратичную форму и, следовательно, не сохраняется знак разности
представляет собой знакопеременную квадратичную форму и, следовательно, не сохраняется знак разности 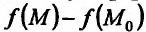 , что свидетельствует об отсутствии экстремума в точке
, что свидетельствует об отсутствии экстремума в точке 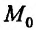 .
.
Пример №4
Исследовать функцию 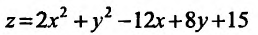 на экстремум.
на экстремум.
Решение:
Функция определена на всей плоскости. Вычислим частные производные заданной функции: 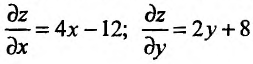 и приравняем их к нулю:
и приравняем их к нулю: 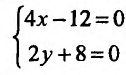
Решив систему, найдем стационарную точку М(3; -4), которая может быть точкой экстремума функции. Для определения существования экстремума функции в этой точке, вычислим частные производные второго порядка:
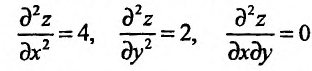
и подставим их значения в выражение: 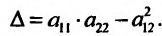 Так как
Так как 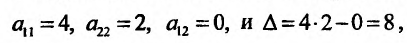 то в точке
то в точке 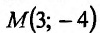 функция имеет минимум.
функция имеет минимум.
Определение экстремума функции широко применяется в экономических исследованиях. Рассмотрим следующий пример.
Пример №5
Фирма имеет два филиала, издержки производства в которых описываются функциями 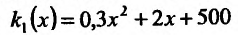 и
и 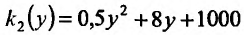 соответственно, где х и у- объемы производимой продукции. Общий спрос на товар фирмы определяется ценой р за единицу продукции, зависящей от объема выпускаемой продукции z = х + у и определяемой функцией z=5000 – 4р. Рассчитать оптимальный объем выпуска продукции для производителя, оптимальную цену в целом и распределение производственной про-граммы по филиалам.
соответственно, где х и у- объемы производимой продукции. Общий спрос на товар фирмы определяется ценой р за единицу продукции, зависящей от объема выпускаемой продукции z = х + у и определяемой функцией z=5000 – 4р. Рассчитать оптимальный объем выпуска продукции для производителя, оптимальную цену в целом и распределение производственной про-граммы по филиалам.
Решение:
Оптимальный выпуск продукции определяется максимальной прибылью фирмы, которая равна разности дохода фирмы от реализуемой продукции по цене р и издержек, то есть функцией прибыли:
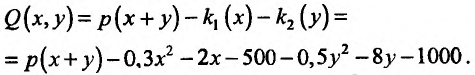 .
.
Найдем значение функции цены р из равенства
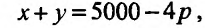
решив которое получим:
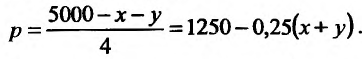
Подставим значение цены в функцию прибыли:
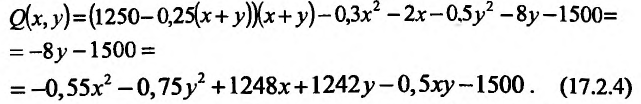
Определим экстремум функции прибыли (17.2.4). Для этого вычислим частные производные первого порядка:
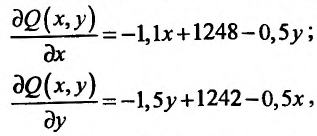
приравняем их к нулю и решим систему: 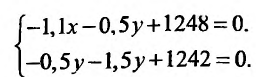
Получим значения: 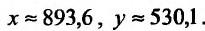 . Характер экстремума в стационарной точке (893,6;530,l) определим, вычислив значение частных производных второго порядка:
. Характер экстремума в стационарной точке (893,6;530,l) определим, вычислив значение частных производных второго порядка:
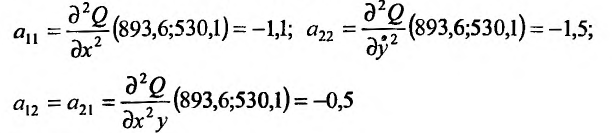
и значение выражения:
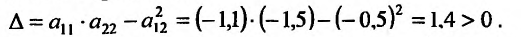 .
.
Так как 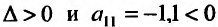 , то точка (893,6;530,l) является точкой максимума и при найденных значениях х и у функция прибыли получает наибольшее значение.
, то точка (893,6;530,l) является точкой максимума и при найденных значениях х и у функция прибыли получает наибольшее значение.
Таким образом, если фирма в первом филиале произведет примерно 894 единицы продукции, а во втором – 530 единиц, то продав ее по цене р = 1250-0,25(894 + 530) = 894 денежных единиц за единицу, она получит максимальную прибыль, равную:
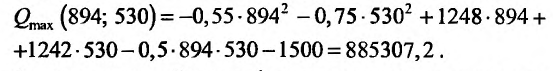
Аналогичным образом формулируются достаточные условия локального экстремума функции n переменных.
Теорема 17.2.2. Пусть функция 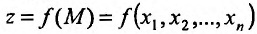 один раз дифференцируема в некоторой окрестности точки и два раза дифференцируема в самой точке
один раз дифференцируема в некоторой окрестности точки и два раза дифференцируема в самой точке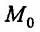 и точка
и точка 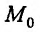 является стационарной точкой функции
является стационарной точкой функции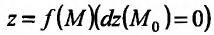 . Тогда, если дифференциал второго порядка
. Тогда, если дифференциал второго порядка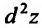 представляет собой положительно определенную (отрицательно определенную) квадратичную форму от переменных
представляет собой положительно определенную (отрицательно определенную) квадратичную форму от переменных 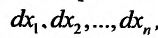 то функция
то функция 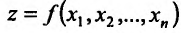 имеет в точке
имеет в точке 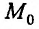 локальный минимум (локаланый максимум)- Если же дифференциал второго порядка (17.2.1), представляет cобой знакопеременную квадратичную фор-щ'( 17.2.2), то функция z = f(м) не имеет локального экстремума точке
локальный минимум (локаланый максимум)- Если же дифференциал второго порядка (17.2.1), представляет cобой знакопеременную квадратичную фор-щ'( 17.2.2), то функция z = f(м) не имеет локального экстремума точке 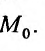
Наибольшее и наименьшее значения функции
В предыдущих параграфах рассмотрены методы определения локального экстремума функции п переменных. Пусть требуется найти наибольшее (наименьшее) значение функции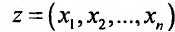 в определенной области D, то есть требуется найти точки глобального экстремума функции.
в определенной области D, то есть требуется найти точки глобального экстремума функции.
Вначале находим точки локального экстремума внутри заданной области D, методами, указанными в предыдущих параграфах. Затем находим экстремумы функции на границе области D и сравниваем ее максимумы (минимумы) внутри области со значениями на границе области. Наибольшее (наименьшее) из всех этих значений и будет наибольшим (наименьшим) значением функции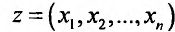 в данной области D.
в данной области D.
Пример №6
Найти наименьшее и наибольшее значение функции 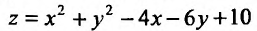 в замкнутой области, ограниченной окружностью
в замкнутой области, ограниченной окружностью 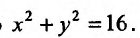
Решение:
Определим вначале локальные экстремумы внутри круга 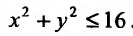 Для этого последовательно вычислим частные производные, приравняем их к нулю, найдем стационарные точки, решив соответствующую систему, и определим характер стационарных точек:
Для этого последовательно вычислим частные производные, приравняем их к нулю, найдем стационарные точки, решив соответствующую систему, и определим характер стационарных точек:
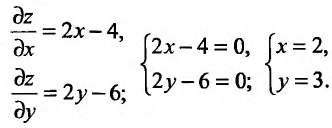
Точка А(2;3) принадлежит кругу 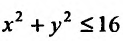 Так как
Так как 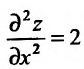 ,
,
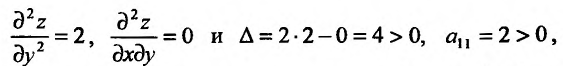 то в точке
то в точке
А(2,3) функция достигает минимума, min z = f(2;3) = -3.
Найдем экстремумы на границе области, то есть на окружности 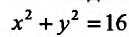 Воспользуемся параметрическими уравнениями этой окружности
Воспользуемся параметрическими уравнениями этой окружности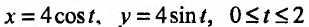 Подставив их в заданную функцию, получим функцию одной переменной t:
Подставив их в заданную функцию, получим функцию одной переменной t: 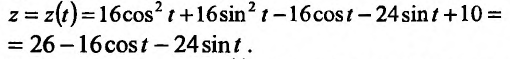
Исследуем функцию 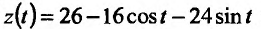 на экстремум:
на экстремум:
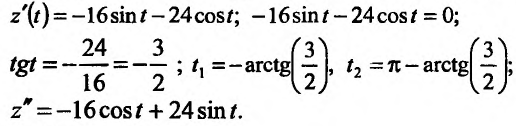
Так как
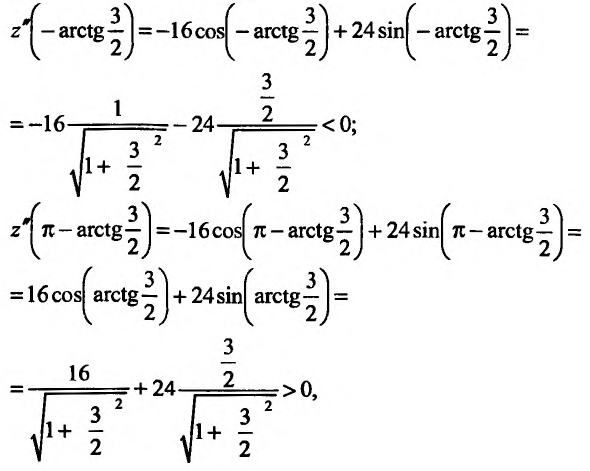
то 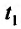 – точка максимума, a
– точка максимума, a 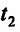 – точка минимума, причем
– точка минимума, причем
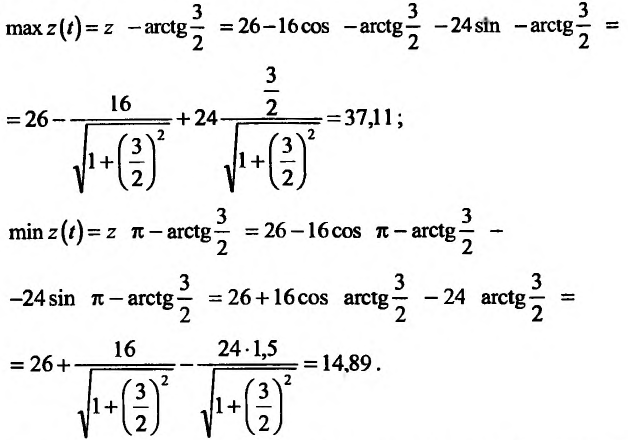
Сравнивая, полученные экстремальные значения функции, замечаем, что в круге 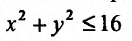 наименьшее значение функции равно «-3», и достигается оно внутри круга в точке А(2;3). а наибольшее значение функции равно 37,11 и достигается оно на окружности
наименьшее значение функции равно «-3», и достигается оно внутри круга в точке А(2;3). а наибольшее значение функции равно 37,11 и достигается оно на окружности 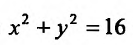 в точке
в точке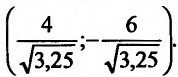
Метод наименьших квадратов
Понятие об эмпирических формулах. При изучении различных процессов и явлений мы почти всегда сталкиваемся с задачей: «Функциональная зависимость между переменными величинами л: и у задана, исходя из тех или иных теоретических соображений Формула, выражающая эту зависимость, содержит постоянные величины, которые необходимо определить по результатам наблюдений.»
Отметим, что нередко при обработке результатов наблюдений (опыта) приходится встречаться и с более сложной задачей, то есть с задачей вида: «В результате наблюдений получен ряд значений переменных х и у, однако характер функциональной зависимости между ними остается неизвестным. Требуется, по наблюденным данным, найти аналитическое выражение зависимости между x и y. Такие формулы, принято называть эмпирическими формулами, то есть формулами, полученными в результате опыта (наблюдений).
Совершенно ясно, что однозначно установить функциональную зависимость между х и у по конечному числу измеренных значений было бы невозможно даже в том случае, если бы они не обладали ошибками, свойственными наблюденным величинам.
Следует поэтому отчетливо представлять, что математическая обработка результатов наблюдений не может ставить перед собой задачу разгадать истинный характер зависимости между имеющимися переменными. Речь идет лишь о том, чтобы охватить результаты опыта наиболее простой формулой, которая позволит применять методы математического анализа к дальнейшему изучению наблюденных данных.
Метод наименьших квадратов. Пусть в результате некоторого опыта мы получили числовые значения, которые дают возможность установить взаимосвязь между исследуемыми величинами в математической форме. Исходя из теоретических соображений, выберем вид этой зависимости:

Функция (17.4.1) — это функция независимой переменной х и (m + l)-ro параметра 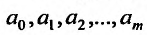 . Эти параметры постоянны и неизвестны, так как они не поддаются непосредственным измерениям заранее. Для их определения производится ряд измерений величин х и у. Подставляя поочередно их в равенство (17.4.1), мы получаем уравнения между параметрами
. Эти параметры постоянны и неизвестны, так как они не поддаются непосредственным измерениям заранее. Для их определения производится ряд измерений величин х и у. Подставляя поочередно их в равенство (17.4.1), мы получаем уравнения между параметрами 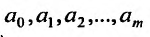 вида:
вида:
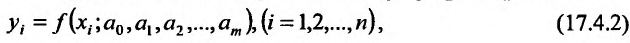
где 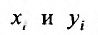 , соответствующие друг другу измерения, а n – число измерений. Если бы значения х и у находились точно, то для отыскания m +1 параметра достаточно было бы произвести m+1 измерение. На самом же деле, значения х и у содержат ошибки и никакие m +1 измерений не позволят определить истинные значения параметров. Поэтому обычно производится большее число измерений (n > m + l), в результате чего число уравнений (17.4.2) будет больше числа неизвестных параметров. Полученная система будет, вообще говоря, несовместной, то есть точные решения каких-либо m + 1 из уравнений системы могут не удовлетворять остальным уравнениям. Наша задача состоит в том, чтобы найти такие значения неизвестных параметров, которые будут удовлетворять этим уравнениям наилучшим образом, хотя и не точно.
, соответствующие друг другу измерения, а n – число измерений. Если бы значения х и у находились точно, то для отыскания m +1 параметра достаточно было бы произвести m+1 измерение. На самом же деле, значения х и у содержат ошибки и никакие m +1 измерений не позволят определить истинные значения параметров. Поэтому обычно производится большее число измерений (n > m + l), в результате чего число уравнений (17.4.2) будет больше числа неизвестных параметров. Полученная система будет, вообще говоря, несовместной, то есть точные решения каких-либо m + 1 из уравнений системы могут не удовлетворять остальным уравнениям. Наша задача состоит в том, чтобы найти такие значения неизвестных параметров, которые будут удовлетворять этим уравнениям наилучшим образом, хотя и не точно.
Так как уравнения (17.4.2) удовлетворяются не точно, то будем иметь:
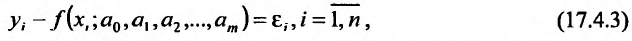
где 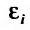 — отклонения измеренных значений yj от вычисленных по формуле (17.4.1). В методе наименьших квадратов утверждается, что наилучшими значениями параметров будут такие, при которых сумма квадратов отклонений
— отклонения измеренных значений yj от вычисленных по формуле (17.4.1). В методе наименьших квадратов утверждается, что наилучшими значениями параметров будут такие, при которых сумма квадратов отклонений 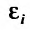 , будет наименьшей, то есть
, будет наименьшей, то есть
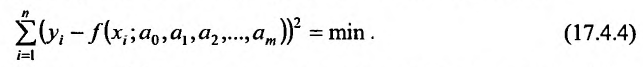
Замечание. Мы не рассматриваем сумму самих отклонений (невязок), так как сумма 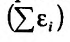 может быть очень малой и тогда, когда отдельные отклонения
может быть очень малой и тогда, когда отдельные отклонения 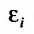 очень велики, но имеют разные знаки и взаимно компенсируют друг друга.
очень велики, но имеют разные знаки и взаимно компенсируют друг друга.
Из минимума суммы квадратов отклонений автоматически вытекает, что все невязки е, в своей совокупности должны быть минимальными.
Рассматривая теперь правую часть выражения (17.4.4) как некоторую функцию независимых переменных 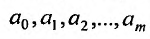 , применим необходимые условия экстремумов для нахождения минимума этой функции. Для этого вычислим частные производные по этим переменным
, применим необходимые условия экстремумов для нахождения минимума этой функции. Для этого вычислим частные производные по этим переменным 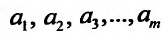 и приравняем их к нулю. Получим в точности m +1 уравнение с m +1 неизвестными. Составление и решение этой системы особенно просто в том случае, когда функция
и приравняем их к нулю. Получим в точности m +1 уравнение с m +1 неизвестными. Составление и решение этой системы особенно просто в том случае, когда функция 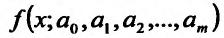 линейна относительно параметров, то есть если она имеет вид:
линейна относительно параметров, то есть если она имеет вид:
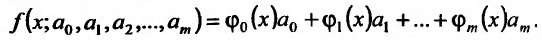
Тогда дифференцируя сумму квадратов отклонений
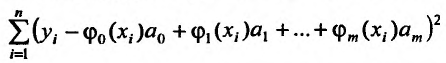
по 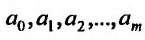 и приравнивая к нулю частные производные, получим:
и приравнивая к нулю частные производные, получим: 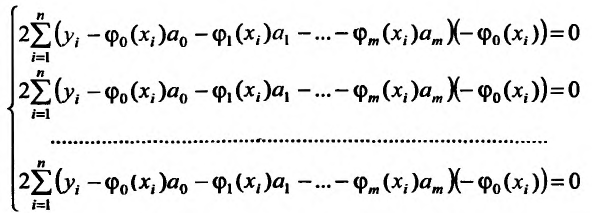
Или после преобразования будем иметь линейную неоднородную систему:
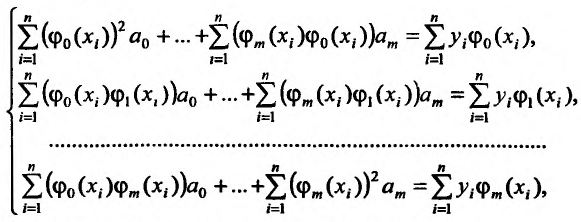
которую решаем любым известным нам способом.
Применим теперь общие выводы в некоторых конкретных случаях.
а) Выравнивание по прямой. Пусть 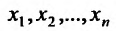 – последовательность значений независимой переменной, а
– последовательность значений независимой переменной, а 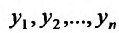 – последовательность соответствующих значений зависимой переменной, полученных из опыта. Требуется подобрать прямую, которая наилучшим образом отображала бы зависимость между х и у, то есть, чтобы отклонения фактических значений функции от подобранной прямой были бы минимальными.
– последовательность соответствующих значений зависимой переменной, полученных из опыта. Требуется подобрать прямую, которая наилучшим образом отображала бы зависимость между х и у, то есть, чтобы отклонения фактических значений функции от подобранной прямой были бы минимальными.
Для решения этой задачи применим метод наименьших квадратов. В этом случае функция 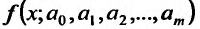 зависит от двух параметров, которые обозначим а и b, и имеет вид:
зависит от двух параметров, которые обозначим а и b, и имеет вид: 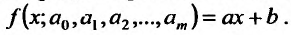 .
.
Отклонения от фактических значений функции составляют: 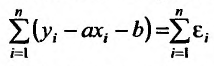
Согласно метода наименьших квадратов, искомыми параметрами а и b будут те, для которых
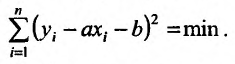
Необходимое условие существования минимума состоит в том, чтобы
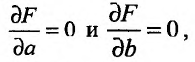
где 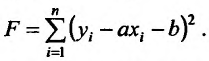
Вычислив частные производные и приравняв их нулю, получим два уравнения для определения а и b:
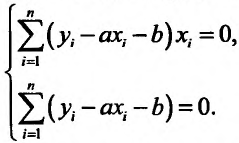
Раскрывая скобки и производя суммирование, получаем систему линейных уравнений: 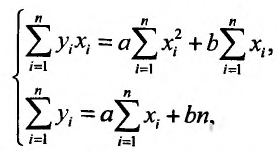
решая которую находим значения а и b: 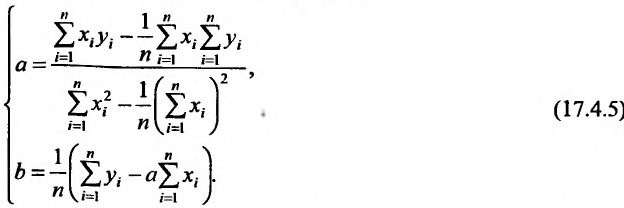
Значения а и b, найденные по формулам (17.4.5), определяют прямую наилучшим образом, в смысле метода наименьших квадратов, описывающую изучаемую зависимость.
Пример:
В течение четырех последовательных лет переменные х и у принимали значения, указанные в таблице 17.1. 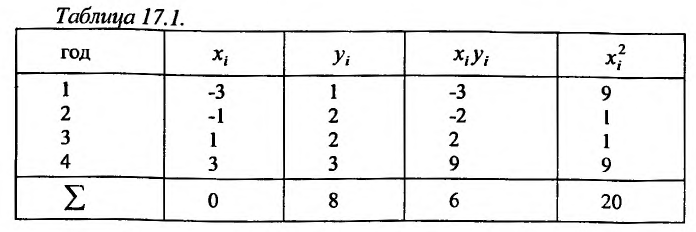
Найти прямую, выражающую зависимость величины у от величины х.
Решение:
Для определения эмпирической прямой у = ах + b, составим систему (17.4.5).Так как
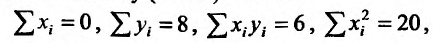
то система (17.4.5) будет иметь вид: 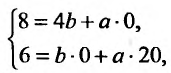
Решив систему, находим: b = 2, а = 0,3.
Тогда искомая прямая, имеет вид: y = 0,Зх + 2.
б) Выравнивание но параболе. Пусть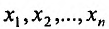 – последовательность значений независимой переменной, а
– последовательность значений независимой переменной, а 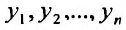 последовательность соответствующих значений зависимой переменной.
последовательность соответствующих значений зависимой переменной.
Предположим, что точки 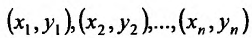 расположены вдоль некоторой параболы. Применим метод наименьших квадратов для определения параметров квадратичной функции, то есть параболы второго порядка:
расположены вдоль некоторой параболы. Применим метод наименьших квадратов для определения параметров квадратичной функции, то есть параболы второго порядка: 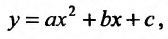
соответствующей наблюденной экспериментальной зависимости, таким образом, чтобы сумма квадратов отклонений эмпирических данных от действительных значений функции была минимальной, то есть 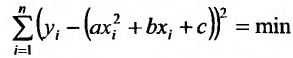 где
где 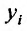 – наблюденные значения, а
– наблюденные значения, а 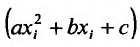 – значения функции в точках
– значения функции в точках 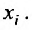
Необходимые условия существования минимума функции 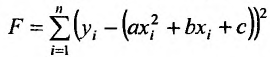 определяют систему уравнений:
определяют систему уравнений:
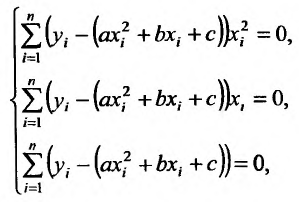
которую можно преобразовать к виду: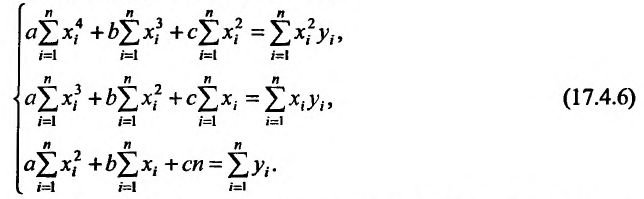
Решая эту систему одним из известных методов, вычисляем неизвестные коэффициенты a, b и с.
в) Выравнивание с помощью гиперболы. Пусть 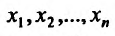 -последовательность значений независимой переменной, а
-последовательность значений независимой переменной, а  – последовательность соответствующих значений зависимой переменной. Предположим, что эмпирические данные
– последовательность соответствующих значений зависимой переменной. Предположим, что эмпирические данные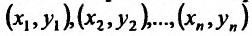 описываются гиперболой
описываются гиперболой
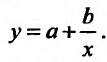
Эта гипербола подобрана наилучшим образом, в смысле способа наименьших квадратов, если функция
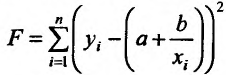
достигает минимума. Необходимые условия минимума функции F определяют систему:
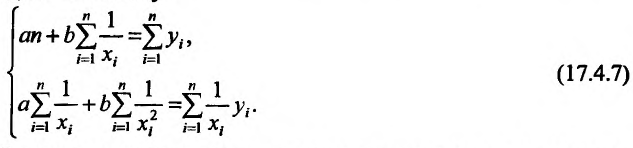
Решая эту систему, находим значения неизвестных параметров а и b.
Зависимость между удельными затратами и объемом производства можно описать гиперболой. Действительно, если переменные издержки составляют а, а постоянные издержки b, то полные затраты определяются уравнением К(х) = ах + b, где х – объем (производства) выпуска продукции. Тогда удельные затраты равны отношению полных затрат к объему производства, т. е.
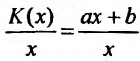
и, следовательно:
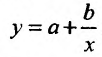
Применяя метод наименьших квадратов, мы можем определить а и b, если за у принять удельные затраты.
г) Выравнивание по показательной функции. Пусть 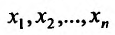 – последовательность значений независимой переменной, а
– последовательность значений независимой переменной, а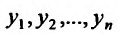 – последовательность соответствующих значений зависимой переменной. Предположим, что точки
– последовательность соответствующих значений зависимой переменной. Предположим, что точки 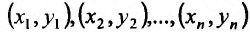 расположены вдоль показательной кривой
расположены вдоль показательной кривой
вида 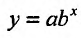 . Найдем параметры а и b, используя метод наименьших квадратов, то есть найдем такую кривую
. Найдем параметры а и b, используя метод наименьших квадратов, то есть найдем такую кривую 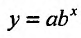 , которая бы наилучшим образом отражала зависимость между переменными х и у.
, которая бы наилучшим образом отражала зависимость между переменными х и у.
Представим уравнение показательной кривой 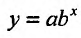 в виде
в виде
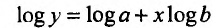 , или, вводя обозначения logа=А, logb = B,
, или, вводя обозначения logа=А, logb = B,
получим:
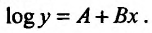
Отсюда следует, что функция у, представленная на графике в системе прямоугольных координат, где ось ординат разделена по логарифмической шкале, а ось абсцисс – по обычной шкале, определяет прямую с угловым коэффициентом В и расстоянием по оси Оу, равным А.
Согласно методу наименьших квадратов, найдем минимум
функции 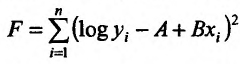 .Применяя необходимые условия
.Применяя необходимые условия
существования минимума, получим:
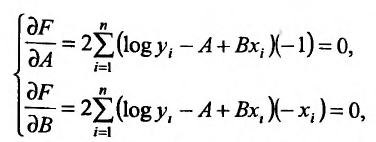
или, раскрывая скобки и производя суммирование, будем иметь систему:
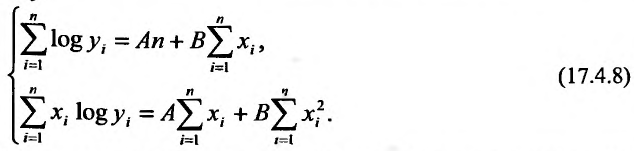
Решая, полученную систему (17.4.8), известными методами, найдем параметры А и В. Потенцируя равенства log а = А и log b = B, находим а и Ь, которые определяют показательную кривую 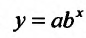 , наилучшим образом описывающую изучаемую зависимость.
, наилучшим образом описывающую изучаемую зависимость.
Необходимые условия условного экстремума
В предыдущем параграфе мы рассмотрели локальный экстремум функции, аргументы которой не связаны никакими дополнительными условиями. Вместе с тем в приложениях математики (в экономических исследованиях) часто встречается задача об отыскании экстремума функции, аргументы которой удовлетворяют дополнительным условиям связи.
Приведем пример задачи об отыскании условного экстремума:
«Пусть требуется найти экстремум функции 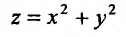 при условии, что аргументы этой функции удовлетворяют условию связи Зх + у —2 = 0.»
при условии, что аргументы этой функции удовлетворяют условию связи Зх + у —2 = 0.»
Таким образом, экстремумы функции ищутся не на всей плоскости Оху , а лишь на прямой Зх + у – 2 = 0. Для решения поставленной задачи подставим значение у (определяемое из условия связи 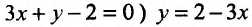 , в функцию z:
, в функцию z:
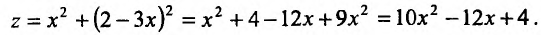
Получили функцию аргумента х и свели поставленную задачу к отысканию безусловного экстремума функции 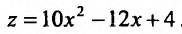
Так как 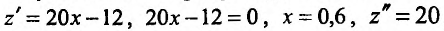 , то функция
, то функция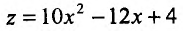 имеет минимум в точке х = 0,6, равный
имеет минимум в точке х = 0,6, равный 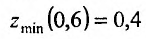 . Таким образом, функция
. Таким образом, функция 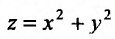 с условием связи Зх + у – 2 = 0 имеет условный минимум
с условием связи Зх + у – 2 = 0 имеет условный минимум 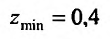 в точке (0,6;0,2). Отметим, что безусловный минимум функции
в точке (0,6;0,2). Отметим, что безусловный минимум функции 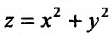 достигается в точке (0;0) и равен z = 0. Это значит, что минимум функции
достигается в точке (0;0) и равен z = 0. Это значит, что минимум функции 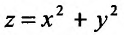 на всей плоскости не совпадает с ее минимумом на прямой
на всей плоскости не совпадает с ее минимумом на прямой 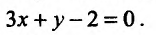
Рассмотрим общую постановку задачи об отыскании условного экстремума.
Пусть требуется найти экстремум функции двух переменных

при условии, что аргументы х и у удовлетворяют уравнению:
F(x,y) = a. (17.5.2)
Определение 17.5.1. Функция z = f(x,y) при условии F(x,y) = а имеет условный максимум (минимум) в точке 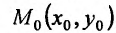 , координаты которой удовлетворяют условиям связи И7.5.2), если существует такая окрестность
, координаты которой удовлетворяют условиям связи И7.5.2), если существует такая окрестность 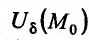 , что для всех точек
, что для всех точек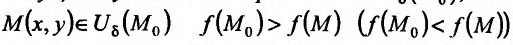 , координаты которых удовлетворяют условиям связи (17.5.2).
, координаты которых удовлетворяют условиям связи (17.5.2).
Геометрическая задача на условный экстремум может быть истолкована следующим образом. Дана поверхность Q с уравнением 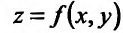 и линия L на этой поверхности, являющаяся линией пересечения поверхности Q с цилиндрической поверхностью F(x,y) = a. (рис. 17.1)
и линия L на этой поверхности, являющаяся линией пересечения поверхности Q с цилиндрической поверхностью F(x,y) = a. (рис. 17.1)
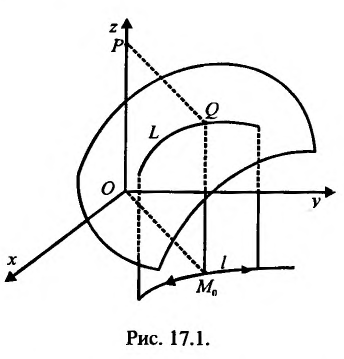
У точек линии L надо найти экстремальную аппликату. Точки поверхности Q, не принадлежащие линии L, не рассматриваются. На рис. 17.1 точка Р имеет максимальную в этом смысле аппликату. Спроектировав линию L на плоскость хОу, получим кривую l с уравнением F(x,y) = a. Точка 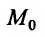 линии I (проекция точки Р-поверхности Q) называется точкой условного экстремума (в данном случае точкой условного максимума) функции z = f(x,y). а аппликата
линии I (проекция точки Р-поверхности Q) называется точкой условного экстремума (в данном случае точкой условного максимума) функции z = f(x,y). а аппликата 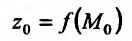 точки Р – условным экстремумом (максимумом).
точки Р – условным экстремумом (максимумом).
Дня нахождения условного экстремума функции z = f(x,y) при наличии связи F(x,y)= а, предположим, что F дифференцируема в окрестности точки 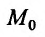 , непрерывна в точке
, непрерывна в точке 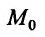 и производная
и производная 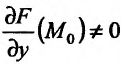 . Тогда существует окрестность точки
. Тогда существует окрестность точки 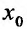 , в которой определена единственная функция
, в которой определена единственная функция 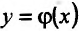 , дифференцируемая в этой окрестности. Подставляя найденную функцию в (17.5.1), сведем вопрос о существовании условного экстремума в точке
, дифференцируемая в этой окрестности. Подставляя найденную функцию в (17.5.1), сведем вопрос о существовании условного экстремума в точке 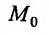 у функции
у функции 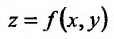 при наличии связи (17.5.2) к вопросу о существовании безусловного экстремума в точке х0 у сложной функции
при наличии связи (17.5.2) к вопросу о существовании безусловного экстремума в точке х0 у сложной функции 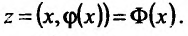
Установим теперь необходимые условия существования условного экстремума в точке 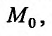 таким образом, чтобы не решать уравнения связи. Итак, пусть функция
таким образом, чтобы не решать уравнения связи. Итак, пусть функция 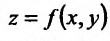 дифференцируема в точке
дифференцируема в точке 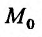 и имеет в этой точке условный экстремум при наличии связи (17.5.2) или (что то же самое) функция
и имеет в этой точке условный экстремум при наличии связи (17.5.2) или (что то же самое) функция 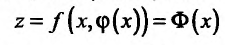 (17.5.3) имеет в точке
(17.5.3) имеет в точке 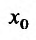 безусловный экстремум. Необходимым условием безусловного экстремума функции (17.5.3) в точке
безусловный экстремум. Необходимым условием безусловного экстремума функции (17.5.3) в точке 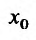 является равенство нулю производной этой функции
является равенство нулю производной этой функции 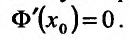 Так как функция Ф сложная неявно заданная функция, то, применяя правило дифференцирования неявно заданной функции, получим:
Так как функция Ф сложная неявно заданная функция, то, применяя правило дифференцирования неявно заданной функции, получим: 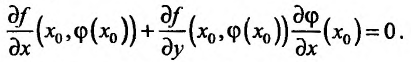 (17.5.4) Подставив в (17.5.2) решение этого уравнения
(17.5.4) Подставив в (17.5.2) решение этого уравнения 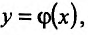 получим тождество. Тогда, дифференцируя это тождество, получим:
получим тождество. Тогда, дифференцируя это тождество, получим: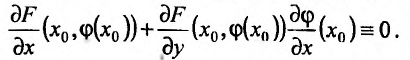 (17.5.5) Умножим, далее, равенство (17.5.5) на произвольный (и пока неизвестный) постоянный множитель
(17.5.5) Умножим, далее, равенство (17.5.5) на произвольный (и пока неизвестный) постоянный множитель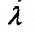 и сложим с (17.5.4). В результате получим следующее равенство:
и сложим с (17.5.4). В результате получим следующее равенство: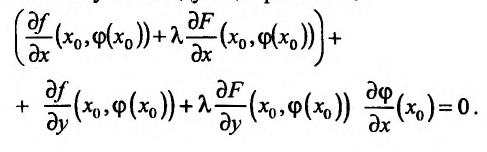 (17.5.6)
(17.5.6)
Пусть
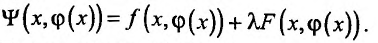
Тогда равенство (17.5.6) можно записать в виде:
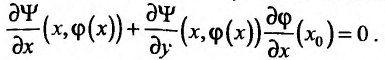
Выберем 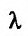 таким, чтобы выполнялось равенство:
таким, чтобы выполнялось равенство:
–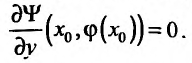
Так как функция 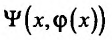 сложная функция, то, применив правило дифференцирования сложной функции, получим:
сложная функция, то, применив правило дифференцирования сложной функции, получим:
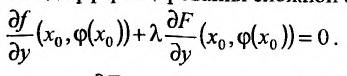 (17.5.8)
(17.5.8)
Так как 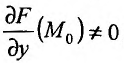 , то из (17.5.8) можно найти
, то из (17.5.8) можно найти 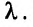 Тогда из (17.5.7) следует:
Тогда из (17.5.7) следует:
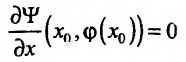 или
или
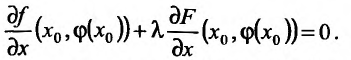 (17.5.9)
(17.5.9)
Присоединив к (17.5.8) и (17.5.9) условие связи (17.5.2), мы получим систему:
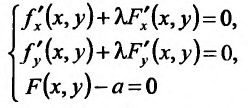
для определения координат точек возможного условного экстремума и 
Практически поступают следующим образом составляют функцию Лагранжа
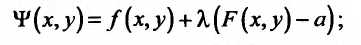 находят точки возможного безусловного экстремума; для исключения множителя
находят точки возможного безусловного экстремума; для исключения множителя 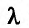 привлекают условие связи (17.5.2).
привлекают условие связи (17.5.2).
Достаточное условие условного экстремума
Рассмотрим далее достаточное условие условного экстремума функции 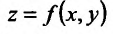 в точке
в точке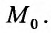 Мы должны определить знак разности
Мы должны определить знак разности 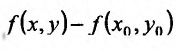 при всех
при всех 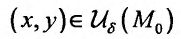 и удовлетворяющих уравнению связи
и удовлетворяющих уравнению связи 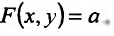 Из уравнения связи непосредственно следует, что вместо разности
Из уравнения связи непосредственно следует, что вместо разности 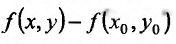 можно рассматривать разность
можно рассматривать разность 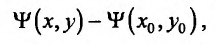 составленную для функции Лагранжа и исследовать ее знак. Разлагая эту функцию
составленную для функции Лагранжа и исследовать ее знак. Разлагая эту функцию 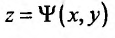 по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки 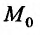 с остаточным членом в форме Пеано при
с остаточным членом в форме Пеано при 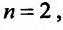 получим:
получим:
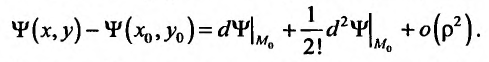
Так как 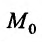 – стационарная точка, то дифференциал первого порядка
– стационарная точка, то дифференциал первого порядка 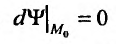 и знак разности определяется знаком второго дифференциала
и знак разности определяется знаком второго дифференциала 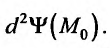 При этом, в точке
При этом, в точке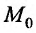 будет минимум, если при наличии связи
будет минимум, если при наличии связи 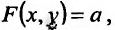 дифференциал второго порядка
дифференциал второго порядка 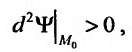 и максимум, если
и максимум, если 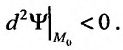 Дифференциал второго порядка
Дифференциал второго порядка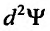 в точке
в точке 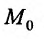 возможного экстремума можно вычислять, гак как если бы переменные
возможного экстремума можно вычислять, гак как если бы переменные 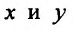 были бы независимыми, то есть по формуле:
были бы независимыми, то есть по формуле: 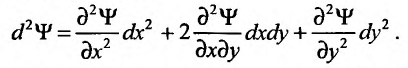 (17.6.1)
(17.6.1)
Однако при проведении вычислений, следует в формулу (17.6.1) подставить вместо дифференциала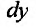 его значение, определяемое из равенства:
его значение, определяемое из равенства:
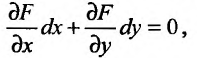 то есть
то есть
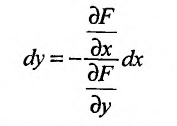
и изучить вопрос о знакоопределенности  в данной точке
в данной точке  . После подстановки значения
. После подстановки значения 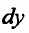 в (17.6.1), получим*
в (17.6.1), получим* 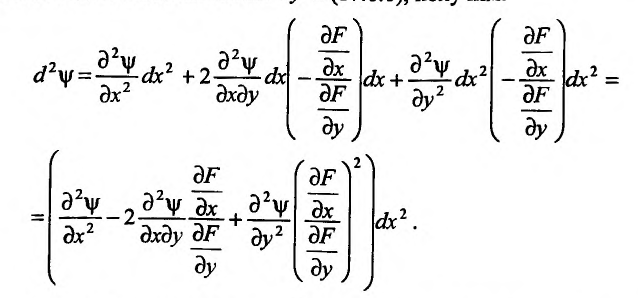
Откуда следует, что знак 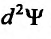 определяется знаком выражения:
определяется знаком выражения: 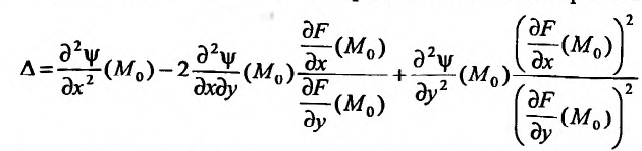 Если
Если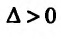 то
то 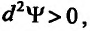 что означает, что в точке
что означает, что в точке 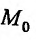 условный минимум, если же
условный минимум, если же 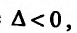 то
то 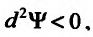 тогда в точке
тогда в точке 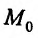 условный максимум.
условный максимум.
Выражение 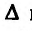 можно записать в матричном виде:
можно записать в матричном виде:
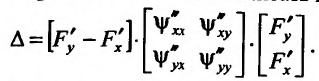 Все элементы матриц вычисляются в точке
Все элементы матриц вычисляются в точке 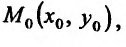 для заданного
для заданного 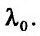
Пример №7
В данный полукруг радиуса R вписать прямоугольник наибольшей площади.
Решение:
Площадь прямоугольника со сторонами х и у (см. рис. 17.2.) выражается формулой:
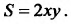
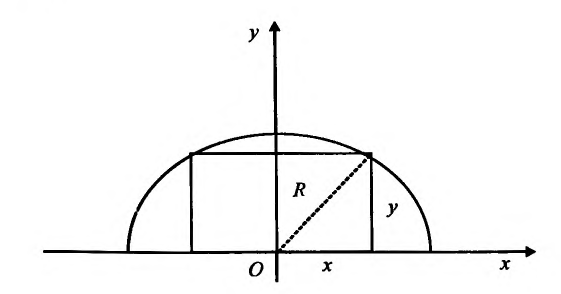
рис.17.2.
Координаты 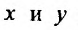 удовлетворяют уравнению
удовлетворяют уравнению 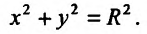 Найдем максимум функции
Найдем максимум функции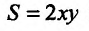 при условии
при условии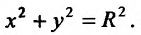 Составляем функцию Лагранжа:
Составляем функцию Лагранжа:
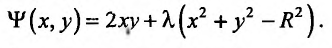
Вычисляем частные производные первого порядка функции 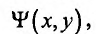 приравниваем их к нулю и, присоединив уравнение связи, получим систему для нахождения точек возможного условного экстремума:
приравниваем их к нулю и, присоединив уравнение связи, получим систему для нахождения точек возможного условного экстремума:
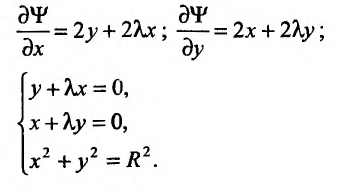 (17.6.2)
(17.6.2)
Из системы (17.6.2) находим:
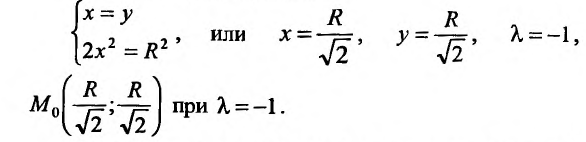 то есть
то есть
Мы получили единственный ответ, и так как наибольшее значение должно существовать, то ему должны соответствовать найденные значения переменных: 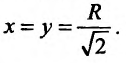 Подставляя эти значения в формулу, получаем:
Подставляя эти значения в формулу, получаем: 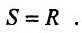
Пример №8
Некоторый цех завода выпускает два вида изделий, причем изделие каждого вида обрабатывается на двух разных станках А и В. Каждая единица первого изделия требует 3-х часов обработки на станке А и 2-х часов – на станке В. Для второго изделия время обработки соответственно 2 и 3 часа. Станок А можно использовать не более 8 часов, станок В – не более 7 часов. Прибыль, получаемая от продажи каждого вида изделия, равна 20 денежных единиц. Составить план работы цеха, обеспечивающий получение максимальной прибыли.
Решение:
Обозначим через 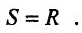 резерв времени работы станков А и В, а через
резерв времени работы станков А и В, а через 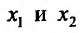 количество изделий первого и второго вида, который должен выпустить цех. Тогда, для составления плана, обеспечивающего максимальную прибыль, нужно найти максимум функции
количество изделий первого и второго вида, который должен выпустить цех. Тогда, для составления плана, обеспечивающего максимальную прибыль, нужно найти максимум функции 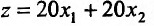 при ограничениях:
при ограничениях:
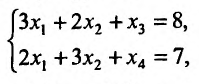
где 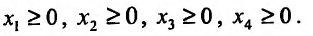
Составляем функцию Лагранжа:
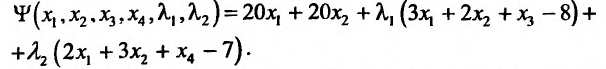
Вычисляем частные производные, приравниваем их к нулю и составляем систему:
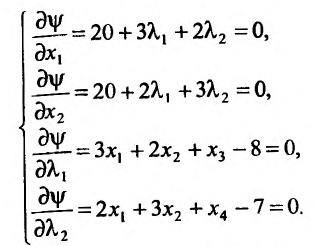
Находим решение системы:
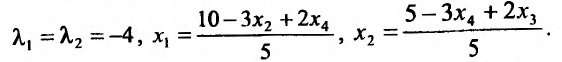 Подставив найденные значения
Подставив найденные значения 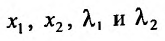 в функцию Лагранжа, получим функцию:
в функцию Лагранжа, получим функцию:
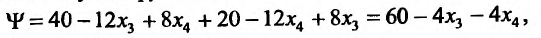
которая достигает максимума, когда 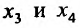 достигают минимума, то есть
достигают минимума, то есть 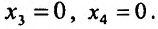 Подставив значения
Подставив значения 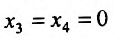 в решение системы, найдем:
в решение системы, найдем:
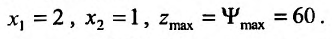
Пример №9
Имеется два технологических процесса производства некоторого продукта. Обозначим через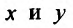 количество продукта, произведенного соответственно первым и вторым способом. Издержки производства при каждом технологическом процессе производства выражаются функциями:
количество продукта, произведенного соответственно первым и вторым способом. Издержки производства при каждом технологическом процессе производства выражаются функциями:
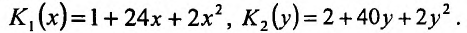
За некоторое время нужно произвести 100 единиц продукта, то есть 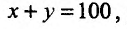 распределив их так, чтобы минимизировать общие издержки.
распределив их так, чтобы минимизировать общие издержки.
Решение:
Составим функцию, характеризующую издержки производства:
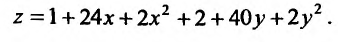
При этом количества продукта удовлетворяю! равенству 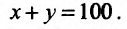 Итак, задача сводится к нахождению минимума функции, описывающей издержки производства при условии, что объемы продукта связаны условием. Это значит, что нужно найти условный минимум функции двух переменных. Для этого составим функцию Лагранжа:
Итак, задача сводится к нахождению минимума функции, описывающей издержки производства при условии, что объемы продукта связаны условием. Это значит, что нужно найти условный минимум функции двух переменных. Для этого составим функцию Лагранжа:
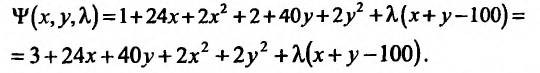
Вычислим частные производные и приравняем их к нулю:
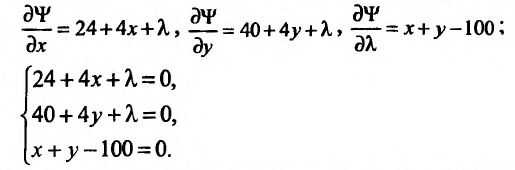
Решив систему (17.6.3), находим 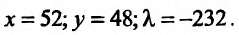
Вычисляем частные производные второго порядка функции Лагранжа:
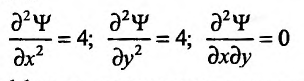
и дифференциал второго порядка при выполнении условий связи, то есть когда 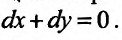 Имеем:
Имеем: 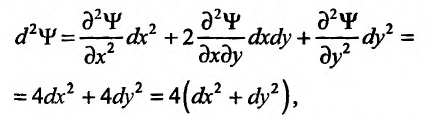 и, значит, при выполнении условий связи
и, значит, при выполнении условий связи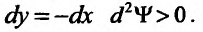 При
При 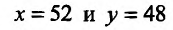 функция
функция 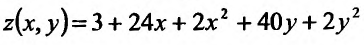 имеет условный минимум.
имеет условный минимум.
Таким образом, если 52 единицы продукта произвести первым технологическим способом, а 48 единиц продукта вторым технологическим способом, то общие издержки производства 100 единиц продукта будут минимальными.
Дифференциальное исчисление функции нескольких переменных
Ранее мы изучали функции одной независимой переменной. Однако многим явлениям, в том числе экономическим, присуща многофакторная зависимость. Исследование таких зависимостей привело к необходимости расширения известного понятия функциональной зависимости и введению понятия функции нескольких переменных.
Будем рассматривать функции двух переменных, т.к. все важнейшие факты теории функций нескольких переменных наблюдаются уже на функциях двух переменных. Эти факты обобщаются на случай большего числа переменных. Кроме того, для функций двух переменных можно дать наглядную геометрическую интерпретацию.
Определение. Пусть дано множество D упорядоченных пар чисел 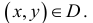 Если каждой паре (х,.у) значений двух, независимых друг от друга, переменных величин х и у, принадлежащих множеству D, соответствует определенное значение величины Z, то говорят, что Z есть функция двух переменных хиу, определенная на множестве D .
Если каждой паре (х,.у) значений двух, независимых друг от друга, переменных величин х и у, принадлежащих множеству D, соответствует определенное значение величины Z, то говорят, что Z есть функция двух переменных хиу, определенная на множестве D .
Символическое обозначение 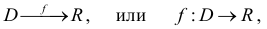 или Z = f(x,y). При этом х и у называются независимыми переменными (аргументами), a Z – зависимой переменной (функцией).
или Z = f(x,y). При этом х и у называются независимыми переменными (аргументами), a Z – зависимой переменной (функцией).
Определение. Совокупность пар (х,y) значений х и у, при которых определяется функция Z = f(х,у) называется областью определения или областью существования этой функции. Множество значений, принимаемых Z в области определения, называется областью изменения этой функции, обозначается 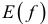 или Е.
или Е.
Пара (х,у) определяет точку M(х,у) в области существования, т.е. область определения – часть плоскости 
Область определения функции 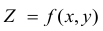 в простейших случаях представляет собой:
в простейших случаях представляет собой:
- либо часть плоскости, ограниченную замкнутой кривой, причем точки этой кривой (границы области) могут принадлежать или не принадлежать области определения,
- либо всю плоскость,
- либо, наконец, совокупность нескольких частей плоскости
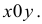
Геометрически изображением функции Z = f(х,у) в системе координат 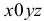 является некоторая поверхность.
является некоторая поверхность.
Примеры:
1. Примером функции двух переменных может служить формула площади прямоугольника S со сторонами, длины которых равны х и у: S = ху. Областью определения этой функции является множество 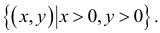
2. Область определения функции Z = 2x-y является вся плоскость.
3. Область определения функции 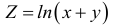 – точки правее (выше) прямой
– точки правее (выше) прямой
у=-х.
4. Для функции, описывающей площадь треугольника S = xy/2, область определения х>0 и у>0. Заметим, что естественной областью определения является вся плоскость.
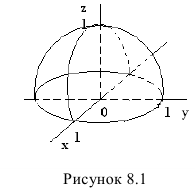
5. Функция 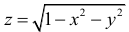 имеет областью определения круг
имеет областью определения круг 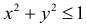 и
и
изображается верхней полусферой с центром в точке O(0,0,0) и радиусом R = 1 (Рисунок 8.1).
Аналогично определяется функция любого конечного числа независимых переменных и 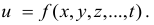
6. Объём параллелепипеда V = xyz .
В области D существует множество точек, в которых функция 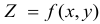 принимает одинаковые значения. Если Z = C = const, тогда уравнение f(х,у) = С определяет линию в плоскости
принимает одинаковые значения. Если Z = C = const, тогда уравнение f(х,у) = С определяет линию в плоскости  во всех точках которой Z = С. Такая линия называется линией уровня.
во всех точках которой Z = С. Такая линия называется линией уровня.
Если задана функция трех переменных  определяет поверхность уровня, во всех точках которой Z = С.
определяет поверхность уровня, во всех точках которой Z = С.
Линию, ограничивающую данную область, будем называть границей области. Точки области, не лежащие на границе области, называются внутренними точками области.
Область, состоящая из одних внутренних точек, называется открытой или незамкнутой.
Область с присоединенной к ней границей называется замкнутой, обозначается  примером замкнутой области является круг с окружностью.
примером замкнутой области является круг с окружностью.
Область называется ограниченной, если существует такое постоянное С, что расстояние любой точки М области от начала координат O меньше С.
Функция двух переменных, как и функция одной переменной, может быть задана разными способами: табличным, аналитическим (с помощью формулы), графическим (например, полусфера – для функции двух аргументов, см. Рисунок 12).
Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично функции одной переменной.
Предел и непрерывность
Введем понятие окрестности точки. Множество всех точек М(х,у) плоскости, координаты которых удовлетворяют неравенству 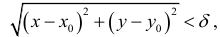 называется
называется 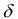 – окрестностью точки
– окрестностью точки 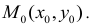
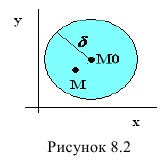
Другими словами 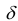 – окрестность точки – это все внутренние точки круга с центром
– окрестность точки – это все внутренние точки круга с центром 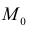 и радиусом
и радиусом 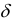 (Рисунок 8.2).
(Рисунок 8.2).
Пусть функция 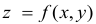 определена в некоторой окрестности точки
определена в некоторой окрестности точки 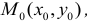 кроме, быть может, самой этой точки.
кроме, быть может, самой этой точки.
Определение. Число А называется пределом функции z = f(x,y) при 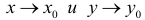 (или, что то же самое, при
(или, что то же самое, при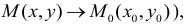 если для любого сколь угодно малого положительного числа
если для любого сколь угодно малого положительного числа 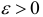 существует
существует 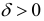 такое, что для всех
такое, что для всех 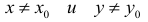 и удовлетворяющих неравенству
и удовлетворяющих неравенству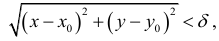 выполняется неравенство
выполняется неравенство 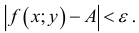
Записывают это так:
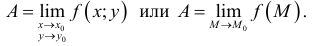
Геометрический смысл предела функции двух переменных состоит в следующем.
Каково бы ни было число 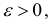 найдется
найдется 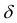 – окрестность точки
– окрестность точки 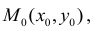 что во всех ее точках М(х,у), отличных от
что во всех ее точках М(х,у), отличных от 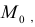 аппликаты соответствующих точек поверхности z = f(x,y) отличаются от числа А по модулю меньше, чем на
аппликаты соответствующих точек поверхности z = f(x,y) отличаются от числа А по модулю меньше, чем на 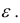
Вычисление пределов функций двух переменных оказывается существенно более трудной задачей по сравнению со случаем одной переменной. Причина заключается в том, что из определения предела следует, что если предел существует, то он не зависит от пути, по которому М стремится к 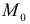 (число таких направлений бесконечно! Для функции одной переменной
(число таких направлений бесконечно! Для функции одной переменной 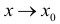 по двум направлениям – справа и слева!). На плоскости – таких направлений – бесконечное множество, и пределы функции по разным направлениям могут не совпадать.
по двум направлениям – справа и слева!). На плоскости – таких направлений – бесконечное множество, и пределы функции по разным направлениям могут не совпадать.
Определение. Функция z = f(x,y) называется непрерывной в точке 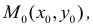 если она:
если она:
а) определена в этой точке и некоторой ее окрестности;
б) имеет предел 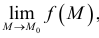
в) этот предел равен значению функции z = f(x,y) в точке 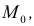 т.е.
т.е.
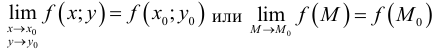
Определение. Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области.
Частные и полное приращение функции нескольких переменных
Пусть дана функция двух переменных z = f(x,у). Полагая у = const, дадим независимой переменной х приращение 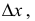 тогда z получит приращение, которое называют частным приращением z по х и обозначают
тогда z получит приращение, которое называют частным приращением z по х и обозначают 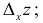
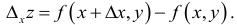
Аналогично, 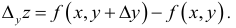
Наконец, сообщив аргументу х приращение 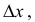 а аргументу у – приращение
а аргументу у – приращение 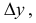 получим для z приращение
получим для z приращение 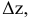 которое называется полным приращением функции z и определяется формулой
которое называется полным приращением функции z и определяется формулой
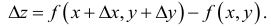
Заметим, что в общем случае 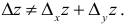
Пример:
Пусть z = ху.
Тогда приращения этой функции будут иметь вид 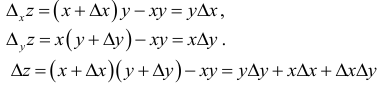
При 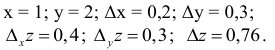
Аналогичным образом определяются частные и полные приращения функции любого количества переменных.
Рассмотрим примеры использования функции нескольких переменных в экономике.
Пример:
Пусть предметами потребления будут два товара: А и В, с соответствующими ценами 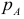 и
и 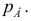 Если цены на другие товары постоянны, а доходы потребителей и структура потребностей на изменяются, то спрос и предложение каждого из товаров зависит от их цен.
Если цены на другие товары постоянны, а доходы потребителей и структура потребностей на изменяются, то спрос и предложение каждого из товаров зависит от их цен.
Запишем несколько функций:
1) Спрос на товар A: 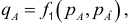
2) Спрос на товар В: 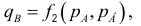
3) Предложение товара А: 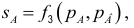
4) Предложение товара В: 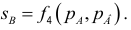
Частные производные
Определение. Частной производной по х от функции z = f(x,y) называется предел отношения частного приращения 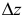 по х к приращению
по х к приращению 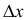 при стремлении
при стремлении 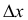 к нулю. Частная производная обозначается одним из символов
к нулю. Частная производная обозначается одним из символов
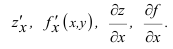
Таким образом, по определению
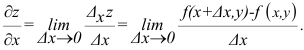
Аналогично определяется частная производная по у.
Заметив, что 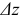 вычисляется при неизменном у, мы можем определить правило нахождения частной производной:
вычисляется при неизменном у, мы можем определить правило нахождения частной производной:
частная производная по одной переменной вычисляется в предположении, что остальные переменные являются величинами постоянными.
- Заказать решение задач по высшей математике
Полный дифференциал функции нескольких переменных
Полным приращением функции z =f(х,у)в точке M(х,у) называют разность
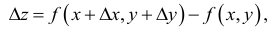
где 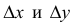 – произвольные приращения аргументов.
– произвольные приращения аргументов.
Функцию 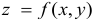 называют дифференцируемой в точке (х,у), если в этой точке полное приращение можно представить в виде
называют дифференцируемой в точке (х,у), если в этой точке полное приращение можно представить в виде
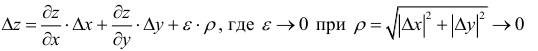
Полным дифференциалом функции z = f(x,y) называют главную часть
полного приращения  линейную относительно приращений аргументов
линейную относительно приращений аргументов  т.е.
т.е.
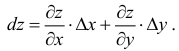
Пусть
1) z = х, найдем: 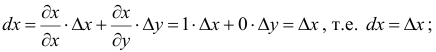
2) z = у, найдем: 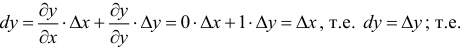
дифференциалы независимых переменных совпадают с их приращениями.
Поэтому полный дифференциал функции z = f(х, у) определяется по формуле
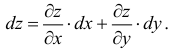
Полный дифференциал равен сумме произведений частных производных на дифференциалы соответствующих независимых переменных.
Из этого следует, что (при достаточно малом 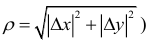 для дифференцируемой функции z = f(x,y) справедливы приближенные равенства
для дифференцируемой функции z = f(x,y) справедливы приближенные равенства
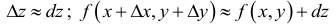
т.е. полное приращение функции приближенно равно ее полному дифференциалу.
Функция f(x,y) называется дифференцируемой в точке (х,у), если она имеет в этой точке полный дифференциал.
Пример №10
Вычислить приближенно 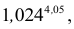 исходя из значения функции
исходя из значения функции 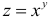 при x = 1,у = 4 и заменяя ее приращение дифференциалом.
при x = 1,у = 4 и заменяя ее приращение дифференциалом.
Решение. Искомое число есть наращенное значение функции z при 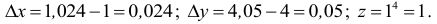
Найдем приращение функции:
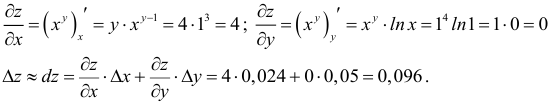
Итак, 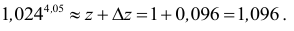
Частные производные и дифференциалы высших порядков
Пусть имеется функция двух переменных 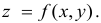
Частными производными второго порядка функции 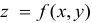 называются частные производные от ее частных производных первого порядка.
называются частные производные от ее частных производных первого порядка.
Частные производные 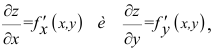 вообще говоря, являются функциями переменных х и у. Поэтому от них можно снова находить частные производные. Следовательно, можно получить четыре частных производных второго порядка:
вообще говоря, являются функциями переменных х и у. Поэтому от них можно снова находить частные производные. Следовательно, можно получить четыре частных производных второго порядка:
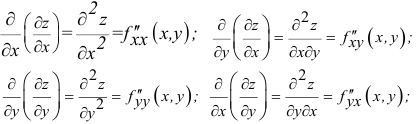
Производные второго порядка можно снова дифференцировать как по х, так и по у. Получим восемь частных производных третьего порядка, и т.д..
Пример №11
Вычислить четвертую производную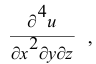 если
если 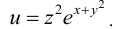
Последовательно дифференцируя заданную функция, получаем
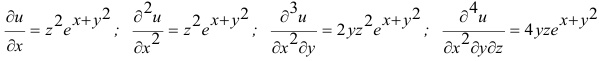
Возникает естественный вопрос – зависит ли результат дифференцирования от порядка (последовательности) дифференцирования?
Теорема. Если функция z = f(x,y) и её частные производные 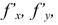
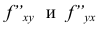 определены и непрерывны в точке М(х,у) и в некоторой её окрестности, то в этой точке смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой:
определены и непрерывны в точке М(х,у) и в некоторой её окрестности, то в этой точке смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой:
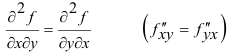
Теорема имеет место и для функции любого числа переменных.
Дифференциалом второго порядка функции 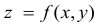 называют
называют
дифференциал от ее полного дифференциала, т.е. 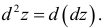 Аналогично определяются дифференциалы третьего
Аналогично определяются дифференциалы третьего 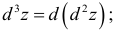 и высших порядков:
и высших порядков:
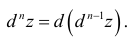
Если х и у-независимые переменные и функция z = f(x,y) имеет непрерывные частные производные, то дифференциалы второго и третьего порядков вычисляются по формулам
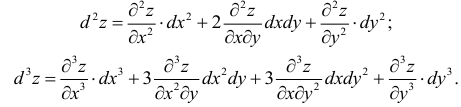
Вообще, имеет место символическая формула, 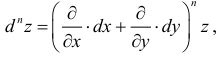
которая формально раскрывается по биномиальному закону.
Дифференцирование сложной функции
а) Пусть 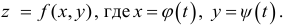 Функции
Функции 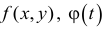 и
и 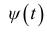
– дифференцируемы. Тогда производная сложной функции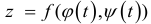 вычисляется по формуле:
вычисляется по формуле:
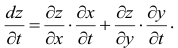
б) Предположим, что в уравнении 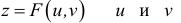 являются функциями независимых переменных х и у:
являются функциями независимых переменных х и у: 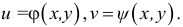 В этом случае z есть сложная функция от аргументов х и у.
В этом случае z есть сложная функция от аргументов х и у.
Предположим, что функции 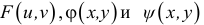 имеют непрерывные частные производные по всем своим аргументам, и поставим задачу:
имеют непрерывные частные производные по всем своим аргументам, и поставим задачу:
вычислить 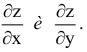
Дадим аргументу х приращение 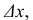 сохраняя значение у неизменным. Тогда
сохраняя значение у неизменным. Тогда 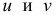 получат приращения, соответственно получит приращение и функция
получат приращения, соответственно получит приращение и функция 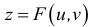
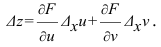
Разделим всё на 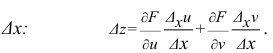
Переходя к пределу при  получим
получим
Следовательно, 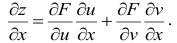
Аналогично получим 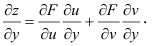
Дифференцирование неявных функций
Функция  называется неявной, если она задается уравнением F(x,y,z)=0, неразрешенным относительно z.
называется неявной, если она задается уравнением F(x,y,z)=0, неразрешенным относительно z.
Найдем частные производные  неявной функции z, заданной уравнением F(x,y,z) = 0. Для этого подставим в уравнение вместо z
неявной функции z, заданной уравнением F(x,y,z) = 0. Для этого подставим в уравнение вместо z
функцию f(х,у), получим тождество 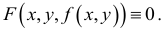
Частные производные по х и по у функции, тождественно равной нулю, также равны нулю:
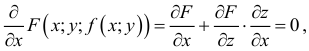 , (у – считаем постоянным),
, (у – считаем постоянным),
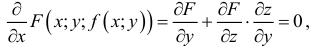 (х – считаем постоянным),
(х – считаем постоянным),
Откуда 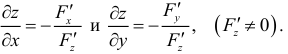
Пример №12
Найти частные производные функции z, заданной уравнением
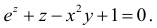
Решение: 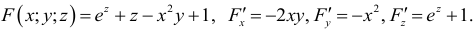
По формуле производной неявной функции имеем:
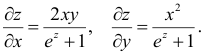
Производная в заданном направлении
Пусть функция z = f(x,y) определена в некоторой окрестности точки М(х,у), L – некоторое направление, задаваемое единичным вектором
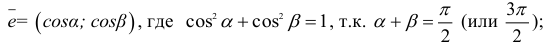
 – косинусы углов, образуемых вектором
– косинусы углов, образуемых вектором  с осями координат и называемые направляющими косинусами.
с осями координат и называемые направляющими косинусами.
При перемещении в данном направлении L точки М(х,у) в точку 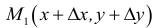 функция z получит приращение
функция z получит приращение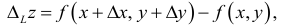 называемое приращением функции z в данном направлении L (рисунок 8.3).
называемое приращением функции z в данном направлении L (рисунок 8.3).
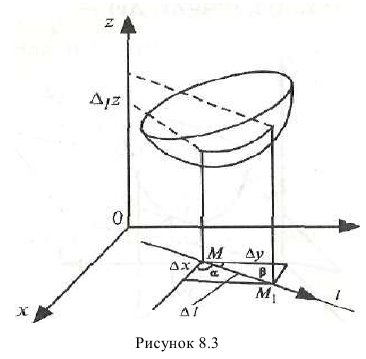
Если 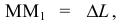 то, очевидно, что
то, очевидно, что 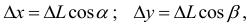 следовательно,
следовательно, 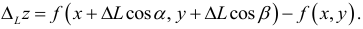
Определение. Производной 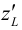 по направлению L функции двух переменных z=f(х,у) называется предел отношения приращения функции в этом направлении к величине перемещения
по направлению L функции двух переменных z=f(х,у) называется предел отношения приращения функции в этом направлении к величине перемещения 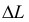 при стремлении последней к
при стремлении последней к
нулю, т.е.
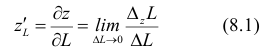
Производная  характеризует скорость изменения функции в направлении L.
характеризует скорость изменения функции в направлении L.
Очевидно, что рассмотренные ранее частные производные  представляют производные по направлениям, параллельным соответственно осям Ох и Оу.
представляют производные по направлениям, параллельным соответственно осям Ох и Оу.
Нетрудно показать, что
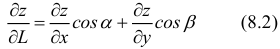
Градиент функции
Определение. Градиентом 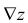 функции z = f(x,y) называется вектор с началом в точке М(х,у), координатами которого являются частные производные функции z = f(x,y).
функции z = f(x,y) называется вектор с началом в точке М(х,у), координатами которого являются частные производные функции z = f(x,y).
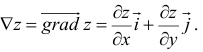
Рассмотрим скалярное произведение векторов 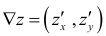 и единичного вектора
и единичного вектора 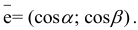 Получим
Получим
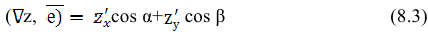
Сравнивая равенства (8.2) и (8.3), получим, что 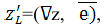 т.е. производная по направлению есть скалярное произведение градиента
т.е. производная по направлению есть скалярное произведение градиента 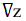 и единичного вектора, задающего направление L.
и единичного вектора, задающего направление L.
Известно, что скалярное произведение двух векторов максимально, если они одинаково направлены. Следовательно, градиент функции 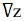 в данной точке характеризует направление максимальной скорости изменения функции в этой точке.
в данной точке характеризует направление максимальной скорости изменения функции в этой точке.
Производная 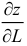 в направлении градиента имеет наибольшее значение, которое определяется по формуле
в направлении градиента имеет наибольшее значение, которое определяется по формуле
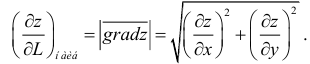
Теорема. Пусть задана дифференцируемая функция z = f(x,y) и пусть в точке, величина градиента отлична от нуля. Тогда градиент перпендикулярен линии уровня, проходящей через данную точку.
Экстремумы функций нескольких переменных
Будем рассматривать функцию двух переменных. Как и в случае одной переменной, функция z = f(x,y) имеет узловые, определяющие структуру графика, точки. В первую очередь это точки экстремума.
Определение. Точка 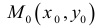 называется точкой максимума (минимума) функции z = f(x,у), если существует такая окрестность, что для всех точек
называется точкой максимума (минимума) функции z = f(x,у), если существует такая окрестность, что для всех точек 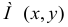 из этой окрестности, удовлетворяющих условию
из этой окрестности, удовлетворяющих условию 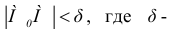 достаточно малое положительное число, выполняется неравенство:
достаточно малое положительное число, выполняется неравенство: 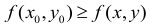
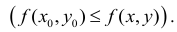
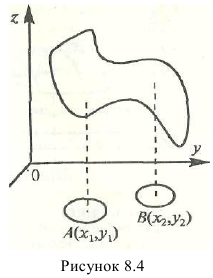
Максимум или минимум функции называется ее экстремумом. Точка  в которой функция имеет экстремум, называется точкой экстремума.
в которой функция имеет экстремум, называется точкой экстремума.
На рисунке 8.4: точка  — есть точка минимума, а точка
— есть точка минимума, а точка  —точка максимума.
—точка максимума.
Следует обратить внимание на локальный характер экстремума (максимума и минимума) функции, так как речь идет о максимальном и минимальном значении лишь в достаточно малой окрестности точки 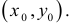
Теорема (необходимый признак существования экстремума).
Если 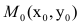 есть точка экстремума функции z = f(x,y), то ее частные производные первого порядка в этой точке равны нулю, т.е.
есть точка экстремума функции z = f(x,y), то ее частные производные первого порядка в этой точке равны нулю, т.е.
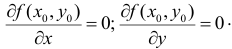
в предположении, что указанные частные производные существуют в точке 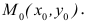
Этот признак — необходимый, т.е. функция может иметь экстремум также в тех точках, где хотя бы одна из частных производных не существует. Точки, в которых первые частные производные обращаются в ноль, или не существуют, называются критическими (стационарными) точками этой функции.
Например, у функции z = xy первые частные производные обращаются в нуль в точке (0;0), однако экстремума у этой функции в этой точке нет.
На рисунке 8.5 изображена так называемая седловая точка  Частные производные
Частные производные  равны нулю, но, очевидно, никакого экстремума в точке
равны нулю, но, очевидно, никакого экстремума в точке  нет. Такие седловые точки являются
нет. Такие седловые точки являются
двумерными аналогами точек перегиба функций одной переменной. Задача заключается в том, чтобы отделить их от точек экстремума. Иными, словами, требуется знать достаточное условие экстремума.
Теорема (достаточное условие экстремума функции двух переменных).
Пусть функция z = f(x,y):
а) определена в некоторой окрестности критической точки 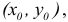 в которой ее частные производные первого порядка равны нулю, т.е.
в которой ее частные производные первого порядка равны нулю, т.е.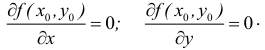
б) имеет в этой точке непрерывные частные производные второго порядка
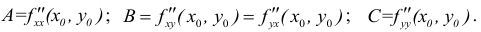
Возможны следующие случаи:
1. 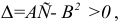 в точке
в точке 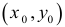 функция
функция 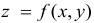 имеет экстремум, причем, если А<0 — максимум; если А>0 — минимум.
имеет экстремум, причем, если А<0 — максимум; если А>0 — минимум.
2. 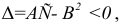 в окрестности точки
в окрестности точки 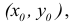 функция
функция 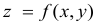 экстремума не имеет, но может быть минимакс (форма «седла», рисунок 17).
экстремума не имеет, но может быть минимакс (форма «седла», рисунок 17).
3. 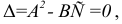 требуется дополнительное исследование.
требуется дополнительное исследование.
Пример №13
Найти экстремумы функции 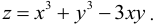
Решение. 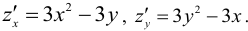 Приравнивая первые частные
Приравнивая первые частные
производные нулю, найдем стационарные точки:
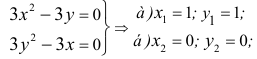
Найдем частные производные второго порядка 
Пример №14
Пусть производится два вида товаров, обозначим их количества через х и у. Пусть цены на эти товары  а функция затрат
а функция затрат 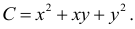 Найти максимум прибыли.
Найти максимум прибыли.
Для решения задачи выразим функцию прибыли /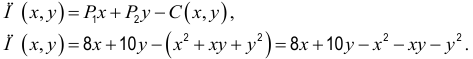
Условия локального экстремума приводят к решению системы двух алгебраических уравнений:
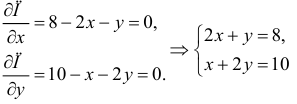
Решение системы дает точку (2,4).
Определим вид экстремума, для этого найдем значения вторых производных функции прибыли:
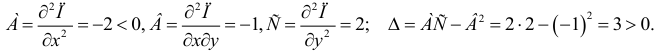
Поскольку 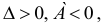 то найденная точка определяет локальный максимум функции прибыли
то найденная точка определяет локальный максимум функции прибыли 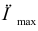 (2,4) = 28.
(2,4) = 28.
Наибольшее и наименьшее значение функции в замкнутой области
Пусть функция z = f(x,y) непрерывна в замкнутой ограниченной области и дифференцируема внутри этой области. Тогда она имеет в этой области наибольшее и наименьшее значения, которые достигаются либо внутри области, либо на её границе. Если наибольшее или наименьшее значение функция принимает во внутренних точках области, то, очевидно, что эти точки являются точками экстремума функции.
Правило нахождения наибольшего и наименьшего значений функции двух переменных:
- найти все критические точки функции, принадлежащие замкнутой области и вычислить значения функции в этих точках;
- найти наибольшее и наименьшее значения функции на границах области;
- сравнить все найденные значения функции, выбрать из них наибольшее и наименьшее.
Замечание. Иногда границу области удобно разбить на части, каждая из которых задается своим уравнением.
Пример №15
Найти наибольшее и наименьшее значения функции 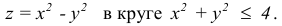
Решение.
Найдем частные производные первого порядка 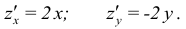
Приравняем их нулю 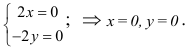
Получаем критическую точку 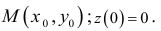 Окружность
Окружность 
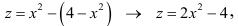 причем
причем 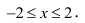
Задача свелась к нахождению наибольшего и наименьшего значений
функции одной переменной 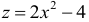 на отрезке
на отрезке 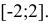 Получаем
Получаем 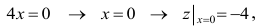 на концах отрезка:
на концах отрезка:
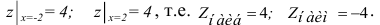
Условный экстремум
Рассмотрим задачу, специфическую для функций нескольких переменных, когда ее экстремум ищется не на всей области определения, а на множестве, удовлетворяющем некоторому условию.
Пусть рассматривается функция z = f(x,y), аргументы х и у которой удовлетворяют условию g(x,y) = С, называемому уравнением связи.
Определение. Точка  называется точкой условного максимума (минимума), если существует такая окрестность этой точки, что для всех точек (х,у) из этой окрестности удовлетворяющих условию g(x,y) = C, выполняется
называется точкой условного максимума (минимума), если существует такая окрестность этой точки, что для всех точек (х,у) из этой окрестности удовлетворяющих условию g(x,y) = C, выполняется
неравенство
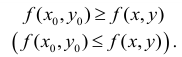
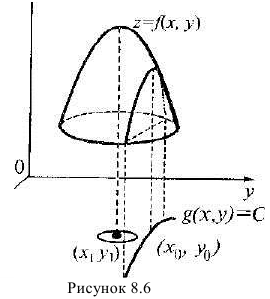
На рис. 18 изображена точка условного максимума 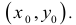 Очевидно, что она не является точкой безусловного экстремума функции z = f(x,y) (на рис. 8.6 это точка
Очевидно, что она не является точкой безусловного экстремума функции z = f(x,y) (на рис. 8.6 это точка 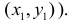
Наиболее простым способом нахождения условного экстремума функции двух переменных является сведение задачи к отысканию экстремума функции одной переменной. Допустим уравнение связи g(x,y) = C удалось разрешить относительно одной из переменных, например, выразить t через х: 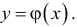 Подставив полученное выражение в функцию двух переменных, получим
Подставив полученное выражение в функцию двух переменных, получим 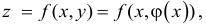 т.е. функцию одной переменной. Ее экстремум и будет условным экстремумом функции z = f(х,у).
т.е. функцию одной переменной. Ее экстремум и будет условным экстремумом функции z = f(х,у).
Пример №16
Найти точки максимума и минимума функции 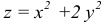 при условии Зх+2у =11.
при условии Зх+2у =11.
Решение. Выразим из уравнения Зх +2у = 11 переменную у через переменную х и подставим полученное выражение 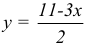 в функцию z.
в функцию z.
Получим 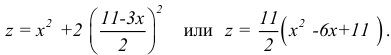 Эта функция имеет единственный минимум
Эта функция имеет единственный минимум 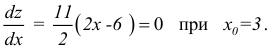 Соответствующее значение функции
Соответствующее значение функции 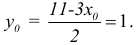 Таким образом, (3; 1) — точка условного экстремума (минимума).
Таким образом, (3; 1) — точка условного экстремума (минимума).
В рассмотренном примере уравнение связи g(x,y) = C оказалось линейным, поэтому его легко удалось разрешить относительно одной из переменных. Однако в более сложных случаях сделать это не удается.
Метод множителей Лагранжа
Для отыскания условного экстремума часто используется метод множителей Лагранжа.
Рассмотрим функцию трех переменных
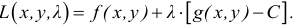
Эта функция называется функцией Лагранжа, а 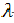 — неопределенным множителем Лагранжа.
— неопределенным множителем Лагранжа.
Теорема. Если точка 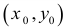 является точкой условного экстремума функции
является точкой условного экстремума функции 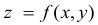 при условии
при условии 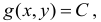 то существует значение
то существует значение 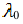 такое,
такое,
что точка  является точкой экстремума функции
является точкой экстремума функции 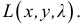
Таким образом, для нахождения условного экстремума функции 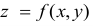 при условии g(x,y) = C требуется найти решение системы
при условии g(x,y) = C требуется найти решение системы
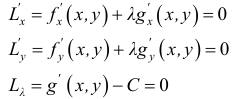
Последнее из этих уравнений совпадает с уравнением связи.
Первые два уравнения системы можно переписать в виде
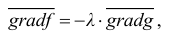
т.е. в точке условного экстремума градиенты функций f(x,y) и g(x,y) коллинеарные.
На рисунке 8.7 показан геометрический смысл условий Лагранжа. Линия  пунктирная, линии уровня
пунктирная, линии уровня 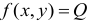 функции z = f(x,y)
функции z = f(x,y)
сплошные.
Пример №17
Найти точки экстремума функции 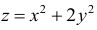 при условии Зх + 2у = 11, используя метод множителей Лагранжа.
при условии Зх + 2у = 11, используя метод множителей Лагранжа.
Решение. Составим функцию Лагранжа 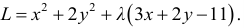 Приравнивая нулю ее частные производные, получим систему уравнений
Приравнивая нулю ее частные производные, получим систему уравнений
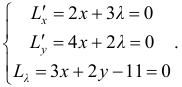
Ее единственное решение 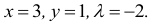 Таким образом, точкой условного экстремума может быть только точка (3;1). Нетрудно убедиться в том, что в этой точке функция z = f(x,y) имеет условный минимум.
Таким образом, точкой условного экстремума может быть только точка (3;1). Нетрудно убедиться в том, что в этой точке функция z = f(x,y) имеет условный минимум.
В случае если число переменных более двух, может рассматриваться и несколько уравнений связи. Соответственно в этом случае будет и несколько множителей Лагранжа.
Мы не рассматриваем здесь достаточные условия условного экстремума. Отметим только, что во многих задачах критическая точка функции Лагранжа оказывается единственной и соответствует не только локальному, но и глобальному условному минимуму или максимуму.
Метод наименьших квадратов
Пусть 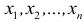 – последовательность значений независимой
– последовательность значений независимой
переменной, а 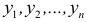 последовательность соответствующих значений зависимой переменной.
последовательность соответствующих значений зависимой переменной.
Требуется подобрать прямую, которая «наилучшим» образом изображала бы зависимость между х и у. Это означает, что отклонения фактических значений функций от «подобранной» прямой должны быть минимальными. Пусть
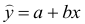
есть уравнение этой прямой. Имеем 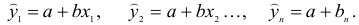
Отклонения от фактических значений функции составляют:
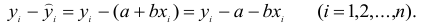
Эти отклонения могут быть положительными или отрицательными; Поэтому прямая подбирается так, чтобы сумма квадратов отклонений
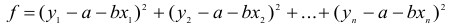 была наименьшей.
была наименьшей.
Следовательно, нужно определить а и b так, чтобы f достигала минимума. Необходимое условие существования минимума состоит в том, чтобы
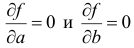
Имеем:
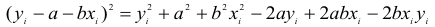
следовательно, 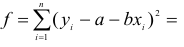
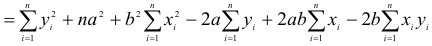
Вычислим 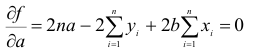
Откуда 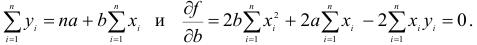
Откуда 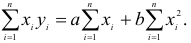
Так мы получаем два уравнения с двумя неизвестными а и b; 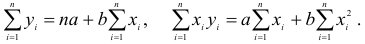
Решение этих двух уравнений дает значения а и b, которые определяют прямую, наилучшим образом отражающую ход изменений функции.
Пример №18
В течении 4-х последних лет переменные х и у принимали следующие значения: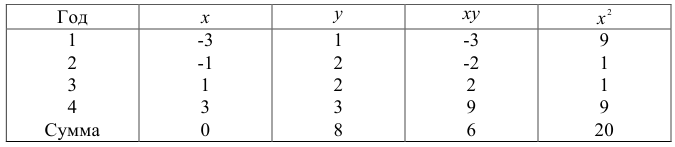
Найти уравнение прямой линии, выражающее зависимость величины у от величины х.
Имеем:
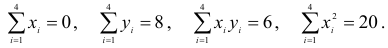
Следовательно, необходимое условие существования минимума суммы квадратов отклонений есть
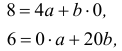
откуда
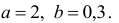
Следовательно, искомая прямая есть
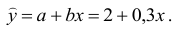
y = a + bx = 2 + 0,3x.
Для сравнения, на рисунке 8.8 изображены точки с координатами, равными значениям х и y пo данным таблицы, а также прямая линия 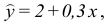 построенная с помощью метода наименьших квадратов.
построенная с помощью метода наименьших квадратов.
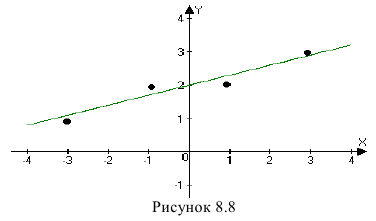
Понятие двойного интеграла
Пусть функция f(x,y) определена в ограниченной замкнутой области D плоскости  Разобьем область D произвольным образом на п элементарных областей, имеющих площади
Разобьем область D произвольным образом на п элементарных областей, имеющих площади  и диаметры
и диаметры 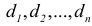 (диаметром области называют наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку
(диаметром области называют наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку 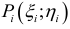 и умножим значение функции в точке
и умножим значение функции в точке  на площадь этой области.
на площадь этой области.
Интегральной суммой для функции f(х,у) по области D называют сумму вида
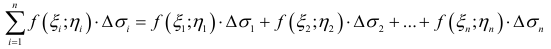
Если при стремлении наибольшего диаметра к нулю, т.е. при max 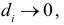 интегральная сумма имеет определенный конечный предел
интегральная сумма имеет определенный конечный предел
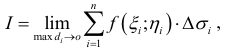 не зависящий от способа разбиения области D на элементарные области и от выбора точек
не зависящий от способа разбиения области D на элементарные области и от выбора точек 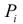 в пределах каждой из них, то этот предел называют двойным интегралом от функции
в пределах каждой из них, то этот предел называют двойным интегралом от функции 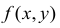 в области D и обозначают следующим образом:
в области D и обозначают следующим образом:
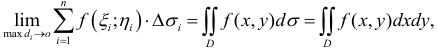
где: D – область интегрирования,  – элемент площади.
– элемент площади.
Геометрический смысл двойного интеграла
Если  в области D, то двойной интеграл
в области D, то двойной интеграл  равен объему D цилиндрического тела, ограниченного сверху поверхностью,
равен объему D цилиндрического тела, ограниченного сверху поверхностью,
сбоку цилиндрической поверхностью с образующими параллельными оси Oz и снизу областью D плоскости 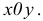
Основные свойства двойного интеграла
Пусть функции 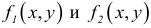 интегрируемы в области D.
интегрируемы в области D.
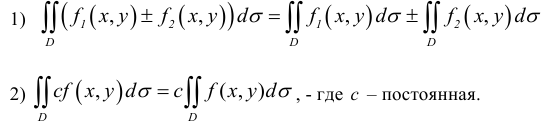
3) Если область интегрирования D разбита на две области 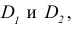 и в каждой из этих областей функция f(x,y) интегрируема, то
и в каждой из этих областей функция f(x,y) интегрируема, то
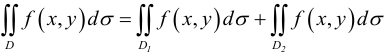
4) Оценка двойного интеграла. Если 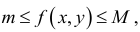 то
то
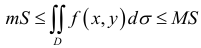
где S — площадь области D, а m и М — соответственно наименьшее и наибольшее значения функции f(x,y) в области D .
Вычисление двойного интеграла
При вычислении двойного интеграла его сводят к повторному, т.е. дважды применяют процесс обычного интегрирования.
Различают два основных вида области интегрирования.
1. Область интегрирования D ограничена слева и справа прямыми
х = а и х = b (а каждая из которых пересекается вертикальной прямой только в одной точке (рисунок 8.9).
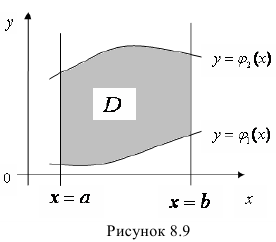
Для такой области двойной интеграл вычисляют по формуле
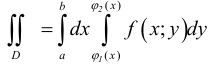
Причем сначала вычисляют внутренний интеграл 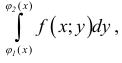 в котором х считают постоянным.
в котором х считают постоянным.
2. Область интегрирования D ограничена снизу и сверху прямыми у = с и y = d (с каждая из которых пересекается
горизонтальной прямой только в одной точке (рисунок 8.10).
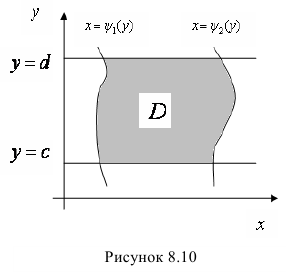
Для такой области двойной интеграл вычисляют по формуле
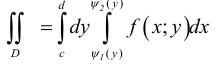
Причем сначала вычисляют внутренний интеграл
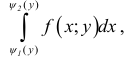
в котором у считают постоянным.
Правые части указанных формул называют двукратными (или повторными) интегралами.
В общем случае область интегрирования с помощью разбиения на части сводят к основным областям.
Пример №19
Вычислить двойные интегралы по указанным областям:
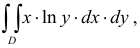 где область D – прямоугольник
где область D – прямоугольник 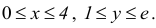
Решение: 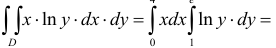
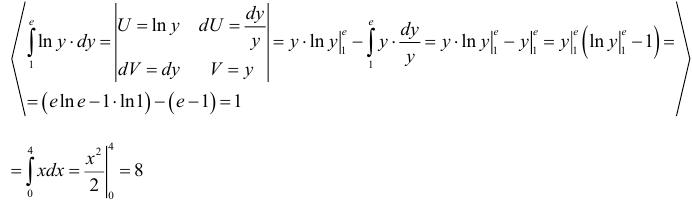
Пример №20
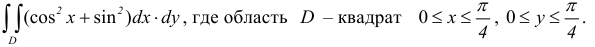
Решение:
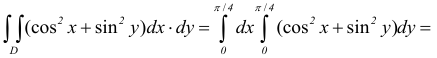
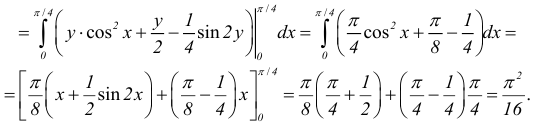
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Линейные дифференциальные уравнения второго порядка
- Системы дифференциальных уравнений
- Производная функции одной переменной
- Приложения производной функции одной переменной
- Исследование поведения функций
- Предел и непрерывность функции двух переменны
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 сентября 2019 года; проверки требуют 7 правок.
Дифференциалом порядка n, где n > 1, от функции 
.
Дифференциал высшего порядка функции одной переменной[править | править код]
Для функции, зависящей от одной независимой переменной 
,
.
Отсюда можно вывести общий вид дифференциала n-го порядка от функции 

.
При вычислении дифференциалов высших порядков очень важно, что 



Дифференциал высшего порядка функции нескольких переменных[править | править код]
Если функция 

Символически общий вид дифференциала n-го порядка от функции

где 


Приращения 
Сложность выражения дифференциала возрастает с увеличением числа переменных.
Неинвариантность дифференциалов высшего порядка[править | править код]
При 




Так, для независимой переменной 
Если же переменная 

.
Аналогично, третий дифференциал примет вид:
.
Для доказательства неинвариантности дифференциалов высшего порядка достаточно привести пример.
При 

С учётом зависимости 
Дополнения[править | править код]
-
- для функции с одной переменной:
,
;
- для функции с несколькими переменными:
,
Примечания[править | править код]
- ↑ 1 2 Баранова Елена Семеновна, Васильева Наталья Викторовна, Федотов Валерий Павлович. Практическое пособие по высшей математике. Типовые расчеты: Учебное пособие. 2-е изд.. — “Издательский дом “”Питер”””, 2012. — С. 196-197. — 400 с. — ISBN 9785496000123.
Литература[править | править код]
- Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
Дифференциалом функции
называется главная (линейная по
) часть приращения функции. Чтобы понять данное определение, рассмотрим следующий рисунок.
На рисунке изображён график функции
и
касательной
к ней в точке
.
Дадим аргументу функции
некоторое приращение
,
тогда функция
также получит некоторое приращение
.
Величина
называется
дифференциалом функции
.
При этом, из графика следует, что
равно приращению ординаты касательной, проведённой в точке
к функции
.
Именно поэтому дифференциалом называют линейную часть приращения функции, т.е. приращение ординаты касательной.
Из рисунка следует, что угол наклона касательной
,
который она образует с положительным направлением оси
и
– равны. Кроме того, тангенс угла наклона касательной равен значению производной функции в точке касания:
Из треугольника
следует, что:
Таким образом, дифференциал функции выражается следующей формулой:
Рассмотрим ещё такой момент: из рисунка следует, что
, причем
. Причем, чем меньше
, тем меньший вклад в величину
вносит значение
. Т.е. при достаточно малых значениях
, можно считать, что
. Данное соотношение позволяет вычислять приближенное значение функции в точке
, если известно её значение в точке
.
Дифференциал высшего порядка (например порядка
) определяется как дифференциал от дифференциала
-ого порядка:
Например, дифференциал второго порядка вычисляется следующим образом:
Аналогичным образом получаем формулу для вычисления дифференциала
-ого порядка:
где
–
-ая производная функции
по переменной
.
Пару слов стоит сказать о вычислении дифференциала функции многих переменных, который в этом случае называется
полным дифференциалом. Полный дифференциал функции, зависящей от
-переменных
определяется по формуле:
Выражения для дифференциалов высших порядков функции многих переменных можно получить исходя из общей формулы:
В общем случае, для возведения суммы в
-ую степень необходимо воспользоваться формулой бинома Ньютона. Рассмотрим процесс получения формулы полного дифференциала второго порядка функции двух переменных:
Наш онлайн калькулятор способен вычислить дифференциалы разных порядков для любых функций одной или нескольких переменных с описанием подробного решения на русском языке.
Содержание:
- Случай независимой переменной
- Случай зависимой переменной
Пусть функция $y=f(x)$ зависит от переменной
$x$ и дифференцируема в точке
$x$. Может оказаться, что в точке
$x$ дифференциал
$d y=f^{prime}(x) d x$, рассматриваемый как функция от
$x$, есть также дифференцируемая функция. Тогда существует
дифференциал от дифференциала $d(dy)$ данной функции,
который называется дифференциалом второго порядка функции $y=f(x)$.
Дифференциал второго порядка обозначается следующим образом:
$d^2y=d(dy)$
Аналогично определяются дифференциалы более высоких порядков.
Определение
Дифференциалом
$n$-го порядка
$d_ny$ функции
$y=f(x)$ называется дифференциал от дифференциала
$(n-1)$-го порядка этой функции, то есть
$$d^{n} y=dleft(d^{n-1} yright)$$
Получим формулы, выражающие дифференциалы высших порядков. Рассмотрим несколько случаев.
Случай независимой переменной
Пусть $y=f(x)$ – функция независимой переменной
$x$, имеющая дифференциалы любого порядка.
Первый дифференциал функции
$$d y=f^{prime}(x) d x$$
где $dx=Delta x$ – некоторое приращение независимой
переменной $x$, которое мы задаем сами и которое не
зависит от $x$. По определению
$$d^{2} y=d(d y)=dleft(f^{prime}(x) d xright)$$
Переменной является аргумент $x$. Значит, для
дифференциала величина $dx$ является постоянной и
поэтому может быть вынесена за знак дифференциала. То есть дифференциал второго порядка
$$d^{2} y=dleft(f^{prime}(x) d xright)=d x cdot dleft(f^{prime}(x)right)$$
Для вычисления дифференциала $dleft(f^{prime}(x)right)$ применим формулу
дифференциала первого порядка к функции $f^{prime}(x)$. Тогда получим:
$$dleft(f^{prime}(x)right)=left(f^{prime}(x)right)^{prime} cdot d x=d x cdot f^{prime prime}(x) d x=f^{prime prime}(x)(d x)^{2}=f^{prime prime}(x) d x^{2}$$
Итак,
$$d^{2} y=f^{prime prime}(x) d x^{2}$$
Рассматривая последовательно дифференциалы все более высокого порядка, получим формулу дифференциала
$n$-го порядка:
$$d^{n} y=f^{n}(x) d x^{n}$$
Пример
Задание. Найти дифференциал третьего порядка функции $y(x)=4x^3-12x+5$
Решение. По формуле
$$d^{3} y=y^{prime prime prime}(x) d x^{3}$$
Найдем третью производную заданной функции:
$$begin{array}{c}
y^{prime}(x)=left(4 x^{3}-12 x+5right)^{prime}=left(4 x^{3}right)^{prime}-(12 x)^{prime}+(5)^{prime}= \
4left(x^{3}right)^{prime}-12(x)^{prime}+0=4 cdot 3 x^{2}-12 cdot 1=12 x^{2}-12 \
y^{prime prime}(x)=left(y^{prime}(x)right)^{prime}=left(12 x^{2}-12right)^{prime}=left(12 x^{2}right)^{prime}-(12)^{prime}= \
=12left(x^{2}right)^{prime}-0=12 cdot 2 x=24 x \
y^{prime prime prime}(x)=left(y^{prime prime}(x)right)^{prime}=(24 x)^{prime}=24(x)^{prime}=24
end{array}$$
Тогда
$$d^{3}y=24dx^3$$
Ответ. $d^{3}y=24dx^3$
Случай зависимой переменной
Пусть задана дифференцируемая функция $y=f(u(x))$. Тогда
$$d y=f^{prime}(u) d u$$
где $d u=u^{prime}(x) d x$ в общем случае не является постоянной величиной.
Поэтому дифференциал от функции $f^{prime}(u) d u$ берем как дифференциал от произведения
$$d^{2} y=dleft(f^{prime}(u) d uright)=dleft(f^{prime}(u)right) cdot d u+f^{prime}(u) cdot d(d u)=f^{prime prime}(u) d u^{2}+f^{prime}(u) d^{2} u$$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти дифференциал второго порядка
$d^{2}u$ функции $f(u)=sqrt{u}$, где
$u(x)=3x+7$ и $x$ – независимая переменная.
Решение. Решим пример разными способами и сравним ответы.
1-ый способ. Согласно формуле, имеем, что искомый дифференциал
$$d^{2} y=f^{prime prime}(u) d u^{2}+f^{prime}(u) d^{2} u$$
Найдем все необходимые компоненты формулы. Из условия имеем:
$$begin{array}{c}
f^{prime}(u)=(sqrt{u})^{prime}=frac{1}{2 sqrt{u}} \
f^{prime prime}(u)=left(f^{prime}(u)right)^{prime}=left(frac{1}{2 sqrt{u}}right)^{prime}=frac{1}{2} cdotleft(u^{-frac{1}{2}}right)^{prime}= \
=frac{1}{2} cdotleft(-frac{1}{2}right) cdot u^{-frac{3}{2}}=-frac{1}{4 sqrt{u^{3}}} \
d u=d(3 x+7)=(3 x+7)^{prime} d x=left[(3 x)^{prime}+(7)^{prime}right] d x= \
=left[3(x)^{prime}+0right] d x=3 cdot 1 cdot d x=3 d x \
d^{2} u=d(3 d x)=d x cdot d(3)=d x cdot 0=0
end{array}$$
А тогда:
$$begin{aligned}
d^{2} y=&-frac{1}{4 sqrt{u^{3}}} d u^{2}+frac{1}{2 sqrt{u}} cdot 0=-frac{1}{4 sqrt{u^{3}}} cdot(3 d x)^{2}=\
&=-frac{9}{4 sqrt{u^{3}}} d x^{2}=-frac{9}{4 sqrt{(3 x+7)^{3}}} d x^{2}
end{aligned}$$
2-ой способ. Из того, что $f(u)=sqrt{u}$ и
$u(x)=3 x+7$, получаем:
$$f(x)=sqrt{3 x+7}$$
А тогда
$$d^{2} y=f^{prime prime}(x) d x^{2}$$
Найдем вторую производную функции $f(x)=sqrt{3 x+7}$:
$$f^{prime}(x)=(sqrt{3 x+7})^{prime}=frac{1}{2 sqrt{3 x+7}} cdot(3 x+7)^{prime}=$$
$$=frac{1}{2 sqrt{3 x+7}} cdotleft[(3 x)^{prime}+(7)^{prime}right]=frac{1}{2 sqrt{3 x+7}} cdotleft[3(x)^{prime}+0right]=$$
$$=frac{3 cdot 1}{2 sqrt{3 x+7}}=frac{3}{2 sqrt{3 x+7}}$$
$$f^{prime prime}(x)=left(f^{prime}(x)right)^{prime}=left(frac{3}{2 sqrt{3 x+7}}right)^{prime}=frac{3}{2}left((3 x+7)^{-frac{1}{2}}right)^{prime}=$$
$$=frac{3}{2} cdotleft(-frac{1}{2}right) cdot(3 x+7)^{-frac{3}{2}} cdot(3 x+7)^{prime}=$$
$$=-frac{3}{4 sqrt{(3 x+7)^{3}}} cdotleft[(3 x)^{prime}+(7)^{prime}right]=-frac{3}{4 sqrt{(3 x+7)^{3}}} cdot 3(x)^{prime}=$$
$$=-frac{3 cdot 3 cdot 1}{4 sqrt{(3 x+7)^{3}}}=-frac{9}{4 sqrt{(3 x+7)^{3}}}$$
Окончательно имеем:
$$d^{2} y=-frac{9}{4 sqrt{(3 x+7)^{3}}} d x^{2}$$
Ответ. $d^{2} y=-frac{9}{4 sqrt{(3 x+7)^{3}}} d x^{2}$
Читать дальше: производная функции, заданной неявно.






