Как найти полный импульс тела - Сайт, где вы сможете решить свои вопросы

Определение

Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:

p = mv

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).

Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.

Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:

10 г = 0,01 кг

Импульс равен:

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

Определение

Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:

p_1отн2 = m₁v_1отн2 = m₁(v₁ – v₂)

p_1отн2 — импульс первого тела относительно второго, m₁ — масса первого тела, v_1отн2 — скорость первого тела относительно второго, v₁ и v₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.

Сначала переведем единицы измерения в СИ:

15 т = 15000 кг

p_1отн2 = m₁(v₁ – v₂) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙10³ (кг∙м/с)

Изменение импульса тела

ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:

∆p = p – p₀ = p + (– p₀)

∆p — изменение импульса тела, p — конечный импульс тела, p₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар
	Конечная скорость после удара: v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0.
Абсолютно упругий удар
	Модули конечной и начальной скоростей равны: v = v₀. Модули конечного и начального импульсов равны: p = p₀. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p₀ = 2p.
Пуля пробила стенку
	Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p₀ – p = m(v₀ – v)
Радиус-вектор тела повернул на 180 градусов
	Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p₀ = 2p = 2mv₀
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
	Модули конечной и начальной скоростей равны: v = v₀. Модули конечного и начального импульсов равны: p = p₀. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:

Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.

В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.

Вычисляем:

Второй закон Ньютона в импульсном виде

Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела

Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Определение

Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.

Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.

Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

V = a∆t

Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Определение

Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса

Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.

Закон сохранения импульса в проекции на горизонтальную ось

Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:

положителен, если его направление совпадает с направлением оси ОХ;
отрицателен, если он направлен противоположно направлению оси ОХ.

Важно!

При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m₁v₁ = (m₁ + m₂)v
Неупругое столкновение движущихся тел	± m₁v₁ ± m₂v₂ = ±(m₁ + m₂)v
В начальный момент система тел неподвижна	0 = m₁v’₁ – m₂v’₂
До взаимодействия тела двигались с одинаковой скоростью	(m₁ + m₂)v = ± m₁v’₁ ± m₂v’₂

Сохранение проекции импульса

В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.

Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.

Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:

m₂v₂ = (m₁+ m₂)v

Отсюда скорость равна:

Задание EF17556

Импульс частицы до столкновения равен −p₁, а после столкновения равен −p₂, причём p₁= p, p₂= 2p, −p₁⊥−p₂. Изменение импульса частицы при столкновении Δ−p равняется по модулю:

а) p

б) p√3

в) 3p

г) p√5

Алгоритм решения

1.Записать исходные данные.

2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.

3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.

4.Подставить известные значения и вычислить.

Решение

Запишем исходные данные:

• Модуль импульса частицы до столкновения равен: p₁= p.

• Модуль импульса частицы после столкновения равен: p₂= 2p.

• Угол между вектором начального и вектором конечного импульса: α = 90^о.

Построим чертеж:

Так как угол α = 90^о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:

Δp=√p21+p22

Подставим известные данные:

Δp=√p2+(2p)2=√5p2=p√5

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17695

На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно

б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено

в) в интервалах 0–1 и 1–2 двигалось равномерно

г) в интервалах 0–1 и 1–2 двигалось равноускорено

Алгоритм решения

1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.

2.Сделать вывод о том, как зависит характер движения от импульса.

3.На основании вывода и анализа графика установить характер движения тела на интервалах.

Решение

Импульс тела есть произведение массы тела на его скорость:

p = mv

Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.

На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.

Верный ответ: б.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22730

Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.

Алгоритм решения

1.Записать исходные данные.

2.Записать закон сохранения импульса применительно к задаче.

3.Записать формулу кинетической энергии тела.

4.Выполнить общее решение.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса камня: m₁ = 3 кг.

• Масса тележки с песком: m₂ = 15 кг.

• Кинетическая энергия тележки с камнем: E_k = 2,25 Дж.

Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:

m1v1+m2v2=(m1+m2)v

Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:

m1v1cosα=(m1+m2)v

Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:

Ek=(m1+m2)v22

Отсюда скорость равна:

v=√2Ekm1+m2

Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:

v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2

Подставим известные данные и произведем вычисления:

v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)

Ответ: 6

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22520

Снаряд, имеющий в точке О траектории импульсp₀, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:

а) −−→AB

б) −−→BC

в) −−→CO

г) −−→OD

Алгоритм решения

1.Сформулировать закон сохранения импульса и записать его в векторной форме.

2.Применить закон сохранения импульса к задаче.

3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.

Решение

Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:

−p1+−p2=−p′
1+−p′2

Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:

−p0=−p1+−p2

Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:

−p2=−p0−−p1

Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18122

Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?

Ответ:

а) 27 г

б) 64 г

в) 81 г

г) 100 г

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.

3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.

4.Выполнить решение задачи в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса пластилиновой пули: m = 9 г.

• Скорость пластилиновой пули: v = 20 м/с.

• Максимальный угол отклонения нити: α = 60°.

Переведем единицы измерения величин в СИ:

Сделаем чертеж:

Нулевой уровень — точка А.

После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:

mv=(m+M)V

После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.

Закон сохранения энергии для точки В:

(m+M)V22=(m+M)gh

V22=gh

Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:

V=√2glcosα

Подставим это выражение в закон сохранения импульса для точки А и получим:

Выразим массу груза:

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 20.1k

Источник

Р
азделим
силы на внутренние и внешние:

– внутренние силы, действующие между
телами, включенными в систему (i,j
= 1,2,…, i

j),
F₁,F₂…-
внешние силы, действующие со стороны
других тел, не включенных в систему.

– теорема об изменении полного импульса
системы материальных точек
(II
закон Ньютона для системы материальных
точек), т.е. импульс системы может
измениться только под действием внешних
сил.

Вопрос 5. Центр масс(центр инерции). Уравнение движения центра масс.

Центром масс
(центром инерции) называется
воображаемая точка, в которой как бы
сосредоточена вся масса тела или системы
тел. Центр
тяжести
практически совпадает с центром масс.

Перепишем первое
уравнение, дифференцируя, найдем скорость
центра масс и получим:

.

–
уравнение
движения центра масс.

Тема 6. Закон сохранения импульса.

Вопрос 1. Замкнутая и незамкнутая системы в механике. Закон сохранения импульса.

Система, на которую
не действуют внешние силы или их действие
скомпенсировано, т.е. для которой

,
называется замкнутой
или
изолированной.
Для такой
системы можно записать:

и,
т.к.

,
следовательно,

– закон
сохранения импульса:
«В замкнутой системе полный импульс
материальных точек остается постоянным».

Пространство
однородно
– это означает, что все точки пространства
эквивалентны, т.е. равноправны. В
однородном пространстве нет каких-либо
особых точек, отличных от других. Если
некоторую систему тел перенести в другое
место пространства, а тела в ней поставить
в те же условия, в которых они находились
в прежнем положении, то это никак не
отразится на ходе всех последующих
явлений. Если взять замкнутую систему
тел, для которой полный импульс системы
равен некоторой величине, то и в любом
другом месте полный импульс будет
оставаться тем же самым. Иначе говоря,
закон
сохранения импульса
является следствием однородности
пространства.

Тема 7. Работа. Мощность. Энергия.

Вопрос 1. Определение элементарной работы, различные выражения.

-элементарная
работа, т.е. работа, совершаемая при
таком малом перемещении, в пределах
которого силу можно считать неизменной,
F_r
проекция силы на направление перемещения.

–
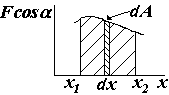
полная работа (это всегда интеграл).

,только
при

,

= 0 и S
=

r.

-работа
на конечном участке, выраженная через
проекции силы и изменения координат.

Н
а
приведенном графике для одномерного
движения 
работа – площадь под кривой зависимости
проекции
силы от перемещения х.Работа
является положительной, если сила
действует в сторону перемещения
(перпендикулярная
сила работы не совершает).

Вопрос 2. Мощность, ее выражение через силу и скорость тела.

Мощность (Дж/с
= Вт) – по смыслу – это работа, совершаемая
за единицу времени.

Используя выражение
для работы, мощность можно выразить как
скалярное произведение вектора силы и
вектора скорости:
.

Вопрос 3. Кинетическая энергия и ее выражение через импульс тела.

Кинетическая
энергия –
это энергия, связанная с движением.
Выражение для кинетической энергии
можно получить, если найти работу,
которую должна совершить сила F,
чтобы сообщить неподвижному телу массой
m
скорость v.

Таким образом,
неподвижное тело за счет работы силы
приобрело скорость и кинетическую
энергию.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Импульс

Второй закон Ньютона в импульсной форме
Пример вычисления силы
Импульс системы тел
Закон сохранения импульса
Закон сохранения проекции импульса

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: импульс тела, импульс системы тел, закон сохранения импульса.

Импульс тела — это векторная величина, равная произведению массы тела на его скорость:

Специальных единиц измерения импульса нет. Размерность импульса — это просто произведение размерности массы на размерность скорости:

$[p]=[m]cdot [upsilon ]= frac{displaystyle kgcdot m}{displaystyle c}$ .

Почему понятие импульса является интересным? Оказывается, с его помощью можно придать второму закону Ньютона несколько иную, также чрезвычайно полезную форму.

к оглавлению ▴

Второй закон Ньютона в импульсной форме

Пусть vec{F} — равнодействующая сил, приложенных к телу массы . Начинаем с обычной записи второго закона Ньютона:

С учётом того, что ускорение тела vec{a} равно производной вектора скорости, второй закон Ньютона переписывается следующим образом:

$mfrac{displaystyle dvec{upsilon } }displaystyle {dt}=vec{F}$ .

Вносим константу под знак производной:

$frac{displaystyle d(mvec{upsilon } )}{displaystyle dt}= vec{F}$ .

Как видим, в левой части получилась производная импульса:

$frac{displaystyle dvec{displaystyle p} }{displaystyle dt}= vec{F}$ . ( 1)

Соотношение ( 1) и есть новая форма записи второго закона Ньютона.

Второй закон Ньютона в импульсной форме. Производная импульса тела есть равнодействующая приложенных к телу сил.

Можно сказать и так: результирующая сила, действующая на тело, равна скорости изменения импульса тела.

Производную в формуле ( 1) можно заменить на отношение конечных приращений:

$frac{displaystyle Delta vec{displaystyle p} }{Delta displaystyle t}= vec{displaystyle F}$ . ( 2)

В этом случае vec{F} есть средняя сила, действующая на тело в течение интервала времени Delta t . Чем меньше величина Delta t , тем ближе отношение к производной , и тем ближе средняя сила vec{F} к своему мгновенному значению в данный момент времени.

В задачах, как правило, интервал времени Delta t достаточно мал. Например, это может быть время соударения мяча со стенкой, и тогда vec{F} — средняя сила, действующая на мяч со стороны стенки во время удара.

Вектор в левой части соотношения ( 2) называется изменением импульса за время Delta t . Изменение импульса — это разность конечного и начального векторов импульса. А именно, если $vec{p} _{0}$ — импульс тела в некоторый начальный момент времени, vec{p} — импульс тела спустя промежуток времени Delta t , то изменение импульса есть разность:

$Delta vec{p} = vec{p} -vec{p} _{0}$ .

Подчеркнём ещё раз, что изменение импульса — это разность векторов (рис. 1):

Рис. 1. Изменение импульса

Пусть, например, мяч летит перпендикулярно стенке (импульс перед ударом равен $vec{p} _{0}$ ) и отскакивает назад без потери скорости (импульс после удара равен $vec{p}= -vec{p} _{0}$ ). Несмотря на то, что импульс по модулю не изменился ( $p= p _{0}$ ), изменение импульса имеется:

$Delta vec{p} = vec{p} -vec{p} _{0}= -vec{p} _{0}-vec{p} _{0}= -2vec{p} _{0}$ .

Геометрически эта ситуация показана на рис. 2:

Рис. 2. Изменение импульса при отскоке назад

Модуль изменения импульса, как видим, равен удвоенному модулю начального импульса мяча: $Delta p= 2p_{0}$ .

Перепишем формулу ( 2) следующим образом:

, ( 3)

или, расписывая изменение импульса, как и выше:

$vec{p} -vec{p} _{0}=vec{F} Delta t$ .

Величина называется импульсом силы. Специальной единицы измерения для импульса силы нет; размерность импульса силы равна просто произведению размерностей силы и времени:

(Обратите внимание, что Hcdot c оказывается ещё одной возможной единицей измерения импульса тела.)

Словесная формулировка равенства ( 3) такова: изменение импульса тела равно импульсу действующей на тело силы за данный промежуток времени. Это, разумеется, снова есть второй закон Ньютона в импульсной форме.

к оглавлению ▴

Пример вычисления силы

В качестве примера применения второго закона Ньютона в импульсной форме давайте рассмотрим следующую задачу.

Задача. Шарик массы m= 100 г, летящий горизонтально со скоростью м/с, ударяется о гладкую вертикальную стену и отскакивает от неё без потери скорости. Угол падения шарика (то есть угол между направлением движения шарика и перпендикуляром к стене) равен $alpha = 60^{circ}$ . Удар длится с. Найти среднюю силу,
действующую на шарик во время удара.

Решение. Покажем прежде всего, что угол отражения равен углу падения, то есть шарик отскочит от стены под тем же углом alpha (рис. 3).

Рис. 3. К задаче (вид сверху)

Тут всё дело в том, что стена — гладкая. Это значит, что трения между шариком и стеной нет. Следовательно, со стороны стены на шарик действует единственная сила vec{N} — сила упругости, направленная перпендикулярно стене (рис. 4).

Рис. 4. К задаче

Согласно ( 3) имеем: . Отсюда следует, что вектор изменения импульса сонаправлен с вектором vec{N} , то есть направлен перпендикулярно стене в сторону отскока шарика (рис. 5).

Рис. 5. К задаче

Векторы $vec{p} _{0}$ и
vec{p} равны по модулю
(так как скорость шарика не изменилась). Поэтому треугольник, составленный из векторов $vec{p} _{0}$ , vec{p} и , является равнобедренным. Значит, угол между векторами vec{p} и равен alpha , то есть угол отражения действительно равен углу падения.

Теперь заметим вдобавок, что в нашем равнобедренном треугольнике есть угол $60^{circ}$ (это угол падения); стало быть, данный треугольник — равносторонний. Отсюда:

$Delta p= p_{0}= mupsilon = 0,1cdot 6= 0,6~Hcdot c$ .

И тогда искомая средняя сила, действующая на шарик:

$N= frac{displaystyle Delta p}{displaystyle Delta t}= frac{displaystyle 0,6}{displaystyle 0,01}= 60~H$ .

к оглавлению ▴

Импульс системы тел

Начнём с простой ситуации системы двух тел. А именно, пусть имеются тело 1 и тело 2 с импульсами $vec{p} _{1}$ и $vec{p} _{2}$ соответственно. Импульс vec{p} системы данных тел — это векторная сумма импульсов каждого тела:

$vec{p} = vec{p} _{1}+vec{p} _{2}$ .

Оказывается, для импульса системы тел имеется формула, аналогичная второму закону Ньютона в виде ( 1). Давайте выведем эту формулу.

Все остальные объекты, с которыми взаимодействуют рассматриваемые нами тела 1 и 2, мы будем называть внешними телами. Силы, с которыми внешние тела действуют на тела 1 и 2, называем внешними силами. Пусть $vec{F} _{1}$ — результирующая внешняя сила, действующая на тело 1. Аналогично $vec{F} _{2}$ — результирующая внешняя сила, действующая на тело 2 (рис. 6).

Рис. 6. Система двух тел

Кроме того, тела 1 и 2 могут взаимодействовать друг с другом. Пусть тело 2 действует на тело 1 с силой vec{T} . Тогда тело 1 действует на тело 2 с силой . По третьему закону Ньютона силы vec{T} и равны по модулю и противоположны по направлению: . Силы vec{T} и — это внутренние силы, действующие в системе.

Запишем для каждого тела 1 и 2 второй закон Ньютона в форме ( 1):

$frac{displaystyle dvec{displaystyle p} _ {displaystyle 1}}{displaystyle dt}=vec{F} _{1}+vec{T}$ , ( 4)

$frac{displaystyle dvec{displaystyle p} _{displaystyle 2}}{displaystyle dt}=vec{F} _{2}+{vec{T}}$ . ( 5)

Сложим равенства ( 4) и ( 5):

$frac{displaystyle dvec{displaystyle p} _{displaystyle 1}}{displaystyle dt}+frac{displaystyle dvec{displaystyle p} _{displaystyle 2}}{displaystyle dt}= vec{F} _{1}+vec{F} _{2}+vec{T} +{vec{T}}$ .

В левой части полученного равенства стоит сумма производных, равная производной суммы векторов $vec{p} _{1}$ и $vec{p} _{2}$ . В правой части имеем в силу третьего закона Ньютона:

$frac{displaystyle d(vec{displaystyle p} _{displaystyle 1}+vec{displaystyle p} _{displaystyle 2})}{displaystyle dt}= vec{F} _{1}+vec{F} _{2}$ .

Но $vec{p} _{1}+vec{p} _{2}= vec{p}$ — это импульс системы тел 1 и 2. Обозначим также $vec{F} _{1}+vec{F} _{2}= vec{F} _{external}$ — это результирующая внешних сил, действующих на систему. Получаем:

$frac{dvec{displaystyle p} }{displaystyle dt}= vec{F} _{external}$ . ( 6)

Таким образом, скорость изменения импульса системы тел есть равнодействующая внешних сил, приложенных к системе. Равенство ( 6), играющее роль второго закона Ньютона для системы тел, мы и хотели получить.

Формула ( 6) была выведена для случая двух тел. Теперь обобщим наши рассуждения на случай произвольного количества тел в системе.

Импульсом системы тел тел называется векторная сумма импульсов всех тел, входящих в систему. Если система состоит из тел, то импульс этой системы равен:

$vec{p} = vec{p} _{1}+vec{p} _{2}+...+vec{p} _{N}$ .

Дальше всё делается совершенно так же, как и выше (только технически это выглядит несколько сложнее). Если для каждого тела записать равенства, аналогичные ( 4) и ( 5), а затем все эти равенства сложить, то в левой части мы снова получим производную импульса системы, а в правой части останется лишь сумма внешних сил (внутренние силы, попарно складываясь, дадут нуль ввиду третьего закона Ньютона). Поэтому равенство ( 6) останется справедливым и в общем случае.

к оглавлению ▴

Закон сохранения импульса

Система тел называется замкнутой, если действия внешних тел на тела данной системы или пренебрежимо малы, или компенсируют друг друга. Таким образом, в случае замкнутой системы тел существенно лишь взаимодействие этих тел друг с другом, но не с какими-либо другими телами.

Равнодействующая внешних сил, приложенных к замкнутой системе, равна нулю: $vec{F} _{external}= vec{0}$ . В этом случае из ( 6) получаем:

$frac{displaystyle dvec{displaystyle p} }{displaystyle dt}= vec{0}$ .

Но если производная вектора обращается в нуль (скорость изменения вектора равна нулю), то сам вектор не меняется со временем:

Закон сохранения импульса. Импульс замкнутой системы тел остаётся постоянным с течением времени при любых взаимодействиях тел внутри данной системы.

Простейшие задачи на закон сохранения импульса решаются по стандартной схеме, которую мы сейчас покажем.

Задача. Тело массы $m_{1}= 800$ г движется со скоростью $upsilon _{1}= 3$ м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы $m_{2}= 200$ г со скоростью $upsilon _{2}= 13$ м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.

Решение. Ситуация изображена на рис. 7. Ось направим в сторону движения первого тела.

Рис. 7. К задаче

Поскольку поверхность гладкая, трения нет. Поскольку поверхность горизонтальная, а движение происходит вдоль неё, сила тяжести и реакция опоры уравновешивают друг друга:

$m_{1}vec{g} +vec{N} _{1}= vec{0}$ ,
$m_{2}vec{g} +vec{N} _{2}= vec{0}$ .

Таким образом, векторная сумма сил, приложенных к системе данных тел, равна нулю. Это значит, что система тел замкнута. Стало быть, для неё выполняется закон сохранения импульса:

$vec{p} _{before~hitting}= vec{p} _{after~hitting}$ . ( 7)

Импульс системы до удара — это сумма импульсов тел:

$vec{p} _{before~hitting}= m_{1}vec{upsilon _{1}} +m_{2}vec{upsilon _{2}}$ .

После неупругого удара получилось одно тело массы $m_{1}+m_{2}$ , которое движется с искомой скоростью :

$vec{p} _{after~hitting}= (m_{1}+m_{2})vec{upsilon }$ .

Из закона сохранения импульса ( 7) имеем:

$m_{1}vec{upsilon _{1}} +m_{2}vec{upsilon _{2}} = (m_{1}+m_{2})vec{upsilon }$ .

Отсюда находим скорость тела, образовавшегося после удара:

$vec{upsilon} = frac{displaystyle m_{displaystyle 1}vec{displaystyle upsilon _{displaystyle 1}} +displaystyle m_{displaystyle 2}vec{displaystyle upsilon _{displaystyle 2}} }{displaystyle m_{displaystyle 1}+displaystyle m_{displaystyle 2}}$ .

Переходим к проекциям на ось :

$upsilon _{x}= frac{displaystyle m_{displaystyle 1}displaystyle upsilon _{displaystyle 1x}+displaystyle m_{displaystyle 2}upsilon _{displaystyle 2x}}{displaystyle m_{displaystyle 1}+displaystyle m_{displaystyle 2}}$ .

По условию имеем: $upsilon _{1x}= 3$ м/с, $upsilon _{2x}= -13$ м/с, так что

$upsilon _{x}= frac{displaystyle 0,8cdot 3-0,2cdot 13}{displaystyle 0,8+0,2}= -0,2frac{m}{c}$ .

Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси . Искомая скорость: м/с.

к оглавлению ▴

Закон сохранения проекции импульса

Часто в задачах встречается следующая ситуация. Система тел не является замкнутой (векторная сумма внешних сил, действующих на систему, не равна нулю), но существует такая ось , сумма проекций внешних сил на ось равна нулю в любой момент времени. Тогда можно сказать, что вдоль данной оси наша система тел ведёт себя как замкнутая, и проекция импульса системы на ось сохраняется.

Покажем это более строго. Спроектируем равенство ( 6) на ось :

$frac{displaystyle dp_{displaystyle x}}{displaystyle dt}= F_{external,x}$ .

Если проекция равнодействующей внешних сил обращается в нуль, $F_{external,x}= 0$ , то

$frac{displaystyle dp_{displaystyle x}}{displaystyle dt}= 0$ .

Следовательно, проекция $p_{x}$ есть константа:

$p_{x}= const$ .

Закон сохранения проекции импульса. Если проекция на ось суммы внешних сил, действующих на систему, равна нулю, то проекция $p_{x}$ импульса системы не меняется с течением времени.

Давайте посмотрим на примере конкретной задачи, как работает закон сохранения проекции импульса.

Задача. Мальчик массы , стоящий на коньках на гладком льду, бросает камень массы со скоростью upsilon под углом alpha к горизонту. Найти скорость , с которой мальчик откатывается назад после броска.

Решение. Ситуация схематически показана на рис. 8. Мальчик изображён прямогольником.

Рис. 8. К задаче

Импульс системы «мальчик + камень» не сохраняется. Это видно хотя бы из того, что после броска появляется вертикальная составляющая импульса системы (а именно, вертикальная составляющая импульса камня), которой до броска не было.

Стало быть, система, которую образуют мальчик и камень, не замкнута. Почему? Дело в том, что векторная сумма внешних сил не равна нулю во время броска. Величина больше, чем сумма Mg+mg , и за счёт этого превышения как раз и появляется вертикальная компонента импульса системы.

Однако внешние силы действуют только по вертикали (трения нет). Стало быть, сохраняется проекция импульса на горизонтальную ось . До броска эта проекция была равна нулю. Направляя ось в сторону броска (так что мальчик поехал в направлении отрицательной полуоси), получим:

$-Mu+mupsilon _{0}cos alpha = 0$ ,

откуда

$u=frac{mupsilon _{0}cos alpha }{M}$ .

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Импульс» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

Содержание:

Импульс:

Основное уравнение динамики (второй закон Ньютона)

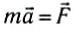
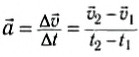
Что такое импульс стела

Импульс тела — физическая векторная величина, совпадающая по направлению со скоростью тела в данный момент времени и равная произведению массы тела на его скорость. Как следует из определения, импульс тела измеряется в СИ в килограмм-метрах в секунду ().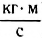

Впервые понятие импульса тела было введено в физику как произведение массы тела на модуль его скорости французским мыслителем и математиком P Декартом. Импульс тела как вектор был введен И. Ньютоном.

Хотя скорость и импульс тела связаны между собой простой зависимостью, они коренным образом отличаются друг от друга. Скорость тела — чисто кинематическая характеристика движения. Импульс тела является динамической характеристикой движения, связанной с причинами (силами), вызывающими движение.

C помощью важнейшего понятия импульса основное уравнение динамики запишется в виде:
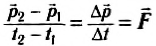(4)

и может быть сформулировано следующим образом.
Изменение импульса тела в единицу времени равно векторной сумме всех сил, действующих на данное тело.

Это более общая формулировка второго закона Ньютона. Именно так сформулировал Ньютон свой основной закон в знаменитой книге «Математические начала натуральной философии».

На первый взгляд уравнение (4) идентично уравнению (I). Это верно в том случае, если масса тела при движении не меняется. Если же масса тела изменяется, например при движении ракет, осьминогов, катеров с водометными движителями и т. д., то для описания движения тел необходимо применять более общее уравнение (4), а не уравнение (1).
Уравнение (4) может быть записано еще и в виде:
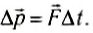(5)

Данное выражение позволяет сделать важнейший вывод: для изменения импульса тела сила должна действовать определенный промежуток времени. Импульс, а следовательно, и скорость тела мгновенно изменить нельзя.

Величина 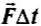называется импульсом силы. Импульс силы в СИ измеряется в ньютон-секундах (Н^.с). Необходимо отметить, что выражение (5) для импульса силы справедливо для случая, когда сила не изменяется в течение промежутка времени △t. Если она изменяется, то вычислить таким образом импульс силы нельзя. Однако можно ввести понятие средней силы, действующей на тело в течение того же промежутка времени.

Действительно, предположим, что на тело действует постоянная сила F₀ в течение некоторого промежутка времени ∆t = t₂-t₁. На рисунке 114 представлен график зависимости модуля силы от времени. Из формулы (5) следует, что величина модуля импульса этой силы численно равна площади прямоугольника.

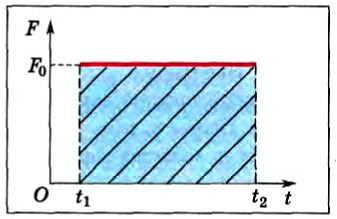
Рис. 114

Если же сила непостоянна во времени, например линейно увеличивается: F = kt (рис. 115) от t₁ = 0 до t₂, то импульс этой силы тоже равен площади под прямой, т. е. площади треугольника. Очевидно, что импульс этой силы равен –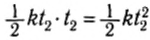. Естественно, можно заменить эту силу такой постоянной силой, которая изменит импульс тела на ту же величину:

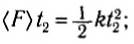
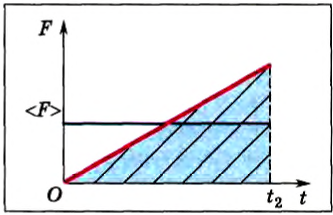
Рис. 115

Вычисленная таким образом сила называется средней силой и обозначается (F).
Поэтому выражение (4) часто записывается в виде:
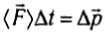(6)
и используется для оценки средней силы при кратковременных взаимодействиях тел (ударах, толчках и т. п.).

Для примера оценим среднюю силу, действующую со стороны пола на теннисный мяч массой m при его падении с высоты h₁. Как показывает опыт, после удара о пол мяч поднимается на меньшую высоту h₂. По этим данным мы можем вычислить скорость мяча по известной формуле 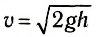в момент касания пола и в момент отскока от пола. Соответственно, изменение импульса мяча за время удара показано на рисунке 116. Модуль этого вектора:

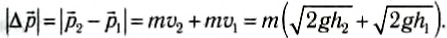
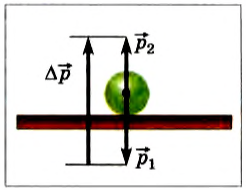
Рис. 116

Это выражение получено в предположении отсутствия сопротивления воздуха. Уменьшение высоты подъема мяча обусловлено тем, что удар неупругий.

Во время удара на мяч действуют две силы: сила реакции пола 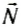и сила тяжести 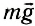. Поскольку сила реакции изменяется в течение времени удара, то необходимо использовать уравнение (6). В проекции на вертикальное направление оно примет вид:

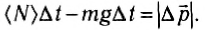
Следовательно,

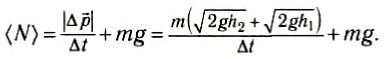(7)

Опыт проводился с мячом массой m = 55 г. Его бросали без начальной скорости с высоты h₁ = 1,0 м. После отскока от пола мяч поднимался на среднюю высоту h₂= 63 см. Считая, что удар происходил за время Δt = 0,15 с, после подстановки численных значений в формулу (7) и вычисления, получим, что (N) = 3,4 H = 6,3 mg.

Если мяч просто лежит на полу (рис. 117), то сила реакции N, действующая на него, равна mg. Значит, средняя сила реакции, действующая на мяч, при ударе в данном опыте в 6,3 раза превосходила силу тяжести.

Рис. 117

Главные выводы:

Импульсом тела (количеством движения) называется векторная физическая величина, равная произведению массы тела на его скорость.
Импульсом силы называется векторная физическая величина, равная произведению постоянной или средней силы на промежуток времени действия силы.
Изменение импульса тела в единицу времени равно векторной сумме всех действующих на тело сил.

Определение импульса

Существует несколько путей решения основной задачи механики. Одним из них является использование законов механики Ньютона. Однако это не всегда возможно. Если массу тела измерить сравнительно легко, то измерение силы связано со значительными трудностями. Для примера рассмотрим два стальных шарика, которые движутся навстречу друг другу и сталкиваются. По законам Ньютона каждый из них при столкновении приобретает некоторое ускорение, которое определяет скорость шариков после взаимодействия. Чтобы найти ускорение, необходимо знать силу, действующую на каждый из шариков во время взаимодействия.

Время, на протяжении которого взаимодействуют шарики, очень незначительное, а потому измерить силу или вызванное ей ускорение сложно.

Пусть два упругих шарика имеют массы 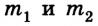и движутся навстречу друг другу со скоростью соответственно 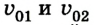(рис. 2.53).

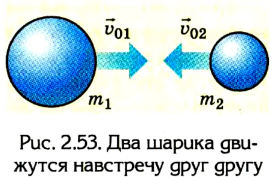
Будем считать, что действие других сил несущественно или скомпенсировано, т. е. шарики образуют замкнутую (изолированную) систему.
Во время столкновения шарики деформируются, вследствие чего возникают силы упругости, которые в соответствии с третьим законом Ньютона равны по модулям, но противоположны по направлению:

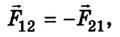
где 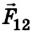– сила действия первого шарика на второй; 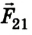– сила действия второго шарика на первый.

Отсюда 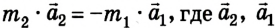– ускорение соответственно второго и первого шариков.

Если считать, что 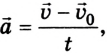то получим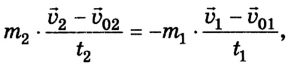

где 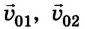– начальная скорость соответственно первого и второго шариков; 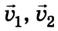– скорость соответственно первого и второго шариков после взаимодействия (рис. 2.54); 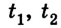– время взаимодействия каждого шарика.

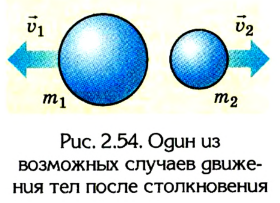
Поскольку время взаимодействия обоих шариков одинаков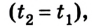о то

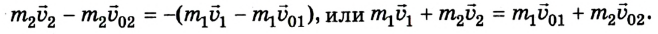
В левой и правой части уравнения суммируются произведения массы тела на его скорость. Как известно, данная физическая величина называется импульсом тела, или количеством движения.

Таким образом, чтобы определить результат взаимодействия, необязательно знать силы, которые возникают во время взаимодействия. Достаточно знать массу и скорость каждого тела: если два тела взаимодействуют только друг с другом, то сумма их импульсов до и после взаимодействия не изменяется.

Для более общего случая: в замкнутой (изолированной) системе сумма импульсов тел после любого взаимодействия между ними остается постоянной: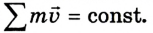

Закон сохранения импульса – один из основных законов природы. Согласно этому закону в замкнутой (изолированной) системе векторная сумма импульсов всех тел остается постоянной. Тела такой системы могут обмениваться импульсами, но суммарный импульс остается постоянным. Это положение справедливо для всех явлений природы.

Закон сохранения импульса

До сих пор мы рассматривали изменение скорости отдельного тела под действием некоторых сил. Теперь давайте рассмотрим вопрос об изменении импульсов нескольких тел под действием сил взаимодействия между ними.

В механике всякая группа тел, выделенная нами, называется механической системой.

Рассмотрим систему, состоящую из двух тележек с пружинными бамперами, находящихся на горизонтальных рельсах. На тележки действуют силы тяжести и силы реакции рельсов. Эти силы действуют со стороны тел, не входящих в систему, и поэтому называются внешними силами.

Итак, внешние силы — это силы, действующие на тела системы со стороны тел, не входящих в выделенную систему.

При столкновении тележек между ними возникают силы взаимодействия. Эти силы принято называть внутренними.

Внутренние силы в любой механической системе — это силы взаимодействия между телами, входящими в данную систему.

Если на тела системы действуют только внутренние силы, то такая система называется замкнутой. В том случае, когда на тела системы действуют еще внешние силы, система тел называется незамкнутой. Хорошим примером замкнутой системы является Солнечная система. Движение любой из планет относительно Солнца происходит вследствие, во-первых, силы притяжения к Солнцу и, во-вторых, сил притяжения к остальным планетам Солнечной системы. Очевидно, что система, состоящая из, например. Солнца, Земли и Луны, не является замкнутой.

Теперь давайте рассмотрим опыт по столкновению двух одинаковых тележек.

Толкнув одну из тележек, мы увидим, что она после столкновения остановится, а покоящаяся ранее тележка придет в движение (рис. 118, а, б) с той же скоростью, т. е. тележки обменяются скоростями.

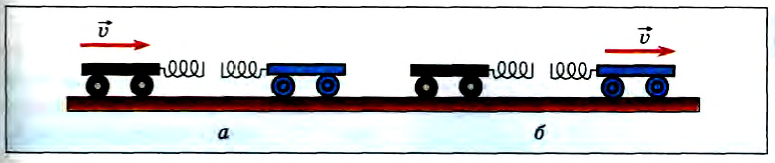
Рис. 118

Видоизменим опыт. Повернем тележки так, чтобы они не были обращены друг к другу пружинными бамперами. На одну из тележек прикрепим пластилиновый шарик. Если толкнуть одну из тележек, то после столкновения с другой они будут двигаться вместе (рис. 119, а, б). При этом скорость тележек будет в 2 раза меньше скорости первой тележки до столкновения. Из этого опыта следует, что скорость изменяется в зависимости от типа столкновения. Однако можно заметить, импульс системы не изменяется. Действительно, до столкновения двигалась одна тележка, и ее импульс был равен 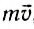, после столкновения движутся обе тележки, и их суммарный импульс равен 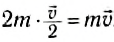. Таким образом, при столкновении тележек их суммарный импульс сохраняется. Можно ли считать систему, состоящую из двух сталкивающихся тележек, замкнутой? Очевидно, нет, поскольку на тележки действуют Земля и рельсы, т. е. внешние силы. Однако эти внешние силы направлены перпендикулярно движению тележек, и они в любой момент времени столкновения взаимно уравновешиваются. Таким образом, они не изменяют скорости движения тележек. Тогда в горизонтальной плоскости систему из двух тележек можно считать замкнутой.

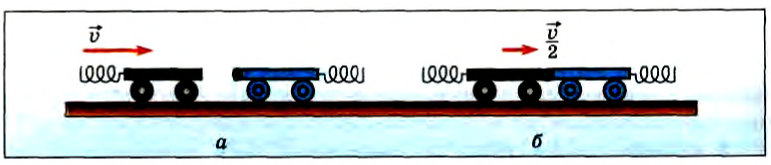
Рис. 119

Изменение скорости тележек происходит только под действием внутренних сил — сил взаимодействия между тележками. Импульс системы до взаимодействия равен импульсу системы после взаимодействия. Суммарный импульс системы не изменяется под действием внутренних сил.

Действительно, рассмотрим изменение состояния движения двух тел под действием только сил взаимодействия между ними. Внешние силы отсутствуют, т. е. наша система является замкнутой (рис. 120). По третьему закону Ньютона: .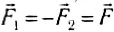

Рис. 120

Запишем уравнение (5) из § 22 для каждого из тел.
Для тела 1:

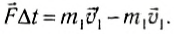
Для тела 2:

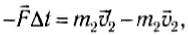
где и — скорости тел до взаимодействия, и 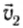— после взаимодействия. Будем также считать промежуток времени ∆t достаточно малым, чтобы силы взаимодействия существенно не изменялись.
Сложим почленно эти равенства:

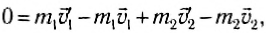или

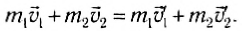
В левой части равенства (3) стоит сумма импульсов обоих тел до взаимодействия, а в правой — сумма их импульсов после взаимодействия. Импульс каждого тела изменился, но сумма осталась неизменной.

Очевидно, что если взаимодействуют не два, а несколько тел, то для каждой пары тел можно написать соотношения (I) и (2) и доказать, что векторная сумма импульсов тел замкнутой системы нс изменяется. В этом и состоит закон сохранения импульса системы.

Если в замкнутой системе п тел и их импульсы до взаимодействия — 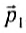, ,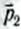…. , 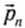после взаимодействия — 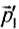, , 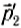…, , 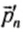то

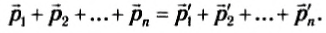
Векторная сумма импульсов всех тел, входящих в замкнутую систему, остается неизменной при любых движениях и взаимодействиях тел системы. Это и есть закон сохранения импульса. Всякий раз, когда под действием сил взаимодействия изменяется импульс одного из тел, непременно изменяются и импульсы других тел замкнутой системы так, что суммарный импульс всех тел остается неизменным.

Закон сохранения импульса для замкнутых систем является одним из фундаментальных законов природы, хотя мы его получили, опираясь на второй и третий законы Ньютона.

Поскольку импульс тела является физической векторной величиной, то, следовательно, закон должен выполняться и для проекций импульса на оси выбранной системы координат. Например, для проекций на ось Ox выбранной системы координат равенство (4) примет вид:

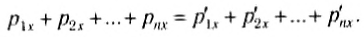
Поскольку при решении практических задач о движении тел в земных условиях в систему обычно Земля не включается, то такая система тел не будет замкнутой. Однако если в каждый момент взаимодействия тел сумма внешних сил в каком-то направлении равна нулю, то в этом направлении импульс системы не изменяется. В плоскости, перпендикулярной этому направлению, систему можно считать замкнутой и применять закон сохранения импульса для определения скоростей движения тел. Этот закон можно применять и для незамкнутых систем, когда внешние силы, действующие на тела, значительно меньше сил взаимодействия между телами системы.

Главные выводы:

Закон сохранения импульса является фундаментальным законом природы. Он всегда выполняется для замкнутых систем.
Если тела выделенной системы движутся только под действием сил взаимодействия между ними, то векторная сумма импульсов тел системы не изменяется с течением времени.
Закон сохранения импульса можно использовать в земных условиях для систем тел. на которые действуют внешние силы, если они взаимно компенсируются или импульсом этих сил можно пренебречь по сравнению с импульсом сил взаимодействия.

Импульс тела и реактивное движение

Многие из вас видели игрушку «колыбель Ньютона» — несколько стальных шаров, подвешенных вплотную друг к другу. Если первый шар отвести в сторону и отпустить, после его удара о систему отклонится последний шар, причем примерно на такой же угол, на который был отведен первый. Вернувшись, последний шар ударит систему из оставшихся шаров, после чего снова отклонится первый шар, а затем все повторится. При этом шары посредине остаются практически неподвижными. Как объяснить действие этой игрушки?

Закон сохранения импульса:

Изучая, вы вспомнили закон сохранения механической энергии, а сейчас вспомните еще одну физическую величину, которая имеет свойство сохраняться, — импульс тела.

Импульс тела 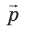— векторная физическая величина, равная произведению массы m тела на скорость 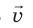его движения:

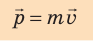
Единица импульса тела в СИ — килограммметр в секунду: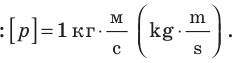

Запишем второй закон Ньютона в импульсном виде: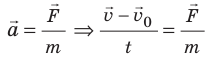

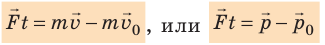
Величину 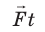называют импульсом силы. Таким образом, импульс силы равен изменению импульса тела: 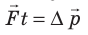(см. рис. 17.1).

Рис. 17.1. Чем большая сила действует на тело и чем дольше ее действие, тем сильнее изменяется импульс тела

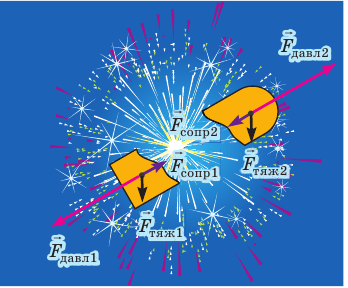
Рис. 17.2. При разрыве снаряда фейерверка суммарный импульс системы сохраняется, поскольку в момент разрыва внешние силы (сила тяжести и сила сопротивления) незначительны по сравнению с силами давления пороховых газов

В замкнутой системе тел — системе, в которой тела взаимодействуют только друг с другом, а внешние силы отсутствуют, уравновешены или пренебрежимо малы (см., например, рис. 17.2), суммарный импульс тел остается неизменным (сохраняется), то есть выполняется закон сохранения импульса:

В замкнутой системе тел векторная сумма импульсов тел до взаимодействия равна векторной сумме импульсов тел после взаимодействия:

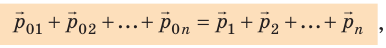
где n — количество тел системы.

Учитывая, что импульс тела равен произведению массы m и скорости 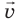движения тела, закон сохранения импульса можно записать так:

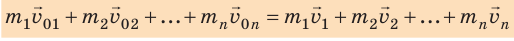
С проявлениями закона сохранения импульса мы имеем дело в природе, технике и т. д. Рассмотрим два примера применения данного закона: реактивное движение и столкновение тел.

Заказать решение задач по физике

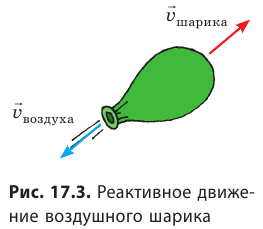
От чего отталкиваются ракеты

Вспомните опыт с шариком, который движется благодаря воздуху, вырывающемуся из его отверстия (рис. 17.3). Это движение — пример реактивного движения. Реактивное движение — это движение, возникающее при отделении с некоторой скоростью от тела его части.

Реактивное движение — это движение, возникающее при отделении с некоторой скоростью от тела его части.

Реактивное движение можно наблюдать в природе (рис. 17.4); его широко используют в технике: простейшие поливные системы, автомобили на реактивной тяге, катера с водометными двигателями, реактивные самолеты и, конечно, ракеты, ведь реактивное движение — это единственный способ передвижения в безвоздушном пространстве.

Рис. 17.4. Благодаря реактивному движению передвигаются многие обитатели морей и океанов (а); «бешеный огурец» может преодолеть расстояние до 12 м, рассеивая по пути семена (б)

Ракета — летательный аппарат, который движется в пространстве благодаря реактивной тяге, возникающей при отбросе ракетой части собственной массы.

Отделяющейся частью ракеты является струя горячего газа, образующегося при сгорании топлива. Когда газовая струя с огромной скоростью выбрасывается из сопла ракеты, оболочка ракеты получает мощный импульс, направленный в сторону, противоположную движению струи.

Если бы топливо сгорало мгновенно, а раскаленный газ сразу весь выбрасывался бы из ракеты, то закон сохранения импульса для системы «оболочка ракеты — раскаленный газ» выглядел бы так: 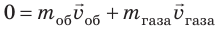(поскольку до старта импульс системы равен нулю), а следовательно, оболочка ракеты приобретала бы скорость: 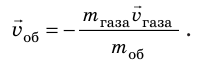К сожалению, топливо сгорает постепенно, поэтому часть газа приходится «разгонять» вместе с оболочкой; к тому же систему «оболочка ракеты — раскаленный газ» нельзя считать замкнутой (с увеличением скорости ракеты значительно возрастает сопротивление воздуха). Вычисления показывают, что для достижения первой космической скорости (8 км/с) масса топлива должна в 200 раз превышать массу оболочки. А ведь на орбиту нужно поднять не только оболочку, но и оборудование, космонавтов, запасы воды, кислорода и т. п. Поэтому возникла идея многоступенчатых ракет: каждая ее ступень содержит запас топлива и собственный реактивный двигатель, который разгоняет ракету, пока не израсходует топливо. После этого ступень отбрасывается, облегчая ракету и сообщая ей дополнительный импульс.

Именно на многоступенчатых ракетах были сделаны первые шаги человечества в космос: 4 октября 1957 г. советские ученые вывели на околоземную орбиту первый искусственный спутник Земли, а 12 апреля 1961 г. — космический корабль «Восток», на борту которого был первый в мире космонавт Юрий Алексеевич Гагарин; 21 июля 1969 г. американские астронавты Нил Армстронг и Базз Олдрин впервые высадились на Луне.

Прошло всего 60 лет, а мы уже не можем представить свою жизнь без космоса. Вспомните: спутниковое телевидение и спутниковая связь, система GPS и спутниковый Интернет, надежный прогноз погоды и спутниковые карты. Сейчас созданы космические корабли многоразового использования, космические аппараты высадились на Венеру, Марс и другие планеты Солнечной системы.

13 апреля 2018 г. исполнилось 25 лет со дня первого запуска ракеты-носителя «Зенит», созданной в конструкторском бюро «Южное» и на заводе «Южмаш» (Днепр). Сейчас усовершенствованная трехступенчатая ракета-носитель «Зенит-3SL» является самым большим и самым мощным летательным аппаратом своего класса в мире. Экологически чистый (работает на кислороде и керосине), недорогой, надежный «Зенит» может быть запущен при любых метеорологических условиях, способен вывести на околоземную орбиту спутники массой до 13 т. Изобретатель и предприниматель Илон Маск, основатель компании SpaceX, работающей в области строительства космического транспорта, на вопрос журналистки о любимой ракете ответил: «Лучшая ракета (после моей) — это “Зенит”».

Упругий и неупругий удары

Кратковременное взаимодействие тел, при котором тела непосредственно касаются друг друга, называют ударом. В системе сталкивающихся тел при ударе обычно возникают большие (по сравнению с внешними) внутренние силы, поэтому при ударе систему тел можно считать замкнутой и, рассматривая удары, использовать закон сохранения импульса. А вот полная механическая энергия сохраняется не всегда. Потенциальная энергия тел непосредственно до столкновения и сразу после него в большинстве случаев одинакова, поэтому далее речь пойдет только о кинетической энергии.

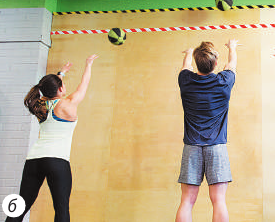
Рис. 17.5. Удар при столкновении бильярдных шаров (а), удары мяча по бетонной стене (б) можно считать упругими

Если после удара суммарная кинетическая энергия тел сохраняется, такой удар называют упругим (рис. 17.5).

Если после удара часть кинетической энергии превращается во внутреннюю энергию (тратится на деформацию и нагревание тел), такой удар называют неупругим.

Неупругий удар, после которого тела движутся как единое целое, называют абсолютно неупругим ударом (рис. 17.6).

Если скорости движения тел до и после удара (упругого или неупругого) направлены вдоль прямой, проходящей через центры масс этих тел, такой удар называют центральным.

Абсолютно неупругий центральный удар и упругий центральный удар рассмотрим на примерах решения задач.

Пример №1

Два шара массами 300 и 200 г, движущиеся со скоростями 4 и 2 м/с соответственно, испытывают центральный абсолютно неупругий удар. Определите, какое количество кинетической энергии шаров превратится во внутреннюю энергию, если: 1) шары двигались навстречу друг другу; 2) шары двигались друг за другом.

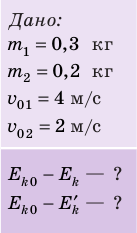
Анализ физической проблемы. Удар абсолютно неупругий, поэтому: 1) после столкновения шары движутся как одно целое; 2) суммарный импульс системы сохраняется; 3) кинетическая энергия системы уменьшается (часть энергии превращается во внутреннюю).

Решение:

Найдем суммарную кинетическую энергию системы шаров до столкновения:

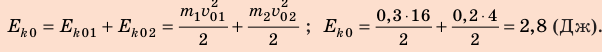
Выполним пояснительные рисунки; ось ОХ направим вдоль движения шаров.

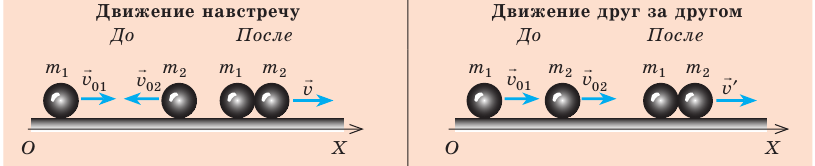
Запишем закон сохранения импульса в векторном виде и в проекциях на ось OX:

Найдем скорость движения шаров после столкновения:

Найдем суммарную кинетическую энергию системы шаров после столкновения:

Выясним, на сколько уменьшилась кинетическая энергия системы шаров:

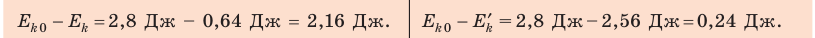
Ответ: 1) 2,16 Дж; 2) 0,24 Дж.

Анализ результатов. Видим, что в случае лобового удара шаров во внутреннюю энергию превращается значительно большее количество механической энергии.

Пример №2

Два шара одинаковой массы, движущиеся со скоростями 4 и 2 м/с соответственно, испытывают центральный упругий удар. Определите скорость движения шаров после столкновения, если: 1) шары двигались навстречу друг другу; 2) шары двигались друг за другом.

Решение:

Удар упругий, поэтому: 1) после столкновения шары движутся с разными скоростями; 2) суммарный импульс системы сохраняется, поскольку внешние силы, действующие на шары, скомпенсированы; 3) кинетическая энергия системы не изменяется. Для решения задачи воспользуемся законом сохранения импульса и законом сохранения механической энергии. Выполним пояснительные рисунки; ось ОХ направим вдоль движения шаров.

Запишем закон сохранения импульса в проекциях на ось ОХ и закон сохранения кинетической энергии:

Учтем, что 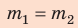= m, и после сокращений получим систему уравнений:

После простых преобразований получим:

Разделим второе уравнение системы на первое и получим более простую систему:

Решим полученную систему уравнений методом сложения и найдем скорости движения шаров после столкновения:

Ответ: для обоих случаев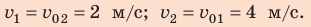

Видим, что при упругом центральном ударе тела одинаковой массы обмениваются скоростями.

Выводы:

Вычисление импульса

Импульс тела — это векторная физическая величина, характеризующая движение, и определяется произведением массы тела и его скорости.

Обозначают импульс буквой р. Единицей импульса в СИ является один килограмм-метр в секунду (1 кг • м/с). Математически это записывают так:

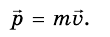
Импульс силы — это векторная физическая величина, характеризующая действие силы за определенный интервал времени.
Определяется произведением среднего значения силы за определенный интервал времени и длительности этого интервала:

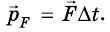
Импульсу присуще очень интересное и важное свойство, которое имеют немного физических величин. Это свойство сохранения. Оно заключается в том, что геометрическая сумма импульсов тел, взаимодействующих только друг с другом, сохраняется неизменной. Сами импульсы тел, конечно, изменяются, поскольку на каждое из тел действуют силы взаимодействия, но сумма импульсов остается неизменной (постоянной).

Это утверждение называют законом сохранения импульса. Закон сохранения импульса – один из самых важных законов природы. Его очень просто доказать, если взаимодействуют друг с другом два тела. Действительно, если первое тело действует на второе с силой 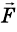, то на первое тело второе действует с силой, которая по третьему закону Ньютона равна –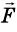. Обозначим массы тел через 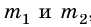, а их скорости движения относительно какой-то системы отсчета 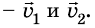В результате взаимодействия тел их скорости спустя некоторое время t изменятся и будут равны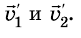

Тогда, согласно формуле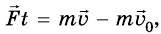запишем: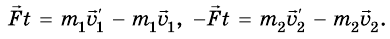

Изменив знаки обеих частей этого равенства на противоположные, перепишем его в виде:

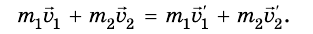
В левой части этого равенства записана сумма начальных импульсов двух тел, а в правой – сумма импульсов этих же тел через время t. Эти суммы равны между собой. Таким образом, хотя импульс каждого из тел при взаимодействии изменяется, их полный импульс, то есть сумма импульсов обоих тел сохраняется неизменной. Что и требовалось доказать.

Можно также доказать, и опыты это подтверждают, если взаимодействуют не два, а много тел, то геометрическая сумма импульсов всех тел или системы тел остается неизменной. Важно только, чтобы эти тела взаимодействовали друг с другом и на них не действовали силы со стороны других тел, которые не входят в систему (или, чтобы эти внешние силы уравновешивались). Такую группу тел, которые не взаимодействуют с другими телами, не входящими в эту группу, называют замкнутой системой.

Именно для замкнутых систем и выполняется закон сохранения импульса:

геометрическая сумма импульсов тел, образующих замкнутую систему, сохраняется постоянной при любых взаимодействиях тел этой системы между собой: 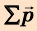= const.

Отсюда следует, что взаимодействие тел сводится к тому, что одни тела передают часть своего импульса другим.

Импульс тела – это векторная величина. Следовательно, если сумма импульсов тел сохранится постоянной, то и сумма проекций этих импульсов на координатные оси также остается постоянной. Вследствие этого геометрическую сумму импульсов можно заменить суммой алгебраических их проекций.

Закон сохранения импульса можно проиллюстрировать такими опытами.

Опыт 1. Поставим на рельсы две тележки одинаковой массы m. К торцу одной тележки прикрепим пластилиновый шарик. Пусть тележки движутся навстречу друг другу с одинаковыми по модулю скоростями 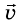(рис. 288).

При столкновении обе тележки остановятся. Объяснить результаты опыта легко. До столкновения импульс левой тележки равен 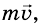, а правой тележки 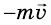(тележки двигались с противоположно направленными скоростями). Следовательно, к моменту встречи тележек их общий импульс равнялся нулю: 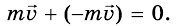После столкновения тележки остановились. Следовательно, и теперь суммарный импульс обеих тележек равен нулю.

Опыт 2. Повернем тележки друг к другу пружинными буферами (рис. 289). Повторив опыт, убедимся в том, что после столкновения обе тележки разъедутся в противоположные стороны. При таком взаимодействии скорости движения тележек изменят свои направления на противоположные, модули скоростей останутся такими же, какими они были до

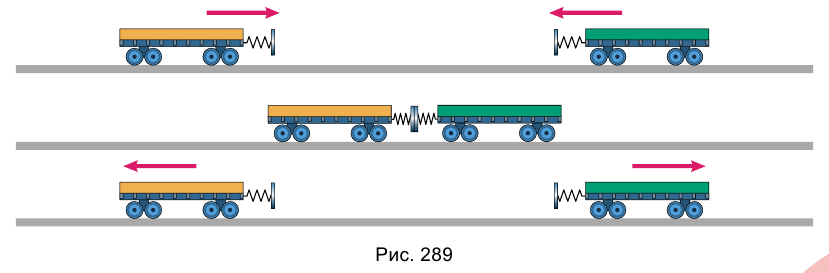
взаимодействия. Если до встречи импульс левой тележки равен 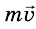, а правой равен –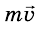, то после встречи импульс левой тележки равен –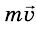, а правой – равен 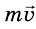. Поэтому суммарный импульс обеих тележек равен нулю как до, так и после столкновения, в соответствии с законом сохранения импульса.

Замкнутая система в физике
Реактивное движение в физике
Освоение космоса – история, этапы и достижения с фотографиями
Закон сохранения механической энергии в физике
Математика – язык физики
Законы Ньютона в физике
Гравитационные силы в физике
Центр тяжести в физике (центр масс)

Источник

Импульс

Размерность	LMT⁻¹
Единицы измерения
СИ	кг·м/с
СГС	г·см/с
Примечания
векторная величина

И́мпульс (коли́чество движе́ния) — векторная физическая величина, являющаяся мерой механического движения тела.

В классической механике импульс тела равен произведению массы этого тела на его скорость направление импульса совпадает с направлением вектора скорости:

В релятивистской физике импульс вычисляется как:

${displaystyle {vec {p}}={frac {m{vec {v}}}{sqrt {1-v^{2}/c^{2}}}},}$

где — скорость света; в пределе для малых формула переходит в классическую.

Важнейший физический закон, в котором фигурирует импульс тела, — второй закон Ньютона:

${displaystyle {frac {{mbox{d}}{vec {p}}}{{mbox{d}}t}}={vec {F}},}$

здесь — время, vec{F} — сила, приложенная к телу.

В записи через импульс (в отличие от — ускорение) закон применим не только в классической, но и в релятивистской механике.

В самом общем виде, определение звучит: импульс — это аддитивный интеграл движения механической системы, связанный согласно теореме Нётер с фундаментальной симметрией — однородностью пространства.

Понятие «импульс» имеет обобщения в теоретической механике, для случая наличия электромагнитного поля (как для частицы в поле, так и для самого поля), а также в квантовой механике.

История появления термина[править | править код]

Средневековые натурфилософы, в соответствии с учением Аристотеля, полагали, что для поддержания движения непременно требуется некоторая сила, без силы движение прекращается. Часть учёных выдвинула возражение против этого утверждения: почему брошенный камень продолжает двигаться, хотя связь с силой руки утрачена?

Для ответа на подобные вопросы Жан Буридан (XIV век) изменил ранее известное в философии понятие «импетус». По Буридану, летящий камень обладает «импетусом», который сохранялся бы в отсутствие сопротивления воздуха. При этом «импетус» прямо пропорционален скорости. В другом месте он пишет о том, что тела с бо́льшим весом способны вместить больше импетуса.

В первой половине XVII века Рене Декартом было введено понятие «количества движения». Он высказал предположение о том, что сохраняется не только количество движения одного тела, изолированного от внешних воздействий, но и любой системы тел, взаимодействующих лишь друг с другом. Физическое понятие массы в то время ещё не было формализовано — и он определил количество движения как произведение «величины тела на скорость его движения». Под скоростью Декарт подразумевал абсолютную величину (модуль) скорости, не учитывая её направление. Поэтому теория Декарта согласовывалась с опытом лишь в некоторых случаях (например, Валлис, Рен и Гюйгенс в 1678 году использовали её для исследования абсолютно упругого столкновения в системе центра масс).

Валлис в 1668 году первым предложил считать количество движения не скалярной, а направленной величиной, учитывая направления с помощью знаков «плюс» и минус”^[1]. В 1670 году он окончательно сформулировал закон сохранения количества движения. Экспериментальным доказательством закона послужило то, что новый закон позволял рассчитывать неупругие удары, а также удары в любых системах отсчёта.

Закон сохранения количества движения был теоретически доказан Исааком Ньютоном через третий и второй закон Ньютона. Согласно Ньютону, «количество движения есть мера такового, устанавливаемая пропорционально скорости и массе».

Формальное абстрактное определение[править | править код]

Импульсом называется сохраняющаяся физическая величина, связанная с однородностью пространства (то есть инвариант относительно трансляций).

Из свойства однородности пространства следует независимость лагранжиана замкнутой системы от её положения в пространстве: для хорошо изолированной системы её поведение не зависит от того, в какое место пространства она помещена. По теореме Нётер из этой однородности следует сохранение некоторой физической величины, которую и называют импульсом.

В разных разделах физики применительно к реальным задачам даются более конкретные определения импульса, с которыми можно работать и производить расчёты.

Определения импульса тела в механике[править | править код]

Классическая механика[править | править код]

В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:

${vec p}=sum _{{i}}m_{i}{vec {v}}_{i},$

соответственно, величина ${vec p}_{i}=m_{i}{vec {v}}_{i}$ называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с).

Импульс тела конечных размеров находится путём его мысленного разбиения на малые части, которые можно считать материальными точками, с последующим интегрированием по ним:

{displaystyle {vec {p}}=int rho (x,y,z){vec {v}}(x,y,z)dxdydz.}

Стоящее под интегралом произведение называют плотностью импульса.

Релятивистская механика[править | править код]

В релятивистской механике импульсом системы материальных точек называется величина:

${displaystyle {vec {p}}=sum _{i}{frac {m_{i}{vec {v}}_{i}}{sqrt {1-v_{i}^{2}/c^{2}}}},}$

где m_i — масса -й материальной точки, vec v_i — её скорость.

Также вводится четырёхмерный импульс, который для одной материальной точки массой определяется как:

${displaystyle p_{mu }=(E/c,{vec {p}})=left({frac {mc}{sqrt {1-v^{2}/c^{2}}}},{frac {m{vec {v}}}{sqrt {1-v^{2}/c^{2}}}}right).}$

На практике часто применяются соотношения между массой, импульсом и энергией частицы:

${displaystyle E^{2}-mathbf {p} ^{2}c^{2}=m^{2}c^{4},qquad qquad mathbf {p} ={frac {E}{c^{2}}},mathbf {v} .}$

Свойства импульса[править | править код]

Сохранение импульса следует из второго и третьего законов Ньютона: записав второй закон для каждой из составляющих систему материальных точек, представив силу, действующую на каждую точку, как внешнюю ${displaystyle {vec {F}}_{i,ext}}$ плюс силу взаимодействия со всеми остальными точками, затем просуммировав, получим:

${displaystyle {frac {d{vec {p}}}{dt}}=sum _{i}{frac {d{vec {p}}_{i}}{dt}}=sum _{i}{vec {F}}_{i}=sum _{i}left({vec {F}}_{i,ext}+sum _{j,jneq j}{vec {F}}_{i,j}right)=sum _{i}{vec {F}}_{i,ext}+sum _{i}sum _{j,jneq i}F_{i,j}.}$

Первое слагаемое равно нулю из-за компенсации внешних сил, а второе — вследствие третьего закона Ньютона (слагаемые ${displaystyle {vec {F}}_{a,b}}$ и ${displaystyle {vec {F}}_{b,a}}$ в двойной сумме попарно уничтожают друг друга).

Импульс не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея^[2]. Свойства сохранения кинетической энергии, сохранения импульса и второго закона Ньютона достаточно для получения математического выражения импульса^[3]^[4].

При наличии электромагнитного взаимодействия между материальными точками третий закон Ньютона может не выполняться — и тогда сохранения суммы импульсов точек не будет. В таких случаях, особенно в релятивистской механике, удобнее включать в понятие «система» не только совокупность точек, но и поле взаимодействия между ними. Соответственно, будут учтены не только импульсы составляющих систему частиц, но и импульс поля взаимодействия. При этом вводится величина — тензор энергии-импульса, которая в полной мере удовлетворяет законам сохранения.

Что касается 4-импульса, то для системы не взаимодействующих материальных точек их совокупный 4-импульс равен сумме по всем частицам. При наличии взаимодействия такое суммирование теряет смысл.

Обобщённый импульс[править | править код]

В теоретической механике в целом[править | править код]

В теоретической механике обобщённым импульсом называется частная производная лагранжиана системы по обобщённой скорости:

${displaystyle p_{i}={{partial {mathcal {L}}} over {partial {dot {q}}_{i}}}.}$

Обобщенный импульс, как и не обобщённый, обозначается буквой обычно из контекста ясно, о чём идёт речь.

Размерность обобщённого импульса зависит от размерности обобщённой координаты. Если размерность $q_{i}$ — длина, то $p_{i}$ будет иметь размерность обычного импульса, если же координатой $q_{i}$ выступает угол (величина безразмерная), то $p_{i}$ обретёт размерность момента импульса. Если лагранжиан системы не зависит от некоторой обобщённой координаты, то из уравнений Лагранжа ${displaystyle dp_{i}/dt=0.}$

Если обобщённая координата — это обычная координата (и тогда её производная по времени — просто скорость), а внешних полей нет, обобщённый импульс тождественен обычному. Так, для свободной частицы функция Лагранжа имеет вид:

${mathcal L}=-mc^{2}{sqrt {1-v^{2}/c^{2}}}$

, отсюда: ${displaystyle {vec {p}}=m{vec {v}}/{sqrt {1-v^{2}/c^{2}}}}$

Для частицы в электромагнитном поле[править | править код]

В электромагнитном поле лагранжиан частицы будет отличаться от приведённого выше наличием дополнительных членов, а именно ${displaystyle {mathcal {L}}=-mc^{2}{sqrt {1-v^{2}/c^{2}}}-qvarphi +q{vec {v}}cdot {vec {A}}.}$ Соответственно, обобщённый импульс частицы равен:

${mathbf {p}}={frac {m{mathbf {v}}}{{sqrt {1-v^{2}/c^{2}}}}}+q{mathbf A},$

где — векторный потенциал электромагнитного поля, — заряд частицы; в выражении для фигурировал также скалярный потенциал varphi .

Импульс электромагнитного поля[править | править код]

Электромагнитное поле, как и любой другой материальный объект, обладает импульсом, который легко можно найти, проинтегрировав вектор Пойнтинга по объёму:

${mathbf p}={frac {1}{c^{2}}}int {mathbf S}dV={frac {1}{c^{2}}}int [{mathbf E}times {mathbf H}]dV$

(в системе СИ).

Существованием импульса у электромагнитного поля объясняется, например, такое явление как давление электромагнитного излучения.

Импульс в квантовой механике[править | править код]

Определение через оператор[править | править код]

В квантовой механике оператором импульса частицы называют оператор — генератор группы трансляций. Это эрмитов оператор, собственные значения которого отождествляются с импульсом системы частиц. В координатном представлении для системы нерелятивистских частиц он имеет вид:

${hat {{mathbf {P}}}}=sum _{j}{hat {{mathbf {p}}}}_{j}=sum _{j}-ihbar nabla _{j}$

где $nabla _{j}$ — оператор набла, соответствующий дифференцированию по координатам -ой частицы.

Гамильтониан системы выражается через оператор импульса:

${hat {H}}=sum _{i}{frac {1}{2m_{i}}}{hat {{mathbf {p}}}}_{i}^{2}+U({mathbf {r_{1}}},dots )$ .

Для замкнутой системы ( U=0 ) оператор импульса коммутирует с гамильтонианом, и импульс сохраняется.

Определение через волны де Бройля[править | править код]

Формула де Бройля связывает импульс и длину волны де Бройля рассматриваемого объекта.

Модуль импульса обратно пропорционален длине волны

$p={frac hlambda }$

где — постоянная Планка.

Для частиц не очень высокой энергии, движущихся со скоростью vll c (скорости света), модуль импульса равен p=mv (где — масса частицы), и:

${displaystyle lambda ={frac {h}{p}}={frac {h}{mv}}}$

Следовательно, длина волны де Бройля тем меньше, чем больше модуль импульса.

В векторном виде это записывается как:

${displaystyle {vec {p}}={frac {h}{2pi }}{vec {k}}=hbar {vec {k}}}$

где {vec k} — волновой вектор.

Как и в классической механике, в квантовой имеет место сохранение импульса в изолированных системах^[5]^[6]. В тех явлениях, когда проявляются корпускулярные свойства частиц, их импульс записывается «классически» как p=mv , а если проявляются волновые свойства, действует^[7] связь ${displaystyle p=hlambda ^{-1}}$ . При этом, как и в классической механике, сохранение импульса выступает следствием симметрии относительно сдвигов по координатам^[8].

Импульс в гидродинамике[править | править код]

В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа При этом вместо импульса фигурирует вектор плотности импульса, совпадающий по смыслу с вектором плотности потока массы

Поскольку в турбулентном потоке характеристики состояния вещества (в том числе плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока в соответствии с методом О. Рейнольдса получаются путём осреднения уравнений Навье-Стокса^[9].

Если в согласии с методом Рейнольдса представить , где черта сверху — знак осреднения, а штрих — отклонения от среднего, то вектор осреднённой плотности импульса приобретёт вид:

{displaystyle {overline {vec {s}}}={overline {rho {vec {v}}}}={overline {rho }}~{overline {vec {v}}}+{vec {S}},}

где — вектор плотности флуктуационного потока массы (или «плотность турбулентного импульса»^[9]).

Импульсное представление в квантовой теории поля[править | править код]

В квантовой теории поля часто употребляется импульсное представление на основе использования преобразования Фурье. Его преимуществами являются: удобство описания физических систем при помощи энергий и импульсов, а не при помощи пространственно-временных координат; более компактная и наглядная структура динамических переменных^[10].

См. также[править | править код]

Импульс силы
Момент импульса
Электрический импульс

Примечания[править | править код]

↑ Григорьян А. Т. Механика от античности до наших дней. — М.: Наука, 1974.
↑ ¹ ² ³ Айзерман, 1980, с. 49.
↑ Айзерман, 1980, с. 54.
↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» Архивная копия от 1 января 2015 на Wayback Machine // УФН, 59, с. 325—362, (1956)
↑ Перкинс Д.^[en] Введение в физику высоких энергий. — М., Мир, 1975. — c. 94
↑ Широков Ю. М., Юдин Н. П. Ядерная физика. — М.: Наука, 1972. — С. 276. — 670 с.
↑ Фейнман Р. Ф. ]. Фейнмановские лекции по физике. Вып. 1 Современная наука о природе. Законы механики.. — М.: Едиториал УРСС, 2004. — С. 194. — 440 с. — ISBN 5-354-00699-6.
↑ Ферми Э. Квантовая механика. — М.: Мир, 1968. — С. 183. — 367 с.
↑ ¹ ² Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
↑ Боголюбов Н. Н., Ширков Д. В. Квантовые поля. — М., Наука, 1980. — с. 25

Литература[править | править код]

Арнольд В. И. Математические методы классической механики. — 5-е изд., стереотипное. — М.: Едиториал УРСС, 2003. — 416 с. — 1500 экз. — ISBN 5-354-00341-5.
Ландау Л. Д., Лифшиц Е. М. Механика. — Издание 4-е, исправленное. — М.: Наука, 1988. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9.
Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
Сивухин Д. В. Общий курс физики. — Издание 4-е. — М.: Физматлит, 2002. — Т. I. Механика. — 792 с. — ISBN 5-9221-0225-7.
Айзерман М. А. Классическая механика. — М.: Наука, 1980. — 368 с.

Источник

Относительный импульс

Изменение импульса тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар

Абсолютно упругий удар

Пуля пробила стенку

Радиус-вектор тела повернул на 180 градусов

Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Второй закон Ньютона в импульсном виде

Реактивное движение

Суммарный импульс системы тел

Закон сохранения импульса

Закон сохранения импульса в проекции на горизонтальную ось

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Сохранение проекции импульса

Вопрос 5. Центр масс(центр инерции). Уравнение движения центра масс.

Тема 6. Закон сохранения импульса.

Вопрос 1. Замкнутая и незамкнутая системы в механике. Закон сохранения импульса.

Тема 7. Работа. Мощность. Энергия.

Вопрос 1. Определение элементарной работы, различные выражения.

Вопрос 2. Мощность, ее выражение через силу и скорость тела.

Вопрос 3. Кинетическая энергия и ее выражение через импульс тела.

Импульс

Второй закон Ньютона в импульсной форме

Пример вычисления силы

Импульс системы тел

Закон сохранения импульса

Закон сохранения проекции импульса

Что такое импульс стела

Определение импульса

Закон сохранения импульса

Импульс тела и реактивное движение

Закон сохранения импульса:

От чего отталкиваются ракеты

Упругий и неупругий удары

Вычисление импульса

История появления термина[править | править код]

Формальное абстрактное определение[править | править код]

Определения импульса тела в механике[править | править код]

Классическая механика[править | править код]

Релятивистская механика[править | править код]

Свойства импульса[править | править код]

Обобщённый импульс[править | править код]

В теоретической механике в целом[править | править код]

Для частицы в электромагнитном поле[править | править код]

Импульс электромагнитного поля[править | править код]

Импульс в квантовой механике[править | править код]

Определение через оператор[править | править код]

Определение через волны де Бройля[править | править код]

Импульс в гидродинамике[править | править код]

Импульсное представление в квантовой теории поля[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Вам также может понравиться

Как найти размер квартиры

Как найти сургутский район

1с эдо подпись неверна как исправить

Добавить комментарий Отменить ответ