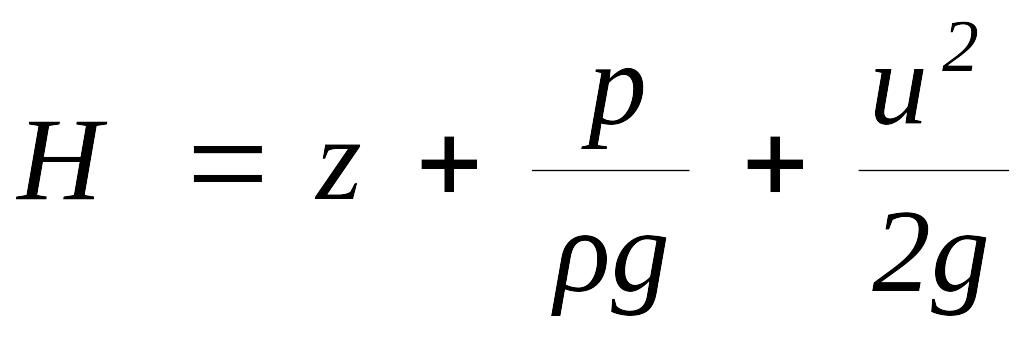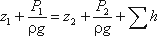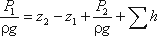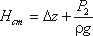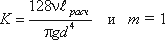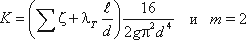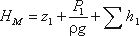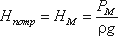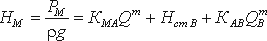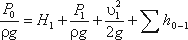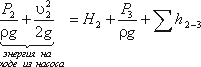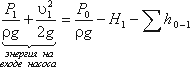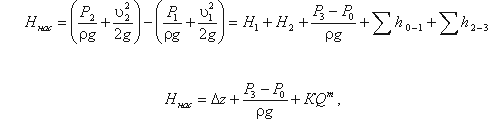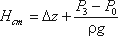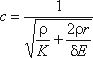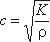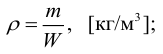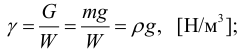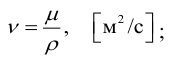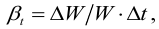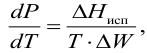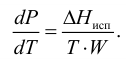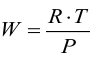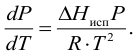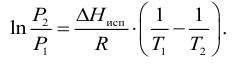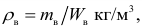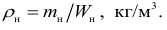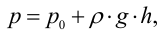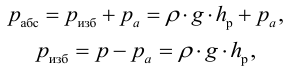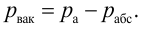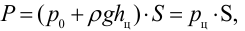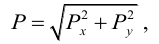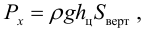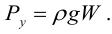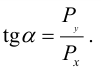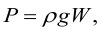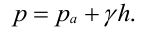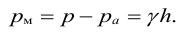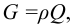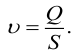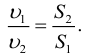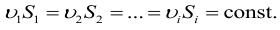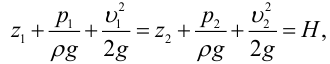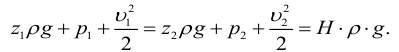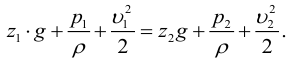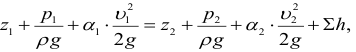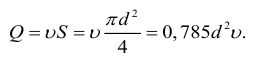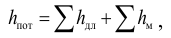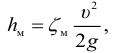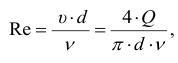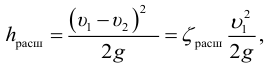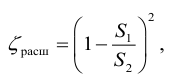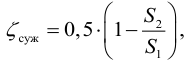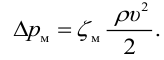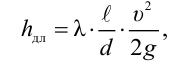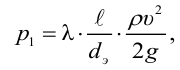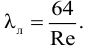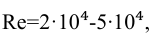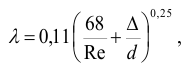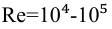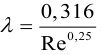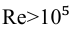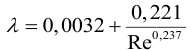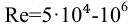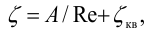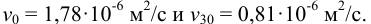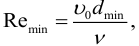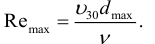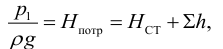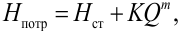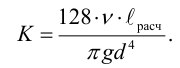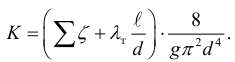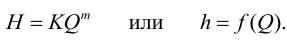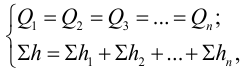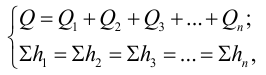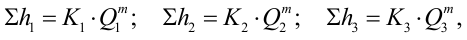Уравнение Бернулли для элементарной
струйки вязкой несжимаемой жидкости
при установившемся движении в поле силы
тяжести имеет вид
(1)
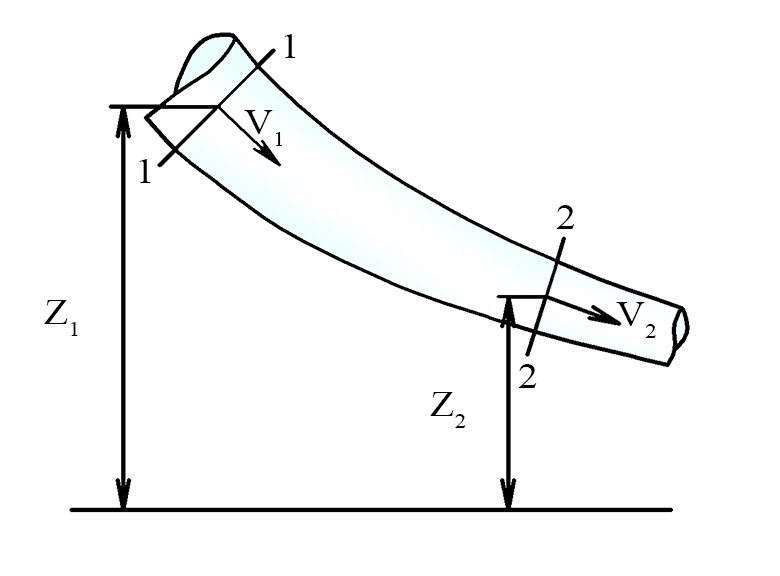
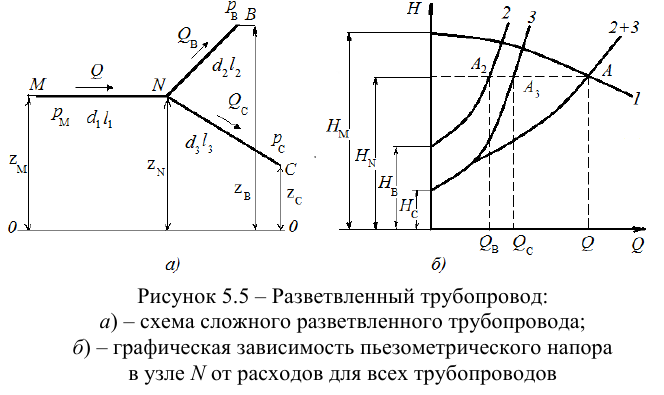
где z1, z2 – расстояния от центров выбранных
живых сечений 1 — 1 и 2 — 2 до некоторой
произвольной горизонтальной плоскости
z = 0 (рис. 1); 1, 2
– скорости; P1,P2 -давления в этих сечениях;
h1-2 — потери напора на участке между
выбранными сечениями.
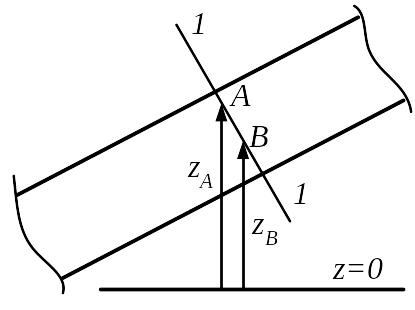
Рис. 1. Живое сечение равномерного потока
Уравнение Бернулли выражает собой закон
сохранения механической энергии.
Величина
(2)
называется полным напором и представляет
собой удельную (приходящуюся на единицу
силы тяжести) механическую энергию
жидкости в рассматриваемом сечении; z
— геометрический напор или удельная
потенциальная энергия положения; p/(g)
— пьезометрический напор или удельная
потенциальная энергия давления; u2/(2g) –
скоростной напор или удельная кинетическая
энергия; h1-2 — потери напора, т.е. часть
удельной механической энергии,
израсходованной на работу сил трения
на участке между сечениями 1 — 1 и 2 — 2
(см. рис. 1).
В случае идеальной жидкости h1-2 =0.
Для плавно изменяющегося потока при
установившемся движении вязкой
несжимаемой жидкости в поле силы тяжести
уравнение Бернулли имеет вид
(3)
где p1, p2 — давления в произвольно взятых
точках сечений 1 — 1 и 2 — 2 с координатами
z1 и z2 соответственно (обычно берутся
точки на оси потока);
1 , 2 — средние
скорости в этих сечениях; а1 , а2 —
коэффициенты Кориолиса, учитывающие
неравномерность распределения скоростей
частиц жидкости в сечениях; при течении
по круглой цилиндрической трубке
= 2 для ламинарного режима течения и
1,1 — для турбулентного;
при решении практических задач обычно
принимается =
1.
При использовании уравнения Бернулли
(2) или (3) необходимо иметь в виду, что
номера сечений возрастают в направлении
течения жидкости. В качестве расчетных
выбираются такие сечения (струйки) , в
которых известны какие-либо из величин
1 , 2
(u1, u2) и р1, р2 .
Плоскость z = 0 бывает удобно располагать
таким образом, чтобы центр одного из
выбранных сечений потока лежал в этой
плоскости.
22. Исходные данные для технологического расчета
В технологический расчет нефтепровода
входит решение следующих основных
вопросов:
определение экономически наивыгоднейших
параметров нефтепровода: диаметра
трубопровода, давления на нефтеперекачивающих
станциях, толщины стенки трубопровода
и числа насосных станций;
определение местонахождения станций
на трассе нефтепровода;
расчет режимов эксплуатации нефтепровода.
Существуют два способа нахождения
оптимальных параметров нефтепровода:
а) сравнением нескольких вариантов; б)
по специальным формулам, учитывающим
как экономические показатели, так и
физические условия перекачки. Обычно
пользуются первым методом. В этом случае
для нескольких значений диаметра и
давления выполняют гидравлический и
механический расчеты, определяющие
(для каждого варианта) число
нефтеперекачивающих станций и толщину
стенки трубопровода. Экономическим
расчетом (по сроку окупаемости или по
приведенным расходам) находят вариант,
имеющий наилучшие параметры.
Расположение нефтеперекачивающих
станций находят графически на чертеже
сжатого профиля трассы.
В расчет режимов эксплуатации входит
определение давлений на станциях,
подпоров перед ними и пропускной
способности нефтепровода при условиях
перекачки, отличающихся от расчетных;
решается вопрос о регулировании работы
нефтепровода.
ИСХОДНЫЕ ДАННЫЕ ДЛЯ ТЕХНОЛОГИЧЕСКОГО
РАСЧЕТА
1. Пропускная способность нефтепровода
является основной исходной величиной
для расчета, она указывается в плановом
задании (в млн. т/год). Для расчетов она
переводится в м3/ч и м3/с при определенном
(расчетном) значении плотности. При этом
считается, что нефтепровод работает
350 дней в году. В основном пропускную
способность определяет диаметр
трубопровода и давление на станциях.
Среднемесячные температуры грунта на
глубине заложения трубопровода могут
быть получены у местных метеостанций
или из климатологических справочников.
Данные о температуре грунта служат для
определения расчетных значений плотности
и вязкости нефти. Обычно наинизшие
температуры бывают в марте — апреле, а
наивысшие в августе — сентябре.
3. Плотность и вязкость нефти определяют
лабораторными анализами или задаются
при определенных температурах: плотностыо
при 20° С — р20, а вязкостью при 20 и 50° С —
v20 и v5o.
4. Механические свойства (прочностные
показатели) сталей, необходимые для
расчета толщины стенки магистральных
трубопроводов.
5. Технико-экономические показатели
необходимы для подсчета капитальных
затрат и эксплуатационных расходов при
определении экономически наивыгоднейшего
варианта.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2018-03-17
Уравнение Бернулли
Содержание:
- Уравнение Бернулли для потока идеальной жидкости
- Физический смысл уравнения Бернулли
- Уравнение Бернулли для потока реальной вязкой жидкости
- Иллюстрация уравнения Бернулли
- Уравнение Бернулли для горизонтальной трубы
- Алгоритм решения задач с помощью уравнения Бернулли
Основные уравнения гидродинамики – уравнение Бернулли и неразрывности позволяют установить взаимосвязь между параметрами плавно изменяющегося потока.
Уравнение Бернулли для потока идеальной жидкости
Рассмотрим установившееся движение потока идеальной несжимаемой жидкости, на которую действует только одна массовая сила – сила тяжести.
Выбреем два живых сечения , 1-1 в начале рассматриваемого участка, 2-2 – в конце.
Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении.
- где z – геометрическая высота,
- p – давление в выбранном сечении,
- V – скорость жидкости в выбранном сечении,
- ρ – плотность жидкости,
- g – ускорение свободного падения.
Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости.
Для каждого рассматриваемого сечения полный напор есть сумма геометрического, пьезометрического и скоростного напора. Для идеальной жидкости (т.е. при отсутствии потерь энергии) полный напор – величина постоянная.
- где z – геометрический напор,
- p/ρg – пьезометрический напор,
- z + p/ρg – статический напор,
- V2/2g – скоростной напор,
- z + p/ρg + V2/2g = Н – полный напор.
Уравнение Бернулли можно записать и в другом виде, умножим обе части уравнения на g получим:
gz1 + p1/ρ + V12/2 = gz2 + p2/ρ + V22/2
Физический смысл уравнения Бернулли
Составляющие уравнения Бернулли являются различными формами удельной (отнесенной к единице массы) механической энергии жидкости:
- gz – удельная энергия положения,
- p/ρ – удельная энергия давления движущейся жидкости,
- V12/2 – удельная кинетическая энергия жидкости,
- gz + p/ρ + V2/2 = Hg – полная удельная энергия движущейся идеальной жидкости.
Физический и энергетический смысл уравнения Бернулли заключается в постоянстве полной удельной энергии вдоль элементарной струйки идеальной жидкости.
Уравнение Бернулли отражает закон сохранения механической энергии для идеальной несжимаемой жидкости.
Уравнение Бернулли для потока реальной вязкой жидкости
Если на участке между расчетными сечениями не совершается механическая работа, а движение является установившимся, без притока и отбора жидкости, и сама жидкость является несжимаемой, то для потока будут справедливы зависимости:
Н1=Н2 + Δh1 – 2
z1 + p1/ρg + V12/2g = z2 + p2/ρg + V22/2g + Δh1 – 2
Уравнение Бернулли устанавливает связь между полными напорами потока жидкости на участке ограниченными сечениями 1-1 и 2-2. В соответствии с уравнением Бернулли полный напор потока Hi уменьшается от сечения 1-1 к сечению 2-2 на величину потерь напора (энергии) h1 – 2, вызванных гидравлическими сопротивлениями участка.
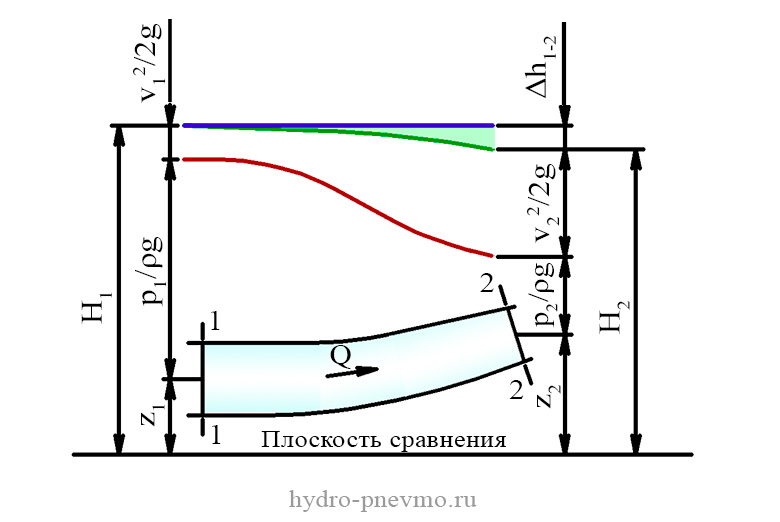
Иллюстрация уравнения Бернулли
Для иллюстрации закона Бернулли на координатной плоскости, совмещенной с принципиальной гидравлической схемой системы изображают напорную и пьезометрическую линии.
Уравнение Бернулли для горизонтальной трубы
Для горизонтальных трубопроводов и силовых гидроприоводов, в которых пьезометрический набор существенно превышает геометрический удобна следующая форма записи уравнения Бернулли:
p1 + ρV12 = p2 + ρV22 + Δp1о
Алгоритм решения задач с помощью уравнения Бернулли
Задачи с помощью уровнения Бернулли удобно решать в следующей последовательности:
- Изобразить принципиальную гидравлическую схему системы
- Провести общую для всего потока плоскость сравнения. Лучше всего провести ее самой нижней точки системы, например на уровне оси самого нижнего трубопровода, или не уровне жилкости самого нижнего резервуара.
- Выбрать два (или несколько) живых сечения. Одно сечение выбирается в, том месте где параметры потока известны, другое там, где нужно определить неизвестные параметры (напрмер давление). Сечения следует выбирать только в тех местах где движение можно считать плавно изменяющимся. Нумеровать сечения следует в направлении движения жидкости.
- Записать уравенение Бернулли для выбранных сечений.
- При необходимости определить гидравлические потери напора на различных участка гидросистемы.
- Вычислить неизвестные параметры, используя уранение Бренулли.
Читайте также:
Все новости
Лекция 6. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ПРОСТЫХ ТРУБОПРОВОДОВ
При расчетах напорных трубопроводов основной задачей является либо определение пропускной способности
(расхода), либо потери напора на том или ином участке, равно как и на всей длине, либо диаметра трубопровода
на заданных расходе и потерях напора.
В практике трубопроводы делятся на короткие и длинные. К первым относятся все трубопроводы,
в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов
обязательно учитывают потери напора в местных сопротивлениях. К ним относят, к примеру, маслопроводы объемных
передач.
Ко вторым относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет
ведется без учета местных потерь. К таким трубопроводам относятся, например, магистральные водоводы,
нефтепроводы.
Учитывая гидравлическую схему работы длинных трубопроводов, их можно разделить также на простые
и сложные. Простыми называются последовательно соединенные трубопроводы одного или различных сечений,
не имеющих никаких ответвлений. К сложным трубопроводам относятся системы труб с одним или несколькими
ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы.
Жидкость по трубопроводу движется благодаря тому, что ее энергия в начале трубопровода больше, чем в
конце. Этот перепад уровней энергии может создаваться несколькими способами: работой насоса, разностью уровней
жидкости, давлением газа.
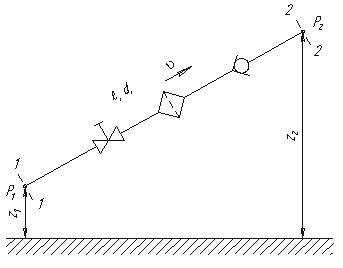
Рассмотрим простой трубопровод постоянного сечения, который расположен произвольно в пространстве
(рис. 6.1), имеет общую длину l и диаметр d, а также содержит ряд местных сопротивлений
(вентиль, фильтр и обратный клапан). В начальном сечении трубопровода 1-1 геометрическая высота равна
z1 и избыточное давление Р1, а в конечном сечении 2-2 –
соответственно z2 и Р2. Скорость потока в этих сечениях вследствие
постоянства диаметра трубы одинакова и равна ν.
Рис. 6.1. Схема простого трубопровода
Запишем уравнение Бернулли для сечений 1-1 и 2-2. Поскольку скорость в обоих сечениях
одинакова и α1 = α2, то скоростной напор можно не
учитывать. При этом получим
или
Пьезометрическую высоту, стоящую в левой части уравнения, назовем потребным напором
Нпотр. Если же эта пьезометрическая высота задана, то ее называют располагаемым напором
Нрасп. Такой напор складывается из геометрической высоты Hпотр, на которую
поднимается жидкость, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.
Назовем сумму первых двух слагаемых статическим напором, который представим как некоторую
эквивалентную геометрическую высоту
а последнее слагаемое Σh – как степенную функцию расхода
Σh = KQm
тогда
Hпотр = Hст + KQm
где K – величина, называемая сопротивлением трубопровода;
Q – расход жидкости;
m – показатель степени, который имеет разные значения в зависимости от режима течения.
Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление
трубопровода равно
где lрасч = l + lэкв.
Численные значения эквивалентных длин lэкв для различных местных сопротивлений обычно
находят опытным путем.
Для турбулентного течения, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход,
получаем
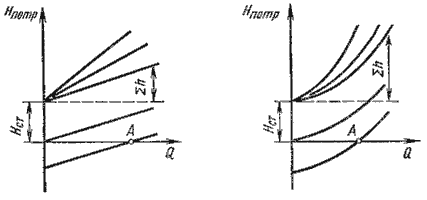
По этим формулам можно построить кривую потребного напора в зависимости от расхода. Чем больше расход
Q, который необходимо обеспечить в трубопроводе, тем больше требуется потребный напор
Нпотр. При ламинарном течении эта кривая изображается прямой линией (рис.6.2, а), при
турбулентном – параболой с показателем степени равном двум (рис.6.2, б).
Рис.6.2. Зависимости потребных напоров от расхода жидкости в трубопроводе
Крутизна кривых потребного напора зависит от сопротивления трубопровода K и возрастает с увеличением
длины трубопровода и уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений.
Величина статического напора Нст положительна в том случае, когда жидкость движется вверх
или в полость с повышенным давлением, и отрицательна при опускании жидкости или движении в полость с
пониженным давлением. Точка пересечения кривой потребного напора с осью абсцисс (точка А) определяет
расход при движении жидкости самотеком. Потребный напор в этом случае равен нулю.
Иногда вместо кривых потребного напора удобнее пользоваться характеристиками трубопровода. Характеристикой
трубопровода называется зависимость суммарной потери напора (или давления) в трубопроводе от расхода:
Σh = f(q)
Простые трубопроводы могут соединяться между собой, при этом их соединение может быть последовательным
или параллельным.
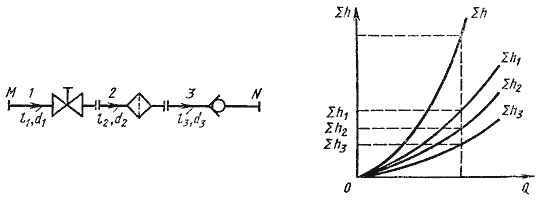
Последовательное соединение. Возьмем несколько труб различной длины, разного диаметра и
содержащих разные местные сопротивления, и соединим их последовательно (рис. 6.3, а).
Рис. 6.3. Последовательное соединение трубопроводов
При подаче жидкости по такому составному трубопроводу от точки М к точке N расход жидкости
Q во всех последовательно соединенных трубах 1, 2 и 3 будет одинаков, а полная
потеря напора между точками М и N равна сумме потерь напора во всех последовательно
соединенных трубах. Таким образом, для последовательного соединения имеем следующие основные уравнения:
Q1 = Q2 = Q3 = Q
ΣhM-N = Σh1 + Σh2 + Σh3
Эти уравнения определяют правила построения характеристик последовательного соединения труб (рис. 6.3, б).
Если известны характеристики каждого трубопровода, то по ним можно построить характеристику всего
последовательного соединения M-N. Для этого нужно сложить ординаты всех трех кривых.
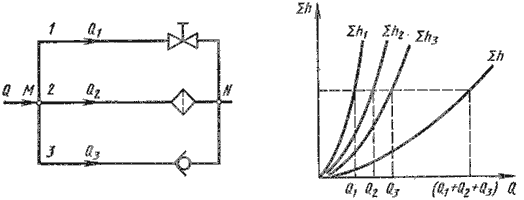
Параллельное соединение. Такое соединение показано на рис. 6.4, а. Трубопроводы 1,
2 и 3 расположены горизонтально.
Рис. 6.4. Параллельное соединение трубопроводов
Обозначим полные напоры в точках М и N соответственно HM и
HN , расход в основной магистрали (т.е. до разветвления и после слияния) – через Q,
а в параллельных трубопроводах через Q1, Q2 и Q3;
суммарные потери в этих трубопроводах через Σ1 , Σ2 и Σ3.
Очевидно, что расход жидкости в основной магистрали
Q = Q1 = Q2 = Q3
Выразим потери напора в каждом из трубопроводов через полные напоры в точках М и N :
Σh1 = HM – HN; Σh2 = HM – HN; Σh3 = HM – HN
Отсюда делаем вывод, что
Σh1 = Σh2 = Σh3
т.е. потери напора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через
соответствующие расходы следующим образом
Σh1 = K1Q1m; Σh2 = K2Q2m; Σh3 = K3Q3m
где K и m – определяются в зависимости от режима течения.
Из двух последних уравнений вытекает следующее правило: для построения характеристики параллельного
соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при
одинаковых ординатах ( Σ h). Пример такого построения дан на рис. 6.3, б.
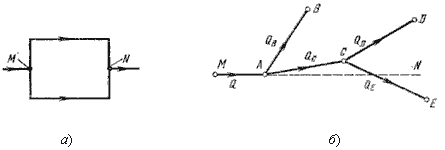
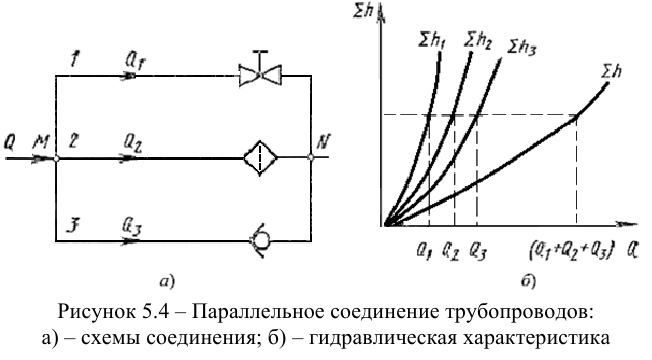
Разветвленное соединение. Разветвленным соединением называется совокупность нескольких
простых трубопроводов, имеющих одно общее сечение – место разветвления (или смыкания) труб.
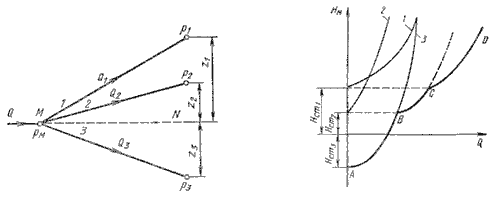
Рис. 6.5. Разветвленный трубопровод
Пусть основной трубопровод имеет разветвление в сечении М-М, от которого отходят, например, три
трубы 1, 2 и 3 разных диаметров, содержащие различные местные сопротивления (рис. 6.5, а).
Геометрические высоты z1, z2 и z3 конечных сечений и
давления P1, P2 и P3 в них будут также различны.
Так же как и для параллельных трубопроводов, общий расход в основном трубопроводе будет равен сумме
расходов в каждом трубопроводе:
Q = Q1 = Q2 = Q3
Записав уравнение Бернулли для сечения М-М и конечного сечения, например первого трубопровода,
получим (пренебрегая разностью скоростных высот)
Обозначив сумму первых двух членов через Hст и выражая третий член через расход (как
это делалось в п.6.1), получаем
HM = Hст 1 + KQ1m
Аналогично для двух других трубопроводов можно записать
HM = Hст 2 + KQ2m
HM = Hст 3 + KQ3m
Таким образом, получаем систему четырех уравнений с четырьмя неизвестными: Q1,
Q2 и Q3 и HM.
Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых
потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 6.5, б) –
сложением абсцисс (Q) при одинаковых ординатах (HM). Кривые потребных напоров для
ветвей отмечены цифрами 1, 2 и 3 , а суммарная кривая потребного напора для всего разветвления обозначена
буквами ABCD. Из графика видно, что условием подачи жидкости во все ветви является неравенство
HM > Hст1.
Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их
соединением (рис. 6.6, а) или с разветвлениями (рис. 6.6, б).
Рис. 6.6. Схемы сложных трубопроводов
Рассмотрим разомкнутый сложный трубопровод (рис. 6.6, б). магистральный трубопровод разветвляется в точках
А и С. Жидкость подается к точкам (сечениям) B, D и E с расходами Q
B и QD и QE .
Пусть известны размеры магистралей и всех ветвей (простых трубопроводов), заданы все местные сопротивления,
а также геометрические высоты конечных точек, отсчитываемые от плоскости M – N и избыточные давления
в конечных точках PB и PD и PE.
Для этого случая возможны два вида задач:
Задача 1. Дан расход Q в основной магистрали MA. Необходимо
определить расходы QB и QD и QE, а также потребный
напор в точке М.
Задача 2. Дан напор в точке М. Определить расход в магистрали Q и расходы в
каждой ветви.
Обе задачи решают на основе одной и той же системы уравнений, число которых на единицу больше числа
конечных ветвей, а именно:
уравнение расходов:
Q = QB = QD = QE
уравнение равенства потребных напоров для ветвей CD и CE
Hст D + KCDQDт = Hст E + KCEQEт
уравнение равенства потребных напоров для ветви АВ и сложного трубопровода АСЕD
Hст B + KABQBт = Hст D + KCDQDт + KAC(QD + QE)т
выражение для потребного напора в точке М
Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т.е. с применением кривых
потребного напора и характеристик трубопроводов. Кривую потребного напора для сложного трубопровода следует
строить следующим образом:
1) сложный трубопровод разбивают на ряд простых;
2) строят кривые потребных напоров для каждого из простых трубопроводов;
3) складывают кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу
сложения характеристик параллельных трубопроводов;
4) полученную кривую складывают с характеристикой последовательно присоединенного трубопровода по
соответствующему правилу (см. п.6.2).
Таким образом, при расчете идут от конечных точек трубопровода к начальной точке, т.е. против течения
жидкости.
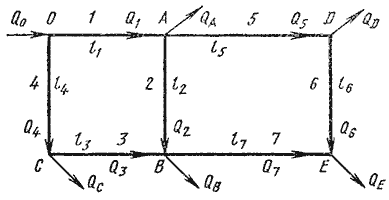
Сложный кольцевой трубопровод. Представляет собой систему смежных замкнутых контуров, с
отбором жидкости в узловых точках или с непрерывной раздачей жидкости на отдельных участках (рис. 6.7).
Рис. 6.7. Схема сложного кольцевого трубопровода
Задачи для таких трубопроводов решают аналогичным методом с применением электроаналогий (закон Кирхгофа).
При этом основываются на двух обязательных условиях. Первое условие – баланс расходов, т.е. равенство
притока и оттока жидкости для каждой узловой точки. Второе условие – баланс напоров, т.е. равенство нулю
алгебраической суммы потерь напора для каждого кольца (контура) при подсчете по направлению движения часовой
стрелки или против нее.
Для расчета таких трубопроводов типичной является следующая задача. Дан максимальный напор в начальной
точке, т.е. в точке 0, минимальный напор в наиболее удаленной точке Е, расходы во всех шести узлах и
длины семи участков. Требуется определить диаметры трубопроводов на всех участках.
Как уже отмечалось выше, перепад уровней энергии, за счет которого жидкость течет по трубопроводу, может
создаваться работой насоса, что широко применяется в машиностроении. Рассмотрим совместную работу трубопровода
с насосом и принцип расчета трубопровода с насосной подачей жидкости.
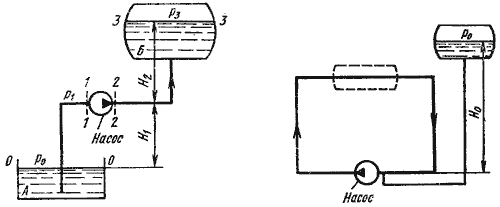
Трубопровод с насосной подачей жидкости может быть разомкнутым, т.е. по которому жидкость
перекачивается из одной емкости в другую (рис. 6.8, а), или замкнутым (кольцевым), в котором
циркулирует одно и то же количество жидкости (рис. 6.8, б).
Рис. 6.8. Трубопроводы с насосной подачей
Рассмотрим трубопровод, по которому перекачивают жидкость из нижнего резервуара с давлением P
0 в другой резервуар с давлением P3 (рис. 6.8, а). Высота расположения оси
насоса H1 называется геометрической высотой всасывания, а трубопровод, по которому
жидкость поступает к насосу, всасывающим трубопроводом или линией всасывания. Высота
расположения конечного сечения трубопровода H2 называется геометрической высотой
нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным или линией
нагнетания.
Составим уравнением Бернулли для потока рабочей жидкости во всасывающем трубопроводе, т.е. для сечений
0-0 и 1-1 (принимая α = 1):
Это уравнение является основным для расчета всасывающих трубопроводов.
Теперь рассмотрим напорный трубопровод, для которого запишем уравнение Бернулли, т.е. для сечений
2-2 и 3-3:
Левая часть этого уравнения представляет собой энергию жидкости на выходе из насоса. А на входе насоса
энергию жидкости можно будет аналогично выразить из уравнения:
Таким образом, можно подсчитать приращение энергии жидкости, проходящей через насос. Эта энергия сообщается
жидкости насосом и поэтому обозначается обычно Hнас.
Для нахождения напора Hнас вычислим уравнение :
где Δz – полная геометрическая высота подъема жидкости, Δz = H
1 + H2;
КQm – сумма гидравлических потерь,
P3 и Р0 – давление в верхней и нижней емкости соответственно.
Если к действительной разности уровней Δz добавить разность пьезометрических высот
( P3 – Р0 ) ( ρg ), то можно рассматривать увеличенную
разность уровней
и формулу можно переписать так:
Hнас = Hст + KQm
Из этой формулы делаем вывод, что
Hнас = Hпотр
Отсюда вытекает следующее правило устойчивой работы насоса: при установившемся течении жидкости в
трубопроводе насос развивает напор, равный потребному.
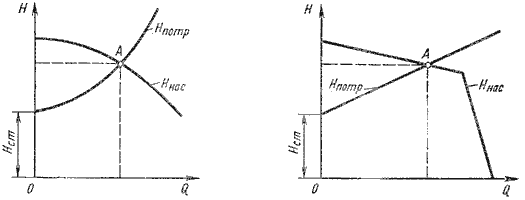
На этом равенстве основывается метод расчета трубопроводов с насосной подачей, который заключается в
совместном построении в одном и том же масштабе и на одном графике двух кривых: напора Hпотр =
f1(Q) и характеристики насоса Hнас = f2(Q) и в
нахождении их точки пересечения (рис. 6.9).
Рис. 6.9. Графическое нахождение рабочей точки
Характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода
жидкости) при постоянной частоте вращения вала насоса. На рис. 6.9 дано два варианта графика: а –
для турбулентного режима; б – для ламинарного режима. Точка пересечения кривой потребного напора с
характеристикой насоса называется рабочей точкой. Чтобы получить другую рабочую точку, необходимо
изменить открытие регулировочного крана (изменить характеристику трубопровода) или изменить частоту вращения
вала насоса.
Гидравлическим ударом называется резкое повышение давления, возникающее в напорном трубопроводе при
внезапном торможении потока рабочей жидкости. Этот процесс является очень быстротечным и характеризуется
чередованием резких повышений и понижений давления, которое связано с упругими деформациями жидкости и
стенок трубопровода. Гидравлический удар чаще всего возникает при резком открытии или закрытии крана или
другого устройства, управляемого потоком.
Пусть в конце трубы, по которой движется жидкость со скоростью υ0, произведено
мгновенное закрытие крана (рис. 6.10, а).
Рис. 6.10. Стадии гидравлического удара
При этом скорость частиц, натолкнувшихся на кран, будет погашена, а их кинетическая энергия перейдет в
работу деформации стенок трубы и жидкости. При этом стенки трубы растягиваются, а жидкость сжимается в
соответствии с увеличением давления на величину ΔPуд, которое называется
ударным. Область (сечение n – n), в которой происходит увеличение давления, называется ударной волной.
Ударная волна распространяется вправо со скоростью c, называемой скоростью ударной волны.
Когда ударная волна переместится до резервуара, жидкость окажется остановленной и сжатой во всей трубе,
а стенки трубы – растянутыми. Ударное повышение давления распространится на всю длину трубы (рис. 6.10, б).
Далее под действием перепада давления ΔPуд частицы жидкости устремятся
из трубы в резервуар, причем это течение начнется с сечения, непосредственно прилегающего к резервуару. Теперь
сечение n-n перемещается обратно к крану с той же скоростью c, оставляя за собой выровненное
давление P0 (рис. 6.10, в).
Жидкость и стенки трубы предполагаются упругими, поэтому они возвращаются к прежнему состоянию,
соответствующему давлению P0. Работа деформации полностью переходит в кинетическую энергию,
и жидкость в трубе приобретает первоначальную скорость υ0, но направленную теперь
в противоположную теперь сторону.
С этой скоростью весь объем жидкости стремится оторваться от крана, в результате возникает отрицательная
ударная волна под давлением P0 – ΔPуд, которая
направляется от крана к резервуару со скоростью c, оставляя за собой сжавшиеся стенки трубы и
расширившуюся жидкость, что обусловлено снижением давления (рис. 6.10, д). Кинетическая энергия жидкости
вновь переходит в работу деформаций, но противоположного знака.
Состояние трубы в момент прихода отрицательной ударной волны к резервуару показано на рис. 6.10, е. Так же
как и для случая, изображенного на рис. 6.10, б, оно не является равновесным. На рис. 6.10, ж, показан процесс
выравнивания давления в трубе и резервуаре, сопровождающийся возникновением движения жидкости со
скоростью υ0.
Очевидно, что как только отраженная от резервуара ударная волна под давлением ΔP
уд достигнет крана, возникнет ситуация, уже имевшая место в момент закрытия крана. Весь цикл
гидравлического удара повторится.
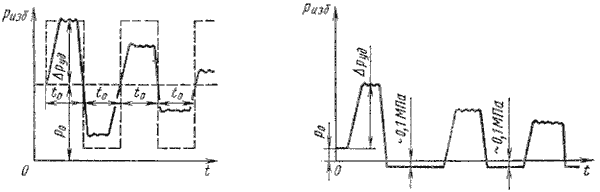
Протекание гидравлического удара во времени иллюстрируется диаграммой, представленной на рис. 6.11, а и б.
Штриховыми линиями показано теоретическое изменение давления у крана в точке А, а сплошной
действительный вид картины изменения давления по времени (рис. 6.11, а). При этом затухание колебаний
давления происходит за счет потерь энергии жидкости на преодоление сил трения и ухода энергии в резервуар.
Если давление P0 невелико (P0 < ΔP
уд), то картина изменения амплитуды давления получается несколько иная, примерно такая, как
показано на рис. 6.11, б.
Рис. 6.11. Изменение давления по времени у крана
Повышение давления при гидравлическом ударе можно определить по формуле
ΔPуд = ρυ0c
Данное выражение носит название формулы Жуковского. В нем скорость распространения ударной волны c
определится по формуле:
где r – радиус трубопровода;
E – модуль упругости материала трубы;
δ – толщина стенки трубопровода;
K – объемный модуль упругости (см. п.1.3)
Если предположить, что труба имеет абсолютно жесткие стенки, т.е. E = 
ударной волны определится из выражения
Для воды эта скорость равна 1435 м/с, для бензина 1116 м/с, для масла 1200 – 1400 м/с.
При проектировании напорных трубопроводов следует учитывать, что их пропускная способность в период
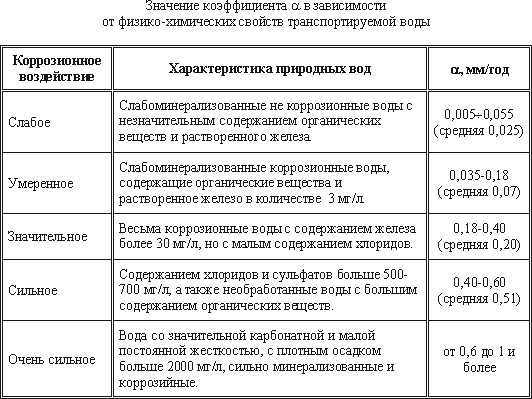
эксплуатации снижается (например, для водопроводных труб до 50% и даже ниже). Вследствие коррозии и
образования отложений в трубах (инкрустации), шероховатость труб увеличивается. Это можно оценить по
формуле:
kt = k0 + αt
где k0 – абсолютная шероховатость для новых труб, (мм),
kt – шероховатость через t лет эксплуатации,
α – коэффициент характеризующий быстроту возрастания шероховатости (мм/год).
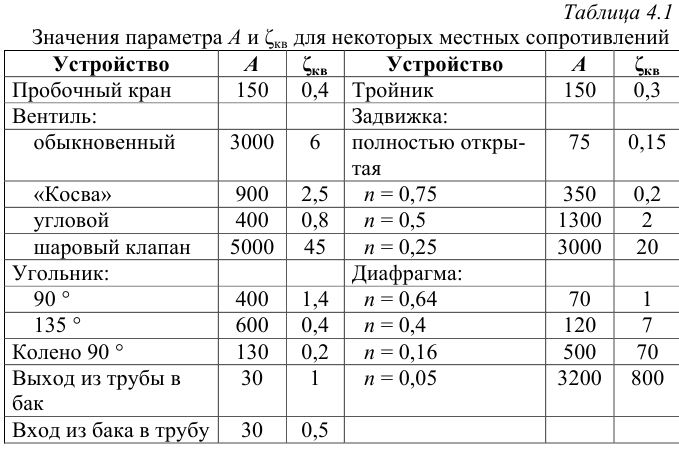
Таблица 6.1
Проверить себя ( Тест )
Наверх страницы
11-я лекция.
11. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ПРОСТЫХ ТРУБОПРОВОДОВ
12.1. Простой трубопровод постоянного сечения.
12.1.1.Общий вид расчетного уравнения простого трубопровода
12.2.Простой трубопровод между двумя резервуарами.
12.3. Простой трубопровод при истечении в атмосферу.
12.4.Сифонный трубопровод. Вакуум на участке трубопровода.
12.5. Использование приблизительных зависимостей при расчете простого трубопровода.
Замена местных сопротивлений.
Рекомендуемые материалы
12.6. Три задачи на расчет простого трубопровода.
12.7 Графики напоров
12.1. Простой трубопровод постоянного сечения
Трубопровод называют простым, если жидкость транспортируется по нему от питателя к приемнику без ответвлений потока, но может иметь различные диаметры и включать местные сопротивления.
Трубопроводы, содержащие последовательные, параллельные соединения и разветвления простых трубопроводов называются сложными.
Жидкость движется по трубопроводу за счет того, что энергия, имеющаяся в начале трубопровода больше, чем в конце.
Энергии может быть обеспечена разностью уровней жидкости, работой насоса или давлением газа, например, за счет применения гидроаккумуляторов.
Движение жидкости за счет разности уровней (разности геометрических высот) применяется в гидротехнике и водоснабжении.
В машиностроении движение жидкости обеспечивается работой насоса и гидроаккумуляторами. Гидроаккмуляторы – емкости с разделителем с одной стороны использующие давление газа или пружины для создания запаса энергии с другой стороны рабочую жидкость, заправленную в гидроаккумулятор и находящуюся под действием давления газа.
На рис.12.1 изображен простой трубопровод постоянного сечения расположенный произвольно в пространстве, состоящий из нескольких участков с длиной li и диаметром di и содержащий местные сопротивления.
Запишем уравнение Бернулли для сечений «1 – 1» и “2-2”. Геометрические высоты: z1 и z2, избыточные давления: Р1 и Р2, скорости: V1 и V2.ρ

Σh – сумма потерь на трение по длине и в местных сопротивлениях, а также потерь на входе и выходе из трубопровода.
Гидростатическим напором называется сумма геометрического и пьзометрического напора в данном сечении трубопровода.
где z – геометрический напор, 
Разность гидростатических напоров в в сечениях 1 и 2, называется располагаемым напором – Нрасп, если величина гидростатического напора Нгст для сечений 1 и 2 известна.
Если величина Нгст не известна, разность гидростатических напоров называется потребным напором – Нпотр
и ее необходимо определить.
Таким образом, разность может быть располагаемым или потребным напором, в зависимости от наличия или отсутствия исходных данных.

Используя разность гидростатических напоров из уравнения баланса напоров Бернулли, получаем общий вид расчетного уравнения простого трубопровода

Это уравнение показывает, что имеющаяся в нашем распоряжении потенциальная энергиия в виде гидростатического напора затрачивается на преодоление разности скоростных напоров и потерь в местных сопротивлениях и на трение по длине.
Если площади питателя и приемника или длины трубопроводов велики по сравнению с сечением трубопровода, тогда скоростными напорами можно пренебречь, уравнение простого трубопровода принимает вид

В этом случае, потребный напор будет равен сумме сопротивлений в трубопроводе. Располагаемый напор будет затрачиваться на преодоление гидравлических сопротивлений.
Таким образом, уравнение простого трубопровода позволяет решить две задачи.
Первая: в случае известного располагаемого напора определить сопротивления, которые он может преодолеть.
Вторая: в случае известной суммы сопротивлений определить располагаемый напор.
Правая часть равенства (12.4) называется характеристикой трубопровода. Уравнение баланса напоров можно записать в виде

где Σh – есть характеристика трубопровода, которая является степенной функцией расхода. Величина К – коэффициент сопротивления трубопровода, а показатель степени m имеет значение, зависящее от режима течения жидкости(ламинарный или турбулентный).
Используя формулу (12.4′) можно построить кривую потребного напора в координатах Н=f(Q), (рис.12.2), то есть зависимость напора от расхода жидкости в трубопроводе.
Величина Нгст определяет положение характеристики трубопровода относительно начала координат Н-Q.
12.2.Простой трубопровод между двумя резервуарами.
Используем уравнение располагаемого напора для расчета простого трубопровода, который соединяет два резервуара с постоянными уровнями жидкости и состоит из k последовательных участков длиной li и диаметром di, а также включает местные сопротивления.
Показанные на рис.12.3 уровни жидкости в резервуарах следует рассматривать, как пьезометрические уровни в питателе и в приемнике, поскольку геометрические напоры в их сечениях равны z1 = z2, а за плоскость сравнения принята ось трубопровода.
Выражая потери на трение по длине и в местных сопротивлениях формулами

получим уравнение простого трубопровода в виде:

где λ i и ξ i – коэффициент сопротивления трению и суммарный коэффициент местных сопротивлений на каждом участке, Vi – средняя скорость на каждом участке, Vk – скорость потока на выходе из трубопровода в резервуар, αkV2k/2g – скоростной напор при выходе из трубопровода в резервуар (потеря напора в выходном сечении трубопровода). Коэффициент Кориолиса αk = 1 – для турбулентного режима течения, αk= 2 для ламинарного режима течения.
Используя уравнение неразрывности потоков
Q=V1F1 =…=ViFi=VkFk ,
получим расчетное уравнение простого трубопровода в виде

где Fk – площадь выходного сечения трубопровода с диаметром dк, Fi – площадь трубопровода с диаметром di.
Если трубопровод имеет длину l и диаметр d, при турбулентном режиме αk = 1, уравнение упрощается

где Σξ – сумма коэффициентов потерь в местных сопротивлениях.
Из уравнения трубопровода можно выразить скорость
и расход 
где 
Выражая скорость V = Q/F через расход и использовав значение ускорения свободного падения g = 9,81 м/с2, получим уравнение простого трубопровода в виде

где l, d, H в м, Q в м3/с.
12.3. Простой трубопровод при истечении в атмосферу.
При истечении из резервуара в атмосферу (рис.12.3) уравнение Бернулли между сечениями 0-0 и 1-1 имеет вид

где Н – располагаемый напор трубопровода, определяемый высотой пьезометрического уровня, 
Так как потери напора при выходе в атмосферу отсутствуют, уравнение (12.9) при подстановке в него суммы потерь переходит в уравнение (12.6),
поэтому уравнение (12.6 ) является общим при истечении под уровень и в атмосферу.
12.4.Сифонный трубопровод. Вакуум на участке трубопровода.
Если часть длины трубопровода находится под вакуумом (например, сифонный трубопровод, область С, рис.12.5), необходимо проверить наибольший вакуум в опасном сечении С:

где h – высота сечения С над начальным уровнем пьезометрическим уровнем в баке питателе; V – скорость в этом сечении; ΣhпС – сумма потерь напора на участке трубопровода до этого сечения. Для обеспечения нормальной бескавитационной работы трубопровода должно выполняться условие
РвС < Рат – Рн.п.,
где РвС – вакуум в точке С, Рат – атмосферное давление, Рн.п. – давление насыщенных паров жидкости при данной температуре.
12.5. Использование приблизительных зависимостей при расчете простого трубопровода. Замена местных сопротивлений.
При достаточно большой длине трубопровода можно пренебречь скоростным напором V2/2g по сравнению с потерями на трение по длине и использовать для расчета приблизительные зависимости, введя в них, если это необходимо замену коэффициентов местных сопротивлений на потери по длине



При такой замене получаем

Для трубопровода, состоящего только из k – последовательных участков труб с различными диаметрами di и длинами Li

12.6 Определение коэффициентов трения
в зависимости от режима течения жидкости.
Расчет трубопроводов связан с выбором коэффициентов ξ местных сопротивлений и коэффициента трения λ.
1. Ламинарный режим. При числе Рейнольдса равном Re ≤ 2300, коэффициент трения определяется по формуле λ=64/Re.
Для определения потерь используем формулу Дарси:

При подстановке λ=64/Re потери на трение в трубопроводе

Если скорость определить через расход V =Q/F = 4Q/(πd2)

2.Турбулентный режим Re > 2300.
А.Область гидравлически гладких труб.
При числах Рейнольдса Reгл ≤ 20d/Δэ, здесь Δэ –эквивалентная абсолютная шероховатость, коэффициент сопротивления трению определяется по формуле Канакова

или по формуле Блазуиса

Подставляя формулу Блазиуcа в формулу Дарси

Зависимость λ от Re для гидравлически гладких труб дана в справочниках или ее можно взять в задачнике на стр.228.
К этой области относятся технически гладкие трубы , цельнотянутые из цветных металлов, во всем диапазоне их практического применения по числам Re, а также стальные трубы до чисел Re ориентировочно равных Reгл ≥ 20d/Δ.
Б. Переходная зона.
При числах Рейнольдса 20d/Δ ≤Re ≤ 500 d/Δ в переходной области λ зависит и от числа Re и от относительной гладкости.
Значения λ в функции Re и относительной гладкости d/Δ по данным теплотехнического института, приведены в справочниках в виде графика Мурина в задачнике.
Можно применять для определения коэффициента λ формулу Альтшуля.

Средние значения эквивалентной шероховатости для новых труб Δ =0,1мм, для бывших в употреблении Δ = 0,2 мм.
В. Область гидравлически шероховатых труб.
При числах Рейнольдса Re ≥ 500 d/Δ коэффициент λ зависит только от шероховатости. Для определения значений коэффициента λ можно использовать формулу Никурадзе

Или формулу Шифринсона

Для старых стальных и чугунных труб, эквивалентная шероховатость до Δ = 1 мм, применимо выражение, где d в м

Зависимость λ от d/Δ для квадратичной области дается по таблицам, пример такой таблицы приведен в задачнике на стр.229.
12.6. Три задачи на расчет простого трубопровода.
Задача 1. Даны: расход жидкости Q, кинематическая вязкость жидкости ν, размеры трубопровода l, d шероховатость стенок – Δ.
Найти требуемый напор – Н
1.По известным Q, d, ν находится число Рейнольдса – Re и определяется режим движения.
1.1 При ламинарном режиме, напор определяется по ф-ле

где L = l + Σlэ – приведенная длина трубопровода, эквивалентные длины lэ местных сопротивлений при ламинарном режиме в трубопроводе существенно зависят от числа Рейнольдса: lэ/d = f(Re) .
1.2.При турбулентном режиме Н определяется по формулам:


Задача 2. Даны: располагаемый напор – Н, размеры трубопровода: l, d, Δ – шероховатость свойства жидкости. Найти расход – Q.
Задача 3. Даны располагаемый напор – Q, длина трубопровода l, шероховатость стенок – Δ. Найти диаметр трубопровода – d.
Из уравнения располагаемого напора определяются искомые величины
12.7 Построение диаграмм напоров в трубопроводе
Последовательность построения диаграмм.
1. Выделение в трубопроводе участков, на которых происходит изменение сечения и участки с местными сопротивлениями.
2. Начало первого участка определяет начало трубопровода, а величину напора – напор в питателе.
Если начало трубопровода связано с потерями, как например, при входе в трубу, начало участка немного смещают влево, чтобы показать качественный участок сжатия струи.
3. Первый участок – вход в трубопровод, в котором происходит сужение потока и увеличение скорости до значения 


Потери, связанные с деформацией потока, входят в величину 
График напоров, построение которого дано на рис.12.8 показывает изменение по длине трубопровода полного напора потока и его составляющих.
4. Линия напора (удельной механической энергии потока ) строится путем последовательного вычитания потерь, нарастающих вдоль потока из начального напора потока (заданного пьезометрическим уровнем в питающем резервуаре).
Там, где имеется местная деформация потока и ход изменения напоров может быть показан только качественно, линии напоров даны штриховой линией).
Построение графика напоров для вертикального трубопровода дано на рис. 12.10.
1. Напоры в каждом сечении откладываются по горизонтали таким образом, чтобы ось трубы являлась началом отсчета пьезометрических напоров.
2.Графики напоров, показывают изменение по длине трубопровода полного напора потока и его составляющих.
Бесплатная лекция: “3. Свойства Z-преобразования” также доступна.
3. Из начального напора потока (заданного пьезометрическим уровнем в питающем резервуаре) вычитаются потери, нарастающие вдоль трубопровода, таким образом, потеря в конце участка формирует (пьезометрический) уровень напора на следующий участок.
4. Пьезометрическая линия (линия изменения гидростатического напора потока) строится путем вычитания скоростного напора в каждом сечении полного напора потока.
Пьезометрический напор Pи/(ρg) в каждом сечении (Ри – избыточное давление) определяется на графике вертикальным расстоянием от центра сечения до пьезометрической линиии;
Скоростной напор 
График напора для длинного трубопровода строится упрощенно (рис.12.11), поскольку малость скоростных напоров позволяет рассматривать линию напора и пьезометрическую линию, как совпадающие.
Решение задач гидравлике уравнение бернулли
Уравнение Бернулли для реальной и идеальной жидкости
Уравнение Бернулли позволяет выполнить расчет водоснабжения и отопления: Подобрать диаметры и насосы. В этой статье будет расписан энергетический и геометрический смысл уравнения Бернулли.
График Бернулли и уравнение Бернулли для идеальной жидкости:
График Бернулли и уравнение Бернулли для реальной жидкости:
Смысл уравнения Бернулли
Смысл уравнения Бернули в том, чтобы показать, что внутри системы заполненной жидкостью (участка трубопровода) сохраняется общая энергия между разными точками. То есть на участке трубопровода необходимо выделить две точки, и эти две точки равны друг другу по значению полной энергии. Полная энергия состоит из потенциальной и кинетической энергии.
Назначение уравнения Бернули
Понять, как распределяется давление в системе трубопроводов. А также с помощью уравнения находить неизвестные параметры внутри системы. Например, найти давление в каждой течке пространства системы заполненной жидкостью.
Подробнее на видео: (для запуска видео кликните по окошку) На видео намного больше информации
Решая задачу с уравнением Бернулли, Вы фактически занимаетесь гидравлическим расчетом. О том, как делать гидравлический расчет – написано тут: Конструктор водяного отопления
Задача. Пример решения уравнения Бернулли
По решению задачи необходимо найти давление в точке 2 при известных параметрах: давление и расход.
Как понять уравнение Бернулли?
Для расчета уравнения Бернулли необходимо выбрать две точки в пространстве
Точка 1 – это место где известно давление
Точка 2 – это место где нужно узнать давление
Поймите, что каждый кусок формулы измеряется давлением: м.в.ст. (метр водяного столба)
То есть для того, чтобы быстро считать гидравлику систем водоснабжения и отопления, необходимо меньше всего выражаться в Барах, Паскалях и тому подобное.
Проще выражать давление в единице измерения: м.в.ст. (метр водяного столба)
Вы этим самым упростите себе жизнь… просто другая единица это еще один процесс, который отнимает время.
Сборка формулы уравнения Бернулли
Как избавится от минуса?
Как избавится от множителя (-1)?
Необходимо множитель (-1) помножить на каждый слагаемый член. Знак каждого слагаемого члена меняется на противоположный. То есть (+ на -) (- на +). Далее перестановка слагаемых.
Что такое идеальная жидкость?
Идеальная жидкость – это жидкость, не обладающая внутренним трением. То есть такая жидкость не создает гидравлическое сопротивление.
Реальная жидкость – это жидкость, которая обладает вязкостью. То есть внутренним сопротивлением.
Формула Бернулли для реальной жидкости
Коэффициент Кориолиса – это поправка кинетической энергии на реальную жидкость.
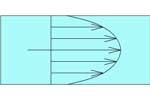
Потому что реальная жидкость движется не равномерно
У реальной жидкости серединная струйка воды движется быстрее остальных. При ламинарном режиме градиент: Чем ближе к стенке, тем медленнее движется поток воды.
Формула коэффициента Кориолиса
Что такое коэффициент Кориолиса?
Коэффициент Кориолиса характеризует отношение действительной кинетической энергии потока жидкости в данном сечении к той кинетической энергии потока, которую он имел бы, если бы все частицы двигались с одинаковой скоростью, равной средней скорости потока.
Чему равен коэффициент Кориолиса?
Нд.п. – Это динамические потери. Это потери вызванные движением воды.
Имеются дополнительные задачи с уравнением Бернули на реальную жидкость:
Посмотрите видеоурок по составлению уравнения Бернулли:
Как сделать гидравлический расчет погружного насоса?
Основы гидравлики
Уравнение Бернулли – фундамент гидродинамики
Бернулли – вне всякого сомнения – имя, знакомое и специалистам, и обывателям, которые хоть немного интересуются науками. Этот человек оставил ослепительный след в истории познавания человечеством окружающего мира, как физик, механик, гидравлик и просто общепризнанный гений, Даниил Бернулли навсегда останется в памяти благодарных потомков за свои идеи и выводы, которые долгое время существования человечества были покрыты мраком неизведанного.
Открытия и законы, которыми Бернулли осветил путь к познанию истины, являются фундаментальными, и придали ощутимый импульс развитию многих естественных наук. К таковым относится и уравнение Бернулли в Гидравлике, которое он вывел почти три века назад. Данное уравнение является основополагающим законом этой сложной науки, объясняющим многие явления, описанные даже древними учеными, например, великим Архимедом.
Попробуем уяснить несложную суть закона Бернулли (чаще его называют уравнением Бернулли), описывающего поведение жидкости в той или иной ситуации.
Выделим в стационарно текущей идеальной жидкости трубку тока, которая ограничена сечениями S1 и S2 , (рис. 1) .
(Понятие идеальной жидкости абстрактно, как и понятие всего идеального. Идеальной считается жидкость, в которой нет сил внутреннего трения, т. е. трения между отдельными слоями и частицами подвижной жидкости).
Пусть в месте сечения S1 скорость течения ν1 , давление p1 и высота, на которой это сечение расположено, h1 . Аналогично, в месте сечения S2 скорость течения ν2 , давление p2 и высота сечения h2 .
За бесконечно малый отрезок времени Δt жидкость переместится от сечения S1 к сечению S1‘ , от S2 к S2‘ .
По закону сохранения энергии, изменение полной энергии E2 – E1 идеальной несжимаемой жидкости равно работе А внешних сил по перемещению массы m жидкости:
где E1 и E2 – полные энергии жидкости массой m в местах сечений S1 и S2 соответственно.
С другой стороны, А – это работа, которая совершается при перемещении всей жидкости, расположенной между сечениями S1 и S2 , за рассматриваемый малый отрезок времени Δt .
Чтобы перенести массу m от S1 до S1‘ жидкость должна переместиться на расстояние L1 = ν1Δt и от S2 до S2‘ – на расстояние L2 = ν2Δt . Отметим, что L1 и L2 настолько малы, что всем точкам объемов, закрашенных на рис. 1 , приписывают постоянные значения скорости ν , давления р и высоты h .
Следовательно,
где F1 = p1S1 и F2 = – p2S2 (сила отрицательна, так как направлена в сторону, противоположную течению жидкости; см. рис. 1).
Полные энергии E1 и E2 будут складываться из кинетической и потенциальной энергий массы m жидкости:
Подставляя (3) и (4) в (1) и приравнивая (1) и (2) , получим
Согласно уравнению неразрывности для несжимаемой жидкости, объем, занимаемый жидкостью, всегда остается постоянным, т. е.
Разделив выражение (5) на ΔV , получим
где ρ – плотность жидкости.
После некоторых преобразований эту формулу можно представить в другом виде:
Поскольку сечения выбирались произвольно, то в общем случае можно записать:
ρv 2 /2 +ρgh +p = const (6) .
Выражение (6) получено швейцарским физиком Д. Бернулли (опубликовано в 1738 г.) и называется уравнением Бернулли.
Даниил Бернулли (Daniel Bernoulli, 1700 – 1782), швейцарский физик, механик и математик, один из создателей кинетической теории газов, гидродинамики и математической физики. Академик и иностранный почётный член (1733) Петербургской академии наук, член Академий: Болонской (1724), Берлинской (1747), Парижской (1748), Лондонского королевского общества (1750).
Уравнение Бернулли по своей сути является интерпретацией закона сохранения энергии применительно к установившемуся течению идеальной жидкости. Уравнение хорошо выполняется и для реальных жидкостей, для которых внутреннее трение не очень велико.
Величина р в формуле (6) называется статическим давлением (давление жидкости на поверхность обтекаемого ею тела) , величина ρν 2 /2 – динамическим давлением, величина ρgh – гидростатическим давлением.
Статическое давление обусловлено взаимодействием поверхности жидкости с внешней средой и является составляющей внутренней энергии рассматриваемого элементарного объема жидкости (т. е. характеризуется взаимодействием внутренних частиц жидкости, вызванных внешним возмущением – давлением) , а гидростатическое – положением этого объема жидкости в пространстве (зависит от высоты над поверхностью Земли) .
Динамическое давление характеризует кинематическую составляющую энергии этого объема, поскольку зависит от скорости потока, в котором движется рассматриваемый элементарный объем жидкости.
Для горизонтальной трубки тока изменение потенциальной составляющей ρgh будет равно нулю (поскольку h2 – h1 = 0) , и выражение (6) примет упрощенный вид:
ρv 2 /2 + p = const (7) .
Выражение p + ρν 2 /2 называется полным давлением.
Таким образом, содержание уравнения Бернулли для элементарной струйки при установившемся движении можно сформулировать так: удельная механическая энергия при установившемся движении элементарной струйки идеальной жидкости, представляющая собой сумму удельной потенциальной энергии положения и давления и удельной кинетической энергии, есть величина постоянная.
Все члены уравнения Бернулли измеряются в линейных единицах.
В гидравлике широко применяют термин напор, под которым подразумевают механическую энергию жидкости, отнесенную к единице ее веса (удельную энергию потока или неподвижной жидкости) .
Величину v 2 /2g называют скоростным (кинетическим) напором, показывающим, на какую высоту может подняться движущаяся жидкость за счет ее кинетической энергии.
Величину hп = p/ρg называют пьезометрическим напором, показывающим на какую высоту поднимается жидкость в пьезометре под действием оказываемого на нее давления.
Величину z называют геометрическим напором, характеризующим положение центра тяжести соответствующего сечения движущейся струйки над условно выбранной плоскостью сравнения.
Сумму геометрического и пьезометрического напоров называют потенциальным напором, а сумму потенциального и скоростного напора – полным напором.
На основании анализа уравнения Бернулли можно сделать вывод, что при прочих неизменных параметрах потока (жидкости или газа) величина давления в его сечениях обратно пропорциональна скорости, т. е. чем выше давление, тем меньше скорость, и наоборот.
Это явление используется во многих технических конструкциях и устройствах, например, в карбюраторе автомобильного двигателя (диффузор), в форме крыла самолета. Увеличение скорости воздушного потока в диффузоре карбюратора приводит к созданию разрежения, всасывающего бензин из поплавковой камеры, а специальная форма сечения самолетного крыла позволяет создавать на его нижней стороне зону повышенного давления, способствующего появлению подъемной силы.
Геометрическая интерпретация уравнения Бернулли
Поскольку напор измеряется в линейных величинах, можно дать графическую (геометрическую) интерпретацию уравнению Бернулли и его составляющим.
На графике (рис. 2) представлена горизонтальная плоскость сравнения 0-0 , относительно которой геометрический напор будет в каждом сечении равен вертикальной координате z центра тяжести сечения (линия геометрического напора проходит по оси струйки) .
Линия К-К , характеризующая потенциальный напор струйки, получена сложением геометрического и пьезометрического напора в соответствующих сечениях (т. е. разница координат точек линии К-К и соответствующих точек оси струйки характеризует пьезометрический напор в данном сечении) .
Полный напор характеризуется линией MN , которая параллельна плоскости сравнения О-О , свидетельствуя о постоянстве полного напора H’e (удельной механической энергии) идеальной струйки в любом ее сечении.
При движении реальной жидкости, обладающей вязкостью, возникают силы трения между ограничивающими поток поверхностями и между слоями внутри самой жидкости. Для преодоления этих сил трения расходуется энергия, которая превращается в теплоту и рассеивается в дальнейшем движущейся жидкостью. По этой причине графическое изображение уравнения Бернулли для идеальной жидкости будет отличаться от аналогичного графика для реальной жидкости.
Если обозначить hf потери напора (удельной энергии) струйки на участке длиной L , то уравнение Бернулли для реальной жидкости примет вид:
Для реальной жидкости полный напор вдоль струйки не постоянен, а убывает по направлению течения жидкости, т. е. его графическая интерпретация имеет вид не прямой линии, а некоторой кривой МЕ (рис. 3) . Заштрихованная область характеризует потери напора.
Падение напора на единице длины элементарной струйки, измеренной вдоль оси струйки, называют гидравлическим уклоном:
Гидравлический уклон положителен, если напорная линия снижается по течению жидкости, что всегда бывает при установившемся движении.
Для практического применения уравнения Бернулли необходимо распространить его на поток реальной жидкости:
где α1 , α2 – коэффициенты Кориолиса, учитывающие различие скоростей в разных точках сечения потока реальной жидкости.
На практике обычно принимают α1 = α2 = α : для ламинарного режима течения жидкости в круглых трубах α = 2, для турбулентного режима α = 1,04. 1,1.
Из уравнения Бернулли для горизонтальной трубки тока и уравнения неразрывности ( S1v1Δt = S2v2Δt ) видно, что при течении жидкости по горизонтальной трубе, которая имеет различные сечения, скорость жидкости больше в более узких местах (где площадь сечения S меньше) , а статическое давление больше в более широких местах, т. е. там, где скорость меньше. Это можно увидеть, установив вдоль трубы ряд манометров.
Данный опыт показывает, что в манометрической трубке В , которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С , которые прикреплены к широкой части трубы, что соответствует уравнению Бернулли.
Так как динамическое давление зависит от скорости движения жидкости (газа) , то уравнение Бернулли можно использовать для измерения скорости потока жидкости. Принципиально это свойство жидкости для определения скорости потока реализовано в так называемой трубке Пито – Прандтля (обычно ее называют трубкой Пито ) .
Трубка Пито – Прандтля ( см. рис. 2 ) состоит из двух тонких стеклянных трубок, одна из которых изогнута под прямым углом (Г-образно) , а вторая – прямая.
Одним из свободных концов каждая трубка присоединена к манометру.
Изогнутая трубка имеет открытый свободный конец, направленный против тока и принимающий напор потока жидкости, а вторая погружена в поток перпендикулярно току, и скорость потока на давление внутри трубки не влияет, т. е. внутри этой трубки действует лишь статическая составляющая давления жидкости.
Разница между давлением в первой трубке (полное давление) и второй трубке (статическое давление) , которую показывает манометр, является динамическим давлением, определяемым по формуле:
Определив с помощью трубки Пито – Прандтля динамическое давление в потоке жидкости, можно легко вычислить скорость этого потока:
Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью, с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости.
Рассмотрим два сечения (на уровне h1 свободной поверхности жидкости в сосуде и на уровне h1 выхода ее из отверстия) и применим уравнение Бернулли:
Так как давления р1 и р2 в жидкости на уровнях первого и второго сечений равны атмосферному, т. е. р1 = р2 , то уравнение будет иметь вид
Из уравнения неразрывности мы знаем, что ν1/ν2 = S2/S1 , где S1 и S2 – площади поперечных сечений сосуда и отверстия.
Если S1 значительно превышает S2 , то слагаемым ν1 2 /2 можно пренебречь и тогда:
Это выражение получило название формулы Торричелли.
Формулу Торричелли можно использовать для подсчета объемного (или массового) расхода жидкости, истекающего из отверстия в сосуде с поддерживаемым постоянно уровнем под действием атмосферного давления.
При этом используется формула Q = vS (для определения массового расхода – m = ρvS ) , по которой определяется расход жидкости за единицу времени.
Если требуется узнать расход жидкости за определенный промежуток времени t , то его определяют, умножив расход за единицу времени на время t .
Следует отметить, что такая методика расчета расхода реальной жидкости через отверстие в стенке сосуда дает некоторые погрешности, обусловленные физическими свойствами реальных жидкостей, поэтому требует применения поправочных коэффициентов (коэффициентов расхода) .
Пример решения задачи на определение расхода жидкости
Определить примерный объемный расход воды, истекающей из отверстия диаметром 10 мм, проделанном в вертикальной стенке широкого сосуда на высоте h = 1 м от верхнего, постоянно поддерживаемого, уровня воды за 10 секунд.
Ускорение свободного падения принять равным g = 10 м/с 2 .
Коэффициент расхода воды через отверстие – µs = 0,62.
По формуле Торричелли определим скорость истечения воды из отверстия:
v = √2gh = √2×10×1 ≈ 4,5 м/с.
Определим расход воды Q за время t = 10 секунд:
Q = µsvSt = 0,62×4,5×3,14×0,012/4 × 10 ≈ 0,0022 м 3 ≈ 2,2 литра.
На практике расход жидкости в трубопроводах измеряют расходомерами, например, расходомером Вентури. Расходомер Вентури (см рис. 2) представляет собой конструкцию из двух конических патрубков, соединенных цилиндрическим патрубком. В сечениях основной трубы и цилиндрического патрубка устанавливают трубки-пьезометры, которые фиксируют уровень жидкости, обусловленный полным давлением в потоке.
При прохождении жидкости через сужающийся конический патрубок часть потенциальной энергии потока преобразуется в кинетическую, и, наоборот, – при прохождении потока по расширяющемуся коническому патрубку, кинетическая энергия уменьшается, а потенциальная растет. Это сказывается на скорости движения жидкости по рассматриваемым участкам. Перепад высоты уровня жидкости в пьезометрах позволяет рассчитать среднюю скорость потока жидкости на рассматриваемых участках и вычислить объемный расход по внутреннему сечению трубы.
В расходомерах учитываются потери напора в самом приборе при помощи коэффициента расхода прибора φ .
Гидравлика задачи с решением
Гидравлика
Гидравлика — это наука, изучающая законы равновесия и движения жидкостей и газов, в том числе паров жидкости, то есть воды. Если строго следовать научно-техническим канонам, то гидравлика, в отличие от теоретической гидромеханики, управляет сложным и строгим математическим аппаратом («Механика жидкостей и газов»), прежде всего, является технической наукой, главной задачей которой является решение проблем на практике. По этой причине разработка практических методов расчета в гидравлике очень часто предполагает использование различных предположений и допущений, во многих случаях ограничиваясь одномерными потоками в стационарных режимах. Во многих случаях используются результаты экспериментальных данных, которые после соответствующей математической обработки используются в качестве математических уравнений для решения целого ряда аналогичных задач.
Основные физические свойства жидкостей и газов
Указания к решению задач:
Основными физическими характеристиками жидкости являются плотность, вязкость, сжимаемость, температурное расширение, испаряемость. Характеристики определяются с помощью следующих формул:
динамическая вязкость 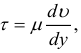
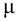
сжимаемость 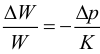
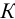
определяется соответствующим коэффициентом, равным относительному изменению объема, при изменении температуры на 1 °С;
испаряемость Жидкости испаряются при любой температуре при наличии свободного объема. Испарение происходит с поверхности, причем тех молекул, которые имеют повышенную в 5-10 раз энергию по сравнению со средней. С повышением внешнего давления температура кипения увеличивается, а с понижением (вакуум) — уменьшается. Зависимость давления насыщенного пара от температуры выражается уравнением Клаузиуса-Клапейрона
где 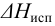
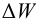
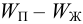
При испарении жидкости резко изменяется объем паровой фазы по сравнению с жидкой, поэтому объемом жидкости в уравнении можно пренебречь, тогда
С учетом уравнения Менделеева-Клапейрона
Интегрировав данное выражение получим формулу Клазиуса-Клапейрона
Возможно эта страница вам будет полезна:
Задача №1.2
Определить плотности воды и нефти при 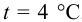
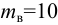
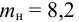
Решение:
плотность воды при заданных условиях:
а плотность нефти:
Гидростатика
Гидростатика — это раздел физики непрерывных сред, изучающий равновесие жидкостей, особенно в области гравитации.
Гидростатика — это теория поведения неподвижных жидкостей. Прежде всего, полезно сравнить гидростатику с теорией упругости, в которой изучается равновесие твердых тел.
Указания к решению задач:
Гидростатика — это раздел гидравлики, изучающий покоящиеся жидкости. Она изучает законы равновесия жидкости и распределение в ней давления. Основные величины, используемые в гидростатике -это давление 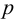
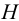
Гидростатическим давлением 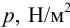
Гидростатическое давление жидкости складывается из давления на ее свободную поверхность 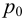
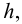
где 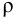
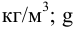
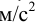
Гидростатическое давление называют абсолютным 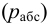
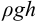
где 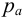
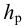
Вакуумметрическое давление, или вакуум, — недостаток давления до атмосферного, т.е. разность между атмосферным или барометрическим и абсолютным давлением:
Полная сила, действующая на плоскую стенку 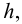
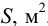
где 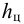
Полная сила, действующая на цилиндрическую поверхность:
где 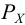
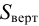
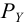
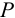
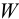
Направление полной силы давления 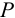
На любое тело, погруженное в жидкость, действует выталкивающая сила, равная весу жидкости, вытесненной телом (закон Архимеда):
где 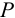
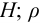
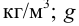
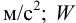
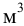
Возможно эта страница вам будет полезна:
Задача №2.1
Определить полное гидростатическое и манометрическое давление на дне сосуда, наполненного водой. Сосуд сверху открыт, давление на свободной поверхности атмосферное. Глубина воды в сосуде 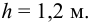
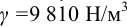
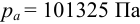
Решение:
1) Определим полное гидростатическое давление в точке:
2) Манометрическое давление на дне сосуда определяется как разность между полным гидростатическим и атмосферным давлениями:
Применение уравнения Бернулли
Основным объектом изучения гидродинамики является поток жидкости. Различают объемный расход 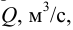
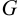
где 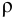
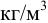
Скорость потока определяется как объемный расход вещества через единицу площади сечения потока, 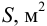
Отсюда следует, что скорости обратно пропорциональны площадям поперечного сечения потоков:
При установившемся движении через любое поперечное сечение потока в единицу времени проходит одно и то же количество жидкости (уравнение неразрывности потока):
Основным уравнением гидравлики, определяющим связь между давлением и скоростью в движущемся потоке идеальной жидкости, является уравнение Берну или, все члены которого имеют размерность длины и измеряются высотой столба жидкости:
где 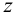
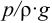
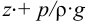
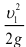
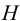
Физически уравнение Бернулли есть математическая запись закона сохранения и превращения энергии применительно к движущейся жидкости. Из уравнения следует, что если на участке потока уменьшается скорость (кинетическая энергия), то на этом участке должно возрастать давление (потенциальная энергия).
Если энергию жидкости отнести к единице ее объема, то члены уравнения Бернулли будут иметь размерность давления, а само уравнение примет вид, которым также часто пользуются:
Если же энергию жидкости отнести к единице массы, можно получить 3-ю формулу записи уравнения:
Для потока реальной (вязкой) жидкости уравнение Бернулли запишем в следующем виде:
где 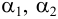
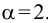
Указания к решению задач:
Часть задач раздела рассчитана на применение уравнения Бернулли для идеальной жидкости, без учета гидравлических потерь. Другая часть задач решается с помощью уравнений Бернулли для потока реальной жидкости.
При применении уравнения Бернулли важно правильно выбрать два сечения, для которых оно записывается.
В качестве сечений рекомендуется выбирать:
Уравнение Бернулли рекомендуется вначале записывать в общем виде, а затем произвести замену его членов заданными параметрами. Члены уравнения Бернулли записываются по потоку жидкости, геометрическая высота 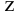
В случае подвода жидкости к резервуару, считается, что теряется вся кинетическая энергия жидкости. Коэффициент Кориолиса « учитывается в случае ламинарного режима.
Возможно эта страница вам будет полезна:
Задача №3.1
Определить расход в водопроводной трубе, если средняя скорость 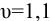
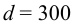
Решение:
Гидравлические сопротивления
Указания к решению задач:
Общие потери напора условно считают равными сумме потерь напора, вызываемых каждым сопротивлением:
где 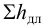
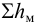
Местные потери определяются по формуле Вейсбаха:
где 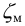
Числовое значение 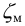
Иногда на него влияет число Рейнольдса. Которое для труб диаметром 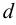
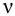
При значениях 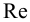
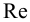
При турбулентном режиме, в случае внезапного расширения потери напора определяются формулой Борда:
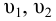
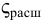
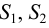
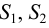
Для других местных сопротивлений коэффициенты находят в справочниках.
Для определения потерь давления на местных сопротивлениях выражение (4.2) приобретает вид:
Потери напора на трение по длине 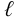
где 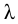
Потери давления на трение по длине находят по следующей формуле
При ламинарном течении
При турбулентном режиме, если
для переходных труб, по формуле Альштуля,
коэффициент 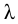
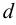

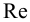
Для гладких труб, по формуле Блазиуса, если
Для гладких труб, по формуле Никурадзе, если
Для области шероховатых труб, по формуле Шифринсона, если
Местные потери в трубах при малых числах Рейнольдса зависят не только от геометрических характеристик сопротивления [1], но и от числа Рейнольдса и могут быть при ориентировочных расчетах найдены по формуле Альтшуля:
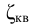
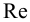
Возможно эта страница вам будет полезна:
Задача №4.1
Применяемые в водоснабжении и канализации трубы имеют минимальный диаметр 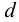
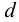
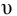
Решение:
Температура воды в системах водоснабжения и канализации изменяется в пределах от 0 °С до 30 °С, кинематические вязкости по таблицам [1] составляют
1) Определим минимальное число Рейнольдса:
2) Определим максимальное число Рейнольдса:
Задачи на гидравлический расчет трубопроводов
Трубопроводы — это система напорных труб, предназначенных для перемещения разнообразных жидкостей и газов [20].
В гидравлике при расчете трубопроводов их подразделяют на короткие и длинные. К первым относятся все трубопроводы, в которых местные потери напора превышают 5-10 % потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. Ко вторым относятся трубопроводы, в которых местные потери менее 5-10% потерь напора по длине. Их расчет ведется без учета местных потерь. Длинные трубопроводы можно разделить на простые и сложные.
Простыми трубопроводами называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений.
К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями, кольцевые и т.д.
Жидкость движется по трубопроводу благодаря тому, что ее энергия в начале трубопровода больше, чем в конце. Запас энергии должен быть создан работой насоса, давлением газа или за счет разности уровней жидкости.
Указания к решению задач:
Основными расчетными формулами для простого напорного трубопровода являются: уравнение Бернулли, уравнение постоянства расход, а также зависимости для определения потерь напора на трение по длине и в местных сопротивлениях [4, 21].
Если в трубопроводе необходимо обеспечить расход жидкости 
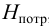
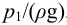
где 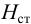
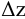
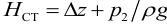
Потери напора выражают через расход 
где 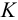
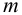
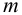
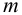
Для ламинарного течения при замене местных сопротивлений эквивалентными длинами сопротивление трубопровода равно
Для турбулентного режима течения жидкости в квадратичной области, используя формулу Вейсбаха-Дарси, и выражая в ней скорость через расход, получаем
Формулы (5.2), дополненная выражениями (5.3) и (5.4), является основной для расчета простых трубопроводов [4, 21].
Если трубопровод лежит в горизонтальной плоскости, а противодавление 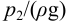
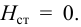
Выражение (5.5) называется гидравлической характеристикой трубопровода, которая показывает зависимость суммарной потери напора (или давления) в трубопроводе от расхода.
При ламинарном режиме течения гидравлическая характеристика представляет собой прямую линию, а при турбулентном в квадратичной области — параболу второй степени [20].
Задачи по расчету простого трубопровода можно разбить на три типа:
Тип 1. Известны: расход жидкости 
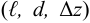
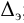
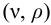
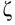
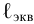
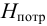
По известным значениям 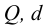
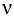
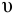
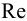
При ламинарном режиме искомый напор находится по формулам (5.2) и (5.3).
При турбулентном режиме задача решается с помощью формул (5.2) и (5.4). Определение зоны сопротивления производится с помощью формул Блазиуса или Альтшуля, в зависимости от шероховатости труб.
Тип 2. Известны: напор в начальном сечении (располагаемый напор 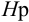

Расчет начинается с предположения о режиме течения жидкости. Так при течении маловязких жидкостей (воды, бензина, керосина и т.п.) целесообразно принимать режим течения турбулентным, при течении вязких жидкостей (масла, нефти и т.п.) — ламинарный.
При ламинарном режиме течения задача решается с помощью формул (5.2) и (5.3).
При турбулентном режиме в уравнениях (5.2) и (5.4) содержатся две неизвестные 
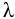
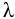
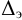
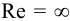
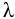
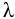
Вторым вариантом решения задачи является графоаналитический метод. Для этого необходимо построить гидравлическую характеристику трубопровода 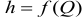
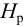

Гидравлическая характеристика трубопровода строится по данным расчета потерь напора при различных величинах расхода, т.е. решения задачи 1-го типа.
По известной величине напора 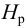
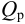
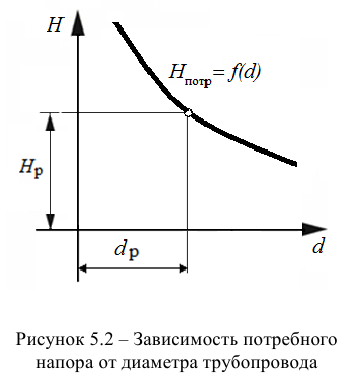
Тип 3. Известны следующие данные: расход жидкости 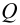
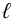
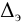
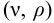
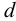
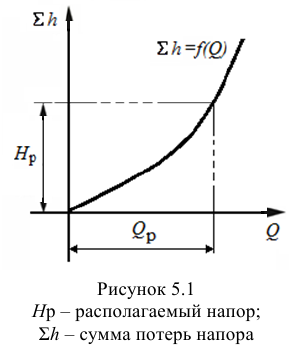
Задачу рекомендуется решать графоаналитическим способом (рис. 5.2), путем построения кривой взаимосвязи между потребным напором 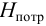
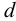
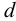
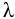
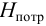
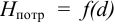
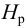
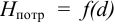
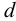
В конечном итоге принимается ближайший стандартный диаметр.
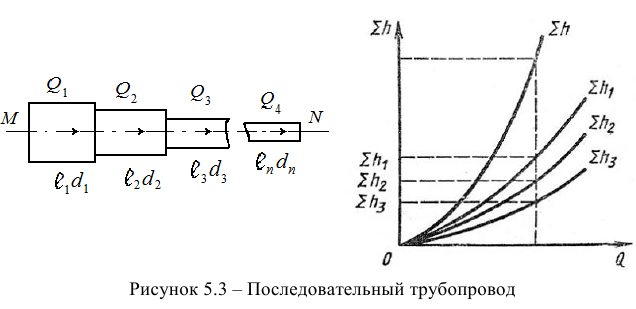
Расчет последовательно соединенного трубопровода
Последовательным называется такое соединение трубопроводов, при котором жидкость протекает по простым трубопроводам разного диаметра, последовательно соединенных в одну нитку (рис. 5.3). По всем участкам трубопровода протекает одинаковый расход жидкости 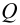
Потери напора в таком трубопроводе равны сумме всех местных потерь и потерь по длине:
где 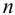
Если известны характеристики каждого участка трубопровода, то по ним можно построить характеристику всего последовательного соединения 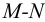
Возможно эта страница вам будет полезна:
Задача на гидравлический расчет сложного напорного трубопровода
Сложный трубопровод обычно состоит из простых трубопроводов, которые соединены параллельно, либо имеет разветвления. Параллельным называется соединение трубопроводов, при котором жидкость, подходя к точке разветвления, течет по ответвлениям и далее снова сливается в один трубопровод, т.е. параллельно соединенные трубопроводы имеют общую точку разветвления и общий узел соединения (рис. 5.4).
Расход жидкости в основной магистрали равен сумме расходов в параллельных трубопроводах, а потери напора равны между собой:
где 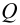
Потери напора можно выразить через соответствующие расходы:
где 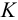
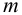
Для построения характеристики параллельного соединения нескольких трубопроводов следует сложить расходы характеристик этих трубопроводов при одинаковых ординатах (рис. 5.4, б).
Разветвленным соединением называется совокупность нескольких простых трубопроводов, имеющих одно общее сечение — место разветвления (или смыкания) труб (рис. 5.5).
Алгоритм расчета разветвленного трубопровода включает следующие действия:
1) разбить сложный трубопровод на ряд простых;
2) рассчитать и построить кривые потребных напоров для каждого из простых трубопроводов;
3) провести графическое сложение параллельных участков;
4) провести графическое сложение последовательных участков.
ВНИМАНИЕ: при расчете разветвленного трубопровода необходимо идти от конечных точек к его начальной точке, т.е. против течения.
Приведем расчет разветвленного трубопровода (рис. 5.5). Трубопровод 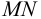
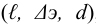
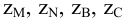
Величины пьезометрических напоров в точках составят:
Для решения задачи составим систему уравнений, связывающих искомые расходы и потери напора на отдельных участках [21]:
Представим три верхних уравнения системы (5.9), в виде системы уравнений пьезометрических напоров для трубопроводов и :
По уравнениям (5.10) строятся графические зависимости пьезометрического напора в узле от расхода для всех трубопроводов (рис. 5.5, б).
Зависимость суммарного расхода (уравнение 4 в системе (5.9)) в трубопроводах и от напора (кривая 2+5) строится сложением абсцисс кривых 2 и 3.
Значение напора при котором суммарный расход в трубопроводах 2 и 3 равен расходу в трубопроводе 1, и является искомым. Поэтому координаты точки пересечения кривых (2+3) и 1 определяют решение задачи: ее абсцисса равна полному расходу , а ордината напору . Абсциссы точек и равны расходам и [21].
Теория из учебников и готовые задачи на продажу тут.
Задача на расчет трубопровода с насосной подачей жидкости
Основными понятиями для расчета таких трубопроводов являют-
- объемная подача насоса (подача ) — это объем жидкости, подаваемый насосом в единицу времени, т.е. объемный расход на выходе из насоса, ;
- напором насоса называется механическая энергия, сообщаемая насосом единице веса перемещаемой жидкости, или разность удельных энергий жидкости на выходе и входе насоса, м;
- мощность насоса (потребляемая) — это энергия, подводимая к насосу от двигателя за единицу времени, Вт;
- мощность насоса (полезная) — это энергия, сообщаемая насосом за единицу времени протекающей через него жидкости весом полезную мощность можно выразить:
— давление, развиваемое насосом.
Мощность насоса превышает полезную мощность на величину потерь насоса, которые оцениваются КПД насоса :
- характеристика насоса — графическое изображение зависимостей напора насоса (или давления ), мощности и КПД от подачи насоса при постоянной частоте вращения;
- разомкнутый трубопровод с насосной подачей — это трубопровод, по которому жидкость перекачивается из одного места в другое;
- замкнутый (кольцевой) трубопровод с насосной подачей — это трубопровод, в котором циркулирует одно и тоже количество жидкости.
Рассмотрим решение задачи по расчету потребного напора разомкнутого трубопровода и построению на одном графике рабочей характеристики насоса и характеристики насосной установки.
Точка пересечения этих характеристик называется рабочей точкой.
1) Запишем уравнение Бернулли для потока жидкости во всасывающем трубопроводе для сечений 1-1 и 2-2 относительно плоскости сравнения 0-0, совпадающей с горизонтальной осыо насоса (рис. 5.6):
где — потери во всасывающем трубопроводе; — скорости жидкости в сечениях 1-1 и 2-2.
Удельная энергия перед входом в насос составит:
2) Запишем уравнение Бернулли для потока жидкости в нагнетательном трубопроводе для сечений 3-3 и 4-4 относительно плоскости сравнения 0-0, совпадающей с горизонтальной осыо насоса:
где — потери в нагнетательном трубопроводе; — скорости жидкости в сечениях 3-3 и 4-4; левая часть уравнения является удельной энергией потока жидкости на выходе из насоса.
Так как скоростные напоры жидкости в баках и очень малы, следовательно ими можно пренебречь, в результате можно выразить напор насоса как разность удельных энергий потока рабочей жидкости на выходе и входе в насос:
где — суммарные потери в трубопроводе; — полная высота подъема жидкости, называется геометрическим напором.
Обозначив через статический напор слагаемые уравнения
получим следующее выражение:
Таким образом, при установившемся режиме работы насоса его напор равен потребному напору системы р:
На полученном равенстве основан метод расчета трубопроводов, питаемых насосом, который заключается в построении на одном графике рабочей характеристики насоса и характеристики насосной установки
Точка пересечения этих характеристик называется рабочей точкой, в которой справедливо равенство (5.19).
В случае замкнутого трубопровода (рис. 5.8) геометрическая высота подъема жидкости равна нулю (геометрический напор = 0).
Следовательно, при значениях получаем потребный напор:
то есть, между потребным напором и напором, развиваемым насосом выполняется равенство (5.19).
Эти страницы вам могут пригодиться:
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
[spoiler title=”источники:”]
http://k-a-t.ru/gidravlika/7_Bernulli/
http://lfirmal.com/reshenie-zadach-po-gidravlike/
[/spoiler]