Как найти полость шаров

Использование теоремы Гаусса для расчета полей

(Примеры решения задач)

Поток электрического поля

Пример 2.1.

Два точечных
заряда q
и –q
расположены на расстоянии 2l
друг от друга. Найдите поток вектора
напряженности через круг радиуса R,
плоскость которого перпендикулярна
отрезку прямой, соединяющей заряды, и
проходит через его середину.

Решение.

Рассмотрим
элементарный поток результирующего
электрического полячерез бесконечно малую кольцевую зону
круга радиусаи ширины(см.рис).
В записи потока учтено, что векторперпендикулярен поверхности круга.
Выразим напряженность электрического
поля через,
используя подобие треугольников
показанных на рисунке:,

.

Вычисление потока сводится к взятию
интеграла:

.

Электрическое поле заряженной сферы

Пример 2.2.

По поверхности сферы радиуса
однородно распределен заряд.
Определите напряженность электрического
поля в произвольной точке пространства
вне сферы и внутри нее. Полученный
результат представьте на графике,
гдепроекция вектора напряженности на осьr, проведенную из
центра сферы.

Решение.

Электрическое поле, порождаемое
сферически-симметричным распределением
заряда сферы, в любой точке пространства
направлено вдоль луча от центра сферы
и в равноудаленных точках имеет одинаковую
величину, т.е.
.
При таком свойстве симметрии поля в
качестве замкнутой гауссовой поверхности
возьмем концентрическую сферу радиуса.
Поток сквозь выбранную поверхность
равен.
Согласно теореме Гаусса, он определяется
зарядом внутри гауссовой поверхности.
Призаряд внутри поверхности равен заряду
сферы,
а приравен нулю. Поэтому:

Знак заряда
определяет знак проекции,
а следовательно и направление самого
вектора.
Он направлен от центра заряженной сферы
()
или к центру ().
Внутри однородно заряженной сферической
поверхности электрическое поле
отсутствует. График зависимости проекции
вектора напряженностина ось,
проведенную из центра сферы, показан
на Рис. 1 в предположении.

Рис 1

Электрическое поле заряженного шара

Пример 2.3.

По объему шара
однородно
распределен заряд.
Пренебрегая влиянием вещества шара,
определите напряженность электрического
поля в произвольной точке пространства
вне шара и внутри него. Полученный
результат представьте на графике,
гдепроекция вектора напряженности на осьr, проведенную из
центра шара.

Решение.

Поле такой системы зарядов
центрально-симметричное, поэтому в
качестве гауссовой замкнутой поверхности
следует взять концентрическую сферу
радиуса
.

1) Найдем напряженность электрического
поля внутри шара
.
Векторы напряженностинаправлены по радиусам выбранной сферы,
а модули векторовзависят только от расстояниядо центра сферы, то есть, одинаковы по
поверхности сферы. Поэтому поток поля
векторачерез выбранную сферуможно записать(Рис.2а).

Заряд, охватываемый сферой
,
равен,
где–
объемная плотность заряда. Согласно
теореме Гаусса.
В результате напряженность поля внутри
однородно заряженного шара равна:

,

т.е. поле
внутри
шара возрастает по линейному закону от
нуля в центре до значенияна
его поверхности.

2) Найдем напряженность электрического
поля вне шара
.
Свойство симметрии поля остается
неизменным. Поэтому гауссову поверхность
представим концентрической сферойрадиуса(Рис.2а). Согласно теореме Гаусса имеем:,
гдезаряд шара. Для величины напряженности
поля получим:

.

Поле
вне однородно заряженного шара убывает
обратно пропорционально.

Объединяя полученные зависимости,
запишем:

.

График зависимости проекции вектора
напряженности
на ось,
проведенную из центра шара, представлен
на Рис. 2б.

Рис.2а	Рис.2б

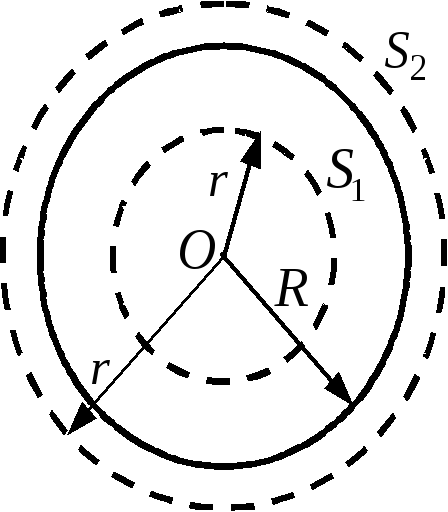
Пример 2.4.

Шар заряжен однородно с объемной
плотностью
.
В шаре сделана сферическая полость,
положение центра которой характеризуется
радиусом-вектором(этот вектор проведен из центра шара в
центр полости). Найти полев полости.

Решение.

Представим, что имеем два шара с центрами
в точках
и,
заряженные однородно с объемной
плотностьюпервый ивторой. Выберем произвольную точку,
которая принадлежит обоим шарам.
Воспользовавшись решениемпримера
2.3., для первого шара в точкеполе равно:

().

Для второго шара в точке
поле равно:

.

Рис.3

Чтобы определить напряженность поля в
полости наложим распределение зарядов
двух шаров, как показано на Рис.3. Тогда
по принципу суперпозиции найдем поле
в полости:

.

Заметим, что поле внутри полости однородно
заряженного шара оказывается однородным,
а его величина и направление определяется
вектором смещения
.

Пример 2.5.

Шар радиуса
имеет положительный заряд, объемная
плотность которого зависит от расстоянияrдо его центра как,
где– положительная постоянная. Пренебрегая
влиянием вещества шара, найдите модуль
вектора напряженности электрического
поля внутри и вне шара как функциюr.

Решение.

Поле этой системы зарядов
центрально-симметричное, поэтому в
качестве замкнутой гауссовой поверхности
выберем сферу, концентрическую с шаром.

1) Для нахождения поля вне шара радиус
сферы
,
согласно теореме Гаусса:

,

где
полный заряд шара. Чтобы найти,
мысленно представим шар в виде набора
бесконечно тонких шаровых слоев радиусаширины(Рис.4а). Объем шарового слоя,
тогда,
а.Интегрируя,
получим:

Подставив полученное выражение для
в правую часть соотношения для потока,
получим напряженность поля вне шара:

.

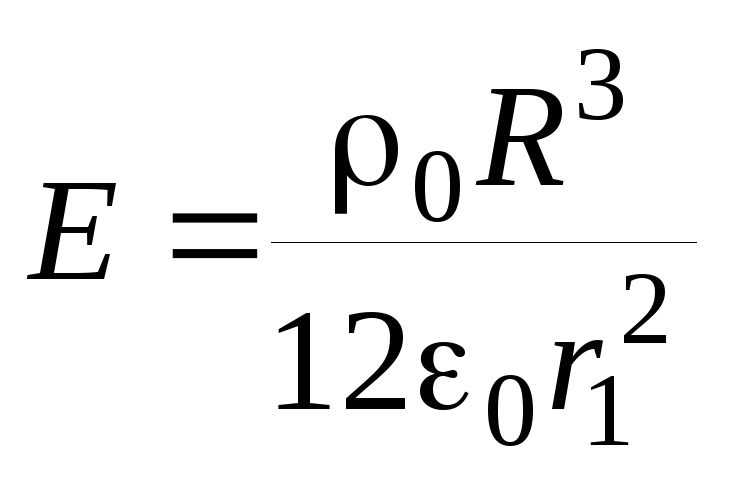
2) Найдем напряженность электрического
поля внутри шара. В качестве замкнутой
гауссовой поверхности снова выберем
сферу, концентрическую с шаром, радиус
которой(рис.4б).

Согласно теореме Гаусса

,

где
заряд внутри выбранной сферы. Величинунайдем также как и в пункте 1), подставив
соответствующие пределы интегрирования:

.

Подставив величину заряда
в соотношение для потока, найдем:

.

График зависимости проекции вектора
на ось,
проведенную из центра шара, показан на
Рис.4в, из которого видно, что напряженность
достигает максимума на расстоянииот центра шара.

Рис.4а	Рис.4б	Рис.4в

Соседние файлы в папке Примеры решений

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

1. Задача №1. Есть ли в теле полость?

Име­ют­ся ли в сталь­ном шаре мас­сой 250 г по­ло­сти, или этот шар сплош­ной, если его объем со­став­ля­ет 0,0005 м³?  

Нач­нем с за­пи­си крат­ко­го усло­вия за­да­чи. В нем го­во­рит­ся, что шар сталь­ной, по­это­му в спра­воч­ных таб­ли­цах мы на­хо­дим плот­ность стали (она равна 7800 кг/м³) и за­пи­сы­ва­ем ее в крат­кое усло­вие на­ря­ду с дан­ны­ми из тек­ста за­да­чи.

Чтобы узнать, име­ют­ся ли в шаре по­ло­сти (пу­сто­ты), необ­хо­ди­мо вы­чис­лить плот­ность шара, раз­де­лив его массу на объем. Мы по­лу­чим так на­зы­ва­е­мую сред­нюю плот­ность, то есть от­но­ше­ние массы шара к его объ­е­му, неза­ви­си­мо от того, за­пол­нен ли шар ве­ще­ством це­ли­ком, или в нем име­ет­ся пу­стое про­стран­ство.

Если плот­ность шара сов­па­да­ет с плот­но­стью стали, зна­чит, шар це­ли­ком со­сто­ит из этого ма­те­ри­а­ла. Если же в шаре име­ют­ся по­ло­сти, то его плот­ность будет мень­ше плот­но­сти стали. Итак, для от­ве­та на во­прос за­да­чи необ­хо­ди­мо срав­нить плот­но­сти шара и стали, что мы и за­пи­сы­ва­ем внизу крат­ко­го усло­вия.

Пре­жде чем пе­ре­хо­дить к ре­ше­нию, необ­хо­ди­мо про­ве­рить, все ли ве­ли­чи­ны за­да­ны в си­сте­ме СИ, и при необ­хо­ди­мо­сти вы­пол­нить пе­ре­вод ве­ли­чин в эту си­сте­му. Так, в нашей за­да­че необ­хо­ди­мо массу шара пе­ре­ве­сти в ки­ло­грам­мы. Масса 250 г со­став­ля­ет 0,25 кг.

Рис. 1. Крат­кое усло­вие за­да­чи № 1.

Далее за­пи­сы­ва­ем рас­чет­ную фор­му­лу и про­во­дим про­вер­ку раз­мер­но­сти ре­зуль­та­та.

 

Под­став­ля­ем дан­ные из усло­вия в рас­чет­ную фор­му­лу

Срав­нив по­лу­чен­ную плот­ность с таб­лич­ным зна­че­ни­ем плот­но­сти стали (7800 кг/м³), по­лу­ча­ем, что в шаре име­ют­ся по­ло­сти. За­фик­си­ру­ем по­лу­чен­ный ре­зуль­тат в от­ве­те. За­да­ча ре­ше­на.

Рис. 2. Пол­ное ре­ше­ние за­да­чи № 1

2. Задача №2. Вычисление массы тела

Опре­де­лить массу свин­цо­во­го тела объ­е­мом 0,35 м³.

Перед за­пи­сью крат­ко­го усло­вия из спра­воч­ных таб­лиц опре­де­лим плот­ность свин­ца. Она со­став­ля­ет 11 300 кг/м³. Так как все ве­ли­чи­ны в усло­вии за­да­ны в си­сте­ме СИ, можно сразу пе­рей­ти к ре­ше­нию за­да­чи.

По­сколь­ку в усло­вии за­да­чи фи­гу­ри­ру­ет плот­ность, то вна­ча­ле за­пи­сы­ва­ем зна­ко­мую фор­му­лу для плот­но­сти, а затем по пра­ви­лам ал­геб­ра­и­че­ских пре­об­ра­зо­ва­ний вы­ра­жа­ем из этой фор­му­лы массу тела.

 

Затем про­во­дим про­вер­ку раз­мер­но­сти.

Об­ра­ти­те вни­ма­ние, что ку­би­че­ские метры в чис­ли­те­ле и в зна­ме­на­те­ле со­кра­ща­ют­ся, и оста­ют­ся толь­ко еди­ни­цы из­ме­ре­ния массы, ки­ло­грам­мы.

Под­ста­вим чис­ло­вые дан­ные

Оста­ет­ся за­пи­сать ответ. Пол­ное ре­ше­ние за­да­чи № 2 вы­гля­дит так.

Рис. 3. Пол­ное ре­ше­ние за­да­чи № 2

3. Заключение

Мы рас­смот­ре­ли толь­ко неболь­шую часть задач на рас­чет па­ра­мет­ров тела по плот­но­сти ма­те­ри­а­ла, из ко­то­ро­го оно из­го­тов­ле­но. Для того, чтобы на­учить­ся ре­шать более слож­ные за­да­чи, необ­хо­ди­мо ре­гу­ляр­но са­мо­сто­я­тель­но вы­пол­нять до­маш­ние за­да­ния.

2018-05-14   

Внутри шара, заряженного равномерно с объемной плотностью $rho$, имеется сферическая полость. Центр полости смещен относительно центра шара на величину $a$. Найти напряженность $E$ поля внутри полости, полагая диэлектрическую проницаемость равной единице.

Решение:

Используя теорему Гаусса, легко показать, что напряженность электрического поля в равномерно заряженная сфера равна $vec{E} = left ( frac{ rho}{3 epsilon_{0} } right ) vec{r}$

Полость в нашей задаче может рассматриваться как суперпозиция двух шаров, одна с плотностью заряда $rho$, а другая с $- rho$.

Пусть P – точка внутри полости, такая, что ее вектор положения относительно центра полости равно $vec{r}_{-}$ и по отношению к центру шара $vec{r}_{+}$. Тогда из принципа суперпозиции, поля внутри полости, в произвольной точке P,

$vec{E} = vec{E}_{+} + vec{E}_{-} = frac{ rho}{3 epsilon_{0} } ( vec{r}_{+} – vec{r}_{0} ) = frac{ rho}{3 epsilon_{0} } vec{a} $

Примечание. Полученное выражение для $vec{E}$ показывает, что оно действительно не зависит от отношения между радиусами сферы и расстоянием между их центрами.