Амплитудно-частотная
характеристика последовательного
контура характеризуется тем, что на
резонансной частоте она имеет максимальное
значение. На частотах, отстоящих
значительно от резонансной частоты,
значения амплитудно-частотной
характеристики близки к нулю. Если к
контуру прикладывать сигналы одинаковой
амплитуды, но с разными частотами, то
сигналы с частотой, равной резонансной
частоте, будут создавать большой ток в
контуре и большие напряжения на реактивных
элементах. В этом случае говорят, что
контур пропускает этот сигнал. Если
частота сигнала значительно отличается
от 0,
то в контуре практически отсутствуют
электрические колебания. В этом случае
говорят, что контур такой сигнал
подавляет. Для оценки этих свойств
контура вводится понятие его полосы
пропускания.
Полосой
пропускания
называется интервал частот, включающий
резонансную частоту контура, на границах
которого значение тока контура меньше
значения тока на резонансной частоте
в заданное число раз.
Как
правило, за исключением особой аппаратуры,
требуется, чтобы на границе полосы
пропускания ток контура был меньше тока
на резонансной частоте в раз.
раз.
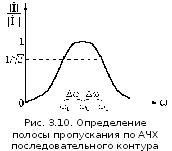
На
рис.3.10 показано определение полосы
пропускания с помощью АЧХ. В соответствии
с заданным уровнем подавления на границе
полосы пропускания должно выполняться
условие:
 . (3.31)
. (3.31)
Значит
на границах полосы пропускания АЧХ
должна иметь значение:
 . (3.32)
. (3.32)
Исходя из этого, на рис.3.10 найдена полоса
пропускания, границы которой обозначаются
частотами 1
и 2.
Полоса пропускания обозначается как
и измеряется в единицах измерения
частоты. Тогда полоса пропускания будет
равна:
 . (3.33)
. (3.33)
В
зоне полосы пропускания АЧХ практически
симметрична относительно резонансной
частоты. Поэтому интервалы между
резонансной частотой и границами полосы
пропускания обозначим как ∆.
 ,
,  .
.
С
учетом этого выражение для полосы
пропускания (3.33) принимает вид:
 . (3.34)
. (3.34)
Рассмотренный
способ определения полосы пропускания
возможен только при наличии графика
АЧХ. Это не всегда удобно.
Найдем
аналитическое выражение для определения
полосы пропускания. Для этого воспользуемся
формулой (3.29) определения АЧХ.
 . (3.35)
. (3.35)
Найдем,
какой имеет вид (3.35) для границ полосы
пропускания. Для этого предварительно
найдем выражение в круглых скобках
формулы (3.35) для 1
и 2.
Для
=1
получаем:
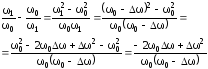
В
контурах радиоаппаратуры полоса
пропускания узкая и составляет единицы
килогерц, а резонансная частота высокая
и составляет сотни килогерц. Это позволяет
пренебречь величиной ∆
в числителе и знаменателе. Тогда
рассматриваемое соотношение принимает
вид:

Для
=2,
с учетом сказанного получаем:

Из
приведенного анализа видно, что
рассматриваемая часть формулы (3.35) на
граничных частотах 1
и 2
имеет
одинаковые выражения, отличающиеся
только знаком. Но так как рассмотренное
соотношение в формуле (3.35) находится в
квадрате, то эта формула для обеих границ
полосы пропускания имеет один и тот же
вид:

(3.36)
При
решении задачи о полосе пропускания в
общем виде вводится понятие коэффициента
неравномерности .
Он показывает, какую часть от резонансного
тока принимает ток контура на границах
полосы пропускания и имеет разные
значения в зависимости от вида аппаратуры
(0.707; 0.1; 0.01 и т. д.) Тогда, в соответствии
с понятием полосы пропускания, приравняем
(3.36) к коэффициенту неравномерности:
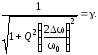
Решаем
это уравнение относительно 2∆
и с учетом (3.34) находим:
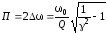 .
.
При
коэффициенте неравномерности

полоса пропускания одиночного
последовательного контура определяется
формулой:
 (3.37)
(3.37)
На
границах полосы пропускания последовательный
одиночный колебательный контур обладает
рядом свойств, которые полезно знать
при расчете схем с его применением.
1.
Мощность, потребляемая контуром на
границах полосы пропускания, в 2 раза
меньше мощности, потребляемой контуром
на резонансной частоте.
Действительно,
на резонансной частоте мощность,
потребляемая контуром, выражается через
действующее значение тока контура
известным соотношением:

Обозначим
действующее значение тока на границе
полосы пропускания через I. Тогда, с
учетом (3.31), мощность, потребляемая
контуром на каждой из границ полосы
пропускания, равна:

2.
На границах полосы пропускания
сопротивление резистора контура R равно
модулю суммы его реактивных элементов:

На
резонансной частоте ток в контуре равен:

На
границах полосы пропускания ток контура
в общем виде (для =1
и =2)
определяется формулой:

С
учетом (3.31) приравняем эти токи:

После
несложных преобразований находим:
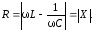 (3.38)
(3.38)
3.
На границах полосы пропускания фаза
тока контура относительно входного
сигнала равна 45.
Комплексное
значение тока контура равно:
 .
.
Фаза
тока равна:
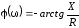 . (3.39)
. (3.39)
Исходя
из (3.38), модуль аргумента (3.39) на границах
полосы пропускания равен 1. Исходя из
свойств ФЧХ, на частотах <0
контур имеет емкостные свойства (Х<0)
и, следовательно:
 .
.
На
частотах >0
контур имеет индуктивные свойства (Х >
0), следовательно:

4.
На границах полосы пропускания обобщенная
расстройка
 .
.
Из
(3.36) видно, что обобщенная расстройка,
с учетом ранее выполненного анализа
для 1
и
2
имеет вид:
 ,
,
где
“плюс” имеет место для 2,
а “минус” – для 1.
Тогда,
учитывая (3.34) и (3.37), получаем:
 .
.
5.
На границе полосы пропускания модуль
полного сопротивления контура равен:
 .
.
Это
легко проверить, учитывая второе из
рассмотренных свойств (3.38). Из выражения
модуля полного сопротивления контура
находим:
 .
.
-
Параллельный
контур
без
диссипаций
в
реактивных
ветвях
–
полное
сопротивление,
резонанс
в
контуре,
напряжение
на
контуре
и
токи
в
ветвях,
векторная
диаграмма.
Параллельные
колебательные контура
Параллельные
одиночные колебательные контура
характеризуются тем, что основные
элементы их – конденсатор и индуктивность
соединены между собой параллельно.
Резисторы могут быть включены как
параллельно с реактивными элементами,
так и последовательно. В первом случае
диссипация энергии в параллельных
ветвях, содержащих реактивные элементы,
отсутствует. Во втором случае в этих
ветвях имеют место диссипативные
процессы. Рассмотрим каждый из названных
видов параллельных контуров.
3.3.1.
Параллельный колебательный контур без
диссипации в реактивных ветвях
Общие
соотношения.
В параллельном колебательном контуре
без диссипации в реактивных ветвях
резистор включен параллельно с
конденсатором и индуктивностью, которые
здесь считаются идеальными (рис.3.18). Их
диссипации могут быть учтены в резисторе
по параллельной схеме замещения
(рис.1.4).
Сопротивление
контура.
Для рассмотрения свойств контура
определим его полное сопротивление
 K
K
(рис.3.18,в). Представим контур в виде
параллельно соединенных реактивных и
резистивного сопротивлений (рис.3.18,б).

Воспользуемся
проводимостями этих элементов:
 ;
;  ;
;  ;
; 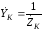 .
.
Как
известно, эквивалентная проводимость
параллельно соединенных элементов
равна сумме проводимостей этих элементов.
Тогда эквивалентная проводимость
контура имеет вид:
 .
.
Отсюда
находим величину эквивалентного
сопротивления контура, выделяя в нем
вещественную и мнимую составляющие:
 (3.50)
(3.50)
Представим
сопротивление контура в показательной
форме:
 , (3.51)
, (3.51)
где  ;
;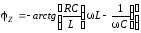 .
.
Напряжение
на контуре.
В отличие от последовательного контура,
в параллельном контуре входным параметром
является ток контура iК(t),
а выходным – напряжение на контуре uК(t).
Это связано с особенностью функционирования
параллельных контуров в радиотехнических
устройствах, таких как резонансные
усилители, резонансные фильтры и др. В
связи с этим задаем ток с определенной
амплитудой и нулевой фазой, который в
гармонической форме записи и в комплексной
форме имеет виды:
 ;
;  .
.
Напряжение
на контуре определяется в соответствии
с законом Ома:
 , (3.52)
, (3.52)
где 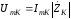 ,
,  .
.
Токи
в контуре.
Определим токи во всех ветвях контура.
Напряжение на контуре, а, значит,
напряжение, приложенное к каждой из
ветвей, имеет вид:
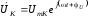 . (3.53)
. (3.53)
Токи
в ветвях определяются по закону Ома:
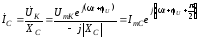 ,где
,где .
.
 , где
, где
(3.54)
 ,где
,где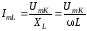
Резонанс
в контуре.
Условие резонанса и резонансная частота.
Как отмечалось, признаком резонанса
являются максимальные значения тока и
напряжения в схеме при определенной
частоте сигнала. При этом в полном
сопротивлении цепи мнимая составляющая
равна нулю. Это мы видели в последовательном
одиночном колебательном контуре.
Воспользуемся этим условием. Тогда из
выражения (3.50) видно, что условием
резонанса в контуре является выполнение
следующего равенства:
 . (3.55)
. (3.55)
Это
значит, что при резонансе сопротивления
конденсатора и катушки индуктивности
равны:
 .
.
Решая
(3.55) относительно частоты, находим
выражение для резонансной частоты
контура:
 . (3.56)
. (3.56)
Определим
сопротивление контура, напряжение на
контуре и токи в ветвях на резонансной
частоте.
Сопротивление
контура на резонансной частоте можно
определить из (3.51). С учётом условия
резонанса (3.55) видно, что на резонансной
частоте модуль и фаза сопротивления
контура принимают значения:
 ,
, 
 .
.
Напряжение
на контуре при резонансе определяется
из (3.53) с учётом равенства нулю фазы
сопротивления контура на резонансной
частоте
где
 ,
,
(3.57)
 .
.
Токи
в ветвях контура при резонансе определяются
из (3.54) с учётом (3.55) и (3.57):
 ,
,
где  ;
;
 ,
,
где
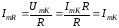 ;
;
(3.58)
 ,
,
где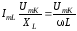 .
.
В
силу равенства
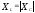
видно, что токи в ветвях с индуктивностью
и конденсатором равны по величине, а по
фазе отличаются друг от друга на 180.
Это хорошо видно на векторной диаграмме
(рис.3.19). Совершенно очевидно,
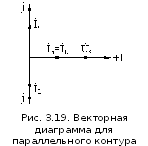 что
что
в соответствии с первым законом Кирхгофа
контурный ток равен сумме токов ветвей
контура:
 .
.
Однако,
как видно из векторной диаграммы, токи
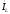
и

при суммировании уничтожают друг друга
и контурный ток определяется током,
протекающим через резистор:
 . (3.59)
. (3.59)
В
силу рассмотренных свойств параллельного
контура, резонанс в параллельном контуре
еще называют резонансом токов.
Мощности
в контуре.
Мгновенная мощность контура определяется
как произведение мгновенного тока
контура на мгновенное напряжение:

На
резонансной частоте  ,
,
тогда
 .
.
Средняя
мощность, потребляемая контуром, равна:
 .
.
С
учетом (3.58) выражение для средней мощности
контура принимает вид:
 .
.
В
полученном выражении мгновенной мощности
контура на резонансной частоте отсутствует
реактивная составляющая мощности.
Однако под действием контурного
напряжения через конденсатор и
индуктивность протекают токи. Определим
мгновенные мощности на этих элементах
так, как это делали при анализе идеальных
емкостного и индуктивного двухполюсников.
Для
емкостной ветви и индуктивной ветви
получим:
 ,
,
 . (3.60)
. (3.60)
При
резонансе
 .
.
Из (3.60) следует, что мгновенные мощности
на конденсаторе и индуктивности равны
по величине и противоположны по фазе.
Добротность
контура.
Добротность контура, как и прежде, найдем
из отношения амплитуды реактивной
мощности контура к средней мощности.
Для этого воспользуемся амплитудными
значениями мощностей на конденсаторе
и индуктивности (3.60). После очевидных
преобразований имеем:
 . (3.61)
. (3.61)
Из
(3.61) видно, что добротность контура без
диссипации в параллельных ветвях
(рис.3.18) тем выше, чем больше величина
R, и тем меньше затухают колебания в
контуре.
С
учетом полученного выражения для
добротности полное сопротивление
контура (3.50) примет вид:
 (3.62)
(3.62)
Последнее
выражение для сопротивления контура
позволяет рассмотреть зависимость от
частоты его модуля и фазы:
 ,
,
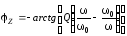 . (3.63)
. (3.63)
На
рис.3.20 представлены эти зависимости.
Модуль сопротивления контура имеет
наибольшее значение на резонансной
частоте. Если R имеет конечное значение
(присутствует в контуре), то ZК0=R
(график 1). Если R стремится к бесконечности
(резистор отсутствует), то ZК0
также стремится к бесконечности (график
2).

Фазовая
характеристика сопротивления контура
позволяет установить его свойства на
различных частотах. Если воспользоваться
треугольником сопротивления, то видно,
что на низких частотах (слева от
резонансной частоты) контур должен
иметь свойства реального индуктивного
двухполюсника, а на высоких частотах
(справа от резонансной частоты) контур
должен иметь свойства реального
емкостного двухполюсника.
Сравним
амплитуды токов IL
и IC
с
амплитудой тока IR.
Используя соотношения (3.58), находим:
 ;
; 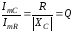 .
.
Амплитудно-частотной
характеристикой (АЧХ)
параллельного контура называется
зависимость от частоты модуля напряжения
на контуре.
Как
и для последовательного контура, удобно
АЧХ для параллельного контура рассматривать
в приведенном виде. Для этого необходимо
найти модуль отношения напряжения на
контуре в комплексной форме при
произвольной частоте к напряжению на
контуре при резонансной частоте.
Напряжение
на контуре при произвольной частот и
на резонансной частоте находятся по
закону Ома:
 ;
;  .
.
Для
удобства рассмотрения АЧХ здесь
напряжение на контуре и сопротивление
контура на резонансной частоте обозначены,
соответственно как
 и
и .
.
Берем
отношение этих напряжений и, с учетом
(3.58) и что ,
,
получаем:
 . (3.64)
. (3.64)
Модуль
полученного выражения (3.60) является
амплитудно-частотной характеристикой
параллельного контура.

 . (3.65)
. (3.65)
На
рис.3.21 представлены графики АЧХ
параллельного контура для двух значений
добротности. Увеличение добротности
делает график АЧХ более крутым.
 Фазо-частотной
Фазо-частотной
характеристикой
параллельного контура называется
зависимость от частоты фазы напряжения
на контуре.
Как
видно из (3.52), фаза напряжения на контуре
равна фазе комплексного сопротивления
контура. Учитывая (3.63), фазо-частотная
характеристика параллельного контура
принимает вид:
 . (3.66)
. (3.66)
 На
На
рис.3.22 представлен график ФЧХ параллельного
контура. Так как фаза контурного тока
равна нулю, то ФЧХ контура показывает,
в каком фазовом соотношении (опережает,
совпадает, отстает) находится напряжение
по отношению к току. Эта информация
позволяет судить о свойствах контура.
Так, на резонансной частоте фаза
контурного напряжения равна нулю. Значит
на резонансной частоте напряжение
контура и ток совпадают по фазе. Исходя
из теории двухполюсников, этим свойством
обладает резистивный двухполюсник.
Следовательно, на резонансной частоте
контур может быть заменен резистором.
Об этом свойстве контура уже говорилось.
На
низких частотах (слева от резонансной
частоты) фаза контурного напряжения
положительная. Значит, в этом интервале
частот напряжение опережает ток контура.
Из теории двухполюсников известно, что
этим свойством обладает реальный
индуктивный двухполюсник. Следовательно,
на низких частотах параллельный контур
может быть заменен последовательно
соединенными резистором и индуктивностью.
На высоких частотах (справа от резонансной
частоты) фаза контурного напряжения
отрицательная. Значит, в этом интервале
частот контурное напряжение отстает
от контурного тока. Следовательно, на
этом интервале частот контур обладает
свойствами реального емкостного
двухполюсника, и может быть заменен
последовательно соединенными резистором
и конденсатором. Необходимо отметить,
что величины индуктивности и емкости
в схемах замещения контура индуктивным
и емкостным двухполюсниками не равны
значениям индуктивности и ёмкости
контура и на различных частотах будут
иметь различные значения.
Полоса
пропускания.
Физический смысл полосы пропускания
резонансных контуров рассматривался
для последовательного одиночного
колебательного контура. Для параллельного
контура физический смысл полосы
пропускания совершенно аналогичен.
Отличительная особенность параллельного
контура состоит в том, что выходным
сигналом является контурное напряжение,
и АЧХ отображает его зависимость от
частоты.
Полосой
пропускания параллельного одиночного
колебательного контура называется
интервал частот, включающий резонансную
частоту контура, на границах которого
значение напряжения контура меньше
значения напряжения на резонансной
частоте в

раз.
Это
требование для значения напряжения на
границе полосы пропускания можно
выразить так:
 ;
;  .
.
Последнее
соотношение позволяет определить
границы полосы пропускания и ее величину
по АЧХ контура (рис.3.23):

 .
.
Пользуясь
полученными соотношениями для
последовательного колебательного
контура, АЧХ для параллельного контура
на границах полосы пропускания примет
вид, аналогичный (3.36):
 .
.
(3.67)
Приравнивая
(3.67) к коэффициенту неравномерности
и решая полученное уравнение относительно
2∆ω, находим:
 ;
;  .
.
Как
отмечалось, для широкого круга
приемно-передающих устройств коэффициент
неравномерности берется равным:
 .
.
С
учетом этого находим выражение для
полосы пропускания одиночного
параллельного резонансного контура:
 . (3.68)
. (3.68)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Частотные методы анализа электрических цепей:
Частотные характеристики являются компонентами комплексных функций цепи.
Комплексная функция цепи (КФЦ)
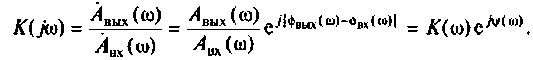
Амплитудно-частотная характеристика (АЧХ)
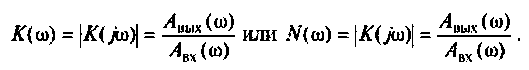
Фазочастотная характеристика (ФЧХ)
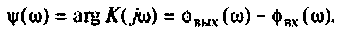
Амплитудно-фазовая частотная характеристика (АФЧХ) (комплексная функция цепи)
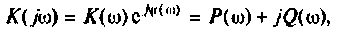
где 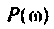 — вещественная частотная характеристика (ВЧХ);
— вещественная частотная характеристика (ВЧХ); 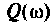 — мнимая частотная характеристика (МЧХ).
— мнимая частотная характеристика (МЧХ).
Комплексные функции простых цепей можно рассчитать непосредственно по закону Ома.
На рис.4.1 показаны АЧХ и ФЧХ, а на рис.4.2 — АФЧХ простейшей интегрирующей цепи (апериодического звена). По АЧХ определяют полосу пропускания
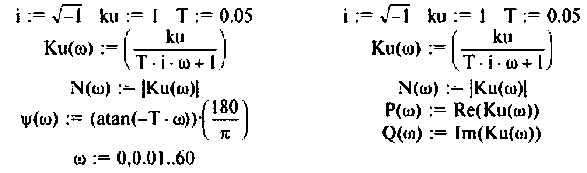
Полосой пропускания П называется диапазон частот, на границах которого мощность сигнала уменьшается в 2 раза, а амплитуда (действующее значение) напряжения (тока) — в 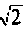 раз по сравнению с максимальными значениями.
раз по сравнению с максимальными значениями.
Полоса пропускания может измеряться в радианах в секунду 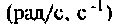 или в герцах (Гц).
или в герцах (Гц).
Например, для простой интегрирующей цепи полоса пропускания (см. рис. 4.1)
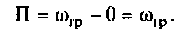
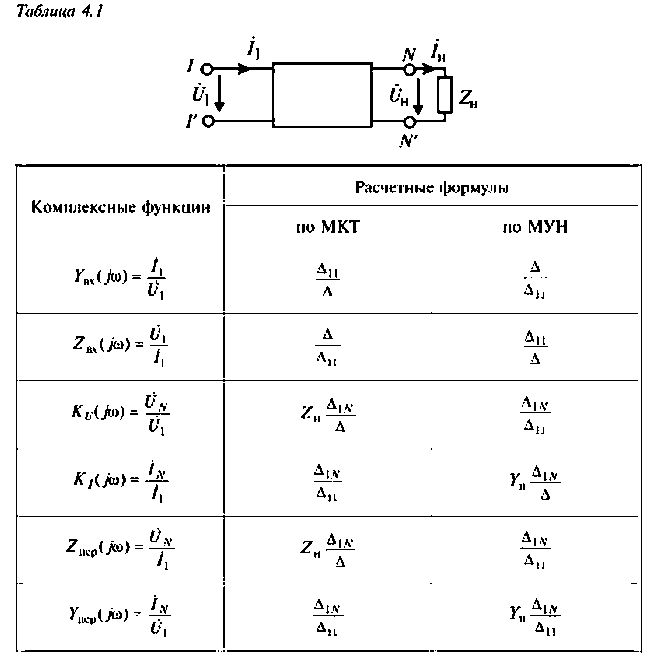
Для сложных цепей КФЦ рассчитывают по MKT или МУН. В табл. 4.1 приведены соотношения для расчета КФЦ, выраженные через определитель и алгебраические дополнения матрицы контурных сопротивлений и узловых проводимостей.
Частотные характеристики цепей с одним реактивным элементом
Примеры решения типовых задач:
Пример 4.2.1.
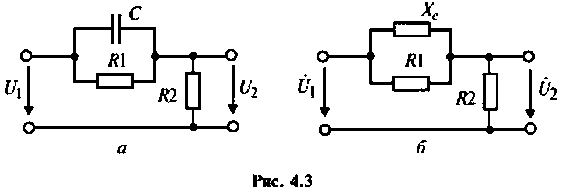
Определить комплексный коэффициент передачи по напряжению для дифференцирующего RC-контура (рис.4.3, а), рассчитать и построить графики АЧХ и ФЧХ.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.3, б).
2. Определим комплексное напряжение на выходе цепи в виде
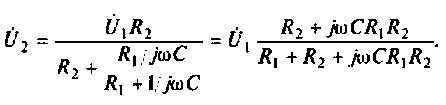
Преобразуем полученное выражение, вынеся зa скобки в числителе и знаменателе члены, не содержащие 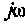 . После преобразований получим
. После преобразований получим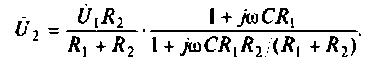
Следовательно.
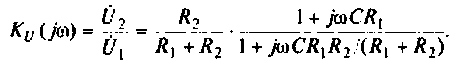
Введем обозначения:
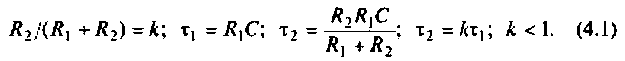
Величина 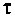 называется постоянной времени цепи и измеряется в секундах. Величина
называется постоянной времени цепи и измеряется в секундах. Величина 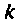 имеет смысл коэффициента усиления по напряжению на постоянном токе, т. е. на частоте
имеет смысл коэффициента усиления по напряжению на постоянном токе, т. е. на частоте 
С учетом принятых обозначений
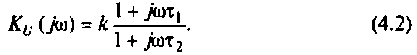
Для получения аналитических выражений АЧХ и ФЧХ запишем комплексную функцию в показательной форме.
Так как выражение (4.2) есть отношение двух полиномов, то удобно числитель и знаменатель записать отдельно в показательной форме, а затем разделить:
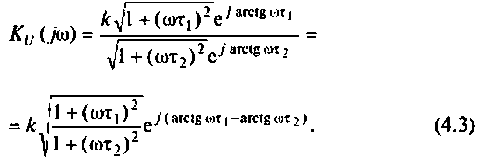
3. Из (4.3) запишем АЧХ и ФЧХ соответственно:
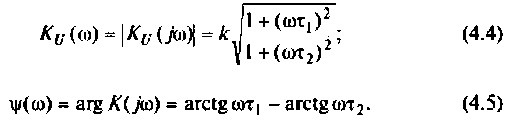
4. Построим график АЧХ и ФЧХ качественно по двум точкам. Для этого рассчитаем значения  для крайних значений частот:
для крайних значений частот:
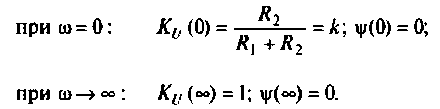
График АЧХ 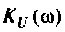 (рис. 4.4, а) является кривой, монотонно возрастающей от значения
(рис. 4.4, а) является кривой, монотонно возрастающей от значения 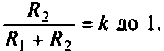
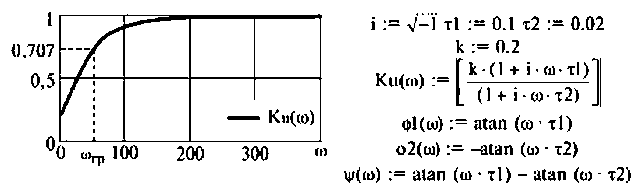
График функции ФЧХ 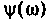 можно построить качественно как сумму двух графиков (рис. 4.4). Из рис. 4.4,б видно, что оба слагаемых монотонно увеличиваются: первое от нуля до +90° и вносит опережение по фазе. Второе до -90° и вносит отставание по фазе. Но первое слагаемое растет быстрее, так как
можно построить качественно как сумму двух графиков (рис. 4.4). Из рис. 4.4,б видно, что оба слагаемых монотонно увеличиваются: первое от нуля до +90° и вносит опережение по фазе. Второе до -90° и вносит отставание по фазе. Но первое слагаемое растет быстрее, так как  что следует из формулы (4.1). Поэтому функция
что следует из формулы (4.1). Поэтому функция  следовательно, дифференцирующий RС-контур вносит опережение по фазе.
следовательно, дифференцирующий RС-контур вносит опережение по фазе.
Исследуя функцию (4.5) на экстремум, можно показать, что она имеет максимум на частоте
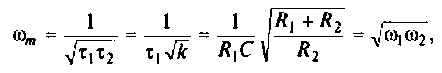
где 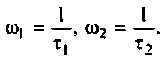
Подставляя 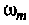 в (4.5), получим
в (4.5), получим
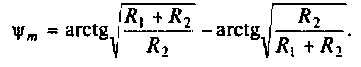
Графики АЧХ и ФЧХ изображены на рис. 4.4.
Пример 4.2.2.
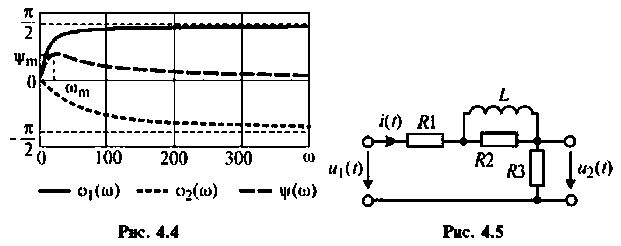
Для электрической цепи, изображенной на рис. 4.5, определить АЧХ 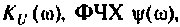 граничную частоту полосы пропускания. Рассчитать АЧХ, ФЧХ и построить графики, если параметры цепи:
граничную частоту полосы пропускания. Рассчитать АЧХ, ФЧХ и построить графики, если параметры цепи: 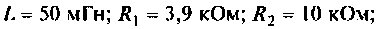
Решение
1. Найдем комплексную функцию К(; (/ш) но формуле делителя напряжения
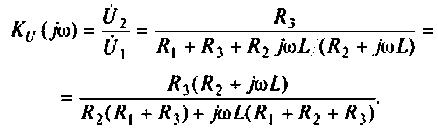
Преобразуем полученное выражение к виду
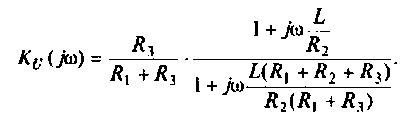
Обозначим:
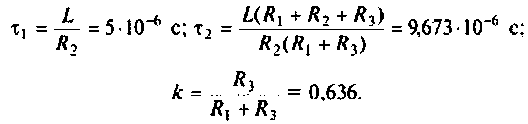
Следовательно,
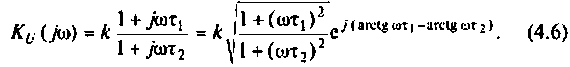
Отсюда: АЧХ
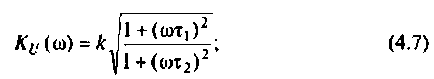
ФЧХ
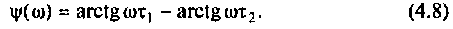
2. Рассчитаем граничную частоту. По определению
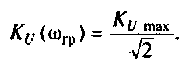
Из (4.7) найдем
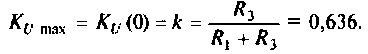
Следовательно,
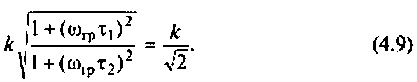
Из уравнения (4.9) получаем, что
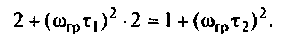
Отсюда 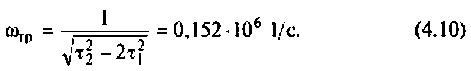
3. Построим график функций.
Вычислим значения (4.7) и (4.8) для частот с дискретностью 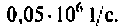
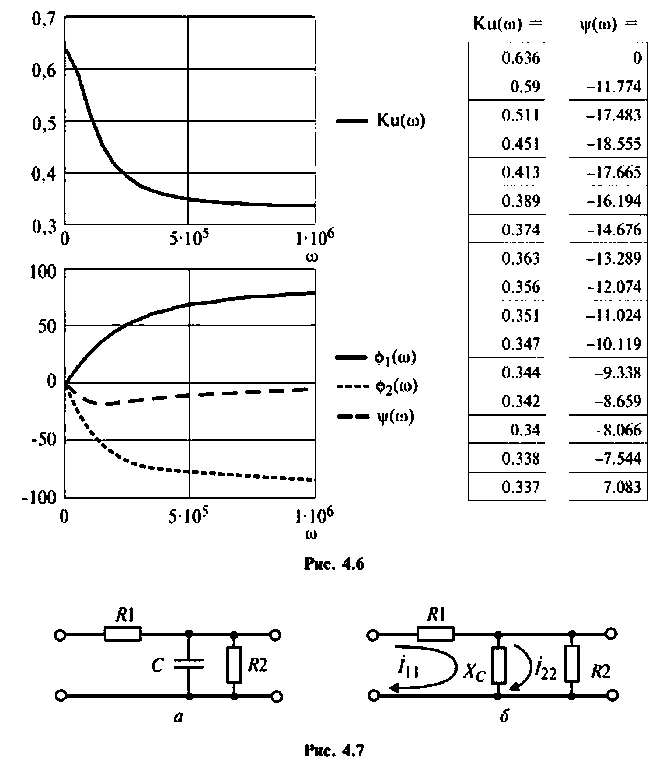
Графики и таблицы выполним в среде Mathcad (рис. 4.6).
Пример 4.2.3.
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.7, а), используя метод контурных токов. Построить в среде Mathcad график АЧХ, определить полосу пропускания.
Параметры цепи: 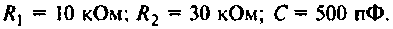
Решение
1. Представим цепь комплексной схемой замещения (рис. 4.7, б). Данная цепь имеет два независимых контура. Ток 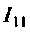 в первом контуре замыкается через источник, который на схеме не изображен. Направления контурных токов выбираем одинаковыми.
в первом контуре замыкается через источник, который на схеме не изображен. Направления контурных токов выбираем одинаковыми.
2.Составим матрицы контурных сопротивлений для двух независимых контуров
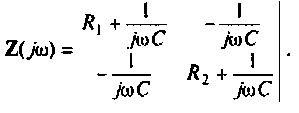
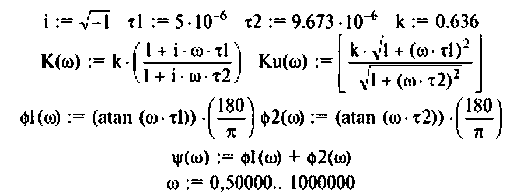
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
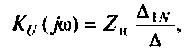
где сопротивление нагрузки равно 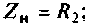
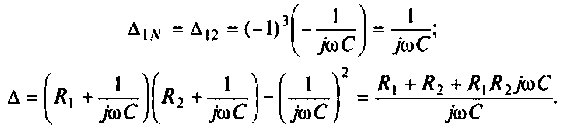
Подставляя найденные выражения, получаем
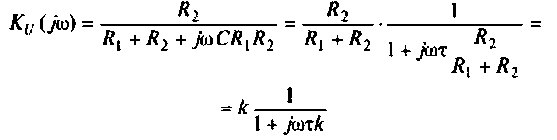
или 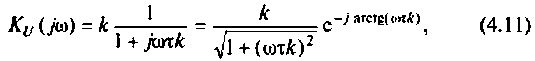
где 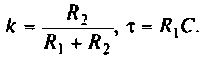
4. Рассчитаем 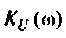 для крайних значений частоты
для крайних значений частоты  и
и 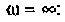
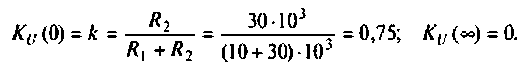
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 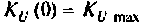
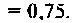 С ростом частоты емкостное сопротивление уменьшается. Если
С ростом частоты емкостное сопротивление уменьшается. Если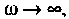 то
то 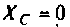 и шунтирует сопротивление
и шунтирует сопротивление 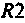 . При этом
. При этом
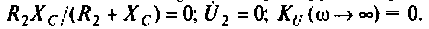 = 0.
= 0.
По полученным выражениям строим график АЧХ (рис. 4.8) и среде Mathcad.
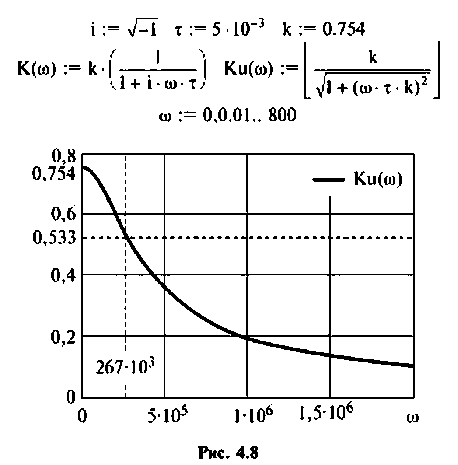
5. Определяем полосу пропускания. По определению
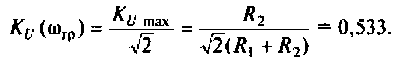
Поэтому из (4.11) имеем
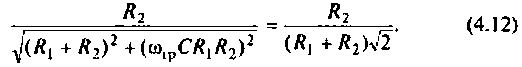
После преобразований уравнения (4.12) получаем
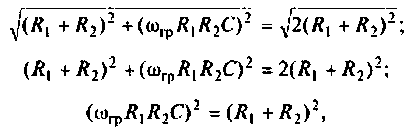
откуда
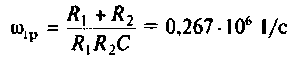
или
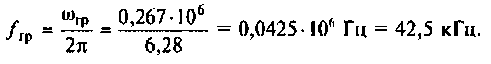
Следовательно, цепь имеет полосу пропускания
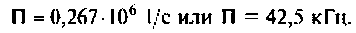
На рис. 4.8 указана граничная частота 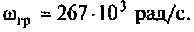
Данная цепь представляет собой фильтр нижних частот с полосой пропускания 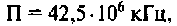 сигналы на частотах
сигналы на частотах  проходят с большим затуханием.
проходят с большим затуханием.
Пример 4.2.4.
Найти комплексную передаточную проводимость 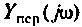 для цепи, изображенной на рис. 4.9, а методом узловых напряжений.
для цепи, изображенной на рис. 4.9, а методом узловых напряжений.
Параметры цепи: 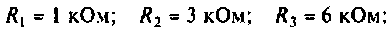
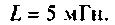
Определить АЧХ и ФЧХ, построить их графики в среде Mathcad.
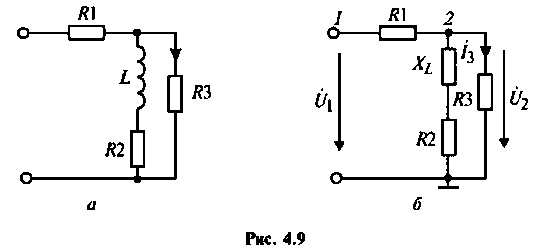
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.9, б). Схема имеет два независимых узла. В данном случае 
2. Составим матрицу узловых проводимостей. При определении собственной проводимости узлов необходимо помнить, что собственная проводимость ветви, состоящей из последовательно включенных пассивных элементов, находится из соотношения  , где
, где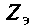 — эквивалентное сопротивление ветви. Как найти проводимость ветви с последовательно включенными
— эквивалентное сопротивление ветви. Как найти проводимость ветви с последовательно включенными 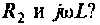
В начале рассчитывают комплексное сопротивление этой ветви, 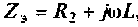 , а затем комплексную проводимость
, а затем комплексную проводимость
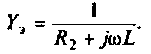
Составим матрицу проводимостей цепи 1 2
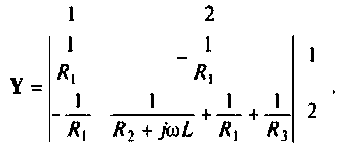
Как видим, общие проводимости узлов взяты со знаком минус, так как узловые напряжения 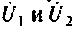 направлены одинаково, к базисному yзлy.
направлены одинаково, к базисному yзлy.
3.Определим комплексную передаточную проводимость по соотношению, приведенному в табл. 4.1
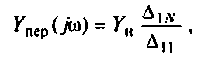
где 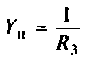 -комплексная проводимость ветви, по которой протекает ток
-комплексная проводимость ветви, по которой протекает ток 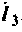 ,так как по определению
,так как по определению
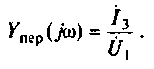
Найдем алгебраические дополнения:
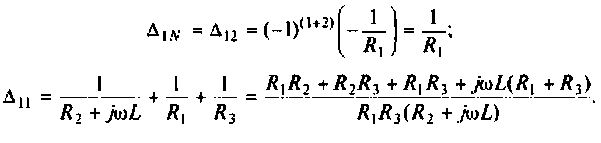
После подстановки найденных значений получим
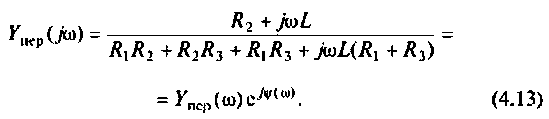
Для определении АЧХ и ФЧХ запишем выражения для модуля и аргумента 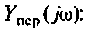
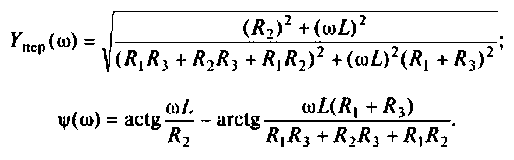
4. Рассчитаем значения 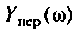 на частотах
на частотах 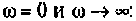
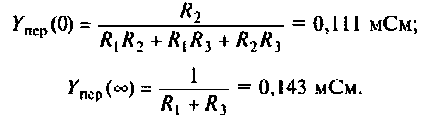
Примечание. Эти значения можно найти без вывода аналитического выражения для 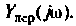 Для этого достаточно воспользоваться эквивалентными схемами цепи на рассматриваемых частотах.
Для этого достаточно воспользоваться эквивалентными схемами цепи на рассматриваемых частотах.
Учитывая, что 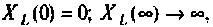 получим две схемы, показанные на рис. 4.10. а, б, соответственно.
получим две схемы, показанные на рис. 4.10. а, б, соответственно.
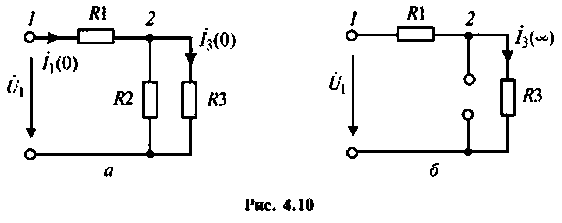
Для первой схемы:
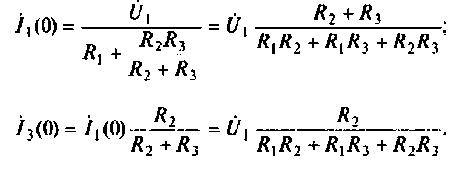
Следовательно,
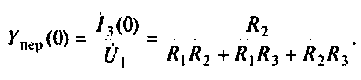
Аналогично для второй схемы получим
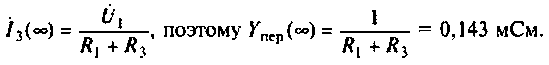
При расчете сложных схем такой прием можно применять для проверки правильности полученного аналитического выражения КФЦ.
Из (4.13) видно, что функция наметен монотонной, но для качественного построения графика АЧХ (рис. 4.11) необходимо воспользоваться ПЭВМ, например построить функцию в среде Mathcad.
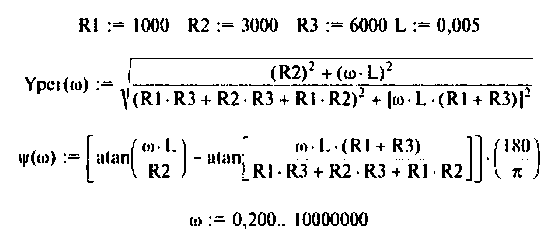
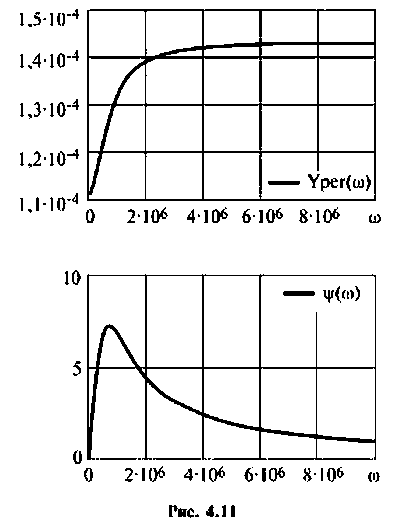
Пример 4.2.5.
Для интегрирующего RС-контура (рис.4.12,а) определить комплексный коэффициент передачи по напряжению, рассчитать АЧХ, ФЧХ, ВЧХ, МЧХ. Построить графики АЧХ, ФЧХ. АФЧХ, если
Решение
1. Составим комплексную схему замещения цепи (рис. 4.12, б).
2. Определим 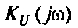 из соотношения
из соотношения 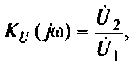 где
где
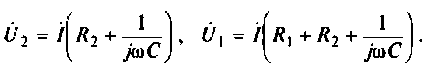
Следовательно.
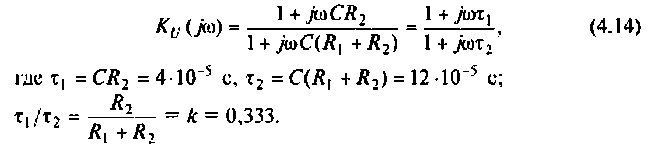
3. Для нахождения АЧХ и ФЧХ комплексную функцию 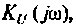 представленную в виде отношения двух полиномов мнимой частоты
представленную в виде отношения двух полиномов мнимой частоты 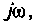 записывают в показательной форме
записывают в показательной форме
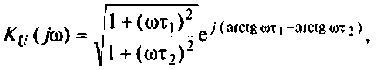
Найдем модуль (АЧХ) и аргумент (ФЧХ) комплексной функции;
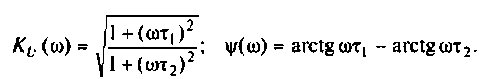
Для определения вещественной и мнимой частотных характеристик запишем КФЦ в алгебраической форме. Для этого умножим и разделим (4.14) на комплексно-сопряженный знаменатель:
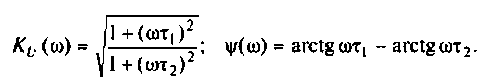
4. Для приближенного построения графиков АЧХ, ФЧХ. АФХ найдем значения 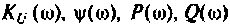 для трех значений частот:
для трех значений частот: 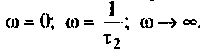 Результаты расчетов для удобства построения графиков сведем в табл. 4.2.
Результаты расчетов для удобства построения графиков сведем в табл. 4.2.

Для более точного и наглядного представления графиков воспользуемся ПЭВМ и математической средой Mathcad.
Графики характеристик приведены на рис. 4.13.
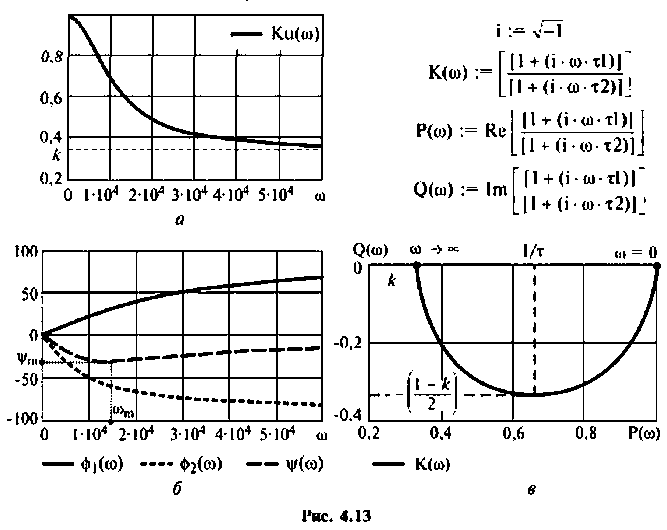
АЧХ представляет монотонно убывающую функцию (рис. 4.13, а).
ФЧХ принимает отрицательные значения, т.е. контур вносит фазовое отставание, а на частоте  ФЧХ имеет экстремум (рис.4.13, б). Найдем из соотношения
ФЧХ имеет экстремум (рис.4.13, б). Найдем из соотношения
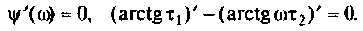
Взяв производную, получим
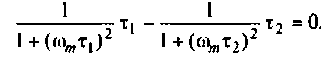
Решая полученное уравнение относительно  , найдем
, найдем
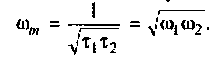
Подставляя  в выражение
в выражение 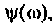 определим максимальное значение фазовой частотной характеристики.
определим максимальное значение фазовой частотной характеристики.
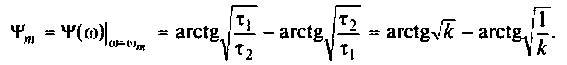
АФХ (рис. 4.13, в) представляет собой полуокружность, расположенную в 4-м квадрате. Центр окружности находится на оси  в точке с абсциссой, равной
в точке с абсциссой, равной
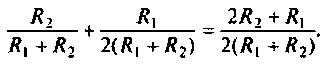
Радиус окружности нетрудно определить из соотношения:
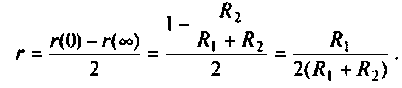
МЧХ:
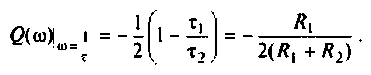
Отрицательное значение 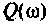 свидетельствует о том, что
свидетельствует о том, что
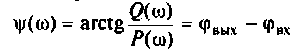 принимает отрицательное значения, т.е. интегрирующий контур вносит запаздывание по фазе.
принимает отрицательное значения, т.е. интегрирующий контур вносит запаздывание по фазе.
5. Проверка расчетов АЧХ. Воспользуемся эквивалентными схемами цепи для частот 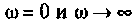 (рис. 4.14).
(рис. 4.14).
На частоте 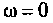 цепь разомкнута (рис. 4.14, а), поэтому
цепь разомкнута (рис. 4.14, а), поэтому
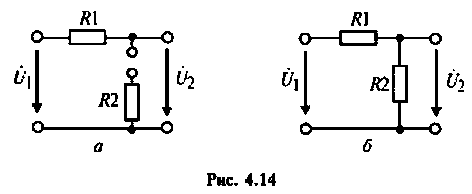
При  схема представляет собой резистивный делитель напряжения (рис. 4.14, б) с коэффициентом передачи
схема представляет собой резистивный делитель напряжения (рис. 4.14, б) с коэффициентом передачи
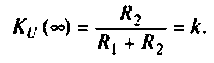
Подставляя эти значения частот в аналитическое выражение (4.14) для 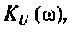 получаем
получаем
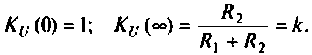
Следовательно, расчет АЧХ выполнен верно.
Частотные характеристики последовательного колебательного контура
Основные теоретические сведения:
В последовательном колебательном контуре (рис. 4.21) возникает резонанс напряжений, если выполняется условие
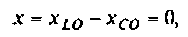
т. е. 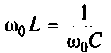
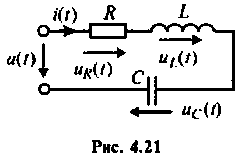
Резонансная частота
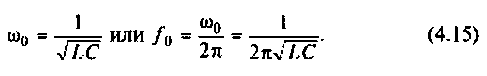
Волновое сопротивление контура 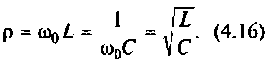
Сопротивление контура при резонансе 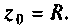
Собственная добротность контура 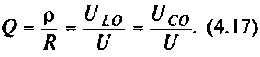
Добротность нагруженного контура 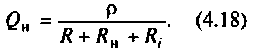
Затухание контура 
Абсолютная расстройка 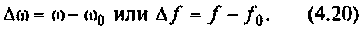
Относительная расстройка 
Обобщенная расстройка
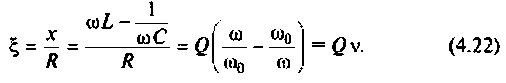
Фактор расстройки: 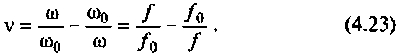
Абсолютная полоса пропускания (рис. 4.22)
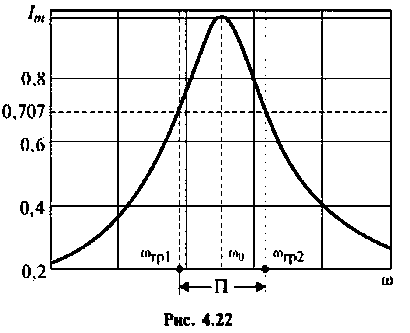
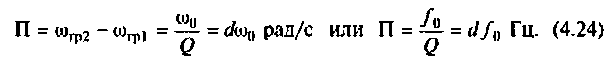
Относительная полоса пропускания

Для нагруженного контура:
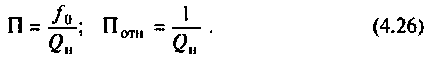
Комплексные коэффициенты передачи по напряжению:
на активном сопротивлении
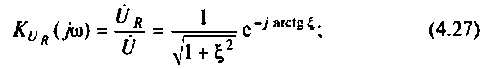
на индуктивности
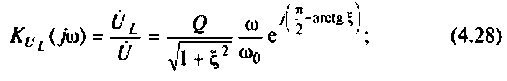
на емкости
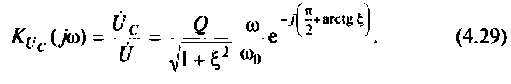
Примеры решения типовых задач:
Пример 4.3.1.
Последовательный колебательный контур (рис. 4.23) подключен к источнику напряжению. Контур настроен в резонанс.
Параметры цепи: 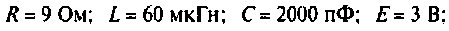
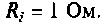
Определить резонансную частоту, волновое сопротивление. добротность и полосу пропускания, ток и напряжения на элементах контура.
Построить АЧХ и ФЧХ по напряжению на конденсаторе в среде Mathcad.
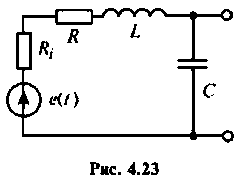
Решение
1. Определяем резонансную частоту контура
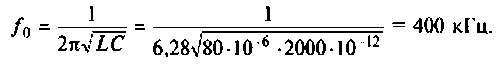
2. Находим волновое сопротивление контура
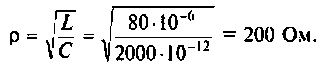
3. Вычисляем добротность нагруженного контура
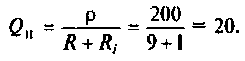
4. Определяем полосу пропускания
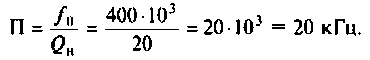
5. Рассчитываем ток и напряжения на элементах контура при резонансе
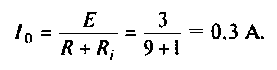
Напряжение на R равно
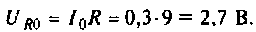
Напряжения на реактивных элементах
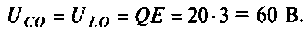
6. Рассчитаем АЧХ и ФЧХ комплексного коэффициента передачи напряжения с емкости.
Учитывая (4.22), из (4.29) получим:
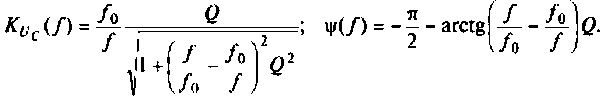
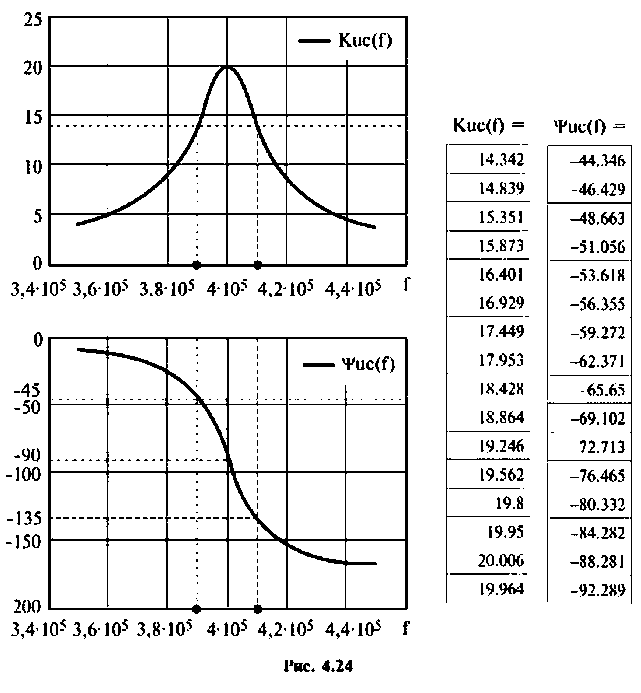
Для построения графиков АЧХ и ФЧХ, выполнения расчетов используем среду Mathcad. АЧХ, ФЧХ в виде графиков и таблиц приведены на рис. 4.24.
Следует заметить, что максимум А11Х достигается на частоте
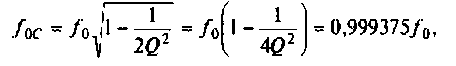
т.е. при 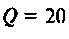 смещение максимума мало, тогда
смещение максимума мало, тогда 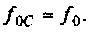
Задача 4.3.2.
К последовательному колебательному контуру (рис. 4.25) с параметрами 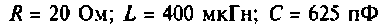 подключена нагрузка
подключена нагрузка 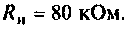
Определить собственную добротность и добротность нагруженного контура, полосу пропускания нагруженного и ненагруженного контура.
Решение
1. Рассчитаем вторичные параметры ненагруженного контура:
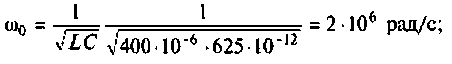
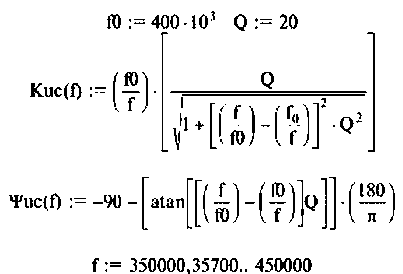
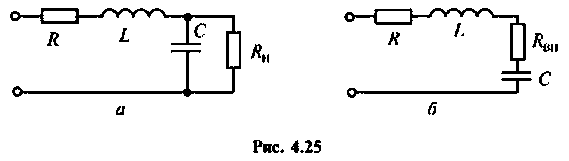
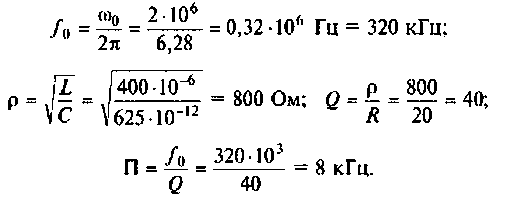
2.Определим вторичные параметры наруженного контура. Так как сопротивление нагрузки активное, причем 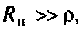 то согласно (4.15) и (4.16) резонансная частота и волновое сопротивление не изменяются.
то согласно (4.15) и (4.16) резонансная частота и волновое сопротивление не изменяются.
Для определения добротности рассчитаем сопротивление 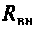 , вносимое в контур за счет нагрузки, и построим эквивалентную схему нагруженного контура (рис. 4.25, б). Так как
, вносимое в контур за счет нагрузки, и построим эквивалентную схему нагруженного контура (рис. 4.25, б). Так как 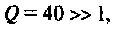 то
то
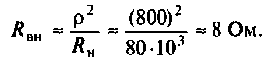
Следовательно,
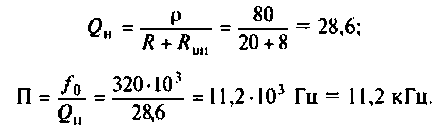
Вывод. Подключение нагрузки ухудшает добротность контура, что приводит к расширению полосы пропускания.
Пример 4.3.3.
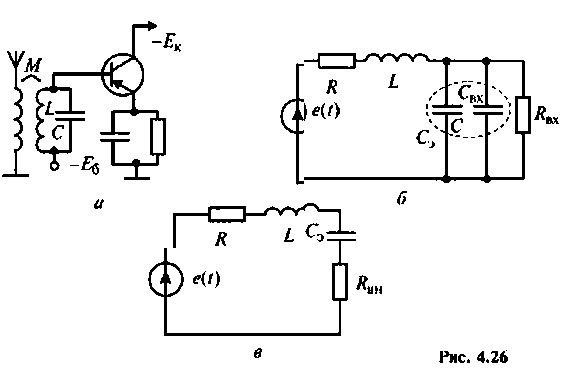
На рис. 4.26, а изображена входная цепь приемника, а на рис. 4.26, б — ее эквивалентная схема. Известны входное сопротивление и входная емкость транзистора входного каскада УВЧ:  . На резонансной частоте антенна наводит в контуре ЭДС
. На резонансной частоте антенна наводит в контуре ЭДС 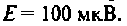 Емкость конденсатора
Емкость конденсатора 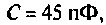 катушка индуктивности имеет
катушка индуктивности имеет 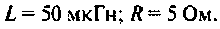
Определить абсолютную полосу пропускания и ток в контуре на резонансной частоте.
Решение
1. Определяем эквивалентную емкость контура
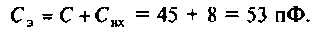
2. Рассчитываем резонансную частоту контура
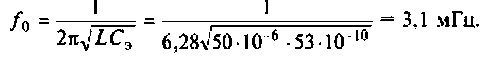
3. Находим волновое сопротивление и сопротивление, вносимое в контур за счет транзистора усилителя (рис. 4.26, в):
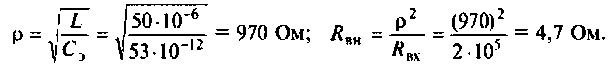
4. Определяем добротность нагруженного контура
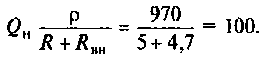
5. Рассчитаем абсолютную полосу пропускания нагруженного контура
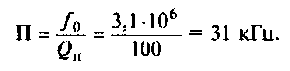
6. Находим ток в контуре
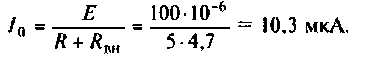
Пример 4.3.4.
Рассчитать емкость последовательного колебательного контура, если резонансная частота контура 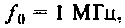 полоса пропускания
полоса пропускания 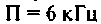 при сопротивлении потерь 0,5 Ом.
при сопротивлении потерь 0,5 Ом.
Построить АЧХ и ФЧХ комплексного коэффициента передачи напряжения с индуктивности в среде Mаthcad.
Решение
1. Определим требуемую добротность контура
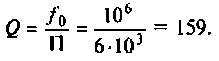
2. Рассчитаем емкость конденсатора. Из формулы 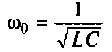 найдем
найдем
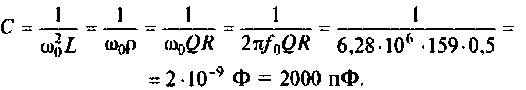
3. Рассчитаем АЧХ и ФЧХ.
Воспользуемся комплексным коэффициентом передачи напряжения с индуктивности по формуле (4.28). Учитывая 4.22), запишем:
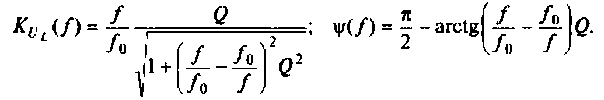
Вычислим значения функций на частотах:
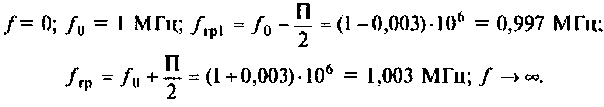
Определим частоту, при которой АЧХ имеет максимум
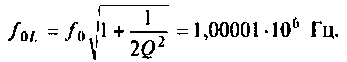
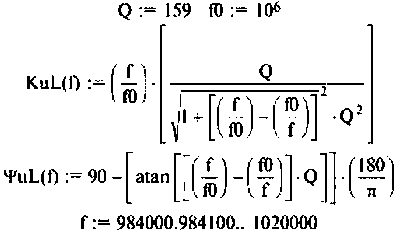
Смещением частоты  можно пренебречь.
можно пренебречь.
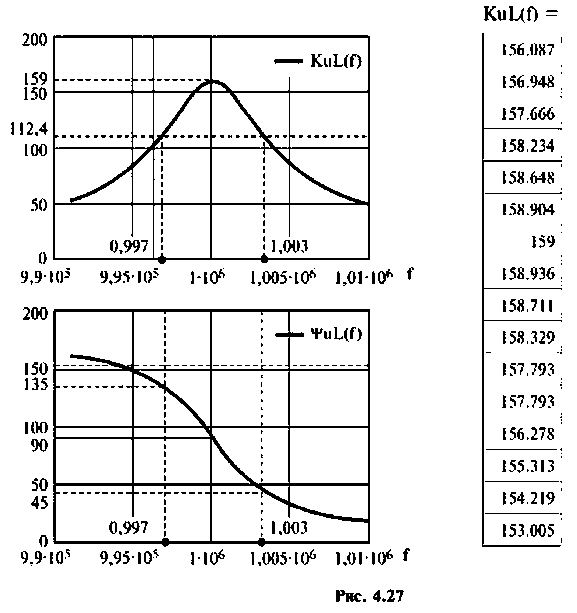
Результаты расчетов АЧХ и ФЧХ б графическом и табличном видах приведены на рис. 4.27.
Частотные характеристики параллельного колебательного контура
Основные теоретические сведения:
Параллельный колебательный контур образуется путем параллельного соединения катушки индуктивности и конденсатора. Оба элемента, кроме основного эффекта (запасания энергии), имеют потери энергии. В расчетной схеме (рис. 4.29, а) тепловые потери в элементах учтены включением условных сопротивлений 
где резонансная частота колебаний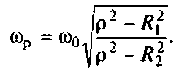
Для реального контура 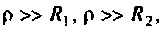 поэтому при расчете можно полагать, что
поэтому при расчете можно полагать, что
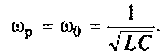
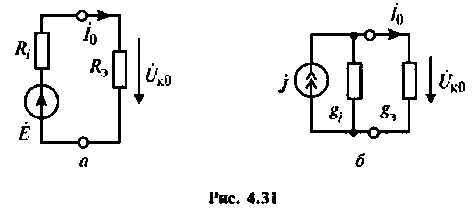
При резонансе сопротивление контура является активным, поэтому ток 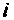 в цепи и напряжение
в цепи и напряжение 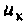 в контуре синфазны. Эквивалентные схемы цепи в режиме резонанса токов показаны на рис. 4.31, а, б.
в контуре синфазны. Эквивалентные схемы цепи в режиме резонанса токов показаны на рис. 4.31, а, б.
Сопротивление параллельного колебательного контура при резонансе максимально и равно (без учета внешней цепи)
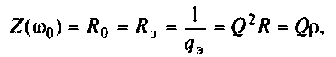
где 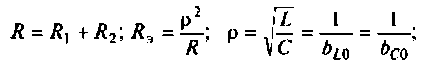
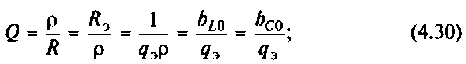
Добротность 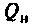 нагруженного контура меньше собственной добротности
нагруженного контура меньше собственной добротности 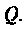 Ее можно выразить через сопротивления элементов цепи
Ее можно выразить через сопротивления элементов цепи
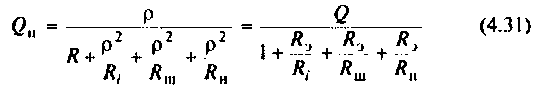
или через их проводимости
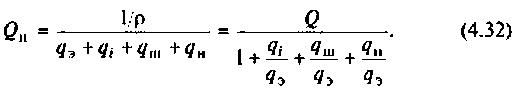
Важными параметрами цепи при резонансе являются токи в ветвях и напряжение на контуре. Ток в обшей ветви (ток источника) при резонансе минимален и равен (см. рис. 4.31)
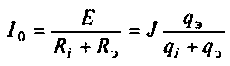
При этом напряжение на контуре максимально и равно
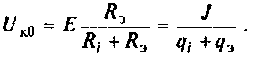
Токи в индуктивности и в емкости при резонансе равны по значению и противоположны по направлению. Они образуют замкнутый ток в контуре, равный
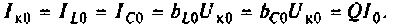
Частотные свойства параллельного колебательного контура обычно оценивают по нормированной АЧХ
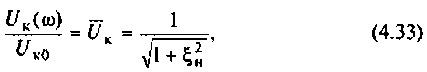
где 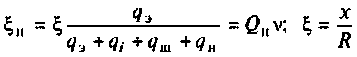 -обобщенная расстройка контура без учета внешних цепей;
-обобщенная расстройка контура без учета внешних цепей; 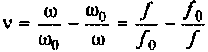 — фактор расстройки.
— фактор расстройки.
Параллельный контур, показанный на рис. 4.29, имеет по одной реактивности в ветвях. Такой контур называется простым или контуром I вида. Для уменьшения шунтирующего действия внешних цепей часто применяют сложные параллельные контуры.
На рис. 4.32, а, б, в показаны контуры II, (III и IV) видов, соответственно.
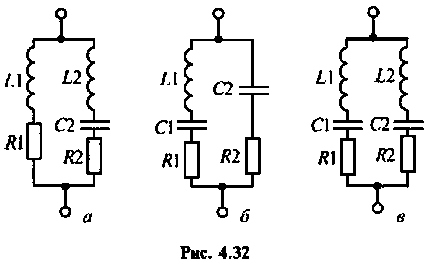
Главной особенностью этих контуров является то, что их резонансное сопротивление меньше резонансного сопротивления простого контура с такими же параметрами.
Сопротивление контуров (рис.4.32) при резонансе рассчитывается по формулам, соответственно:
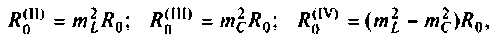
где 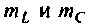 — коэффициенты включения:
— коэффициенты включения:
Примеры решения типовых задач:
Пример 4.4.1.
Параллельный контур (см. рис. 4.29, а) подключен к источнику с параметрами 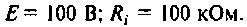 Контур настроен в резонанс на длину волны, равную 1000 м.
Контур настроен в резонанс на длину волны, равную 1000 м.
Параметры катушки индуктивности: 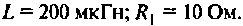
Определить действующие значения тока в контуре, тока на входе цепи и напряжения на контуре при резонансе, абсолютную и относительную полосы пропускания контура, добавочное сопротивление необходимое для расширения полосы пропускания в 2 раза.
Решение
1. Определим резонансную частоту колебания
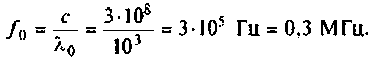
2. Рассчитаем волновое сопротивление
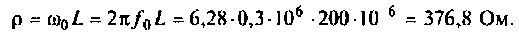
3. Определим сопротивление контура при резонансе
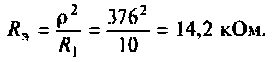
4. Найдем действующее значение тока на входе контура (см. рис. 4.31, а) при резонансе
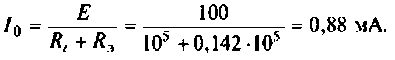
5. Определим соответственную добротность контура
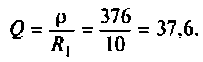
6. Найдем ток в контуре и напряжение на нем:
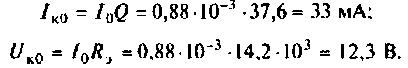
7. Определим добротность нагруженного контура
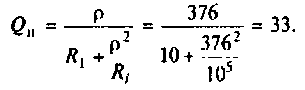
8. Рассчитаем абсолютную и относительную полосы пропускания:
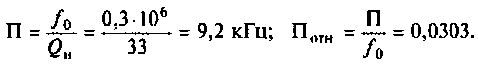
9. Определяем добавочное cопротивление 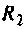 из (4.31)
из (4.31)
Пример 4.4.2.
Рассчитать полосу пропускания колебательного контура (см. рис. 4.30, а).
Дано: 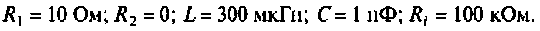
Определить сопротивление 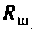 шунта, необходимого для расширения полосы пропускания до 10 кГц.
шунта, необходимого для расширения полосы пропускания до 10 кГц.
Решение
1. Рассчитаем волновое сопротивление и резонансную частоту контура:
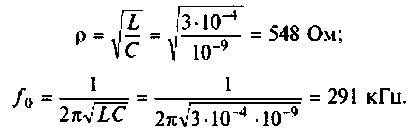
2.Рассчитаем добротность цепи без шунта. Воспользуемся трехветвевой эквивалентной схемой цепи и соотношением (4.32). Найдем проводимость элементов схемы:
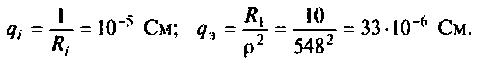
Тогда
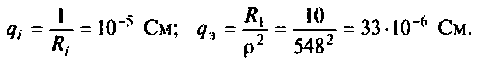
3. Определим полосу пропускания
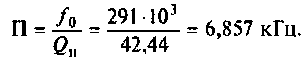
4. Найдем сопротивление шунта, необходимою для расширения полосы до 10 кГц,
В этом случае добротность цепи должна быть равна
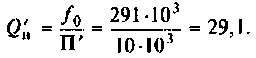
Тогда из (4.32) получаем
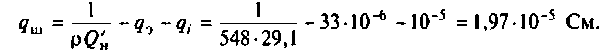
Следовательно, сопротивление шунта должно быть равно
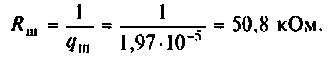
Пример 4.4.3.
Параллельный колебательный контур с параметрами: 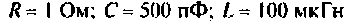 подключен к источнику
подключен к источнику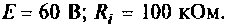
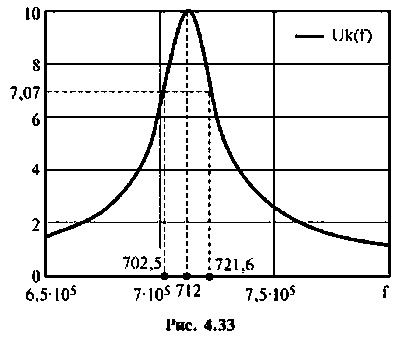
Определить собственную добротность контура, добротность нагруженного контура, абсолютную полосу пропускания и граничные частоты полосы пропускания. Построить резонансную кривую по напряжению на ЭВМ.
Решение
1. Определим волновое сопротивление контура
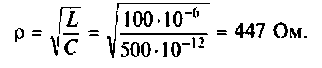
2. Рассчитаем собственную добротность контура
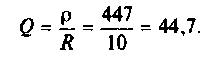
3. Найдем сопротивление контура при резонансе
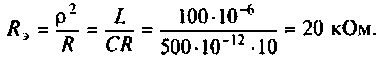
4. Определим добротность нагруженного контура по формуле (4.31)
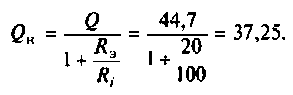
5. Рассчитаем резонансную частоту
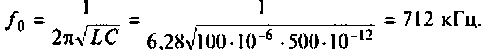
6. Найдем полосу пропускания
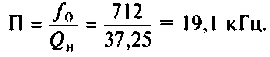
7. Определим граничные частоты полосы пропускания:
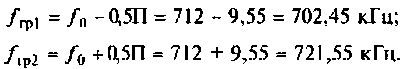
8. Построим резонансную характеристику контура но напряжению. Из выражения (4.33) запишем
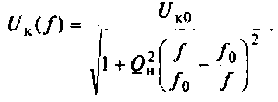
Напряжение па контуре при резонансе
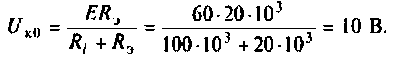
Для построения резонансной характеристики задаемся характерными значениями частот:  Результаты расчетов в графическом виде представлены на рис. 4.33.
Результаты расчетов в графическом виде представлены на рис. 4.33.
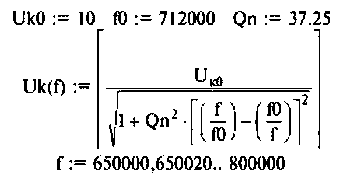
Пример 4.4.4.
Определить резонансную частоту, эквивалентное сопротивление при резонансе и добротность сложного контура (рис. 4.32, а), подключенного к источнику напряжения.
Дано: 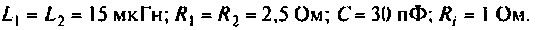
Решение
1. Определим резонансную частоту и сопротивление параллельного контура при резонансе:
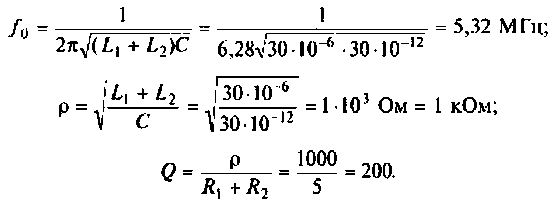
Сопротивление контура при резонансе
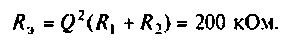
2. Рассчитаем эквивалентное сопротивление сложного контура II вида
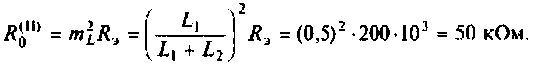
3. Найдем добротность нагруженного контура II вида
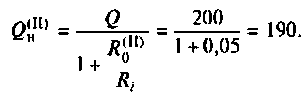
Сравним значения 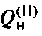 с добротностью простого нагруженного контура
с добротностью простого нагруженного контура
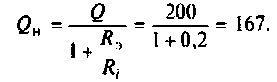
Вывод. За счет неполного включения индуктивности  уменьшилось шунтирующее действие источника. Поэтому добротность сложного контура больше, чем простого с теми же параметрами элементов.
уменьшилось шунтирующее действие источника. Поэтому добротность сложного контура больше, чем простого с теми же параметрами элементов.
Частотные характеристики связанных колебательных контуров
Основные теоретические сведения:
С целью повышения коэффициента прямоугольности АЧХ контуров применяют связанные контуры последовательного и параллельного питания (рис. 4.37, а, б).
Частотные характеристики связанных контуров рассмотрим на примере системы из двух контуров.
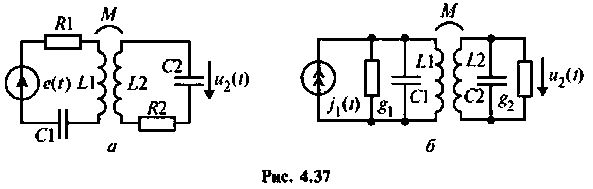
Эквивалентные схемы связанных контуров
Во всех случаях систему связанных контуров можно представить в виде Т- или П-образной эквивалентной схемы (рис. 4.38).
Количественной характеристикой связи является сопротивление связи 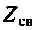 в Т-образной эквивалентной схеме (рис. 4.38,а) или проводимость связи
в Т-образной эквивалентной схеме (рис. 4.38,а) или проводимость связи 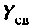 в П-образной эквивалентной схеме (рис. 4.38, б).
в П-образной эквивалентной схеме (рис. 4.38, б).
Удобным параметром для оценки связи является коэффициент связи
В случае реактивной связи для Т-образной схемы
Для П-образной схемы
где — сопротивление (проводимость) связи;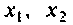
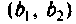 — сопротивления (проводимости) контуров, однотипные элементу связи. Для анализа связанных контуров удобно применять схемы, приведенные к первичному (рис. 4.39, а) или ко вторичному (рис. 4.39, б) контуру.
— сопротивления (проводимости) контуров, однотипные элементу связи. Для анализа связанных контуров удобно применять схемы, приведенные к первичному (рис. 4.39, а) или ко вторичному (рис. 4.39, б) контуру.
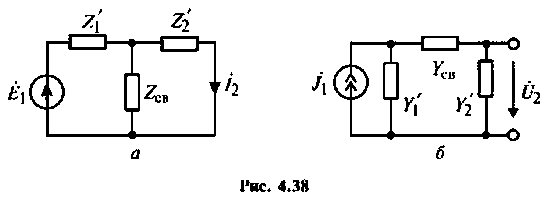
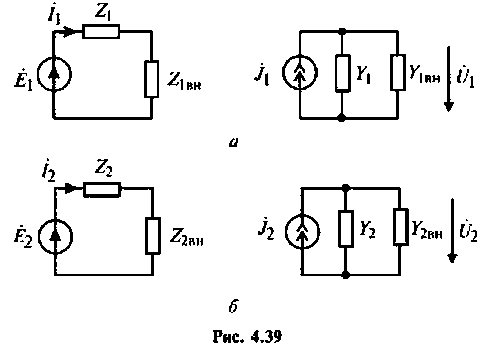
Для этого используют понятия вносимого сопротивления 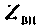 и вносимой проводимости
и вносимой проводимости 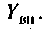 Эти схемы представляют собой одиночные последовательные (параллельные) контуры с параметрами:
Эти схемы представляют собой одиночные последовательные (параллельные) контуры с параметрами:
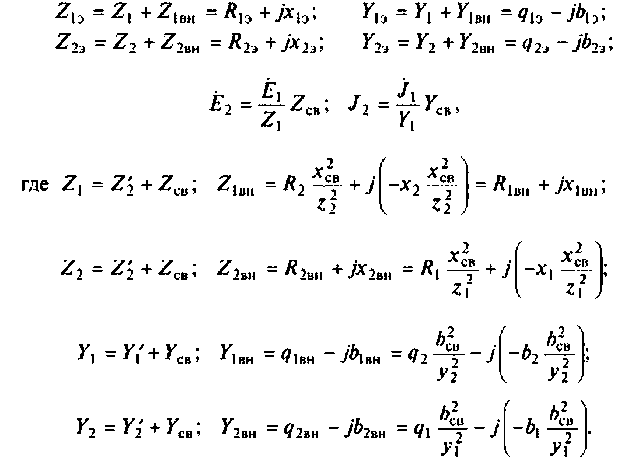
Резонансы в связанных контурах:
При настройке контуров в резонанс добиваются максимального тока (напряжения) во вторичном контуре.
Настройка связанных контуров может производиться различными способами, поэтому различают шесть резонансов. В табл. 4.3, 4.4 приведены виды и условия резонансов, способы настройки и соотношения для токов (напряжений) в связанных контурах последовательного (параллельного) питания.


Резонансные характеристики связанных контуров:
Для двух неидентичных связанных контуров: последовательного питания
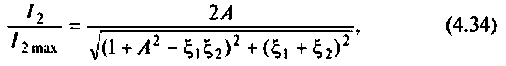
где 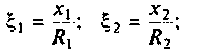
параллельного питания:
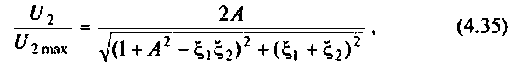
где 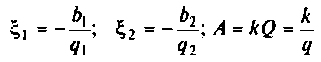 — параметр связи.
— параметр связи.
Если контуры идентичны, то обобщенная расстройка 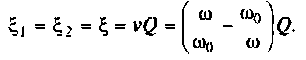
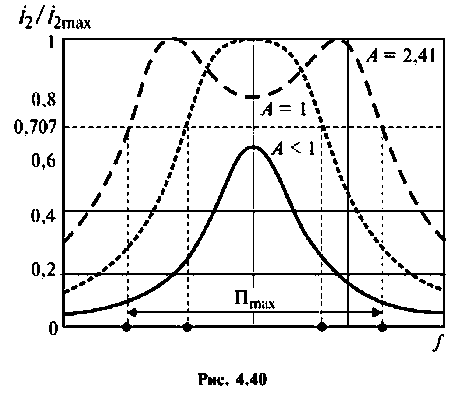
На рис. 4.40 приведены резонансные характеристики при различных факторах связи.
Относительная полоса пропускания:
а) связь слабая 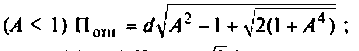
б) связь критическая 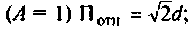
в) связь сильная 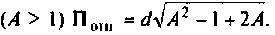
При 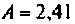 достигается максимально возможная полоса пропускания
достигается максимально возможная полоса пропускания 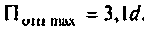
Примеры решения типовых задач:
Пример 4.5.1.
В системе двух индуктивно связанных контуров (см. рис.4.37,а) известны следующие параметры: коэффициент связи
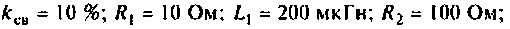
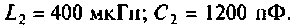
Определить емкость 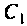 при которой в системе наступает первый частный резонанс, если частота источника равна 500 кГц.
при которой в системе наступает первый частный резонанс, если частота источника равна 500 кГц.
Решение
Емкость конденсатора 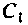 определим но реактивному сопротивлению первого контура:
определим но реактивному сопротивлению первого контура:
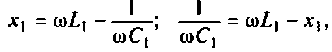
отсюда
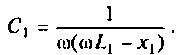
Определим реактивное сопротивление 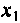 , первого контура из условия первого частного резонанса (см. табл. 4.3)
, первого контура из условия первого частного резонанса (см. табл. 4.3)
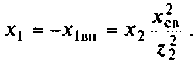
Peaктивное сопротивление второго контура
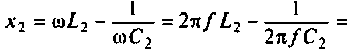
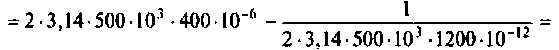
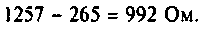
Рассчитаем полное сопротивление второго контура
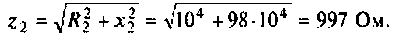
Определим сопротивление связи контуров
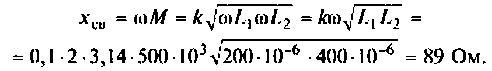
Следовательно
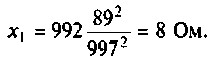
Находим емкость первого контура
Пример 4.5.2.
Рассчитать емкости связанных контуров (см. рис. 4.37,а) и оптимальное сопротивление связи, если система настроена и полный резонанс. Определить токи, мощности в контурах при этом режиме, а также КПД системы.
Дано: 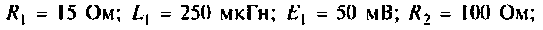
Решение
1. Определим емкость конденсатора 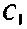 , полагая, что
, полагая, что
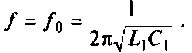
Отсюда
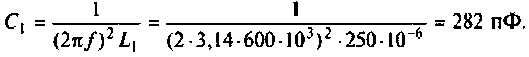
2. Сопротивление оптимальной связи при полном резонансе
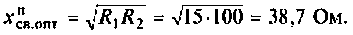
3. Рассчитаем токи в первом и втором контурах при полном резонансе
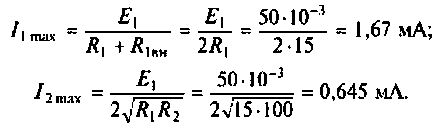
4. Определим активные мощности в первом и втором контурах и КПД связанных контуров:
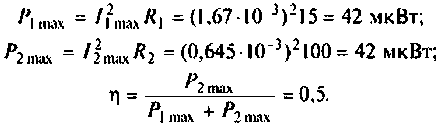
Пример 4.5.3.
На рис. 4.37, а показана система из двух идентичных связанных контуров с параметрами: 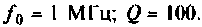 Рассчитать полосы пропускания одиночного контура и связанных контуров при различной связи:
Рассчитать полосы пропускания одиночного контура и связанных контуров при различной связи: 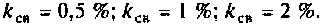
Решение
1. Определим полосу пропускания одиночного контура
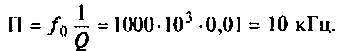
2. Рассчитаем полосу пропускания системы связанных контуров:
1) определим параметр связи для 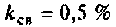
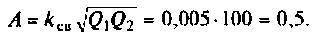
Таким образом при 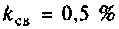 связь меньше критической
связь меньше критической 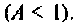 При этом относительная полоса пропускания
При этом относительная полоса пропускания
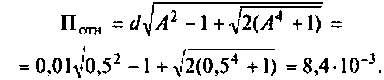
Абсолютная полоса пропускания (рис. 4.41, резонансная кривая А = 0,5)
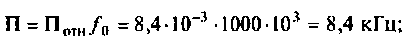
2) при 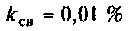 параметр связи
параметр связи 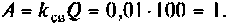 Таким образом, коэффициент связи является оптимальным, а связь критическая, система настроена в полный резонанс. Полоса пропускания в этом случае
Таким образом, коэффициент связи является оптимальным, а связь критическая, система настроена в полный резонанс. Полоса пропускания в этом случае
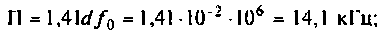
3) если 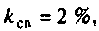 то параметр связи
то параметр связи 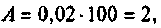 следовательно, связь больше критической.
следовательно, связь больше критической.
Рассчитаем полосу пропускания для этого случая.
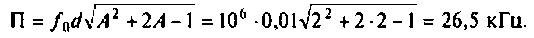
Вид резонансных кривых по току и полоса пропускания для критической и сильной связи показаны на рис. 4.41, кривые А = 1 и А = 2.

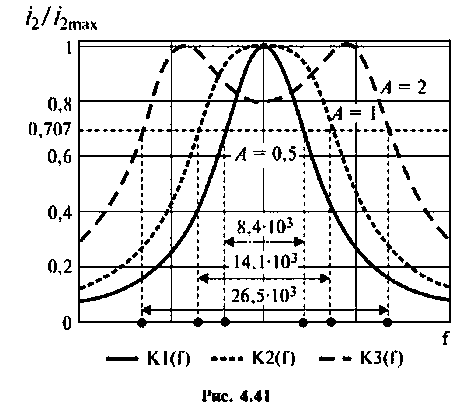
Пример 4.5.4.
Антенный контур (см. рис. 4.37,б) индуктивно связан с входным контуром усилителя высокой частоты. Оба контура настроены в резонанс на частоту 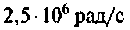 принимаемого сигнала. В антенном контуре наводится
принимаемого сигнала. В антенном контуре наводится 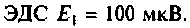
Дано: 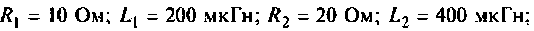
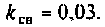
Входное сопротивление УВЧ считать бесконечно большим.
Определить емкости и добротности контуров, их взаимную индуктивность, а также ток и напряжение на емкости во вторичном контуре.
Решение
1.Емкости контуров определим из формулы резонансной частоты. Емкость конденсатора первого контура
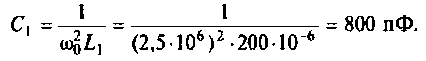
Емкость конденсатора второго контура
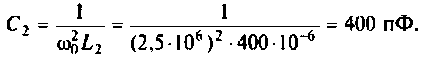
2. Рассчитаем волновое сопротивление контуров:
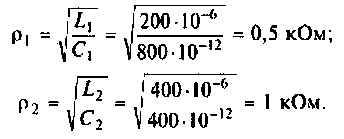
3. Рассчитаем добротности контуров и параметр связи:
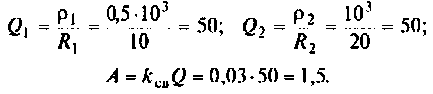
4. Определим взаимную индуктивность двух связанных контуров
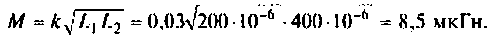
5. Рассчитаем ток во вторичном контуре. Известно (см. табл. 4.3), что при полном резонансе 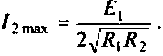
Тогда, учитывая, что контуры настроены в резонанс, то из (4.34) получаем
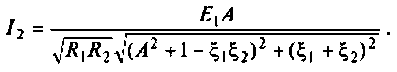
Оба контура по условию настроены в резонанс, поэтому расстройки равны нулю:
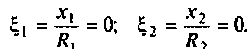
С учетом этого рассчитаем ток во втором контуре
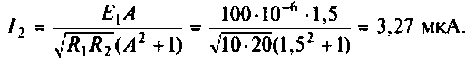
6. Найдем напряжение на конденсаторе вторичного контура
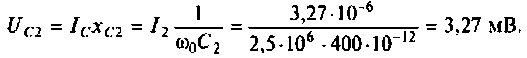
Пример 4.5.5.
На рис. 4.42 приведена схема одного каскада УПЧ радиоприемника, в котором избирательность обеспечивается двумя связанными контурами с емкостной связью. Оба контура настроены в резонанс на промежуточную частоту 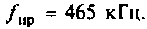
Эквивалентная схема этого каскада (рис. 4.43) имеет следующие параметры: 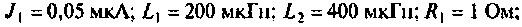
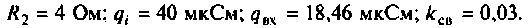
Определить емкости и добротности контуров, емкость связи, напряжение на емкости во вторичном контуре, а также полосу пропускания каскада УПЧ.
Решение
1. Из формулы резонансной частоты найдем емкость первого контура. С учетом влияния выходной емкости транзистора  и емкости монтажа получаем
и емкости монтажа получаем
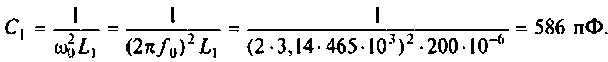
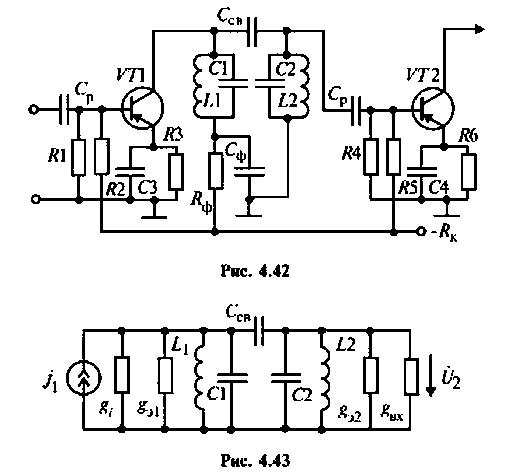
Емкость второго контура с учетом влияния входной емкости транзистора  и емкости монтажа
и емкости монтажа
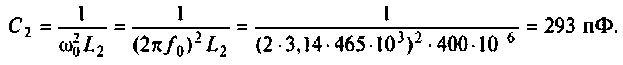
2. Определим емкость связи
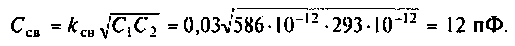
3. Рассчитаем добротности нагруженных контуров при отсутствии связи между ними. Для расчета воспользуемся формулой (4.31)
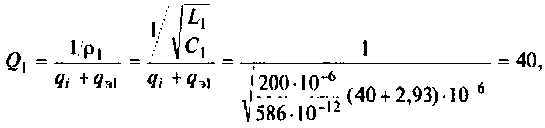
где
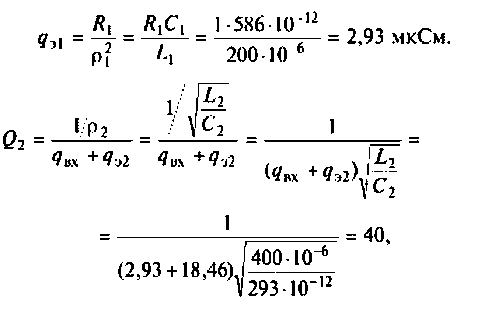
где
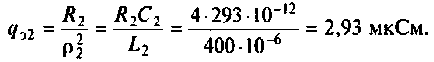
4. Рассчитаем параметр связи 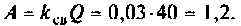
5. Рассчитаем напряжение на втором контуре. Известно (см. табл. 4.4), что при полном резонансе
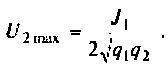
Тогда, учитывая, что контуры настроены в резонанс 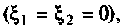 из (4.35) получаем
из (4.35) получаем
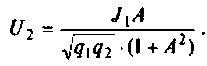
Найдем проводимость контуров
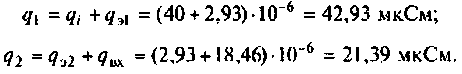
Тогда
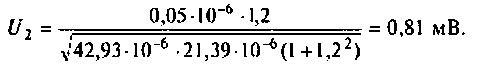
6. Рассчитаем полосу пропускания каскадов УПЧ. учитывая, что А = 1,2.
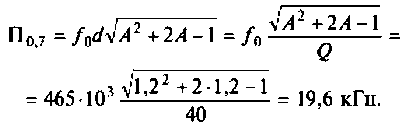
Частотные методы расчета и построения переходных и установившихся процессов в электрических цепях
Основные теоретические сведения:
Зная частотную характеристику электрической цепи 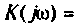
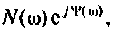 можно определить ее выходную величину при подаче на вход синусоидального (гармонического) сигнала. Действительно, если на вход цепи подано синусоидальное напряжение комплексное изображение которого
можно определить ее выходную величину при подаче на вход синусоидального (гармонического) сигнала. Действительно, если на вход цепи подано синусоидальное напряжение комплексное изображение которого 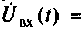
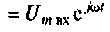 то в установившемся режиме комплексное изображение выходного напряжения
то в установившемся режиме комплексное изображение выходного напряжения
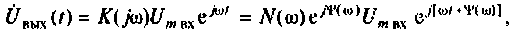
где 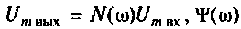 амплитуда и сдвиг по фазе выходных колебаний соответственно.
амплитуда и сдвиг по фазе выходных колебаний соответственно.
С помощью частотной характеристики электрической цели можно не только определить выходную величину цепи в установившемся режиме при гармоническом входном воздействии, но и найти реакцию цепи в переходном процессе на произвольное воздействие 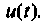 . Действительно, представляя это воздействие в зависимости от того, является оно периодической или непериодической функцией, в виде ряда или интеграла Фурье, т.е. в виде бесконечной суммы гармонических колебаний. По частотной характеристике можно определить реакцию электрической цепи на каждое из этих элементарных колебаний, а затем, просуммировав все реакции, найти результирующую реакцию в виде суммы или интеграла [4].
. Действительно, представляя это воздействие в зависимости от того, является оно периодической или непериодической функцией, в виде ряда или интеграла Фурье, т.е. в виде бесконечной суммы гармонических колебаний. По частотной характеристике можно определить реакцию электрической цепи на каждое из этих элементарных колебаний, а затем, просуммировав все реакции, найти результирующую реакцию в виде суммы или интеграла [4].
Найдем реакцию цепи на единичную ступенчатую функцию (т.е. найдем переходную функцию цепи), используя ее частотную характеристику. Как известно, интеграл Фурье для единичной ступенчатой функции имеет вид
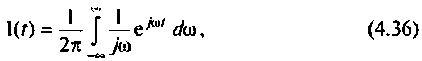
т.е. единичная ступенчатая функция может быть представлена как бесконечная сумма элементарных колебаний вида 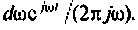
Каждому из этих колебаний соответствует выходное колебание 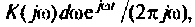 а реакция системы на единичную ступенчатую функцию выражается интегралом
а реакция системы на единичную ступенчатую функцию выражается интегралом
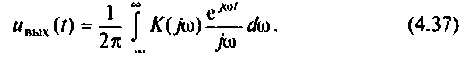
Представляя 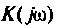 в алгебраической форме
в алгебраической форме 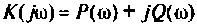 и преобразуя выражение (4.37), получаем следующую формулу для переходной функции |4, 6|:
и преобразуя выражение (4.37), получаем следующую формулу для переходной функции |4, 6|:
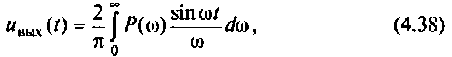
где 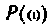 — вещественная частотная характеристика (ВЧХ) КФ электрической цепи. Полученное выражение связывает ВЧХ КПФ цепи с ее переходной функцией. Таким образом, при частотном методе анализа косвенной характеристикой переходной функции является вещественная частотная характеристика КФ электрической цепи.
— вещественная частотная характеристика (ВЧХ) КФ электрической цепи. Полученное выражение связывает ВЧХ КПФ цепи с ее переходной функцией. Таким образом, при частотном методе анализа косвенной характеристикой переходной функции является вещественная частотная характеристика КФ электрической цепи.
Построение переходной функции с помощью вещественной частотной характеристики методами численного интегрирования:
Выражение (4.38) позволяет вычислить переходную функцию ЭЦ и определить качество переходного процесса. Однако интегрирование этого выражения аналитическими методами — задача весьма трудоемкая, а чаще всего просто практически невыполнимая. С применением современных ЭВМ и методов численного интегрирования (метод прямоугольников, трапеций, метод Симпсона и др.) эта задача существенно упрощается, ее решение сводится к составлению программы для ПЭВМ. В инженерной практике интегрирование достаточно осуществлять в области существенных частот от 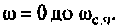 В области частот
В области частот  влияние ВЧХ
влияние ВЧХ 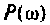 на переходную функцию (4.38) мало и им можно пренебречь. В dtom случае используют модифицированное выражение от (4.38) [4]
на переходную функцию (4.38) мало и им можно пренебречь. В dtom случае используют модифицированное выражение от (4.38) [4]
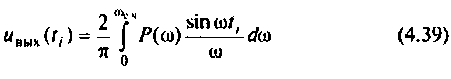
В результате интегрирования получают совокупность значений 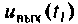 переходной функции системы и исследуемом интервале времени и строят график переходной функции, по которой определяют показатели качества переходного процесса.
переходной функции системы и исследуемом интервале времени и строят график переходной функции, по которой определяют показатели качества переходного процесса.
В качестве примера построения алгоритма численного интегрирования рассмотрим интегрирование с точки зрения простоты вычислений и точности результата. Сущность метода заключается в следующем. Пусть необходимо вычислить определенный интеграл
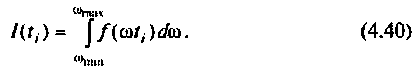
Вид подынтегральной функции, соответствующей выражению
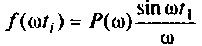
при фиксированном времени 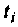 приведен на рис. 4.47, кривая
приведен на рис. 4.47, кривая 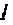 для t = 10 с, кривая 2 для
для t = 10 с, кривая 2 для 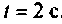 , а кривая 3 изображает ВЧХ электрической цепи. Функция
, а кривая 3 изображает ВЧХ электрической цепи. Функция 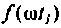 представляет функцию
представляет функцию 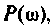 модулированную «замечательным» синусом. Известно, что интеграл (4.40) численно равен площади под кривой функции
модулированную «замечательным» синусом. Известно, что интеграл (4.40) численно равен площади под кривой функции 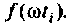 Если интервал аргумента
Если интервал аргумента 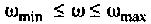 разбить на
разбить на 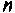 равных частей, то длина одного интервала будет равна
равных частей, то длина одного интервала будет равна 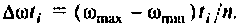 Площадь под кривой можно аппроксимировать суммой площадей прямоугольных трапеций с основаниями
Площадь под кривой можно аппроксимировать суммой площадей прямоугольных трапеций с основаниями 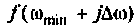
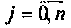 и высотой
и высотой  Тогда интеграл (4.40) можно представить как сумму площадей прямоугольных трапеций:
Тогда интеграл (4.40) можно представить как сумму площадей прямоугольных трапеций:
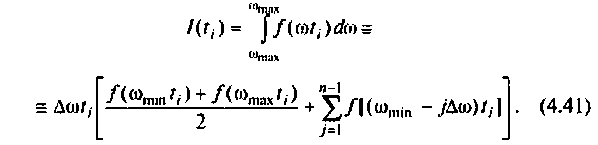
Очевидно, что погрешность численного интегрирования зависит и от выбора числа интервалов  разбиения аргумента
разбиения аргумента  при конкретном времени
при конкретном времени  При увеличении времени , как видно из рис. 4.47, период подынтегральной функции уменьшается. Следовательно, необходимо увеличивать число интервалов, которое определился выражением
При увеличении времени , как видно из рис. 4.47, период подынтегральной функции уменьшается. Следовательно, необходимо увеличивать число интервалов, которое определился выражением

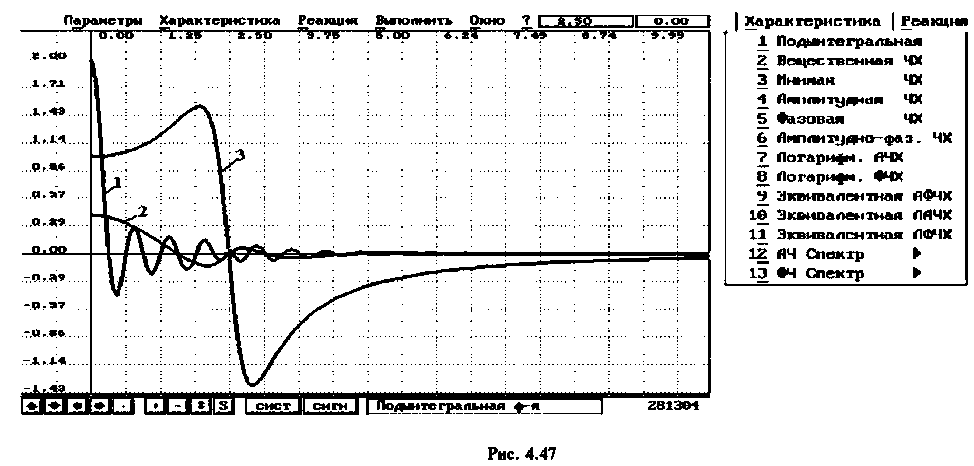
При этом одно полное колебание подынтегральной функции представляется не менее чем шестнадцатью трапециями.
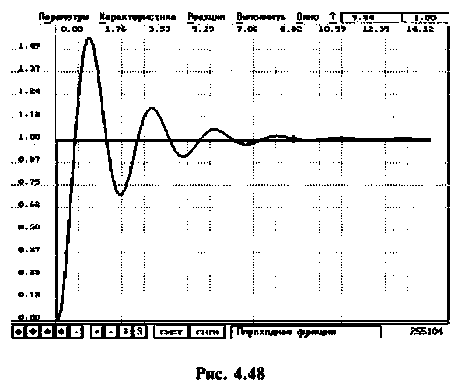
В качестве примера для построения переходной функции возьмем электрическую цепь, ВЧХ которой была построена и приведена на рис. 4.47 (кривая 3). На рис. 4.48 приведена переходная функция этой сложной электрической цепи.
Переходная функция на рис. 4.48 получена с помощью пакета ПП «Сигнал» [5].
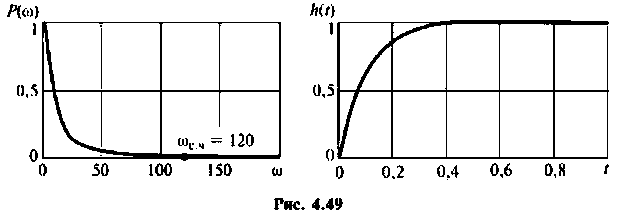
Для вычисления интеграла (4.39) необходимо определить значение частоты для верхнего предела интегрирования  Это значение легко может быть определено из кривой вещественной частотной характеристики (ВЧХ) КФ электрической цепи. В качестве примера возьмем простую интегрирующую цепь (см. рис. 4.1), КФ которой имеет вид
Это значение легко может быть определено из кривой вещественной частотной характеристики (ВЧХ) КФ электрической цепи. В качестве примера возьмем простую интегрирующую цепь (см. рис. 4.1), КФ которой имеет вид
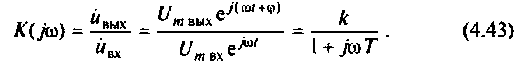
Алгебраическая форма КФ
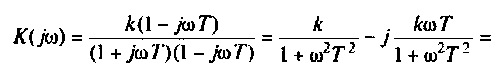
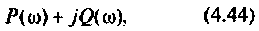
где 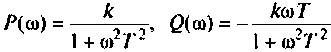 — вещественная и мнимая части КФ. Построим кривую
— вещественная и мнимая части КФ. Построим кривую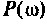 (рис. 4.49) в среде Mathcad, если
(рис. 4.49) в среде Mathcad, если 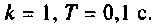 .
.
Из графика ВЧХ видно, что при 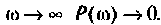 Влияние ВЧХ в области больших частот на переходную функцию несущественно, поэтому за частоту
Влияние ВЧХ в области больших частот на переходную функцию несущественно, поэтому за частоту 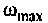 можно принять частоту, при которой ВЧХ принимает значение
можно принять частоту, при которой ВЧХ принимает значение 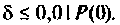 Эту частоту принято называть «существенной частотой» и обозначать
Эту частоту принято называть «существенной частотой» и обозначать 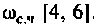 . В нашем примере
. В нашем примере 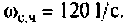 Переходная функция, вычисленная по выражению (4.39), приведена на рис. 4.49.
Переходная функция, вычисленная по выражению (4.39), приведена на рис. 4.49.
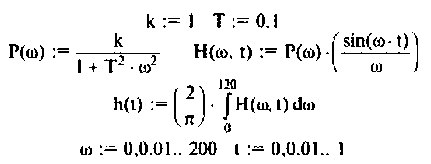
Для случая электрических цепей с дифференцирующими свойствами может оказаться, что при  ВЧХ КФ этой цепи
ВЧХ КФ этой цепи 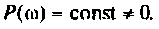 Тогда для расчета переходной функции необходимо использовать мнимую частотную характеристику (МЧХ) в соответствии с выражением
Тогда для расчета переходной функции необходимо использовать мнимую частотную характеристику (МЧХ) в соответствии с выражением
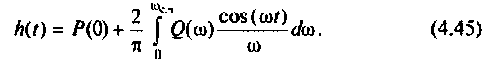
Приведенный пример наглядно показывает, что использование частотных характеристик для построения временных характеристик с помощью ЭВМ существенно расширяет возможности частотных методов анализа электрических цепей.
Спектральный метод расчета и построения выходных величин электрических цепей при сложных входных воздействиях:
Применение частотных методов при анализе и синтезе электрических цепей с требуемыми динамическими характеристиками и использованием ЭВМ позволяет не только строить переходные характеристики, но и строить реакцию цепи на любые детерминированные воздействия, оценивать их в установившихся режимах.
Математической основой частотных методов анализа электрических цепей и систем автоматического управления является обратное преобразование Фурье, позволяющее получать изображение выходного сигнала системы y(t) с помощью вещественной и мнимой частотных характеристик систем. В свою очередь, по вещественной или мнимой частотным характеристикам можно построить переходный процесс выходной величины и оценить реакцию цепи в переходном и установившемся режимах.
Как известно, реакция системы определяется по формуле обратного преобразования Фурье [4]
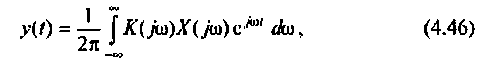
где 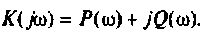
После соответствующих преобразований выражение (4.46) примет вид:
I) для ступенчатой входной функции 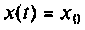 спектром
спектром 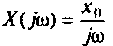
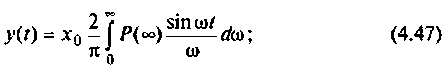
2) для линейной входной функции 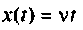 со спектром
со спектром 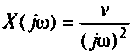
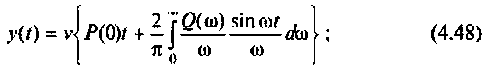
y{t) = vP(0)t+±l
2 r0(
Л» И
(4.48)
О)
3) для параболической входной функции 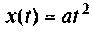 со спектром
со спектром 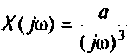
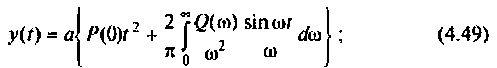
4) для полиномиального воздействия вида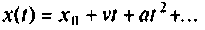
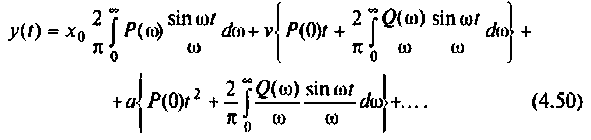
Применение ЭВМ и численных методов интегрирования позволяет отказаться от графических и табличных методов построения переходных и других необходимых функций в электрических цепях.
Примеры решения типовых задач:
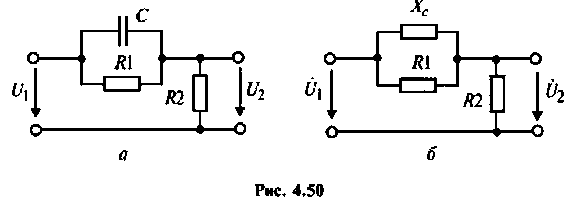
Пример 4.6.1.
Определить комплексный коэффициент передачи по напряжению для дифференцирующего 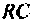 -контура (рис. 4.50,а), рассчитать и построить переходную функцию контура с помощью ВЧХ.
-контура (рис. 4.50,а), рассчитать и построить переходную функцию контура с помощью ВЧХ.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.50, б).
2. Определим комплексное напряжение на выходе цепи в виде
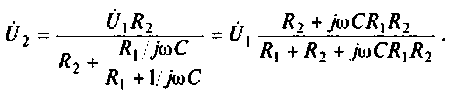
Преобразуем полученное выражение, вынеся за скобки в числителе и знаменателе члены, не содержащие 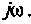 После преобразований получим
После преобразований получим
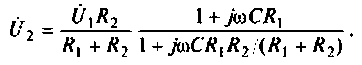
Следовательно
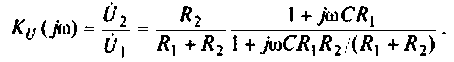
Введем обозначения:
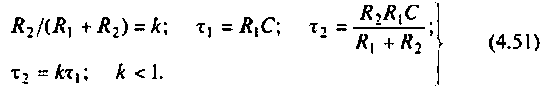
Величина 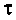 называется постоянной времени цепи и измеряется в секундах. Величина k имеет смысл коэффициента усиления по напряжению на постоянном токе, т. е. на частоте
называется постоянной времени цепи и измеряется в секундах. Величина k имеет смысл коэффициента усиления по напряжению на постоянном токе, т. е. на частоте 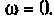 С учетом принятых обозначений
С учетом принятых обозначений
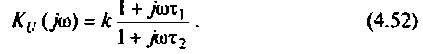
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
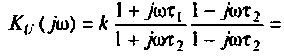
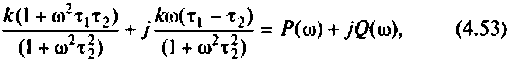
где 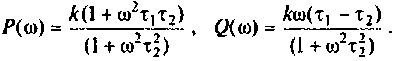
Примем: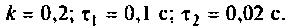
Для определения частоты 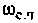 в среде Mathcad построим кривые ВЧХ и МЧХ (рис. 4.51).
в среде Mathcad построим кривые ВЧХ и МЧХ (рис. 4.51).
Из частотных характеристик КПФ принимаем 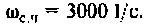 Для построения переходной функции воспользуемся выражением (4.45). Построение проведем также в среде Mathcad.
Для построения переходной функции воспользуемся выражением (4.45). Построение проведем также в среде Mathcad.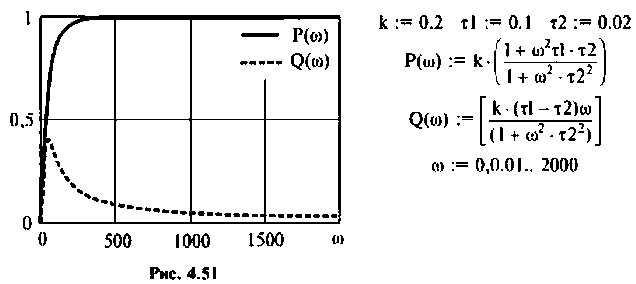
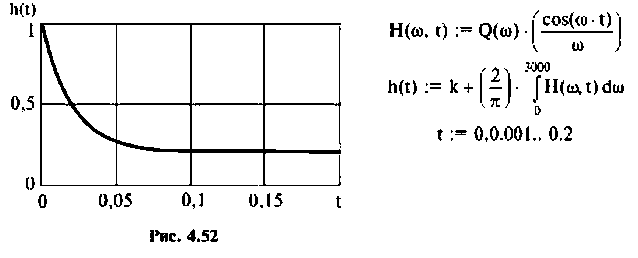
Переходная функция, показанная на рис.4.52, соответствует дифференцирую щему фазоопережающему контуру, который широко применяется в электронных и радиотехнических устройствах, системах автоматического управления.
Пример 4.6.2.
Для электрической цепи, изображенной на рис, 4.53, определить КПФ 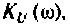 построить ВЧХ
построить ВЧХ 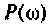 и МЧХ
и МЧХ 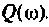 . Рассчитать и построить график переходной функции. Параметры цепи:
. Рассчитать и построить график переходной функции. Параметры цепи: 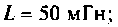
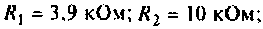
Решение
1. Найдем комплексную функцию 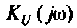 по формуле делителя напряжения
по формуле делителя напряжения
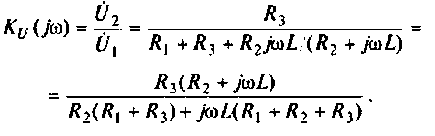
Преобразуем полученное выражение к виду
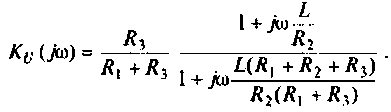
Обозначим:
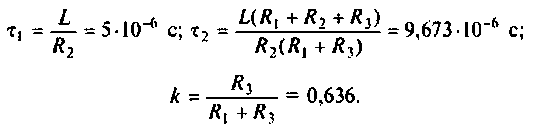
Следовательно,
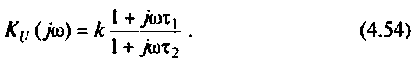
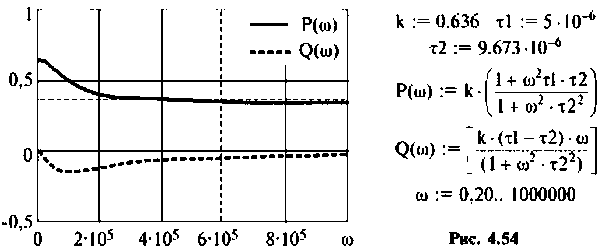
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
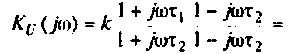
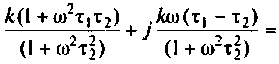
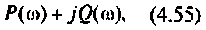
где 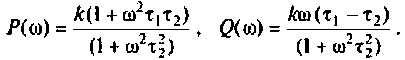
Для определения частоты 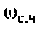 в среде Mathcad построим кривые ВЧХ и МЧХ (рис. 4.54).
в среде Mathcad построим кривые ВЧХ и МЧХ (рис. 4.54).
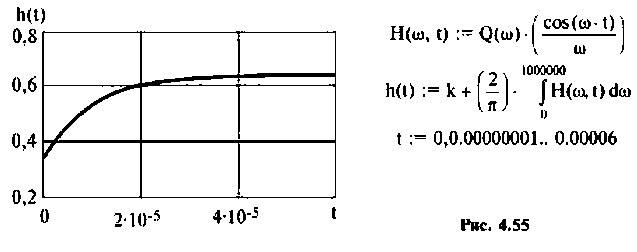
По виду ВЧХ и МЧХ определяем, что для построения переходной функции необходимо применить МЧХ. Примем из графика МЧХ 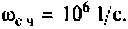 Переходная функция и программа для ее вычисления и построения приведена на рис. 4.55.
Переходная функция и программа для ее вычисления и построения приведена на рис. 4.55.
Из рис. 4.55 видно, что переходная функция соответствует интегрирующему контуру.
Пример 4.6.3.
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.56, а), используя метод контурных токов. Построить в среде Mathcad графики АЧХ, ВЧХ, МЧХ. Рассчитать и построить эпюру входного и выходного напряжения, если на вход цепи поступает напряжение вида 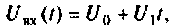 где
где 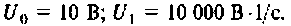
Параметры цепи: 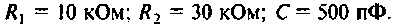
Решение
1.Представим цепь комплексной схемой замещения (рис. 4.56, б). Данная цепь имеет два независимых контура. Ток  в первом контуре замыкается через источник, который на схеме не изображен. Направление контурных тиков выбираем одинаковым.
в первом контуре замыкается через источник, который на схеме не изображен. Направление контурных тиков выбираем одинаковым.
2.Составим матрицы контурных сопротивлений для двух независимых контуров
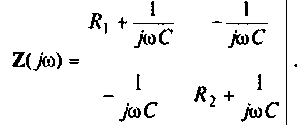
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
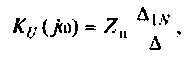
где сопротивление нагрузки 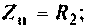
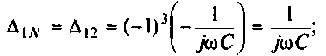
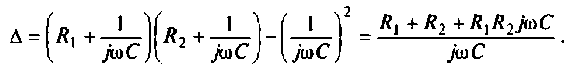
Подставляя найденные выражения, получаем
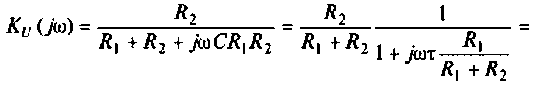
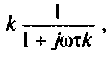
т.е. 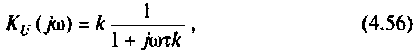
где 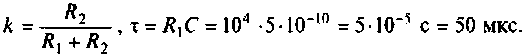
4. Рассчитаем  для крайних значений частоты
для крайних значений частоты 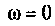 и
и 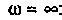
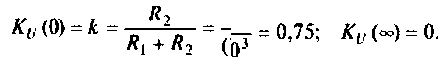
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 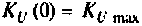 = = 0,75. С ростом частоты емкостное сопротивление уменьшается. Если
= = 0,75. С ростом частоты емкостное сопротивление уменьшается. Если 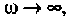 то
то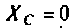 и шунтирует сопротивление
и шунтирует сопротивление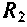 . При этом
. При этом
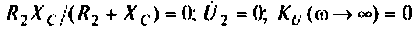
5.Определим выражения для АЧХ, ВЧХ, МЧХ. Представим КГ1Ф (4.55) в алгебраической форме
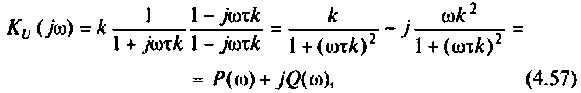
где 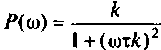 вещественная частотная характеристика:
вещественная частотная характеристика:
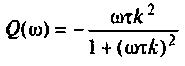 — мнимая частотная характеристика.
— мнимая частотная характеристика.
Амплитудно-частотную характеристику запишем в виде
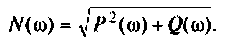
6. В среде Mathcad построим частотные характеристики и определим 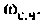
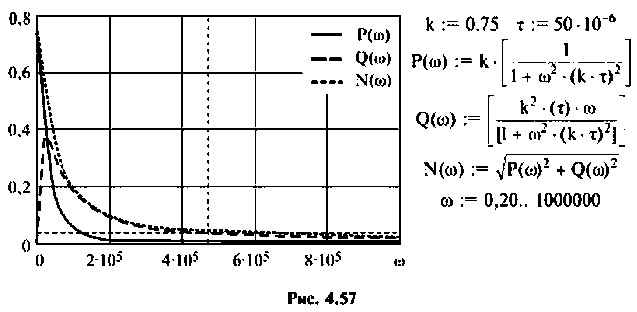
По ВЧХ на рис. 4.57 определяем, что существенная частота 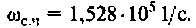
7. Построим переходную функцию электрической цепи, которая представлена на рис. 4.58.
Переходная функция электрической цепи соответствует апериодическому звену.
8. Построим реакцию электрической цепи на напряжение, изменяющееся но линейному закону (рис. 4.59).
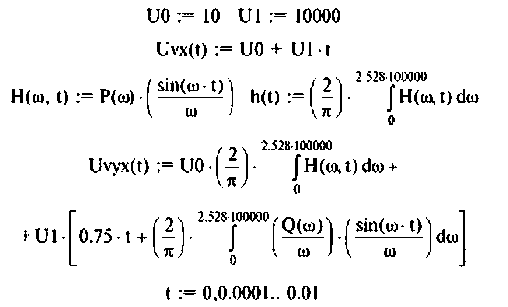
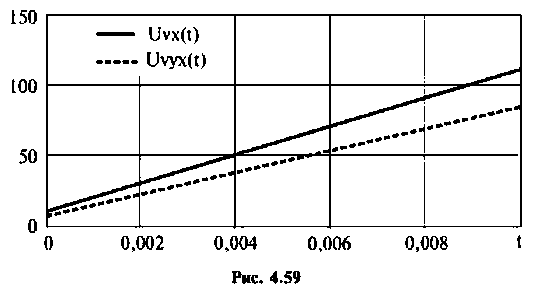
- Операторные передаточные функции
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей
Во время передачи тех или иных сигналов ток высокой частоты в антенне радиопередатчика состоит из нескольких токов различной частоты. Такой же сложный характер имеют электромагнитные волны, распространяющиеся от антенны передатчика, и токи, возникающие под действием радиоволн в приемной антенне.
Для каждого вида передачи (радиотелефония, радиотелеграфия, телевизионная передача и т. д.) частоты этих токов занимают определенную полосу. При радиовещании на средних волнах она составляет примерно 9 кГц, т. е. радиовещательный передатчик создает сложный ток, состоящий из нескольких токов, у которых наиболее высокая частота на 9 кГц больше наиболее низкой частоты. Например, для радиовещательного передатчика, работающего на частоте 173 кГц (? =1734 м), это будут частоты от 168,5 до 177,5 кГц. В случае служебной радиотелефонной связи полоса частот не больше 2 — 2,5 кГц, а для радиотелеграфной передачи она еще меньше. Зато при телевизионной передаче полоса частот расширяется до нескольких мегагерц.
При воздействии на контур электродвижущих сил различной частоты наиболее сильные колебания получаются в случае, когда эдс имеет резонансную частоту или частоту, близкую к ней. А при значительном отклонении частоты внешней эдс от резонансного значения, т. е. когда контур расстроен относительно частоты внешней эдс, амплитуда колебаний получается сравнительно малой.
Можно сказать, что каждый контур хорошо пропускает колебания в пределах некоторой полосы частот, располагающейся по обе стороны от резонансной частоты. Ее называют полосой пропускания контура Ппр и условно определяют по резонансной кривой на уровне 0,7 от максимального значения тока или напряжения, соответствующего резонансной частоте (рис.1).
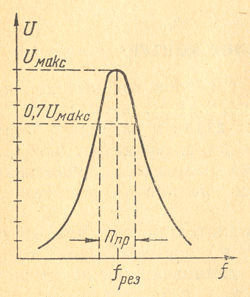
Рис.1 — Полоса пропускания контура
Иначе говоря, считают, что контур хорошо пропускает колебания тогда, когда их амплитуда уменьшается не более, чем на 30% по сравнению с амплитудой при резонансе. Полосу пропускания контура иногда называют также шириной кривой резонанса. Качество контура влияет на форму резонансной кривой. Из этого рисунка видно, что чем ниже качество контура, тем больше его полоса пропускания. Кроме того, полоса пропускания получается больше при более высокой резонансной частоте контура.
Зависимость полосы пропускания контура от его затухания или добротности Q дается следующей простой формулой
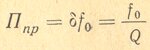
Например, контур, настроенный на частоту fо = 2000 кГц и обладающий затуханием ? = 0,01, имеет полосу пропускания Ппр =0,01 * 2000 = 20 кГц.
Как видно, для получения узкой полосы пропускания необходимо применять контур с высокой добротностью, а для широкой полосы добротность, либо работать на весьма высокой резонансной частоте.
Из приведенной формулы следует, что fo = Q * Ппp. Так как у контура среднего качества Q не менее 20, то рабочая частота должна не менее, чем в 20 раз, превышать полосу пропускания. Например, телевизионную передачу, для которой Ппр составляет несколько мегагерц, нужно вести на частотах не ниже нескольких десятков мегагерц, т.е. на ультракоротких волнах.
Желательно, чтобы контур имел полосу пропускания соответствующую полосе частот, которая характерна для данного вида передачи. Если полоса пропускания меньше, то получатся искажения за счет плохого пропускания некоторых колебаний. Более широкая полоса нежелательна, так как могут быть помехи от сигналов радиостанций, работающих на соседних частотах.
Если необходима широкая полоса пропускания, то приходится часто применять контуры с низкой добротностью. Добротность контура снижается, а полоса пропускания увеличивается, если параллельно контуру присоединяют активное сопротивление R, называемое шунтирующим (рис.2). Действительно, переменное напряжение U, имеющееся на контуре, приложено к сопротивлению R и создает в нем ток. Следовательно, в этом сопротивлении будет расходоваться мощность. Чем меньше сопротивление R, тем больше в нем потери мощности и тем больше затухание контура. Если сопротивление R будет очень малым, то оно замкнет накоротко один из элементов контура (конденсатор на (рис.2 а) или весь контур (рис.2 б). Тогда контур вообще не сможет работать как колебательная система и проявлять свои резонансные свойства.
Рис.1 — Шунтирование контура активным сопротивлением
Шунтирование контура активным сопротивлением делают иногда специально с целью расширения полосы пропускания. Кроме того, подобное шунтирование существует вследствие того, что контур соединен с другими деталями и цепями. За счет этого происходит нежелательное ухудшение качества контура.
Внутреннее сопротивление генератора, питающего параллельный контур, также влияет на добротность контура и его полосу пропускания. Это можно легко объяснить следующим образом.
Пусть генератор в какой-то момент прекратил свое действие. Тогда колебания в контуре станут затухать, а внутреннее сопротивление генератора, присоединенного к контуру, будет играть роль шунтирующего сопротивления, увеличивающего затухание.
Чем больше Ri генератора, тем слабее его влияние, а значит, кривая резонанса контура острее и его полоса пропускания меньше, т.е. резонансные свойства контура выражены резче. При малом Ri генератора добротность контура настолько снижается и полоса пропускания становится такой широкой, что резонансные свойства у контура практически отсутствуют.
К подобному выводу о влиянии Ri генератора мы пришли уже ранее при рассмотрении работы параллельного контура.
Другой разновидностью линейных цепей являются колебательные контуры. С их помощью решается одна из важнейших задач радиотехники – осуществление частотной селекции (избирательности). Из множества несущих частот различных радиостанций, поступающих в антенну радиоприемника, необходимо выбрать узкую полосу частот интересующей нас радиостанции. Для решения этой задачи нужны частотно–избирательные цепи в виде колебательных контуров. Колебательный контур – это линейная электрическая цепь, составленная из конденсатора ![]() и катушки индуктивности
и катушки индуктивности ![]()
3.4.1.Свободные колебания в идеальном контуре
Рассмотрим вначале колебательный контур, в котором отсутствуют потери электрической энергии, то есть контур из идеальной катушки индуктивности и идеального конденсатора. Зарядим однократно конденсатор от внешней батареи до напряжения ![]() . При этом электрическая энергия, запасенная конденсатором, будет равна
. При этом электрическая энергия, запасенная конденсатором, будет равна
 (3.45)
(3.45)
За счет разряда конденсатора через катушку индуктивности происходит преобразование электрической энергии в магнитную энергию. При этом магнитная энергия, запасенная катушкой индуктивности, становится равной
 . (3.46)
. (3.46)
Затем происходит обратное преобразование магнитной энергии в электрическую энергию. В результате в контуре происходит колебательный процесс на некоторой частоте ![]() , Которая называется резонансной частотой. Такие колебания называются свободными. Найдем частоту свободных колебаний из равенства электрической и магнитной энергий:
, Которая называется резонансной частотой. Такие колебания называются свободными. Найдем частоту свободных колебаний из равенства электрической и магнитной энергий:
 . (3.47)
. (3.47)
Учитывая, что ![]() , подставим значение
, подставим значение ![]() В предыдущее выражение:
В предыдущее выражение:
 (3.48)
(3.48)
Отсюда резонансная частота колебаний
![]() , (3.49)
, (3.49)
А период колебаний
 . (3.50)
. (3.50)
Из равенства энергий найдем волновое (характеристическое) сопротивление контура ![]() :
:
 . (3.51)
. (3.51)
На резонансной частоте модуль реактивного сопротивления катушки индуктивности равен модулю реактивного сопротивления конденсатора:
 (3.52)
(3.52)
Подставляя значение резонансной частоты в выражения для модулей реактивных сопротивлений, получим:
 , (3.53)
, (3.53)
![]() =
=![]() (3.54)
(3.54)
Таким образом, на резонансной частоте сопротивления реактивных элементов контура равны волновому сопротивлению. В идеальном контуре колебания будут незатухающими.
3.4.2.Свободные колебания в реальном контуре
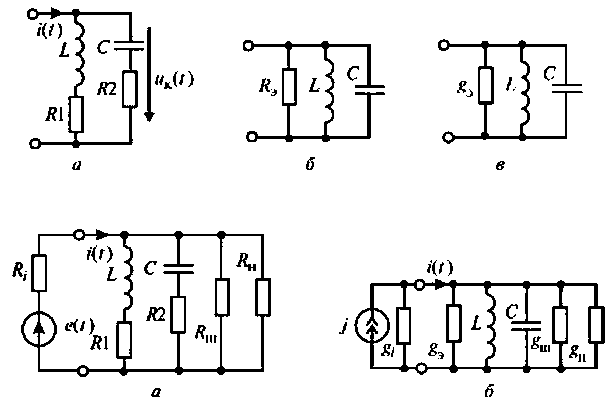
Рассмотрим физические процессы в реальном контуре, состоящем из последовательно соединенных катушки индуктивности, конденсатора и некоторого активного сопротивления потерь ![]() . Сопротивление
. Сопротивление ![]() эквивалентно омическому сопротивлению катушки индуктивности и сопротивлению потерь электрической энергии в конденсаторе.
эквивалентно омическому сопротивлению катушки индуктивности и сопротивлению потерь электрической энергии в конденсаторе.

Рис. 3.11. Последовательный колебательный контур
Если зарядить однократно от внешней батареи конденсатор, то в контуре возникнет колебательный процесс. На основе второго закона Кирхгофа можно записать:
![]() . (3.55)
. (3.55)
Или:
![]() (3.56)
(3.56)
Продифференцируем все слагаемые уравнения (2.55) по времени и разделим на ![]() :
:
 (3.57)
(3.57)
Обозначим ![]() , Где
, Где ![]() — коэффициент затухания.
— коэффициент затухания.
Учитывая, что ![]() , перепишем уравнение в следующем виде:
, перепишем уравнение в следующем виде:
 (3.58)
(3.58)
Ищем решение этого уравнения в виде: ![]()
![]() .
.
Подставим это решение в уравнение:
 (3.59)
(3.59)
Или:
 , (3.60)
, (3.60)
Где: ![]() .
.
![]() — резонансная частота реального контура.
— резонансная частота реального контура.![]()
Решение последнего уравнения имеет вид:
![]() (3.61)
(3.61)
Отсюда ток в контуре равен:
![]() . (3.62)
. (3.62)
Полагая начальную фазу j=0, ток в контуре будет равен:
![]() (3.63)
(3.63)
Если a=0, то колебания не затухают. При этом:
![]() (3.64)
(3.64)
![]() (3.65)
(3.65)
В реальном контуре ![]() , поэтому колебания на частоте
, поэтому колебания на частоте ![]() Будут затухающими.
Будут затухающими.

![]()
Рис. 3.12. Затухающие колебания в контуре с потерями
Период колебаний реального контура:
![]()
![]()
 (3.66)
(3.66)
Если ![]() , то период колебаний
, то период колебаний ![]() . При этом колебательный процесс невозможен, а имеет место апериодический разряд конденсатора через катушку индуктивности и сопротивление потерь.
. При этом колебательный процесс невозможен, а имеет место апериодический разряд конденсатора через катушку индуктивности и сопротивление потерь.
Колебательный процесс возможен только, когда ![]() или
или ![]() .
.
Отсюда:  или
или ![]() .
.
У радиотехнических контуров волновое сопротивление ![]() .
.
Поэтому с большой степенью точности можно считать, что период колебаний и резонансная частота в реальном контуре определяются следующими выражениями:
![]() (3.67)
(3.67)
![]() (3.68)
(3.68)
По степени затухания колебательного процесса можно судить о качестве контура, которое оценивается добротностью:
![]() (3.69)
(3.69)
Для радиотехнических контуров добротность ![]()
Добротность контура равна отношению напряжения на индуктивности ![]() или на емкости
или на емкости ![]() к напряжению на активном сопротивлении при резонансе:
к напряжению на активном сопротивлении при резонансе:
 (3.70)
(3.70)
В этом выражении ![]() — Ток в контуре на резонансной частоте.
— Ток в контуре на резонансной частоте.
Умножим числитель и знаменатель на ![]() :
:
![]()
 . (3.71)
. (3.71)
Добротность равна умноженному на 2![]() отношению энергии, запасенной в контуре, к энергии, теряемой за один период колебаний.
отношению энергии, запасенной в контуре, к энергии, теряемой за один период колебаний.
Величина обратная добротности называется затуханием контура:
 . (3.72)
. (3.72)
3.4.3.Последовательный контур. Вынужденные колебания.
На рис. 3.13 представлен последовательный колебательный контур, к которому подключен генератор гармонических сигналов ![]() , внутреннее сопротивление которого равно нулю.
, внутреннее сопротивление которого равно нулю.

Рис3.13. Последовательный контур с внешним генератором
На основании второго закона Кирхгофа запишем:
![]() . (3.73)
. (3.73)
Ток в контуре будет равен:
 (3.74)
(3.74)
Входное сопротивление
![]()
![]() . (3.75)
. (3.75)
Реактивная составляющая входного сопротивления
![]() . (3.76)
. (3.76)
В зависимости от расстройки контура относительно резонансной частоты возможны три случая:
![]() — При этом реактивная составляющая входного сопротивления
— При этом реактивная составляющая входного сопротивления ![]() носит индуктивный характер;
носит индуктивный характер;
![]() При этом реактивная составляющая входного сопротивления
При этом реактивная составляющая входного сопротивления ![]() носит емкостный характер;
носит емкостный характер;
![]() при этом реактивная составляющая входного сопротивления равна нулю. Реактивные сопротивления будут равны на резонансной частоте.
при этом реактивная составляющая входного сопротивления равна нулю. Реактивные сопротивления будут равны на резонансной частоте.
На резонансной частоте входное сопротивление контура равно активному сопротивлению и ток в контуре равен значению ![]() .
.
Эквивалентная схема контура при резонансе приведена на рисунке.

Рис. 3.14. Эквивалентная схема последовательного контура на
Резонансной частоте.
Амплитуды напряжений на реактивных элементах на резонансной частоте равны по величине и противоположны по фазе.
 . (3.77)
. (3.77)
Из этого выражения найдем резонансную частоту:
![]() . (3.78)
. (3.78)
Оценим величину отношения напряжений на реактивных элементах на резонансной частоте к напряжению внешнего генератора:
 , (3.79)
, (3.79)
 . (3.80)
. (3.80)
Таким образом, на резонансной частоте в последовательном контуре напряжения на реактивных элементах равны по абсолютной величине и в Q раз превышают напряжение внешнего генератора. Такой резонанс называется резонансом напряжений.
3.4.4.Амплитудно-частотная характеристика последовательного контура.
Зависимость тока в контуре или напряжения на реактивных элементах от частоты питающего генератора при постоянном по величине напряжении генератора называется резонансной кривой или амплитудно-частотной характеристикой контура.
Для сравнения различных контуров резонансные кривые строят в относительном масштабе. Амплитудно-частотная характеристика в относительном масштабе контура, представленного на рис. 2.14, запишется как отношение тока в контуре на любой частоте к току в контуре на резонансной частоте:
 =
= . (3.81)
. (3.81)
Реактивная составляющая входного сопротивления контура равна:
 (3.82)
(3.82)
Здесь
![]() (3.83)
(3.83)
— относительная расстройка контура.
Для небольших абсолютных расстроек контура ![]() (в пределах полосы пропускания)
(в пределах полосы пропускания)
![]() (3.84)
(3.84)
С учетом этого амплитудно-частотная характеристика контура
 , (3.85)
, (3.85)
Где:  — обобщенная расстройка контура.
— обобщенная расстройка контура.
Окончательно уравнение амплитудно-частотной характеристики контура запишется в виде:
 . (3.86)
. (3.86)
Фазовая характеристика контура
![]() (3.87)
(3.87)
При настройке контура в резонанс ![]() , обобщенная расстройка
, обобщенная расстройка ![]() , реактивная составляющая входного сопротивления равна нулю и эквивалентное сопротивление контура равно
, реактивная составляющая входного сопротивления равна нулю и эквивалентное сопротивление контура равно ![]() . Характер зависимости
. Характер зависимости ![]() свидетельствует о том, что колебательный контур обладает свойством избирательности. Количественно избирательность контура оценивается коэффициентом прямоугольности
свидетельствует о том, что колебательный контур обладает свойством избирательности. Количественно избирательность контура оценивается коэффициентом прямоугольности ![]() , который равен отношению ширины резонансной кривой на уровне 0,7 к ширине на уровне 0,1. Чем больше значение добротности, тем лучше избирательность контура. Для одиночных колебательных контуров
, который равен отношению ширины резонансной кривой на уровне 0,7 к ширине на уровне 0,1. Чем больше значение добротности, тем лучше избирательность контура. Для одиночных колебательных контуров ![]()
![]() . АЧХ последовательного контура в относительном масштабе представлена на рис. 3.15.
. АЧХ последовательного контура в относительном масштабе представлена на рис. 3.15.
Рис.2.15 АЧХ последовательного контура
Найдем выражение для полосы пропускания колебательного контура. Полоса пропускания оценивается по уменьшению тока в контуре или напряжений на реактивных элементах в ![]() раз по сравнению с их значениями на резонансной частоте. Из формулы для АЧХ контура найдем полосу пропускания:
раз по сравнению с их значениями на резонансной частоте. Из формулы для АЧХ контура найдем полосу пропускания:
 . (3.88)
. (3.88)
Отсюда полоса пропускания контура на уровне ![]() Будет равна:
Будет равна:
 (3.89)
(3.89)
Зная резонансную частоту и полосу пропускания, можно рассчитать добротность контура:
 (3.90)
(3.90)
Фазовая характеристика последовательного контура, построенная по выражению (2.98), приведена на рис. 3.16.
 (3.91)
(3.91)

Рис.3.16. Фазовая характеристика последовательного контура
3.4.5. Параллельный колебательный контур.
Параллельный колебательный контур состоит из параллельно включенных катушки индуктивности и конденсатора, как показано на рис. 3.17. Активное сопротивление катушки индуктивности равно ![]() , а потери электромагнитной энергии в конденсаторе эквивалентны некоторому активному сопротивлению
, а потери электромагнитной энергии в конденсаторе эквивалентны некоторому активному сопротивлению ![]() . Контур питается идеальным генератором тока.
. Контур питается идеальным генератором тока.

Рис. 3.17. Параллельный колебательный контур.
Входное сопротивление контура равно:
 . (3.92)
. (3.92)
Для высокодобротных контуров в области резонансной частоты  и
и  . Учитывая это, можно записать:
. Учитывая это, можно записать:
 (3.93)
(3.93)
Где: ![]() ;
; ![]() .
.
Таким образом, входное сопротивление зависит от частоты. Токи в ветвях контура также зависят от частоты. На резонансной частоте ![]() сопротивление катушки индуктивности по модулю становится равным модулю сопротивления конденсатора и токи в ветвях контура будут равны по абсолютной величине и противоположны по фазе. При этом ток в общей ветви в случае идеального контура был бы равен 0. На резонансной частоте в контуре протекает ток
сопротивление катушки индуктивности по модулю становится равным модулю сопротивления конденсатора и токи в ветвях контура будут равны по абсолютной величине и противоположны по фазе. При этом ток в общей ветви в случае идеального контура был бы равен 0. На резонансной частоте в контуре протекает ток
 . (3.94)
. (3.94)
Входное сопротивление контура при резонансе становится активным и равно:
![]() (3.95)
(3.95)
Следовательно, ток в контуре на резонансной частоте равен:
 (3.96)
(3.96)
Таким образом, токи в ветвях контура при резонансе в ![]() раз превышают ток внешнего генератора. Поэтому говорят, что в параллельном контуре имеет место резонанс токов.
раз превышают ток внешнего генератора. Поэтому говорят, что в параллельном контуре имеет место резонанс токов.
Зависимость отношения амплитуды напряжения на контуре ![]() на текущей частоте к амплитуде напряжения на контуре на резонансной частоте
на текущей частоте к амплитуде напряжения на контуре на резонансной частоте ![]() от частоты называют амплитудно-частотной характеристикой параллельного контура.
от частоты называют амплитудно-частотной характеристикой параллельного контура.
Запишем выражение для амплитудно-частотной характеристики параллельного контура:
 (3.97)
(3.97)
Входное сопротивление контура равно:
![]() (3.98) Умножим числитель и знаменатель этого выражения на (
(3.98) Умножим числитель и знаменатель этого выражения на (![]() ):
):
 . (3.99)
. (3.99)
Найдем модуль входного сопротивления:
 . (3.100)
. (3.100)
Подставив модуль входного сопротивления в выражение (3.97), окончательно получим:
 . (3.101)
. (3.101)
Таким образом, АЧХ параллельного и последовательного контуров описываются одним и тем же выражением.
Фазовая характеристика параллельного контура (рис. 2.18) построена на основании выражения
![]() (3.102)
(3.102)

Рис. 3.18. Фазовая характеристика параллельного контура
3.4.6. Методы измерения добротности колебательных контуров
Существует несколько методов измерения добротности колебательных контуров.
Если подключить к контуру генератор гармонических сигналов и, изменяя частоту генератора, снять резонансную кривую контура, то добротность можно рассчитать по формуле:
 , (3.103)
, (3.103)
Где: ![]() — резонансная частота;
— резонансная частота;
![]() — полоса пропускания контура на уровне 0,7 от максимального значения коэффициента передачи.
— полоса пропускания контура на уровне 0,7 от максимального значения коэффициента передачи.
Добротность контура можно также измерить по затухающим колебаниям в контуре, если подключить к контуру генератор прямоугольных импульсов. При этом прямоугольные импульсы должны быть достаточно короткими и с большим периодом, чтобы к моменту прихода следующего импульса колебания в контуре уже успели закончится (рис. 3.19).

Рис. 3.19. Определение добротности по затухающим колебаниям
Если обозначить начальную амплитуду затухающих колебаний ![]() , то, отсчитав число периодов колебаний, через которое начальная амплитуда уменьшится в
, то, отсчитав число периодов колебаний, через которое начальная амплитуда уменьшится в ![]() раз, можно рассчитать добротность, исходя из следующих выражений:
раз, можно рассчитать добротность, исходя из следующих выражений:
![]() , (3.104)
, (3.104)
 , (3.105)
, (3.105)
![]() . (3.106)
. (3.106)
Таким образом, добротность равна умноженному на ![]() числу периодов, в течение которых начальная амплитуда колебаний уменьшается в
числу периодов, в течение которых начальная амплитуда колебаний уменьшается в ![]() Раз.
Раз.
Кроме названных методов измерения добротности существуют специальные приборы — измерители добротности колебательных контуров.
3.4.7. Связанные контуры.
Недостатком одиночных колебательных контуров является их плохая избирательность. Количественно избирательность оценивается коэффициентом прямоугольности, который равен отношению ширины полосы пропускания на уровне 0,7 к ширине полосы пропускания на уровне 0,1 (иногда на уровне 0,01):
 . (3.107)
. (3.107)
Чем ближе значение коэффициента прямоугольности к 1, тем лучше избирательность контура.
Коэффициент прямоугольности одиночного контура ![]() = 0,1, а двух одиночных контуров, настроенных на одну частоту, примерно 0,21. При неограниченном числе одиночных контуров, настроенных на одну частоту, их коэффициент прямоугольности не превзойдет величину 0,39. Четыре одиночных взаимно расстроенных контура дадут приемлемую прямоугольность АЧХ, но при этом в приемнике надо иметь четыре каскада усиления.
= 0,1, а двух одиночных контуров, настроенных на одну частоту, примерно 0,21. При неограниченном числе одиночных контуров, настроенных на одну частоту, их коэффициент прямоугольности не превзойдет величину 0,39. Четыре одиночных взаимно расстроенных контура дадут приемлемую прямоугольность АЧХ, но при этом в приемнике надо иметь четыре каскада усиления.
Ценным свойством связанных контуров является возможность осуществить АЧХ по форме, близкую к прямоугольной. Связанные контуры взаимно влияют друг на друга. Степень влияния зависит от сопротивления связи. В качестве элементов связи используют конденсаторы и индуктивности. Чаще всего используют индуктивную (трансформаторную) связь. В этом случае степень связи определяется коэффициентом взаимной индукции ![]() . В общем виде два индуктивно связанных контура и их эквивалентная схема представлены на рис. 3.20, где
. В общем виде два индуктивно связанных контура и их эквивалентная схема представлены на рис. 3.20, где ![]() — коэффициент взаимной индукции,
— коэффициент взаимной индукции, ![]() – сопротивление связи.
– сопротивление связи.


Рис. 3.20. Связанные контуры и их эквивалентная схема
Коэффициент взаимной индукции равен:
![]() , (3.108)
, (3.108)
Где: ![]() — магнитный поток, создаваемый током первого контура, сквозь поверхность, охватываемую витками катушки индуктивности второго контура;
— магнитный поток, создаваемый током первого контура, сквозь поверхность, охватываемую витками катушки индуктивности второго контура;
![]() — магнитный поток, создаваемый током второго контура, сквозь поверхность, охватываемую витками катушки индуктивности первого контура.
— магнитный поток, создаваемый током второго контура, сквозь поверхность, охватываемую витками катушки индуктивности первого контура.
Для неферромагнитной среды ![]() .
.
Эдс, индуцируемая во втором контуре, равна:
![]()
![]() (3.109)
(3.109)
Сопротивление связи равно
![]() . (3.110)
. (3.110)
Степень связи между контурами оценивается коэффициентом связи ![]() , который зависит от коэффициентов передачи напряжения от одного контура к другому. Под коэффициентом передачи понимают отношение напряжения (тока или энергии), переданного из первого контура во второй, к тому максимальному напряжению (току или энергии), которое можно было бы передать из первого контура во второй контур.
, который зависит от коэффициентов передачи напряжения от одного контура к другому. Под коэффициентом передачи понимают отношение напряжения (тока или энергии), переданного из первого контура во второй, к тому максимальному напряжению (току или энергии), которое можно было бы передать из первого контура во второй контур.
Коэффициент передачи напряжения из первого контура во второй равен:
![]()
![]() (3.111)
(3.111)
Если включить генератор во второй контур, то получим коэффициент передачи напряжения из второго контура в первый:
 . (3.112)
. (3.112)
Коэффициент связи между контурами равен среднему геометрическому из коэффициентов передачи:
 (3.113)
(3.113)
Коэффициент связи выражает отношение общего магнитного потока, пронизывающего обе катушки индуктивности, к полному магнитному потоку. Величина (![]() ) характеризует поток рассеяния.
) характеризует поток рассеяния.
Выясним характер и форму амплитудно-частотной характеристики системы из двух индуктивно связанных контуров, представленных на рис.2.20. Для упрощения предположим, что контуры состоят из одинаковых элементов ![]() и поэтому имеют одинаковую резонансную частоту
и поэтому имеют одинаковую резонансную частоту ![]() . АЧХ связанных контуров зависит от степени связи между ними. При слабой связи (катушки далеки друг от друга) степень взаимного влияния контуров мала и на резонансной кривой будет один максимум. По мере сближения катушек взаимное влияние контуров возрастает и при некотором коэффициенте связи резонансная кривая становится двугорбой и на ней появляются два максимума (рис.2.22). Максимальная связь, при которой АЧХ остается с одним максимумом, называется критической связью. При связи больше критической АЧХ связанных контуров имеет три экстремальные точки. Одна из них соответствует минимуму коэффициента передачи и будет на резонансной частоте частоте
. АЧХ связанных контуров зависит от степени связи между ними. При слабой связи (катушки далеки друг от друга) степень взаимного влияния контуров мала и на резонансной кривой будет один максимум. По мере сближения катушек взаимное влияние контуров возрастает и при некотором коэффициенте связи резонансная кривая становится двугорбой и на ней появляются два максимума (рис.2.22). Максимальная связь, при которой АЧХ остается с одним максимумом, называется критической связью. При связи больше критической АЧХ связанных контуров имеет три экстремальные точки. Одна из них соответствует минимуму коэффициента передачи и будет на резонансной частоте частоте ![]() . Две другие соответствуют максимуму коэффициента передачи и будут на частотах
. Две другие соответствуют максимуму коэффициента передачи и будут на частотах
 , (3.114)
, (3.114)
 . (3.115) .
. (3.115) .
Частоты ![]() зависят от коэффициента связи
зависят от коэффициента связи ![]() и величины затухания контуров
и величины затухания контуров ![]() и называются частотами связи. Чем больше коэффициент связи, тем больше разнос между частотами связи.
и называются частотами связи. Чем больше коэффициент связи, тем больше разнос между частотами связи. ![]() — быстрая частота связи, а
— быстрая частота связи, а ![]() — медленная частота связи. Зависимость частот связи от коэффициента связи показана на рисунке 3.21.
— медленная частота связи. Зависимость частот связи от коэффициента связи показана на рисунке 3.21.

Рис. 3.21. Зависимость частот связи от коэффициента связи
При критической связи ![]() и на резонансной кривой будет один максимум на частоте
и на резонансной кривой будет один максимум на частоте ![]() .
.
При связи меньше критической ![]() формулы для частот связи
формулы для частот связи ![]() и
и ![]() не имеют смысла и на АЧХ будет только один максимум на частоте
не имеют смысла и на АЧХ будет только один максимум на частоте ![]() .
.
При связи больше критической (![]() ) на АЧХ появляются два максимума на частотах
) на АЧХ появляются два максимума на частотах ![]() и
и ![]() .
.

Рис. 3.22. АЧХ одиночного и двух связанных контуров (![]() ).
).
Полоса пропускания связанных контуров определяется, как ширина АЧХ на уровне 0,7 от максимальной ординаты при этом минимум АЧХ также должен быть на уровне 0,7. Можно показать, что при одинаковом затухании и ![]() Относительная ширина полосы пропускания для связанных контуров получается в 3,1 раза больше, чем для одиночного контура. Коэффициент прямоугольности двух связанных контуров при критической связи равен 0,32. При связи выше критической для системы из двух каскадов связанных контуров коэффициент прямоугольности
Относительная ширина полосы пропускания для связанных контуров получается в 3,1 раза больше, чем для одиночного контура. Коэффициент прямоугольности двух связанных контуров при критической связи равен 0,32. При связи выше критической для системы из двух каскадов связанных контуров коэффициент прямоугольности ![]() = 0,6 , а для трёх – 0,65.
= 0,6 , а для трёх – 0,65.
В серийно выпускаемой радиоаппаратуре в качестве элементов, обеспечивающих высокую избирательность используют пъезофильтры, созданные на основе пьезоэлектриков. Пьезоэлектрики – кристаллические вещества, в которых при сжатии или растяжении в определенных направлениях возникает электрическая поляризация (прямой пьезоэффект). Следствием прямого пьезоэффекта является обратный пьезоэффект – появление механической деформации под действием электрического поля. Пьезофильтр состоит из отдельных, объединенных в группы пьезоэлементов (стержней, пластинок) с нанесенными на определенные поверхности электродами, к которым подводится электрическое напряжение, для создания деформации в результате обратного пьезоэффекта. Пьезофильтр обеспечивает хорошую прямоугольность АЧХ. Добротность керамических пьезофильтров составляет несколько тысяч, а затухание вне полосы составляет -60дБ.
4. Последовательный колебательный контур
4.1. Схема последовательного колебательного контура

 Последовательным колебательным контуром называют электрическую цепь, представляющую собой последовательное соединение катушки индуктивности и конденсатора. Его возможные варианты включения как четырехполюсника показа- ны на рис. 4.1 (выход-
Последовательным колебательным контуром называют электрическую цепь, представляющую собой последовательное соединение катушки индуктивности и конденсатора. Его возможные варианты включения как четырехполюсника показа- ны на рис. 4.1 (выход-
ное напряжение сни- Рис. 4.1
мается с конденсатора
или с катушки индуктивности).
Конденсатор и катушка индуктивности имеют внутренние потери энергии, которые учитываются последовательно соединенными с ними эквивалентными сопротивлениями потерь  и
и  соответственно. На практике в керамических конденсаторах всегда
соответственно. На практике в керамических конденсаторах всегда  и потерями в них пренебрегают, тогда эквивалентные схемы последовательных колебательных контуров рис. 4.1 примут вид, показанный на рис. 4.2.
и потерями в них пренебрегают, тогда эквивалентные схемы последовательных колебательных контуров рис. 4.1 примут вид, показанный на рис. 4.2.

Рис. 4.2
Рекомендуемые материалы
В дальнейшем будем рассматривать схему на рис. 4.2а, в которой выходное напряжение снимается с емкости, а схему
71
на рис. 4.2б аналогично рассмотрите самостоятельно.
4.2. Входное сопротивление последовательного
колебательного контура
Определим входное сопротивление последовательного колебательного контура показанного на рис. 4.3. Полное комплексное сопротивление  равно
равно
 . (4.1)
. (4.1)
Рис. 4.3 Его модуль  , аргумент
, аргумент  , активная
, активная
 и реактивная
и реактивная  составляющие соответственно равны:
составляющие соответственно равны:

Зависимости этих функций от частоты сигнала при  Ом,
Ом,  мГн,
мГн,  нФ показаны на рис. 4.4. На частоте
нФ показаны на рис. 4.4. На частоте
 (4.2)
(4.2)
реактивное сопротивление  и
и  принимает минималь-
принимает минималь-
72
ное значение, равное  ,
,
 . (4.3)
. (4.3)

Рис. 4.4
При отклонении частоты от  модуль сопротивления контура резко возрастает. В области
модуль сопротивления контура резко возрастает. В области  реактивное сопротивление положительно, то есть контур имеет индуктивный характер сопротивления, сдвиг фаз между напряжением и током
реактивное сопротивление положительно, то есть контур имеет индуктивный характер сопротивления, сдвиг фаз между напряжением и током  . В области
. В области  реактивное сопротивление отрицательно и сопротивление контура имеет емкостный характер
реактивное сопротивление отрицательно и сопротивление контура имеет емкостный характер  .
.
4.3. Ток и напряжения в контуре, резонансные явления
Подключим к контуру рис. 4.2а идеальный источник гармонического напряжения, получим схему на рис. 4.5.
73
 Комплексная амплитуда ЭДС источника равна
Комплексная амплитуда ЭДС источника равна  , тогда для комплексной амплитуды тока в контуре получим
, тогда для комплексной амплитуды тока в контуре получим
Рис. 4.5  , (4.4)
, (4.4)
а для его амплитуды  и начальной фазы
и начальной фазы  соответственно
соответственно
 , (4.5)
, (4.5)
 . (4.6)
. (4.6)
Зависимости амплитуды и начальной фазы тока от частоты при  Ом,
Ом,  мГн,
мГн,  нФ,
нФ,  В и
В и  представлены на рис. 4.6.
представлены на рис. 4.6.

Рис. 4.6
74
Ток в контуре резко нарастает при приближении частоты источника к частоте  (4.3), его максимальное значение равно
(4.3), его максимальное значение равно
 . (4.7)
. (4.7)
Однако резонанс тока в последовательном колебательном контуре отсутствует, так как ток в контуре равен току источника, а не возрастает по сравнению с ним.
Так как изменения тока происходят в малой окрестности около частоты  , то целесообразно строить графики в координатах абсолютной расстройки, равной
, то целесообразно строить графики в координатах абсолютной расстройки, равной
 , (4.8)
, (4.8)
то есть производится смещение начала координат в точку  .
.
Те же графики, что и на рис. 4.6, но в координатах  , показаны на рис. 4.7.
, показаны на рис. 4.7.

Рис.4.7
Как видно, координаты абсолютной расстройки удобны для построения графиков частотных характеристик колебательного контура.
75
Определим комплексные амплитуды напряжений на элементах контура:
 , (4.9)
, (4.9)
 , (4.10)
, (4.10)
 . (4.11)
. (4.11)
Тогда для амплитуд этих напряжений получим:
 , (4.12)
, (4.12)
 , (4.13)
, (4.13)
 . (4.14)
. (4.14)
76
а их начальные фазы равны
 , (4.15)
, (4.15)
 , (4.16)
, (4.16)
 . (4.17)
. (4.17)
На рис. 4.8 показаны зависимости амплитуд напряжений на элементах контура при  Ом,
Ом,  мГн,
мГн,  нФ,
нФ,  В и
В и  (обратите внимание, что сопротивление потерь в 10 раз больше, чем в предыдущем примере)
(обратите внимание, что сопротивление потерь в 10 раз больше, чем в предыдущем примере)

Рис. 4.8
77
На рис. 4.8а кривые представлены в широком диапазоне частот, а на рис. 4.8б – в координатах абсолютной расстройки и узком частотном интервале в окрестности  .
.
Как видно на частоте  напряжения на индуктивности и емкости резко возрастают по сравнению с напряжением (ЭДС) источника (становятся много больше
напряжения на индуктивности и емкости резко возрастают по сравнению с напряжением (ЭДС) источника (становятся много больше  ), то есть в последовательном колебательном контуре имеет место резонанс напряжений на реактивных элементах. Напряжение на сопротивлении
), то есть в последовательном колебательном контуре имеет место резонанс напряжений на реактивных элементах. Напряжение на сопротивлении  не превышает входной ЭДС, поэтому о его резонансе говорить не приходится.
не превышает входной ЭДС, поэтому о его резонансе говорить не приходится.
Частоты, на которых напряжения  и
и  максимальны, примерно равны
максимальны, примерно равны  , поэтому частоту (4.2)
, поэтому частоту (4.2)

называют резонансной.
Точные значения резонансных частот нетрудно найти, определив производные  и
и  по частоте
по частоте  и приравняв результат нулю (проделайте это самостоятельно). Как видно из кривых рис. 4.8б, эти частоты отличаются от
и приравняв результат нулю (проделайте это самостоятельно). Как видно из кривых рис. 4.8б, эти частоты отличаются от  весьма незначительно (резонансная частота напряжения емкости меньше
весьма незначительно (резонансная частота напряжения емкости меньше  , а индуктивности – больше) и тем сильнее, чем больше сопротивление
, а индуктивности – больше) и тем сильнее, чем больше сопротивление  (для того, чтобы это увидеть графически и было выбрано
(для того, чтобы это увидеть графически и было выбрано  Ом).
Ом).
Принимая резонансную частоту равной  , определим резонансные амплитуды напряжений,
, определим резонансные амплитуды напряжений,
 , (4.18)
, (4.18)
 , (4.19)
, (4.19)
78
 . (4.20)
. (4.20)
Подстановкой  нетрудно убедиться, что
нетрудно убедиться, что
 , (4.21)
, (4.21)
тогда резонансные напряжения на реактивных элементах одинаковы и равны
 . (4.22)
. (4.22)
Величину
 (4.23)
(4.23)
называют добротностью колебательного контура. Согласно (4.22) добротность является важнейшей характеристикой резонансных явлений.
На рис. 4.9 приведены зависимости от частоты сдвигов фаз напряжений на элементах контура относительно фазы ЭДС источника,
 ,
,
 , (4.24)
, (4.24)
 ,
,
начальные фазы напряжений определяются из (4.15)-(4.17). Как видно, напряжение на индуктивности опережает по фазе
79
напряжение на сопротивлении на  , а на емкости – отстает от него на
, а на емкости – отстает от него на  . Напряжение на индуктивности
. Напряжение на индуктивности  опережает по фазе напряжение на емкости
опережает по фазе напряжение на емкости  на
на  , то есть эти напряжения противофазны.
, то есть эти напряжения противофазны.

Рис. 4.9
4.4. Вторичные параметры колебательного контура
Последовательный колебательный контур полностью описывается своими первичными параметрами  ,
,  и
и  . Однако их численные значения малоинформативны, и на практике широко используются дополнительные (вторичные) параметры.
. Однако их численные значения малоинформативны, и на практике широко используются дополнительные (вторичные) параметры.
Резонансная частота контура
 (4.25)
(4.25)
измеряется в радианах делить на секунду, или
 , (4.26)
, (4.26)
80
которая измеряется в герцах. Ее значение сразу определяет частоту настройки колебательного контура.
Характеристическое сопротивление контура
 (4.27)
(4.27)
измеряется в Омах и численно равно модулю реактивного сопротивления индуктивности или емкости (отдельно) на резонансной частоте  .
.
Добротность контура
 (4.28)
(4.28)
– величина безразмерная, характеризует резонансные свойства колебательного контура. Физический смысл добротности – это отношение максимальной энергии, накапливаемой в реактивных элементах, к энергии потерь в контуре за период колебаний на резонансной частоте.
Как видно из (2.28), добротность возрастает с уменьшением сопротивления потерь контура, которое практически полностью определяется потерями мощности сигнала в катушке индуктивности. На практике добротность  . В большинстве случаев добротность составляет 70-100. Для получения высоких добротностей 150-300 используют специальный провод (покрытый тонким слоем серебра – «серебрянку»), вжигание серебряного проводника в керамический каркас и ряд других инженерных решений. Более высокие значения добротности LC колебательных контуров получить не удается.
. В большинстве случаев добротность составляет 70-100. Для получения высоких добротностей 150-300 используют специальный провод (покрытый тонким слоем серебра – «серебрянку»), вжигание серебряного проводника в керамический каркас и ряд других инженерных решений. Более высокие значения добротности LC колебательных контуров получить не удается.
Явление резонанса и понятие добротности используются и в механических колебательных системах. Например,
81
в кристаллах кварца (горного хрусталя) очень малы потери энергии механических колебаний, то есть они имеют высокую добротность. Поэтому изготовленные из него бокалы при слабом ударе издают продолжительный звон. В железе, алюминии или пластмассе эти потери велики, поэтому сделанные их них бокалы не обладают соответствующим звучанием.
Помимо малых потерь энергии механических колебаний монокристаллы кварца характеризуются явлением пьезоэффекта (повторите материал по физике): при возникновении в кварцевой пластине механических колебаний на ее гранях возникает переменное напряжение и наоборот, приложенное к кристаллу переменное напряжение вызывает механические колебания кристалла. Из кварцевых пластин изготавливают электронные устройства – кварцевые резонаторы. С электрической точки зрения они эквивалентны последовательному колебательному контуру с очень высокой добротностью  .
.
4.5. Частотные характеристики контура
Под частотными характеристиками последовательного колебательного контура (рис. 4.2) понимают зависимость от частоты характеристик комплексного коэффициента передачи по напряжению вида
 (4.29)
(4.29)
или
 , (4.30)
, (4.30)
где  – комплексная амплитуда напряжения на емкости (обычно полагают, что потери в емкости отсутствуют),
– комплексная амплитуда напряжения на емкости (обычно полагают, что потери в емкости отсутствуют),  – комплексная амплитуда напряжения на последовательном со-
– комплексная амплитуда напряжения на последовательном со-
82
единении индуктивности  с ее сопротивлением потерь
с ее сопротивлением потерь  (напряжение на реальной катушке индуктивности).
(напряжение на реальной катушке индуктивности).
Рассмотрим комплексный коэффициент передачи напряжения емкости  (аналогичный анализ
(аналогичный анализ  проведите самостоятельно). Из (4.29) с учетом (4.11) получим
проведите самостоятельно). Из (4.29) с учетом (4.11) получим
 . (4.31)
. (4.31)
Из (4.31) АЧХ  и ФЧХ
и ФЧХ  контура имеют вид
контура имеют вид
 , (4.32)
, (4.32)
 . (4.33)
. (4.33)
Частотные характеристики последовательного колебательного контура при  мГн,
мГн,  нФ для двух значений
нФ для двух значений  Ом (сплошные линии) и
Ом (сплошные линии) и  Ом (пунктир) в различных масштабах показаны на рис. 4.10 в координатах абсолютной расстройки. Кривые резко возрастает при приближении частоты сигнала
Ом (пунктир) в различных масштабах показаны на рис. 4.10 в координатах абсолютной расстройки. Кривые резко возрастает при приближении частоты сигнала  к резонансной частоте контура
к резонансной частоте контура  (4.25). Максимум коэффициента передачи имеет место приближенно
(4.25). Максимум коэффициента передачи имеет место приближенно
83
на частоте  и равен добротности контура,
и равен добротности контура,
 . (4.34)
. (4.34)

Рис. 4.10
На рис. 4.10а приведены АЧХ в абсолютном, а на рис. 4.10б в относительном масштабах по оси ординат. На рис. 4.11 показаны ФЧХ этих контуров.

 Рис. 4.11.
Рис. 4.11.
Как видно, с ростом сопротивления потерь  в колеба-
в колеба-
84
тельном контуре максимум АЧХ падает (так как уменьшается добротность) и кривая АЧХ становится «шире», а ФЧХ – более пологой.


По форме АЧХ видно, что последовательный колебательный контур является узкополосным частотным фильтром.
4.6. Обобщенная расстройка
Исследование частотных характеристик колебательного контура удобнее всего проводить в координатах обобщенной расстройки  , равной
, равной
 . (4.35)
. (4.35)
Как видно, она зависит от частоты сигнала и параметров контура. Проведем преобразования
 . (4.36)
. (4.36)
Обозначая абсолютную расстройку
 , (4.37)
, (4.37)
85
и приближенно полагая в первой дроби  , получим
, получим
 . (4.38)
. (4.38)
Из (4.38) видно, что обобщенная расстройка прямо пропорциональна абсолютной расстройке, то есть частоте сигнала (начало координат смещено в точку  ).
).
4.7. Частотные характеристики в координатах обобщенной
расстройки
Комплексное входное сопротивление контура (4.1) в координатах  можно записать в виде
можно записать в виде
 , (4.39)
, (4.39)
а его модуль, аргумент, активную и реактивную составляющие соответственно
 (4.40)
(4.40)
Эти характеристики как функции обобщенной расстройки показаны на рис. 4.12. Сплошной линией показаны точные, а пунктирной – приближенные значения, полученные из (4.40).
86

Рис. 4.12
Проведем расчет комплексного коэффициента передачи, приближенно заменив в числителе (4.31)  на
на  ,
,
 . (4.41)
. (4.41)
Частотные характеристики последовательного колебательного контура в координатах обобщенной расстройки имеют вид
 , (4.42)
, (4.42)
 (4.43)
(4.43)
Зависимости АЧХ  и ФЧХ
и ФЧХ  показаны на рис. 4.13 пунктирными линиями. Их точные значения показаны сплошными кривыми.
показаны на рис. 4.13 пунктирными линиями. Их точные значения показаны сплошными кривыми.
Как видно, расчеты частотных характеристик в координатах обобщенной расстройки имеют вполне удовлетворитель-
87
ную точность в достаточно широкой окрестности резонансной частоты, то есть там, где они и представляют практический интерес.

Рис. 4.13
С помощью обобщенной расстройки можно проводить расчеты токов и напряжений в контуре:
 , (4.44)
, (4.44)
 , (4.45)
, (4.45)
 , (4.46)
, (4.46)
 , (4.47)
, (4.47)
Выражения и вычисления существенно упрощаются.
Запишите самостоятельно выражения для амплитуд и начальных фаз тока и напряжений на элементах контура. Постройте их зависимости от частоты и обобщенной расстройки, оцените погрешность вычислений в координатах  .
.
88
4.8. Полоса пропускания и коэффициент
прямоугольности
Определим полосу пропускания контура, расчет проведем в координатах обобщенной расстройки (рис. 4.14).
 Максмум АЧХ контура равен добротности
Максмум АЧХ контура равен добротности  , тогда полоса пропускания определяется на уровне
, тогда полоса пропускания определяется на уровне
 .
.
С учетом (4.42) урав-
нение имеет
вид Рис. 4.14
 (4.48)
(4.48)
и его решения равны

Интервал обобщенной расстройки в полосе пропускания
 ,
,
с другой стороны из (4.38)
 ,
,
89
тогда получим уравнение
 ,
,
а полоса пропускания будет равна
 . (4.49)
. (4.49)
Как видно, полоса пропускания контура с заданной частотой настройки  определяется только его добротностью. Высокодобротный контур позволяет реализовать узкополосный частотный фильтр. Как уже отмечалось, большие значения
определяется только его добротностью. Высокодобротный контур позволяет реализовать узкополосный частотный фильтр. Как уже отмечалось, большие значения  обеспечить достаточно сложно.
обеспечить достаточно сложно.


Для определения коэффициента прямоугольности  необходимо найти полосу пропускания контура
необходимо найти полосу пропускания контура  на уровне 1/10 от максимума. Для этого составим уравнение в координатах
на уровне 1/10 от максимума. Для этого составим уравнение в координатах  ,
,
 , (4.50)
, (4.50)
решения которого равны

90
Интервал величин обобщенной расстройки в полосе пропускания на уровне 1/10 от максимума равен
 ,
,
тогда получим уравнение
 ,
,
а полоса пропускания  будет равна
будет равна
 . (4.51)
. (4.51)
В результате коэффициент прямоугольности колебательного контура оказывается равным
 .
.
Как видно, последовательный колебательный контур является полосовым частотным фильтром с низкой избирательностью.
4.9. Влияние внутреннего сопротивления источника
сигнала и нагрузки на резонансные свойства контура
Рассмотрим контур с подключенным реальным источником напряжения  (
( – его внутреннее сопротивление) и сопротивлением нагрузки
– его внутреннее сопротивление) и сопротивлением нагрузки  (рис. 4.15). Можно провести анализ этой цепи отдельно, однако целесообразнее преобразовать
(рис. 4.15). Можно провести анализ этой цепи отдельно, однако целесообразнее преобразовать
91
ее к уже рассмотренной цепи вида рис. 4.5 (с идеальным источником напряжения и без нагрузки) и воспользоваться уже полученными результатами анализа.

Рис. 4.15
 Как видно, сопротивление источника
Как видно, сопротивление источника  просто складывается с
просто складывается с  , увеличивая сопротивление потерь контура. Нагрузка же подключена параллельно емкости, и тогда параллельное соединение
, увеличивая сопротивление потерь контура. Нагрузка же подключена параллельно емкости, и тогда параллельное соединение  необходимо эквивалентно преобразовать в последовательное соединение элементов
необходимо эквивалентно преобразовать в последовательное соединение элементов  (как по-
(как по-
Рис. 4.16 казано на рис. 4.16). Эти
цепи эквивалентны, если равны их полные комплексные сопротивления, тогда получим
 .
.
Преобразуя дроби и приводя обе части равенства к алгебраической форме записи комплексных чисел, можно записать
 .
.
92
Комплексные числа равны тогда и только тогда, когда равны отдельно их действительные и мнимые части, поэтому после алгебраических преобразований получим два уравнения для неизвестных  ,
,
 , (4.52)
, (4.52)
 . (4.53)
. (4.53)
Проделайте необходимые преобразования самостоятельно.
Как видно, эквивалентные параметры последовательной цепи зависят от частоты и, строго говоря, такое преобразование возможно только на фиксированной частоте. При анализе колебательного контура интерес представляет окрестность его резонансной частоты  , поэтому в (4.52) и (4.53), приняв
, поэтому в (4.52) и (4.53), приняв  и условие
и условие
 , (4.54)
, (4.54)
получим
 , (4.55)
, (4.55)
 . (4.56)
. (4.56)
Эти равенства является точными на частоте  и приближенными в ее окрестности. На рис. 4.17 показаны зависимости эквивалентных сопротивления
и приближенными в ее окрестности. На рис. 4.17 показаны зависимости эквивалентных сопротивления  и емкости
и емкости  от абсолютной
от абсолютной
93
расстройки при  нФ и
нФ и  рад/с и различных значениях сопротивления нагрузки
рад/с и различных значениях сопротивления нагрузки  . Как видно, при больших
. Как видно, при больших  , и особенно при выполнении условия (4.54), величины
, и особенно при выполнении условия (4.54), величины  и
и  практически постоянны в широкой окрестности резонансной частоты.
практически постоянны в широкой окрестности резонансной частоты.

Рис. 4.17
 Таким образом эквивалентная схема последовательного колебательного контура с реальным источником сигнала и нагрузкой имеет вид, показанный на рис. 4.18, где
Таким образом эквивалентная схема последовательного колебательного контура с реальным источником сигнала и нагрузкой имеет вид, показанный на рис. 4.18, где  – эквивалентное сопротивление потерь, рав-
– эквивалентное сопротивление потерь, рав-
Рис. 4.18 ное
 . (4.56)
. (4.56)
Контур рис. 4.18 уже изучен, его резонансные свойства определяются эквивалентной добротностью  ,
,
94
 . (4.57)
. (4.57)
Как видно, внутреннее сопротивление источника сигнала  снижает эквивалентную добротность, его влияние будет мало, если
снижает эквивалентную добротность, его влияние будет мало, если
 или
или  , (4.58)
, (4.58)
Собственное сопротивление потерь  достаточно мало (доли Ома – единицы Ом), поэтому источник сигнала для последовательного колебательного контура должен быть практически идеальным.
достаточно мало (доли Ома – единицы Ом), поэтому источник сигнала для последовательного колебательного контура должен быть практически идеальным.
Нагрузка контура также снижает его добротность, чем больше  , тем меньше падает
, тем меньше падает  . Для того, чтобы влияние нагрузки было невелико, необходимо выполнение условия
. Для того, чтобы влияние нагрузки было невелико, необходимо выполнение условия
 или
или  . (4.59)
. (4.59)
На практике величина характеристического сопротивления  составляет сотни Ом – килоОмы, добротность лежит в пределах от нескольких десятков до 150, тогда произведение
составляет сотни Ом – килоОмы, добротность лежит в пределах от нескольких десятков до 150, тогда произведение  составляет десятки – сотни килоОм. С учетом сделанных оценок необходимое сопротивление нагрузки при условии (4.59) оказывается достаточно большим, например, 1 МОм, что крайне сложно обеспечить на практике.
составляет десятки – сотни килоОм. С учетом сделанных оценок необходимое сопротивление нагрузки при условии (4.59) оказывается достаточно большим, например, 1 МОм, что крайне сложно обеспечить на практике.
Для ослабления влияния нагрузки на добротность контура используют ее неполное включение, один из вариантов схемы показан на рис. 4.19.
95

Рис. 4.19
Проведите самостоятельно анализ этой цепи аналогично предыдущей, преобразовав параллельное соединение  в последовательное, получите выражение для эквивалентной добротности, в результате можно записать
в последовательное, получите выражение для эквивалентной добротности, в результате можно записать
 , (4.60)
, (4.60)
где  – коэффициент включения нагрузки в контур, равный
– коэффициент включения нагрузки в контур, равный
 . (4.61)
. (4.61)
Требования к сопротивлению нагрузки определяются неравенством
 , (4.62)
, (4.62)
что значительно слабее (4.59). Например, при  кОм и
кОм и  (типичное значение) необходимо выполнение условия
(типичное значение) необходимо выполнение условия  кОм, что вполне приемлемо на практике.
кОм, что вполне приемлемо на практике.
96
4.10. Расчеты цепей с последовательными
колебательными контурами
Расчет гармонических токов и напряжений в электрических цепях с колебательными контурами проводится методом комплексных амплитуд чаще всего в координатах обобщенной расстройки.
 Рассмотрим пример, показанный на рис. 4.20, в котором на заданной частоте
Рассмотрим пример, показанный на рис. 4.20, в котором на заданной частоте  рад/с при
рад/с при  Ом,
Ом,  мГн,
мГн,  нФ,
нФ,  Ом и
Ом и  В необходимо определить комплексную амплитуду напряжения на нагрузке
В необходимо определить комплексную амплитуду напряжения на нагрузке  . Расчет в координатах частоты
. Расчет в координатах частоты  будет достаточно громоздким (проведите его самостоятельно, чтобы убедиться в этом). Рис. 4.20
будет достаточно громоздким (проведите его самостоятельно, чтобы убедиться в этом). Рис. 4.20
Резонансная частота 
контура равна
 ,
,
а добротность соответственно
 .
.
В координатах обобщенной расстройки  , равной
, равной
 ,
,
97
сопротивление  последовательного колебательного контура
последовательного колебательного контура  равно
равно  Ом.
Ом.
Сопротивление  параллельного соединения контура с нагрузкой определяется выражением
параллельного соединения контура с нагрузкой определяется выражением
 Ом.
Ом.
Вычислим общее сопротивление цепи,
 ,
,
в результате получим
 Ом.
Ом.
Комплексная амплитуда тока в цепи равна

а напряжения на нагрузке соответственно
 В.
В.
Переход к координатам обобщенной расстройки существенно упрощает расчеты цепей с колебательными контурами. При расчетах широко используют известные выражения для коэффициента передачи и других характеристик контура.
98

 Рассмотрим пример, показанный на рис.4.21 при
Рассмотрим пример, показанный на рис.4.21 при  В
В  рад/с,
рад/с,  Ом,
Ом,  мГн и
мГн и  нФ. Необходимо рассчитать мгновенные значения напряжения на емкости последовательного колебательного контура
нФ. Необходимо рассчитать мгновенные значения напряжения на емкости последовательного колебательного контура  .
.
Резонансная частота  и добротность
и добротность  равны Рис. 4.21
равны Рис. 4.21
 ,
,  ,
,
тогда для обобщенной расстройки получим
 .
.
Комплексный коэффициент передачи  определяется выражением
определяется выражением
 ,
,
тогда комплексная амплитуда напряжения на емкости равна
 В,
В,
а для его мгновенных значений получим
 В.
В.
99
4.11. Моделирование последовательного колебательного
контура
На рис. 4.22 показана модель последовательного колебательного контура  Ом,
Ом,  мГн и
мГн и  пФ с нагрузкой
пФ с нагрузкой  МОм в пакете программ MicroCAP7. На рис. 4.23 приведены результаты моделирования в АЧХ и ФЧХ режиме «Stepping» при изменении сопротивления потерь
МОм в пакете программ MicroCAP7. На рис. 4.23 приведены результаты моделирования в АЧХ и ФЧХ режиме «Stepping» при изменении сопротивления потерь  от 50 Ом (верхние кривые) до 150 Ом (нижние
от 50 Ом (верхние кривые) до 150 Ом (нижние
кривые) с шагом 50 Ом.
Рис.4.22 На рис. 4.24 пока-
заны аналогичные зависимости при  Ом и изменении сопротивления нагрузки от
Ом и изменении сопротивления нагрузки от  МОм (нижние кривые) до
МОм (нижние кривые) до  МОм верхние кривые) с шагом 1МОм .
МОм верхние кривые) с шагом 1МОм .
Как видно по результатам моделирования, максимум АЧХ снижается с ростом сопротивления потерь и уменьшением сопротивления нагрузки, причем даже при большом  МОм добротность контура существенно уменьшается. При этих условиях АЧХ и ФЧХ становятся более пологими.
МОм добротность контура существенно уменьшается. При этих условиях АЧХ и ФЧХ становятся более пологими.
На рис. 4.25 представлены результаты моделирования контура при изменении его емкости от 100пФ (правая кривая) до 200пФ (левая кривая) с шагом 50 пФ для  Ом. Такие изменения происходят при настройке колебательного контура в радиоприемнике с помощью конденсатора переменной емкости.
Ом. Такие изменения происходят при настройке колебательного контура в радиоприемнике с помощью конденсатора переменной емкости.
Проведите расчеты, подтверждающие результаты моделирования, например, вычислите максимальные значения АЧХ при соответствующих параметрах цепи.
100


101


102



103
4.12. Применение последовательного колебательного
контура
Последовательный колебательный контур широко используется как узкополосный частотный фильтр. Таким фильтром является преселектор (предварительный селектор), который присутствует в любом супергетеродинном радиоприемнике (факультативно поинтересуйтесь у преподавателя, как работает супергетеродинный радиоприемник), его условная схема показана на рис. 4.26. Антенна приемника включена в контур как источник сигнала, а напряжение с емкости  подается на вход усилителя высокочастотного сигнала (УВЧ), входное сопротивление которого является нагрузкой колебательного контура. Так как транзисторный УВЧ имеет невысо-
подается на вход усилителя высокочастотного сигнала (УВЧ), входное сопротивление которого является нагрузкой колебательного контура. Так как транзисторный УВЧ имеет невысо-
Рис. 4.26 кое входное сопротивление,
то используется неполное включение нагрузки. Задача преселектора – фильтрация «зеркального канала» приема в супергетеродинном приемнике.
 На базе последовательного колебательного контура можно реализовать режекторный фильтр, пример которого показан на рис. 4.27. На рис 4.28 показана его модель при
На базе последовательного колебательного контура можно реализовать режекторный фильтр, пример которого показан на рис. 4.27. На рис 4.28 показана его модель при  мГн,
мГн,  нФ и
нФ и  Ом, сопротив-
Ом, сопротив-
лении потерь катушки ин-
дуктивности  Ом и сопротивлении нагрузки
Ом и сопротивлении нагрузки
Рис. 4.27  кОм, а на рис. 4.29 –
кОм, а на рис. 4.29 –
АЧХ и ФЧХ.
104

Рис. 4.28

Рис. 4.29
Как видно, фильтр подавляет сигнал в окрестности частоты 160 кГц. Нетрудно спроектировать такой фильтр на частоту 50 или 100 Гц, что часто необходимо в биомедицинской аппаратуре, питающейся от силовой сети переменного тока 220В с частотой 50 Гц (проведите необходимые расчеты и схемотехническое моделирование).
105
4.13. Задания для самостоятельного решения
Задание 4.1. Определите сопротивление потерь колебательного контура при  ,
,  рад/с и
рад/с и  мГн.
мГн.
Задание 4.2. Определите сопротивление потерь колебательного контура при полосе пропускания  рад/с и
рад/с и  мГн.
мГн.
Задание 4.4. Определите полосу пропускания колебательного контура при  рад/с,
рад/с,  нФ и сопротивлении потерь
нФ и сопротивлении потерь  Ом.
Ом.
Задание 4.4. Определите добротность  колебательного контура при
колебательного контура при  рад/с и полосе пропускания
рад/с и полосе пропускания  рад/с.
рад/с.
Задание 4.5. Определите напряжение на катушке индуктивности контура рис. 4.30 при  мГн,
мГн,  пФ,
пФ,

 Ом,
Ом,  В,
В,  Ом и
Ом и  рад/с. Расчет проведите обычным методом комплексных амплитуд и используя теорию колебательных контуров в координатах обобщенной расстройки, сравните результаты.
рад/с. Расчет проведите обычным методом комплексных амплитуд и используя теорию колебательных контуров в координатах обобщенной расстройки, сравните результаты.
Рис. 4.30
Задание 4.6. Определите напряжение на емкости контура рис. 4.31 при  мГн,
мГн,  нФ,
нФ,  Ом,
Ом,  В,
В,  Ом и
Ом и  рад/с. Расчет проведите обычным
рад/с. Расчет проведите обычным
106
 методом комплексных амплитуд и используя теорию колебательных контуров в координатах обобщенной расстройки
методом комплексных амплитуд и используя теорию колебательных контуров в координатах обобщенной расстройки
сравните результаты. Рис. 4.31
Рекомендуем посмотреть лекцию “9. Районирование в экономической и социальной географии”.
Задание 4.7. Вычислите резонансные значения тока и напряжение на емкости контура при  мГн,
мГн,  нФ,
нФ,  Ом и ЭДС идеального источника напряжения
Ом и ЭДС идеального источника напряжения  В.
В.
 Задание 4.8. В координатах обобщенной расстройки вычислите напряжение
Задание 4.8. В координатах обобщенной расстройки вычислите напряжение  на нагрузке в цепи на рис. 4.32 при
на нагрузке в цепи на рис. 4.32 при  В,
В,  мГн,
мГн,  нФ,
нФ,  Ом, Рис. 4.32
Ом, Рис. 4.32
 Ом,
Ом,  кОм и
кОм и  рад/с.
рад/с.
 Задание 4.9. Получите выражение для АЧХ цепи, показанной на рис. 4.33, постройте ее график. Проанализируйте влияние нагрузки
Задание 4.9. Получите выражение для АЧХ цепи, показанной на рис. 4.33, постройте ее график. Проанализируйте влияние нагрузки  и сопротивлений
и сопротивлений  и
и  на форму АЧХ.
на форму АЧХ.
Рис. 4.33
