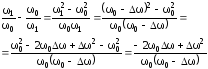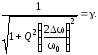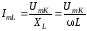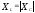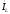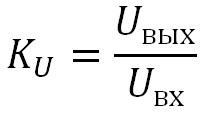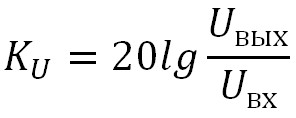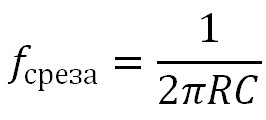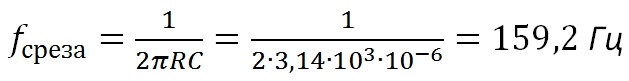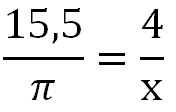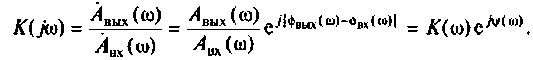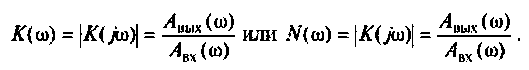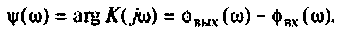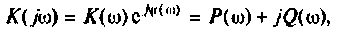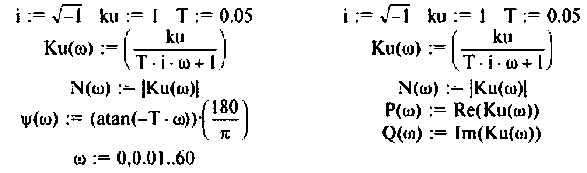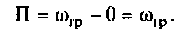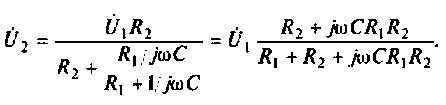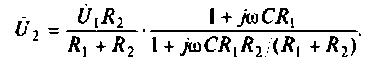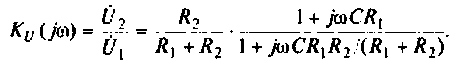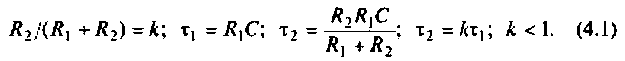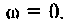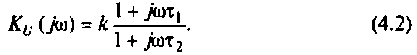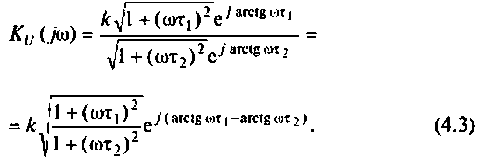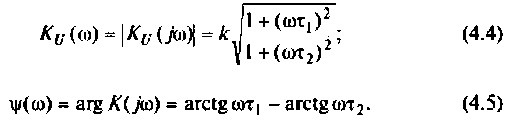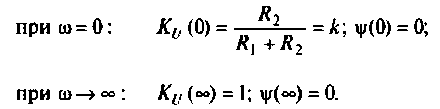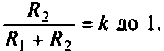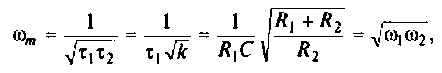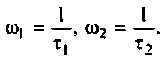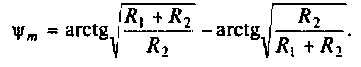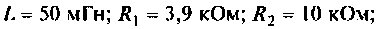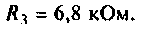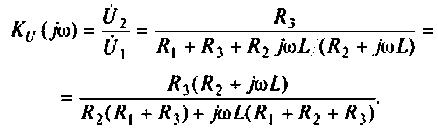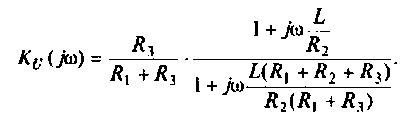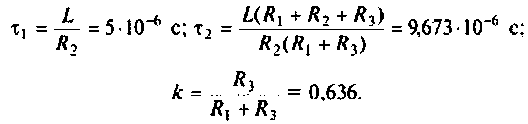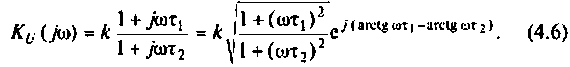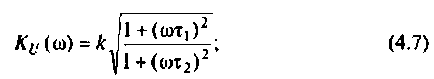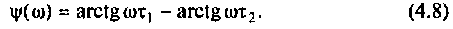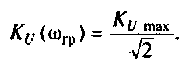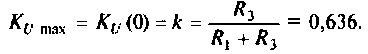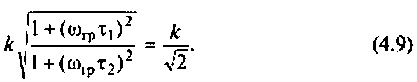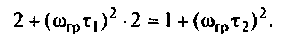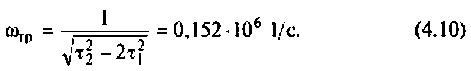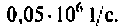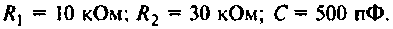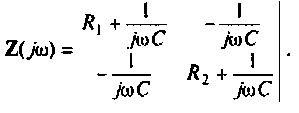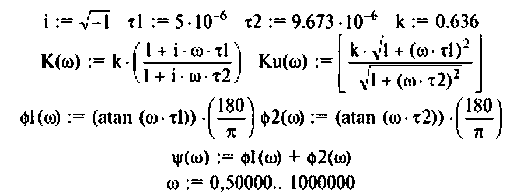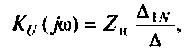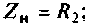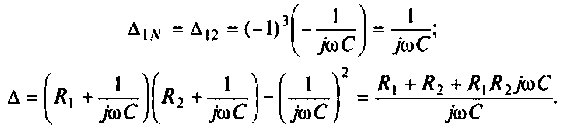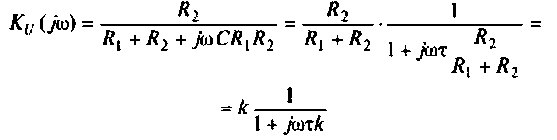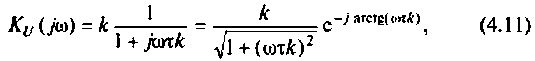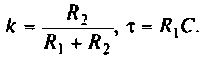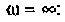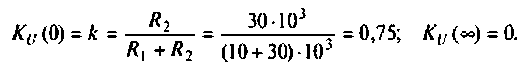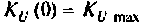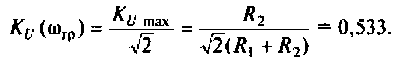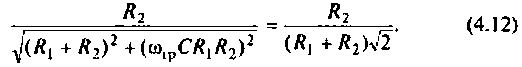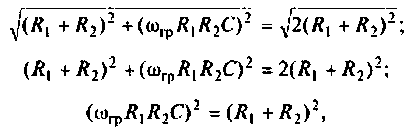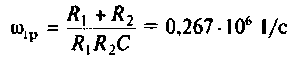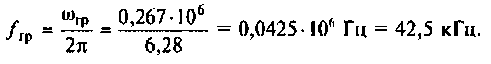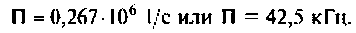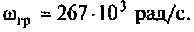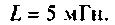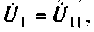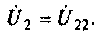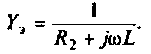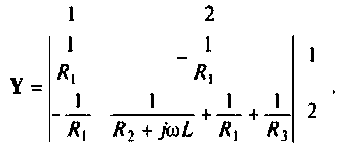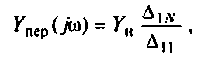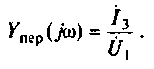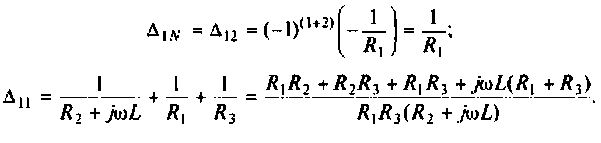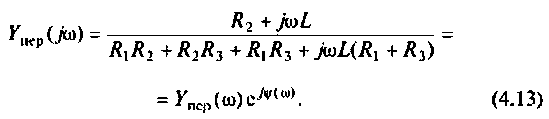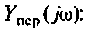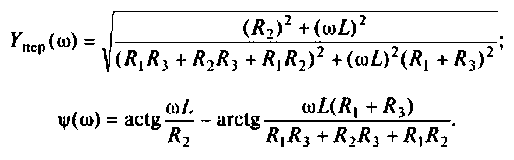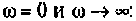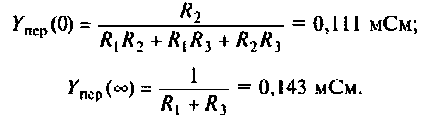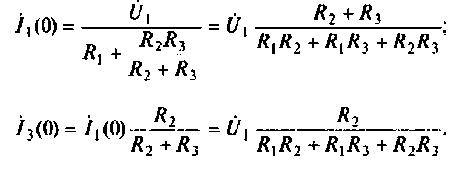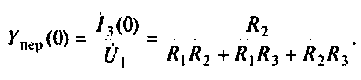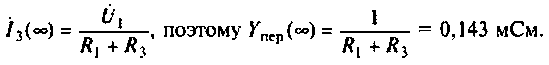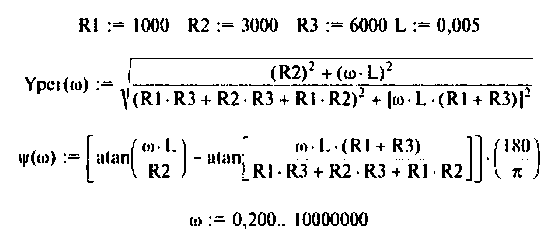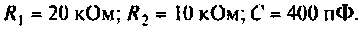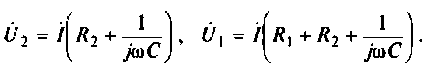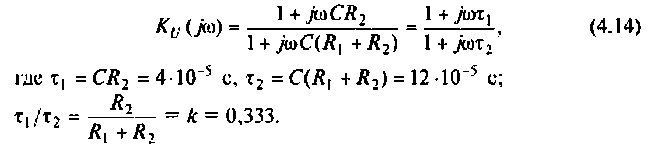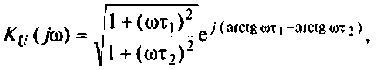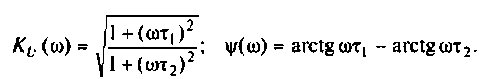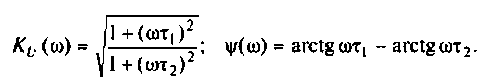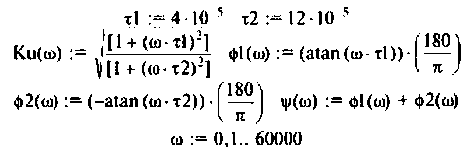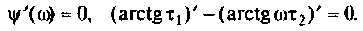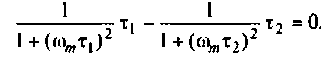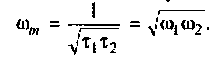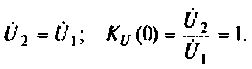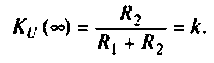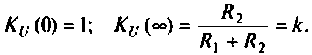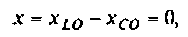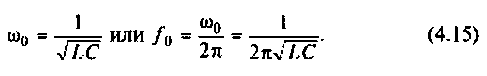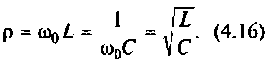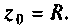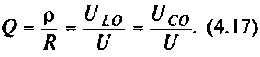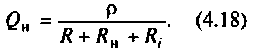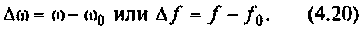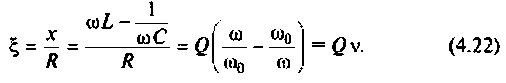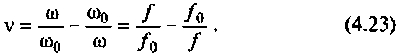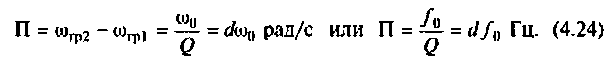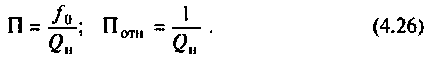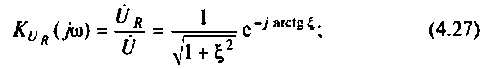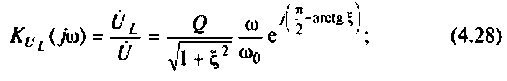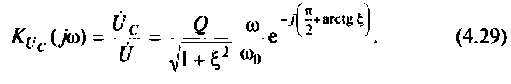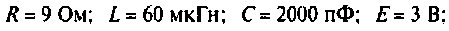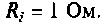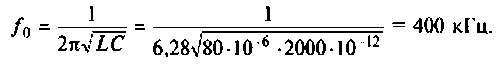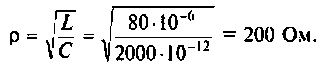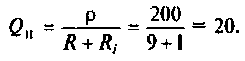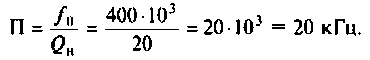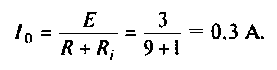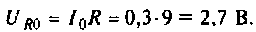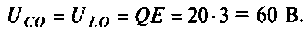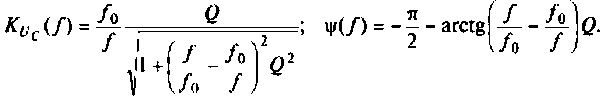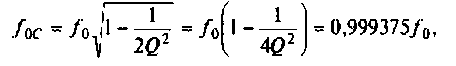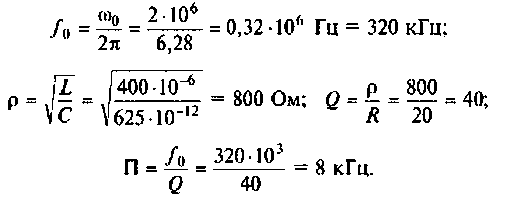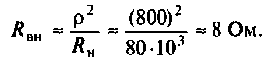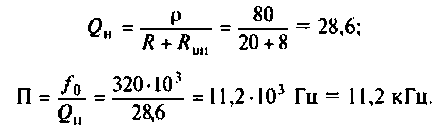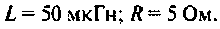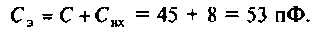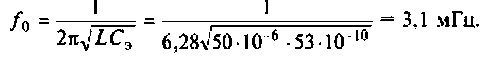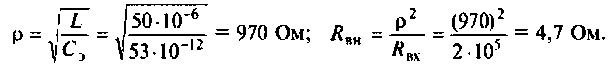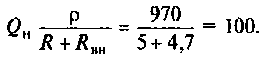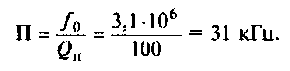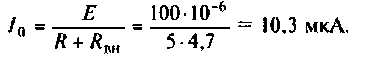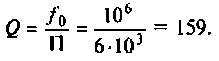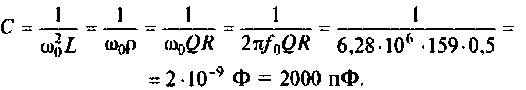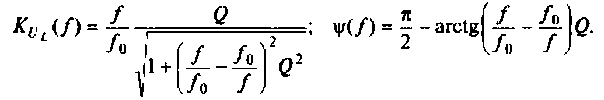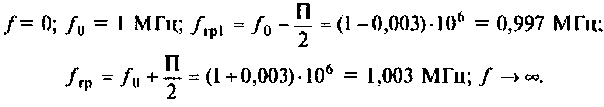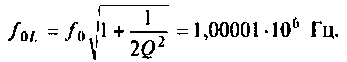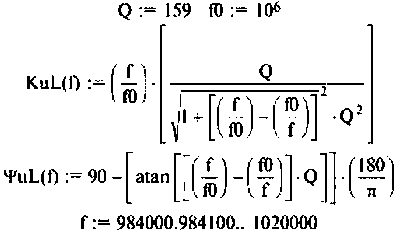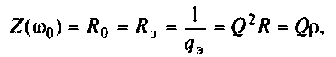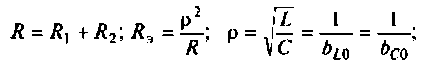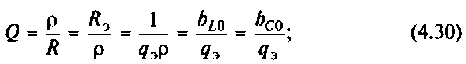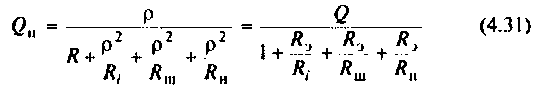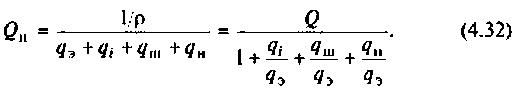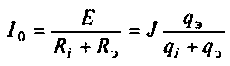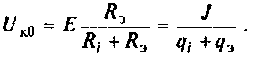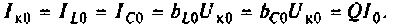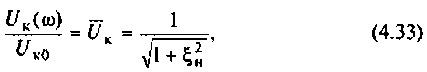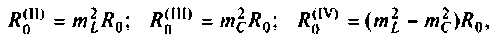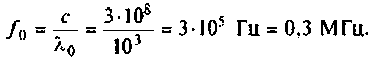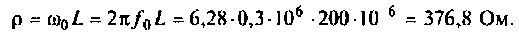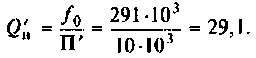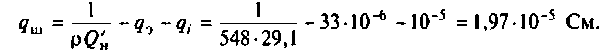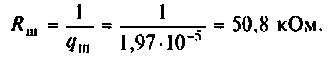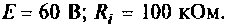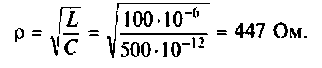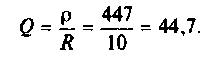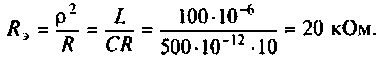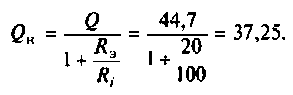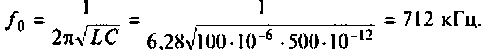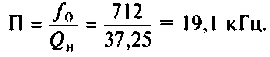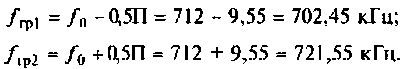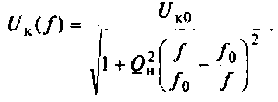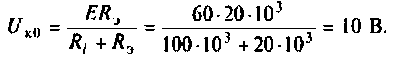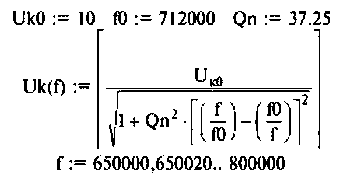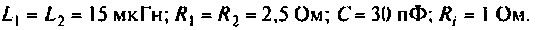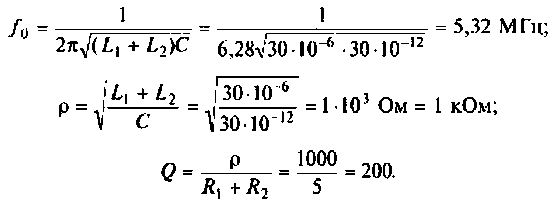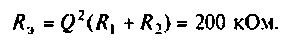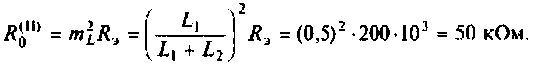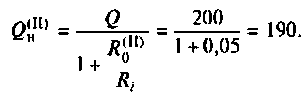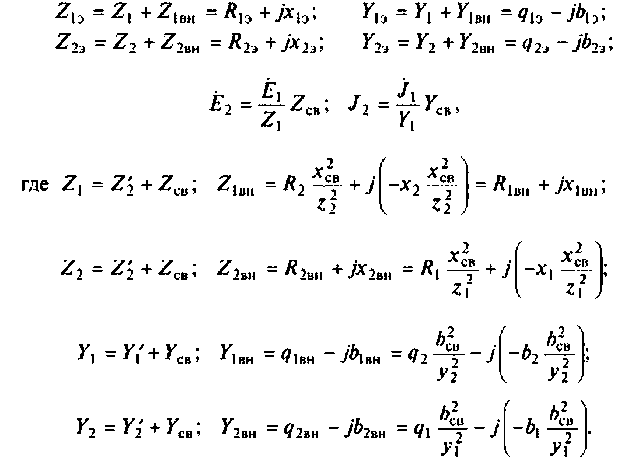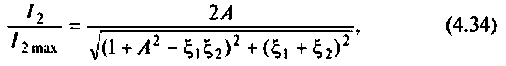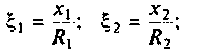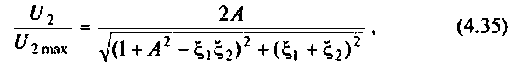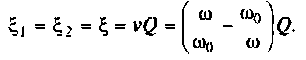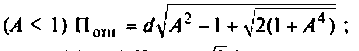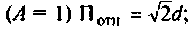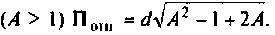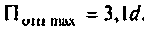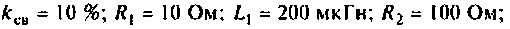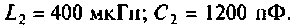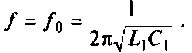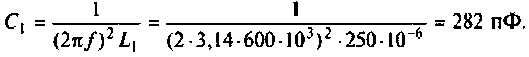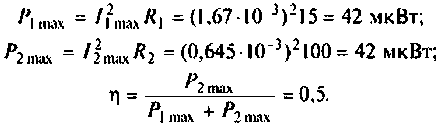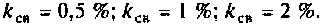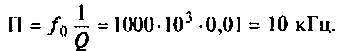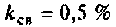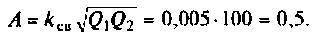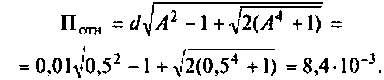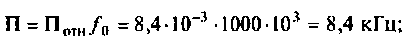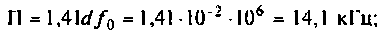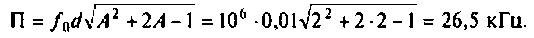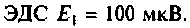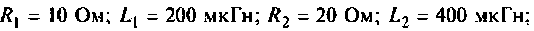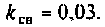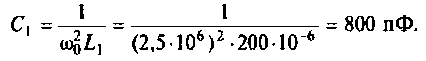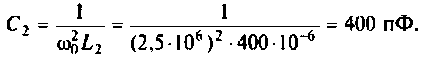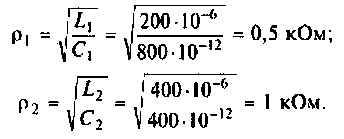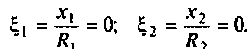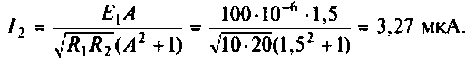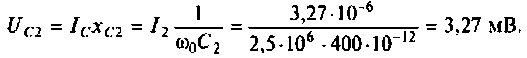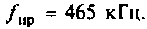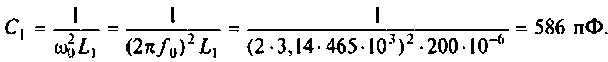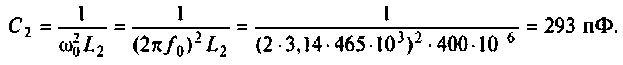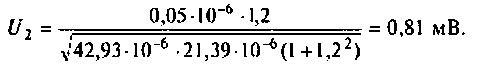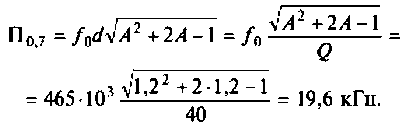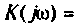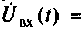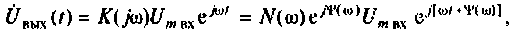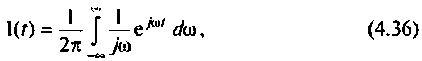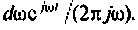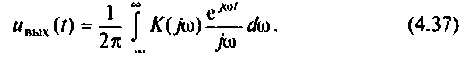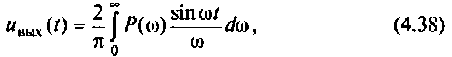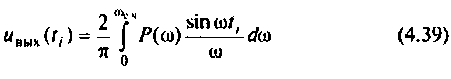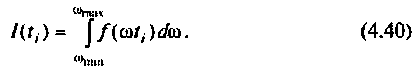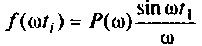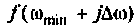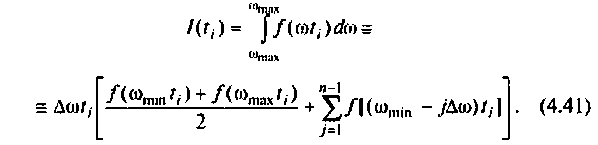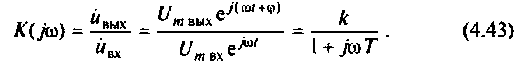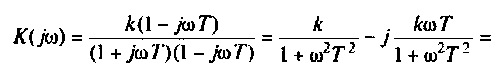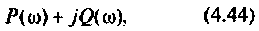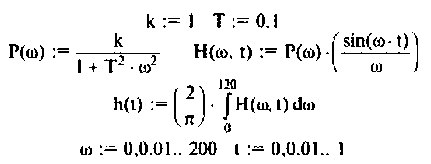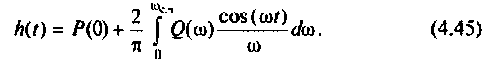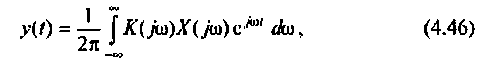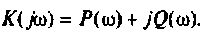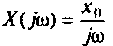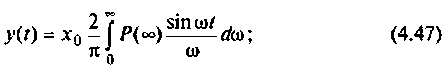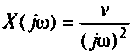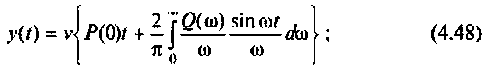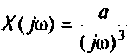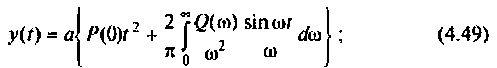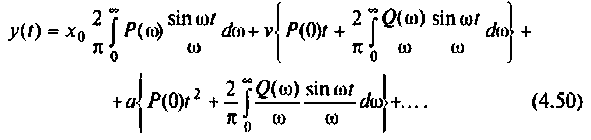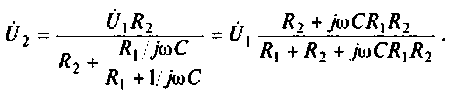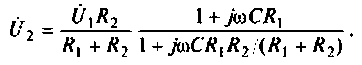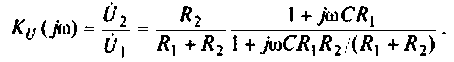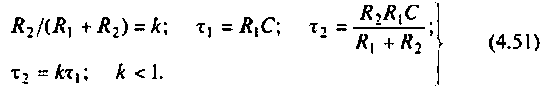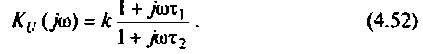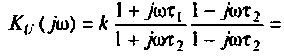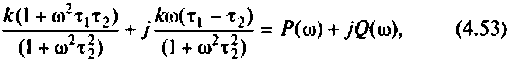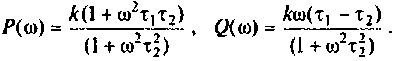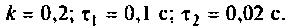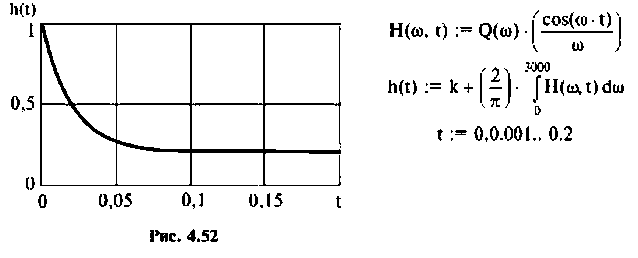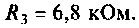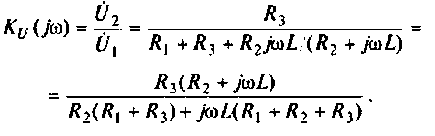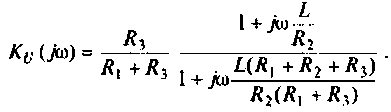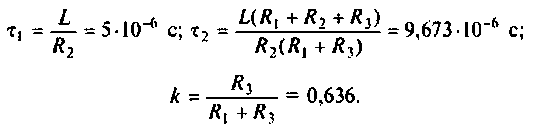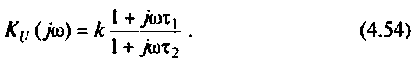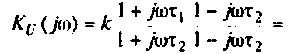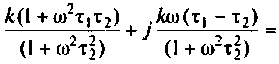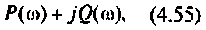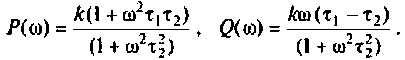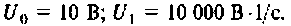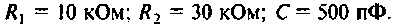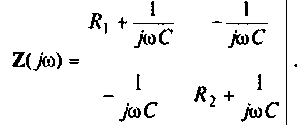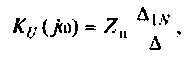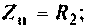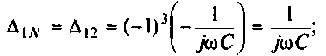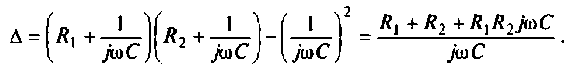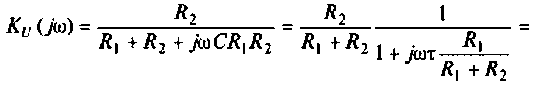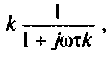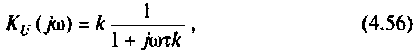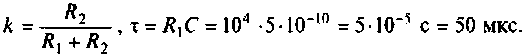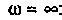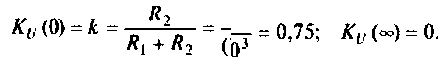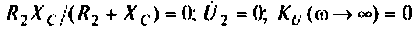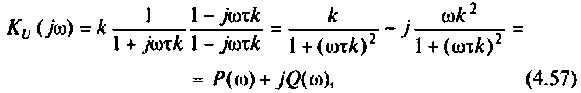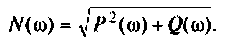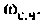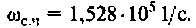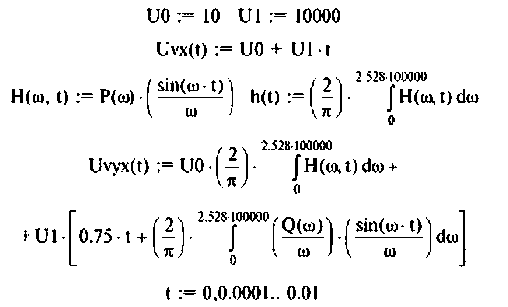Амплитудно-частотная
характеристика последовательного
контура характеризуется тем, что на
резонансной частоте она имеет максимальное
значение. На частотах, отстоящих
значительно от резонансной частоты,
значения амплитудно-частотной
характеристики близки к нулю. Если к
контуру прикладывать сигналы одинаковой
амплитуды, но с разными частотами, то
сигналы с частотой, равной резонансной
частоте, будут создавать большой ток в
контуре и большие напряжения на реактивных
элементах. В этом случае говорят, что
контур пропускает этот сигнал. Если
частота сигнала значительно отличается
от 0,
то в контуре практически отсутствуют
электрические колебания. В этом случае
говорят, что контур такой сигнал
подавляет. Для оценки этих свойств
контура вводится понятие его полосы
пропускания.
Полосой
пропускания
называется интервал частот, включающий
резонансную частоту контура, на границах
которого значение тока контура меньше
значения тока на резонансной частоте
в заданное число раз.
Как
правило, за исключением особой аппаратуры,
требуется, чтобы на границе полосы
пропускания ток контура был меньше тока
на резонансной частоте в
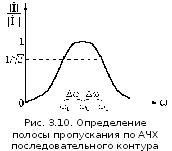
На
рис.3.10 показано определение полосы
пропускания с помощью АЧХ. В соответствии
с заданным уровнем подавления на границе
полосы пропускания должно выполняться
условие:

Значит
на границах полосы пропускания АЧХ
должна иметь значение:

Исходя из этого, на рис.3.10 найдена полоса
пропускания, границы которой обозначаются
частотами 1
и 2.
Полоса пропускания обозначается как
и измеряется в единицах измерения
частоты. Тогда полоса пропускания будет
равна:

В
зоне полосы пропускания АЧХ практически
симметрична относительно резонансной
частоты. Поэтому интервалы между
резонансной частотой и границами полосы
пропускания обозначим как ∆.


С
учетом этого выражение для полосы
пропускания (3.33) принимает вид:

Рассмотренный
способ определения полосы пропускания
возможен только при наличии графика
АЧХ. Это не всегда удобно.
Найдем
аналитическое выражение для определения
полосы пропускания. Для этого воспользуемся
формулой (3.29) определения АЧХ.

Найдем,
какой имеет вид (3.35) для границ полосы
пропускания. Для этого предварительно
найдем выражение в круглых скобках
формулы (3.35) для 1
и 2.
Для
=1
получаем:
В
контурах радиоаппаратуры полоса
пропускания узкая и составляет единицы
килогерц, а резонансная частота высокая
и составляет сотни килогерц. Это позволяет
пренебречь величиной ∆
в числителе и знаменателе. Тогда
рассматриваемое соотношение принимает
вид:
Для
=2,
с учетом сказанного получаем:
Из
приведенного анализа видно, что
рассматриваемая часть формулы (3.35) на
граничных частотах 1
и 2
имеет
одинаковые выражения, отличающиеся
только знаком. Но так как рассмотренное
соотношение в формуле (3.35) находится в
квадрате, то эта формула для обеих границ
полосы пропускания имеет один и тот же
вид:
(3.36)
При
решении задачи о полосе пропускания в
общем виде вводится понятие коэффициента
неравномерности .
Он показывает, какую часть от резонансного
тока принимает ток контура на границах
полосы пропускания и имеет разные
значения в зависимости от вида аппаратуры
(0.707; 0.1; 0.01 и т. д.) Тогда, в соответствии
с понятием полосы пропускания, приравняем
(3.36) к коэффициенту неравномерности:
Решаем
это уравнение относительно 2∆
и с учетом (3.34) находим:
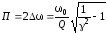
При
коэффициенте неравномерности
полоса пропускания одиночного
последовательного контура определяется
формулой:

На
границах полосы пропускания последовательный
одиночный колебательный контур обладает
рядом свойств, которые полезно знать
при расчете схем с его применением.
1.
Мощность, потребляемая контуром на
границах полосы пропускания, в 2 раза
меньше мощности, потребляемой контуром
на резонансной частоте.
Действительно,
на резонансной частоте мощность,
потребляемая контуром, выражается через
действующее значение тока контура
известным соотношением:
Обозначим
действующее значение тока на границе
полосы пропускания через I. Тогда, с
учетом (3.31), мощность, потребляемая
контуром на каждой из границ полосы
пропускания, равна:
2.
На границах полосы пропускания
сопротивление резистора контура R равно
модулю суммы его реактивных элементов:
На
резонансной частоте ток в контуре равен:
На
границах полосы пропускания ток контура
в общем виде (для =1
и =2)
определяется формулой:
С
учетом (3.31) приравняем эти токи:
После
несложных преобразований находим:
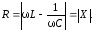
3.
На границах полосы пропускания фаза
тока контура относительно входного
сигнала равна 45.
Комплексное
значение тока контура равно:

Фаза
тока равна:
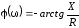
Исходя
из (3.38), модуль аргумента (3.39) на границах
полосы пропускания равен 1. Исходя из
свойств ФЧХ, на частотах <0
контур имеет емкостные свойства (Х<0)
и, следовательно:

На
частотах >0
контур имеет индуктивные свойства (Х >
0), следовательно:
4.
На границах полосы пропускания обобщенная
расстройка

Из
(3.36) видно, что обобщенная расстройка,
с учетом ранее выполненного анализа
для 1
и
2
имеет вид:

где
“плюс” имеет место для 2,
а “минус” – для 1.
Тогда,
учитывая (3.34) и (3.37), получаем:

5.
На границе полосы пропускания модуль
полного сопротивления контура равен:

Это
легко проверить, учитывая второе из
рассмотренных свойств (3.38). Из выражения
модуля полного сопротивления контура
находим:

-
Параллельный
контур
без
диссипаций
в
реактивных
ветвях
–
полное
сопротивление,
резонанс
в
контуре,
напряжение
на
контуре
и
токи
в
ветвях,
векторная
диаграмма.
Параллельные
колебательные контура
Параллельные
одиночные колебательные контура
характеризуются тем, что основные
элементы их – конденсатор и индуктивность
соединены между собой параллельно.
Резисторы могут быть включены как
параллельно с реактивными элементами,
так и последовательно. В первом случае
диссипация энергии в параллельных
ветвях, содержащих реактивные элементы,
отсутствует. Во втором случае в этих
ветвях имеют место диссипативные
процессы. Рассмотрим каждый из названных
видов параллельных контуров.
3.3.1.
Параллельный колебательный контур без
диссипации в реактивных ветвях
Общие
соотношения.
В параллельном колебательном контуре
без диссипации в реактивных ветвях
резистор включен параллельно с
конденсатором и индуктивностью, которые
здесь считаются идеальными (рис.3.18). Их
диссипации могут быть учтены в резисторе
по параллельной схеме замещения
(рис.1.4).
Сопротивление
контура.
Для рассмотрения свойств контура
определим его полное сопротивление

(рис.3.18,в). Представим контур в виде
параллельно соединенных реактивных и
резистивного сопротивлений (рис.3.18,б).
Воспользуемся
проводимостями этих элементов:



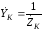
Как
известно, эквивалентная проводимость
параллельно соединенных элементов
равна сумме проводимостей этих элементов.
Тогда эквивалентная проводимость
контура имеет вид:

Отсюда
находим величину эквивалентного
сопротивления контура, выделяя в нем
вещественную и мнимую составляющие:

Представим
сопротивление контура в показательной
форме:

где 
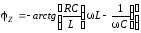
Напряжение
на контуре.
В отличие от последовательного контура,
в параллельном контуре входным параметром
является ток контура iК(t),
а выходным – напряжение на контуре uК(t).
Это связано с особенностью функционирования
параллельных контуров в радиотехнических
устройствах, таких как резонансные
усилители, резонансные фильтры и др. В
связи с этим задаем ток с определенной
амплитудой и нулевой фазой, который в
гармонической форме записи и в комплексной
форме имеет виды:


Напряжение
на контуре определяется в соответствии
с законом Ома:

где 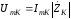

Токи
в контуре.
Определим токи во всех ветвях контура.
Напряжение на контуре, а, значит,
напряжение, приложенное к каждой из
ветвей, имеет вид:
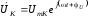
Токи
в ветвях определяются по закону Ома:
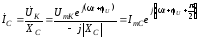


(3.54)

Резонанс
в контуре.
Условие резонанса и резонансная частота.
Как отмечалось, признаком резонанса
являются максимальные значения тока и
напряжения в схеме при определенной
частоте сигнала. При этом в полном
сопротивлении цепи мнимая составляющая
равна нулю. Это мы видели в последовательном
одиночном колебательном контуре.
Воспользуемся этим условием. Тогда из
выражения (3.50) видно, что условием
резонанса в контуре является выполнение
следующего равенства:

Это
значит, что при резонансе сопротивления
конденсатора и катушки индуктивности
равны:

Решая
(3.55) относительно частоты, находим
выражение для резонансной частоты
контура:

Определим
сопротивление контура, напряжение на
контуре и токи в ветвях на резонансной
частоте.
Сопротивление
контура на резонансной частоте можно
определить из (3.51). С учётом условия
резонанса (3.55) видно, что на резонансной
частоте модуль и фаза сопротивления
контура принимают значения:


Напряжение
на контуре при резонансе определяется
из (3.53) с учётом равенства нулю фазы
сопротивления контура на резонансной
частоте
где

(3.57)

Токи
в ветвях контура при резонансе определяются
из (3.54) с учётом (3.55) и (3.57):

где 

где
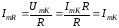
(3.58)

где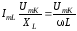
В
силу равенства
видно, что токи в ветвях с индуктивностью
и конденсатором равны по величине, а по
фазе отличаются друг от друга на 180.
Это хорошо видно на векторной диаграмме
(рис.3.19). Совершенно очевидно,
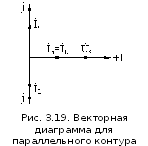
в соответствии с первым законом Кирхгофа
контурный ток равен сумме токов ветвей
контура:

Однако,
как видно из векторной диаграммы, токи
и
при суммировании уничтожают друг друга
и контурный ток определяется током,
протекающим через резистор:

В
силу рассмотренных свойств параллельного
контура, резонанс в параллельном контуре
еще называют резонансом токов.
Мощности
в контуре.
Мгновенная мощность контура определяется
как произведение мгновенного тока
контура на мгновенное напряжение:
На
резонансной частоте 
тогда

Средняя
мощность, потребляемая контуром, равна:

С
учетом (3.58) выражение для средней мощности
контура принимает вид:

В
полученном выражении мгновенной мощности
контура на резонансной частоте отсутствует
реактивная составляющая мощности.
Однако под действием контурного
напряжения через конденсатор и
индуктивность протекают токи. Определим
мгновенные мощности на этих элементах
так, как это делали при анализе идеальных
емкостного и индуктивного двухполюсников.
Для
емкостной ветви и индуктивной ветви
получим:


При
резонансе

Из (3.60) следует, что мгновенные мощности
на конденсаторе и индуктивности равны
по величине и противоположны по фазе.
Добротность
контура.
Добротность контура, как и прежде, найдем
из отношения амплитуды реактивной
мощности контура к средней мощности.
Для этого воспользуемся амплитудными
значениями мощностей на конденсаторе
и индуктивности (3.60). После очевидных
преобразований имеем:

Из
(3.61) видно, что добротность контура без
диссипации в параллельных ветвях
(рис.3.18) тем выше, чем больше величина
R, и тем меньше затухают колебания в
контуре.
С
учетом полученного выражения для
добротности полное сопротивление
контура (3.50) примет вид:

Последнее
выражение для сопротивления контура
позволяет рассмотреть зависимость от
частоты его модуля и фазы:

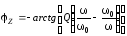
На
рис.3.20 представлены эти зависимости.
Модуль сопротивления контура имеет
наибольшее значение на резонансной
частоте. Если R имеет конечное значение
(присутствует в контуре), то ZК0=R
(график 1). Если R стремится к бесконечности
(резистор отсутствует), то ZК0
также стремится к бесконечности (график
2).
Фазовая
характеристика сопротивления контура
позволяет установить его свойства на
различных частотах. Если воспользоваться
треугольником сопротивления, то видно,
что на низких частотах (слева от
резонансной частоты) контур должен
иметь свойства реального индуктивного
двухполюсника, а на высоких частотах
(справа от резонансной частоты) контур
должен иметь свойства реального
емкостного двухполюсника.
Сравним
амплитуды токов IL
и IC
с
амплитудой тока IR.
Используя соотношения (3.58), находим:

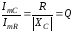
Амплитудно-частотной
характеристикой (АЧХ)
параллельного контура называется
зависимость от частоты модуля напряжения
на контуре.
Как
и для последовательного контура, удобно
АЧХ для параллельного контура рассматривать
в приведенном виде. Для этого необходимо
найти модуль отношения напряжения на
контуре в комплексной форме при
произвольной частоте к напряжению на
контуре при резонансной частоте.
Напряжение
на контуре при произвольной частот и
на резонансной частоте находятся по
закону Ома:


Для
удобства рассмотрения АЧХ здесь
напряжение на контуре и сопротивление
контура на резонансной частоте обозначены,
соответственно как


Берем
отношение этих напряжений и, с учетом
(3.58) и что
получаем:

Модуль
полученного выражения (3.60) является
амплитудно-частотной характеристикой
параллельного контура.

На
рис.3.21 представлены графики АЧХ
параллельного контура для двух значений
добротности. Увеличение добротности
делает график АЧХ более крутым.

характеристикой
параллельного контура называется
зависимость от частоты фазы напряжения
на контуре.
Как
видно из (3.52), фаза напряжения на контуре
равна фазе комплексного сопротивления
контура. Учитывая (3.63), фазо-частотная
характеристика параллельного контура
принимает вид:


рис.3.22 представлен график ФЧХ параллельного
контура. Так как фаза контурного тока
равна нулю, то ФЧХ контура показывает,
в каком фазовом соотношении (опережает,
совпадает, отстает) находится напряжение
по отношению к току. Эта информация
позволяет судить о свойствах контура.
Так, на резонансной частоте фаза
контурного напряжения равна нулю. Значит
на резонансной частоте напряжение
контура и ток совпадают по фазе. Исходя
из теории двухполюсников, этим свойством
обладает резистивный двухполюсник.
Следовательно, на резонансной частоте
контур может быть заменен резистором.
Об этом свойстве контура уже говорилось.
На
низких частотах (слева от резонансной
частоты) фаза контурного напряжения
положительная. Значит, в этом интервале
частот напряжение опережает ток контура.
Из теории двухполюсников известно, что
этим свойством обладает реальный
индуктивный двухполюсник. Следовательно,
на низких частотах параллельный контур
может быть заменен последовательно
соединенными резистором и индуктивностью.
На высоких частотах (справа от резонансной
частоты) фаза контурного напряжения
отрицательная. Значит, в этом интервале
частот контурное напряжение отстает
от контурного тока. Следовательно, на
этом интервале частот контур обладает
свойствами реального емкостного
двухполюсника, и может быть заменен
последовательно соединенными резистором
и конденсатором. Необходимо отметить,
что величины индуктивности и емкости
в схемах замещения контура индуктивным
и емкостным двухполюсниками не равны
значениям индуктивности и ёмкости
контура и на различных частотах будут
иметь различные значения.
Полоса
пропускания.
Физический смысл полосы пропускания
резонансных контуров рассматривался
для последовательного одиночного
колебательного контура. Для параллельного
контура физический смысл полосы
пропускания совершенно аналогичен.
Отличительная особенность параллельного
контура состоит в том, что выходным
сигналом является контурное напряжение,
и АЧХ отображает его зависимость от
частоты.
Полосой
пропускания параллельного одиночного
колебательного контура называется
интервал частот, включающий резонансную
частоту контура, на границах которого
значение напряжения контура меньше
значения напряжения на резонансной
частоте в
раз.
Это
требование для значения напряжения на
границе полосы пропускания можно
выразить так:


Последнее
соотношение позволяет определить
границы полосы пропускания и ее величину
по АЧХ контура (рис.3.23):

Пользуясь
полученными соотношениями для
последовательного колебательного
контура, АЧХ для параллельного контура
на границах полосы пропускания примет
вид, аналогичный (3.36):

(3.67)
Приравнивая
(3.67) к коэффициенту неравномерности
и решая полученное уравнение относительно
2∆ω, находим:


Как
отмечалось, для широкого круга
приемно-передающих устройств коэффициент
неравномерности берется равным:

С
учетом этого находим выражение для
полосы пропускания одиночного
параллельного резонансного контура:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Амплитудно-частотная характеристика
Аббревиатура АЧХ расшифровывается как амплитудно-частотная характеристика. На английском этот термин звучит как «frequency response», что в дословном переводе означает «частотный отклик». Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства. АЧХ может быть определена аналитически через формулы, либо экспериментально. Любое устройство предназначено для передачи (или усиления) электрических сигналов. АЧХ устройства определяется по зависимости коэффициента передачи (или коэффициента усиления) от частоты.
Коэффициент передачи
Что такое коэффициент передачи? Коэффициент передачи — это отношение напряжения на выходе цепи к напряжению на ее входе. Или формулой:
где
Uвых — напряжение на выходе цепи
Uвх — напряжение на входе цепи
В усилительных устройствах коэффициент передачи больше единицы. Если устройство вносит ослабление передаваемого сигнала, то коэффициент передачи меньше единицы.
Коэффициент передачи может быть выражен через децибелы:
Строим АЧХ RC-цепи в программе Proteus
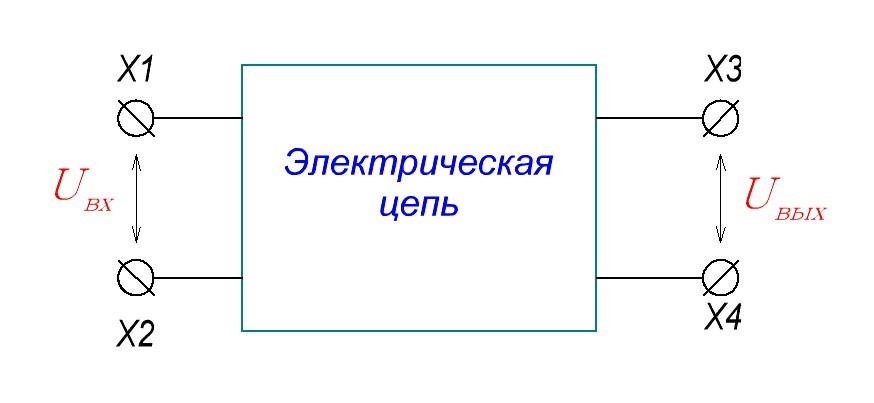
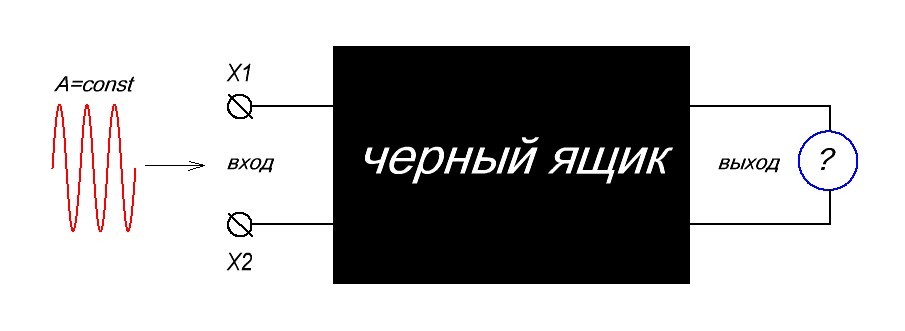
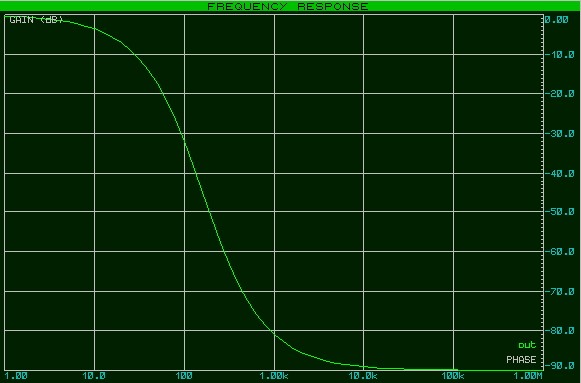
Для того, чтобы досконально разобраться, что такое АЧХ, давайте рассмотрим рисунок ниже.
Итак, имеем «черный ящик», на вход которого мы будем подавать синусоидальный сигнал, а на выходе черного ящика мы будем снимать сигнал. Должно соблюдаться условие: нужно менять частоту входного синусоидального сигнала, но его амплитуда должна быть постоянной.
Что нам делать дальше? Надо измерить амплитуду сигнала на выходе после черного ящика при интересующих нас значениях частоты входного сигнала. То есть мы должны изменять частоту входного сигнала от 0 Герц (постоянный ток) и до какого-либо конечного значения, которое будет удовлетворять нашим целям, и смотреть, какая амплитуда сигнала будет на выходе при соответствующих значениях на входе.
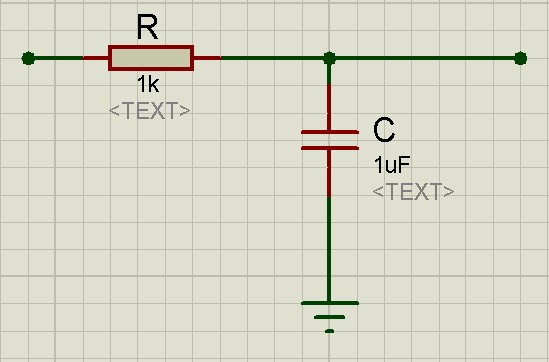
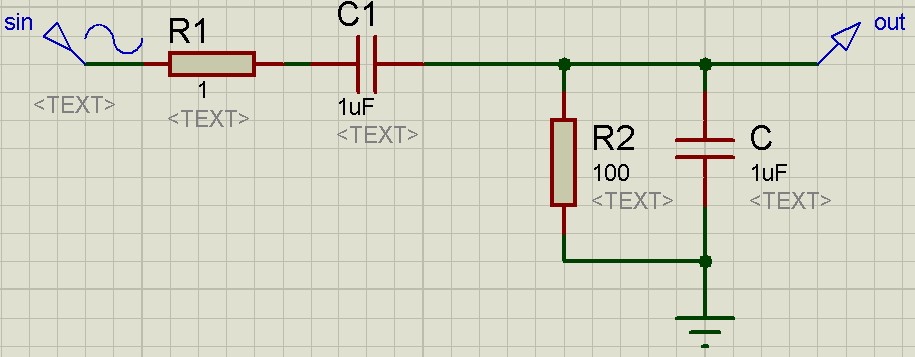
Давайте разберем все это дело на примере. Пусть в черном ящике у нас будет самая простая RC-цепь с уже известными номиналами радиоэлементов.
Как я уже говорил, АЧХ может быть построено экспериментально, а также с помощью программ-симуляторов. На мой взгляд, самый простой и мощный симулятор для новичков — это Proteus. С него и начнем.
Собираем данную схему в рабочем поле программы Proteus
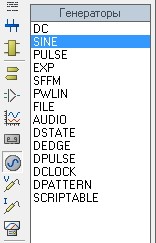
Для того, чтобы подать на вход схемы синусоидальный сигнал, мы кликаем на кнопочку «Генераторы», выбираем SINE, а потом соединяем его со входом нашей схемы.
Для измерения выходного сигнала достаточно кликнуть на значок с буквой «V» и соединить выплывающий значок с выходом нашей схемы:
Для эстетики, я уже поменял название входа и выхода на sin и out. Должно получиться как-то вот так:
Ну вот, пол дела уже сделано.
Теперь осталось добавить важный инструмент. Он называется «frequency response», как я уже говорил, в дословном переводе с английского — «частотный отклик». Для этого нажимаем кнопочку «Диаграмма» и в списке выбираем «frequency»
На экране появится что-то типа этого:
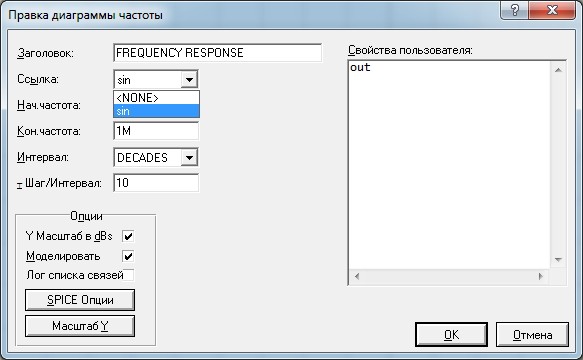
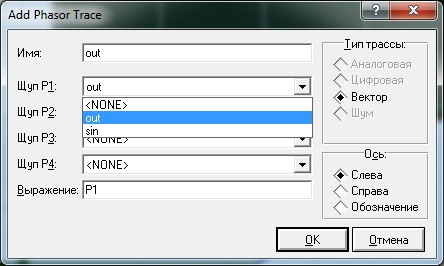
Кликаем ЛКМ два раза и открывается вот такое окошко, где в качестве входного сигнала мы выбираем наш генератор синуса (sin), который у нас сейчас задает частоту на входе.
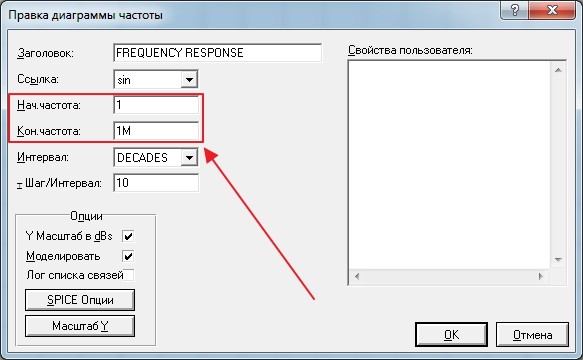
Здесь же выбираем диапазон частоты, который будем «загонять» на вход нашей цепи. В данном случае это диапазон от 1 Гц и до 1 МГц. При установке начальной частоты в 0 Герц Proteus выдает ошибку. Поэтому, ставьте начальную частоту близкую к нулю.
Нажимаем ОК.
Далее нажимаем ПКМ на самой табличке Frequency Response и видим вот такой выплывающий список, в котором нажимаем «Добавить трассы»
Долго не думая, выбираем в первом же окошке наш выход out
и в результате должно появится окошко с нашим выходом
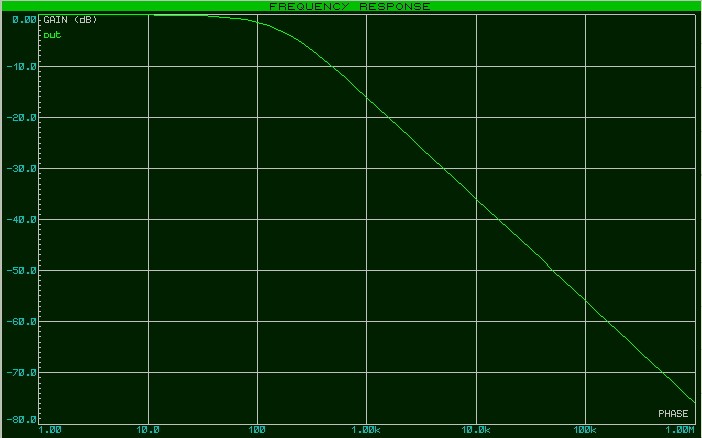
Нажимаем пробел и радуемся результату
Итак, что интересного можно обнаружить, если взглянуть на нашу АЧХ? Как вы могли заметить, амплитуда на выходе цепи падает с увеличением частоты. Это означает, что наша RC-цепь является своеобразным частотным фильтром. Такой фильтр пропускает низкие частоты, в нашем случае до 100 Герц, а потом с ростом частоты начинает их «давить». И чем больше частота, тем больше он ослабляет амплитуду выходного сигнала. Поэтому, в данном случае, наша RC-цепь является самым простейшим фильтром низкой частоты (ФНЧ).
Полоса пропускания
В среде радиолюбителей и не только встречается также такой термин, как полоса пропускания. Полоса пропускания — это диапазон частот, в пределах которого АЧХ радиотехнической цепи или устройства достаточно равномерна, чтобы обеспечить передачу сигнала без существенного искажения его формы.
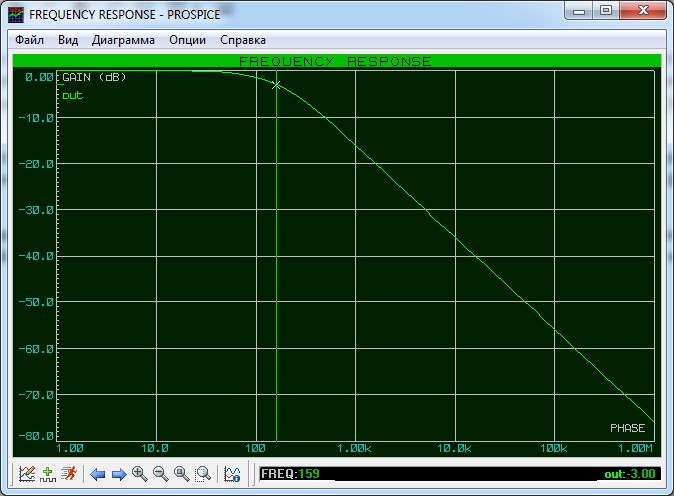
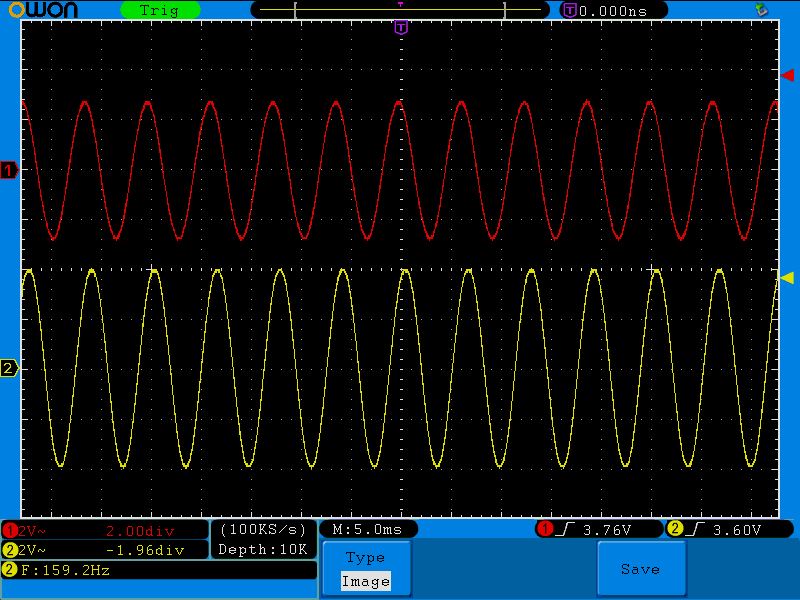
Как же определить полосу пропускания? Это сделать довольно легко. Достаточно на графике АЧХ найти уровень в -3 дБ от максимального значения АЧХ и найти точку пересечения прямой с графиком. В нашем случае это можно сделать легче пареной репы. Достаточно развернуть нашу диаграмму на весь экран и с помощью встроенного маркера посмотреть частоту на уровне в -3 дБ в точке пересечения с нашим графиком АЧХ. Как мы видим, она равняется 159 Герц.
Частота, которая получается на уровне в -3 дБ, называется частотой среза. Для RC-цепи ее можно найти по формуле:
Для нашего случая расчетная частота получилась 159,2 Гц, что подтверждает и Proteus.
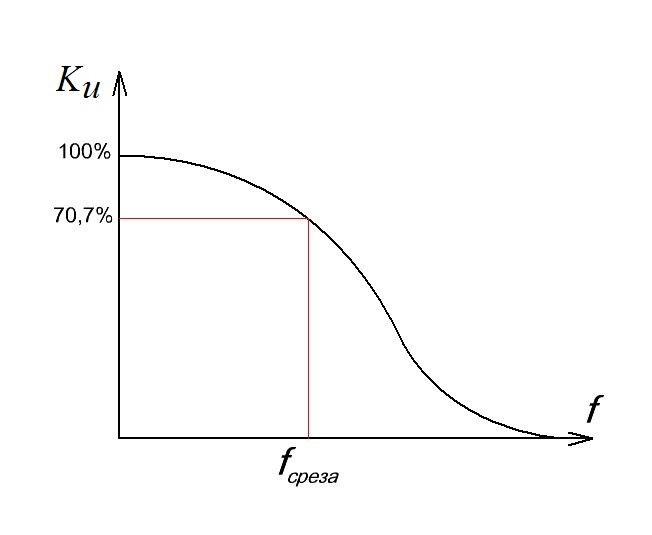
Кто не желает связываться с децибелами, то можно провести линию на уровне 0,707 от максимальной амплитуды выходного сигнала и смотреть пересечение с графиком. В данном примере, для наглядности, я взял максимальную амплитуду за уровень в 100%.
Как построить АЧХ на практике?
Как построить АЧХ на практике, имея в своем арсенале генератор частоты и осциллограф?
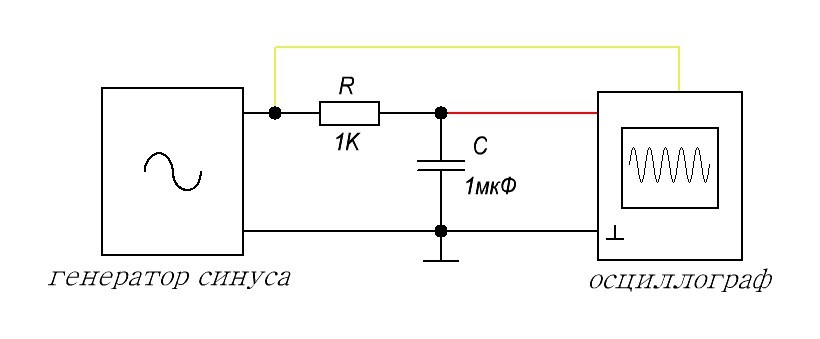
Итак, поехали. Собираем нашу цепь в реале:
Ну а теперь цепляем ко входу схемы генератор частоты, а с помощью осциллографа следим за амплитудой выходного сигнала, а также будем следить за амплитудой входного сигнала, чтобы мы были точно уверены, что на вход RC-цепи подается синус с постоянной амплитудой.
Для экспериментального изучения АЧХ нам потребуется собрать простенькую схемку:
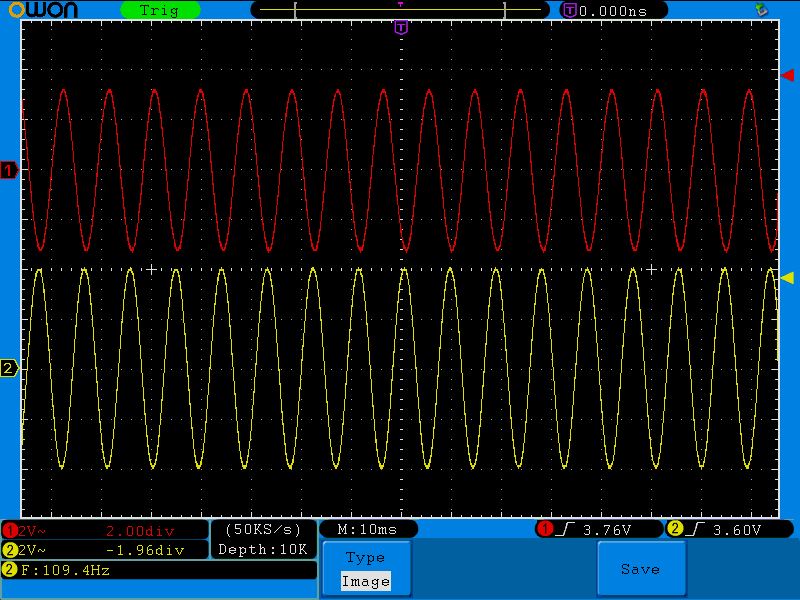
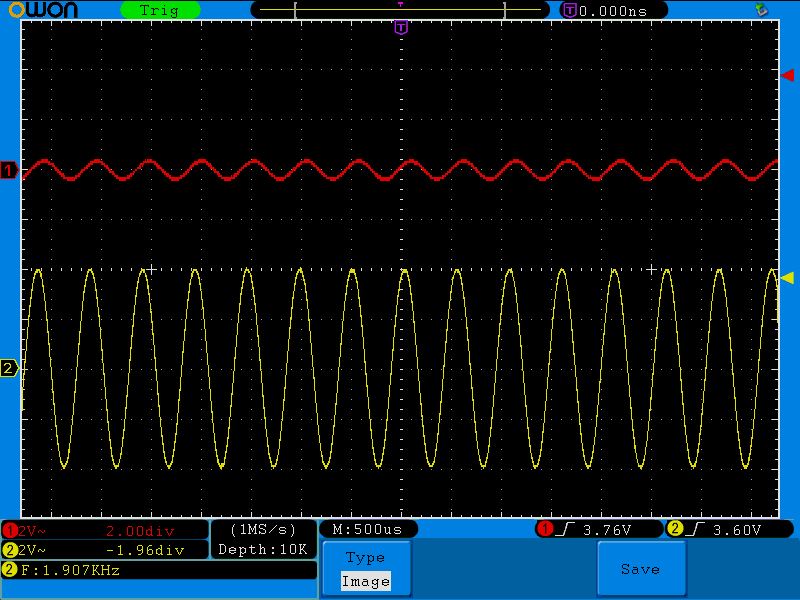
Наша задача состоит в том, чтобы менять частоту генератора и уже наблюдать, что покажет осциллограф на выходе цепи. Мы будем прогонять нашу цепь по частотам, начиная от самой малой. Как я уже сказал, желтый канал предназначен для визуального контроля, что мы честно проводим опыт.
Постоянный ток, проходящий через эту цепь, на выходе будет давать амплитудное значение входного сигнала, поэтому первая точка будет иметь координаты (0;4), так как амплитуда нашего входного сигнала 4 Вольта.
Следующее значение смотрим на осциллограмме:
Частота 15 Герц, амплитуда на выходе 4 Вольта. Итак, вторая точка (15;4)
Третья точка (72;3.6). Обратите внимание на амплитуду выходного красного сигнала. Она начинает проседать.
Четвертая точка (109;3.2)
Пятая точка (159;2.8)
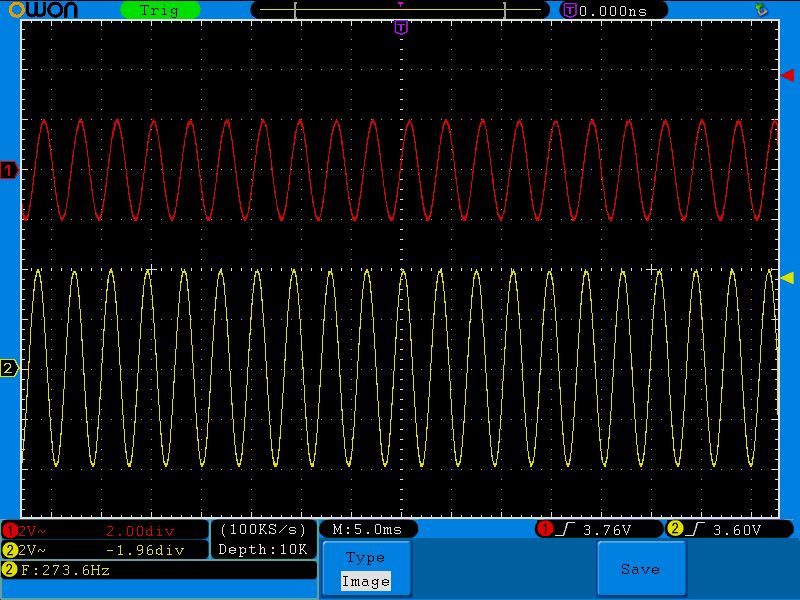
Шестая точка (201;2.4)
Седьмая точка (273;2)
Восьмая точка (361;1.6)
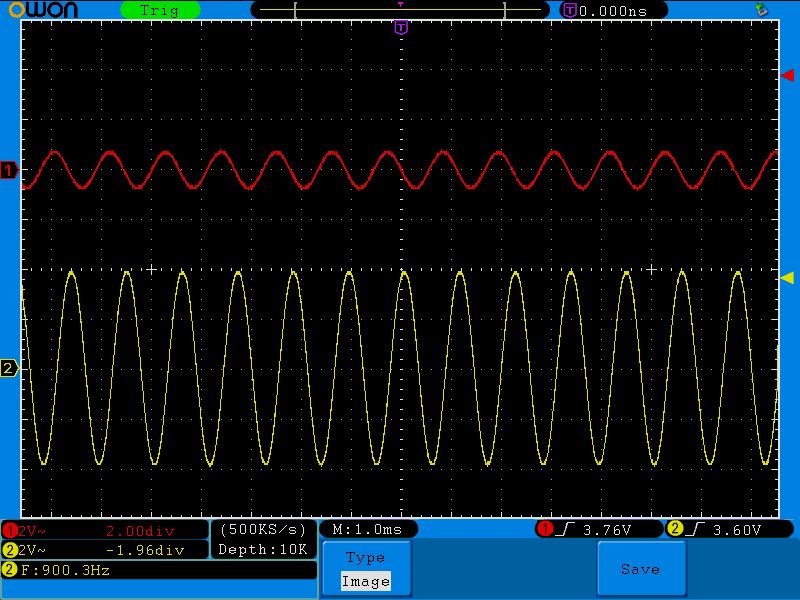
Девятая точка (542;1.2)
Десятая точка (900;0.8)
Ну и последняя одиннадцатая точка (1907;0.4)
В результате измерений у нас получилась табличка:
Строим график по полученным значениям и получаем нашу экспериментальную АЧХ 😉
Получилось не так, как в технической литературе. Оно и понятно, так как по Х берут логарифмический масштаб, а не линейный, как у меня на графике. Как вы видите, амплитуда выходного сигнала будет и дальше понижаться с увеличением частоты. Для того, чтобы еще более точно построить нашу АЧХ, требуется взять как можно больше точек.
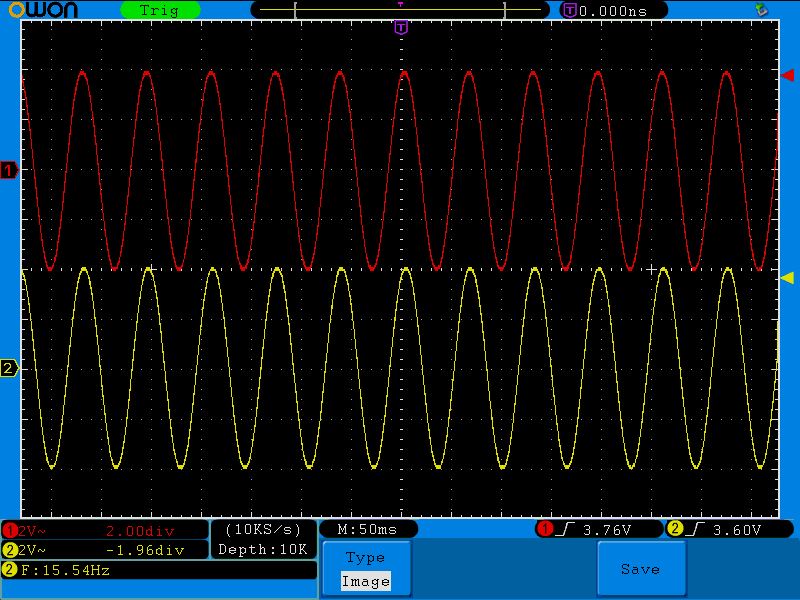
Давайте вернемся к этой осциллограмме:
Здесь на частоте среза амплитуда выходного сигнала получилась ровно 2,8 Вольт, которые как раз и находятся на уровне в 0,707. В нашем случае 100% это 4 Вольта. 4х0,707=2,82 Вольта.
АЧХ полосового фильтра
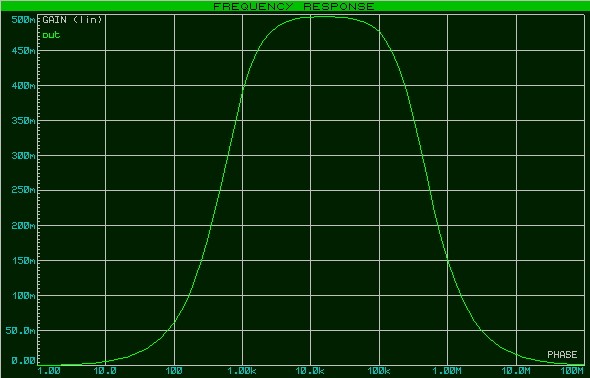
Существуют также схемы, АЧХ которых имеет вид холма или ямы. Давайте рассмотрим один из примеров. Мы будем рассматривать так называемый полосовой фильтр, АЧХ которого имеет вид холма.
Собственно сама схема:
А вот ее АЧХ:
Особенность таких фильтров, что они имеют две частоты среза. Определяются они также на уровне в -3дБ или на уровне в 0,707 от максимального значения коэффициента передачи, а еще точнее Ku max/√2.
Так как в дБ смотреть график неудобно, поэтому я переведу его в линейный режим по оси Y, убирая маркер
В результате перестроения получилась такая АЧХ:
Максимальное значение на выходе составило 498 мВ при амплитуде входного сигнала в 10 Вольт. Мдя, неплохой «усилитель») Итак, находим значение частот на уровне в 0,707х498=352мВ. В результате получились две частоты среза — это частота в 786 Гц и в 320 КГц. Следовательно, полоса пропускания данного фильтра от 786Гц и до 320 КГц.
На практике для получения АЧХ используются приборы, называемые характериографами для исследования АЧХ. Вот так выглядит один из образцов Советского Союза
Фазо-частотная характеристика
ФЧХ расшифровывается как фазо-частотная характеристика, phase response — фазовый отклик. Фазо-частотная характеристика — это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.
Разность фаз
Думаю, вы не раз слышали такое выражение, как » у него произошел сдвиг по фазе». Это выражение не так давно пришло в наш лексикон и обозначает оно то, что человек слегка двинулся умом. То есть было все нормально, а потом раз! И все :-). И в электронике такое тоже часто бывает) Разницу между фазами сигналов в электронике называют разностью фаз. Вроде бы «загоняем» на вход какой-либо сигнал, а выходной сигнал ни с того ни с сего взял и сдвинулся по времени, относительно входного сигнала.
Для того, чтобы определить разность фаз, должно выполняться условие: частоты сигналов должны быть равны. Пусть даже один сигнал будет с амплитудой в Киловольт, а другой в милливольт. Неважно! Лишь бы соблюдалось равенство частот. Если бы условие равенства не соблюдалось, то сдвиг фаз между сигналами все время бы изменялся.
Для определения сдвига фаз используют двухканальный осциллограф. Разность фаз чаще всего обозначается буквой φ и на осциллограмме это выглядит примерно так:
Строим ФЧХ RC-цепи в Proteus
Для нашей исследуемой цепи
Для того, чтобы отобразить ее в Proteus мы снова открываем функцию «frequency response»
Все также выбираем наш генератор
Не забываем проставлять испытуемый диапазон частот:
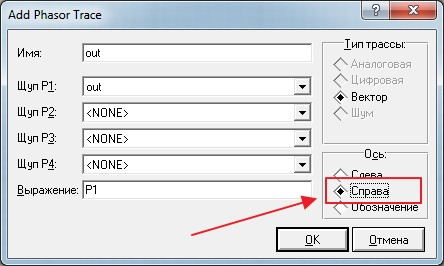
Далее нажимаем ПКМ на самой табличке Frequency Response и видим вот такой выплывающий список, в котором нажимаем «Добавить трассы»
Долго не думая, выбираем в первом же окошке наш выход out
И теперь главное отличие: в колонке «Ось» ставим маркер на «Справа»
Нажимаем пробел и вуаля!
Можно его развернуть на весь экран
При большом желании эти две характеристики можно объединить на одном графике
Обратите внимание, что на частоте среза сдвиг фаз между входным и выходным сигналом составляет 45 градусов или в радианах п/4 (кликните для увеличения)
В данном опыте при частоте более 100 КГц разность фаз достигает значения в 90 градусов (в радианах π/2) и уже не меняется.
Строим ФЧХ на практике
ФЧХ на практике можно измерить также, как и АЧХ, просто наблюдая разность фаз и записывая показания в табличку. В этом опыте мы просто убедимся, что на частоте среза у нас действительно разность фаз между входным и выходным сигналом будет 45 градусов или π/4 в радианах.
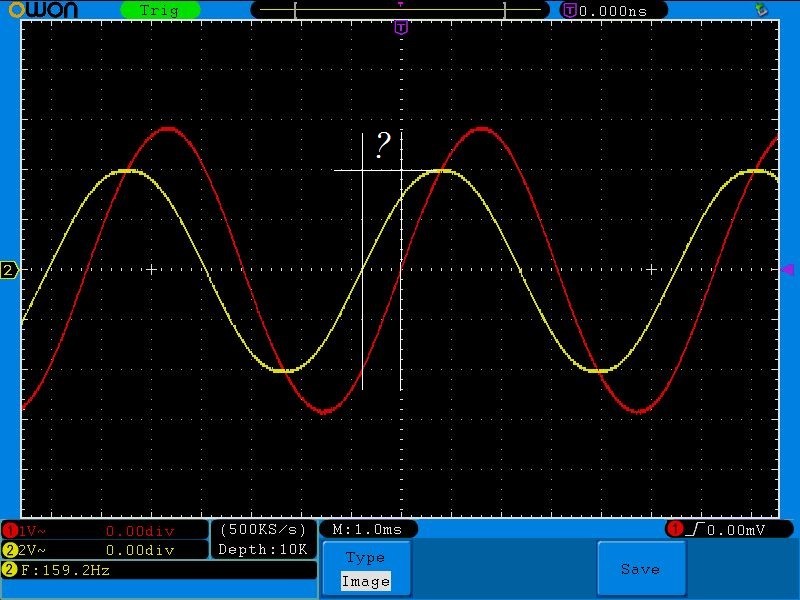
Итак, у меня получилась вот такая осциллограмма на частоте среза в 159,2 Гц
Нам надо узнать разность фаз между этими двумя сигналами
Весь период — это 2п, значит половина периода — это π. На полупериод у нас приходится где-то 15,5 делений. Между двумя сигналами разность в 4 деления. Составляем пропорцию:
Отсюда х=0,258п или можно сказать почти что 1/4п. Следовательно, разница фаз между двумя этими сигналами равняется п/4, что почти в точности совпало с расчетными значениями в Proteus.
Если Вы лучше воспринимаете информацию через видео, то к Вашему вниманию:
Резюме
Амплитудно-частотная характеристика цепи показывает зависимость уровня сигнала на выходе данного устройства от частоты передаваемого сигнала при постоянной амплитуде синусоидального сигнала на входе этого устройства.
И еще интересная статья — последовательное и параллельное соединение проводников.
Фазо-частотная характеристика — это зависимость сдвига по фазе между синусоидальными сигналами на входе и выходе устройства от частоты входного колебания.
Коэффициент передачи — это отношение напряжения на выходе цепи к напряжению на ее входе. Если коэффициент передачи больше единицы, то электрическая цепь усиливает входной ссигнал, если же меньше единицы, то ослабляет.
Полоса пропускания — это диапазон частот, в пределах которого АЧХ радиотехнической цепи или устройства достаточно равномерна, чтобы обеспечить передачу сигнала без существенного искажения его формы. Определяется по уровню 0,707 от максимального значения АЧХ.
Содержание:
Частотные методы анализа электрических цепей:
Частотные характеристики являются компонентами комплексных функций цепи.
Комплексная функция цепи (КФЦ)
Амплитудно-частотная характеристика (АЧХ)
Фазочастотная характеристика (ФЧХ)
Амплитудно-фазовая частотная характеристика (АФЧХ) (комплексная функция цепи)
где 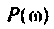
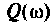
Комплексные функции простых цепей можно рассчитать непосредственно по закону Ома.
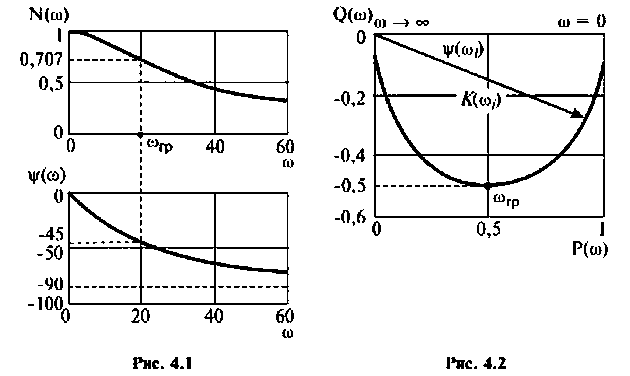
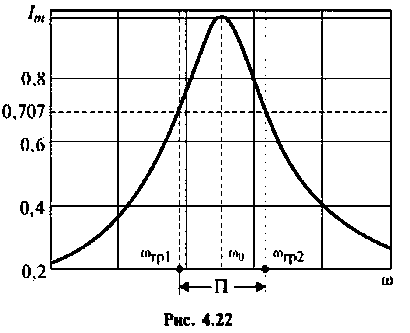
На рис.4.1 показаны АЧХ и ФЧХ, а на рис.4.2 — АФЧХ простейшей интегрирующей цепи (апериодического звена). По АЧХ определяют полосу пропускания
Полосой пропускания П называется диапазон частот, на границах которого мощность сигнала уменьшается в 2 раза, а амплитуда (действующее значение) напряжения (тока) — в 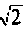
Полоса пропускания может измеряться в радианах в секунду 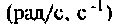
Например, для простой интегрирующей цепи полоса пропускания (см. рис. 4.1)
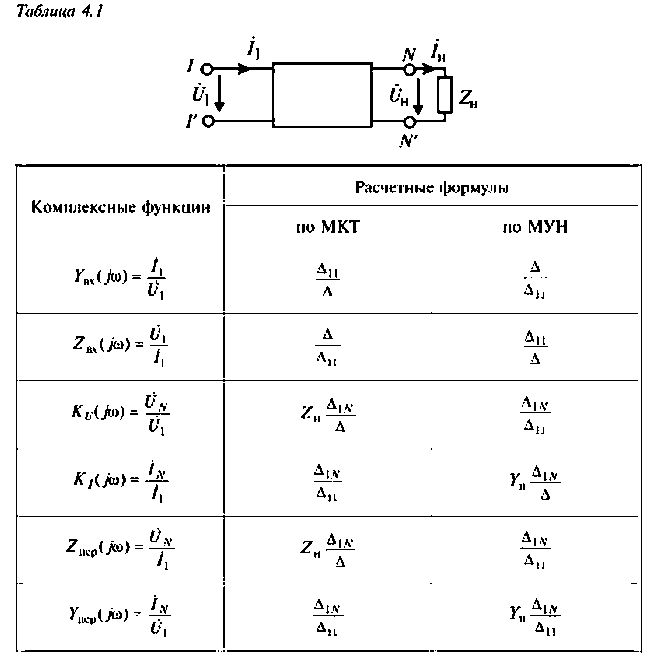
Для сложных цепей КФЦ рассчитывают по MKT или МУН. В табл. 4.1 приведены соотношения для расчета КФЦ, выраженные через определитель и алгебраические дополнения матрицы контурных сопротивлений и узловых проводимостей.
Частотные характеристики цепей с одним реактивным элементом
Примеры решения типовых задач:
Пример 4.2.1.
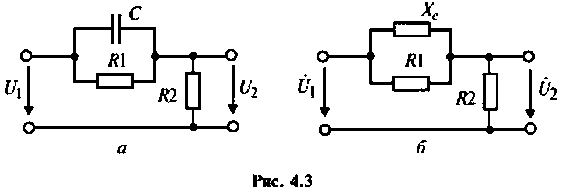
Определить комплексный коэффициент передачи по напряжению для дифференцирующего RC-контура (рис.4.3, а), рассчитать и построить графики АЧХ и ФЧХ.
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.3, б).
2. Определим комплексное напряжение на выходе цепи в виде
Преобразуем полученное выражение, вынеся зa скобки в числителе и знаменателе члены, не содержащие 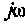
Следовательно.
Введем обозначения:
Величина 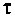
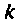
С учетом принятых обозначений
Для получения аналитических выражений АЧХ и ФЧХ запишем комплексную функцию в показательной форме.
Так как выражение (4.2) есть отношение двух полиномов, то удобно числитель и знаменатель записать отдельно в показательной форме, а затем разделить:
3. Из (4.3) запишем АЧХ и ФЧХ соответственно:
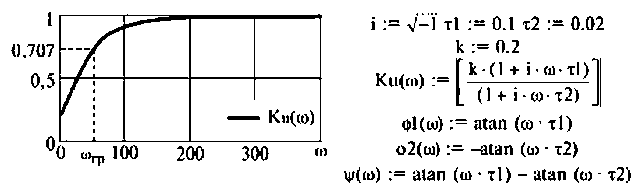
4. Построим график АЧХ и ФЧХ качественно по двум точкам. Для этого рассчитаем значения 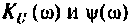
График АЧХ 
График функции ФЧХ 
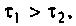
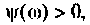
Исследуя функцию (4.5) на экстремум, можно показать, что она имеет максимум на частоте
где
Подставляя 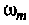
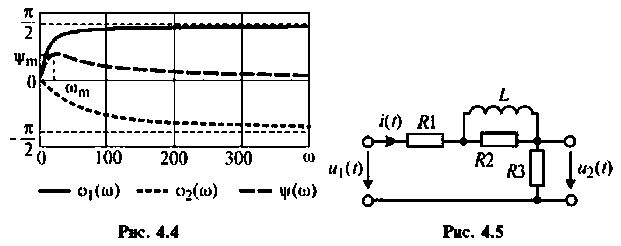
Графики АЧХ и ФЧХ изображены на рис. 4.4.
Пример 4.2.2.
Для электрической цепи, изображенной на рис. 4.5, определить АЧХ 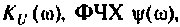
Решение
1. Найдем комплексную функцию К(; (/ш) но формуле делителя напряжения
Преобразуем полученное выражение к виду
Обозначим:
Следовательно,
Отсюда: АЧХ
ФЧХ
2. Рассчитаем граничную частоту. По определению
Из (4.7) найдем
Следовательно,
Из уравнения (4.9) получаем, что
Отсюда
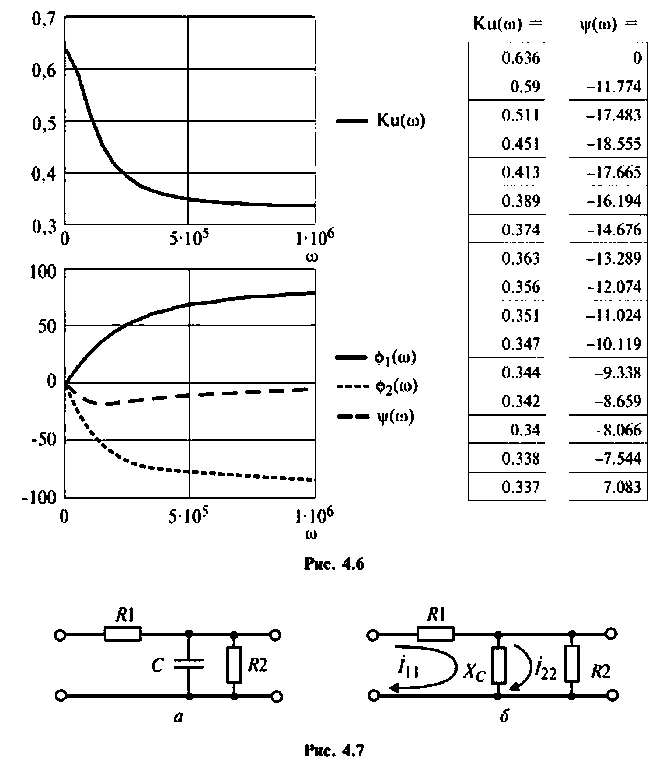
3. Построим график функций.
Вычислим значения (4.7) и (4.8) для частот с дискретностью
Графики и таблицы выполним в среде Mathcad (рис. 4.6).
Пример 4.2.3.
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.7, а), используя метод контурных токов. Построить в среде Mathcad график АЧХ, определить полосу пропускания.
Параметры цепи:
Решение
1. Представим цепь комплексной схемой замещения (рис. 4.7, б). Данная цепь имеет два независимых контура. Ток 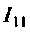
2.Составим матрицы контурных сопротивлений для двух независимых контуров
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
где сопротивление нагрузки равно
Подставляя найденные выражения, получаем
или
где
4. Рассчитаем 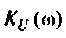
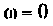
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 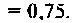
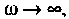
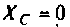
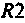
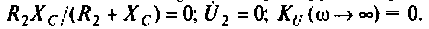
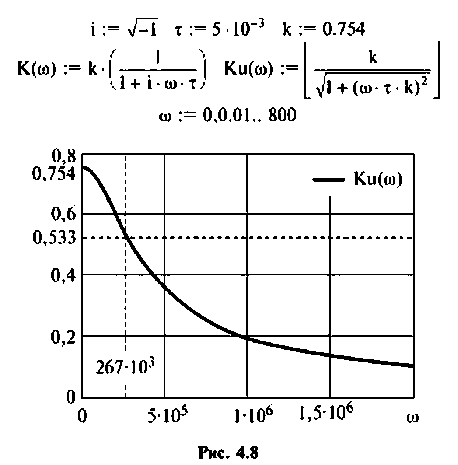
По полученным выражениям строим график АЧХ (рис. 4.8) и среде Mathcad.
5. Определяем полосу пропускания. По определению
Поэтому из (4.11) имеем
После преобразований уравнения (4.12) получаем
откуда
или
Следовательно, цепь имеет полосу пропускания
На рис. 4.8 указана граничная частота
Данная цепь представляет собой фильтр нижних частот с полосой пропускания 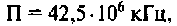

Пример 4.2.4.
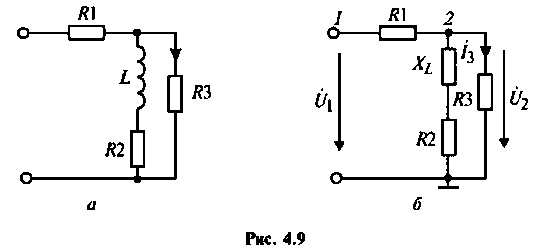
Найти комплексную передаточную проводимость 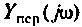
Параметры цепи: 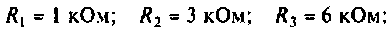
Определить АЧХ и ФЧХ, построить их графики в среде Mathcad.
Решение
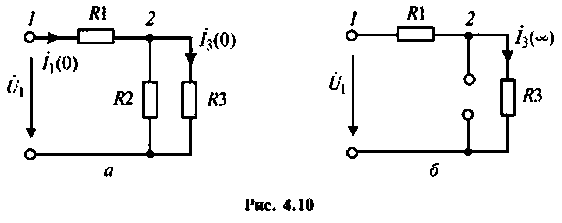
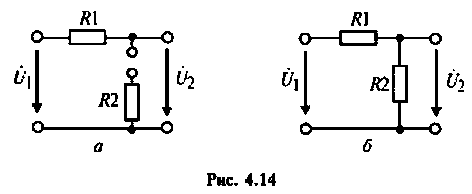
1. Изобразим комплексную схему замещения цепи (рис. 4.9, б). Схема имеет два независимых узла. В данном случае
2. Составим матрицу узловых проводимостей. При определении собственной проводимости узлов необходимо помнить, что собственная проводимость ветви, состоящей из последовательно включенных пассивных элементов, находится из соотношения 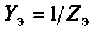
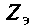
В начале рассчитывают комплексное сопротивление этой ветви, 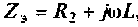
Составим матрицу проводимостей цепи 1 2
Как видим, общие проводимости узлов взяты со знаком минус, так как узловые напряжения 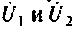
3.Определим комплексную передаточную проводимость по соотношению, приведенному в табл. 4.1
где 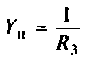
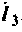
Найдем алгебраические дополнения:
После подстановки найденных значений получим
Для определении АЧХ и ФЧХ запишем выражения для модуля и аргумента
4. Рассчитаем значения 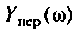
Примечание. Эти значения можно найти без вывода аналитического выражения для 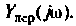
Учитывая, что 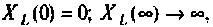
Для первой схемы:
Следовательно,
Аналогично для второй схемы получим
При расчете сложных схем такой прием можно применять для проверки правильности полученного аналитического выражения КФЦ.
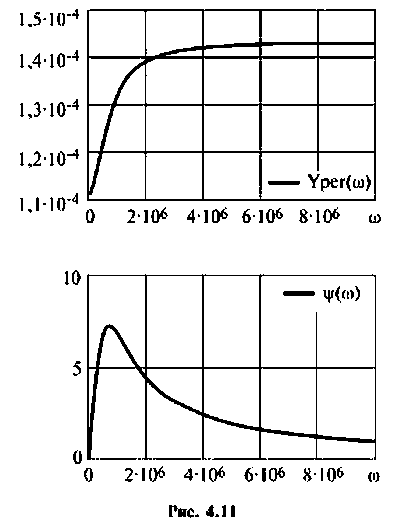
Из (4.13) видно, что функция наметен монотонной, но для качественного построения графика АЧХ (рис. 4.11) необходимо воспользоваться ПЭВМ, например построить функцию в среде Mathcad.
Пример 4.2.5.
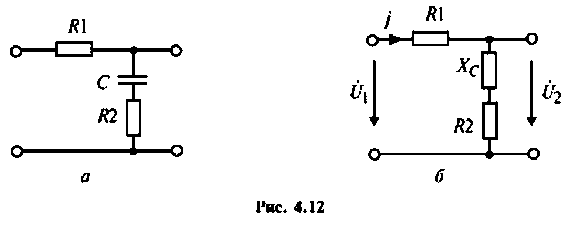
Для интегрирующего RС-контура (рис.4.12,а) определить комплексный коэффициент передачи по напряжению, рассчитать АЧХ, ФЧХ, ВЧХ, МЧХ. Построить графики АЧХ, ФЧХ. АФЧХ, если
Решение
1. Составим комплексную схему замещения цепи (рис. 4.12, б).
2. Определим 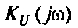
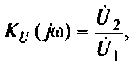
Следовательно.
3. Для нахождения АЧХ и ФЧХ комплексную функцию 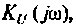
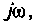
Найдем модуль (АЧХ) и аргумент (ФЧХ) комплексной функции;
Для определения вещественной и мнимой частотных характеристик запишем КФЦ в алгебраической форме. Для этого умножим и разделим (4.14) на комплексно-сопряженный знаменатель:
4. Для приближенного построения графиков АЧХ, ФЧХ. АФХ найдем значения 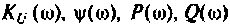
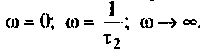
Для более точного и наглядного представления графиков воспользуемся ПЭВМ и математической средой Mathcad.
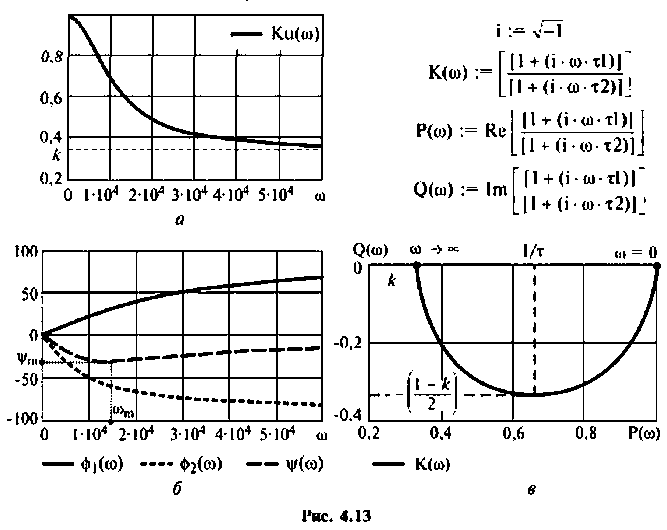
Графики характеристик приведены на рис. 4.13.
АЧХ представляет монотонно убывающую функцию (рис. 4.13, а).
ФЧХ принимает отрицательные значения, т.е. контур вносит фазовое отставание, а на частоте 
Взяв производную, получим
Решая полученное уравнение относительно 
Подставляя 
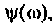
АФХ (рис. 4.13, в) представляет собой полуокружность, расположенную в 4-м квадрате. Центр окружности находится на оси 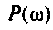
Радиус окружности нетрудно определить из соотношения:
МЧХ:
Отрицательное значение 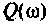
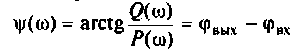
5. Проверка расчетов АЧХ. Воспользуемся эквивалентными схемами цепи для частот 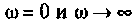
На частоте 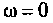
При 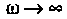
Подставляя эти значения частот в аналитическое выражение (4.14) для 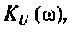
Следовательно, расчет АЧХ выполнен верно.
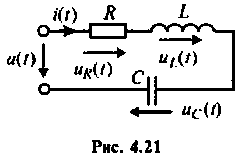
Частотные характеристики последовательного колебательного контура
Основные теоретические сведения:
В последовательном колебательном контуре (рис. 4.21) возникает резонанс напряжений, если выполняется условие
т. е. 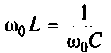
Резонансная частота
Волновое сопротивление контура
Сопротивление контура при резонансе
Собственная добротность контура
Добротность нагруженного контура
Затухание контура
Абсолютная расстройка
Относительная расстройка
Обобщенная расстройка
Фактор расстройки:
Абсолютная полоса пропускания (рис. 4.22)
Относительная полоса пропускания
Для нагруженного контура:
Комплексные коэффициенты передачи по напряжению:
на активном сопротивлении
на индуктивности
на емкости
Примеры решения типовых задач:
Пример 4.3.1.
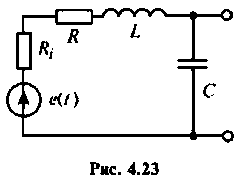
Последовательный колебательный контур (рис. 4.23) подключен к источнику напряжению. Контур настроен в резонанс.
Параметры цепи:
Определить резонансную частоту, волновое сопротивление. добротность и полосу пропускания, ток и напряжения на элементах контура.
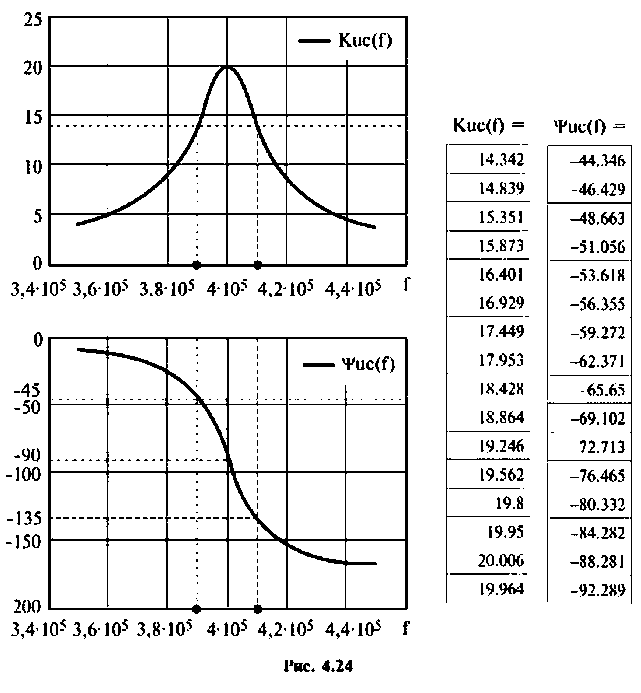
Построить АЧХ и ФЧХ по напряжению на конденсаторе в среде Mathcad.
Решение
1. Определяем резонансную частоту контура
2. Находим волновое сопротивление контура
3. Вычисляем добротность нагруженного контура
4. Определяем полосу пропускания
5. Рассчитываем ток и напряжения на элементах контура при резонансе
Напряжение на R равно
Напряжения на реактивных элементах
6. Рассчитаем АЧХ и ФЧХ комплексного коэффициента передачи напряжения с емкости.
Учитывая (4.22), из (4.29) получим:
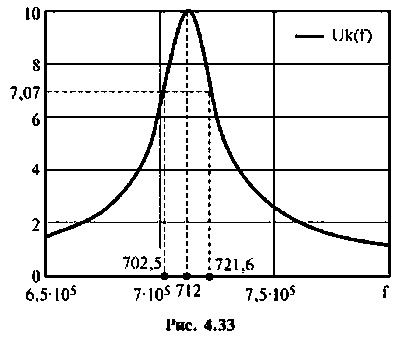
Для построения графиков АЧХ и ФЧХ, выполнения расчетов используем среду Mathcad. АЧХ, ФЧХ в виде графиков и таблиц приведены на рис. 4.24.
Следует заметить, что максимум А11Х достигается на частоте
т.е. при 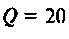
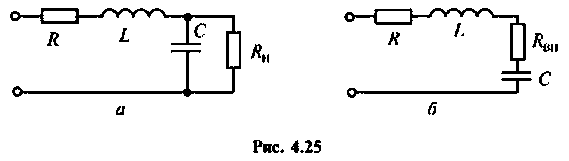
Задача 4.3.2.
К последовательному колебательному контуру (рис. 4.25) с параметрами 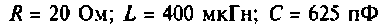
Определить собственную добротность и добротность нагруженного контура, полосу пропускания нагруженного и ненагруженного контура.
Решение
1. Рассчитаем вторичные параметры ненагруженного контура:
2.Определим вторичные параметры наруженного контура. Так как сопротивление нагрузки активное, причем 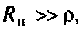
Для определения добротности рассчитаем сопротивление 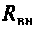
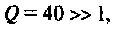
Следовательно,
Вывод. Подключение нагрузки ухудшает добротность контура, что приводит к расширению полосы пропускания.
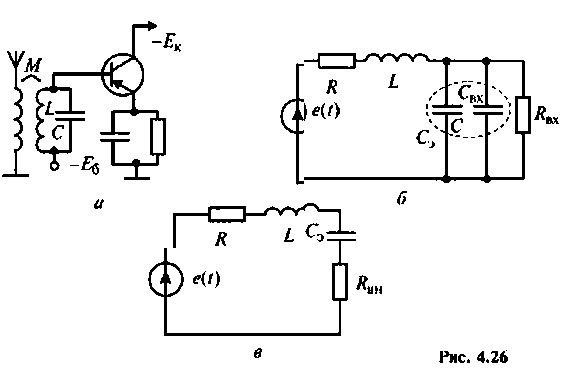
Пример 4.3.3.
На рис. 4.26, а изображена входная цепь приемника, а на рис. 4.26, б — ее эквивалентная схема. Известны входное сопротивление и входная емкость транзистора входного каскада УВЧ: 
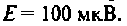
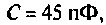
Определить абсолютную полосу пропускания и ток в контуре на резонансной частоте.
Решение
1. Определяем эквивалентную емкость контура
2. Рассчитываем резонансную частоту контура
3. Находим волновое сопротивление и сопротивление, вносимое в контур за счет транзистора усилителя (рис. 4.26, в):
4. Определяем добротность нагруженного контура
5. Рассчитаем абсолютную полосу пропускания нагруженного контура
6. Находим ток в контуре
Пример 4.3.4.
Рассчитать емкость последовательного колебательного контура, если резонансная частота контура 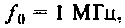
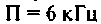
Построить АЧХ и ФЧХ комплексного коэффициента передачи напряжения с индуктивности в среде Mаthcad.
Решение
1. Определим требуемую добротность контура
2. Рассчитаем емкость конденсатора. Из формулы 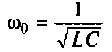
3. Рассчитаем АЧХ и ФЧХ.
Воспользуемся комплексным коэффициентом передачи напряжения с индуктивности по формуле (4.28). Учитывая 4.22), запишем:
Вычислим значения функций на частотах:
Определим частоту, при которой АЧХ имеет максимум
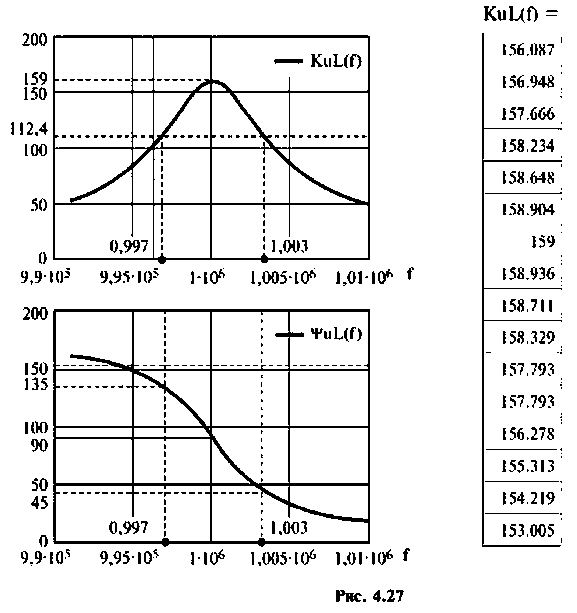
Смещением частоты 
Результаты расчетов АЧХ и ФЧХ б графическом и табличном видах приведены на рис. 4.27.
Частотные характеристики параллельного колебательного контура
Основные теоретические сведения:
Параллельный колебательный контур образуется путем параллельного соединения катушки индуктивности и конденсатора. Оба элемента, кроме основного эффекта (запасания энергии), имеют потери энергии. В расчетной схеме (рис. 4.29, а) тепловые потери в элементах учтены включением условных сопротивлений
где резонансная частота колебаний
Для реального контура 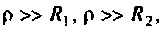
При резонансе сопротивление контура является активным, поэтому ток 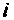
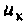
Сопротивление параллельного колебательного контура при резонансе максимально и равно (без учета внешней цепи)
где
Добротность 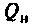
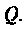
или через их проводимости
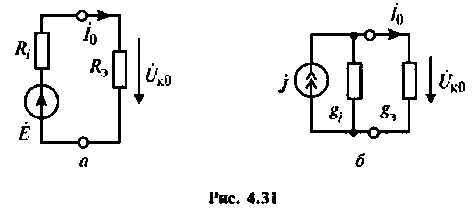
Важными параметрами цепи при резонансе являются токи в ветвях и напряжение на контуре. Ток в обшей ветви (ток источника) при резонансе минимален и равен (см. рис. 4.31)
При этом напряжение на контуре максимально и равно
Токи в индуктивности и в емкости при резонансе равны по значению и противоположны по направлению. Они образуют замкнутый ток в контуре, равный
Частотные свойства параллельного колебательного контура обычно оценивают по нормированной АЧХ
где 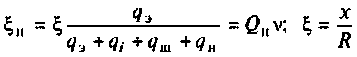
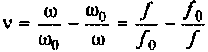
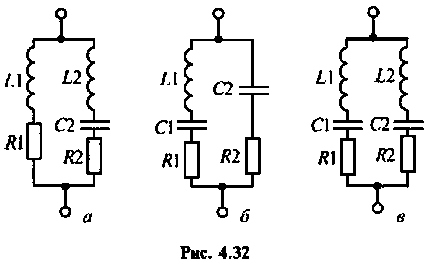
Параллельный контур, показанный на рис. 4.29, имеет по одной реактивности в ветвях. Такой контур называется простым или контуром I вида. Для уменьшения шунтирующего действия внешних цепей часто применяют сложные параллельные контуры.
На рис. 4.32, а, б, в показаны контуры II, (III и IV) видов, соответственно.
Главной особенностью этих контуров является то, что их резонансное сопротивление меньше резонансного сопротивления простого контура с такими же параметрами.
Сопротивление контуров (рис.4.32) при резонансе рассчитывается по формулам, соответственно:
где 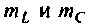
Примеры решения типовых задач:
Пример 4.4.1.
Параллельный контур (см. рис. 4.29, а) подключен к источнику с параметрами 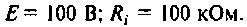
Параметры катушки индуктивности:
Определить действующие значения тока в контуре, тока на входе цепи и напряжения на контуре при резонансе, абсолютную и относительную полосы пропускания контура, добавочное сопротивление необходимое для расширения полосы пропускания в 2 раза.
Решение
1. Определим резонансную частоту колебания
2. Рассчитаем волновое сопротивление
3. Определим сопротивление контура при резонансе
4. Найдем действующее значение тока на входе контура (см. рис. 4.31, а) при резонансе
5. Определим соответственную добротность контура
6. Найдем ток в контуре и напряжение на нем:
7. Определим добротность нагруженного контура
8. Рассчитаем абсолютную и относительную полосы пропускания:
9. Определяем добавочное cопротивление 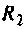
Пример 4.4.2.
Рассчитать полосу пропускания колебательного контура (см. рис. 4.30, а).
Дано:
Определить сопротивление 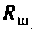
Решение
1. Рассчитаем волновое сопротивление и резонансную частоту контура:
2.Рассчитаем добротность цепи без шунта. Воспользуемся трехветвевой эквивалентной схемой цепи и соотношением (4.32). Найдем проводимость элементов схемы:
Тогда
3. Определим полосу пропускания
4. Найдем сопротивление шунта, необходимою для расширения полосы до 10 кГц,
В этом случае добротность цепи должна быть равна
Тогда из (4.32) получаем
Следовательно, сопротивление шунта должно быть равно
Пример 4.4.3.
Параллельный колебательный контур с параметрами: 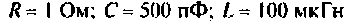
Определить собственную добротность контура, добротность нагруженного контура, абсолютную полосу пропускания и граничные частоты полосы пропускания. Построить резонансную кривую по напряжению на ЭВМ.
Решение
1. Определим волновое сопротивление контура
2. Рассчитаем собственную добротность контура
3. Найдем сопротивление контура при резонансе
4. Определим добротность нагруженного контура по формуле (4.31)
5. Рассчитаем резонансную частоту
6. Найдем полосу пропускания
7. Определим граничные частоты полосы пропускания:
8. Построим резонансную характеристику контура но напряжению. Из выражения (4.33) запишем
Напряжение па контуре при резонансе
Для построения резонансной характеристики задаемся характерными значениями частот: 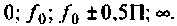
Пример 4.4.4.
Определить резонансную частоту, эквивалентное сопротивление при резонансе и добротность сложного контура (рис. 4.32, а), подключенного к источнику напряжения.
Дано:
Решение
1. Определим резонансную частоту и сопротивление параллельного контура при резонансе:
Сопротивление контура при резонансе
2. Рассчитаем эквивалентное сопротивление сложного контура II вида
3. Найдем добротность нагруженного контура II вида
Сравним значения 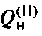
Вывод. За счет неполного включения индуктивности 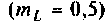
Частотные характеристики связанных колебательных контуров
Основные теоретические сведения:
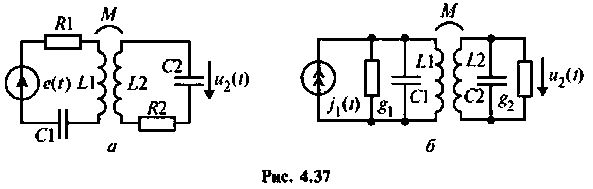
С целью повышения коэффициента прямоугольности АЧХ контуров применяют связанные контуры последовательного и параллельного питания (рис. 4.37, а, б).
Частотные характеристики связанных контуров рассмотрим на примере системы из двух контуров.
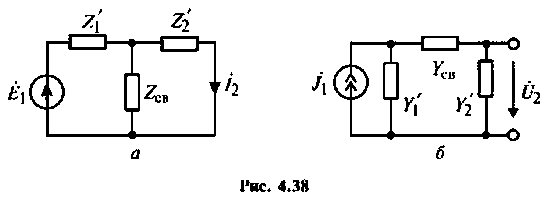
Эквивалентные схемы связанных контуров
Во всех случаях систему связанных контуров можно представить в виде Т- или П-образной эквивалентной схемы (рис. 4.38).
Количественной характеристикой связи является сопротивление связи 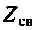
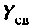
Удобным параметром для оценки связи является коэффициент связи
В случае реактивной связи для Т-образной схемы
Для П-образной схемы
где — сопротивление (проводимость) связи;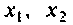
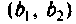
Для этого используют понятия вносимого сопротивления 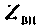
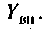
Резонансы в связанных контурах:
При настройке контуров в резонанс добиваются максимального тока (напряжения) во вторичном контуре.
Настройка связанных контуров может производиться различными способами, поэтому различают шесть резонансов. В табл. 4.3, 4.4 приведены виды и условия резонансов, способы настройки и соотношения для токов (напряжений) в связанных контурах последовательного (параллельного) питания.
Резонансные характеристики связанных контуров:
Для двух неидентичных связанных контуров: последовательного питания
где
параллельного питания:
где 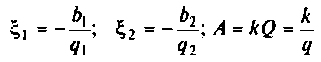
Если контуры идентичны, то обобщенная расстройка
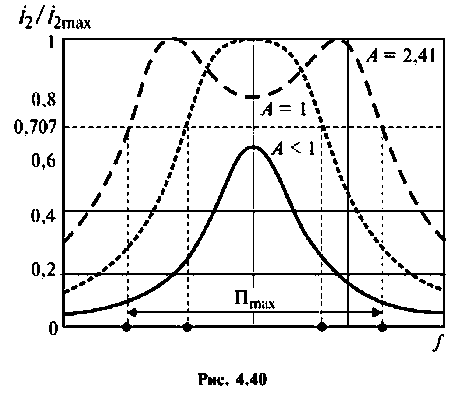
На рис. 4.40 приведены резонансные характеристики при различных факторах связи.
Относительная полоса пропускания:
а) связь слабая
б) связь критическая
в) связь сильная
При 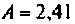
Примеры решения типовых задач:
Пример 4.5.1.
В системе двух индуктивно связанных контуров (см. рис.4.37,а) известны следующие параметры: коэффициент связи
Определить емкость 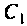
Решение
Емкость конденсатора 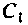
отсюда
Определим реактивное сопротивление 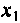
Peaктивное сопротивление второго контура
Рассчитаем полное сопротивление второго контура
Определим сопротивление связи контуров
Следовательно
Находим емкость первого контура
Пример 4.5.2.
Рассчитать емкости связанных контуров (см. рис. 4.37,а) и оптимальное сопротивление связи, если система настроена и полный резонанс. Определить токи, мощности в контурах при этом режиме, а также КПД системы.
Дано:
Решение
1. Определим емкость конденсатора 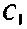
Отсюда
2. Сопротивление оптимальной связи при полном резонансе
3. Рассчитаем токи в первом и втором контурах при полном резонансе
4. Определим активные мощности в первом и втором контурах и КПД связанных контуров:
Пример 4.5.3.
На рис. 4.37, а показана система из двух идентичных связанных контуров с параметрами: 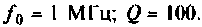
Решение
1. Определим полосу пропускания одиночного контура
2. Рассчитаем полосу пропускания системы связанных контуров:
1) определим параметр связи для
Таким образом при 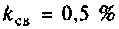
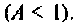
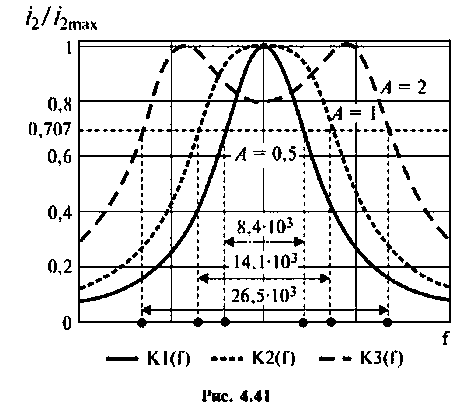
Абсолютная полоса пропускания (рис. 4.41, резонансная кривая А = 0,5)
2) при 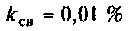
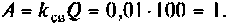
3) если 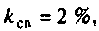
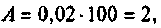
Рассчитаем полосу пропускания для этого случая.
Вид резонансных кривых по току и полоса пропускания для критической и сильной связи показаны на рис. 4.41, кривые А = 1 и А = 2.
Пример 4.5.4.
Антенный контур (см. рис. 4.37,б) индуктивно связан с входным контуром усилителя высокой частоты. Оба контура настроены в резонанс на частоту 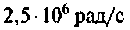
Дано:
Входное сопротивление УВЧ считать бесконечно большим.
Определить емкости и добротности контуров, их взаимную индуктивность, а также ток и напряжение на емкости во вторичном контуре.
Решение
1.Емкости контуров определим из формулы резонансной частоты. Емкость конденсатора первого контура
Емкость конденсатора второго контура
2. Рассчитаем волновое сопротивление контуров:
3. Рассчитаем добротности контуров и параметр связи:
4. Определим взаимную индуктивность двух связанных контуров
5. Рассчитаем ток во вторичном контуре. Известно (см. табл. 4.3), что при полном резонансе
Тогда, учитывая, что контуры настроены в резонанс, то из (4.34) получаем
Оба контура по условию настроены в резонанс, поэтому расстройки равны нулю:
С учетом этого рассчитаем ток во втором контуре
6. Найдем напряжение на конденсаторе вторичного контура
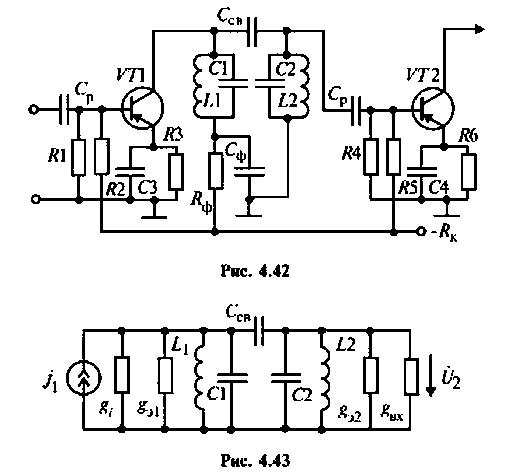
Пример 4.5.5.
На рис. 4.42 приведена схема одного каскада УПЧ радиоприемника, в котором избирательность обеспечивается двумя связанными контурами с емкостной связью. Оба контура настроены в резонанс на промежуточную частоту
Эквивалентная схема этого каскада (рис. 4.43) имеет следующие параметры: 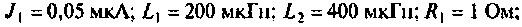
Определить емкости и добротности контуров, емкость связи, напряжение на емкости во вторичном контуре, а также полосу пропускания каскада УПЧ.
Решение
1. Из формулы резонансной частоты найдем емкость первого контура. С учетом влияния выходной емкости транзистора 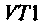
Емкость второго контура с учетом влияния входной емкости транзистора 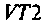
2. Определим емкость связи
3. Рассчитаем добротности нагруженных контуров при отсутствии связи между ними. Для расчета воспользуемся формулой (4.31)
где
где
4. Рассчитаем параметр связи
5. Рассчитаем напряжение на втором контуре. Известно (см. табл. 4.4), что при полном резонансе
Тогда, учитывая, что контуры настроены в резонанс 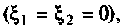
Найдем проводимость контуров
Тогда
6. Рассчитаем полосу пропускания каскадов УПЧ. учитывая, что А = 1,2.
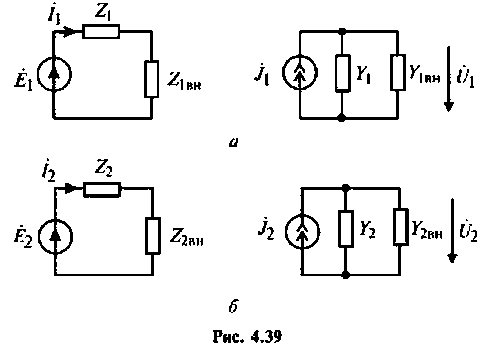
Частотные методы расчета и построения переходных и установившихся процессов в электрических цепях
Основные теоретические сведения:
Зная частотную характеристику электрической цепи 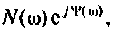
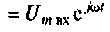
где 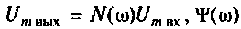
С помощью частотной характеристики электрической цели можно не только определить выходную величину цепи в установившемся режиме при гармоническом входном воздействии, но и найти реакцию цепи в переходном процессе на произвольное воздействие 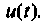
Найдем реакцию цепи на единичную ступенчатую функцию (т.е. найдем переходную функцию цепи), используя ее частотную характеристику. Как известно, интеграл Фурье для единичной ступенчатой функции имеет вид
т.е. единичная ступенчатая функция может быть представлена как бесконечная сумма элементарных колебаний вида
Каждому из этих колебаний соответствует выходное колебание 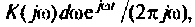
Представляя 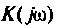
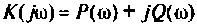
где 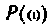
Построение переходной функции с помощью вещественной частотной характеристики методами численного интегрирования:
Выражение (4.38) позволяет вычислить переходную функцию ЭЦ и определить качество переходного процесса. Однако интегрирование этого выражения аналитическими методами — задача весьма трудоемкая, а чаще всего просто практически невыполнимая. С применением современных ЭВМ и методов численного интегрирования (метод прямоугольников, трапеций, метод Симпсона и др.) эта задача существенно упрощается, ее решение сводится к составлению программы для ПЭВМ. В инженерной практике интегрирование достаточно осуществлять в области существенных частот от 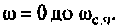

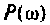
В результате интегрирования получают совокупность значений 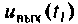
В качестве примера построения алгоритма численного интегрирования рассмотрим интегрирование с точки зрения простоты вычислений и точности результата. Сущность метода заключается в следующем. Пусть необходимо вычислить определенный интеграл
Вид подынтегральной функции, соответствующей выражению
при фиксированном времени 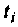
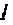
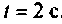
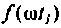
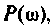
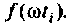
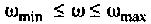
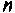
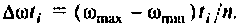
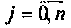

Очевидно, что погрешность численного интегрирования зависит и от выбора числа интервалов 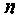
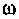
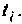
При этом одно полное колебание подынтегральной функции представляется не менее чем шестнадцатью трапециями.
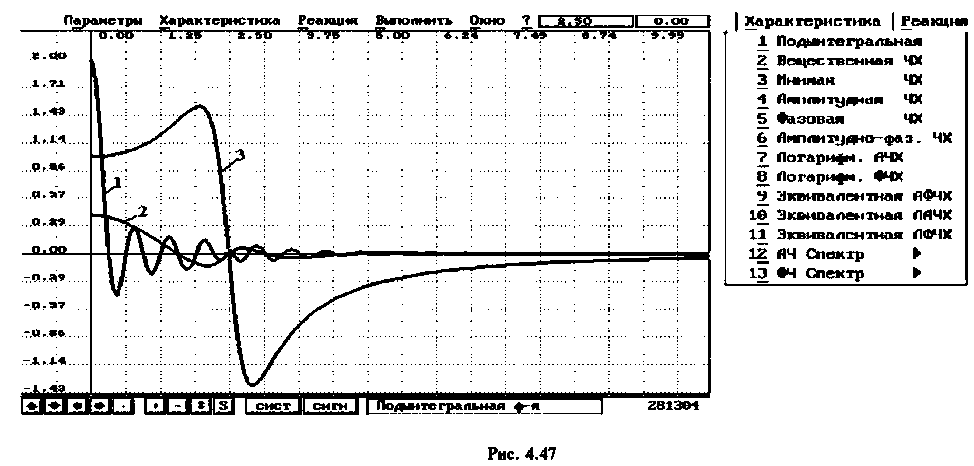
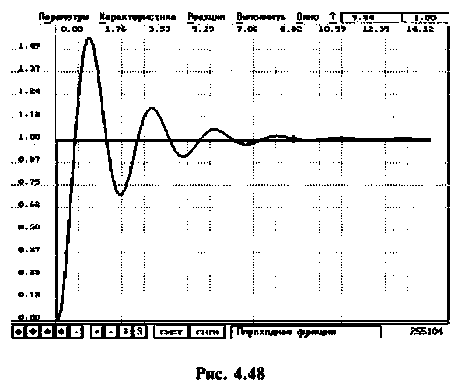
В качестве примера для построения переходной функции возьмем электрическую цепь, ВЧХ которой была построена и приведена на рис. 4.47 (кривая 3). На рис. 4.48 приведена переходная функция этой сложной электрической цепи.
Переходная функция на рис. 4.48 получена с помощью пакета ПП «Сигнал» [5].
Для вычисления интеграла (4.39) необходимо определить значение частоты для верхнего предела интегрирования 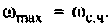
Алгебраическая форма КФ
где 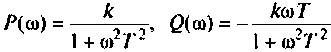
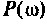
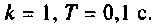
Из графика ВЧХ видно, что при 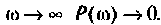
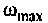
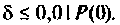
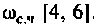
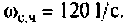
Для случая электрических цепей с дифференцирующими свойствами может оказаться, что при 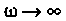
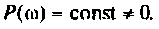
Приведенный пример наглядно показывает, что использование частотных характеристик для построения временных характеристик с помощью ЭВМ существенно расширяет возможности частотных методов анализа электрических цепей.
Спектральный метод расчета и построения выходных величин электрических цепей при сложных входных воздействиях:
Применение частотных методов при анализе и синтезе электрических цепей с требуемыми динамическими характеристиками и использованием ЭВМ позволяет не только строить переходные характеристики, но и строить реакцию цепи на любые детерминированные воздействия, оценивать их в установившихся режимах.
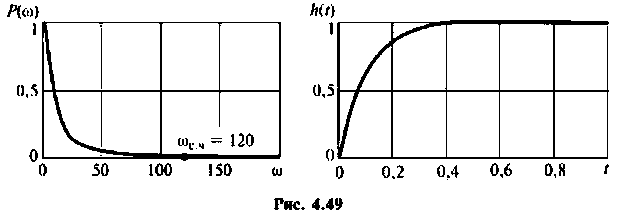
Математической основой частотных методов анализа электрических цепей и систем автоматического управления является обратное преобразование Фурье, позволяющее получать изображение выходного сигнала системы y(t) с помощью вещественной и мнимой частотных характеристик систем. В свою очередь, по вещественной или мнимой частотным характеристикам можно построить переходный процесс выходной величины и оценить реакцию цепи в переходном и установившемся режимах.
Как известно, реакция системы определяется по формуле обратного преобразования Фурье [4]
где
После соответствующих преобразований выражение (4.46) примет вид:
I) для ступенчатой входной функции 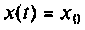
2) для линейной входной функции 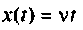
y{t) = vP(0)t+±l
2 r0(
Л» И
(4.48)
О)
3) для параболической входной функции 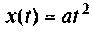
4) для полиномиального воздействия вида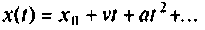
Применение ЭВМ и численных методов интегрирования позволяет отказаться от графических и табличных методов построения переходных и других необходимых функций в электрических цепях.
Примеры решения типовых задач:
Пример 4.6.1.
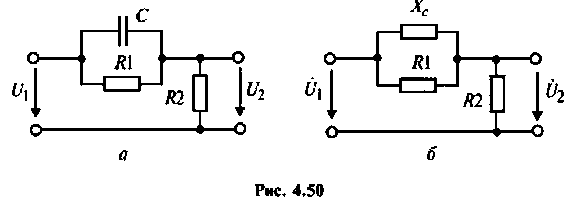
Определить комплексный коэффициент передачи по напряжению для дифференцирующего 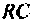
Решение
1. Изобразим комплексную схему замещения цепи (рис. 4.50, б).
2. Определим комплексное напряжение на выходе цепи в виде
Преобразуем полученное выражение, вынеся за скобки в числителе и знаменателе члены, не содержащие 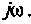
Следовательно
Введем обозначения:
Величина 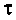
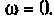
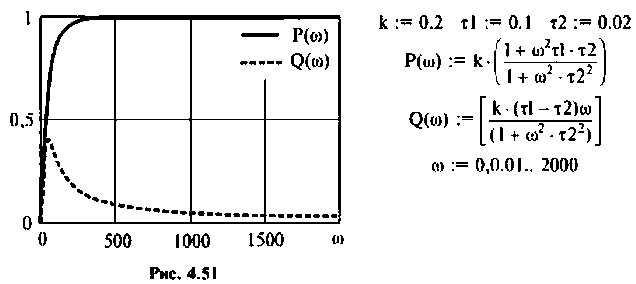
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
где
Примем:
Для определения частоты 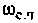
Из частотных характеристик КПФ принимаем 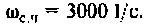
Переходная функция, показанная на рис.4.52, соответствует дифференцирую щему фазоопережающему контуру, который широко применяется в электронных и радиотехнических устройствах, системах автоматического управления.
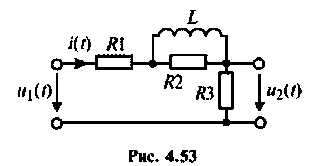
Пример 4.6.2.
Для электрической цепи, изображенной на рис, 4.53, определить КПФ 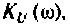
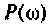
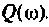
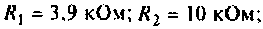
Решение
1. Найдем комплексную функцию 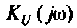
Преобразуем полученное выражение к виду
Обозначим:
Следовательно,
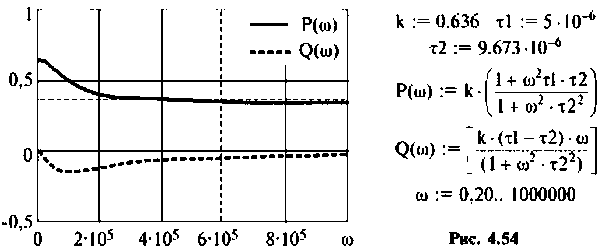
Для получения аналитических выражений ВЧХ и МЧХ запишем комплексную функцию и алгебраической форме
где
Для определения частоты 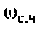
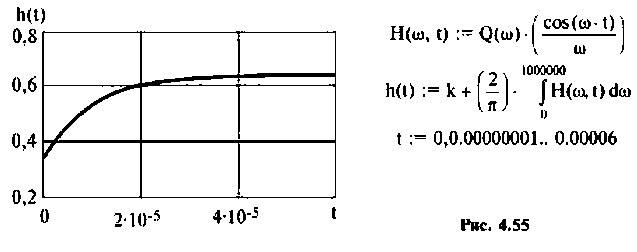
По виду ВЧХ и МЧХ определяем, что для построения переходной функции необходимо применить МЧХ. Примем из графика МЧХ 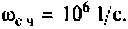
Из рис. 4.55 видно, что переходная функция соответствует интегрирующему контуру.
Пример 4.6.3.
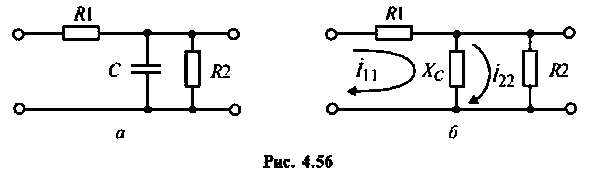
Определить комплексный коэффициент передачи интегрирующей цепи (рис. 4.56, а), используя метод контурных токов. Построить в среде Mathcad графики АЧХ, ВЧХ, МЧХ. Рассчитать и построить эпюру входного и выходного напряжения, если на вход цепи поступает напряжение вида 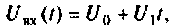
Параметры цепи:
Решение
1.Представим цепь комплексной схемой замещения (рис. 4.56, б). Данная цепь имеет два независимых контура. Ток 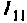
2.Составим матрицы контурных сопротивлений для двух независимых контуров
3.Определим комплексный коэффициент передачи, используя соотношение, приведенное в табл. 4.1.
где сопротивление нагрузки
Подставляя найденные выражения, получаем
т.е.
где
4. Рассчитаем 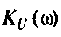
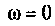
Объяснить полученные результаты можно, рассуждая так: на нулевой частоте (режим постоянного тока) сопротивление емкости бесконечно велико, ток в ней равен нулю, что эквивалентно разрыву этой ветви. При этом цепь становится резистивным делителем напряжения с передаточной функцией 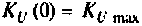
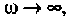
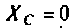
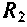
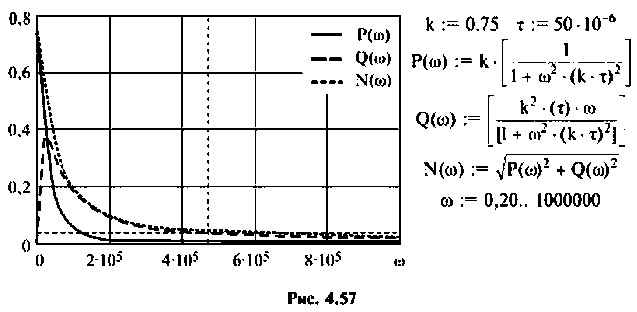
5.Определим выражения для АЧХ, ВЧХ, МЧХ. Представим КГ1Ф (4.55) в алгебраической форме
где 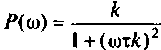
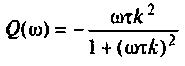
Амплитудно-частотную характеристику запишем в виде
6. В среде Mathcad построим частотные характеристики и определим
По ВЧХ на рис. 4.57 определяем, что существенная частота
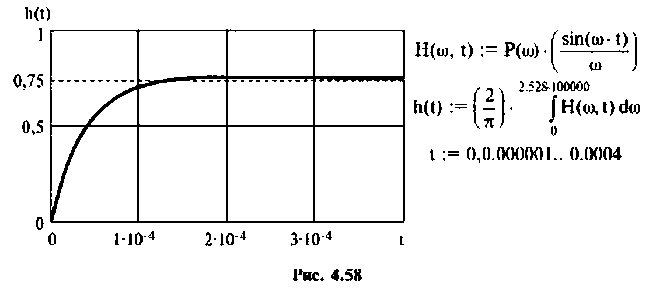
7. Построим переходную функцию электрической цепи, которая представлена на рис. 4.58.
Переходная функция электрической цепи соответствует апериодическому звену.
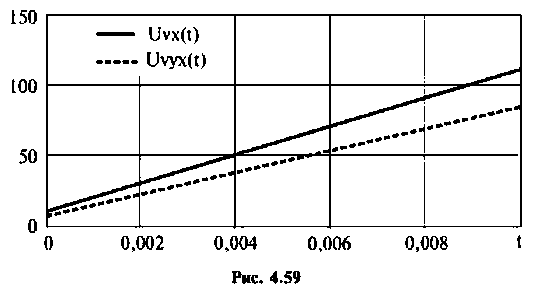
8. Построим реакцию электрической цепи на напряжение, изменяющееся но линейному закону (рис. 4.59).
- Операторные передаточные функции
- Свободные колебания в пассивных электрических цепях
- Цепи с распределёнными параметрами
- Волновые параметры длинной линии
- Энергетические характеристики двухполюсников
- Комплексные функции электрических цепей
- Гармонические колебания в колебательном контуре
- Частотные характеристики линейных электрических цепей