Уровень сложности
Средний
Время на прочтение
7 мин
Количество просмотров 11K

Представьте: вы принимаете аналоговый сигнал, смотрите на результаты показаний и видите, что синусоиду «перекосило». Все из-за плохой селективности вашего приемника и шумов, которые он принимает. Чтобы выделить и выровнять полезный сигнал и не слушать бесконечное шипение, в радиоприемнике должны быть качественные фильтры. Но что это такое, как они работают и какими бывают? Давайте разбираться.
Используйте навигацию, если не хотите читать текст полностью:
→ Что такое частотный фильтр
→ Очередной резистивный делитель, или из чего состоят фильтры
→ Немного о параметрах частотных фильтров
→ Рассчитывать фильтры — это сложно
→ Собираем фильтр Чебышева
Что такое частотный фильтр
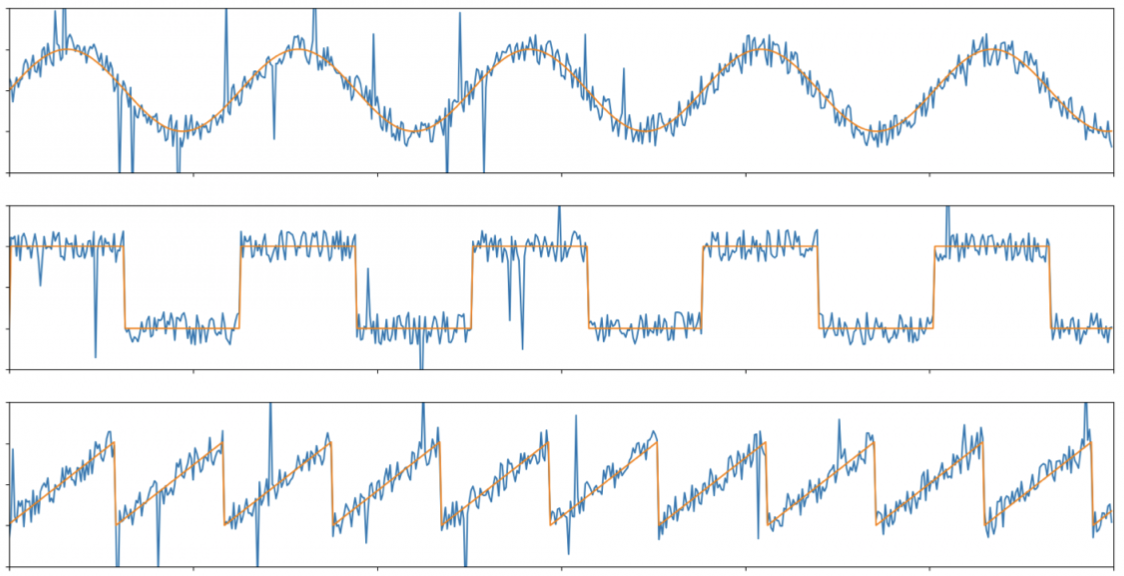
Синий сигнал — с шумами, оранжевый — идеальный, абсолютно чистый. Фильтр не может на 100% выпрямить сигнал, флуктуации все равно будут (см. пример, зеленый — отфильтрованный сигнал).
Частотный фильтр — это электрическая цепь, которая эффективно пропускает только одну область частот. Устройство позволяет «игнорировать» лишние частоты. Тем самым выделять и выравнивать сигналы любой формы — квадратные, синусоидальные, треугольные и другие.

Пример диапазона частот усиливаемого сигнала. Зависимость коэффициента пропускания по напряжению от частоты сигнала.
Фильтры широко применяют в измерительной, электронно вычислительной и радиотехнике. Яркий пример из схемотехники приемно-передающих устройств — ФНЧ/ ФПЧ в супергетеродинах и приемниках прямого преобразования, которые помогают выделить определенную частоту из диапазона.
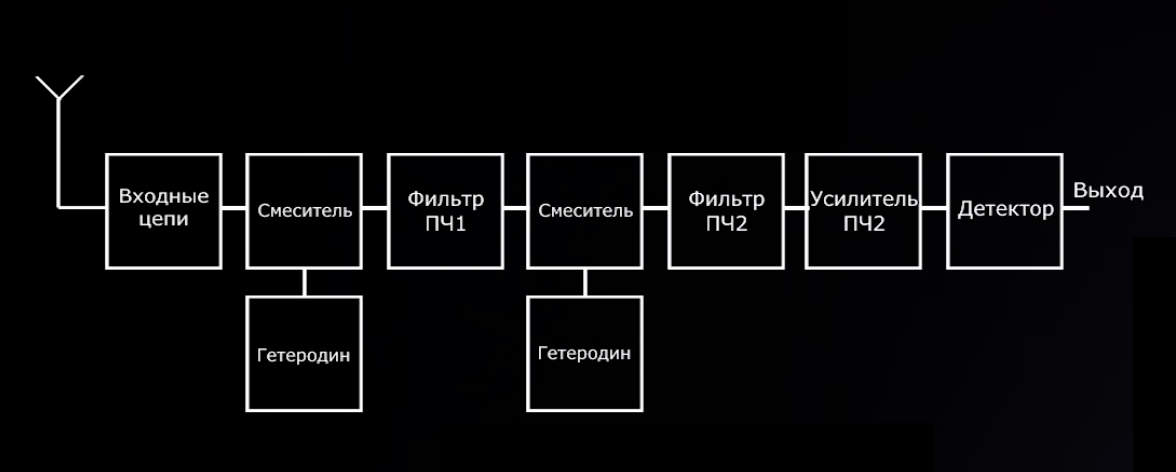
Типичная схема супергетеродина.
Фильтры используют не только в радиостанциях, усилителях и другой профессиональной технике. Их можно встретить в любом приемно-передающем устройстве — например, в смартфоне или роутере. Если говорить о более «прекрасном», то фильтры используют в эквалайзерах для обработки аудиосигналов.
Эквалайзер FabFilter Pro-Q2.
Какие бывают фильтры
Чаще всего можно встретить фильтры нижних частот (ФНЧ) и верхних (ФВЧ), а также полосовые и заградительные.
Фильтр верхних частот — пропускает частоты выше частоты среза.
Фильтр нижних частот — пропускает частоты ниже частоты среза.
Полосовой фильтр — пропускает определенную полосу.
Заградительный фильтр — не пропускает частоты определенной полосы, но пропускает колебания, выходящие за ее пределы.
Частота среза — это такая частота, после которой идет фронт (спад) с полосы пропускания на полосу заграждения. Посмотрим, как это выглядит на АЧХ ФНЧ:
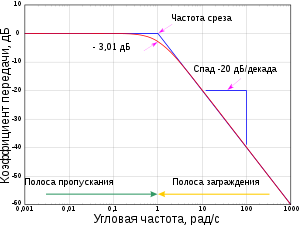
Видно, что с увеличением частоты падает коэффициент передачи.
И вот простое правило: чем круче спад, тем круче фильтр.
Соответственно, для названных видов фильтров АЧХ будут следующими:
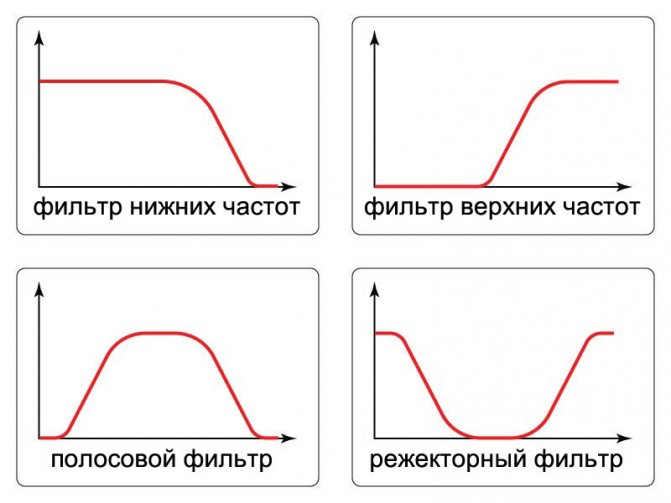
АЧХ для ФНЧ, ФВЧ, полосового и режекторного (заградительного) фильтров.
Согласитесь — красивые рисунки! Но как получить это на
плате
практике?

Очередной резистивный делитель, или из чего состоят фильтры
На самом деле, схема фильтра напоминает резистивный делитель (делитель напряжения на резисторах). Посмотрите сами:
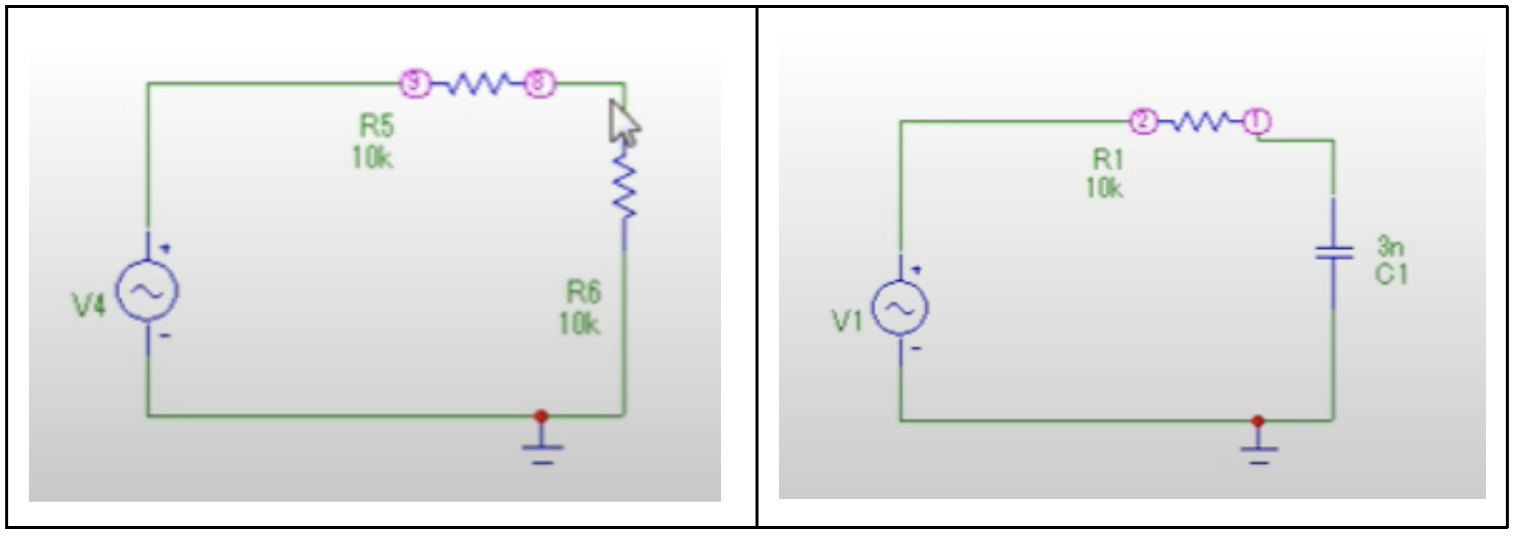
Слева — резистивный делитель, справа — электрический фильтр.
Разница буквально в одном элементе: вместо резистора стоит конденсатор. Но на АЧХ это влияет очень сильно. При включении делителя АЧХ будет стабильна, то есть частота источника на выходную амплитуду никак влиять не будет. Другая ситуация с фильтром: на определенной частоте появляется явный срез.
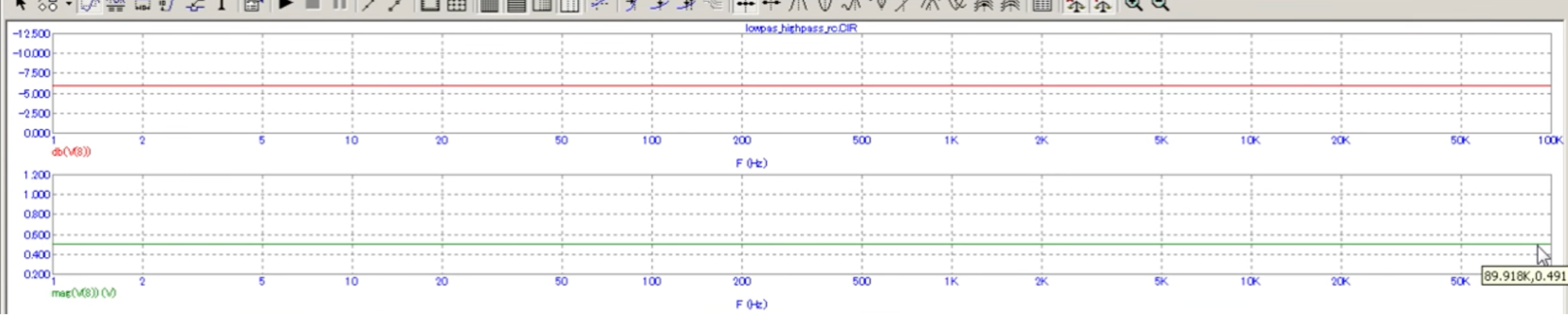
АЧХ резистивного делителя.

АЧХ ФНЧ.
Это связано с тем, что при увеличении частоты тока сопротивление на конденсаторе уменьшается и напряжение падает — по такому принципу работают ФНЧ.
Запомните правило. Емкостное сопротивление обратно пропорционально частоте тока и емкости конденсатора — чем больше их величины, тем меньше емкостное сопротивление.
АЧХ можно «отразить», если поменять емкость и резистор местами — превратить ФНЧ в ФВЧ. Но это не все варианты схемотехнического многообразия
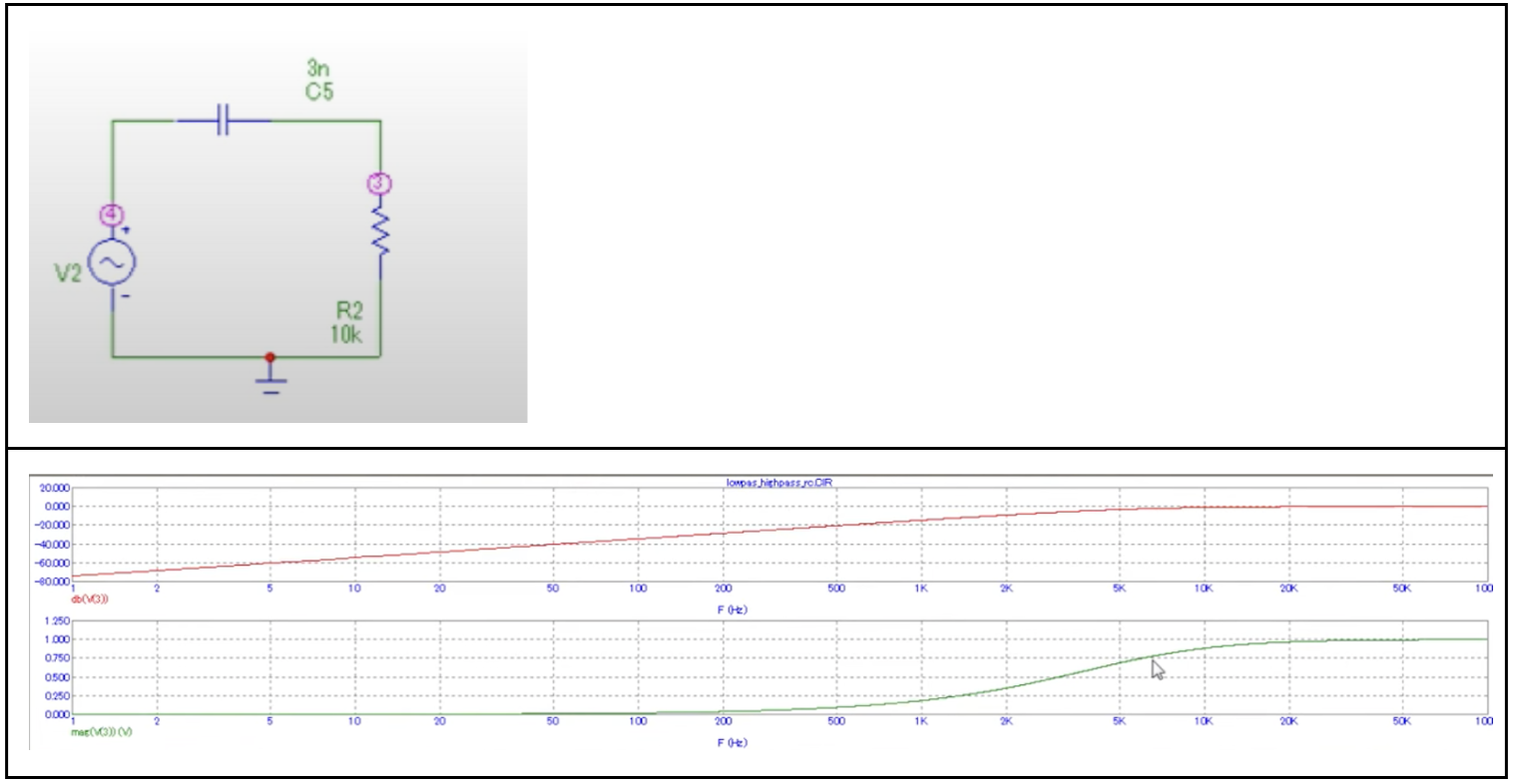
Схема и АЧХ для RC-ФВЧ.
LC-фильтры
Вместо резистора можно поставить индуктивность, и тогда вместо привычного ФНЧ (RC-ФНЧ) получим LC-ФНЧ. Суть та же: у него будет своя частота среза и так далее. Но добротность фильтра будет выше — соответственно, область частот, которую пропускает фильтр (она же полоса пропускания), будет меньше, а спад АЧХ — круче. Именно LC-контуры используются в фильтрах для работы с высокочастотным диапазоном.
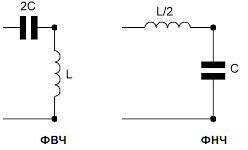
LC-фильтры.
Принцип построения LC-фильтров основан на свойствах емкостей и индуктивностей по-разному вести себя в цепях переменного тока.
Индуктивное сопротивление катушки прямо пропорционально частоте тока, проходящего через нее. Следовательно, чем выше частота тока на катушке, тем большее реактивное сопротивление она этому току оказывает — сильнее задерживает переменные токи на более высоких частотах и легче пропускает на более низких.
У конденсатора наоборот: чем выше частота тока, тем легче протекает переменный ток. А чем ниже его частота, тем большим препятствием для тока оказывается этот конденсатор.
Схемы режекторного и полосового фильтров чуть сложней. Режекторный фильтр — это цепь с параллельно соединенными индуктивностью и емкостью, а полосовой — с последовательно соединенными.
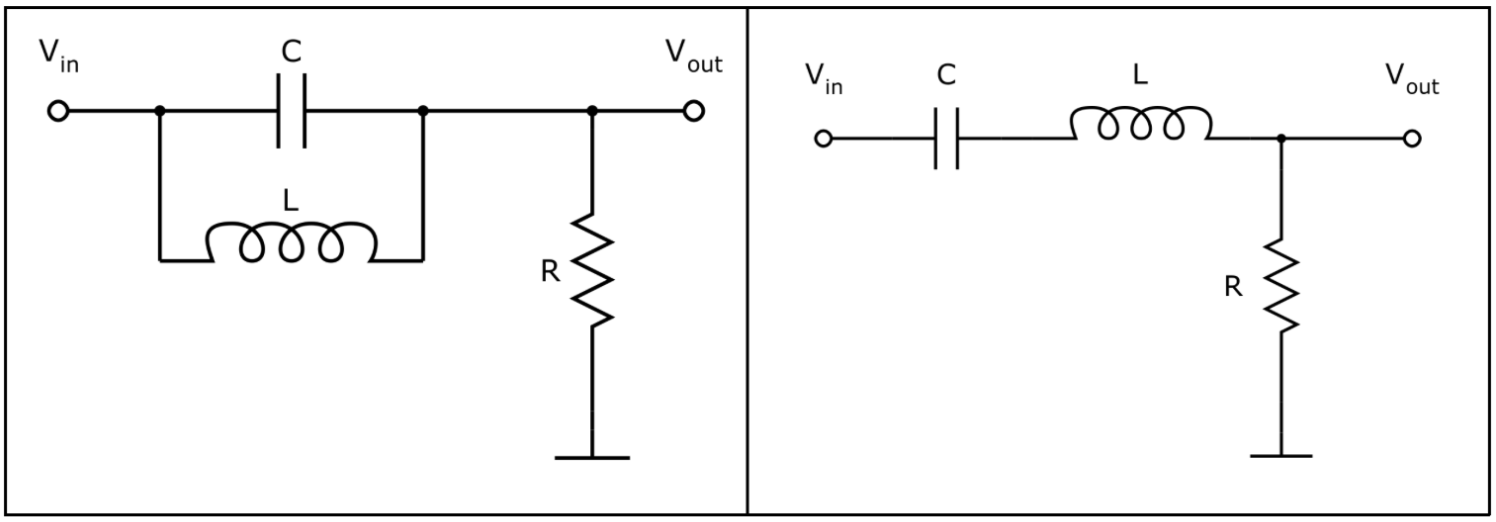
Слева — режекторный фильтр, справа — полосовой.
Г-, Т- и П-образные фильтры
Схематически ФНЧ и ФВЧ бывают Г-образными, Т-образными и П-образными (многозвенными).
Г-образные — это схемы ФНЧ и ФВЧ, которые мы рассмотрели выше. Их входные сопротивления всегда меньше выходных. Г-образные фильтры часто применяют в качестве трансформаторных сопротивлений. В качестве фильтров обычно используют П- и Т-образные схемы.
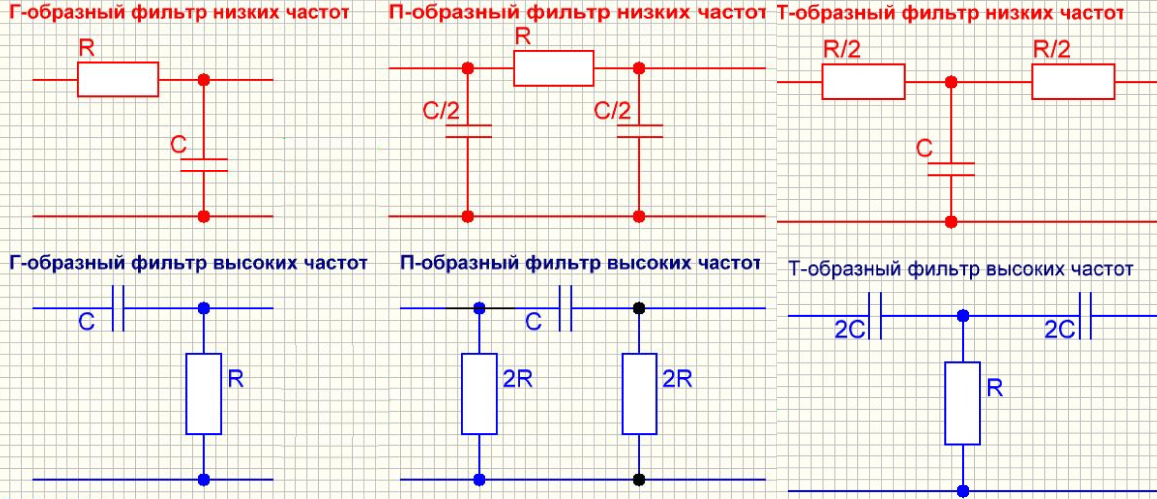
Г-, П- и Т-образные RC-фильтры.
Тип схемы обычно выбирают из экономических соображений. Например, для сборки LC-ФНЧ лучше использовать П-образную схему, чтобы сэкономить катушки индуктивности, а для LC-ФВЧ — Т-образную.
Немного о параметрах частотных фильтров
Вот мы упомянули, что у фильтров есть ширина полосы пропускания, добротность, частота среза. Но все ли это параметры и как они связаны? Давайте разбираться.
Ключевые параметры
При проектировании частотных фильтров учитывают следующие параметры:
- наклон АЧХ — чем круче, тем лучше,
- частота среза — выбирается разработчиком,
- неравномерность АЧХ — чем меньше, тем лучше,
- отношение входного и выходного сопротивлений — особенно важный параметр для ВЧ-фильтров,
- ослабление в полосе задержания — оно же ослабление в полосе заграждения, но без учета переходного участка (длительности фронта).
Самый важный параметр — это частота среза. С помощью нее мы можем регулировать, какую долю частотного диапазона «проигнорировать», а какую — оставить. Поговорим о ней чуть подробнее.
Подробнее о частоте среза
Частота среза — это такая частота, на которой ослабление фильтра равно -3 дБ в логарифмическом масштабе (в линейном это 0,707).
Важно отметить, что частота среза для ФНЧ и ФВЧ вычисляется по одному выражению:
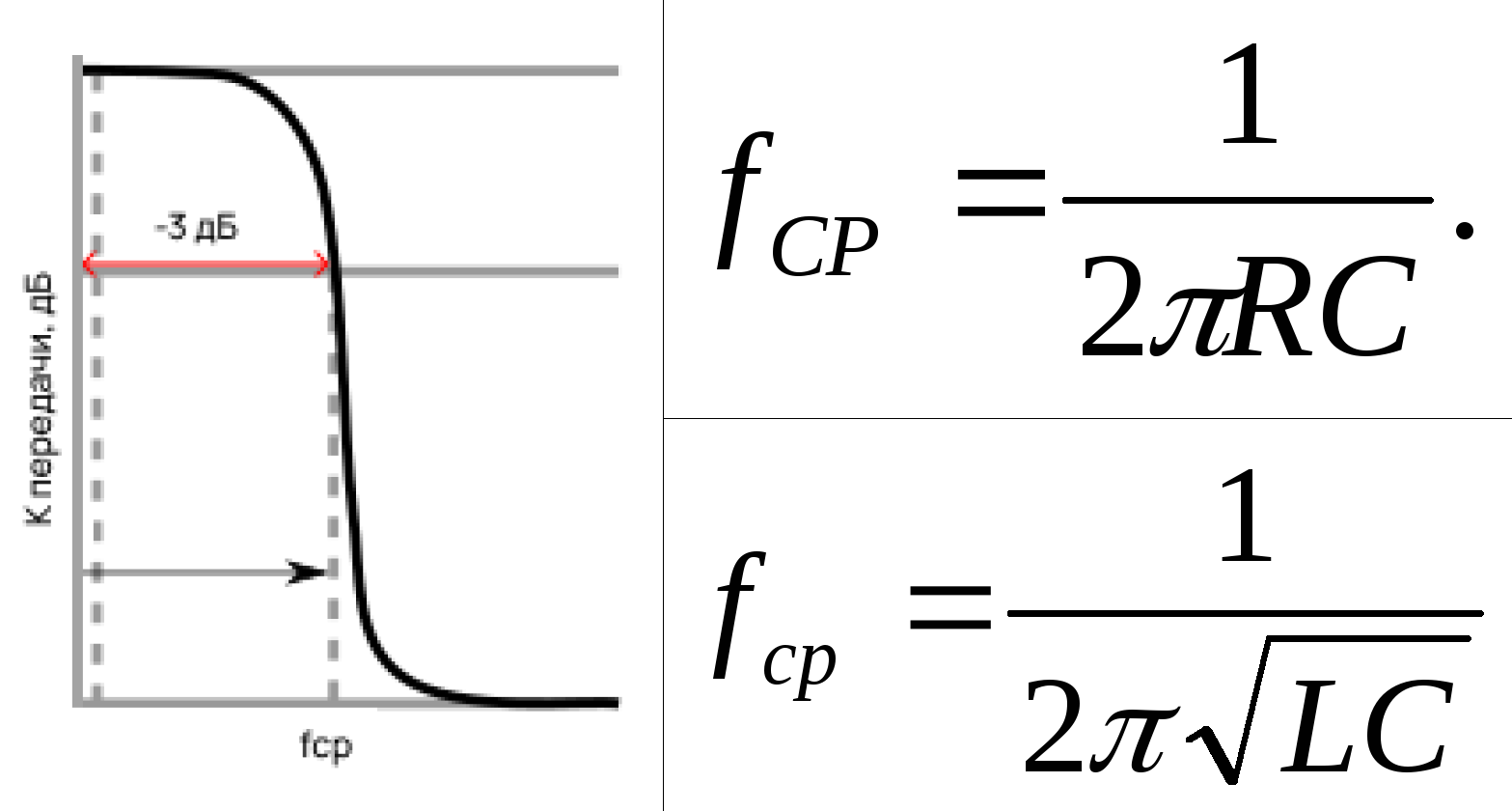
Зная сопротивление/ индуктивность и емкость, можно определить, на какой частоте случится ослабление на -3 дБ. То есть, опираясь на нужную частоту среза, мы можем рассчитать и спроектировать фильтр. Или не все так просто?
Что такое порядок фильтра
Допустим, вы знаете частоту среза и хотите спроектировать фильтр. Но что такое R, C и L? Обычные номиналы для сопротивления, емкости и индуктивности? Вы можете ответить «да» и будете правы: для ФНЧ и ФВЧ второго порядка (самых обычных Г-образных RC- и LC-фильтров) достаточно подобрать резистор, конденсатор и катушку с нужными параметрами. Но для фильтров больших порядков ответ неоднозначный.
Наклон АЧХ удовлетворяет не всегда: если он сильно пологий, то радиоприемное устройство может поймать лишние частоты. Чтобы избавиться от такого эффекта, разработчики стараются делать фильтры с крутым наклоном АЧХ.
Наклон АЧХ тем круче, чем больше ослабление в полосе задержания и выше порядок фильтра. Последнее указывает на количество L- и C- элементов: в фильтре пятого порядка будет, например, три емкости и две индуктивности.
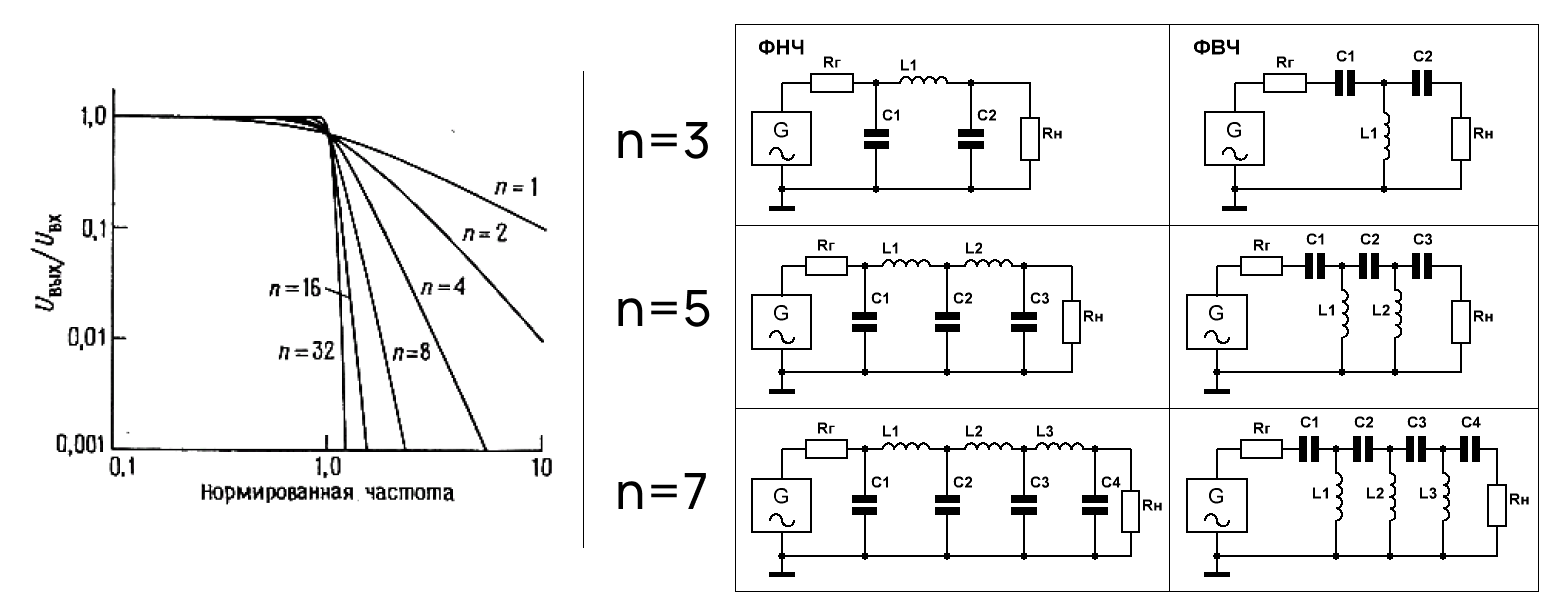
Зависимость крутизны наклона АЧХ от количества порядков (n).
Можно сказать, что каждый LC-элемент — индуктивность или емкость — дает уклонение АЧХ на 12 дБ на октаву, тогда как RC — всего 6 дБ на октаву.
Октава — это область частотного диапазона, на которой значение частоты увеличивается в два раза. Иногда в литературе предпочитают измерять в декадах, которые обозначают область с увеличением частоты в десять раз.
Рассчитывать фильтры — это сложно
Теперь вы знаете, что означают те самые R, C и L в формулах для частоты среза: это «суммы» номиналов для элементов фильтра. Стало ли от этого проще рассчитывать фильтры под определенную частоту среза? Не особо.
Расчет фильтров — это отдельная наука, объединяющая теорию электрических цепей, электротехнику и математические методы.
Чтобы рассчитать фильтр большого порядка по заданным условиям, применяют специальные методики. Среди них — формулы на базе полиномов Баттерворта и Чебышева, функций Бесселя.
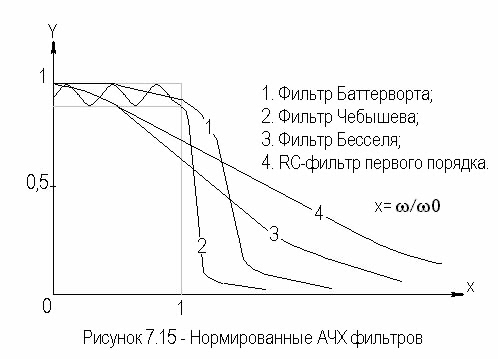
Нормированные АЧХ фильтров.
По сути, выбирая конкретную методику, вы выбираете фильтр:
- Фильтр Баттерворта — обладает самой плоской характеристикой затухания в полосе пропускания, за счет этого имеет плавный спад.
- Фильтр Чебышева — обладает самым крутым спадом, но у него самые неравномерные характеристики в полосе пропускания.
- Фильтр Бесселя — имеет хорошую фазочастотную характеристику и крутой спад.
Чтобы понять теорию расчета фильтров, рекомендую почитать книгу «Аналоговые и цифровые фильтры». Если хотите утонуть в полиномах, аналитических вычислениях комплексных расчетах, сохраняйте в закладки.
Но рассчитать фильтр можно проще, если «схитрить» и использовать онлайн-калькулятор. Так можно узнать, например, номиналы для фильтра Чебышева пятого порядка с частотой среза 4 МГц. Проверим, работает ли он на практике.
Возможно, эти тексты тоже вас заинтересуют:
→ Как геймифицировать аренду серверов со скидкой, связав сайт с внутренней панелью администрирования
→ Первая «зеркалка» от Polaroid, робот-пылесос iRobot, гомеопатия начала XX века и кое-что еще: новые находки на барахолке
→ Проблемы безопасности SNMP на практике: имитация атак и меры профилактики
Собираем фильтр Чебышева
Предварительно я узнал номиналы через онлайн-калькулятор и проверил фильтр в Multisim. Если подключить параллельно Bode Plotter и правильно установить масштабы, программа покажет идеальную АЧХ фильтра Чебышева.
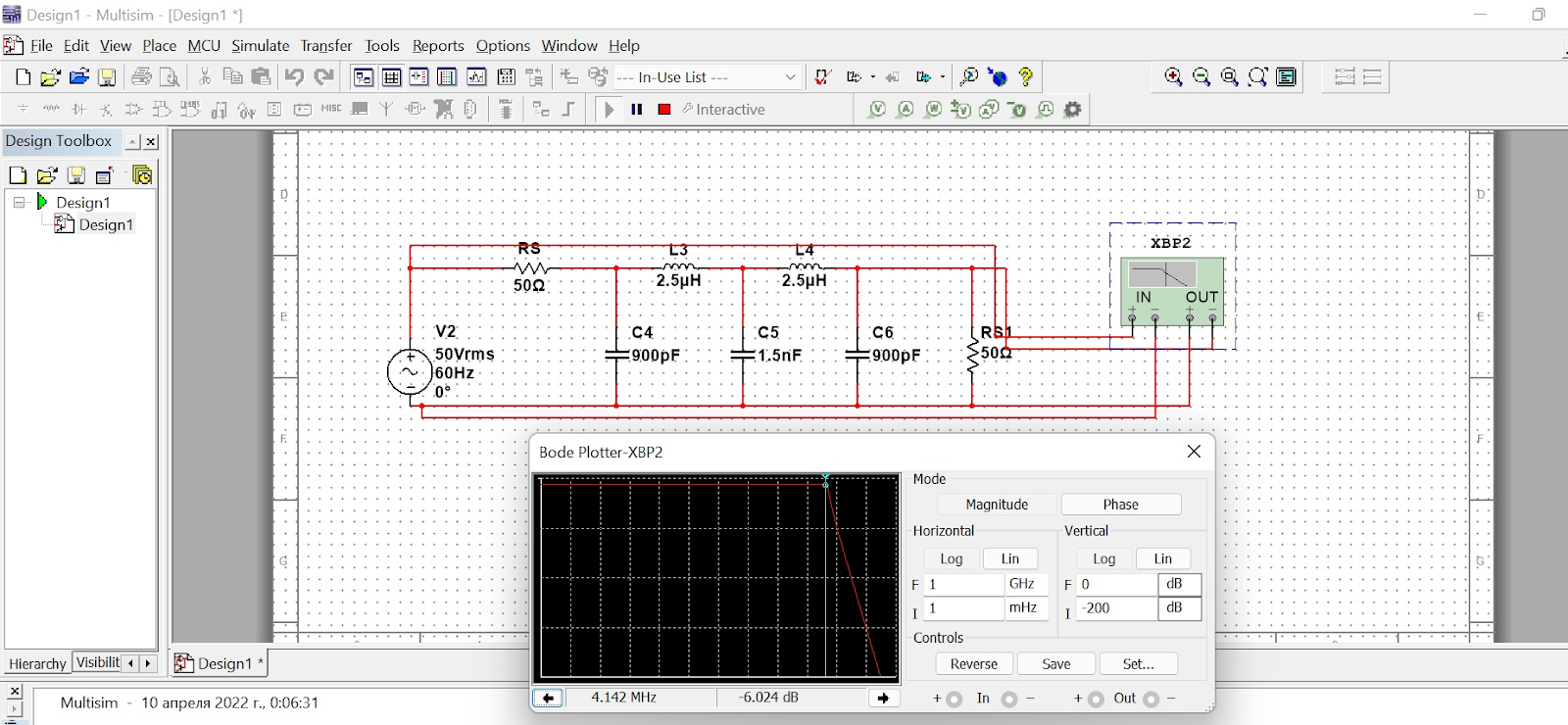
Multisim, схема ФНЧ Чебышева пятого порядка.
Супер — схему можно «перенести» на макетную плату.
Понадобится генератор гармонических колебаний и осциллограф, подключенный к выходам фильтра. Если у вас есть анализатор цепей, можно использовать его.
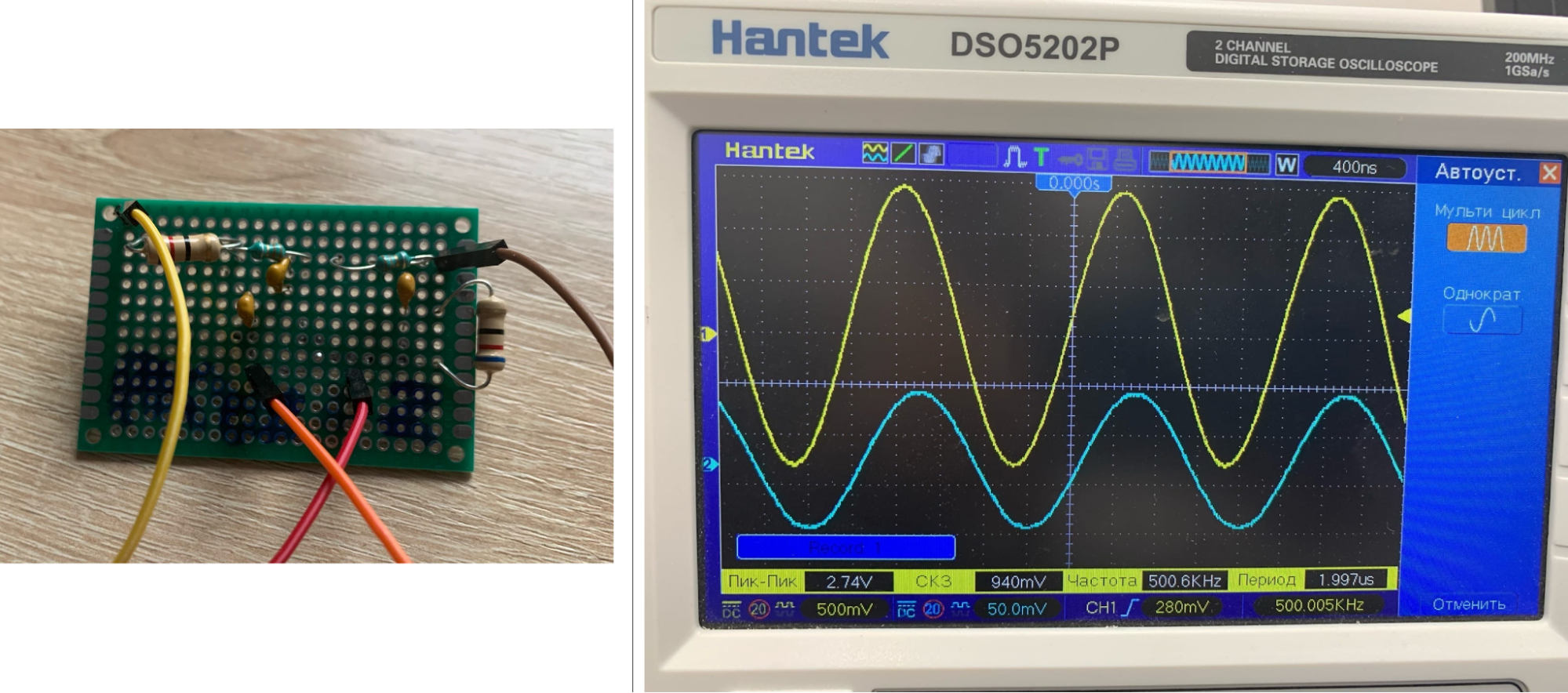
Синусоида синего цвета — выходной сигнал, желтого — входной.
Обратите внимание. Электрическая схема может отличаться по номиналам от идеальной, которую вы рассчитали под свою частоту среза. Не всегда возможно точно повторить значения емкостей и индуктивностей, потому что элементов с такими номиналами может просто и не быть.
Постепенно увеличивая частоту входного сигнала, можно составить таблицу для построения графика.
Если отразить значения на системе координат, получится график для фильтра Чебышева.
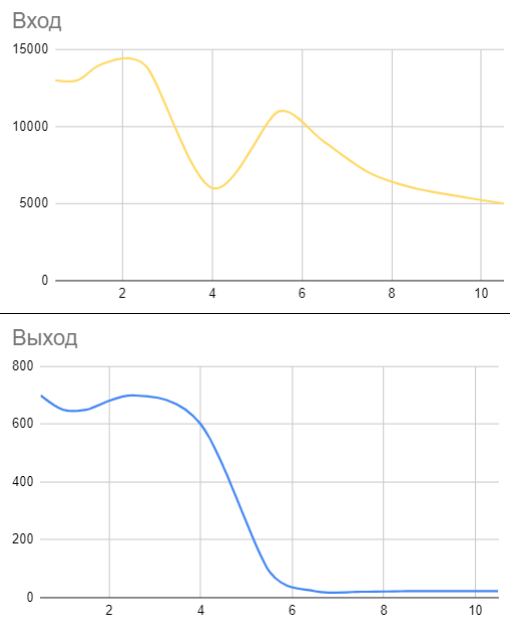
Готово — у нас получилось добиться вполне крутого спада на частоте 4 МГц, ФНЧ Чебышева работает.
В статье рассмотрена лишь малая часть теоретических и практических аспектов. Фильтров гораздо больше: есть активные на базе операционных усилителей, микроконтроллеров, рассчитанные топологии Саллена-Ки и программные фильтры. Обо всем этом — в следующей статье.
Расчет полосового фильтра
Сложную отрицательную
обратную связь можно использовать для
построения полосовых фильтров.
Соответствующая схема приведена на
рис.4.2.

Рис.4.1.
Амплитудно—частотная характеристика
полосового
фильтра второго порядка
fР
–резонансная
(центральная) частота, определяемая
выражением
fР
=
![]() ,
,
где fl
–нижняя
частота по уровню –3 дБ; fh
–верхняя частота по уровню –3 дБ.

Рис.4.2. Полосовой
фильтр со сложной отри-
цательной обратной
связью. (фильтр Баттеворта)
Передаточная
функция полосового фильтра имеет вид
f
(S)
=
![]() ,
,
(4.1)
где
![]() =2,
=2,
![]() s
s
– оператор Лапласа.
Отсюда находим
резонансную частоту:
fР
=
 .
.
(4.2), (резонансная частота)
Коэффициент
передачи на резонансной частоте –АV
= R2
/ 2R1.
Добротность Q
=
R2CfР,
(4.3)
Ширина полосы В
= 1 /
R2C.
(4.4)
Подставив это
выражение для резонансной частоты о
передаточную функцию и приравняв
соответствующие коэффициенты, получим
остальные формулы для вычисления
характеристик фильтра:
AV
= R2
/ 2R1
, (4.5.)
Q
=
=
R2CfР
, (4.6)
из которых видно,
что коэффициент передачи , добротность
и резонансная частота рассматриваемого
фильтра могут выбираться произвольно.
Выражение для
полосы пропускания фильтра получим из
формулы (4.6)
В = fР
/ Q
= 1 /
R2C
(4.7)
Таким образом,
величина В
не зависит
от R1
и R3.
Из формулы (4.5) следует, что AV
не зависит
от R3.
Поэтому можно изменять резонансную
частоту fР
, варьируя величину сопротивления R3
, что не приведет к изменению ширины
пропускания фильтра и коэффициента
передачи AV
.
Основное уравнение
можно записать из (4.1) в виде:
fР
= 0,159 Q
/ R1C1
, (4.8)
и по соглашению
R2 =
R1R3
/
(4Q2R1—R3),
R3
=
2R1
, C1=C2.
(4.9)
Пример 4.1.
Спроектируем фильтр, имеющий верхнюю
частоту по уровню –3 дБ, равную 525 Гц, а
нижнюю частоту по уровню –3 дБ, равную
475 Гц. Положим С2
= 1 мкФ.
fр
=
![]()
![]() 500
500
Гц (приблизительно)
Согласно (4.7 ),
Q
= 500 / (525-475),
![]() f
f
= 500 / 50 = 10 (ширина полосы пропускания)
Согласно (4.9),
R1
=
0,159*10 / (500*1*10-6),
R1
= 3180 Ом,
По соглашению
R3
= 6360 Ом,
С1
= 1 мкФ,
R
3
= 3180*6380 /
(4*102*3180—6380),
R3
=16
Ом
Расчет источников питания
Электропитание
большинства электронных схем осуществляется
от стабилизированных источников
постоянного напряжения в пределах от
5В до 25В. Для питания ряда схем (например,
операционных усилителей) требуется
симметричное относительно общей точки
(«земли») напряжение
![]() ±9В,
±9В,
±12В или ±15В.
На рис.5.1 показан
широко используемый в маломощных
устройствах диодный выпрямитель
переменного тока в сочетании с изолирующим
сетевым трансформатором и емкостным
фильтром.

Рис.5.1. Схема
однофазного выпрямителя переменного
тока
В таблице 5.1
приведены основные соотношения между
напряжением и током
Таблица
5.1 Соотношения
для схемы рис.5.1
|
Параметр |
Соотношение |
|
Выходное |
1,41Uac |
|
Входной |
0,62Iac |
|
Входное |
0,71Udc |
|
Входной |
1,61Idc |
|
Минимальная |
2200Idc |
Для увеличения
надежности схемы рекомендуется выбирать
конденсатор с рабочим напряжением 2Udc
.
Большинство
источников электропитания включает в
себя интегральный стабилизатор,
позволяющий уменьшать пульсации
напряжения и обеспечивающий возможность
его регулирования. Для нормального
функционирования регулятора на нем
падает напряжение порядка 2 В. Учитывая
нестабильность первичного источника
(промышленная сеть, аккумуляторная
батарея), необходимо выбирать напряжение
на регуляторе в пределах от 3 до 6 В.
Очевидно, чем выше это напряжение, тем
большая мощность выделяется в регуляторе
и тем труднее его охлаждать. Обычно
3 В ≤ UРЕГ
≤ 6 В
Если Udc
– напряжение на входе регулятора, а UH
–напряжение
на нагрузке, то можно записать
UРЕГ
= Udc
– UH
.
Мощность, выделяющаяся
в регуляторе, определяется из соотношения
PРЕГ
= IH
UРЕГ
= IH
(Udc
–UH),
где IH
– ток
нагрузки.
Пример 5.1.
Требуется обеспечить напряжение 12 В на
нагрузке, потребляющей ток 1 А. Первичная
сеть переменного тока питается напряжением
220 В, которое может изменяться в пределах
±15%. В схеме используется стабилизатор
К142 ЕН 12.
Тогда минимальное
напряжение на стабилизаторе выбираем
равным 3 В.
Тогда минимальное
напряжение на выходе выпрямителя
переменного напряжения тока при
минимальном напряжении в первичной
сети
Udc
min
= UРЕГ
+ UH
= 3
+ 12 = 15 B;
при максимальном
напряжении в первичной сети
Udc
max
= 20,3 В.
В этом случае
на стабилизаторе будет напряжение
UРЕГ
= Udc
–UH
= 20,3 – 12 = 8,3 B/
При номинальном
напряжении сети
Udc
= 17,7
B.
напряжение
регулятора
UРЕГ
= Udc
–UH
= 17,7 –12 = 5,7
B.
Если в качестве
выпрямителя использовать мостовую
схему, то на диодах будет теряться
напряжение около 1 В. Это нужно учесть
при расчете трансформатора. Напряжение
действующее напряжение на вторичной
обмотке трансформатора
Udc
= 0,71(Udc
+ 1B)
= 0,71*18,7 = 13,3 B.
Максимальный ток
вторичной обмотки трансформатора
Iac
=
IH
(Udc
max
– UH
)
= 1 (20,3 – 12 ) = 8,3 Вт.
Конденсатор фильтра
С1
выбираем К50—35 –2200 мкФ – 64 В.
Стабилизатор
необходимо установить на радиатор с
тепловым сопротивлением не выше 3
![]() Схема источника электропитания приведена
Схема источника электропитания приведена
на рис.5.2.

Рис.5.2.
Стабилизированный источник питания
Соседние файлы в папке Практикум
- #
- #
- #
Полосовой, он же полосно-пропускающий фильтр – это фильтр, пропускающий частоты в некоторой полосе частот,
находящейся между нижней и верхней частотами среза, и может быть легко представлен в виде последовательности,
состоящей из фильтра нижних частот и фильтра верхних частот.
Однако более рациональными с точки зрения оптимизации характеристик, являются фильтры, рассчитанные через ФНЧ-прототип.
Преобразование фильтра низких частот в полосовой фильтр осуществляется заменой емкостей ФНЧ прототипа параллельными контурами,
а индуктивностей – последовательными.
Примеры таких полосовых фильтров 3-го, 5-го и 7-го порядков приведены на Рис.1.
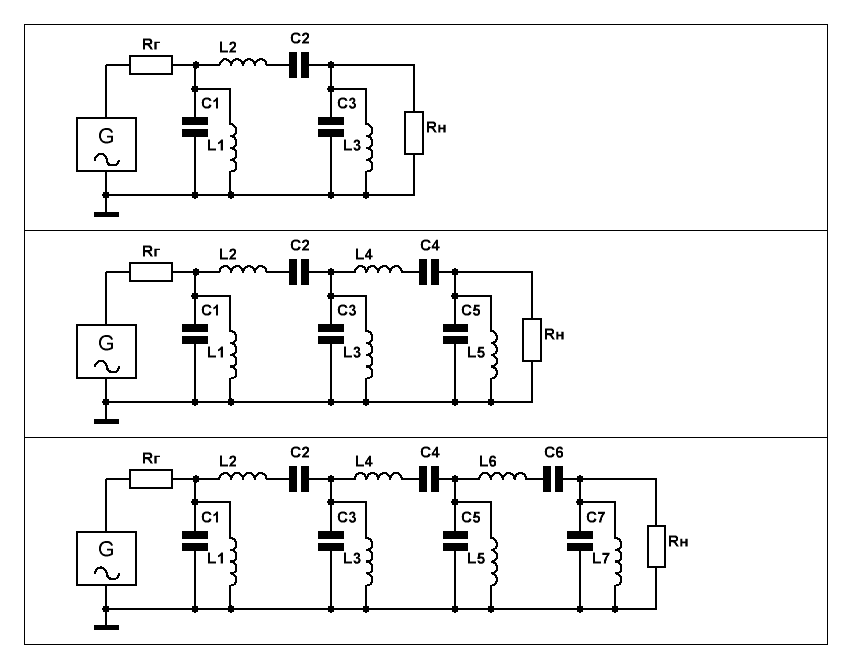
Рис.1
Расчёт поведём, используя прототипы фильтров нижних частот имени уважаемого Пафнутия Чебышева и
таблицы не менее уважаемого господина Гранта Ханзела, приведённые в справочнике по расчёту фильтров.
ТАБЛИЦА РАСЧЁТА ПОЛОСОВЫХ LC ФИЛЬТРОВ.
Порядок фильтра |
||
|
Верхняя частота среза фильтра |
|
|
Сопротивление Rг и Rн (Ом) |
||
C1 |
||
C2 |
||
C3 |
||
C4 |
||
C5 |
||
C6 |
||
C7 |
||
L1 |
||
L2 |
||
L3 |
||
L4 |
||
L5 |
||
L6 |
||
L7 |
На Рис.2 приведены амплитудно-частотные характеристики полосовых фильтров 3-го, 5-го и 7-го порядков с полосой пропускания
3-5 МГц.
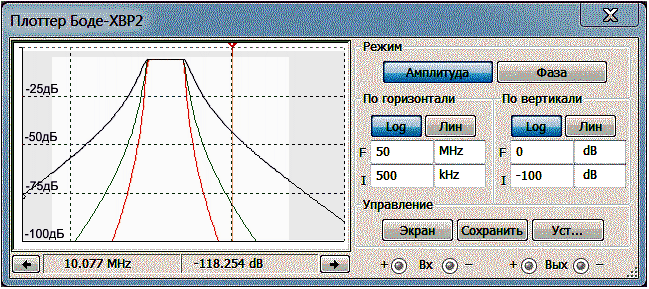
Рис.2
Характеристики затухания фильтров вне полосы пропускания симметричны и составляют величины: 38 дБ на октаву для фильтров
3-го порядка, 75 дБ – для фильтров 5-го порядка и 112 дБ – для фильтров 7-го порядка. Неравномерность в полосе пропускания
– менее 0,5 дБ.
Приведённая таблица может стать хорошим подспорьем при расчёте входных диапазонных фильтров радиоприёмников и трансиверов,
однако следует учитывать маленький, но ЖИРНЫЙ “НЮАНС”:
Фильтры Чебышева значительно лучше других справляются с подавлением внеполосных сигналов, но становятся
крайне неудобными (с точки зрения критически малых значений номиналов некоторых элементов) при выборе узкой полосы
прозрачности.
Поэтому наиболее выигрышно они будут смотреться в устройствах относительно широкополосных – с не менее, чем полуоктавной полосой
пропускания.
![]()
Электрическим фильтром называется четырехполюсник, устанавливаемый между источником
питания и нагрузкой и служащий для беспрепятственного (с малым затуханием) пропускания
токов одних частот и задержки (или пропускания с большим затуханием) токов других частот.
Диапазон частот, пропускаемых фильтром без затухания (с малым затуханием),
называется полосой пропускания или полосой прозрачности; диапазон
частот, пропускаемых с большим затуханием, называется полосой затухания или
полосой задерживания. Качество фильтра считается тем выше, чем ярче выражены
его фильтрующие свойства, т.е. чем сильнее возрастает затухание в полосе задерживания.
В качестве пассивных фильтров обычно применяются четырехполюсники на основе
катушек индуктивности и конденсаторов. Возможно также применение пассивных RC-фильтров,
используемых при больших сопротивлениях нагрузки.
Фильтры применяются как в радиотехнике и технике связи, где имеют место токи достаточно высоких частот, так и в силовой электронике и электротехнике.
Для упрощения анализа будем считать, что фильтры составлены из идеальных катушек
индуктивности и конденсаторов, т.е. элементов соответственно с нулевыми активными
сопротивлением и проводимостью. Это допущение достаточно корректно при высоких
частотах, когда индуктивные сопротивления катушек много больше их активных сопротивлений
( ![]() ), а емкостные проводимости конденсаторов
), а емкостные проводимости конденсаторов
много больше их активных проводимостей ( ![]() ).
).
Фильтрующие свойства четырехполюсников обусловлены возникающими в них резонансными
режимами – резонансами токов и напряжений. Фильтры обычно собираются по симметричной
Т- или П-образной схеме, т.е. при ![]() или
или ![]() (см. лекцию №14). В этой связи
(см. лекцию №14). В этой связи
при изучении фильтров будем использовать введенные в предыдущей лекции понятия
коэффициентов затухания и фазы.
Классификация фильтров в зависимости от диапазона пропускаемых частот приведена в табл. 1.
Таблица 1. Классификация фильтров
|
Название фильтра |
Диапазон пропускаемых частот |
|
Низкочастотный фильтр (фильтр нижних частот) |
|
|
Высокочастотный фильтр (фильтр верхних частот) |
|
|
Полосовой фильтр (полосно-пропускающий фильтр) |
|
|
Режекторный фильтр (полосно-задерживающий фильтр) |
 и и  , где , где  |
В соответствии с материалом, изложенным в предыдущей лекции, если фильтр имеет
нагрузку, сопротивление которой при всех частотах равно характеристическому,
то напряжения и соответственно токи на его входе и выходе связаны соотношением
. . . |
(1) |
В идеальном случае в полосе пропускания (прозрачности) ![]() , т.е. в соответствии с (1)
, т.е. в соответствии с (1) ![]() ,
, ![]() и
и ![]() . Следовательно, справедливо и
. Следовательно, справедливо и
равенство ![]() , которое указывает на отсутствие
, которое указывает на отсутствие
потерь в идеальном фильтре, а значит, идеальный фильтр должен быть реализован
на основе идеальных катушек индуктивности и конденсаторов. Вне области пропускания
(в полосе затухания) в идеальном случае ![]() , т.е.
, т.е. ![]() и
и ![]() .
.
Рассмотрим схему простейшего низкочастотного фильтра, представленную
на рис. 1,а.

Связь коэффициентов четырехполюсника с параметрами элементов Т-образной схемы
замещения определяется соотношениями (см. лекцию № 14)
![]()
или конкретно для фильтра на рис. 1,а
 ; ; |
(2) |
 ; ; |
(3) |
 . . |
(4) |
Из уравнений четырехполюсника, записанных с использованием гиперболических
функций (см. лекцию № 14), вытекает, что
![]() .
.
Однако в соответствии с (2) ![]() – вещественная переменная, а следовательно,
– вещественная переменная, а следовательно,
| (5) |
Поскольку в полосе пропускания частот коэффициент затухания ![]() , то на основании (5)
, то на основании (5)
![]() .
.
Так как пределы изменения ![]() :
: ![]() , – то границы полосы пропускания
, – то границы полосы пропускания
определяются неравенством
![]() ,
,
которому удовлетворяют частоты, лежащие в диапазоне
 . . |
(6) |
Для характеристического сопротивления фильтра на основании (3) и (4) имеем
 . . |
(7) |
Анализ соотношения (7) показывает, что с ростом частоты w в пределах,
определяемых неравенством (6), характеристическое сопротивление фильтра уменьшается
до нуля, оставаясь активным. Поскольку, при нагрузке фильтра сопротивлением,
равным характеристическому, его входное сопротивление также будет равно ![]() , то, вследствие вещественности
, то, вследствие вещественности
![]() , можно сделать заключение, что
, можно сделать заключение, что
фильтр работает в режиме резонанса, что было отмечено ранее. При частотах, больших
![]() , как это следует из (7), характеристическое
, как это следует из (7), характеристическое
сопротивление приобретает индуктивный характер.

На рис. 2 приведены качественные зависимости
![]() и
и ![]() .
.
Следует отметить, что вне полосы пропускания ![]() . Действительно, поскольку коэффициент
. Действительно, поскольку коэффициент
А – вещественный, то всегда должно удовлетворяться равенство
| (8) |
Так как вне полосы прозрачности ![]() , то соотношение (8) может выполняться
, то соотношение (8) может выполняться
только при ![]() .
.
В полосе задерживания коэффициент затухания ![]() определяется из уравнения (5) при
определяется из уравнения (5) при ![]() . Существенным при этом является
. Существенным при этом является
факт постепенного нарастания ![]() , т.е. в полосе затухания фильтр
, т.е. в полосе затухания фильтр
не является идеальным. Аналогичный вывод о неидеальности реального фильтра можно
сделать и для полосы прозрачности, поскольку обеспечить практически согласованный
режим работы фильтра во всей полосе прозрачности невозможно, а следовательно,
в полосе пропускания коэффициент затухания ![]() будет отличен от нуля.
будет отличен от нуля.
Другим вариантом простейшего низкочастотного фильтра может служить четырехполюсник
по схеме на рис. 1,б.
Схема простейшего высокочастотного фильтра приведена на рис. 3,а.

Для данного фильтра коэффициенты четырехполюсника определяются выражениями
 ; ; |
(9) |
 ; ; |
(10) |
 . . |
(11) |
Как и для рассмотренного выше случая, А – вещественная переменная. Поэтому
на основании (9)
![]() .
.
Данному неравенству удовлетворяет диапазон изменения частот
 . . |
(12) |
Характеристическое сопротивление фильтра
 , , |
(13) |

изменяясь в пределах от нуля до ![]() с ростом частоты, остается вещественным.
с ростом частоты, остается вещественным.
Это соответствует, как уже отмечалось, работе фильтра, нагруженного характеристическим
сопротивлением, в резонансном режиме. Поскольку такое согласование фильтра с
нагрузкой во всей полосе пропускания практически невозможно, реально фильтр
работает с ![]() в ограниченном диапазоне частот.
в ограниченном диапазоне частот.
Вне области пропускания частот ![]() определяется из уравнения
определяется из уравнения
| (14) |
при ![]() . Плавное изменение коэффициента
. Плавное изменение коэффициента
затухания в соответствии с (14) показывает, что в полосе задерживания фильтр
не является идеальным.
Качественный вид зависимостей ![]() и
и ![]() для низкочастотного фильтра представлен
для низкочастотного фильтра представлен
на рис. 4.
Следует отметить, что другим примером простейшего высокочастотного фильтра
может служить П-образный четырехполюсник на рис. 3,б.
Полосовой фильтр формально получается путем последовательного соединения
низкочастотного фильтра с полосой пропускания ![]() и высокочастотного с полосой пропускания
и высокочастотного с полосой пропускания
![]() , причем
, причем ![]() . Схема простейшего полосового
. Схема простейшего полосового
фильтра

приведена на рис. 5,а, а на рис. 5,б представлены качественные зависимости
![]() для него.
для него.
У режекторного фильтра полоса прозрачности разделена на две части полосой
затухания. Схема простейшего режекторного фильтра и качественные зависимости
![]() для него приведены на рис.6.
для него приведены на рис.6.

В заключение необходимо отметить, что для улучшения характеристик фильтров
всех типов их целесообразно выполнять в виде цепной схемы, представляющей собой
каскадно включенные четырехполюсники. При обеспечении согласованного режима
работы всех n звеньев схемы коэффициент затухания  такого фильтра возрастает в соответствии
такого фильтра возрастает в соответствии
с выражением  , что приближает фильтр к идеальному.
, что приближает фильтр к идеальному.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Каплянский А. Е. и др. Электрические основы электротехники. Изд.
2-е. Учеб. пособие для электротехнических и энергетических специальностей
вузов. -М.: Высш. шк., 1972. -448с.
Контрольные вопросы и задачи
- Для чего служат фильтры?
- Что такое полосы прозрачности и затухания?
- Как классифицируются фильтры в зависимости от диапазона пропускаемых частот?
- В каком режиме работают фильтры в полосе пропускания частот?
- Почему рассмотренные фильтры нельзя считать идеальными?
- Как можно улучшить характеристики фильтра?
- Определить границы полосы прозрачности фильтров на рис. 1,а и 3,а, если
L=10 мГн, а С=10 мкФ.
Ответ: ![]() ,
, ![]() .
.
Разрабатывая “радиоуправляемое реле” я решил использовать частотный способ кодирования команд управления. При этом фильтр было принято решение построить на ОУ, так как в корпусе оставался еще не задействованный блок ОУ. Но на этом фантазировать я еще не закончил, немного подумал и решил, что можно еще с экономить на деталях используя элементы, которые есть в наличии. Это и привело к написанию этой статьи “расчет полосового фильтра на ОУ”. Покопавшись в книгах, собрав всю необходимую информацию составил алгоритм расчета фильтра с однополярным питанием. Но об этом потом, а сейчас не много теории.
Все фильтры разделяются на: активные фильтры, использующие для формирования частотной характеристики заданного вида как пассивные (резисторы и конденсаторы), так и активные (транзисторы, микросхемы) элементы, и пассивные фильтры, которые для формирования частотной характеристики заданного вида используют только пассивные (резисторы и конденсаторы) элементы. А сейчас поговорим о полосовых фильтрах.
Полосовой фильтр так называется потому, что он пропускает только тот частотный диапазон на который настроен, при этом частоты находящиеся за пределами данного диапазона ослабляются. Любой полосовой фильтр имеет несколько основных параметров определяющих его характеристики: полоса пропускания (полоса в которой сигнал проходя через фильтр имеет наименьшее затухание), полоса затухания (полоса в которой, сигналы ослабляются), коэффициент усиления (характеристика фильтра, которая отвечает за то во сколько раз сигнал будет усилен или ослаблен в полосе пропускания).
Идеальный полосовой фильтр имеет прямоугольную полосу пропускания, но на практике этого добиться невозможно, а можно только в какой-то степени лишь приблизиться такой форме. Реальный фильтр неспособен полностью задержать частоты за границами желаемого диапазона частот, в результате имеется область у границ заданного диапазона, где сигнал только частично ослабляется. Эта область называется крутизной спада фильтра, и измеряется в “дБ” затухания на октаву.
Принцип работы полосового фильтра основан на изменении коэффициента усиления в зависимости от частоты входного сигнала. Основной в фильтре является RC-цепочка, включенная в цепь обратной связи которая, при изменении частоты влияет на коэффициента усиления. Ну все думаю теории хватит перейдем к расчетам.
Расчет произведем по ниже приведенной схеме. Элементы R1-R3 и C1, C2 – определяют полосу пропускания и коэффициент усиления. R4, R5 – смещение рабочей точки, это необходимо для питания от однополярного источника. Микросхема ОУ выполняет роль активного элемента и подключать ее необходимо согласно Datasheet. Ниже схемы на картинках приведен расчет полосового фильтра на ОУ, но вы так же можете воспользоваться файлами расчета в Mathcad 14 и модели в Multisim 11.
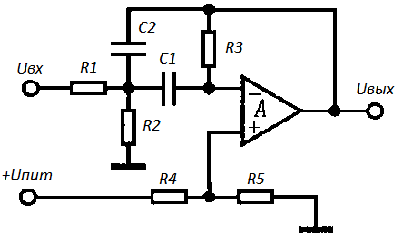
Схема полосового фильтра на ОУ


Данный фильтр можно использовать в светомузыкальных устройствах, радиоуправлении, датчиках и так далее.
Список радиоэлементов
| Обозначение | Тип | Номинал | Количество | Примечание | Магазин | Мой блокнот |
|---|---|---|---|---|---|---|
| A | Операционный усилитель |
LM358 |
1 | Поиск в магазине Отрон | В блокнот | |
| С1, C2 | Конденсатор | 3300 пФ | 2 | Поиск в магазине Отрон | В блокнот | |
| R1 | Резистор |
3.3 кОм |
1 | Поиск в магазине Отрон | В блокнот | |
| R2 | Резистор |
240 Ом |
1 | Поиск в магазине Отрон | В блокнот | |
| R3 | Резистор |
1.5 мОм |
1 | Поиск в магазине Отрон | В блокнот | |
| R4 | Резистор |
24 кОм |
1 | Поиск в магазине Отрон | В блокнот | |
| R5 | Резистор |
20 кОм |
1 | Поиск в магазине Отрон | В блокнот | |
| Добавить все |
Скачать список элементов (PDF)
Теги:

 Опубликована: 20.05.2015
Опубликована: 20.05.2015

 0
0
![]()
 Вознаградить
Вознаградить
Я собрал
0
0
x
Оценить статью
- Техническая грамотность
- Актуальность материала
- Изложение материала
- Орфография
0
Средний балл статьи: 0
Проголосовало: 0 чел.
