Как найти половинный аргумент синус - Сайт, где вы сможете решить свои вопросы

Алгебра и начала математического анализа, 10 класс

Урок №36. Формулы половинного аргумента.

Перечень вопросов, рассматриваемых в теме

1) Формулы синуса, косинуса, тангенса и котангенса половинного аргумента;

2) Преобразовывать тригонометрические выражений на основе использования формулы синуса, косинуса, тангенса и котангенса половинного аргумента;

3) Решение уравнения с использованием формулы синуса, косинуса половинного аргумента.

Глоссарий по теме

Формулы половинного угла (аргумента) представляют собой противоположность формулам двойного угла, так как они выражают синус, косинус, тангенс и котангенс угла при помощи тригонометрических функций угла α.

Основная литература:

Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.

Теоретический материал для самостоятельного изучения

Сегодня мы узнаем формулы, позволяющие нам по известным значениям ; находить ; ; . Их называют формулы половинного аргумента.

Повторим формулу косинуса двойного аргумента .

А если учесть, что и , то получим ещё две формулы, которые нам сегодня понадобятся:

Пример. а) Найти , если .

Вычислим по формуле

б) Найти , если .

Вычислим по формуле .

, получаем

(1) формула синуса половинного аргумента.

Запишем формулу косинуса двойного угла, где в виде

(2) формула косинуса половинного угла.

По формулам (1) и (2) можно найти или , если известны значения и положение угла , т.е. в какой координатной четверти он находится, чтобы определить знак выражения или .

Эти формулы ещё имеют название «формулы понижения степени», так как в левой части находится вторая степень синуса и косинуса, а в правой – первая, т.е. степень понизилась. Но будьте внимательны: степень понижается, а аргумент удваивается.

Например, .

Пример. Известно, что . Найдите ; ;

1) найдём по формуле: ; .

По условию . Разделив обе части неравенства на 2, получаем , значит угол во второй четверти, здесь синус положительный. .

2) ; найдём по формуле ,

Мы уже выяснили, что угол во второй четверти, косинус отрицательный.

3) Так как тангенс это отношение синуса на косинус, то

Выведем формулу для тангенса половинного аргумента. Для этого разделим левую часть формулы (1) на левую часть формулы (2) и правую часть формулы (1) на правую часть формулы (2).

сократим на 2 , и учитывая, что , получим:

формула тангенса половинного аргумента (3).

Так как котангенс это число, взаимообратное тангенсу, то

Пример. Найти и , если известно, что и .

По формуле (3) находим , а Найдём положение угла

По условию ,( разделим на 2)

, угол в первой четверти, тангенс положительный, , а .

Для этого используем формулу синуса двойного угла , заменив в ней х на . Получаем , учтём, что , то

, разделим числитель и знаменатель на , получаем:

(4)

(5)

Пример. Найти , если .

По формуле (5) .

С помощью доказанных на этом уроке формул можно не только вычислять значения выражений, но и упрощать выражения, доказывать тождества и решать тригонометрических уравнений.

Пример. Доказать тождество .

Представим , а , преобразуем левую часть тождества

, но , то

Левая часть равна правой части, тождество доказано.

Примеры и разбор решения заданий тренировочного модуля

№1.Известно, что и . Найдите ; ;

Установите соответствие между множествами значений А и В:

А В

а) 1)

б) cos 2)

в) tg 3)

г) ctg 4)3

Ответ:

Подсказка: используйте формулы половинного аргумента и определение тангенса и котангенса.

№2. Известно, что . Найти ;

Установите соответствие между множествами значений А и В:

А В

а) 1)

б) ; 2)

в) 3)

г) ; 4)

Ответ:

Подсказка: используйте формулы половинного аргумента.

№3.Вычислите

Ответ:12.

Подсказка: используйте формулу синуса двойного угла, где .

№4. Известно, что , Найти ;

Установите соответствие между множествами значений А и В:

А В

а) 1)

б) ; 2)

в) 3)

г) ; 4)

Ответ:

Подсказка: используйте формулы половинного аргумента, зависимость синуса от косинуса, определения тангенса и котангенса.

№5.Вычислите .

Ответ: 0,5.

Подсказка: используйте формулу половинного аргумента.

№6. Известно, что. Найти ;

Установите соответствие между множествами значений А и В:

А В

а) 1)

б) ; 2)

в) 3)-

г) ; 4)

Ответ:

Подсказка: используйте формулы половинного аргумента, определения тангенса и котангенса.

№7. Вычислите и установите соответствие между множествами значений А и В:

А В

а) ; 1)

б) ; 2)

в) ; 3) 0,25

Ответ:

Подсказка: используйте формулу синуса и косинуса двойного угла, где .

№8.Упростите выражения и установите соответствие между множествами выражений А и В:

А В

а); 1)

б); 2)

в) ; 3)

Ответ:

Подсказка: используйте формулу синуса и косинуса двойного угла, где и определение тангенса.

№9*. Упростите выражение .

Выберите правильный ответ:1)2)3)2.

Ответ:2)

Подсказка: используйте формулу синуса двойного угла, где .

№10*. Известно, что . Найти ;

Установите соответствие между множествами значений А и В:

А В

а) 1)

б) ; 2)

в) 3)

г) ; 4)

Ответ:

№11*.Вычислите .

Ответ:1,5.

Подсказка: используйте формулы синуса двойного угла, где ; квадрата суммы и основное тригонометрическое тождество.

№12*.Известно, что , Найти ;

Установите соответствие между множествами значений А и В:

А В

а) 1)

б) ; 2)

в) 3)

г) ; 4)

Ответ:

№13*.Вычислите. Установите соответствие между множествами значений А и В:

А В

а) 1)

б) ; 2)

в) 3)

г) ; 4)

Ответ:

Подсказка: используйте формулу синуса и косинуса двойного угла, где и определение тангенса и котангенса.

№14*.Решите уравнения и выберите верный ответ:

1); 2);3)

Ответ: 2)

Подсказка: используйте формулу половинного аргумента, разделив предварительно обе части уравнения на 2.

Проверочная работа:

№1.

а) Известно, что , ,

Вычислите и установите соответствие между множествами А и В:

А В

а) ; 1)

б) cos; 2)

в) ; 3)

г) ; 4)

5)2

Ответ:

Подсказка: используй формулы половинного аргумента и определение тангенса и котангенса.

б) Известно, что , ,

Вычислите и установите соответствие между множествами А и В:

А В

а) ; 1)

б) cos; 2)

в) ; 3)

г) ; 4)

Ответ:

Подсказка: используй формулы половинного аргумента и определение тангенса и котангенса.

№2.Вычислите: а); б)

Ответ: а) 5; б) 6

Подсказка: используйте формулу тангенса двойного угла, где .

№3.

а)Упростите выражение:

Выберите верный ответ:1)

Ответ: 1)

б) Упростите выражение:

Выберите верный ответ:1)

Ответ: 1)

Подсказка: используйте определение тангенса и котангенса, основное тригонометрическое тождество, формулу синуса и косинуса двойного угла, где .

Источник

Формулы половинного угла (аргумента) представляют собой противоположность формулам двойного угла , так как они выражают синус, косинус, тангенс и котангенс угла α2 при помощи тригонометрических функций угла α. В статье раскрыты формулы половинного угла и добавлены их доказательства с примерами решений.

Список формул половинного угла

Стандартные формулы половинного угла:

sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα

Формулы для sin и cos половинного угла справедливы при любом значении заданного угла α. Формулу для tg любого угла αопределяет tgα2, значение угла α≠π+2π·z при z равном любому целому числу ( выражение 1+cosα с таким же значением α не должно принимать значение 0). Формула ctg угла считается справедливой для любого угла α, где половинный угол имеет место быть, α≠2π·z.

Самые значимые формулы половинного угла для квадратов тригонометрических функций выводятся через положительное или отрицательное значение арифметического квадратного корня. Имеем формулы половинного угла:

sinα2=±1-cosα2, cosα2=±1+cosα2, tgα2=±1-cosα1+cosα, ctgα2=±1+cosα1-cosα

Знак «-» указывает, что тригонометрическая функция принадлежит определенной четверти угла α2.

Применим формулы на практике.

Доказательство формул половинного угла

Доказательство формул половинного угла основывается на формулах cos двойного угла cosα=1-2·sin2α2 и cosα=2·cos2α2-1. Упростив первое выражение по sin2α2, получим саму формулу половинного угла sin2α2=1-cosα2, второе выражение по cos2α2 получим cos2α2=1+cosα2.

Чтобы доказать формулы половинного угла для tg и ctg угла α2, необходимо применить основные тригонометрические тождества tgα2=sinα2cosα2 и ctgα2=cosα2sinα2, к ним необходимо добавить формулы половинного угла cos и sin, которые доказали выше. При подстановке получим выражения, имеющие вид:

tg2α2=sin2α2cos2α2=1-cosα21+cosα2=1-cosα1+cosα;ctg2α2=cos2α2sin2α2=1-cosα21+cosα2=1+cosα1-cosα;

Все формулы половинного угла были доказаны.

Примеры использования

Покажем применение формул половинного угла при решении примера.

Пример 1

Известно, что cos30°=32. Необходимо вычислить значение cos 15 градусов, используя формулы половинного угла.

Решение

Данный пример рассматривает применение формулы половинного угла для косинуса, имеющей вид cos2α2=1+cosα2.

Следуя из условия, подставляем числовые значения и получаем: cos215°=1+cos30°2=1+322=2+34. После получения значения косинуса 15 градусов, необходимо найти само значение косинуса. Для этого вспомним, что угол в 15 градусов принадлежит первой четверти. Там косинус угла имеет положительное значение ( чтобы вспомнить знаки тригонометрических функций, необходимо повторить теорию знаков синуса, косинуса, тангенса и котангенса по четвертям). Следуя из вышесказанного, имеем cos215°=2+34, тогда cos 15°=2+34=2+32. Ответ: cos 15°=2+32.

Применяя формулу половинного угла, стоит учитывать тот факт, что угол может быть не явного вида α2 и α, а потребует дальнейшего приведения к стандартному виду. Главное условие – нахождение аргумента в правой части формул половинного угла было в 2 раза больше, чем в левой. Иначе применение формулы будет невозможно.

Если формула позволит записывать данное равенство таким образом sin27α=1-cos14α2 или sin2 5α17=1-cos10α172, то формула будет применима.

Для правильного преобразования и применения формул половинного аргумента необходимо досконально изучить свойства тригонометрических функций. Не любое выражение поддается такому преобразованию в тригонометрии. Необходимо внимательно следить за значениями углов тригонометрических функций и их нахождение в четвертях для определения знака для выражения.

Все формулы половинного угла в тригонометрии:

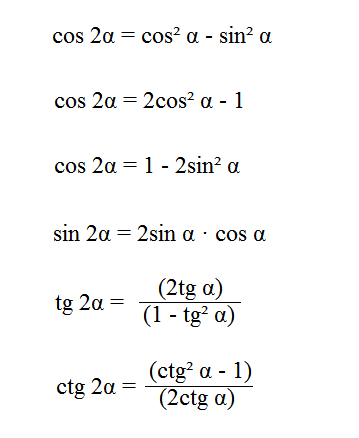
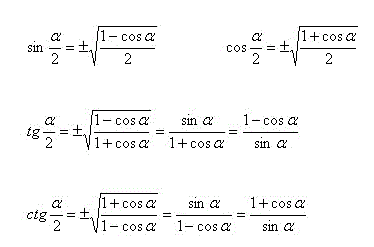
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Формулы двойного и половинного аргумента. Универсальная подстановка

Формулы двойного аргумента
Формулы половинного аргумента
Формулы универсальной подстановки
Примеры

п.1. Формулы двойного аргумента

Выведем формулы двойного аргумента, исходя из формул суммы (см. §13 и §14 данного справочника)

begin{gather*} sin2alpha=sin(alpha+alpha)=sinalpha cosalpha+cosalpha sinalpha=2sinalpha cosalpha\ cos2alpha=cos(alpha+alpha)=cosalpha cosalpha-sinalpha sinalpha=cos^2alpha-sin^2alpha\ tg2alpha=tg(alpha+alpha)=frac{tgalpha+tgalpha}{1-tgalphacdot tgalpha}=frac{2tgalpha}{1-tg^2alpha} end{gather*}

Умножим полученное выражение на котангенс вверху и внизу дроби, и получим еще одно полезное выражение:

begin{gather*} tg2alpha=frac{2tgalpha}{1-tg^2alpha}=frac{2tgalpha}{1-tg^2alpha}cdot{ctgalpha}{ctgalpha}=frac{2}{ctgalpha-tgalpha}\ ctg2alpha=ctg(alpha+alpha)=frac{ctgalphacdot ctgalpha-1}{ctgalpha+ctgalpha}=frac{ctg^2alpha-1}{2ctgalpha}=frac{ctgalpha-tgalpha}{2} end{gather*}

begin{gather*} sin2alpha=2sinalpha cosalpha\ cos2alpha=cos^2alpha-sin^2alpha=2cos^alpha-1=1-2sin^2alpha\ tg2alpha=frac{2tgalpha}{1-tg^2alpha}=frac{2}{ctgalpha-tgalpha}\ ctg2alpha=frac{ctg^2alpha-1}{2ctgalpha}=frac{ctgalpha-tgalpha}{2} end{gather*}

Например:
Найдем (sin2alpha) и (tg2alpha), если (sinalpha=0,8, fracpi2ltalphaltpi)
Угол (alpha) во 2-й четверти, косинус отрицательный:
(cosalpha=-sqrt{1-sin^2alpha}=-sqrt{1-0,8^2}=-0,6)
(tgalpha=frac{sinalpha}{cosalpha}=frac{0,8}{-0,6}=-frac43)
Синус двойного угла: (sin2alpha=2sinalpha cosalpha=2cdot 0,8cdot(-0,6)=-0,96)
Тангенс двойного угла: (tg2alpha=frac{2tgalpha}{1-tg^2alpha}=frac{2cdot left(-frac43right)}{1-left(-frac43right)^2}=frac{-frac83}{1-frac{16}{9}}=frac83 : frac79=frac83cdotfrac97=frac{24}{7}=3frac37)

п.2. Формулы половинного аргумента

По формуле двойного аргумента для косинуса: (cos2alpha=2cos^2alpha-1)
Заменим слева угол (2alpharightarrow alpha), а справа угол (alpharightarrowfrac{alpha}{2}).
Получаем: begin{gather*} cosalpha=2cos^2frac{alpha}{2}-1Rightarrow 2cos^2frac{alpha}{2}=1+cosalphaRightarrow cos^2frac{alpha}{2}=frac{1+cosalpha}{2} end{gather*} Из другой формулы двойного аргумента для косинуса: (cos2alpha=1-2sin^2alpha), получаем: begin{gather*} cosalpha=1-2sin^2frac{alpha}{2}Rightarrow 2sin^2frac{alpha}{2}=1-cosalphaRightarrow sin^2frac{alpha}{2}=frac{1-cosalpha}{2} end{gather*} Для квадрата тангенса и котангенса половинного угла: begin{gather*} tg^2frac{alpha}{2}=frac{sin^2frac{alpha}{2}}{cos^2frac{alpha}{2}}=frac{1-cosalpha}{1+cosalpha}, ctg^2frac{alpha}{2}=frac{1}{tg^2frac{alpha}{2}}=frac{1+cosalpha}{1-cosalpha} end{gather*}

begin{gather*} sin^2frac{alpha}{2}=frac{1-cosalpha}{2}, cos^2frac{alpha}{2}=frac{1+cosalpha}{2}\ tg^2frac{alpha}{2}=frac{1-cosalpha}{1+cosalpha}, ctg^2frac{alpha}{2}=frac{1+cosalpha}{1-cosalpha} end{gather*}

Например:
Найдем (cosfrac{alpha}{2}) и (ctgfrac{alpha}{2}), если (sinalpha=-frac{-sqrt{3}}{2}, piltalphaltfrac{3pi}{2})
Угол (alpha) в 3-й четверти, косинус отрицательный: (cosalpha=-frac12)
Половинный угол (fracpi2ltfrac{alpha}{2}ltfrac{3pi}{4}) во 2-й четверти, косинус отрицательный:
(cosfrac{alpha}{2}=-sqrt{frac{1+cosalpha}{2}}=-sqrt{frac{1-frac12}{2}}=-frac12)
Котангенс тоже отрицательный:
(ctgfrac{alpha}{2}=-sqrt{frac{1+cosalpha}{1-cosalpha}}=-sqrt{frac{1-frac12}{1+frac12}}=-frac{1}{sqrt{3}})

п.3. Формулы универсальной подстановки

Любую тригонометрическую функцию можно выразить через тангенс половинного угла.

Для тангенса формула универсальной подстановки получается из формулы двойного угла: $$ tgalpha=frac{2tgfrac{alpha}{2}}{1-tg^2frac{alpha}{2}} $$ Тогда котангенс через тангенс половинного угла: $$ ctgalpha=frac{1-tg^2frac{alpha}{2}}{2tgfrac{alpha}{2}} $$ Для синуса: $$ sinalpha=2sinfrac{alpha}{2}cosfrac{alpha}{2}=2frac{sinfrac{alpha}{2}}{cosfrac{alpha}{2}}cos^2frac{alpha}{2}=2tgfrac{alpha}{2}cos^2frac{alpha}{2}=frac{2tgfrac{alpha}{2}}{1+tg^2frac{alpha}{2}} $$ Для косинуса: $$ cosalpha=frac{sinalpha}{tgalpha}=frac{2tgfrac{alpha}{2}}{1+tg^2frac{alpha}{2}} : frac{2tgfrac{alpha}{2}}{1-tg^2frac{alpha}{2}}=frac{1-tg^2frac{alpha}{2}}{1+tg^2frac{alpha}{2}} $$

begin{gather*} sinalpha=frac{2tgfrac{alpha}{2}}{1+tg^2frac{alpha}{2}}\ \ cosalpha=frac{1-tg^2frac{alpha}{2}}{1+tg^2frac{alpha}{2}}\ \ tgalpha=frac{2tgfrac{alpha}{2}}{1-tg^2frac{alpha}{2}}\ \ ctgalpha=frac{1-tg^2frac{alpha}{2}}{2tgfrac{alpha}{2}} end{gather*}

Универсальная подстановка эффективна при решении тригонометрических уравнений, а также интегрировании.

п.4. Примеры

Пример 1. Вычислите:
a) begin{gather*} 2cosfrac{pi}{8}sinfrac{7pi}{8}=2cosfrac{pi}{8}sinleft(pi-frac{pi}{8}right)=2cosfrac{pi}{8}sinfrac{pi}{8}=sinfrac{pi}{4}=frac{sqrt{2}}{2} end{gather*}
б) begin{gather*} 6cos^2frac{pi}{12}-3=3left(2cos^2frac{pi}{12}-1right)=3cdot cosfrac{pi}{6}=3cdot frac{sqrt{3}}{2}=frac{3sqrt{3}}{2} end{gather*}
в) begin{gather*} cos^4frac{23pi}{12}-sin^4frac{13pi}{12}=cos^4left(2pi-frac{pi}{12}right)-sin^4left(pi+frac{pi}{12}right)=cos^4frac{pi}{12}-sin^4frac{pi}{12}=\ =left(cos^2frac{pi}{12}-sin^2frac{pi}{12}right)underbrace{left(cos^2frac{pi}{12}+sin^2frac{pi}{12}right)}_{=1}=cos^2frac{pi}{12}-sin^2frac{pi}{12}=cosfrac{pi}{6}=frac{sqrt{3}}{2} end{gather*}
г) begin{gather*} ctgfrac{7pi}{8}+tgfrac{7pi}{8}=ctgleft(pi-frac{pi}{8}right)+tgleft(pi-frac{pi}{8}right)=-ctgfrac{pi}{8}-tgfrac{pi}{8}=\ =-left(frac{cosfrac{pi}{8}}{sinfrac{pi}{8}}+frac{sinfrac{pi}{8}}{cosfrac{pi}{8}}right)=-frac{cos^2frac{pi}{8}+sin^2frac{pi}{8}}{sinfrac{pi}{8}cdot cosfrac{pi}{8}}=-frac{1}{frac12 sinfrac{pi}{4}}=-frac{1}{frac12cdot frac{sqrt{2}}{2}}=-frac{4}{sqrt{2}}=-2sqrt{2} end{gather*}
д) begin{gather*} frac{1+ctg15^{circ}}{1-ctg15^{circ}}=frac{1+ctg15^{circ}}{1-ctg15^{circ}}cdot frac{sin15^{circ}}{sin15^{circ}}=frac{sin15^{circ}+cos15^{circ}}{sin15^{circ}-cos15^{circ}}=\ =frac{(sin15^{circ}+cos15^{circ})^2}{(sin15^{circ}-cos15^{circ})(sin15^{circ}+cos15^{circ})}=frac{sin^2 15^{circ}+2sin15^{circ}cos15^{circ}+cos^2 15^{circ}}{sin^2 15^{circ}-cos^2 15^{circ}}=\ =-frac{1+2sin15^{circ}cos15^{circ}}{cos^2 15^{circ}-sin^2 15^{circ}}=-frac{1+sin30^{circ}}{cos30^{circ}}=-frac{1+frac12}{frac{sqrt{3}}{2}}=-frac{3}{sqrt{3}}=-sqrt{3} end{gather*}
e*) begin{gather*} sinfrac{pi}{10}sinfrac{3pi}{10}=frac{2cosfrac{pi}{10}}{2cosfrac{pi}{10}}cdot sinfrac{pi}{10}sinfrac{3pi}{10}=frac{left(2cosfrac{pi}{10}sinfrac{pi}{10}right)}{2cosfrac{pi}{10}}sinfrac{3pi}{10}=\ =frac{sinfrac{pi}{5}}{2cosfrac{pi}{10}}sinleft(frac{pi}{2}-frac{pi}{5}right)=frac{sinfrac{pi}{5}cosfrac{pi}{5}}{2cosfrac{pi}{10}}=frac{sinfrac{2pi}{5}}{4cosleft(frac{pi}{2}-frac{2pi}{5}right)}=frac{sinfrac{2pi}{5}}{4sinfrac{2pi}{5}}=frac14 end{gather*}

Пример 2.Упростите выражение:
a) begin{gather*} frac{1-tg^2alpha}{1+tg^2alpha}=frac{1-tg^2alpha}{frac{1}{cos^2alpha}}=(1-tg^2alpha)cos^2alpha=cos^2alpha-sin^2alpha=cos2alpha end{gather*}
б) begin{gather*} cos^4left(2alpha+frac{5pi}{2}right)-sin^4left(2alpha-frac{3pi}{2}right)=cos^4left(2alpha+2pi+frac{pi}{2}right)-sin^4left(2alpha-2pi+frac{pi}{2}right)=\ =cos^4left(2alpha+frac{pi}{2}right)-sin^4left(2alpha+frac{pi}{2}right)=sin^4 2alpha-cos^4 2alpha=\ =(sin^2 2alpha-cos^2 2alpha)underbrace{(sin^2 2alpha+cos^2 2alpha)}_{=1}=sin^2 2alpha-cos^2 2alpha=-cos4alpha end{gather*}
в) begin{gather*} sin2alpha+2sin^2left(alpha-frac{5pi}{4}right)=sin2alpha+1-cosleft(2left(alpha-frac{5pi}{4}right)right)=\ =sin2alpha+1-cosleft(2alpha-frac{5pi}{2}right)=sin2alpha+1-cosleft(2alpha-2pi-fracpi2right)=\ =sin2alpha+1-cosleft(2alpha-fracpi2right)=sin2alpha+1-sin2alpha=1 end{gather*}
г) begin{gather*} frac{ctgalpha(sin2alpha-sinalpha)}{cos2alpha-cosalpha+1}=frac{frac{cosalpha}{sinalpha}(2sinalpha cosalpha-sinalpha)}{cos2alpha-cos alpha+1}=frac{cosalpha(2cosalpha-1)}{cos2alpha-cosalpha+1}=\ =frac{2cos^2alpha-cosalpha}{2cos^2alpha-1-cosalpha+1}=frac{2cos^2alpha-cosalpha}{2cos^2alpha-cosalpha}=1 end{gather*}
д) begin{gather*} frac{tg^2left(2alpha-fracpi4right)-1}{tg^2left(2alpha-frac{5pi}{4}right)+1}=frac{tg^2left(2alpha-fracpi4right)-1}{tg^2left(2alpha-fracpi4-piright)+1}=frac{tg^2left(2alpha-fracpi4right)-1}{tg^2left(2alpha-fracpi4right)+1}=\ =left(tg^2left(2alpha-fracpi4right)-1right)cos^2left(2alpha-fracpi4right)=sin^2left(2alpha-fracpi4right)-cos^2left(2alpha-fracpi4right)=\ =-cos2left(2alpha-fracpi4right)=-cosleft(4alpha-fracpi2right)=-sin4alpha end{gather*}

Пример 3.Найдите:
a) (sin2alpha) и (ctg2alpha), если (cosalpha=frac{12}{13}, -fracpi2ltalphalt 0)
Угол (alpha) в 4-й четверти, синус отрицательный: (sinalpha=-sqrt{1-cos^2alpha}=-sqrt{1-left(frac{12}{13}right)^2}=-frac{5}{13})
Котангенс: (ctgalpha=frac{cosalpha}{sinalpha}=frac{12}{13} : left(-frac{5}{13}right)=-frac{12}{5}=-2,4)
Синус двойного угла: (sin2alpha=2sinalpha cosalpha=2cdot left(-frac{5}{13}right)cdot frac{12}{13}=-frac{120}{169})
Котангенс двойного угла: (ctg2alpha=frac{ctg^2alpha-1}{2ctgalpha}=frac{left(-frac{12}{5}right)^2-1}{2cdotleft(-frac{12}{5}right)}=frac{144-25}{25} : left(-frac{24}{5}right)=-frac{119}{5cdot 24}=-frac{119}{120})
Ответ: (-frac{120}{169}) и (-frac{119}{120})

б) (tg^2left(fracpi4+alpharight)), если (sin2alpha=frac15) begin{gather*} tg^2left(fracpi4+alpharight)=left(tgleft(fracpi4+alpharight)right)^2=left(frac{tgfracpi4+tgalpha}{1-tgfracpi4cdot tgalpha}right)^2=left(frac{1+tgalpha}{1-tgalpha}right)^2=\ =left(frac{1+tgalpha}{1-tgalpha}cdot frac{cosalpha}{cosalpha}right)^2=left(frac{cosalpha+sinalpha}{cosalpha-sinalpha}right)^2=frac{cos^2alpha+2sinalpha cosalpha+sin^2alpha}{cos^2alpha-2sinalpha cosalpha+sin^2alpha}=\ =frac{1+2sinalpha cosalpha}{1-2sinalpha cosalpha}=frac{1+sin2alpha}{1-sin2alpha} end{gather*} Подставляем:
(tg^2left(fracpi4+alpharight)=frac{1+frac15}{1-frac15}=frac64=1,5)
Ответ: 1,5

в) ( frac{sin(60^{circ}+alpha)}{4sinleft(15^{circ}+fracalpha4right)sinleft(75^{circ}-fracalpha4right)}), если (sinleft(30^{circ}+fracalpha2right)=0,8, 0^{circ}ltalphalt 90^{circ}) begin{gather*} frac{sin(60^{circ}+alpha)}{4sinleft(15^{circ}+fracalpha4right)sinleft(75^{circ}-fracalpha4right)}=frac{sin(60^{circ}+alpha)}{4sinleft(15^{circ}+fracalpha4right)sinleft(90^{circ}-left(15^{circ}+fracalpha4right)right)}=\ =frac{sin(60^{circ}+alpha)}{4sinleft(15^{circ}+fracalpha4right)cosleft(15^{circ}+fracalpha4right)}=frac{sin(60^{circ}+alpha)}{2sinleft(2left(15^{circ}+fracalpha4right)right)}=frac{sin(60^{circ}+alpha)}{2sinleft(30^{circ}+fracalpha2right)}=\ =frac{2sinleft(30^{circ}+fracalpha2right)cosleft(30^{circ}+fracalpha2right)}{2sinleft(30^{circ}+fracalpha2right)}=cosleft(30^{circ}+fracalpha2right) end{gather*} Нужно найти косинус при известном синусе. $$ 0^{circ}ltalphalt 90^{circ}Rightarrow 0^{circ}ltfracalpha2lt 45^{circ}Rightarrow 30^{circ}+fracalpha2lt 75^{circ} $$ Угол (left(30^{circ}+fracalpha2right)) в 1-й четверти, косинус положительный:
$$ cosleft(30^{circ}+fracalpha2right)=sqrt{1-sin^2left(30^{circ}+fracalpha2right)}=sqrt{1-0,8^2}=0,6 $$ Ответ: 0,6

г) ( sin2alpha), если (frac{2cosalpha+3sinalpha}{3cosalpha-2sinalpha}=-2) begin{gather*} frac{2cosalpha+3sinalpha}{3cosalpha-2sinalpha}=frac{frac{2cosalpha+3sinalpha}{cosalpha}}{frac{3cosalpha-2sinalpha}{cosalpha}}=frac{2+3tgalpha}{3-2tgalpha}=-2\ 2+3tgalpha=-2(3-2tgalpha)\ 3tgalpha-4tgalpha=-6-2\ tgalpha=8\ sin2alpha=2sinalpha cosalpha=2frac{sinalpha}{cosalpha}cos^2alpha=2tgalphacdot cos^2alpha=frac{2tgalpha}{1+tg^2alpha} end{gather*} Подставляем: (sin2alpha=frac{2cdot 8}{1+8^2}=frac{16}{65})
Ответ: (frac{16}{65})

Пример 4*.Упростите:
a) ( cosfrac{pi}{33}cosfrac{2pi}{33}cosfrac{4pi}{33}cosfrac{8pi}{33}cosfrac{16pi}{33} )
Умножим и разделим на (sinfrac{pi}{33}): begin{gather*} frac{sinfrac{pi}{33}cosfrac{pi}{33}}{sinfrac{pi}{33}}cosfrac{2pi}{33}cosfrac{4pi}{33}cosfrac{8pi}{33}cosfrac{16pi}{33}=frac{sinfrac{2pi}{33}cosfrac{2pi}{33}}{2sinfrac{pi}{33}}cosfrac{4pi}{33}cosfrac{8pi}{33}cosfrac{16pi}{33}=\ =frac{sinfrac{4pi}{33}cosfrac{4pi}{33}}{4sinfrac{pi}{33}}cosfrac{8pi}{33}cosfrac{16pi}{33}=frac{sinfrac{8pi}{33}cosfrac{8pi}{33}}{8sinfrac{pi}{33}}cosfrac{16pi}{33}=frac{sinfrac{16pi}{33}cosfrac{16pi}{33}}{16sinfrac{pi}{33}}=\ =frac{sinfrac{32pi}{33}}{32sinfrac{pi}{33}}=frac{sinleft(pi-frac{pi}{33}right)}{32sinfrac{pi}{33}}=frac{sinfrac{pi}{33}}{32sinfrac{pi}{33}}=frac{1}{32} end{gather*} Ответ: (frac{1}{32})

б) ( sin18^{circ}sin54^{circ} ) begin{gather*} sin18^{circ}sin54^{circ}=sin18^{circ}sin(90^{circ}-36^{circ})=sin18^{circ}cos36^{circ}=frac{sin18^{circ}cos18^{circ}cos36^{circ}}{cos18^{circ}}=\ =frac{sin36^{circ}cos36^{circ}}{2cos18^{circ}}=frac{sin72^{circ}}{4cos18^{circ}}=frac{sin72^{circ}}{4cos18^{circ}}=frac{sin(90^{circ}-18^{circ})}{4cos18^{circ}}=frac{cos18^{circ}}{4cos18^{circ}}=frac14 end{gather*} Ответ: (frac14)

в) ( sqrt{2+sqrt{2+2cos4alpha}} ), где (0le alphalefracpi2) begin{gather*} sqrt{2+sqrt{2+2cos4alpha}}=sqrt{2+sqrt{2(1+cos4alpha)}}=sqrt{2+sqrt{2cdot 2cos^2 2alpha}}=\ =sqrt{2+2cdot |cos2alpha|}=sqrt{2(1+|cos2alpha|)}= left[ begin{array} {l l} sqrt{2(1+cos2alpha)}, cos2alphageq 0\ sqrt{2(1-cos2alpha)}, cos2alphalt 0 end{array} right. =\ = left[ begin{array} {l l} sqrt{2cdot 2cos^2alpha}, 0leq 2alphaleqfracpi2\ sqrt{2cdot 2sin^2alpha}, fracpi2lt 2alphaleq pi end{array} right. = left[ begin{array} {l l} 2cosalpha, 0leq alphaleqfracpi4\ 2sinalpha, fracpi4lt alphaleq fracpi2 end{array} right. end{gather*} Ответ: (2cosalpha) при (0leq alphaleqfracpi4; 2sinalpha) при (fracpi4lt alphaleq fracpi2)
г) ( 4(sin^4x+cos^4x)-4(sin^6x+cos^6x)-1 )
Основное тригонометрическое тождество: (sin^2x+cos^2x=1)
Возведём в квадрат: begin{gather*} (sin^2x+cos^2x)^2=sin^4x+cos^4x+2sin^2x cos^2x=1\ sin^4x+cos^4x=1-frac{(2sinx cosx)^2}{2}=1-frac{sin^2 2x}{2} end{gather*} Возведём в куб: begin{gather*} (sin^2x+cos^2x)^3=sin^6x+cos^6x+3sin2x cos^4x+3sin^4x cos^2x=1\ sin^6x+cos^6x = 1-3sin^2x cos^2xunderbrace{(cos^2x+sin^2x)}_{=1}=\ =1-frac34(2sinx cosx)^2=1-frac{3sin^2 2x}{4} end{gather*}

begin{gather*} sin^4x+cos^4x=1-frac{sin^2 2x}{2}\ \ sin^6x+cos^6x = 1-frac{3sin^2 2x}{4} end{gather*}

Подставляем: begin{gather*} 4left(1-frac{sin^2 2x}{2}right)-4left(1-frac{3sin^2 2x}{4}right)=1=4-2sin^2 2x-4+3sin^2 2x-1=\ =sin^2 2x-1=-cos^2 2x end{gather*} Ответ: (-cos^2 2x)

Источник

Формулы половинного угла (половинного аргумента) – это часть от всех основных тригонометрических формул. Они выражают функции синус, косинус, тангенс, котангенс угла `frac{alpha}2` через эти ж функции аргумента `alpha`. Они, можно сказать, противоположны формулам двойного угла. Ниже приведены все формулы половинных углов, их вывод, а также примеры решения задач с их использованием.

Список всех формул половинного угла

Их можно встретить записанными в двух видах. В первом каждая из тригонометрических функций выражается через радикал:

`sin frac alpha 2=pm sqrt{frac {1-cos alpha}2}`
`cos frac alpha 2=pm sqrt{frac {1+cos alpha}2}`
`tg frac alpha 2=pm sqrt{frac {1-cos alpha}{1+cos alpha}}=` `frac {sin alpha}{1+cos alpha}=frac {1-cos alpha}{sin alpha}`
`ctg frac alpha 2=pm sqrt{frac {1+cos alpha}{1-cos alpha}}=` `frac {sin alpha}{1-cos alpha}=frac {1+cos alpha}{sin alpha}`

Знак «+» или «-» перед корнями зависит от того, в какую из координатных четвертей попадает угол `frac{alpha}2`.

Во втором варианте имеем дело с квадратами тригонометрических функций половинного угла:

`sin^2 frac alpha 2=frac {1-cos alpha}2`
`cos^2 frac alpha 2=frac {1+cos alpha}2`
`tg^2 frac alpha 2=frac {1-cos alpha}{1+cos alpha}`
`ctg^2 frac alpha 2=frac {1+cos alpha}{1-cos alpha}`

Формула синуса и косинуса половинного угла имеет место при любом угле `alpha`.

Формула тангенса половинного угла справедлива для тех углов `alpha`, при которых определен `tg frac alpha 2`, то есть при ` alphanepi+2pi n, n in Z`.

Формула котангенса выполняется для тех `alpha`, при которых определен `ctg frac alpha 2`, то есть при ` alphane 2pi n, n in Z`.

С помощью следующего набора формул можно выразить каждую из тригонометрических функций угла `alpha` через тангенс половинного угла.

`sin alpha= frac{2tgfrac{alpha}{2}}{1 + tg^{2}frac{alpha}{2}},` ` alphane pi +2pi n, n in Z`
`cos alpha= frac{1 — tg^{2}frac{alpha}{2}}{1 + tg^{2}frac{alpha}{2}},` ` alpha ne pi +2pi n, n in Z`
`tg alpha= frac{2tgfrac{alpha}{2}}{1 — tg^{2}frac{alpha}{2}},` ` alpha ne pi +2pi n, n in Z,` ` alpha ne frac{pi}{2}+ pi n, n in Z`
`ctg alpha = frac{1 — tg^{2}frac{alpha}{2}}{2tgfrac{alpha}{2}},` ` alpha ne pi n, n in Z,` `alpha ne pi + 2pi n, n in Z`

Вывод формул половинного угла

Формула косинуса и синуса половинного угла выводится из формул косинуса двойного угла `cos 2alpha=1-2 sin^2 alpha` и `cos 2alpha=2 cos^2 alpha-1`. Запишем их в следующем виде: `cos alpha=1-2 sin^2 frac alpha 2` и `cos alpha=2 cos^2 frac alpha 2-1`. Выразив из первого равенства ` sin frac alpha 2` получим `sin frac alpha 2=pm sqrt{frac {1-cos alpha}2}`. Аналогично разрешив второе равенство относительно ` cos frac alpha 2` в результате будем иметь `cos frac alpha 2=pm sqrt{frac {1+cos alpha}2}`.

Формулы тангенса и котангенса половинного угла можно вывести, используя определения этих функций в виде `tg frac alpha 2=frac{sinfrac alpha 2}{cos frac alpha 2}` и `ctg frac alpha 2=frac{cos frac alpha 2}{sin frac alpha 2}`, а также две уже доказанные выше формулы для синуса и косинуса.

В результате будем иметь: `tg frac alpha 2=frac{sinfrac alpha 2}{cos frac alpha 2}=` `frac{pm sqrt{frac {1-cos alpha}2}}{pm sqrt{frac {1+cos alpha}2}}=` `pm sqrt{frac {1-cos alpha}{1+cos alpha}}` и `ctg frac alpha 2=frac{cosfrac alpha 2}{sin frac alpha 2}=` `frac{pm sqrt{frac {1+cos alpha}2}}{pm sqrt{frac {1-cos alpha}2}}=` `pm sqrt{frac {1+cos alpha}{1-cos alpha}}`.

Примеры использования при решении задач

Пример 1. Найти `cos 15^circ`, если известно, что `cos 30^circ=frac{sqrt3}2`.

Решение. Формула половинного угла для тригонометрической функции косинус имеет вид `cos^2 frac alpha 2=frac {1+cos alpha}2`. Подставив известные значения, имеем `cos^2 15^circ=frac {1+cos 30^circ}2=` `frac{1+frac{sqrt3}2}2=frac{2+sqrt3}4`. Имея значение `cos^2 15^circ`, найдем `cos 15^circ`. Поскольку угол 15 градусов лежит в первой координатной четверти, а косинус в этой четверти имеет знак «+», то `cos 15^circ=sqrt{frac{2+sqrt3}4}=` `frac{sqrt{2+sqrt3}}2`.

Ответ. `cos 15^circ=frac{sqrt{2+sqrt3}}2`.

Пример 2. Вычислить значение выражения `4cos frac {alpha}2+2cos alpha+5`, если `cos alpha=frac {1}8`.

Решение. Используя ту же формулу, что и в первом примере (`cos frac alpha 2=pm sqrt{frac {1+cos alpha}2}`) и известное значение косинуса, упростим выражение: `4sqrt{frac {1+cos alpha}2}+2cos alpha+5=4sqrt{frac {1+frac {1}8}2}+2 cdot frac {1}8+5=` `4sqrt{frac {9}16}+frac{1}4+5=8frac{1}4`.

Ответ. `4cos frac {alpha}2+2cos alpha+5=8frac{1}4`.

Еще несколько примеров с подробным объяснением посмотрите на видео:

В большинстве случаев формулы половинного угла используются при преобразовании тригонометрических выражений.

Материалы по теме:

Тригонометрические формулы: косинус, синус и тангенс двойного угла
Формулы понижения степени в тригонометрии: вывод и примеры
Все формулы по тригонометрии
Формулы приведения тригонометрических функций

Загрузка…

Источник

Формулы половинного угла (аргумента) онлайн

С помощю этого онлайн калькулятора можно получить формулы половинного угла (и другие формулы) тригонометрических функций. Для получения формулы выберите нужную тригонометрическую функцию, выберите нужный аргумент, нажав на аргумент в формуле. В результате получится формула для этой функции и аргумента. Теоретическую часть и численные примеры смотрите ниже.

Формулы половинного угла (аргумента) − теория, доказательство, примеры

Формулы половинного угла выражают тригонометрические функции синус, косинус, тангенс и котангенс угла через тригонометрические функции угла . Выведем формулы половинного угла для функций синус, косинус, тангенс, котангенс. Воспользуемся следующими формулами двойного угла (подробнее смотрите на странице Формулы двойного и тройного угла (аргумента) онлайн):

Подставим в (1) и (2) . Тогда имеем

Из равенств (3) и (4) найдем соответвсвенно и :

Следовательно:

Равенства (5) и (6) (или (7) и (8)) являются формулами половинного угла для функций синус и косинус. Для выведения формул для тангенса и котангенса запишем основные тригонометрические тождества для этих функций:

Тогда

Откуда:

Отметим, что в знак формулах (7), (8), (11) и (12) совпадает со знаком тригонометрической функции для угла .

Выражения (11) и (12) являются формулами половинного угла для функций тангенс и котангенс. Отметим, что определен тогда, когда (т.е. , где Z -множество целых чисел). определен тогда, когда (т.е. ).