Как найти половинный дискриминант

Квадратное уравнение с чётным вторым коэффициентом

Если в квадратном уравнении ax 2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D₁ = k 2 − ac , а корни по формулам и .

Примеры

Решим квадратное уравнение x 2 + 6x − 16 = 0 . В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k .

Любое четное число n можно представить в виде произведения числа 2 и числа k , то есть 2k .

Например, число 10 можно представить как 2 × 5 .

В этом произведении k = 5 .

Число 12 можно представить как 2 × 6 .

В этом произведении k = 6 .

Число −14 можно представить как 2 × (−7)

В этом произведении k = −7 .

Как видим, сомножитель 2 не меняется. Меняется только сомножитель k .

В уравнении x 2 + 6x − 16 = 0 вторым коэффициентом является число 6 . Это число можно представить как 2 × 3 . В этом произведении k = 3 . Теперь можно воспользоваться формулами для чётного коэффициента.

Найдем дискриминант по формуле D₁ = k 2 − ac

Теперь вычислим корни по формулам: и .

Значит корнями уравнения x 2 + 6x − 16 = 0 являются числа 2 и −8 .

В отличие от стандартной формулы для вычисления дискриминанта ( D=b 2 − 4ac ), в формуле D₁ = k 2 − ac не нужно выполнять умножение числа 4 на ac .

И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.

Пример 2. Решить квадратное уравнение 5x 2 − 6x + 1=0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3) . То есть k = −3 . Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Пример 3. Решить квадратное уравнение x 2 − 10x − 24 = 0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5) . То есть k = −5 . Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

Обычно для определения числа k поступают так: делят второй коэффициент на 2.

Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2 k . Чтобы из этого равенства выразить сомножитель k , нужно произведение b разделить на сомножитель 2

Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2

Пример 5. Решить квадратное уравнение

Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k . Получается, что

Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.

В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .

Вычислим второй корень уравнения:

Вывод формул

Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.

Рассмотрим квадратное уравнение ax 2 + bx + c = 0 . Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k

Заменим в уравнении ax 2 + bx + c = 0 коэффициент b на выражение 2k

Теперь вычислим дискриминант по ранее известной формуле:

Вынесем в получившемся выражении за скобки общий множитель 4

Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k 2 − ac .

В выражении 4(k 2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k 2 − ac . Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.

То есть выражение k 2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D₁

Теперь посмотрим как выводятся формулы и .

В нашем уравнении ax 2 + bx + c = 0 коэффициент b заменён на выражение 2k . Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k . Также на забываем, что D у нас равно выражению 4(k 2 − ac)

Но ранее было сказано, что выражение k 2 − ac обозначается через D₁ . Тогда в наших преобразованиях следует сделать и эту замену:

Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:

Теперь в получившемся выражении вынесем за скобки общий множитель 2

Сократим получившуюся дробь на 2

Аналогично вывóдится формула для вычисления второго корня:

Формулы корней квадратных уравнений, разложение на множители

В разных практических деятельностях человека вроде физики, инженерии, архитектуры и других точных наук, часто встречаются задачи с математическими моделями, какой являются уравнения, имеющие переменную (x) в иной степени. Именно они помогают учёным в изучении внешней среды и её использовании.

Квадратные уравнения

Квадратным называется равенство вида ax² + bc + c = 0, где x является переменой, a (первый коэффициент), b (второй) и c (свободный) — это действительные числа, которые должны приводить в условии задачи. Нужно помнить при решении, что a ≠ 0. Как уже понятно, оно очень отличается от линейного уравнения, его все изучали в младших классах школы.

Чтобы понять, как решать квадратные уравнения, нужно представить футбольное поле, длина которого на 10 метров больше его ширины, а площадь равна 380 квадратных метров. Нужно найти ширину футбольного поля.

Пусть переменная x — это определённая ширина, тогда её длина будет (х +10) метров. Потом x * (x + 10) = 380, ведь дана площадь 380 квадратных метров в условии задачи, то есть x² + 10x 380 равно нулю. Здесь а = 1, b = 10, а c = -375 Это был один из примеров квадратных равенств.

Различают два вида уравнений:

• Приведённые — это случай, когда в квадратном равенстве a = 1.
• Непривёденные если a ≠ 1.

При этом x² — приведённое, а уже при 5x² оно станет непривёденным.

Понятие дискриминант

Существует определенная система решения таких уравнений. Чтобы найти чётный корень такого равенства, достаточно запомнить приведённую ниже формулу квадратного уравнения.

Буква D — это дискриминант. Звучит сложно, но не стоит пугаться, ведь с латинского языка слово переводится, как разность. Он равен: D = b² 4 ac. Следуя этому, можно записать, что (2ax + b)² = D. Есть определенные правила, как надо решать дискриминант:

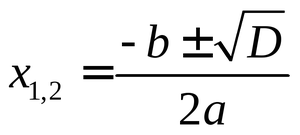• Если D меньше нуля, то действительных корней нет.
• В случае когда D равняется нулю, в решении получается только один действительный корень, но есть редкие случаи с двумя, то есть можно писать при решении в формуле либо +, либо -.
• Если D больше нуля, то в уравнении два действительных корня, то есть и плюс, и минус. Но чтобы укоротить решение достаточно записать ±, вместо двух вариантов решения задачи.

Пример первого способа нахождения через формулу дискриминанта квадратного уравнения и правильным разложением чисел:

• 9х²-6х+1=0,
• D = (-6)² 4 × 9 ×1 = 0,
• D эквивалентен нулю,
• x = -6/2×9 = 1/3.

Как пример можно показать уравнивание: -8x² = 0, у которого b и с равны нулю. Или 2x² 3 = 0, b ничему не равно. В уравнении -7x² + 4x² = 0 c эквивалентно нулю.

Разные квадратные уравнения

Помимо обычных дискриминантов, есть и половинные. Их ищут для равенств, у которых второй коэффициент — это чётное число, по формуле: D1 = 4 k² 4 ac = 4 (k² ac). Чтобы делать меньше ошибок, лучше использовать формулу со скобками. Благодаря этому в ответе получается четверть дискриминанта.

Квадратные равенства с комплексными переменными почти ничем не отличаются от плоскости действительных чисел и тем, которые должны проходить в восьмых классах. И чтобы без проблем их решать, нужно использовать формулу.

Если в квадратном равенстве хотя бы один из общих коэффициентов квадратного трехчлена B или C равен нулю, то такое равенство называют неполным.

Следовательно оно бывает только трёх видов:

• Уравнение вида ax² равно нулю. Поскольку а ≠ 0, имеем случай, когда x² = 0, корнем которого есть число ноль. Как уже понятно, имеется единственный корень х равен нулю.
• ax² + c равно нулю, тогда с не будет равняться нулю. Чтобы это лучше понять, приводится уравнение ах² = -c, x² = -c/a. Поскольку c ≠ 0 тогда и -с/а также не равно нулю. Если -с/а больше нуля, то получается два корня: х1 = корень из -с/а и ещё х2 = корень из с/а. Также можно написать вместо минуса и плюса одно уравнение из знаком: ±. Возможен случай, когда ситуация является обратной (-с/а <, 0), тогда корней совсем нет. Пример: -2х² + 50 равняется нулю. -2х²= -50, х² = 25, х1,2 = ±5.
• ах² + bx = 0, и при этом b нулю не равно. Разложим левую часть уравнения на множители и решим полученное х * (ах + b) = 0. Ответ: x равен нулю или ax + b = 0, но x = -b/a, поскольку a ≠ 0. В итоге должно выйти два корня: х1 = 0 и х2 = -b/a. Один из примеров: 2х² + 5х эквивалентен нулю, х(2х+ 5) = 0, х= 0 или 2х + 5 = 0. На данный момент очевидно, что x2 = -2,5 и х1 эквивалентен нулю.

Из истории математики

Неполные квадратные равенства и некоторые виды неизвестных корней вавилонские математики умели решить и создать ещё 4000 лет тому назад. Такие произведения в Древней Греции решали тем же способом. Люди, обладающие знаниями точных наук, решали некоторые квадратные уравнения геометрическими приёмами.

Это показал древнегреческий учёный Диофант. Много внимания таким уравнениям также выделял арабский математик Мухаммед Альхорезми. Он нашёл как решать уравнение видов: ах²=bx, ax²=c, ax²+bx=c, ax²+c=bx, bc+c=ax² и получил положительные корни.

Формулы, что связывают между собой корни равенства и его коэффициенты, впервые нашёл французский математик Франсуа Виет в 1591 году. Его заключения в современных обозначениях имеют вид: (а + b)x x² = 0.

После быстрой публикации работы нидерландского математика Жераром, а также француза Декарда и англичанина Ньютона равенство корней квадратного уравнения приобрело современный вид.

Уравнения	х1 и х2	х1+х2	х1×х2
х² -6х + 8 = 0	2 и 4	6	8
x²+x-12=0	-4 и 3	-1	-12
x²-4x-5=0	-3 и -2	-5	6
x²-4x-5=0	-1 и 5	4	-5

Сейчас речь идёт о теореме Виета, на которую нужно обратить внимание. Её так называют из-за известного французского математика Франсуа Виета, которым и было открыто это свойство. Сумма корней сведенного квадратного равенства равно другому коэффициенту, взятому с отрицательным знаком, а произведение корней — свободному члену. Часто его записывают в таком виде: х² + px + q эквивалентно нулю.

Теорему можно сформулировать так.

Если х1 и х2 — корни сведенного квадратного равенства х²+px+q эквивалентны нулю, то х1 + х2 = -p, x1 * x2 = q. Поскольку a ≠ 0, поделим две части уравнения на а и получается современная формула: x² b/a * x + c/a равно нулю.

Об отдельных случаях вычисления дискриминанта

Сложно встретить старшеклассника, НЕ умеющего находить корни квадратного уравнения через дискриминант.

Но, к сожалению, в отдельных случаях, получая громоздкий дискриминант, многие начинают паниковать (без калькулятора).

А на ЕГЭ по математике, например, в задачах №11, вам вполне может встретиться причудливый дискриминант.

Нет безвыходных ситуаций!

На чем можно сэкономить силы при вычислении дискриминанта

Прежде чем разбирать примеры, вспомним все же формулу дикриминанта для вычисления корней квадратного уравнения

Тогда корни уравнения находим по формуле

Надеюсь, вы помните, что удобно искать корни уравнения через дискриминант в случае, если имеем дело с полным квадратным уравнением ( и – ненулевые).

I. Используем формулу «разность квадратов» + показать

Допустим, нам нужно решить уравнение

Ясно, что дискриминант следующий:

Не спешим возводить 53 в квадрат! Замечаем, что , поэтому

Корни данного уравнения, думаю, теперь каждый из вас найдет без труда…

II. Используем прием вынесения общего множителя за скобки + показать

Допустим, нам нужно решить уравнение (кстати, оно взято из реальной текстовой задачи из открытого банка заданий ЕГЭ по математике).

Ясно, что дискриминант следующий:

Нет, мы не пойдем напролом!

Замечаем, что , а .

Мы можем вынести за скобку общий множитель

Корни найти – уже не проблема…

III. Формула сокращенного дискриимнанта + показать

Допустим, нам нужно решить уравнение

Вы знаете, что такое ? [spoiler]

Его очень удобно применять в случае четности второго коэффициента (при ).

Вот формулы дискриминанта и корней в этом случае:

для уравнения , где – четное

Тогда корни следующие: , то есть или

Хоть на чуть-чуть, но упростили вычисления. Считаете, что неоправданно, – лишней формулой забивать голову… Выбор за вами.

IV. Вместо дискриминанта – т. Виета + показать

Допустим, нам нужно решить уравнение

Вспоминаем теорему Виета:

Для приведенного квадратного уравнения (т.е. такого, коэффициент при в котором равен единице) сумма корней равна коэффициенту , взятому с обратным знаком, а произведение корней равно свободному члену , то есть ,

Так вот, очевидно, на роль корней уравнения претендуют числа и , так как и

[spoiler title=”источники:”]

http://tvercult.ru/nauka/formulyi-korney-kvadratnyih-uravneniy-razlozhenie-na-mnozhiteli

[/spoiler]

В разных практических деятельностях человека вроде физики, инженерии, архитектуры и других точных наук, часто встречаются задачи с математическими моделями, какой являются уравнения, имеющие переменную (x) в иной степени. Именно они помогают учёным в изучении внешней среды и её использовании.

Квадратные уравнения

Квадратным называется равенство вида ax² + bc + c = 0, где x является переменой, a (первый коэффициент), b (второй) и c (свободный) — это действительные числа, которые должны приводить в условии задачи. Нужно помнить при решении, что a ≠ 0. Как уже понятно, оно очень отличается от линейного уравнения, его все изучали в младших классах школы.

Чтобы понять, как решать квадратные уравнения, нужно представить футбольное поле, длина которого на 10 метров больше его ширины, а площадь равна 380 квадратных метров. Нужно найти ширину футбольного поля.

Пусть переменная x — это определённая ширина, тогда её длина будет (х +10) метров. Потом x * (x + 10) = 380, ведь дана площадь 380 квадратных метров в условии задачи, то есть x² + 10x 380 равно нулю. Здесь а = 1, b = 10, а c = -375 Это был один из примеров квадратных равенств.

Различают два вида уравнений:

• Приведённые — это случай, когда в квадратном равенстве a = 1.
• Непривёденные если a ≠ 1.

При этом x² — приведённое, а уже при 5x² оно станет непривёденным.

Понятие дискриминант

Существует определенная система решения таких уравнений. Чтобы найти чётный корень такого равенства, достаточно запомнить приведённую ниже формулу квадратного уравнения.

Буква D — это дискриминант. Звучит сложно, но не стоит пугаться, ведь с латинского языка слово переводится, как разность. Он равен: D = b² 4 ac. Следуя этому, можно записать, что (2ax + b)² = D. Есть определенные правила, как надо решать дискриминант:

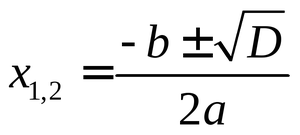• Если D меньше нуля, то действительных корней нет.
• В случае когда D равняется нулю, в решении получается только один действительный корень, но есть редкие случаи с двумя, то есть можно писать при решении в формуле либо +, либо -.
• Если D больше нуля, то в уравнении два действительных корня, то есть и плюс, и минус. Но чтобы укоротить решение достаточно записать ±, вместо двух вариантов решения задачи.

Пример первого способа нахождения через формулу дискриминанта квадратного уравнения и правильным разложением чисел:

• 9х²-6х+1=0,
• D = (-6)² 4 × 9 ×1 = 0,
• D эквивалентен нулю,
• x = -6/2×9 = 1/3.

Как пример можно показать уравнивание: -8x² = 0, у которого b и с равны нулю. Или 2x² 3 = 0, b ничему не равно. В уравнении -7x² + 4x² = 0 c эквивалентно нулю.

Разные квадратные уравнения

Помимо обычных дискриминантов, есть и половинные. Их ищут для равенств, у которых второй коэффициент — это чётное число, по формуле: D1 = 4 k² 4 ac = 4 (k² ac). Чтобы делать меньше ошибок, лучше использовать формулу со скобками. Благодаря этому в ответе получается четверть дискриминанта.

Квадратные равенства с комплексными переменными почти ничем не отличаются от плоскости действительных чисел и тем, которые должны проходить в восьмых классах. И чтобы без проблем их решать, нужно использовать формулу.

Если в квадратном равенстве хотя бы один из общих коэффициентов квадратного трехчлена B или C равен нулю, то такое равенство называют неполным.

Следовательно оно бывает только трёх видов:

• Уравнение вида ax² равно нулю. Поскольку а ≠ 0, имеем случай, когда x² = 0, корнем которого есть число ноль. Как уже понятно, имеется единственный корень х равен нулю.
• ax² + c равно нулю, тогда с не будет равняться нулю. Чтобы это лучше понять, приводится уравнение ах² = -c, x² = -c/a. Поскольку c ≠ 0 тогда и -с/а также не равно нулю. Если -с/а больше нуля, то получается два корня: х1 = корень из -с/а и ещё х2 = корень из с/а. Также можно написать вместо минуса и плюса одно уравнение из знаком: ±. Возможен случай, когда ситуация является обратной (-с/а &lt, 0), тогда корней совсем нет. Пример: -2х² + 50 равняется нулю. -2х²= -50, х² = 25, х1,2 = ±5.
• ах² + bx = 0, и при этом b нулю не равно. Разложим левую часть уравнения на множители и решим полученное х * (ах + b) = 0. Ответ: x равен нулю или ax + b = 0, но x = -b/a, поскольку a ≠ 0. В итоге должно выйти два корня: х1 = 0 и х2 = -b/a. Один из примеров: 2х² + 5х эквивалентен нулю, х(2х+ 5) = 0, х= 0 или 2х + 5 = 0. На данный момент очевидно, что x2 = -2,5 и х1 эквивалентен нулю.

Из истории математики

Неполные квадратные равенства и некоторые виды неизвестных корней вавилонские математики умели решить и создать ещё 4000 лет тому назад. Такие произведения в Древней Греции решали тем же способом. Люди, обладающие знаниями точных наук, решали некоторые квадратные уравнения геометрическими приёмами.

Это показал древнегреческий учёный Диофант. Много внимания таким уравнениям также выделял арабский математик Мухаммед Альхорезми. Он нашёл как решать уравнение видов: ах²=bx, ax²=c, ax²+bx=c, ax²+c=bx, bc+c=ax² и получил положительные корни.

Формулы, что связывают между собой корни равенства и его коэффициенты, впервые нашёл французский математик Франсуа Виет в 1591 году. Его заключения в современных обозначениях имеют вид: (а + b)x x² = 0.

После быстрой публикации работы нидерландского математика Жераром, а также француза Декарда и англичанина Ньютона равенство корней квадратного уравнения приобрело современный вид.

Уравнения	х1 и х2	х1+х2	х1×х2
х² -6х + 8 = 0	2 и 4	6	8
x²+x-12=0	-4 и 3	-1	-12
x²-4x-5=0	-3 и -2	-5	6
x²-4x-5=0	-1 и 5	4	-5

Сейчас речь идёт о теореме Виета, на которую нужно обратить внимание. Её так называют из-за известного французского математика Франсуа Виета, которым и было открыто это свойство. Сумма корней сведенного квадратного равенства равно другому коэффициенту, взятому с отрицательным знаком, а произведение корней — свободному члену. Часто его записывают в таком виде: х² + px + q эквивалентно нулю.

Теорему можно сформулировать так.

Если х1 и х2 — корни сведенного квадратного равенства х²+px+q эквивалентны нулю, то х1 + х2 = -p, x1 * x2 = q. Поскольку a ≠ 0, поделим две части уравнения на а и получается современная формула: x² b/a * x + c/a равно нулю.

• Если b = 0, то квадратное уравнение принимает вид ax 2 + 0x+c=0 и оно равносильно ax 2 + c = 0.
• Если c = 0, то квадратное уравнение выглядит так ax 2 + bx + 0 = 0, иначе его можно написать как ax 2 + bx = 0.
• Если b = 0 и c = 0, то квадратное уравнение выглядит так ax 2 = 0.

Такие уравнения отличны от полного квадратного тем, что их левые части не содержат либо слагаемого с неизвестной переменной, либо свободного члена, либо и того и другого. Отсюда и их название — неполные квадратные уравнения.

Решение неполных квадратных уравнений

Как мы уже знаем, есть три вида неполных квадратных уравнений:

• ax 2 = 0, ему отвечают коэффициенты b = 0 и c = 0;
• ax 2 + c = 0, при b = 0;
• ax 2 + bx = 0, при c = 0.

Давайте рассмотрим по шагам, как решать неполные квадратные уравнения по видам.

Как решить уравнение ax 2 = 0

Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax 2 = 0.

Уравнение ax 2 = 0 равносильно x 2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x 2 = 0 является нуль, так как 0 2 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.

Таким образом, неполное квадратное уравнение ax 2 = 0 имеет единственный корень x = 0.

Пример 1. Решить −6x 2 = 0.

1. Замечаем, что данному уравнению равносильно x 2 = 0, значит исходное уравнение имеет единственный корень — нуль.
2. По шагам решение выглядит так:

Как решить уравнение ax 2 + с = 0

Обратим внимание на неполные квадратные уравнения вида ax 2 + c = 0, в которых b = 0, c ≠ 0. Мы давно знаем, что слагаемые в уравнениях носят двусторонние куртки: когда мы переносим их из одной части уравнения в другую, они надевает куртку на другую сторону — меняют знак на противоположный.

Еще мы знаем, что если обе части уравнения поделить на одно и то же число (кроме нуля) — у нас получится равносильное уравнение. Ну есть одно и то же, только с другими цифрами.

Держим все это в голове и колдуем над неполным квадратным уравнением (производим «равносильные преобразования»): ax 2 + c = 0:

• перенесем c в правую часть: ax 2 = — c,
• разделим обе части на a: x 2 = — c/а.

Ну все, теперь мы готовы к выводам о корнях неполного квадратного уравнения. В зависимости от значений a и c, выражение — c/а может быть отрицательным или положительным. Разберем конкретные случаи.

Если — c/а 2 = — c/а не имеет корней. Все потому, что квадрат любого числа всегда равен неотрицательному числу. Из этого следует, что при — c/а 0, то корни уравнения x 2 = — c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а) 2 = — c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а) 2 = — c/а. Ура, больше у этого уравнения нет корней.

Неполное квадратное уравнение ax 2 + c = 0 равносильно уравнению х 2 = -c/a, которое:

• не имеет корней при — c/а 0.

В двух словах

Пример 1. Найти решение уравнения 8x 2 + 5 = 0.

Перенесем свободный член в правую часть:

Разделим обе части на 8:

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ: уравнение 8x 2 + 5 = 0 не имеет корней.

Как решить уравнение ax 2 + bx = 0

Осталось разобрать третий вид неполных квадратных уравнений, когда c = 0.

Неполное квадратное уравнение ax 2 + bx = 0 можно решить методом разложения на множители. Как разложить квадратное уравнение:

Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x.

Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax 2 + bx = 0 имеет два корня:

Пример 1. Решить уравнение 0,5x 2 + 0,125x = 0

Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.

Решить линейное уравнение:

0,5x = 0,125,
х = 0,125/0,5

Значит корни исходного уравнения — 0 и 0,25.

Ответ: х = 0 и х = 0,25.

Как разложить квадратное уравнение

С помощью теоремы Виета можно получить формулу разложения квадратного трехчлена на множители. Выглядит она так:

Формула разложения квадратного трехчлена

Если x₁ и x₂ — корни квадратного трехчлена ax 2 + bx + c, то справедливо равенство ax 2 + bx + c = a (x − x₁) (x − x₂).

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b 2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b 2 −4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = −b/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4x 2 + 28x — 49 = 0.

1. Найдем дискриминант: D = 28 2 — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6x 2 = 0.

Произведем равносильные преобразования. Умножим обе части на −1

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x 2 — х = 0.

Преобразуем уравнение так, чтобы появились множители

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x 2 — 10 = 39.

Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3x 2 — 4x+94 = 0.

Найдем дискриминант по формуле

D = (-4) 2 — 4 * 3 * 94 = 16 — 1128 = −1112

Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Формула корней для четных вторых коэффициентов

Рассмотрим частный случай. Формула решения корней квадратного уравнения , где D = b 2 — 4ac, помогает получить еще одну формулу, более компактную, при помощи которой можно решать квадратные уравнения с четным коэффициентом при x. Рассмотрим, как появилась эта формула.

Например, нам нужно решить квадратное уравнение ax 2 + 2nx + c = 0. Сначала найдем его корни по известной нам формуле. Вычислим дискриминант D = (2n) 2 — 4ac = 4n 2 — 4ac = 4(n 2 — ac) и подставим в формулу корней:

2 + 2nx + c = 0″ height=»705″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc11a460e2f8354381151.png» width=»588″>

Для удобства вычислений обозначим выражение n 2 -ac как D₁. Тогда формула корней квадратного уравнения со вторым коэффициентом 2·n примет вид:

где D₁ = n 2 — ac.

Самые внимательные уже заметили, что D = 4D₁, или D₁= D/4. Проще говоря, D₁ — это четверть дискриминанта. И получается, что знак D1 является индикатором наличия или отсутствия корней квадратного уравнения.

Сформулируем правило. Чтобы найти решение квадратного уравнения со вторым коэффициентом 2n, нужно:

• вычислить D₁= n 2 — ac;
• если D₁ 0, значит можно найти два действительных корня по формуле

Формула Виета

Если в школьной геометрии чаще всего используется теорема Пифагора, то в школьной алгебре ведущую роль занимают формулы Виета. Теорема звучит так:

Сумма корней x 2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

Если дано x 2 + bx + c = 0, где x₁ и x₂ являются корнями, то справедливы два равенства:

Знак системы, который принято обозначать фигурной скобкой, означает, что значения x₁ и x₂ удовлетворяют обоим равенствам.

Рассмотрим теорему Виета на примере: x 2 + 4x + 3 = 0.

Пока неизвестно, какие корни имеет данное уравнение. Но в соответствии с теоремой можно записать, что сумма этих корней равна второму коэффициенту с противоположным знаком. Он равен четырем, значит будем использовать минус четыре:

Произведение корней по теореме соответствует свободному члену. В данном случае свободным членом является число три. Значит:

Необходимо проверить равна ли сумма корней −4, а произведение 3. Для этого найдем корни уравнения x 2 + 4x + 3 = 0. Воспользуемся формулами для чётного второго коэффициента:
2 + 4x + 3 = 0″ height=»215″ src=»https://lh5.googleusercontent.com/E_X403ETh_88EANRWdQN03KRT8yxP2HO4HoCrxj__c8G0DqmNJ1KDRqtLH5Z1p7DtHm-rNMDB2tEs41D7RHpEV5mojDTMMRPuIkcW33jVNDoOe0ylzXdHATLSGzW4NakMkH2zkLE» width=»393″>

Получилось, что корнями уравнения являются числа −1 и −3. Их сумма равняется второму коэффициенту с противоположным знаком, а значит решение верное.
2 + 4x + 3 = 0″ height=»52″ src=»https://lh5.googleusercontent.com/VzGPXO9B0ZYrr9v0DpJfXwuzeZtjYnDxE_ma76PUC8o7jVWwa8kZjTJhq2Lof0TiJXAp_ny3yRwI_OyRzeucv9xUZ63yoozGPP4xd4OxvElVT7Pt-d6xL5w17e_mQNs5qZJQiwfG» width=»125″>

Произведение корней −1 и −3 по теореме Виета должно равняться свободному члену, то есть числу 3. Это условие также выполняется:
2 + 4x + 3 = 0″ height=»52″ src=»https://lh4.googleusercontent.com/Cq-LCFmY3YGNSan1VF3l3CqIeojoJYAvGAiTBWnzyoZu_xJFrF5NfQ3xCe59apJklw6uYbmQ4lAkBTeC-TJmEGicN3rgGtsezhuqdNiOWjZT39NziOB5uOmQr3cr9-5fNnepdZDo» width=»112″>

Результат проделанных вычислений в том, что мы убедились в справедливости выражения:

Когда дана сумма и произведение корней квадратного уравнения, принято начинать подбор подходящих корней. Теорема, обратная теореме Виета, при таких условиях может быть главным помощником. Вот она:

Обратная теорема Виета

Если числа x₁ и x₂ таковы, что их сумма равна второму коэффициенту уравнения x 2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа и есть корни x 2 + bx + c = 0.

Обычно вся суть обратных теорем в том самом выводе, которое дает первая теорема. Так, при доказательстве теоремы Виета стало понятно, что сумма x₁ и x₂ равна −b, а их произведение равно c. В обратной теореме это и есть утверждение.

Пример 1. Решить при помощи теоремы Виета: x 2 − 6x + 8 = 0.

Для начала запишем сумму и произведение корней уравнения. Сумма будет равна 6, так как второй коэффициент равен −6. А произведение корней равно 8.

2 − 6x + 8 = 0″ height=»59″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc101ce2e346034751939.png» width=»117″>

Когда у нас есть эти два равенства, можно подобрать подходящие корни, которые будут удовлетворять обоим равенствам системы.

Чтобы проще подобрать корни, нужно их перемножить. Число 8 можно получить путем перемножения чисел 4 и 2 либо 1 и 8. Но значения x₁ и x₂ надо подбирать так, чтобы они удовлетворяли и второму равенству тоже.

Можно сделать вывод, что значения 1 и 8 не подходят, так как они не удовлетворяют равенству x₁ + x₂ = 6. А значения 4 и 2 подходят обоим равенствам:

Значит числа 4 и 2 — корни уравнения x 2 − 6x + 8 = 0. p>

Упрощаем вид квадратных уравнений

Если мы ходили в школу всегда одной тропинкой, а потом вдруг обнаружили путь короче — это значит теперь у нас есть выбор: упростить себе задачу и сократить время на дорогу или прогуляться по привычному маршруту.

Так же и при вычислении корней квадратного уравнения. Ведь проще посчитать уравнение 11x 2 — 4 x — 6 = 0, чем 1100x 2 — 400x — 600 = 0.

Часто упрощение вида квадратного уравнения можно получить через умножение или деление обеих частей на некоторое число. Например, в предыдущем абзаце мы упростили уравнение 1100x 2 — 400x — 600 = 0, просто разделив обе части на 100.

Такое преобразование возможно, когда коэффициенты не являются взаимно простыми числами. Тогда принято делить обе части уравнения на наибольший общий делитель абсолютных величин его коэффициентов.

Покажем, как это работает на примере 12x 2 — 42x + 48 = 0. Найдем наибольший общий делитель абсолютных величин его коэффициентов: НОД (12, 42, 48) = 6. Разделим обе части исходного квадратного уравнения на 6, и придем к равносильному уравнению 2x 2 — 7x + 8 = 0. Вот так просто.

А умножение обеих частей квадратного уравнения отлично помогает избавиться от дробных коэффициентов. Умножать в данном случае лучше на наименьшее общее кратное знаменателей его коэффициентов. Например, если обе части квадратного уравнения

умножить на НОК (6, 3, 1) = 6, то оно примет более простой вид x 2 + 4x — 18 = 0.

Также для удобства вычислений можно избавиться от минуса при старшем коэффициенте квадратного уравнения — для этого умножим или разделим обе части на −1. Например, удобно от квадратного уравнения −2x 2 — 3x + 7 = 0 перейти к решению 2x 2 + 3x — 7 = 0.

Связь между корнями и коэффициентами

Мы уже запомнили, что формула корней квадратного уравнения выражает корни уравнения через его коэффициенты:

Из этой формулы, можно получить другие зависимости между корнями и коэффициентами.

Например, можно применить формулы из теоремы Виета:

Для приведенного квадратного уравнения сумма корней равна второму коэффициенту с противоположным знаком, а произведение корней — свободному члену. Например, по виду уравнения 3x 2 — 7x + 22 = 0 можно сразу сказать, что сумма его корней равна 7/3, а произведение корней равно 22/3.

Можно активно использовать уже записанные формулы и с их помощью получить ряд других связей между корнями и коэффициентами квадратного уравнения. Таким образом можно выразить сумму квадратов корней квадратного уравнения через его коэффициенты:

Формулы корней квадратных уравнений, разложение на множители

В разных практических деятельностях человека вроде физики, инженерии, архитектуры и других точных наук, часто встречаются задачи с математическими моделями, какой являются уравнения, имеющие переменную (x) в иной степени. Именно они помогают учёным в изучении внешней среды и её использовании.

Квадратные уравнения

Квадратным называется равенство вида ax² + bc + c = 0, где x является переменой, a (первый коэффициент), b (второй) и c (свободный) — это действительные числа, которые должны приводить в условии задачи. Нужно помнить при решении, что a ≠ 0. Как уже понятно, оно очень отличается от линейного уравнения, его все изучали в младших классах школы.

Чтобы понять, как решать квадратные уравнения, нужно представить футбольное поле, длина которого на 10 метров больше его ширины, а площадь равна 380 квадратных метров. Нужно найти ширину футбольного поля.

Пусть переменная x — это определённая ширина, тогда её длина будет (х +10) метров. Потом x * (x + 10) = 380, ведь дана площадь 380 квадратных метров в условии задачи, то есть x² + 10x 380 равно нулю. Здесь а = 1, b = 10, а c = -375 Это был один из примеров квадратных равенств.

Различают два вида уравнений:

• Приведённые — это случай, когда в квадратном равенстве a = 1.
• Непривёденные если a ≠ 1.

При этом x² — приведённое, а уже при 5x² оно станет непривёденным.

Понятие дискриминант

Существует определенная система решения таких уравнений. Чтобы найти чётный корень такого равенства, достаточно запомнить приведённую ниже формулу квадратного уравнения.

Буква D — это дискриминант. Звучит сложно, но не стоит пугаться, ведь с латинского языка слово переводится, как разность. Он равен: D = b² 4 ac. Следуя этому, можно записать, что (2ax + b)² = D. Есть определенные правила, как надо решать дискриминант:

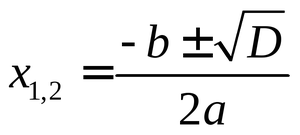• Если D меньше нуля, то действительных корней нет.
• В случае когда D равняется нулю, в решении получается только один действительный корень, но есть редкие случаи с двумя, то есть можно писать при решении в формуле либо +, либо -.
• Если D больше нуля, то в уравнении два действительных корня, то есть и плюс, и минус. Но чтобы укоротить решение достаточно записать ±, вместо двух вариантов решения задачи.

Пример первого способа нахождения через формулу дискриминанта квадратного уравнения и правильным разложением чисел:

• 9х²-6х+1=0,
• D = (-6)² 4 × 9 ×1 = 0,
• D эквивалентен нулю,
• x = -6/2×9 = 1/3.

Как пример можно показать уравнивание: -8x² = 0, у которого b и с равны нулю. Или 2x² 3 = 0, b ничему не равно. В уравнении -7x² + 4x² = 0 c эквивалентно нулю.

Разные квадратные уравнения

Помимо обычных дискриминантов, есть и половинные. Их ищут для равенств, у которых второй коэффициент — это чётное число, по формуле: D1 = 4 k² 4 ac = 4 (k² ac). Чтобы делать меньше ошибок, лучше использовать формулу со скобками. Благодаря этому в ответе получается четверть дискриминанта.

Квадратные равенства с комплексными переменными почти ничем не отличаются от плоскости действительных чисел и тем, которые должны проходить в восьмых классах. И чтобы без проблем их решать, нужно использовать формулу.

Если в квадратном равенстве хотя бы один из общих коэффициентов квадратного трехчлена B или C равен нулю, то такое равенство называют неполным.

Следовательно оно бывает только трёх видов:

• Уравнение вида ax² равно нулю. Поскольку а ≠ 0, имеем случай, когда x² = 0, корнем которого есть число ноль. Как уже понятно, имеется единственный корень х равен нулю.
• ax² + c равно нулю, тогда с не будет равняться нулю. Чтобы это лучше понять, приводится уравнение ах² = -c, x² = -c/a. Поскольку c ≠ 0 тогда и -с/а также не равно нулю. Если -с/а больше нуля, то получается два корня: х1 = корень из -с/а и ещё х2 = корень из с/а. Также можно написать вместо минуса и плюса одно уравнение из знаком: ±. Возможен случай, когда ситуация является обратной (-с/а &lt, 0), тогда корней совсем нет. Пример: -2х² + 50 равняется нулю. -2х²= -50, х² = 25, х1,2 = ±5.
• ах² + bx = 0, и при этом b нулю не равно. Разложим левую часть уравнения на множители и решим полученное х * (ах + b) = 0. Ответ: x равен нулю или ax + b = 0, но x = -b/a, поскольку a ≠ 0. В итоге должно выйти два корня: х1 = 0 и х2 = -b/a. Один из примеров: 2х² + 5х эквивалентен нулю, х(2х+ 5) = 0, х= 0 или 2х + 5 = 0. На данный момент очевидно, что x2 = -2,5 и х1 эквивалентен нулю.

Из истории математики

Неполные квадратные равенства и некоторые виды неизвестных корней вавилонские математики умели решить и создать ещё 4000 лет тому назад. Такие произведения в Древней Греции решали тем же способом. Люди, обладающие знаниями точных наук, решали некоторые квадратные уравнения геометрическими приёмами.

Это показал древнегреческий учёный Диофант. Много внимания таким уравнениям также выделял арабский математик Мухаммед Альхорезми. Он нашёл как решать уравнение видов: ах²=bx, ax²=c, ax²+bx=c, ax²+c=bx, bc+c=ax² и получил положительные корни.

Формулы, что связывают между собой корни равенства и его коэффициенты, впервые нашёл французский математик Франсуа Виет в 1591 году. Его заключения в современных обозначениях имеют вид: (а + b)x x² = 0.

После быстрой публикации работы нидерландского математика Жераром, а также француза Декарда и англичанина Ньютона равенство корней квадратного уравнения приобрело современный вид.

Уравнения	х1 и х2	х1+х2	х1×х2
х² -6х + 8 = 0	2 и 4	6	8
x²+x-12=0	-4 и 3	-1	-12
x²-4x-5=0	-3 и -2	-5	6
x²-4x-5=0	-1 и 5	4	-5

Сейчас речь идёт о теореме Виета, на которую нужно обратить внимание. Её так называют из-за известного французского математика Франсуа Виета, которым и было открыто это свойство. Сумма корней сведенного квадратного равенства равно другому коэффициенту, взятому с отрицательным знаком, а произведение корней — свободному члену. Часто его записывают в таком виде: х² + px + q эквивалентно нулю.

Теорему можно сформулировать так.

Если х1 и х2 — корни сведенного квадратного равенства х²+px+q эквивалентны нулю, то х1 + х2 = -p, x1 * x2 = q. Поскольку a ≠ 0, поделим две части уравнения на а и получается современная формула: x² b/a * x + c/a равно нулю.

Квадратное уравнение с чётным вторым коэффициентом

Если в квадратном уравнении ax 2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D₁ = k 2 − ac , а корни по формулам и .

Примеры

Решим квадратное уравнение x 2 + 6x − 16 = 0 . В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k .

Любое четное число n можно представить в виде произведения числа 2 и числа k , то есть 2k .

Например, число 10 можно представить как 2 × 5 .

В этом произведении k = 5 .

Число 12 можно представить как 2 × 6 .

В этом произведении k = 6 .

Число −14 можно представить как 2 × (−7)

В этом произведении k = −7 .

Как видим, сомножитель 2 не меняется. Меняется только сомножитель k .

В уравнении x 2 + 6x − 16 = 0 вторым коэффициентом является число 6 . Это число можно представить как 2 × 3 . В этом произведении k = 3 . Теперь можно воспользоваться формулами для чётного коэффициента.

Найдем дискриминант по формуле D₁ = k 2 − ac

Теперь вычислим корни по формулам: и .

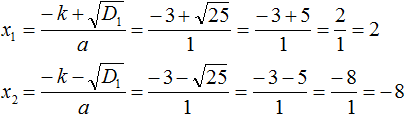
Значит корнями уравнения x 2 + 6x − 16 = 0 являются числа 2 и −8 .

В отличие от стандартной формулы для вычисления дискриминанта ( D=b 2 − 4ac ), в формуле D₁ = k 2 − ac не нужно выполнять умножение числа 4 на ac .

И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.

Пример 2. Решить квадратное уравнение 5x 2 − 6x + 1=0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3) . То есть k = −3 . Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

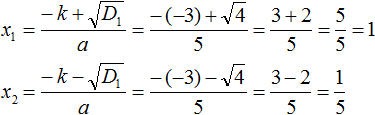
Пример 3. Решить квадратное уравнение x 2 − 10x − 24 = 0

Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5) . То есть k = −5 . Найдём дискриминант по формуле D₁ = k 2 − ac

Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

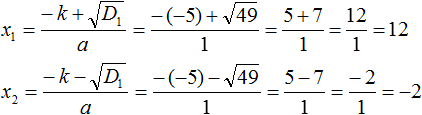
Обычно для определения числа k поступают так: делят второй коэффициент на 2.

Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2 k . Чтобы из этого равенства выразить сомножитель k , нужно произведение b разделить на сомножитель 2

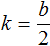
Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2

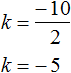
Пример 5. Решить квадратное уравнение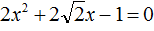

Коэффициент b равен 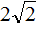. Это выражение состоит из множителя 2 и выражения 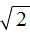. То есть оно уже представлено в виде 2k . Получается, что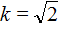

Найдём дискриминант по формуле D₁ = k 2 − ac

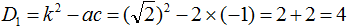
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и

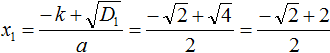
При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2. Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.

В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .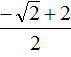

Вычислим второй корень уравнения:

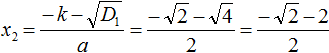
Вывод формул

Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.

Рассмотрим квадратное уравнение ax 2 + bx + c = 0 . Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k

Заменим в уравнении ax 2 + bx + c = 0 коэффициент b на выражение 2k

Теперь вычислим дискриминант по ранее известной формуле:

Вынесем в получившемся выражении за скобки общий множитель 4

Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k 2 − ac .

В выражении 4(k 2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k 2 − ac . Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.

То есть выражение k 2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D₁

Теперь посмотрим как выводятся формулы и .

В нашем уравнении ax 2 + bx + c = 0 коэффициент b заменён на выражение 2k . Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k . Также на забываем, что D у нас равно выражению 4(k 2 − ac)

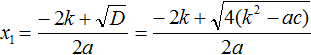
Но ранее было сказано, что выражение k 2 − ac обозначается через D₁ . Тогда в наших преобразованиях следует сделать и эту замену:

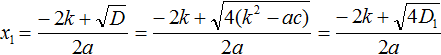
Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:

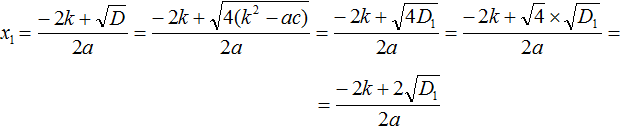
Теперь в получившемся выражении вынесем за скобки общий множитель 2

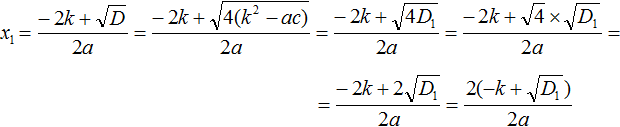
Сократим получившуюся дробь на 2

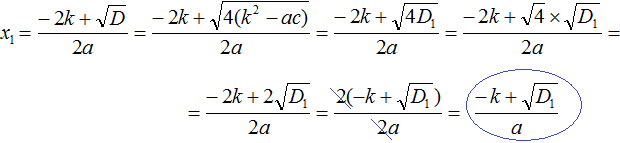
Аналогично вывóдится формула для вычисления второго корня:

В 8 классе по алгебре начинают изучать квадратные уравнения и самый популярный способ их решения –  через дискриминант. Формула вычисления дискриминанта известна

   

Дискриминант в математике используется чтобы определить сколько корней в уравнении — 1 корень, 2 корня или действительных корней нет. В этой статье определим, что такое дискриминант и выведем формулу дискриминанта.

Определение

Определим что такое дискриминант и зачем он нужен в математике, а также как его рассчитать.

Дискриминантом называют число, описывающее свойство коэффициентов квадратного многочлена. Хотя есть дискриминанты и кубических многочленов.

По этому числу определяют характер корней уравнения, полученному если многочлен приравнять к нулю. Так, если дискриминант больше нуля, то уравнение будет иметь два корня, равен нулю, то 1 корень, а если будет меньше нуля, то корней не будет.

Дискриминант (определение) помогает определить наличие или отсутствие корней квадратного уравнения, не решая его.

Обозначается дискриминант квадратного уравнения буквой или знаком Δ. И находится по формуле:

D=b^2-4ac , где

, и  — коэффициенты уравнения:

ax^2+bx+c=0

Корни через дискриминант определяются по формулам:

displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}

Пример вычисления дискриминанта:

Вычислим дискриминант в уравнении 6x^2+4x+2=0 .

По формуле находим:

D=b^2-4ac=4^2-4cdot 6 cdot 2=16-48=-32

Мы получили отрицательный дискриминант, значит, данное уравнение не имеет действительных корней. Действительно, так как корни квадратного уравнения находят по формулам:

displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}

Подставим значения для исходного уравнения:

displaystyle x_1=frac{-4-sqrt{-32}}{12} и displaystyle x_2=frac{-4+sqrt{-32}}{12}

Как видим, мы никак не сможем посчитать корни — у нас отрицательное число под знаком радикала. И, действительно, если вы построите график функции f (x)=6x^2+4x+2 — он нигде не пересечет ось , то есть ни при каком мы не получим ноль.

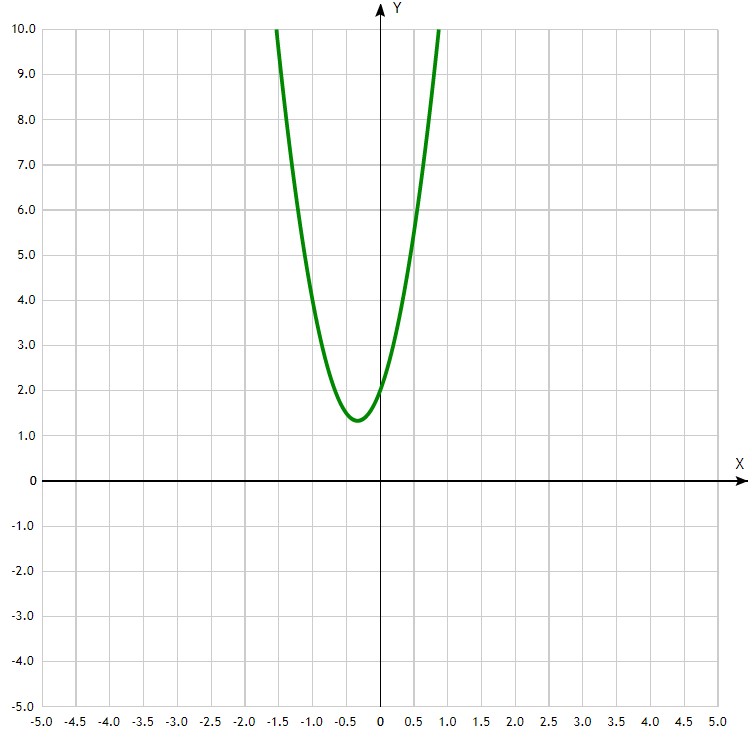
Геометрический смысл дискриминанта

Что означает дискриминант на графике, каков его геометрический смысл? Графически дискриминант квадратного уравнения характеризует расстояние по оси абсцисс между точкой — вершиной параболы (парабола — график квадратичной функции) и точкой пересечения графика с осью абсцисс. Посмотрите на рисунок. На нем видно:

1. Если дискриминант равен нулю (D=0), это значит, что вершина параболы и является точкой пересечения с осью абсцисс — расстояние между точкой пересечения и вершиной параболы равно нулю.
2. Когда D>0, то справа и слева от точки абсцисс вершины параболы на одинаковом расстоянии displaystyle frac{sqrt{D}}{2a} будут находиться точки пересечения параболы ax^2+bx+c=y, которые являются корнями уравнения ax^2+bx+c=0.
3. Когда D<0 — это означает, что точек действительных отметить на оси абсцисс нельзя, то есть от вершины отложить расстояние до точек пересечения графика с осью абсцисс невозможно, то есть этих точек пересечения нет. График не пересекает ось абсцисс и корней уравнения [katex]ax^2+bx+c=0[/katex] нет.

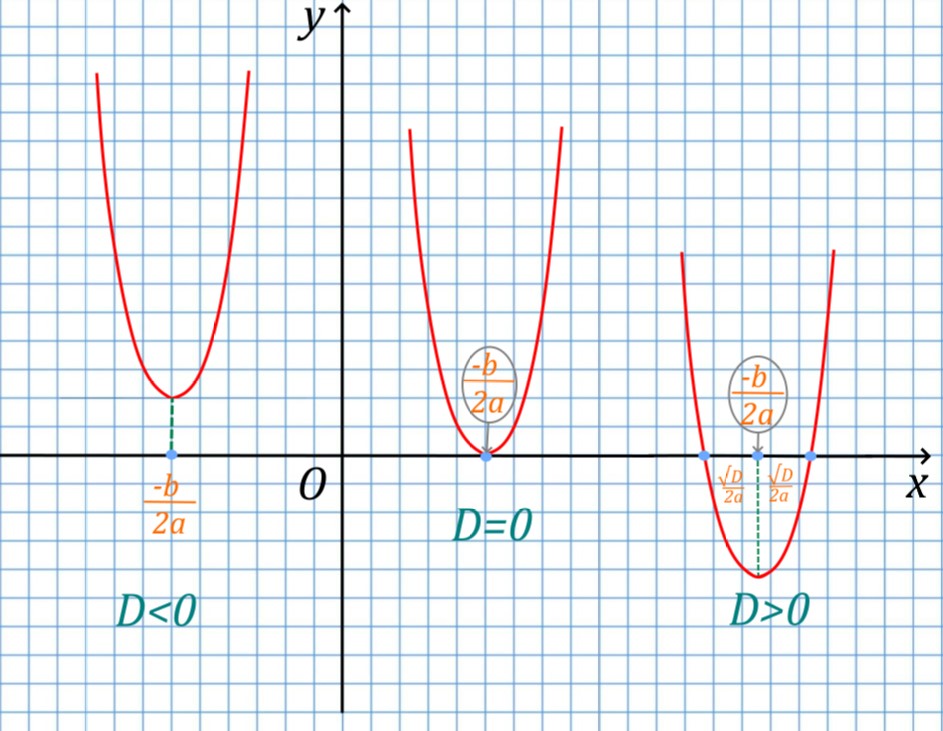
Корни квадратного уравнения через дискриминант.

Полное квадратное уравнение

Пусть нам дано уравнение вида ax^2+bx+c=0. Вычисляем дискриминант по известной формуле. Затем определяем корни уравнения.

1. Если D>0 получаем два вещественных корня displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}.
2. Если D=0 корни будут совпадать: displaystyle x_1=x_2=frac{-b}{2a}
3. Если D<0, вещественных корней нет, но есть мнимые корни или так называемые комплексные корни (обычно изучаются в курсе математического анализа в ВУЗах, хотя иногда и встречаются в алгебре 9-11 классов).

Неполное квадратное уравнение

Неполным называется такое квадратное уравнение, когда один из коэффициентов такого уравнения равен нулю.

1. Пусть коэффициент a=0, тогда уравнение сводится к линейному уравнению вида kx+b=0 и уже не будет считаться неполным.
2. Если равны нулю два коэффициента: 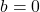и 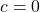, тогда 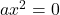. Решением такого уравнения будет: .
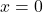3. Если равен нулю коэффициент b, то имеем D=-4ac и displaystyle x_1= frac{sqrt{D}}{2a} и displaystyle x_2= -frac{sqrt{D}}{2a}.
4. При равенстве нулю свободного члена c=0 имеем D=b^2 и displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}.

Приведенное квадратное уравнение

Приведенным квадратным уравнением называется такое уравнение вида , в котором старший коэффициент равен a=1. Оно решается обычно по теореме Виета.

Дискриминант находится по формуле: .

Если второй коэффициент кратен 2

Если коэффициент b можно разделить на 2 (с четным вторым коэффициентом), то тогда вычисляется не полный дискриминант, а displaystyle frac{D}{4} по формуле:

displaystyle frac{D}{4}=left ( frac{b}{2} right)^2-ac,

а корни: displaystyle x_1=frac{-frac{b}{2}-sqrt{frac{D}{4}}}{a} и второй корень displaystyle x_2=frac{-frac{b}{2}+sqrt{frac{D}{4}}}{a}.

Примеры нахождения корней уравнения с помощью дискриминанта

Пример 1

Решим уравнение: 4x^2+5x-5=0

Находим дискриминант: D=25-4 cdot 4 cdot (-5)=25+80=105

Пример 2

Сколько корней в данном уравнении 2x^2-3x+6=0?

Для ответа на этот вопрос необходимо найти дискриминант:

D=3^2-4 cdot 2 cdot 6=9-48=-39
D<0[/katex] — действительных корней нет.</p> <h3>Пример 3</h3> <p>[katex]x^2-6x-72=0 — найти корень.
D=b^2-4ac=(-6)^2-4 cdot (-72)=36+288=324

Так как , имеем два корня:

displaystyle x_1=frac{6-sqrt{324}}{2},      x_2=frac{6+sqrt{324}}{2}
displaystyle x_1=frac{6-18}{2}=-6,      x_2=frac{6+18}{2}=12   

Пример 4

Решить неполное уравнение

x^2-4=0

Способ 1

Разложим левую часть по формуле разность квадратов:

(x-2)(x+2)=0

Тогда корни:

x_1=-2,  x_2=2

Способ 2

Решим задачу с помощью дискриминанта: , тогда displaystyle x_1=sqrt{D}/2=sqrt{16}/2=4/2=2,

displaystyle x_2=-sqrt{D}/2=-sqrt{16}/2=-4/2=-2

Пример 5

Придумайте такое квадратное уравнение, в котором будет нулевой дискриминант.

Решение:

Так как формула дискриминанта: D=b^2-4ac, то выберем любые коэффициенты и , а найдем, если приравняем D=b^2-4ac к нулю.

Пусть , a , тогда displaystyle D=4^2-4cdot 7cdot c=0
4^2-4cdot 7cdot c=0
16-28c=0
-28c=-16 Разделим левую и правую части на -4.

7c=4
displaystyle c=frac{4}{7}

И, получаем: displaystyle 7x^2+4x+frac{4}{7}=0

Ответ: displaystyle 7x^2+4x+frac{4}{7}=0

Выводы

Самое важное, что надо запомнить, это формулу:

D=b^2-4ac

и как определяются корни квадратного уравнения:

displaystyle x_1=frac{-b-sqrt{D}}{2a} и displaystyle x_2=frac{-b+sqrt{D}}{2a}

Можно забыть, как определяются корни в разных видах квадратных уравнений, неполных, приведенных, но если вы знаете главное — как определяется дискриминант и корни в полном квадратном уравнении, то вы сможете решить любое уравнение второй степени.

Доброго времени суток, дорогие любители математики! Предлагаю Вам сегодня еще раз разобраться, как решать квадратные уравнения. Думаю, для многих читателей данный вопрос покажется простым, но сможете ли Вы навскидку назвать семь способов? А их, конечно, больше! Думаю, другие способы вспомните в комментариях.

Кстати, о комментариях! Там я часто вижу вопрос: «Почему Вы игнорируете формулы Виета?». Мне кажется, что на широкую аудиторию стоит транслировать наиболее простой способ — решение через дискриминант. Он понятный, его все помнят, а значит смогут разобраться в решении [и дочитают статью ;)].

Всем известно, что квадратное уравнение имеет вид:

Коэффициенты a, b и c здесь — это некоторые числа, а x — неизвестная. Для решения квадратного уравнения придумали общие формулы, понятные и простые.

Способ первый. Дискриминант.

Для решения квадратного уравнения через дискриминант его нужно вычислить:

А затем найти корни:

Все супер просто! Берем числа, получаем результат.

Пример:

Способ первый с половиной. Дискриминант, деленный на четыре.

Существует еще одна формула — для случая, когда второй коэффициент четный. Выведем ее:

Как видите, для четного коэффициента двойка будет всегда сокращаться, поэтому говорят о дискриминанте, деленном на четыре:

А корни будут находиться по такой формуле:

Проверим на нашем примере:

Корни сошлись, работает!

Способ второй. Выделение полного квадрата.

Формулы для дискриминанта очень занятные, но откуда они взялись?

Вернемся к началу:

Поделим все уравнение на a:

А дальше начнем шаманить. Мы хотим собрать полный квадрат по формуле сокращенного умножения:

В нашем уравнении на первом месте стоит x². На втором должно находиться удвоенное произведение. Создадим двойку искусственно, умножив и поделив на нее одномоментно:

Теперь у нас есть произведение двойки, x и некоторого числа. Для того чтобы получить формулу квадрата суммы прибавим это “некоторое число” в квадрате и сразу вычтем, дабы сумма не изменилась:

Все готово для формулы сокращенного умножения:

Перенесем все числа в правую часть:

Приведем к общему знаменателю:

Извлечем корень [считаем, что мы можем это сделать]:

Выразим икс и посмотрим, что же у нас получилось:

Да это же и есть формула из предыдущего способа!

Рассмотрим на примере:

Нам повезло и здесь двойка уже есть в наличии. Выделим полный квадрат:

Соберем полный квадрат:

Согласитесь, в числах выглядит гораздо проще и приятнее! Двигаемся дальше.

Способ третий. Разложение на множители.

Тут даже не буду пытаться сделать общие выкладки. Просто берем и раскладываем, как учили в восьмом классе.

Добавим «лишний» икс, получится:

Из первых двух слагаемых вынесем икс, из оставшихся — минус:

Вынесем за скобки общий множитель:

Произведение равно нулю, когда хотя бы один из множителей равен нулю:

Просто и надежно!

Способ четвертый. Формулы Виета.

Мы можем разложить квадратное уравнение на множители (как в прошлом способе). Получим такую картину:

Раскроем скобки:

Получили соответствие коэффициентам исходного уравнения:

Или, в привычном виде:

Удобнее всего пользоваться этими формулами, когда a = 1.

Приведем пример:

Здесь все еще можно воспользоваться дискриминантом, но вычисления будут некрасивые. Поэтому запишем формулы Виета:

Осталось подобрать корни. Для этого разложим 98 на множители:

Если первый способ разложения ничего не дает [ 2 + 49 = 51 ≠ 21]. То второй вариант дает нам корни:

Нахождение корней уравнения по формулам Виета — это простой и быстрый способ, всем рекомендую!

Способ пятый. Метод переброски.

Данный способ — эффективная модификация предыдущего способа для случая, когда a ≠ 1. Возьмем квадратное уравнение в общем виде:

И умножим все на a:

Введем замену:

Получим новое квадратное уравнение:

Таким образом мы как бы перебросили a к c. Теперь корни легко найдутся по формулам Виета. А для того, чтобы найти корни исходного уравнения, поделим найденные корни на a:

Приведем пример:

Произведем переброску:

О, а эти корни мы уже знаем:

Найдем иксы:

На мой взгляд, неплохо. Для участников олимпиад — обязательно к изучению.

Способ шестой. По свойствам коэффициентов.

Здесь все просто. Нужно запомнить, если:

То корни будут:

При этом второй корень мы нашли по формулам Виета.

И второе важное свойство, если:

То корни:

Список свойств не исчерпывающий, но другие свойства сильно сложнее, поэтому не будем их приводить.

В этот раздел также можно отнести старый добрый подбор корней.

Пример:

Здесь уже никакими дискриминантам и перебросками не поможешь. Но если заметить, что:

То сразу запишем:

Способ седьмой. Графический.

Есть два возможных варианта решения и оба имеют не очень хорошую точность. Во-первых, можно представить квадратное уравнение в виде:

И изобразить на координатной плоскости два графика: параболу и прямую.

Приведем пример:

Изобразим графики:

Получаем корни:

Конечно, график построенный автоматически позволяет достаточно точно углядеть корни. Но если у вас под рукой компьютер, то легче будет воспользоваться калькулятором и посчитать их. А вот изобразив график на бумаге определить корни будет сложно.

Разберем еще один графический вариант решения. На этот раз с помощью окружности.

Возьмем на оси абсцисс точки B ( x₁ ; 0 ) и C ( x₂ ; 0 ).

Посередине, между этими точками, будет находиться точка F, с координатами:

По формулам Виета:

На оси ординат возьмем точки A ( 0 ; 1 ) и D ( 0 ; c / a ). Посередине между ними будет находиться точка:

Точка S будет центром окружности:

Пусть O начало координат. Тогда OB · OC=OA · OD :

Таким образом для x₁ и x₂ выполняются формулы Виета.

Приведем пример:

Центр окружности будет иметь координаты:

Проведем окружность через точку A ( 0 ; 1 ) :

Получаем точки B ( 2 ; 0 ) и C ( 3 ; 0 ). А значит:

Как видите — способ рабочий, но опять же требует точности, которую на бумаге получить достаточно трудно.

Существует еще способ решения с помощью номограммы. Про него говорят “незаслуженно забытый”. Но на мой взгляд он забыт абсолютно заслуженно, так как преимуществ у него особых нет, а понять его сложнее, чем решение через дискриминант.

На практике я чаще всего использую формулы Виета и дискриминант. А какими способами пользуетесь Вы?

Спасибо за внимание и удачи!

Если вам понравилась статья, то ставьте лайк и подписывайтесь на канал. Математики будет много!