Как найти половину цены деления в физике

В этом задании вы должны записать результат измерения с учетом погрешности

Измерения в физике могут быть прямые и косвенные. При прямом измерении вы снимаете показания с самого прибора. Например, вы зафиксировали, что градусник показывает 25 градусов, это прямое измерение

При косвенных измерениях искомая величина рассчитывается по формуле. Например, книга имеет толщину 5 см и содержит 200 страниц. Тогда толщину одной страницы можно рассчитать поделив 5 на 200 (предполагаем, что обложки книги имеют такую же толщину, как и страницы)

Задание №22 из ЕГЭ посвящено этим двум видам измерений. Как правило ученики относятся к этому заданию несерьезно и считают, что нужно уметь только определять цену деления. Однако они наполнены подводными камнями, на которые многие натыкаются и теряют баллы. В данной статье разберемся с проблемами, с которыми сталкиваются ученики в этом задании

ПРОБЛЕМА №1.

Вы не знаете, где взять погрешность измерений.

Информация о том, какую брать погрешность, всегда есть в самом задании. Погрешность может быть:

1. Равна цене деления
2. Равна половине цены деления
3. В явном виде указана в самом задании (см. Рисунок 1)

ПРОБЛЕМА №2.

Вы банально не умеете записывать ответ на это задание в бланк.

Показания и погрешность нужно записать в бланк без знака ± и без пробелов. Пример смотри на Рисунке 2

ПРОБЛЕМА №3.

Вы не знаете, что результат измерения необходимо округлить до того же десятичного знака, что и погрешность.

То есть, если у погрешности 2 знака после запятой (разряд – сотые), а у измерения 1 знак (разряд – десятые), то измерению необходимо в конце добавить 0, чтобы его разряд был такой же. Смотри Рисунок 3

ПРОБЛЕМА №4.

Прибор имеет несколько шкал, и вы не знаете по какой смотреть.

Информация об этом также находится в самом задании, главное внимательно его прочитать. Примеры смотри на Рисунке 4

ПРОБЛЕМА №5.

В задачах на косвенные измерения вы не производите с погрешностью те же действия, что и с измерением.

Если вы рассчитываете величину по формуле (косвенно), то с погрешностью необходимо проводить те же действия, что и с измерением. Смотри пример на Рисунке 5

Теперь ты точно не ошибешься в этом задании и наберешь свою сотку!

Если было полезно, поставь лайк и подпишись на блог, будет еще много интересного!

Цена деления – это расстояние между двумя ближайшими делениями на нём (в термометре обычно градус) , а погрешность – это половина цены деления (т. е. полградуса)
чтобы определить цену деления, нужно взять 2 деления шкалы, возле которых стоят цифры, из большего числа вычесть меньшее и разделить на количество делений между этими цифрами.
Погре́шность измер́ния — оценка отклонения величины измеренного значения величины от её истинного значения. Погрешность измерения является характеристикой (мерой) точности измерения. Погрешность измерения равна половине цены деления прибора

ПРЯМОЕ ИЗМЕРЕНИЕ- определение значения физ. величины непосредственно средствами измерения. Косвенное измерение-определение значения физ. величины по формуле, связывающей её с другими физич. величинами, определяемыми прямыми измерениями.
Расчет, погрешностей по формулам см. http://ru.wikipedia.org/wiki/

Содержание:

При измерении разных физических величин мы получаем их числовые значения с определенной точностью. Например, при определении размеров листа бумаги (длины, ширины) мы можем указать их с точностью до миллиметра; размеры стола – с  точностью до сантиметра, размеры дома, стадиона – с точностью до метра.

Нет необходимости указывать размеры стола с точностью до миллиметра, а размеры стадиона с точностью до сантиметра или миллиметра. Мы сами в каждой ситуации, опыте и эксперименте определяем, с какой точностью нам нужны данные физические величины. Однако очень важно оценивать, насколько точно мы определяем физическую величину, какую ошибку (погрешность) в ее измерении допускаем.

При измерении мы не можем определить истинное значение измеряемой величины, а только пределы, в которых она находится.

Пример:

Измерим ширину стола рулеткой с сантиметровыми и миллиметровыми делениями на ней (рис. 5.1). Значение наименьшего деления шкалы называют ценой деления и обозначают буквой С. Видно, что цена деления рулетки С = 1 мм (или 0,1 см).

Совместим нулевое деление рулетки с краем стола и посмотрим, с каким значением 
шкалы линейки совпадает второй край стола  (рис. 5.1). Видно, что ширина стола составляет чуть больше 70 см и 6 мм, или 706 мм. Но результат наших измерений мы запишем с точностью до 1 мм, то есть L = 706 мм.

Абсолютная погрешность измерения ∆ (ДЕЛЬТА)

Из рис. 5.1 видно, что мы допускаем определенную погрешность и определить ее «на глаз» достаточно трудно. Эта погрешность составляет не более половины цены деления шкалы рулетки. Эту погрешность называют погрешностью измерения и помечают ∆L («дельта эль»). В данном эксперименте ее можно записать

Сам результат измерения принято записывать таким образом: ширина стола L = (706,0 ± 0,5) мм, читают: 706 плюс-минус 0,5 мм. Эти 0,5 мм в нашем примере называют абсолютной погрешностью. Значения измеряемой величины (706,0 мм) и абсолютной погрешности (0,5 мм) должны иметь одинаковое количество цифр после запятой, то есть нельзя записывать 706 мм ± 0,5 мм.  

Такая запись результата измерения означает, что истинное значение измеряемой величины находится между 705,5 мм и 706,5 мм, то есть 705,5 мм ≤ L ≤ 706,5 мм.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения 
измеряемой величины. Для этого разделим 0,5 мм на 706 мм. В результате получим: .  То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой  (эпсилон): 

     (5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения –  плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 0,5) мм – Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.

На точность измерения влияет много факторов, в частности:

1. При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» – смотреть можно под разными углами.
2. Не вполне ровно установили рулетку.
3. Наша рулетка является копией эталона и может несколько отличаться от оригинала.

Все это необходимо учитывать при проведении измерений.

Итоги:

• Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
• Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора. 
• Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:   и указывает на качество измерения. Ее можно выразить в процентах.

Измерительные приборы

Устройства, с помощью которых измеряют физические величины, называют измерительными приборами.

Простейший и хорошо известный вам измерительный прибор — линейка с делениями. На ее примере вы видите, что у измерительного прибора есть шкала, на которой нанесены деления, причем возле некоторых делений написано соответствующее значение физической величины. Так, значения длины в сантиметрах нанесены на линейке возле каждого десятого деления (рис. 3.11). Значения же, соответствующие «промежуточным» делениям шкалы, можно найти с помощью простого подсчета.

Разность значений физической величины, которые соответствуютближайшим делениям шкалы, называют ценой деления прибора. Ёе находят так: берут ближайшие деления, возле которых написаны значения величины, и делят разность этих значений на количество промежутков между делениями, расположенными между ними.

Например, ближайшие сантиметровые деления на линейке разделены на десять промежутков. Значит, цена деления линейки равна 0,1 см = 1 мм.

Как определяют единицы длины и времени

В старину мерами длины служили большей частью размеры человеческого тела и его частей. Дело в том, что собственное тело очень удобно как «измерительный прибор», так как оно всегда «рядом». И вдобавок «человек есть мера всех вещей»: мы считаем предмет большим или малым, сравнивая его с собой.

Так, длину куска ткани измеряли «локтями», а мелкие предметы — «дюймами» (это слово происходит от голландского слова, которое означает «большой палец»).

Однако человеческое тело в качестве измерительного прибора имеет существенный недостаток: размеры тела и его частей у разных людей заметно отличаются. Поэтому ученые решили определить единицу длины однозначно и точно. Международным соглашением было принято, что один метр равен пути, который проходит свет в вакууме за 1/299792458 с. А секунду определяют с помощью атомных часов, которые сегодня являются самыми точными.

Можно ли расстояние измерять годами

Именно так и измеряют очень большие расстояния — например, расстояния между звездами! Но при этом речь идет не о годах как промежутках времени, а о «световых годах». А один световой год — это расстояние, которое проходит свет за один земной год. По нашим земным меркам это очень большое расстояние — чтобы убедиться в этом, попробуйте выразить его в километрах! А теперь вообразите себе, что расстояние от Солнца до ближайшей к нему звезды составляет больше четырех световых лет! И по астрономическим масштабам это совсем небольшое расстояние: ведь с помощью современных телескопов астрономы тщательно изучают звезды, расстояние до которых составляет много тысяч световых лет!

Что надо знать об измерительных приборах

Приступая к измерениям, необходимо, прежде всего, подобрать приборы. Что надо знать об измерительных приборах?

Минимальное (нижний предел) и максимальное (верхний предел) значения шкалы прибора — это пределы измерения. Чаще всего предел измерения один, но может быть и два. Например, линейка имеет один предел — верхний. У линейки на рисунке 32 он равен 25 см. У термометра на рисунке 33 два предела: верхний предел измерения температуры равен +50 °С; нижний -40 °С.

На рисунке 34 изображены три линейки с одинаковыми верхними пределами (25 см). По эти линейки измеряют длину с различной точностью. Наиболее точные результаты измерений дает линейка 7, наименее точные — линейка 3. Что же такое точность измерений и от чего она зависит? Для ответа на эти вопросы рассмотрим сначала понятие цена деления шкалы прибора.

Цена деления — это значение наименьшего деления шкалы прибора.

Как определить цену деления шкалы? Для этого необходимо:

1. выбрать на шкале линейки два соседних значения, например 3 см и 4 см;
2. подсчитать число делений (не штрихов!) между этими значениями; например, на линейке 1 (см. рис. 34) число делений между значениями 3 см и 4 см равно 10;
3. вычесть из большего значения меньшее (4 см – 3 см = 1 см) и результат разделить на число делений.

Полученное значение и будет ценой деления шкалы прибора. Обозначим ее буквой С.

• Для линейки 1: 
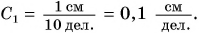
• Для линейки 2: 
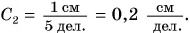
• Для линейки 3: 

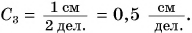
Точно так же можно определить и цену деления шкалы мензурок 1 и 2 (рис. 35). Цена деления шкалы мензурки 1:

Цена деления шкалы мензурки 2: 

А какими линейкой и мензуркой можно измерить точнее?

Измерим один и тот же объем мензуркой 1 и мензуркой 2. Но показаниям шкал в мензурке 1 объем воды V = 35 мл; в мензурке 2 — V = 37 мл.

Понятно, что точнее измерен объем воды мензуркой 2, цена деления которой меньше  Значит, чем меньше цена деления шкалы, тем точнее можно измерить данным прибором. Говорят: мензуркой 1 мы измерили объем с точностью до 5 мл (сравните с ценой деления шкалы ), мензуркой 2 – с точностью до 1 мл (сравните с ценой деления ). Точность измерения температуры термометрами 1 и 2 (рис. 36) определите самостоятельно.

Итак, любым прибором, имеющим шкалу, измерить физическую величину можно с точностью, не превышающей цены деления шкалы.

Линейкой 1 (см. рис. 34) можно измерить длину с точностью до 1 мм. Точность измерения длины линейками 2 и 3 определите самостоятельно.

Главные выводы:

1. Верхний и нижний пределы измерения — это максимальное и минимальное значения шкалы прибора.
2. Цена деления шкалы равна значению наименьшего деления шкалы.
3. Чем меньше цена деления шкалы, тем точнее будут проведены измерения данным прибором.

Для любознательных:

В истории науки есть немало случаев, когда повышение точности измерений давало толчок к новым открытиям. Более точные измерения плотности азота, выделенного из воздуха, позволили в 1894 г. открыть новый инертный газ — аргон. Повышение точности измерений плотности воды привело к открытию в 1932 г. одной из разновидностей тяжелых атомов водорода — дейтерия. Позже дейтерий вошел в состав ядерного горючего. Оценить расстояния до звезд и создать их точные каталоги ученые смогли благодаря повышению точности при измерении положения ярких звезд на небе.

• Заказать решение задач по физике

Пример решения задачи

Для измерения величины угла используют транспортир. Определите: 1) цену деления каждой шкалы транспортира, изображенного на рисунке 38; 2) значение угла BАС, используя каждую шкалу; укажите точность измерения угла ВАС в каждом случае.

Решение:

1) Цена деления нижней шкалы:

Цена деления средней шкалы: 

Цена деления верхней шкалы:

2) Определенный но нижней шкале с точностью до 10° определенный по средней шкале с точностью до 5° определенный по верхней шкале с точностью до 1°

Физические
величины. Точность и погрешность измерений

Измерять
– значит, познавать

Данная
тема посвящена физическим величина и их измерениям. В физике часто приходится
измерять те или иные величины. Измерить можно высоту дома или длину улицы.

Можно
измерить объём воды в колбе или массу воды в стакане.

Но
что означают эти измерения? Измерить какую-либо величину – значит
сравнить её с однородной величиной, принятой за единицу. Из приведённых
выше примеров, можно заметить, что, например, единицей объёма является литр,
а единицей массы является грамм. Для удобства была введена международная
система единиц, которая называется СИ.

В
этой системе длина измеряется в метрах, масса в килограммах, объём – в
кубических метрах, время – в секундах и так далее. В процессе
изучения физики будут вводиться новые величины и соответствующие им единицы
измерения. Иногда физические величины можно не измерять, а вычислять по
формуле. Например, для того, чтобы вычислить среднюю скорость нужно
пройденное расстояние разделить на время. То есть, данная формула помогает
вычислить такую физическую величину, как средняя скорость.

Известно
что, иногда применяются единицы измерения, которые в десятки, сотни, тысячи и
так далее раз больше принятых единиц измерения. Такие единицы измерения
называются кратными.

Каждая
приставка соответствует тому или иному множителю. Например, «Дека»
означает в 10 раз больше, «гекто» – в сто раз больше, «кило» –
в тысячу раз больше, «мега» – в миллион раз больше и так далее. Необходимо
отметить, что в физике принято записывать такие множители в виде степени числа
10. Например, вместо миллиона записывается 10⁶. Также, могут быть
использованы единицы, которые в десятки, сотни, тысячи и так далее раз меньше
принятых единиц измерения. Такие единицы измерения называются дольными.

Каждая
приставка соответствует тому или иному множителю. Например, «Деци»
означает в 10 раз меньше, «санти» – в сто раз меньше, «милли»
– в тысячу раз меньше, «микро» – в миллион раз меньше и так далее.
Эти приставки также записываются в виде степени числа 10. Например, вместо
записи числа 0,000001 записывается 10^–6.

У
каждого ученика имеется линейка, длина которой измеряется в сантиметрах, то
есть в единицах, которые в сто раз меньше метра. Поэтому, если длина линейки
составляет 15 сантиметров, мы можем сказать, что её длина 0,15 метра.

Линейка
– это прибор для измерения длины. Конечно, линейка относится к
самым простым измерительным приборам. Существуют значительно более сложные
приборы: например, термометр, который применяется для измерения температуры,
гигрометр, который используется для измерения влажности или амперметр, который
используется для измерения силы электрического тока.

Важно
знать, как пользоваться измерительными приборами и насколько могут быть точны
те или иные измерения. У каждого ученика есть линейка и карандаш.
Можно попытаться измерить длину карандаша. В первую очередь нужно определить,
какова цена деления измерительного прибора. Для этого необходимо найти
два ближайших штриха шкалы, возле которых указаны значения величины (например, 1 см и 2 см). Далее нужно сосчитать число делений, заключенных между цифрами 1 и 2. При подсчёте
получается, что количество этих делений равно 10. Таким образом, между
отметками 1 см и 2 см заключено десять делений. Вычитаем из большего числа
меньшее и делим на количество делений между ними. В результате вычислений
получаем, что цена деления линейки составляет 0,1 см или 1 мм. Данный пример объясняет, как определить цену деления любого
измерительного прибора.

Как
видно из рисунка, длина карандаша чуть меньше десяти сантиметров. Если бы на
этой линейке не было миллиметровых делений, то можно было сказать, что длина
карандаша равна десяти сантиметрам. Но это было бы не совсем точное
измерение. Такую неточность называют погрешностью измерения. В представленном
случае, на линейке есть миллиметровые деления, поэтому можно измерить длину
карандаша с более высокой точностью – 9,8 см. Это говорит о том, что чем меньше цена деления, тем больше точность измерения. Ну а большая точность
измерения означает меньшую погрешность. Однако абсолютно точных
измерений не существует. Если дать один и тот же карандаш каждому
ученику из класса и попросить измерить длину карандаша, не у всех получится
одинаковый результат. Тем не менее, погрешность измерения не может быть
больше цены деления. Например, если видно, что длина карандаша не точно 9,8 см, а чуточку больше, то понятно, что длина карандаша находится в промежутке от 9,8 см до 9,9 см.

Погрешность
измерений принято считать равной половине цены деления измерительного прибора. То
есть, в рассмотренном случае, погрешность измерений составляет 0,5 мм.
Поэтому, после того, как измерили карандаш и записали, что его длина равна 9,8 см, следует записать погрешность.

Знак
«±» означает, что указанная длина может быть на полмиллиметра больше или на
полмиллиметра меньше. Таким образом, истинное значение длины карандаша
находится в промежутке от 9,75 см до 9,85 см.

В
общем случае запись измеряемых величин с учетом погрешности имеет следующий
вид:

где А
– измеряемая величина;

а –
результат измерения;

Da –
погрешность измерений.

Необходимо
отметить, что при сложении или вычитании величин с погрешностью, погрешность
результата равна сумме погрешностей каждой величины. В этом легко убедиться
на примере. На рисунке показаны два отрезка AB
и
CD, длины которых измерены с определенной погрешностью.

Рассчитаем
сумму длин этих отрезков. Из рисунка видно, что отрезок AB равен 1 м ± 1 см.
Истинная длина этого отрезка находится в промежутке 99 см ≤ АВ ≤ 101 см.
Отрезок CD равен 12 см ± 0,5 см.
Истинная длина этого отрезка находится в промежутке от 11,5 см ≤ CD ≤ 12,5 см.
Поэтому, сумма длин этих отрезков будет иметь еще большую погрешность. Прежде
чем производить вычисления, необходимо перевести обе длины в одинаковые единицы
измерения.

Таким
образом, получаем, что сумма длин отрезков AB
и
CD равна

Важно
отметить, что этот же промежуток мы бы получили, если бы сложили наименьшие и
наибольшие длины отрезков AB и CD. Следовательно,
при сложении или вычитании величин, измеренных с погрешностями, погрешность
результата равна сумме погрешностей каждой из величин.

Упражнения.

Упражнение
1.
Заполните таблицу, указав, что из перечисленных слов является физическим телом,
единицей измерения, физической величиной или физическим явлением: ветер,
Луна, килограмм, дерево, длина, скорость, испарение.

Решение:

Упражнение
2.
Родители измерили рост братьев Димы и Васи с помощью рулетки, цена деления
которой 1 см. Подсчитайте, насколько см Дима выше, чем Вася.

Решение:

Упражнение
3.
Найдите суммарную массу животных с погрешностью.

Решение:

Основные
выводы:

–
Для описания физических тел или физических явлений вводится физическая
величина, которую можно измерить с помощью измерительных приборов или
вычислить по формуле.

–
Измерение величины – это сравнение её с однородной величиной, принятой
за единицу.

–
Кратные приставки – это приставки означающие увеличение в десятки,
сотни, тысячи и так далее раз.

–
Дольные приставки – это приставки, означающие
уменьшение в десятки, сотни, тысячи и так далее раз.

–
Погрешность измерений – неточность допускаемая при измерении. За
погрешность измерений данного прибора принимают половину цены деления этого
прибора.

–
При сложении или вычитании величин с погрешностями, погрешность результата
вычислений равна сумме погрешностей каждой величины.