14 декабря 2022 21:49
1066
Посмотреть ответы
b*корень из 2
считается по теореме пифагора
Можно и по теореме Пифагора. Можно и иначе. .
Вся диагональ равна 2 b
Формула диагонали квадрата d=а√2
2b=а√2
Сторона квадрата
а= 2b:√2= 2b·√2:√2·√2=2b·√2:2=b·√2
а= b√2
Еще вопросы по категории Геометрия
Высота, проведенная к основанию равнобедренного треугольника, равна 9 см, а само основание равно, 24 см. Найдите радиусы вписанной в треугольник и опи…
прямая m пересекает сторону AB треугольника ABC . Каково взаимное расположение прямых m и BC ,если : а) прямая m лежит в плоскости ABC и не имеет общи…
Найдите sin A и sin B, если АС=12, ВС=16, АВ=20. Найдите tg A и tg B, если АС=5, ВС=12.…
Осевое сечение цилиндра – квадрат, диагональ которого равна 16см. Найдите площадь и объем полной поверхности цилиндра. Заранее спасибо. Если возможно…
сторона ab треугольника abc равна 12 см Сторона BC разделена на 3 равные части и через точки деления проведены прямые,параллельные стороне AB. Найдите…
Знаток
(356),
закрыт
11 лет назад
Roma Gromak
Мастер
(1345)
11 лет назад
У квадрата все углы равны 90 градусов.
Значит прямоугольный треугольник.
Половина диагонали квадрата равна B, значит, сама диагональ равна 2B.
По теореме Пифагора
С^2=A^2+B^2
Это квадрат, значит, С^2=2A^2
2A^2=4B^2
A^2=2B^2
A= корень из 2B^2
А если быть совсем точным то сторона равна B корней из 2
Квадрат принадлежит к рангу правильных многоугольников, то есть это равносторонний четырехугольник. Являясь синтезом ромба и прямоугольника, каждый из которых в свою очередь представляет собой производную фигуру от, параллелограмма, квадрат объединяет в себе все свойства вышеперечисленных фигур.
Как это поможет найти диагональ квадрата? Рассмотрим два его основных свойства:
– Все стороны квадрата равны (от ромба)
– Все углы квадрата являются прямыми, то есть равны 90 градусам (от прямоугольника)
Если провести диагональ квадрата, то она образует с его сторонами не просто прямоугольный треугольник (как в прямоугольнике), но равнобедренный прямоугольный треугольник, который по теореме Пифагора будет связывать всего два параметра – диагональ квадрата и его сторону. Стороны квадрата будут катетами для треугольника, а диагональ гипотенузой.
a2+b2=c2
a2+b2=d2
2a2=d2
Чтобы из данного тождества вывести формулу диагонали, нужно поместить удвоенный квадрат стороны под квадратный корень, и так как сторона квадрата также возведена во вторую степень, ее можно будет сразу вынести из под корня. В итоге формула диагонали квадрата через сторону будет выглядеть как сторона квадрата, умноженная на корень из двух:
d=√(2a2)
d=a√2
Данная формула применима ко всем случаям, когда необходимо найти диагональ квадрата. При этом в задаче может быть дан не сам квадрат, а форма квадрата как осевое сечение цилиндра, например, тогда длина диагонали квадрата равна диагонали сечения.
Следует также учитывать, что точка пересечения диагоналей делит их на две равные части (свойство параллелограмма), соответственно каждый отрезок, полученный в результате пересечения диагоналей, будет равен половине диагонали квадрата.
Формулы диагонали квадрата через площадь, периметр 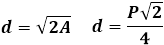
Загрузить PDF
Загрузить PDF
Диагональ квадрата — это отрезок, который соединяет противолежащие углы квадрата и проходит через его центр. Чтобы вычислить диагональ квадрата, воспользуйтесь формулой 

-

1
Найдите длину стороны квадрата. Скорее всего, значение длины стороны квадрата будет дано в условии задачи. Если же вы работаете с реальным предметом, измерьте его сторону при помощи линейки или рулетки. Так как у квадрата все стороны равны, измерьте или найдите длину любой стороны. Если длина стороны квадрата неизвестна, этим методом пользоваться нельзя.
- Например, дан квадрат со стороной 5 см.
-

2
-

3
Подставьте в формулу значение длины стороны квадрата. То есть данное значение нужно подставить вместо
.
- Например, если сторона квадрата равна 5 см, формула запишется так:
- Например, если сторона квадрата равна 5 см, формула запишется так:
-

4
Умножьте сторону квадрата на
, чтобы найти диагональ квадрата. Вычисление лучше выполнить на калькуляторе, чтобы получить точный ответ. Если калькулятора нет, округлите
до 1,414.
Реклама
-

1
-

2
Подставьте в формулу значение периметра квадрата. То есть данное значение нужно подставить вместо
.
- Например, периметр квадрата равен 20 см. Запишите формулу так:
- Например, периметр квадрата равен 20 см. Запишите формулу так:
-

3
Найдите
. Для этого разделите каждую сторону уравнения на 4. В результате будет вычислена сторона квадрата.
-

4
-

5
Подставьте в формулу значение длины стороны квадрата. То есть данное значение нужно подставить вместо
.
- Например, если сторона квадрата равна 5 см, формула запишется так:
- Например, если сторона квадрата равна 5 см, формула запишется так:
-

6
Умножьте сторону квадрата на
, чтобы найти диагональ квадрата. Вычисление лучше выполнить на калькуляторе, чтобы получить точный ответ. Если калькулятора нет, округлите
до 1,414.
Реклама
-

1
-

2
В формулу подставьте значение площади квадрата. То есть данное значение нужно подставить вместо
.
- Например, площадь квадрата равна 25 см2. Запишите формулу так:
.
- Например, площадь квадрата равна 25 см2. Запишите формулу так:
-

3
Найдите
. Для этого извлеките квадратный корень из значения площади квадрата. В результате будет вычислена сторона квадрата. Воспользуйтесь калькулятором, чтобы извлечь квадратный корень. Если квадратный корень нужно извлечь вручную, прочитайте эту статью.
-

4
-

5
Подставьте в формулу значение длины стороны квадрата. То есть данное значение нужно подставить вместо
.
- Например, если сторона квадрата равна 5 см, формула запишется так:
- Например, если сторона квадрата равна 5 см, формула запишется так:
-

6
Умножьте сторону квадрата на
, чтобы найти диагональ квадрата. Вычисление лучше выполнить на калькуляторе, чтобы получить точный ответ. Если калькулятора нет, округлите
до 1,414.
Реклама
Что вам понадобится
- Калькулятор
Об этой статье
Эту страницу просматривали 425 059 раз.
Была ли эта статья полезной?
1. Формулы диагонали квадрата через стороны, площадь, периметр
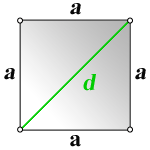
a – сторона квадрата
S – площадь квадрата
P – периметр квадрата
d – диагональ квадрата
Формулы диагонали квадрата, (d ):
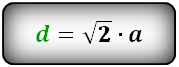
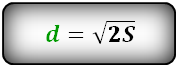
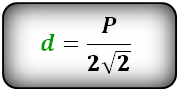
2. Формула диагонали квадрата через радиус вписанной окружности
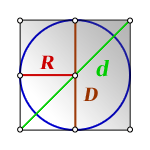
R – радиус вписанной окружности
D – диаметр вписанной окружности
d – диагональ квадрата
Формула диагонали квадрата, (d ):
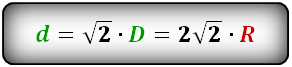
3. Формула диагонали квадрата через радиус описанной окружности
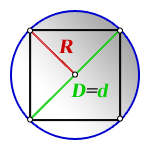
R – радиус описанной окружности
D – диаметр описанной окружности
d – диагональ
Формула диагонали квадрата, (d ):
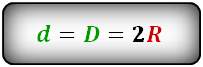
4. Формула диагонали квадрата через линию выходящую из угла на середину стороны квадрата
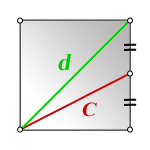
C – линия выходящая из угла на середину стороны квадрата
d – диагональ
Формула диагонали квадрата, (d ):
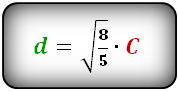
Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
- Подробности
-
Опубликовано: 19 октября 2011
-
Обновлено: 13 августа 2021


