Основные сведения
Чтобы найти площадь квадрата, нужно длину его стороны возвести во вторую степень.
Найдём площадь квадрата, длина стороны которого 3 см
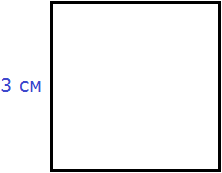
S = 32 = 9 см2
Теперь решим обратную задачу. А именно, зная площадь квадрата определим длину его стороны. Для этого воспользуемся таким инструментом как кóрень. Корень бывает квадратный, кубический, а также n-й степени.
Сейчас наш интерес вызывает квадратный корень. По другому его называют кóрнем второй степени.
Для нахождения длины стороны нашего квадрата, нужно найти число, вторая степень которого равна 9. Таковым является число 3. Это число и является кóрнем.
Введём для работы с корнями новые обозначения.
Символ кóрня выглядит как ![]() . Это по причине того, что слово корень в математике употребляется как радикал. А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня
. Это по причине того, что слово корень в математике употребляется как радикал. А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня ![]() .
.
Под корнем располагáют подкореннóе выражение. В нашем случае подкоренным выражением будет число 9 (площадь квадрата)
![]()
Нас интересовал квадратный корень (он же корень второй степени), поэтому слева над корнем указываем число 2. Это число называют показателем корня (или степенью корня)
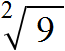
Получили выражение, которое читается так: «квадратный корень из числа 9». С этого момента возникает новая задача по поиску самогó корня.
Если число 3 возвести во вторую степень, то получится число 9. Поэтому число 3 и будет ответом:
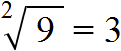
Значит квадрат площадью 9 см2 имеет сторону, длина которой 3 см. Приведённое действие называют извлечéнием квадрáтного кóрня.
Нетрудно догадаться, что квадратным корнем из числа 9 также является отрицательное число −3. При его возведении во вторую степень тоже получается число 9
![]()
Получается, что выражение ![]() имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.
имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.
Вообще, квадратный корень имеет два противоположных значения: положительное и отрицательное.
Например, извлечём квадратный корень из числа 4
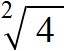
Это выражение имеет два значения: 2 и −2, поскольку при возведении этих чисел во вторую степень, получится один и тот же результат 4
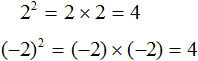
Поэтому ответ к выражению вида ![]() записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.
записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.
Запишем ответ к выражению ![]() с плюсом и минусом:
с плюсом и минусом:
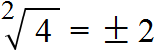
Определения
Дадим определение квадратному корню.
Квадратным корнем из числа a называют такое число b, вторая степень которого равна a.
То есть число b должно быть таким, чтобы выполнялось равенство b2 = a. Число b (оно же корень) обозначается через радикал ![]() так, что
так, что ![]() . На практике левая и правая часть поменяны местами и мы видим привычное выражение
. На практике левая и правая часть поменяны местами и мы видим привычное выражение ![]()
Например, квадратным корнем из числá 16 есть число 4, поскольку число 4 во второй степени равно 16
42 = 16
Корень 4 можно обозначить через радикал ![]() так, что
так, что ![]() .
.
Также квадратным корнем из числá 16 есть число −4, поскольку число −4 во второй степени равно 16
(−4)2 = 16
Если при решении задачи интересует только положительное значение, то корень называют не просто квадратным, а арифметическим квадратным.
Арифметический квадратный корень из числá a — это неотрицательное число b (b ≥ 0), при котором выполняется равенство b2 = a.
В нашем примере квадратными корнями из числá 16 являются корни 4 и −4, но арифметическим из них является только корень 4.
В разговорном языке можно использовать сокращение. К примеру, выражение ![]() полностью читается так: «квадратный корень из числá шестнадцать», а в сокращённом варианте можно прочитать так: «корень из шестнадцати».
полностью читается так: «квадратный корень из числá шестнадцать», а в сокращённом варианте можно прочитать так: «корень из шестнадцати».
Не следует путать понятия корень и квадрат. Квадрат это число, которое получилось в результате возведения какого-нибудь числá во вторую степень. Например, числа 25, 36, 49 являются квадратами, потому что они получились в результате возведения во вторую степень чисел 5, 6 и 7 соответственно.
Корнями же являются числа 5, 6 и 7. Они являются теми числами, которые во второй степени равны 25, 36 и 49 соответственно.
Чаще всего в квадратных корнях показатель кóрня вообще не указывается. Так, вместо записи ![]() можно использовать запись
можно использовать запись![]() . Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.
. Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.
Квадратный корень из единицы равен единице. То есть справедливо следующее равенство:
![]()
Это по причине того, что единица во второй степени равна единице:
12 = 1
и квадрат, состоящий из одной квадратной единицы, имеет сторону, равную единице:
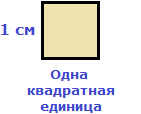
Квадратный корень из нуля равен нулю. То есть справедливо равенство ![]() , поскольку 02 = 0.
, поскольку 02 = 0.
Выражение вида ![]() смысла не имеет. Например, не имеет смысла выражение
смысла не имеет. Например, не имеет смысла выражение ![]() , поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.
, поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.
Если выражение вида ![]() возвести во вторую степень, то есть если записать
возвести во вторую степень, то есть если записать ![]() , то это выражение будет равно подкореннóму выражению a
, то это выражение будет равно подкореннóму выражению a
![]()
Например, выражение ![]() равно 4
равно 4
![]()
Это потому что выражение ![]() равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.
равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.
Еще примеры:
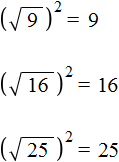
Корень из квадрата числá равен модулю этого числá:
![]()
Например, корень из числá 5, возведённого во вторую степень, равен модулю числá 5
![]()
Это же правило будет срабатывать, если во вторую степень возвóдится отрицательное число. То есть, ответ опять же станет положительным. Например, корень из числá −5, возведённого во вторую степень, равен модулю числá −5. А модуль числа −5 равен 5
![]()
Действительно, если не пользуясь правилом ![]() , вычислять выражение
, вычислять выражение ![]() обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5
обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5
![]()
Не следует путать правило ![]() с правилом
с правилом ![]() . Правило
. Правило ![]() верно при любом a, тогда как правило
верно при любом a, тогда как правило ![]() верно в том случае, если выражение
верно в том случае, если выражение ![]() имеет смысл.
имеет смысл.
В некоторых учебниках знак корня может выглядеть без верхней линии. Выглядит это так:
![]()
Примеры: √4, √9, √16.
Мéньшему числу соответствует мéньший корень, а бóльшему числу соответствует бóльший корень.
Например, рассмотрим числа 49 и 64. Число 49 меньше, чем число 64.
49 < 64
Если извлечь квадратные корни из этих чисел, то числу 49 будет соответствовать меньший корень, а числу 64 — бóльший. Действительно, √49 = 7, а √64 = 8,
√49 < √64
Отсюда:
7 < 8
Примеры извлечения квадратных корней
Рассмотрим несколько простых примеров на извлечение квадратных корней.
Пример 1. Извлечь квадратный корень √36
Данный квадратный корень равен числу, квадрат которого равен 36. Таковым является число 6, поскольку 62 = 36
√36 = 6
Пример 2. Извлечь квадратный корень √49
Данный квадратный корень равен числу, квадрат которого равен 49. Таковым является число 7, поскольку 72 = 49
√49 = 7
В таких простых примерах достаточно знать таблицу умножения. Так, мы помним, что число 49 входит в таблицу умножения на семь. То есть:
7 × 7 = 49
Но 7 × 7 это 72
72 = 49
Отсюда, √49 = 7.
Пример 3. Извлечь квадратный корень √100
Данный квадратный корень равен числу, квадрат которого равен 100. Таковым является число 10, поскольку 102 = 100
√100 = 10
Число 100 это последнее число, корень которого можно извлечь с помощью таблицы умножения. Для чисел, бóльших 100, квадратные корни можно находить с помощью таблицы квадратов.
Пример 3. Извлечь квадратный корень √256
Данный квадратный корень равен числу, квадрат которого равен 256. Чтобы найти это число, воспользуемся таблицей квадратов.
Нахóдим в таблице квадратов число 256 и двигаясь от него влево и вверх определяем цифры, которые образуют число, квадрат которого равен 256.
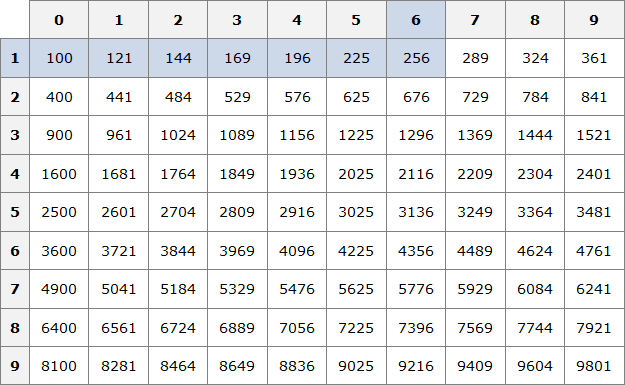
Видим, что это число 16. Значит √256 = 16.
Пример 4. Найти значение выражения 2√16
В данном примере число 2 умножается на выражение с корнем. Сначала вычислим корень √16, затем перемнóжим его с числом 2
![]()
Пример 7. Решить уравнение ![]()
В данном примере нужно найти значение переменной x, при котором левая часть будет равна 4.
Значение переменной x равно 16, поскольку ![]() . Значит корень уравнения равен 16.
. Значит корень уравнения равен 16.
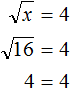
Примечание. Не следует путать корень уравнения и квадратный корень. Корень уравнения это значение переменной, при котором уравнение обращается в верное числовое равенство. А квадратный корень это число, вторая степень которого равна выражению, находящемуся под радикалом ![]() .
.
Подобные примеры решают, пользуясь определением квадратного корня. Давайте и мы поступим так же.
Из определения мы знаем, что квадратный корень ![]() равен числу b, при котором выполняется равенство b2 = a.
равен числу b, при котором выполняется равенство b2 = a.
![]()
Применим равенство b2 = a к нашему примеру ![]() . Роль переменной b у нас играет число 4, а роль переменной a — выражение, находящееся под корнем
. Роль переменной b у нас играет число 4, а роль переменной a — выражение, находящееся под корнем ![]() , а именно переменная x
, а именно переменная x
![]()
В выражении 42 = x вычислим левую часть, полýчим 16 = x. Поменяем левую и правую часть местами, полýчим x = 16. В результате приходим к тому, что нашлось значение переменной x.
Пример 8. Решить уравнение ![]()
Перенесем −8 в правую часть, изменив знак:
![]()
Возведем правую часть во вторую степень и приравняем её к переменной x
![]()
Вычислим правую часть, полýчим 64 = x. Поменяем левую и правую часть местами, полýчим x = 64. Значит корень уравнения ![]() равен 64
равен 64
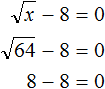
Пример 9. Решить уравнение ![]()
Воспользуемся определением квадратного корня:
![]()
Роль переменной b играет число 7, а роль переменной a — подкореннóе выражение 3 + 5x. Возведем число 7 во вторую степень и приравняем его к 3 + 5x
![]()
В выражении 72 = 3 + 5x вычислим левую часть полýчим 49 = 3 + 5x. Получилось обычное линейное уравнение. Решим его:
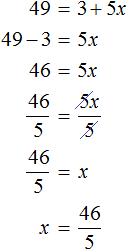
Корень уравнения ![]() равен
равен ![]() . Выполним проверку, подставив его в исходное уравнение:
. Выполним проверку, подставив его в исходное уравнение:
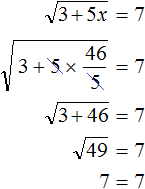
Пример 10. Найти значение выражения ![]()
В этом выражении число 2 умножается на квадратный корень из числа 49.
Сначала нужно извлечь квадратный корень и перемножить его с числом 2
![]()
Приближённое значение квадратного корня
Не каждый квадратный корень можно извлечь. Извлечь квадратный корень можно только в том случае, если удаётся найти число, вторая степень которого равна подкореннóму выражению.
Например, извлечь квадратный корень ![]() можно, потому что удаётся найти число, вторая степень которого равна подкореннóму выражению. Таковым является число 8, поскольку 82 = 64. То есть
можно, потому что удаётся найти число, вторая степень которого равна подкореннóму выражению. Таковым является число 8, поскольку 82 = 64. То есть ![]()
А извлечь квадратный корень ![]() нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.
нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.
Зато можно извлечь квадратный корень из числа 3 приближённо. Извлечь квадратный корень приближённо означает найти значение, которое при возведении во вторую степень будет максимально близко к подкореннóму выражению.
Приближённое значение ищут с определенной точностью: с точностью до целых, с точностью до десятых, с точностью до сотых и так далее.
Найдём значение корня ![]() приближённо с точностью до десятых. Словосочетание «с точностью до десятых» говорит о том, что приближённое значение корня
приближённо с точностью до десятых. Словосочетание «с точностью до десятых» говорит о том, что приближённое значение корня ![]() будет представлять собой десятичную дробь, у которой после запятой одна цифра.
будет представлять собой десятичную дробь, у которой после запятой одна цифра.
Для начала найдём ближайшее меньшее число, корень которого можно извлечь. Таковым является число 1. Корень из этого числа равен самому этому числу:
√1 = 1
Аналогично находим ближайшее бóльшее число, корень которого можно извлечь. Таковым является число 4. Корень из этого числа равен 2
√4 = 2
√1 меньше, чем √4
√1 < √4
А √3 больше, чем √1 но меньше, чем √4. Запишем это в виде двойного неравенства:
√1 < √3 < √4
Точные значения корней √1 и √4 известны. Это числа 1 и 2
1 < √3 < 2
Тогда очевидно, что значение корня √3 будет представлять собой десятичную дробь, потому что между числами 1 и 2 нет целых чисел.
Для нахождения приближённого значения квадратного корня √3 будем проверять десятичные дроби, располагающиеся в интервале от 1 до 2, возводя их в квадрат. Делать это будем до тех пор пока не полýчим значение, максимально близкое к 3. Проверим к примеру дробь 1,1
1,12 = 1,21
Получился результат 1,21, который не очень близок к подкореннóму выражению 3. Значит 1,1 не годится в качестве приближённого значения квадратного корня √3, потому что оно малó.
Проверим тогда дробь 1,8
1,82 = 3,24
Получился результат 3,24, который близок к подкореннóму выражению, но превосходит его на 0,24. Значит 1,8 не годится в качестве приближенного значения корня √3, потому что оно великó.
Проверим тогда дробь 1,7
1,72 = 2,89
Получился результат 2,89, который уже близок к подкореннóму выражению. Значит 1,7 и будет приближённым значением квадратного корня √3. Напомним, что знак приближенного значения выглядит как ≈
√3 ≈ 1,7
Значение 1,6 проверять не нужно, потому что в результате получится число 2,56, которое дальше от трёх, чем значение 2,89. А значение 1,8, как было показано ранее, является уже большим.
В данном случае мы нашли приближенное значение корня √3 с точностью до десятых. Значение можно получить ещё более точно. Для этого его следует находить с точностью до сотых.
Чтобы найти значение с точностью до сотых проверим десятичные дроби в интервале от 1,7 до 1,8
1,7 < √3 < 1,8
Проверим дробь 1,74
1,742 = 3,0276
Получился результат 3,0276, который близок к подкореннóму выражению, но превосходит его на 0,0276. Значит значение 1,74 великó для корня √3.
Проверим тогда дробь 1,73
1,732 = 2,9929
Получился результат 2,9929, который близок к подкореннóму выражению √3. Значит 1,73 будет приближённым значением квадратного корня √3 с точностью до сотых.
Процесс нахождения приближённого значения квадратного корня продолжается бесконечно. Так, корень √3 можно находить с точностью до тысячных, десятитысячных и так далее:
√3 = 1,732 (вычислено с точностью до тысячных)
√3 = 1,7320 (вычислено с точностью до десятитысячных)
√3 = 1,73205 (вычислено с точностью до ста тысячных).
Ещё квадратный корень можно извлечь с точностью до целых. Приближённое значение квадратного корня √3 с точностью до целых равно единице:
√3 ≈ 1
Значение 2 будет слишком большим, поскольку при возведении этого числа во вторую степень получается число 4, которое больше подкоренного выражения. Нас же интересуют значения, которые при возведении во вторую степень равны подкореннóму выражению или максимально близки к нему, но не превосходят его.
В зависимости от решаемой задачи допускается находить значение, вторая степень которого больше подкоренного выражения. Это значение называют приближённым значением квадратного корня с избытком. Поговорим об этом подробнее.
Приближенное значение квадратного корня с недостатком или избытком
Иногда можно встретить задание, в котором требуется найти приближённое значение корня с недостатком или избытком.
В предыдущей теме мы нашли приближённое значение корня √3 с точностью до десятых с недостатком. Недостаток понимается в том смысле, что до значения 3 нам недоставало ещё некоторых частей. Так, найдя приближённое значение √3 с точностью до десятых, мы получили 1,7. Это значение является значением с недостатком, поскольку при возведении этого числа во вторую степень полýчим результат 2,89. Этому результату недостаёт ещё 0,11 чтобы получить число 3. То есть, 2,89 + 0,11 = 3.
С избытком же называют приближённые значения, которые при возведении во вторую степень дают результат, который превосходит подкореннóе выражение. Так, вычисляя корень √3 приближённо, мы проверили значение 1,8. Это значение является приближённым значением корня √3 с точностью до десятых с избытком, поскольку при возведении 1,8 во вторую степень, получаем число 3,24. Этот результат превосходит подкореннóе выражение на 0,24. То есть 3,24 − 3 = 0,24.
Приближённое значение квадратного корня √3 с точностью до целых тоже был найден с недостатком:
√3 ≈ 1
Это потому что при возведении единицы в квадрат получаем единицу. То есть до числа 3 недостаёт ещё 2.
Приближённое значение квадратного корня √3 с точностью до целых можно найти и с избытком. Тогда этот корень приближённо будет равен 2
√3 ≈ 2
Это потому что при возведении числа 2 в квадрат получаем 4. Число 4 превосходит подкореннóе выражение 3 на единицу. Извлекая приближённо квадратный корень с избытком желательно уточнять, что корень извлечен именно с избытком:
√3 ≈ 2 (с избытком)
Потому что приближённое значение чаще всего ищется с недостатком, чем с избытком.
Дополнительно следует упомянуть, что в некоторых учебниках словосочетания «с точностью до целых», «с точностью до десятых», с «точностью до сотых», заменяют на словосочетания «с точностью до 1», «с точностью до 0,1», «с точностью до 0,01» соответственно.
Так, если в задании сказано извлечь квадратный корень из числа 5 с точностью до 0,01, то это значит что корень следует извлекать приближённо с точностью до сотых:
√5 ≈ 2,23
Пример 2. Извлечь квадратный корень из числа 51 с точностью до 1
√51 ≈ 7
Пример 3. Извлечь квадратный корень из числа 51 с точностью до 0,1
√51 ≈ 7,1
Пример 4. Извлечь квадратный корень из числа 51 с точностью до 0,01
√51 ≈ 7,14
Границы, в пределах которых располагаются корни
Если исходное число принадлежит промежутку [1; 100], то квадратный корень из этого исходного числа будет принадлежать промежутку [1; 10].
Например, пусть исходным числом будет 64. Данное число принадлежит промежутку [1; 100]. Сразу делаем вывод, что квадратный корень из числа 64 будет принадлежать промежутку [1; 10]. Теперь вспоминаем таблицу умножения. Какое перемножение двух одинаковых сомножителей даёт в результате 64? Ясно, что перемножение 8 × 8, а это есть 82 = 64. Значит квадратный корень из числа 64 есть 8
![]()
Пример 2. Извлечь квадратный корень из числа 49
Число 49 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 7, поскольку 72 = 49
√49 = 7
Пример 2. Извлечь квадратный корень из числа 1
Число 1 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 1, поскольку 12 = 1
√1 = 1
Пример 3. Извлечь квадратный корень из числа 100
Число 100 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 10, поскольку 102 = 100
√100 = 10
Понятно, что промежуток [1; 100] содержит ещё и числа, квадратные корни из которых не извлекаются. Для таких чисел корень нужно извлекать приближённо. Тем не менее, приближённый корень тоже будет располагаться в пределах промежутка [1; 10].
Например, извлечём квадратный корень из числа 37. Нет целого числа, вторая степень которого была бы равна 37. Поэтому извлекать квадратный корень следует приближённо. Извлечём его к примеру с точностью до сотых:
√37 ≈ 6,08
Для облегчения можно находить ближайшее меньшее число, корень из которого извлекается. Таковым в данном примере было число 36. Квадратный корень из него равен 6. И далее отталкиваясь от числа 6, можно находить приближённое значение корня √37, проверяя различные десятичные дроби, целая часть которых равна 6.
Квадраты чисел от 1 до 10 обязательно нужно знать наизусть. Ниже представлены эти квадраты:
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
И обратно, следует знать значения квадратных корней этих квадратов:

Если к любому числу от 1 до 10 в конце дописать ноль (или несколько нулей), и затем возвести это число во вторую степень, то в полученном числе будет в два раза больше нулей.
Например, 62 = 36. Допишем к числу 6 один ноль, полýчим 60. Возведём число 60 во вторую степень, полýчим 3600
602 = 3600
А если к числу 6 дописать два нуля, и возвести это число во вторую степень, то полýчим число, в котором четыре нуля. То есть в два раза больше нулей:
6002 = 360000
Тогда можно сделать следующий вывод:
Если исходное число содержит знакомый нам квадрат и чётное количество нулей, то можно извлечь квадратный корень из этого числа. Для этого следует извлечь корень из знакомого нам квадрата и затем записать половину количества нулей из исходного числа.
Например, извлечём квадратный корень из числа 900. Видим, что в данном числе есть знакомый нам квадрат 9. Извлекаем из него корень, получаем 3
![]()
Теперь из исходного числа записываем половину от количества нулей. В исходном числе 900 содержится два нуля. Половина этого количества нулей есть один ноль. Записываем его в ответе после цифры 3
![]()
Пример 2. Извлечём квадратный корень из числа 90000
Здесь опять же имеется знакомый нам квадрат 9 и чётное количество нулей. Извлекаем корень из числа 9 и записываем половину от количества нулей. В исходном числе содержится четыре нуля. Половиной же этого количества нулей будет два нуля:
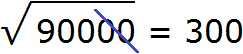
Пример 3. Извлечем квадратный корень из числа 36000000
Здесь имеется знакомый нам квадрат 36 и чётное количество нулей. Извлекаем корень из числа 36 и записываем половину от количества нулей. В исходном числе шесть нулей. Половиной же будет три нуля:
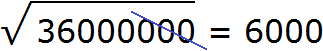
Пример 4. Извлечем квадратный корень из числа 2500
Здесь имеется знакомый нам квадрат 25 и чётное количество нулей. Извлекаем корень из числа 25 и записываем половину от количества нулей. В исходном числе два нуля. Половиной же будет один ноль:
![]()
Если подкореннóе число увеличить (или уменьшить) в 100, 10000 то корень увеличится (или уменьшится) в 10, 100 раз соответственно.
Например, ![]() . Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз:
. Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз:
![]()
И наоборот, если в равенстве ![]() уменьшим подкореннóе число в 100 раз, то квадратный корень уменьшится в 10 раз:
уменьшим подкореннóе число в 100 раз, то квадратный корень уменьшится в 10 раз:
![]()
Пример 2. Увеличим в равенстве ![]() подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз
подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз
![]()
Пример 3. Уменьшим в равенстве ![]() подкореннóе число в 100 раз, тогда квадратный корень 70 уменьшится в 10 раз
подкореннóе число в 100 раз, тогда квадратный корень 70 уменьшится в 10 раз
![]()
Эта закономерность позволяет извлечь квадратный корень из десятичной дроби, если в данной дроби после запятой содéржатся две цифры, и эти две цифры образуют знакомый нам квадрат. В таких случаях данную десятичную дробь следует умножить на 100. Затем извлечь квадратный корень из получившегося числа и уменьшить подкореннóе число в сто раз.
Например, извлечём квадратный корень из числа 0,25. В данной десятичной дроби после запятой содержатся две цифры и эти две цифры образуют знакомый нам квадрат 25.
Умнóжим десятичную дробь 0,25 на 100, полýчим 25. А из числа 25 квадратный корень извлекается легко:
![]()
Но нам изначально нужно было извлечь корень из 0,25, а не из 25. Чтобы исправить ситуацию, вернём нашу десятичную дробь. Если в равенстве ![]() подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз:
подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз:
![]()
Обычно в таких случаях достаточно уметь передвигáть запятую. Потому что сдвинуть в числе запятую вправо на две цифры это всё равно что умножить это число на 100.
В предыдущем примере в подкоренном числе 0,25 можно было сдвинуть запятую вправо на две цифры, а в полученном ответе сдвинуть её влево на одну цифру.
Например, извлечем корень из числа 0,81. Мысленно передвинем запятую вправо на две цифры, полýчим 81. Теперь извлечём квадратный корень из числа 81, полýчим ответ 9. В ответе 9 передвинем запятую влево на одну цифру, полýчим 0,9. Значит, ![]() .
.
Это правило работает и в ситуации, когда после запятой содержатся четыре цифры и эти цифры образуют знакомый нам квадрат.
Например, десятичная дробь 0,1225 содержит после запятой четыре цифры. Эти четыре цифры образуют число 1225, квадратный корень из которого равен 35.
Тогда можно извлечь квадратный корень и из 0,1225. Умнóжим данную десятичную дробь на 10000, полýчим 1225. Из числа 1225 квадратный корень можно извлечь с помощью таблицы квадратов:
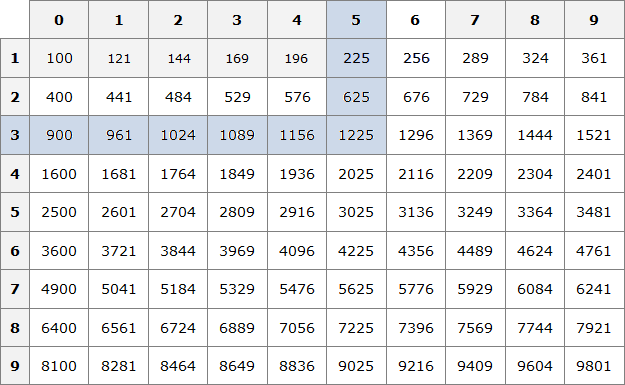
![]()
Но нам изначально нужно было извлечь корень из 0,1225, а не из 1225. Чтобы исправить ситуацию, в равенстве ![]() подкореннóе число уменьшим в 10000 раз. В результате под корнем образуется десятичная дробь 0,1225, а правая часть уменьшится в 100 раз
подкореннóе число уменьшим в 10000 раз. В результате под корнем образуется десятичная дробь 0,1225, а правая часть уменьшится в 100 раз
![]()
Эта же закономерность будет работать и при извлечении корней из дробей вида 12,25. Если цифры из которых состоит десятичная дробь образуют знакомый нам квадрат, при этом после запятой содержится чётное количество цифр, то можно извлечь корень из этой десятичной дроби.
Умнóжим десятичную дробь 12,25 на 100, полýчим 1225. Извлечём корень из числа 1225
![]()
Теперь в равенстве ![]() уменьшим подкореннóе число в 100 раз. В результате под корнем образуется число 12,25, и соответственно ответ уменьшится в 10 раз
уменьшим подкореннóе число в 100 раз. В результате под корнем образуется число 12,25, и соответственно ответ уменьшится в 10 раз
![]()
Если исходное число принадлежит промежутку [100; 10000], то квадратный корень из этого исходного числа будет принадлежать промежутку [10; 100].
В этом случае применяется таблица квадратов:
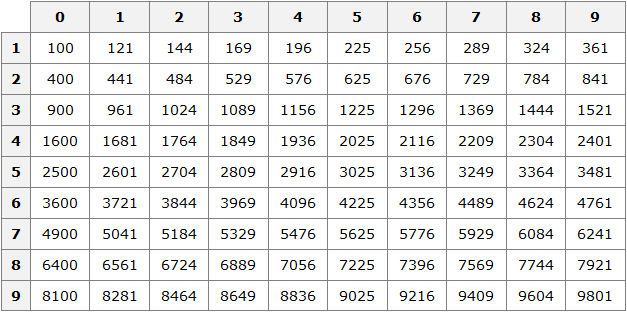
Например, пусть исходным числом будет 576. Данное число принадлежит промежутку [100; 10000]. Сразу делаем вывод, что квадратный корень из числа 576 будет принадлежать промежутку [10; 100]. Теперь открываем таблицу квадратов и смотрим какое число во второй степени равно 576
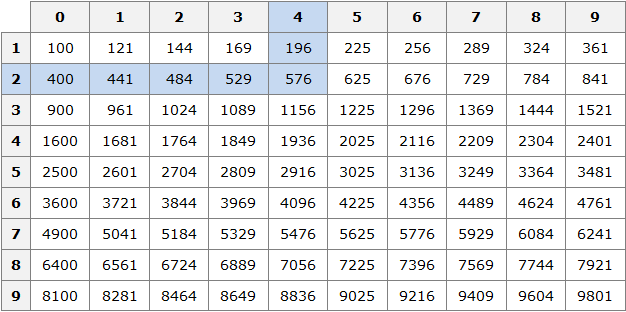
Видим, что это число 24. Значит ![]() .
.
Пример 2. Извлечь квадратный корень из числа 432.
Число 432 принадлежит промежутку [100; 10000]. Значит квадратный корень следует искать в промежутке [10; 100]. Открываем таблицу квадратов и смотрим какое число во второй степени равно 432. Обнаруживаем, что число 432 в таблице квадратов отсутствует. В этом случае квадратный корень следует искать приближённо.
Извлечем квадратный корень из числа 432 с точностью до десятых.
В таблице квадратов ближайшее меньшее число к 432 это число 400. Квадратный корень из него равен 20. Отталкиваясь от числа 20, будем проверять различные десятичные дроби, целая часть которых равна 20.
Проверим, например, число 20,8. Для этого возведём его в квадрат:
20,82 = 432,64
Получилось число 432,64 которое превосходит исходное число 432 на 0,64. Видим, что значение 20,8 великó для корня √432. Проверим тогда значение 20,7
20,72 = 428,49
Значение 20,7 годится в качестве корня, поскольку в результате возведения этого числа в квадрат получается число 428,49, которое меньше исходного числа 432, но близко к нему. Значит √432 ≈ 20,7.
Необязательно запоминать промежутки чтобы узнать в каких границах располагается корень. Можно воспользоваться методом нахождения ближайших квадратов с чётным количеством нулей на конце.
Например, извлечём корень из числа 4225. Нам известен ближайший меньший квадрат 3600, и ближайший больший квадрат 4900
3600 < 4225 < 4900
Извлечём квадратные корни из чисел 3600 и 4900. Это числа 60 и 70 соответственно:
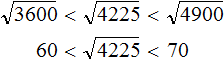
Тогда можно понять, что квадратный корень из числа 4225 располагается между числами 60 и 70. Можно даже найти его методом подбора. Корни 60 и 70 исключаем сразу, поскольку это корни чисел 3600 и 4900. Затем можно проверить, например, корень 64. Возведём его в квадрат (или умнóжим данное число само на себя)
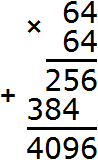
Корень 64 не годится. Проверим корень 65
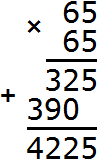
Получается 4225. Значит 65 является корнем числа 4225
![]()
Тождественные преобразования с квадратными корнями
Над квадратными корнями можно выполнять различные тождественные преобразования, тем самым облегчая их вычисление. Рассмотрим некоторые из этих преобразований.
Квадратный корень из произведения
Квадратный корень из произведения это выражение вида ![]() , где a и b некоторые числа.
, где a и b некоторые числа.
Например, выражение ![]() является квадратным корнем из произведения чисел 4 и 9.
является квадратным корнем из произведения чисел 4 и 9.
Чтобы извлечь такой квадратный корень, нужно по отдельности извлечь квадратные корни из множителей 4 и 9, представив выражение ![]() в виде произведения корней
в виде произведения корней ![]() . Вычислив по отдельности эти корни полýчим произведение 2 × 3, которое равно 6
. Вычислив по отдельности эти корни полýчим произведение 2 × 3, которое равно 6
![]()
Конечно, можно не прибегать к таким манипуляциям, а вычислить сначала подкореннóе выражение 4 × 9, которое равно 36. Затем извлечь квадратный корень из числа 36
![]()
Но при извлечении квадратных корней из больших чисел это правило может оказаться весьма полезным.
Допустим, потребовалось извлечь квадратный корень из числа 144. Этот корень легко определяется с помощью таблицы квадратов — он равен 12
![]()
Но предстáвим, что таблицы квадратов под рукой не оказалось. В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составить числа, квадратные корни из которых извлекаются.
Итак, разлóжим число 144 на простые множители:

Получили следующее разложение:
![]()
В разложéнии содержатся четыре двойки и две тройки. При этом все числа, входящие в разложение, перемнóжены. Это позволяет предстáвить произведения одинаковых сомножителей в виде степени с показателем 2.
Тогда четыре двойки можно заменить на запись 22 × 22, а две тройки заменить на 32
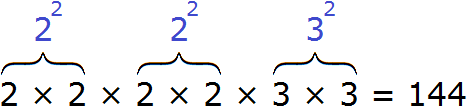
В результате будем иметь следующее разложение:
![]()
Теперь можно извлекáть квадратный корень из разложения числа 144
![]()
Применим правило извлечения квадратного корня из произведения:
![]()
Ранее было сказано, что если подкореннóе выражение возведенó во вторую степень, то такой квадратный корень равен модулю из подкореннóго выражения.
Тогда получится произведение 2 × 2 × 3, которое равно 12
![]()
Простые множители представляют в виде степени для удобства и короткой записи. Допускается также записывать их под кóрнем как есть, чтобы впоследствии перемнóжив их, получить новые сомножители.
Так, разложив число 144 на простые множители, мы получили разложение 2 × 2 × 2 × 2 × 3 × 3. Это разложение можно записать под кóрнем как есть:
![]()
затем перемнóжить некоторые сомножители так, чтобы получились числа, квадратные корни из которых извлекаются. В данном случае можно дважды перемнóжить две двойки и один раз перемнóжить две тройки:
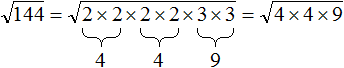
Затем применить правило извлечения квадратного корня из произведения и получить окончательный ответ:
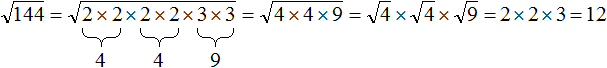
С помощью правила извлечения квадратного корня из произведения можно извлекать корень и из других больших чисел. В том числе, из тех чисел, которых нет в таблице квадратов.
Например, извлечём квадратный корень из числа 13456. Этого числа нет в таблице квадратов, поэтому воспользуемся правилом извлечения квадратного корня из произведения, предварительно разложив число 13456 на простые множители.
Итак, разложим число 13456 на простые множители:

В разложении имеются четыре двойки и два числа 29. Двойки дважды предстáвим как 22. А два числа 29 предстáвим как 292. В результате полýчим следующее разложение числа 13456
![]()
Теперь будем извлекать квадратный корень из разложения числа 13456
![]()
Итак, если a ≥ 0 и b ≥ 0, то ![]() . То есть корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
. То есть корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Докажем равенство ![]() . Для этого воспользуемся определением квадратного корня.
. Для этого воспользуемся определением квадратного корня.
Согласно определению, квадратным корня из числа a есть число b, при котором выполняется равенство b2 = a.
В нашем случае нужно удостовериться, что правая часть равенства ![]() при возведении во вторую степень даст в результате подкореннóе выражение левой части, то есть выражение ab.
при возведении во вторую степень даст в результате подкореннóе выражение левой части, то есть выражение ab.
Итак, выпишем правую часть равенства ![]() и возведём ее во вторую степень:
и возведём ее во вторую степень:
![]()
Теперь воспользуемся правилом возведения в степень произведения. Согласно этому правилу, каждый множитель данного произведения нужно возвести в указанную степень:
![]()
Ранее было сказано, что если выражение вида ![]() возвести во вторую степень, то получится подкореннóе выражение. Применим это правило. Тогда полýчим ab. А это есть подкореннóе выражение квадратного корня
возвести во вторую степень, то получится подкореннóе выражение. Применим это правило. Тогда полýчим ab. А это есть подкореннóе выражение квадратного корня ![]()
![]()
Значит равенство ![]() справедливо, поскольку при возведéнии правой части во вторую степень, получается подкореннóе выражение левой части.
справедливо, поскольку при возведéнии правой части во вторую степень, получается подкореннóе выражение левой части.
Правило извлечения квадратного корня из произведения работает и в случае, если под кóрнем располагается более двух множителей. То есть справедливым будет следующее равенство:
![]() , при a ≥ 0 и b ≥ 0, c ≥ 0.
, при a ≥ 0 и b ≥ 0, c ≥ 0.
Пример 1. Найти значение квадратного корня ![]()
Запишем корень ![]() в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
![]()
Пример 2. Найти значение квадратного корня ![]()
Предстáвим число 250 в виде произведения чисел 25 и 10. Делать это будем под знáком корня:
![]()
Теперь под кóрнем образовалось два одинаковых множителя 10 и 10. Перемнóжим их, полýчим 100
![]()
Далее применяем правило извлечения квадратного кóрня из произведения и получáем окончательный ответ:
![]()
Пример 3. Найти значение квадратного корня ![]()
Воспользуемся правилом возведения степени в степень. Степень 114 предстáвим как (112)2.
![]()
Теперь воспользуемся правилом извлечения квадратного кóрня из квадрата числа:
![]()
В нашем случае квадратный корень из числа (112)2 будет равен 112. Говоря простым языком, внешний показатель степени 2 исчезнет, а внутренний останется:
![]()
Далее возводим число 11 во вторую степень и получаем окончательный ответ:
![]()
Этот пример также можно решить, воспользовавшись правилом извлечения квадратного корня из произведения. Для этого подкореннóе выражение 114 нужно записать в виде произведения 112 × 112. Затем извлечь квадратный корень из этого произведения:
![]()
Пример 4. Найти значение квадратного корня ![]()
Перепишем степень 34 в виде (32)2, а степень 56 в виде (53)2
![]()
Далее используем правило извлечения квадратного кóрня из произведения:
![]()
Далее используем правило извлечения квадратного кóрня из квадрата числа:
![]()
Вычислим произведение получившихся степеней и полýчим окончательный ответ:
![]()
Сомножители, находящиеся под корнем, могут быть десятичными дробями. Например, извлечём квадратный корень из произведения ![]()
Запишем корень ![]() в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
![]()
Пример 6. Найти значение квадратного корня ![]()
![]()
Пример 7. Найти значение квадратного корня ![]()
![]()
Если первый сомножитель умножить на число n, а второй сомножитель разделить на это число n, то произведение не изменится.
Например, произведение 8 × 4 равно 32
8 × 4 = 32
Умнóжим сомножитель 8 скажем на число 2, а сомножитель 4 раздéлим на это же число 2. Тогда получится произведение 16 × 2, которое тоже равно 32.
(8 × 2) × (4 : 2) = 32
Это свойство полезно при решении некоторых задач на извлечение квадратных корней. Сомножители подкореннóго выражения можно умнóжить и разделить так, чтобы корни из них извлекались.
Например, извлечём квадратный корень из произведения ![]() . Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.
. Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.
Проанализировав подкореннóе выражение 1,6 × 90, можно заметить, что если первый сомножитель 1,6 умножить на 10, а второй сомножитель 90 разделить на 10, то полýчится произведение 16 × 9. Из такого произведения квадратный корень можно извлечь, пользуясь правилом извлечения квадратного корня из произведения.
Запишем полное решение данного примера:
![]()
Процесс умножения и деления можно выполнять в уме. Также можно пропустить подробную запись извлечения квадратного корня из каждого сомножителя. Тогда решение станóвится короче:
![]()
Пример 9. Найти значение квадратного корня ![]()
Умнóжим первый сомножитель на 10, а второй раздéлим на 10. Тогда под кóрнем образуется произведение 36 × 0,04, квадратный корень из которого извлекается:
![]()
Если в равенстве ![]() поменять местами левую и правую часть, то полýчим равенство
поменять местами левую и правую часть, то полýчим равенство ![]() . Это преобразовáние позволяет упрощáть вычисление некоторых корней.
. Это преобразовáние позволяет упрощáть вычисление некоторых корней.
Например, узнáем чему равно значение выражения ![]() .
.
Квадратные корни из чисел 10 и 40 не извлекаются. Воспользуемся правилом ![]() , то есть заменим выражение из двух корней
, то есть заменим выражение из двух корней ![]() на выражение с одним корнем, под которым будет произведение из чисел 10 и 40
на выражение с одним корнем, под которым будет произведение из чисел 10 и 40
![]()
Теперь найдём значение произведения, находящегося под корнем:
![]()
А квадратный корень из числа 400 извлекается. Он равен 20
![]()
Сомножители, располагáющиеся под корнем, можно расклáдывать на множители, группировáть, представлять в виде степени, а также перемножáть для получения новых сомножителей, корни из которых извлекаются.
Например, найдём значение выражения ![]() .
.
Воспользуемся правилом ![]()
![]()
Сомножитель 32 это 25. Предстáвим этот сомножитель как 2 × 24
![]()
Перемнóжим сомножители 2 и 2, полýчим 4. А сомножитель 24 предстáвим в виде степени с показателем 2
![]()
Теперь воспóльзуемся правилом ![]() и вычислим окончательный ответ:
и вычислим окончательный ответ:
![]()
Пример 12. Найти значение выражения ![]()
Воспользуемся правилом ![]()
![]()
Сомножитель 8 это 2 × 2 × 2, а сомножитель 98 это 2 × 7 × 7
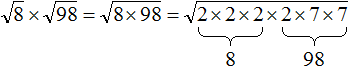
Теперь под кóрнем имеются четыре двойки и две семёрки. Четыре двойки можно записать как 22 × 22, а две семёрки как 72
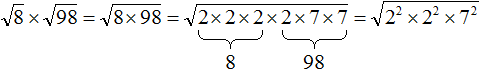
Теперь воспользуемся правилом ![]() и вычислим окончательный ответ:
и вычислим окончательный ответ:
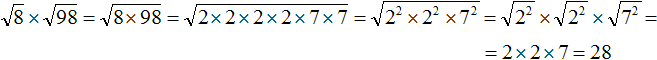
Квадратный корень из дроби
Квадратный корень вида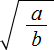 равен дроби, в числителе которой квадратный корень из числа a, а в знаменателе — квадратный корень из числа b
равен дроби, в числителе которой квадратный корень из числа a, а в знаменателе — квадратный корень из числа b

Например, квадратный корень из дроби ![]() равен дроби, в числителе которой квадратный корень из числа 4, а в знаменателе — квадратный корень из числа 9
равен дроби, в числителе которой квадратный корень из числа 4, а в знаменателе — квадратный корень из числа 9
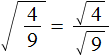
Вычислим квадратные корни в числителе и знаменателе:
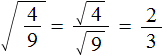
Значит, квадратный корень из дроби ![]() равен
равен .
Докáжем, что равенство  является верным.
является верным.
Возведём правую часть во вторую степень. Если в результате полýчим дробь ![]() , то это будет означать, что равенство
, то это будет означать, что равенство  верно:
верно:
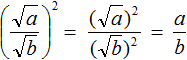
Пример 1. Извлечь квадратный корень 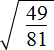
Воспользуемся правилом извлечения квадратного корня из дроби:
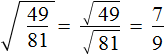
Пример 2. Извлечь квадратный корень 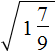
Переведём подкореннóе выражение в неправильную дробь, затем воспользуемся правилом извлечения квадратного корня из дроби:
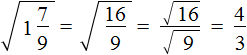
Пример 3. Извлечь квадратный корень ![]()
Квадратным корнем из числа 0,09 является 0,3. Но можно извлечь этот корень, воспользовавшись правилом извлечения квадратного корня из дроби.
Предстáвим подкоренное выражение в виде обыкновенной дроби. 0,09 это девять сотых:
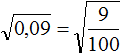
Теперь можно воспользоваться правилом извлечения квадратного корня из дроби:
Пример 4. Найти значение выражения ![]()
Извлечём корни из 0,09 и 0,25, затем сложим полученные результаты:
![]()
Также можно воспользоваться правилом извлечения квадратного корня из дроби:
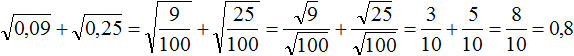
В данном примере первый способ оказался проще и удобнее.
Пример 5. Найти значение выражения ![]()
Сначала вычислим квадратный корень, затем перемнóжим его с 10. Получившийся результат вычтем из 4
![]()
Пример 6. Найти значение выражения ![]()
Сначала найдём значение квадратного корня ![]() . Он равен 0,6 поскольку 0,62 = 0,36
. Он равен 0,6 поскольку 0,62 = 0,36
![]()
Теперь вычислим получившееся выражение. Согласно порядку действий, сначала надо выполнить умножение, затем сложение:
![]()
Вынесение множителя из-под знака корня
В некоторых задачах может быть полезным вынесение множителя из-под знака корня.
Рассмотрим квадратный корень из произведения ![]() . Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения:
. Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения:
![]()
В нашем примере квадратный корень извлекается только из множителя 4. Его мы извлечём, а выражение ![]() оставим без изменений:
оставим без изменений:
![]()
Это и есть вынесение множителя из-под знака корня.
На практике подкореннóе выражение чаще всего требуется разложить на множители.
Пример 2. Вынести множитель из-под знака корня в выражении ![]()
Разлóжим подкореннóе выражение на множители 9 и 2. Тогда полýчим:
![]()
Теперь воспользуемся правило извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 9. Множитель 2 остáвим под кóрнем:
![]()
Пример 3. Вынести множитель из-под знака корня в выражении ![]()
Разлóжим подкореннóе выражение на множители 121 и 3. Тогда полýчим:
![]()
Теперь воспользуемся правилом извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 121. Выражение √3 остáвим под корнем:
![]()
Пример 4. Вынести множитель из-под знака корня в выражении ![]()
Воспользуемся правилом извлечения квадратного корня из произведения:
![]()
Квадратный корень извлекается только из числа 121. Извлечём его, а выражение √15 оставим без изменений:
![]()
Получается, что множитель 11 вынесен из-под знака корня. Вынесенный множитель принято записывать до выражения с корнем. Поменяем выражения √15 и 11 местами:
![]()
Пример 5. Вынести множитель из-под знака корня в выражении ![]()
Разлóжим подкореннóе выражение на множители 4 и 3
![]()
Воспользуемся правилом извлечения квадратного корня из произведения:
![]()
Извлечём корень из числа 4, а выражение √3 остáвим без изменений:
![]()
Пример 6. Упростить выражение ![]()
Предстáвим второе слагаемое ![]() в виде
в виде ![]() . А третье слагаемое
. А третье слагаемое ![]() предстáвим в виде
предстáвим в виде ![]()
![]()
Теперь в выражениях ![]() и
и ![]() вынесем множитель из-под знака корня:
вынесем множитель из-под знака корня:
![]()
Во втором слагаемом ![]() перемнóжим числа −4 и 4. Остальное перепишем без изменений:
перемнóжим числа −4 и 4. Остальное перепишем без изменений:
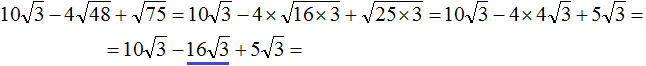
Замечáем, что получившемся выражении квадратный корень √3 является общим множителем. Вынесем его за скобки:
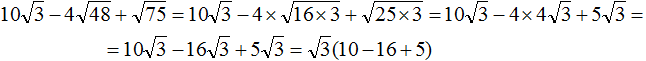
Вычислим содержимое скобок, полýчим −1
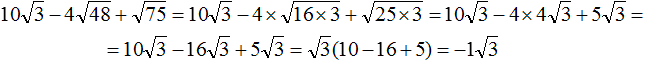
Если множителем является −1, то записывают только минус. Единица опускается. Тогда полýчим окончательный ответ −√3
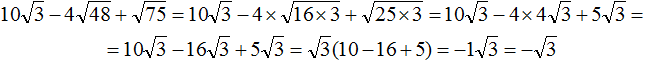
Внесение множителя под знак корня
Рассмотрим следующее выражение:
![]()
В этом выражении число 5 умнóжено на квадратный корень из числа 9. Найдём значение этого выражения.
Сначала извлечём квадратный корень, затем перемнóжим его с числом 5.
Квадратный корень из 9 равен 3. Перемнóжим его с числом 5. Тогда полýчим 15
![]()
Число 5 в данном случае было множителем. Внесём этот множитель под знак корня. Но сделать это нужно таким образом, чтобы в результате наших действий значение исходного выражения не изменилось. Проще говоря, после внесения множителя 5 под знак корня, получившееся выражение по-прежнему должно быть равно 15.
Значение выражения не изменится, если число 5 возвести во вторую степень и только тогда внести его под корень:
![]()
Итак, если данó выражение ![]() , и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень:
, и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень:
![]()
Пример 1. Внести множитель под знак корня в выражении ![]()
Возведём число 7 во вторую степень и внесём его под знак корня:
![]()
Пример 2. Внести множитель под знак корня в выражении ![]()
Возведём число 10 во вторую степень и внесем его под знак корня:
![]()
Пример 3. Внести множитель под знак корня в выражении ![]()
![]()
Вносить под знак корня можно только положительный множитель. Ранее было сказано, что выражение вида ![]() не имеет смысла.
не имеет смысла.
Однако, если перед знаком кóрня располагается отрицательный множитель, то минус можно оставить за знáком корня, а самó число внести под знак корня.
Пример 4. Внести множитель по знак корня в выражении ![]()
В этом примере под знак корня внóсится только 3. Минус остаётся за знáком корня:
![]()
Пример 5. Выполнить возведéние в степень в следующем выражении:
![]()
Воспользуемся формулой квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Роль переменной a в данном случае играет выражение √3, роль переменной b — выражение √2. Тогда полýчим:
![]()
Теперь необходимо упростить получившееся выражение.
Для выражений ![]() и
и ![]() применим правило
применим правило ![]() . Ранее мы говорили, что если выражение вида
. Ранее мы говорили, что если выражение вида ![]() возвести во вторую степень, то это выражение будет равно подкореннóму выражению a.
возвести во вторую степень, то это выражение будет равно подкореннóму выражению a.
А в выражении ![]() для множителей
для множителей ![]() и
и ![]() применим правило
применим правило ![]() . То есть заменим произведение корней на один общий корень:
. То есть заменим произведение корней на один общий корень:
![]()
Приведём подобные слагаемые. В данном случае можно сложить слагаемые 3 и 2. А в слагаемом ![]() вычислить произведение, которое под кóрнем:
вычислить произведение, которое под кóрнем:
![]()
Задания для самостоятельного решения
Задание 1. Найдите значение квадратного корня:
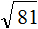
Решение:

Задание 2. Найдите значение квадратного корня:

Решение:
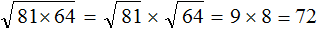
Задание 3. Найдите значение квадратного корня:
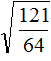
Решение:
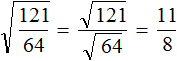
Задание 4. Найдите значение выражения:
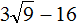
Решение:

Задание 5. Найдите значение квадратного корня:
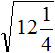
Решение:
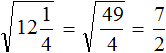
Задание 6. Найдите значение квадратного корня:
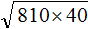
Решение:
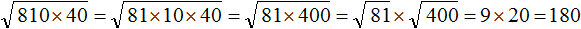
Задание 7. Найдите значение квадратного корня:
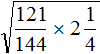
Решение:
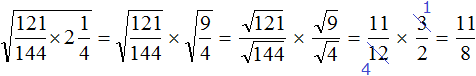
Задание 8. Найдите значения следующих выражений:
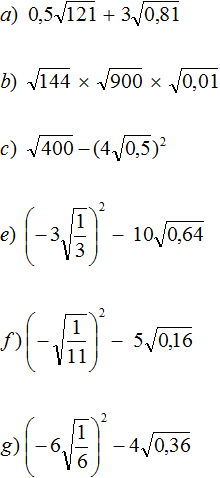
Решение:
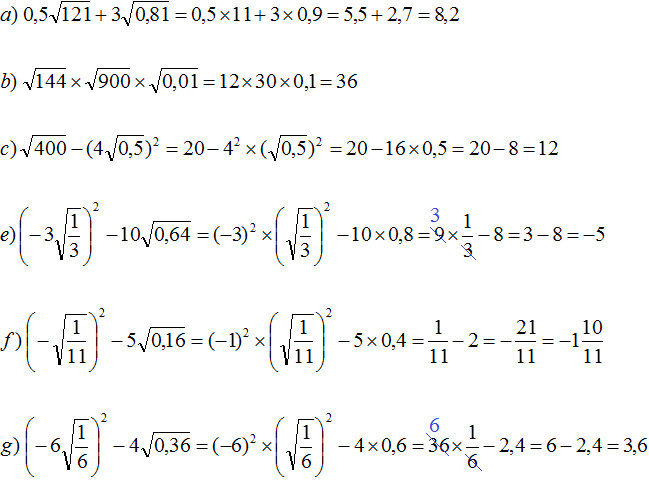
Задание 9. Извлеките квадратный корень из числа 4624
Решение:
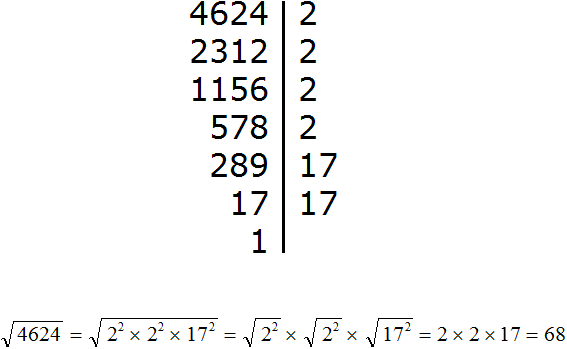
Задание 10. Извлеките квадратный корень из числа 11025
Решение:

Задание 11. Найдите значение квадратного корня:
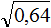
Решение:

Задание 12. Найдите значение квадратного корня:
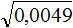
Решение:

Задание 13. Найдите значение квадратного корня:
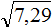
Решение:

Задание 14. Найдите значение квадратного корня:
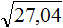
Решение:
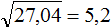
Задание 15. Найдите значение квадратного корня:
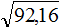
Решение:
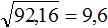
Задание 16. Найдите значение выражения:
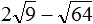
Решение:
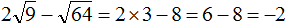
Задание 17. Найдите значение выражения:
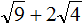
Решение:
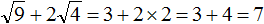
Задание 18. Найдите значение выражения:

Решение:

Задание 19. Найдите значение выражения:
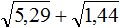
Решение:

Задание 20. Найдите значение выражения:

Решение:

Задание 21. Найдите значение выражения:

Решение:

Задание 22. Найдите значение выражения:
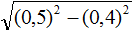
Решение:
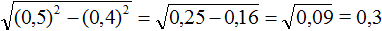
Задание 23. Найдите значение выражения:
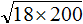
Решение:
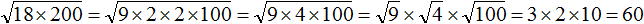
Задание 24. Найдите значение выражения:
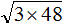
Решение:

Задание 25. Найдите значение выражения:
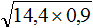
Решение:
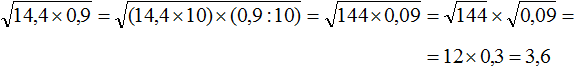
Задание 26. Найдите значение выражения:
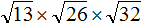
Решение:

Задание 27. Найдите значение выражения:
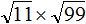
Решение:

Задание 28. Найдите значение выражения:

Решение:

Задание 29. Найдите значение выражения:
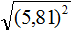
Решение:

Задание 30. Найдите значение выражения:
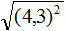
Решение:

Задание 31. Найдите значение выражения:
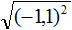
Решение:
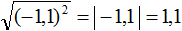
Задание 32. Найдите значение выражения:

Решение:
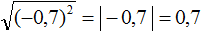
Задание 33. Найдите значение выражения:

Решение:
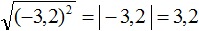
Задание 34. Вынести множитель из-под знака корня:

Решение:
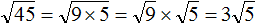
Задание 35. Вынести множитель из-под знака корня:
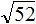
Решение:

Задание 36. Вынести множитель из-под знака корня:
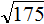
Решение:
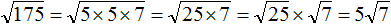
Задание 37. Вынести множитель из-под знака корня:
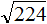
Решение:
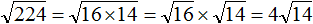
Задание 38. Вынести множитель из-под знака корня:
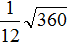
Решение:

Задание 39. Вынести множитель из-под знака корня:
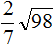
Решение:
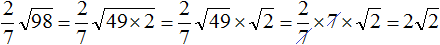
Задание 40. Вынести множитель из-под знака корня:
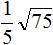
Решение:

Задание 41. Вынести множитель из-под знака корня:

Решение:

Задание 42. Вынести множитель из-под знака корня:
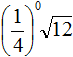
Решение:

Задание 43. Вынести множитель из-под знака корня:
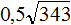
Решение:

Задание 44. Вынести множитель из-под знака корня в следующих выражениях:

Решение:
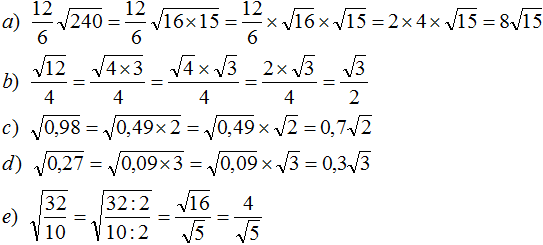
Задание 45. Внести множитель под знак корня:
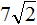
Решение:

Задание 46. Внести множитель под знак корня:
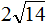
Решение:
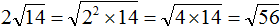
Задание 47. Внести множитель под знак корня:

Решение:
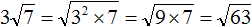
Задание 48. Внести множитель под знак корня:
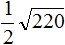
Решение:
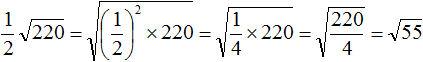
Задание 49. Внести множитель под знак корня:
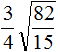
Решение:
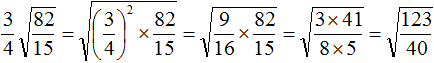
Задание 50. Внести множитель под знак корня в следующих выражениях:
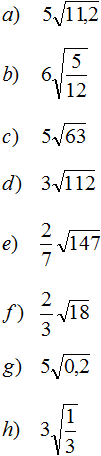
Решение:

Задание 51. Упростить выражение:

Решение:
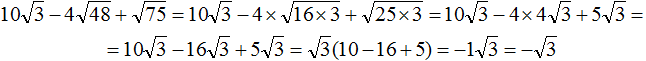
Задание 52. Упростить выражение:

Решение:

Задание 53. Упростить выражение:

Решение:

Задание 54. Упростить выражение:
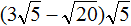
Решение:

Задание 55. Упростить выражение:
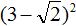
Решение:

Задание 56. Упростить выражение:

Решение:
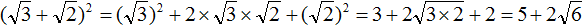
Задание 57. Упростить выражение:

Решение:
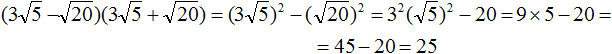
Задание 58. Упростить выражение:
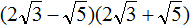
Решение:
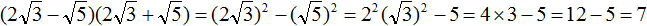
Задание 59. Упростить выражение:
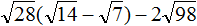
Решение:

Задание 60. Упростить выражение:
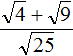
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Методы вычисления квадратных корней — это вычислительные алгоритмы для вычисления приближённых значений главных (или неотрицательных) квадратных корней (обычно обозначаемых как 
![{displaystyle {sqrt[{2}]{S}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e80c8b45982396fb6de8e12e2bef49659bb16e3)




Любое вещественное число имеет два корня[1]. Главное значение квадратного корня большинства чисел является иррациональным числом с бесконечной последовательностью десятичных цифр. Как результат, десятичное представление любого такого квадратного корня может быть вычислено только приближённо с конечной точностью (знаков после запятой). Однако, даже если мы берём корень от полного квадрата целого числа, так что результат имеет конечное представление, некоторые процедуры, используемые для вычисления корня, могут вернуть лишь ряд приближений с возрастающей точностью.
Представление вещественного числа в виде цепной дроби может быть использовано вместо десятичного или двоичного разложения и это представление имеет свойство, что квадратный корень любого рационального числа (который не является полным квадратом) имеет период, то есть периодическое разложение, похожее на то, как рациональные числа имеют повторяющееся разложения десятичной системе счисления.
Большинство общепризнанных аналитических методов являются итеративными и состоят из двух шагов: нахождения подходящего начального значения с последующим итеративным уточнением пока не будет достигнут определённый критерий остановки. Начальным значением может быть любое число, но если оно ближе к конечному значению, число требуемых итераций потребуется меньше. Наиболее известным таким методом, да ещё и удобным для программирования, является метод Ньютона, который основывается на вычислении производной. Несколько методов, такие как обычное деление вручную по схеме Горнера или разложение в ряд, не требуют задание начального значения. В некоторых приложениях требуется найти целочисленный квадратный корень, который является квадратным корнем, округлённым до ближайшего целого (в этом случае может быть использована модифицированная процедура).
Используемый метод зависит от того, как результат будет использован (то есть, насколько точен должен быть результат) и какие средства есть под рукой. Методы можно грубо разбить на те, которые можно выполнить в уме, которые требуют карандаша и листа бумаги, или те, которые реализуются в виде программы и выполняются на компьютерах или других вычислительных устройствах. Могут приниматься в расчёт скорость сходимости (сколько итераций потребуется для достижения заданной точности), вычислительной сложности отдельных операций (таких как деление) или итераций, и распределение ошибок (точность результата).
Процедуры поиска квадратных корней (в частности, корня из 2) известны по меньшей мере со времён древнего Вавилона (17-й век до нашей эры). Метод Герона из Египта первого века был первым проверяемым алгоритмом для вычисления квадратного корня. Современные аналитические методы начались разрабатываться после принятия арабских цифр в Западной Европе в Раннем Ренессансе. В настоящие дни почти все вычислительные устройства имеют функцию быстрого и точного вычисления квадратного корня в виде встроенной конструкции языка программирования, библиотечной функции или аппаратного оператора, которые основываются на описанных ниже процедурах.
Начальная оценка[править | править код]
Многие итеративные алгоритмы вычисления квадратного корня требуют задания начального случайного значения. Это значение должно быть ненулевым положительным числом. Оно должно быть между 1 и 



Вообще говоря, оценка рассматривается на произвольном интервале, в котором известно, что в нём содержится корень (таком как ![{displaystyle [x_{0},S/x_{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6b4547a4f0e1b1d3ed33a5a51d943916fff3a5c)

Десятичная оценка[править | править код]
Обычно число 




Скалярные оценки[править | править код]
Скалярные методы делят весь диапазон на интервалы и оценка в каждом интервале представлена одним числом. Если диапазон рассматривается как один интервал, то арифметическое среднее (5,5) или геометрическое среднее (
Для двух интервалов, разбитых геометрически, квадратный корень 
Эта оценка имеет максимальную абсолютную погрешность 
Например, для 



Линейная оценка[править | править код]
Лучшей оценкой и стандартным методом является линейное приближение функции 

![{displaystyle [1,100]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/691b8a5a7718ae3a31861edcfade2fdc51b1b41e)
Прямая, получающаяся методом наименьших квадратов, минимизирует среднее расстояние между оценкой и значением функции. Её уравнение — 

Это лучшая оценка в среднем, которую можно получить одной попыткой линейной аппроксимации функции 
![{displaystyle [1,100]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/691b8a5a7718ae3a31861edcfade2fdc51b1b41e)
Чтобы разделить на 10, вычитаем единицу из показателя степени 
![{displaystyle [1,100]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/691b8a5a7718ae3a31861edcfade2fdc51b1b41e)
Существенно лучшую оценку можно получить при помощи кусочно–линейной аппроксимации, то есть с помощью нескольких отрезков, которые приближают поддугу исходной дуги. Чем больше отрезков используется, тем лучше приближение. Наиболее употребительно применение касательных. Критичным моментом является как делить дугу и где располагать точки касания. Действенным методом деления дуги от y=1 до y=100 является геометрический — для двух интервалов границей интервалов является квадратный корень исходного интервала, 1*100, то есть ![{displaystyle [1,{sqrt[{2}]{100}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1148314c98c621d190b2e61369cd37868e7c64cc)
![{displaystyle [{sqrt[{2}]{100}},100]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/563876988da2d89347d7994a96d06217beab52a1)
![{displaystyle [1,{sqrt[{3}]{100}}],[{sqrt[{3}]{100}},({sqrt[{3}]{100}})^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bf83cf8365349c94e685807e6467c5771175aa6)
![{displaystyle [({sqrt[{3}]{100}})^{2},100]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd12badd3328081e44b7f76ed0af1ad5b1456902)
![{displaystyle {sqrt[{2}]{100}}=10}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f70489e7084dcb53ce60f6582675109116dbd76c)







Максимальные абсолютные значения оказываются в правых границах интервалов, в точках a=10 и 100, и равны 0,54 и 1,7 соответственно. Максимальные относительные ошибки появляются на концах интервалов, в точках a=1, 10 и 100, и равны 17%. 17% или 0,17. Они больше, чем 1/10, так что метод даёт точность менее одной значащей цифры.
Гиперболическая оценка[править | править код]
В некоторых случаях может оказаться действенной гиперболическая оценка, поскольку гипербола также является выпуклой кривой и может лежать вдоль дуги Y = x2 лучше, чем прямая. Гиперболическая оценка вычислительно более сложная, поскольку для неё нужно деление на число с плавающей запятой. Почти оптимальной гиперболической аппроксимацией к x2 на интервале ![{displaystyle [1,100]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/691b8a5a7718ae3a31861edcfade2fdc51b1b41e)



Деление с плавающей запятой должно быть с точностью до одного десятичного знака, поскольку вся оценка даёт такую точность, и такое деление можно выполнить в уме. Гиперболическая оценка в среднем лучше, чем скалярная или линейная оценка. Её максимальная абсолютная ошибка составляет 1,58 в точке 100, а максимальная относительная ошибка составляет 16,0% в точке 10. Для худшего случая a=10 оценка равна 3,67. Если начать с 10 и применять итерации Нютона-Рапсона напрямую, требуется две итерации, которые дают 3,66, прежде чем достичь точности гиперболической оценки. Для более типичного случая наподобие 75 гиперболическая оценка даёт 8,00 и требуется 5 итераций Ньютона-Рапсона с начальным значением 75, чтобы получить более точный результат.
Арифметическая оценка[править | править код]
Метод, аналогичный кусочно-линейной аппроксимации, но использующий лишь арифметические операции вместо алгебраических уравнений, использует таблицу умножения в обратную сторону — квадратный корень чисел между 1 и 100 где-то между 1 и 10, так что, поскольку мы знаем, что 25 является точным квадратом (5 × 5) и 36 является точным квадратом (6 × 6), то квадратный корень из числа, которое больше 25, но меньше 36, начинается с цифры 5. Аналогично для чисел между другими квадратами. Этот метод даёт правильный первый знак, но точность его всего одна цифра — первая цифра квадратного корня из 35, например, равна 5, но сам корень из 35 почти равен 6.
Лучше делить интервал между двумя квадратами пополам. Так что корень любого числа между 25 и половины пути до 36 (что есть 30,5) оценивается как 5, остальные числа, большие 30,5 вплоть до 36 оцениваются как 6[4]. Процедура требует очень мало арифметики для нахождения середины двух произведений из таблицы. Вот таблица таких чисел:
| a | nearest square |  est. est.
|
|---|---|---|
| 1 to 2,5 | 1 (= 12) | 1 |
| 2,5 to 6,5 | 4 (= 22) | 2 |
| 6,5 to 12,5 | 9 (= 32) | 3 |
| 12,5 to 20,5 | 16 (= 42) | 4 |
| 20,5 to 30,5 | 25 (= 52) | 5 |
| 30,5 to 42,5 | 36 (= 62) | 6 |
| 42,5 to 56,5 | 49 (= 72) | 7 |
| 56,5 to 72,5 | 64 (= 82) | 8 |
| 72,5 to 90,5 | 81 (= 92) | 9 |
| 90,5 to 100 | 100 (= 102) | 10 |
Конечной операцией будет умножение оценки k на степень десятки, делённой пополам, так что для 
Метод даёт точность в одну значащую цифру, поскольку он округляет до лучшей первой цифры.
Метод можно распространить до 3 значащих цифр в большинстве случаев, интерполируя между ближайшими квадратами. Если 


где
Конечной операцией, как и выше, служит умножение результата на степень десятки, делённой пополам
Число k есть десятичная цифра, а R есть дробь, которую следует превратить в десятичную. Дробь имеет обычно одну цифру в числителе и одну или две цифры в знаменателе, так что преобразование в десятичную дробь можно провести в уме.
Пример: найти квадратный корень из 75. 





Двоичная оценка[править | править код]
Когда работа ведётся в двоичной системе счисления (скажем, в процессоре компьютера), 



что является регрессией методом наименьших квадратов по 3 старшим битам. 


[5]
которая имеет максимальную абсолютную ошибку 0,086 в точке 2 и максимальную относительную ошибку в 6,1% в точках 

Для 


Оценку для 

Вавилонский метод[править | править код]
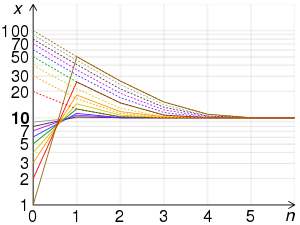
Полулогарифмические графики сравнения скорости сходимости вавилонского метода нахождения квадратного корня для 100 различных начальных значений. Отрицательное начальное значение приводит к отрицательному корню. Заметим, что более близкие к корню значения сходятся быстрее, и все приближения являются завышенными. В SVG файле наведите курсор мыши на конкретный график, чтобы видеть точки этого графика.
Возможно первым алгоритмом, используемым для аппроксимации 


Точнее, если x является начальным приближением для 


поскольку
.
Следовательно, мы можем компенсировать ошибку и обновить нашу старую оценку
Поскольку вычисленная ошибка не была точной, она станет нашим следующим приближением. Процесс обновления продолжается пока не достигнем нужной точности. Это алгоритм с квадратичной сходимостью, что означает, что число верных цифр приближения (грубо говоря) удваивается с каждой итерацией. Работает он так:
- Начинаем с любого положительного начального значения
(чем ближе к истинному квадратному корню числа S, тем лучше).
- Положим
равным среднему между
и
(используем среднее арифметическое для аппроксимации среднего геометрического).
- Повторяем шаг 2 пока не достигнем нужной точности.
Алгоритм можно представить следующим образом:
Алгоритм работает также хорошо и для p-адических чисел, но не может быть использован для отождествления вещественных квадратных корней с p-адичными квадратными корнями. Можно, например, построить последовательность рациональных чисел, полученных этим методом, которая сходится к +3 в случае вещественных чисел, но к -3 в 2-адичных числах.
Пример[править | править код]
Для вычисления √S, где S = 125348, с точностью до шести значащих цифр используем метод грубой оценки, описанный выше
Поэтому 
Сходимость[править | править код]
Предположим, что x0 > 0 и S > 0. Тогда для любого n xn > 0. Относительная ошибка[en] xn определена как
а тогда
Теперь можно показать, что
а следовательно
а отсюда следует гарантированная сходимость и эта сходимость квадратичная.
Сходимость в худшем случае[править | править код]
Если использовать метод грубой оценки с вавилонским методом, то наихудшие случаи точности в нисходящей последовательности:
А тогда в любом случае
Ошибки округления ослабляют сходимость. Рекомендуется хранить по меньшей мере одну лишнюю цифру выше желаемой точности xn, чтобы минимизировать ошибки округления.
Метод Бакхшали[править | править код]
Этот метод для поиска приближения квадратного корня был написан в древнеиндийской рукописи, называемой манускриптом Бакхшали. Метод эквивалентен двум итерациям вавилонского метода с начальным значением x0. Таким образом, алгоритм является квадратично сходящимся, что означает, что число верных знаков приближения увеличивается примерно в четыре раза с каждой итерацией[8]. Представление алгоритма в современной нотации следующее: Следует вычислить 
Это можно использовать для построения рационального приближения к квадратному корню, начав с целого числа. Если 


Метод Бакхшали может быть обобщён для вычисления произвольного корня, включая дробные корни[9].
Пример[править | править код]
Используем тот же пример, что был приведён для вавилонского метода. Пусть 
Аналогично вторая итерация даёт
Цифра за цифрой[править | править код]
Это метод последовательного поиска каждой цифры квадратного корня. Метод медленнее вавилонского, но имеет некоторые преимущества
- Он проще для вычислений вручную.
- Каждый найденный знак корня заведомо верный, то есть он не будет изменён на следующих итерациях.
- Если представление квадратного корня имеет конечное число цифр, алгоритм завершается после последней найденной цифры. Таким образом, он может быть использован для проверки, что данное число является полным квадратом.
- Алгоритм работает в любой системе счисления, и естественно, работа алгоритма зависит от выбранной системы счисления.
Палочки Непера включают дополнительные средства для выполнения этого алгоритма. Алгоритм вычисления n-го корня цифра за цифрой[en] является обобщением этого метода.
Основной принцип[править | править код]
Рассмотрим сначала случай нахождения квадратного корня из числа Z, являющегося квадратом двузначного числа XY, где X — это цифра десятков, а Y — цифра единиц. Имеем:
Сначала определим значение X. X — это наибольшая цифра, такая что X2 не превосходит Z, от которого отброшены две последние цифры.
На следующей итерации соединяем пару цифр, умножая X на 2 и помещая результат в позицию десятков, а затем пытаемся найти, чему же равно Y.
Поскольку в нашем случае ответом является точный квадратный корень, алгоритм останавливается.
Та же идея может быть распространена на вычисление произвольного квадратного корня. Представим, что мы можем найти квадратный корень из N как сумму n положительных чисел, таких что
Путём многократного использования тождества
правую часть можно представить в виде
Это выражение позволяет нам найти квадратный корень последовательным подбором значений 

![{displaystyle Y_{m}=[2P_{m-1}+a_{m}]a_{m},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f44cbdda22b202c32f5420b0ab8051e609ffe16)


так что 





Например, в десятичной системе мы имеем
где 



Поскольку указатели положения 

Очевидно, что подобный метод может быть использован для вычисления квадратного корня в любой системе счисления, не обязательно в десятичной. Например, нахождение цифра за цифрой квадратного корня в двоичной системе довольно эффективно, поскольку значение 











Десятичная система счисления[править | править код]
Запишем исходное число в десятичном виде. Числа, записываются по аналогии алгоритму деления столбиком, и, как и в длинном делении, квадратный корень будет писаться в верхней строке. Теперь разобьём цифры на пары, начиная с запятой, в обе стороны от неё. Десятичная запятая квадратного корня будет на десятичной запятой квадрата. Одна цифра квадратного корня записывается над парой цифр квадрата.
Начиная с крайне левой позиции выполняем следующую процедуру для каждой пары цифр:
- Сносим вниз старшую пару ещё неиспользованных цифр (если все цифры использованы, пишем “00”) и записываем их справа от остатка предыдущего шага (на первом шаге остатка нет). Другими словами, умножаем остаток на 100 и добавляем две цифры. Это будет текущим значением c.
- Находим p, y и x следующим образом:
- Вычитаем y из c для образования нового остатка.
- Если остаток равен нулю и нет больше цифр, которые можно спустить вниз, алгоритм останавливается. В противном случае возвращаемся на шаг 1 и выполняем следующую итерацию.
Примеры[править | править код]
Находим квадратный корень из 152,2756.
1 2. 3 4
/
/ 01 52,27 56
01 1*1 <= 1 < 2*2 x = 1
01 y = x*x = 1*1 = 1
00 52 22*2 <= 52 < 23*3 x = 2
00 44 y = (20+x)*x = 22*2 = 44
08 27 243*3 <= 827 < 244*4 x = 3
07 29 y = (240+x)*x = 243*3 = 729
98 56 2464*4 <= 9856 < 2465*5 x = 4
98 56 y = (2460+x)*x = 2464*4 = 9856
00 00 Алгоритм останавливается: Ответ 12,34
Двоичная система счисления[править | править код]
Этот раздел использует формализм раздела «Вычисление цифра за цифрой» с небольшими изменениями, что 



Теперь мы пробегаем по всем 




Чтобы определить, равно ли 








Чтобы избежать возведения в квадрат 



Первоначально мы устанавливаем 


В качестве дополнительной оптимизации сохраняем 







Заметим, что
, что является конечным результатом, возвращаемым функцией, представленной ниже.
Реализация алгоритма на языке C[10]:
int32_t isqrt(int32_t n)
{ assert(("входное значение должно быть неотрицательным", n > 0));
int32_t x = n; //  int32_t c = 0; //
int32_t c = 0; //  //
//  начинается с наибольшей степени четырёх <= n
int32_t d = 1 << 30; // Второй старший бит устанавливаем в 1.
// То же самое, что ((unsigned)INT32_MAX + 1) / 2.
while (d > n) d >>= 2;
while (d != 0) // для
начинается с наибольшей степени четырёх <= n
int32_t d = 1 << 30; // Второй старший бит устанавливаем в 1.
// То же самое, что ((unsigned)INT32_MAX + 1) / 2.
while (d > n) d >>= 2;
while (d != 0) // для  { if (x >= c + d) // если
{ if (x >= c + d) // если  , то
, то  { x -= c + d; //
{ x -= c + d; //  c = (c >> 1) + d; //
c = (c >> 1) + d; //  } else
c >>= 1; //
} else
c >>= 1; //  d >>= 2; //
d >>= 2; //  }
return c; //
}
return c; //  }
}
Можно реализовать более быстрый алгоритм как в двоичной, так и в десятичной системе счисления, если использовать таблицы для выбора, то есть реализация принципа использование больше памяти сокращает время исполнения[11].
Экспоненциальное тождество[править | править код]
Карманные калькуляторы обычно реализуют хорошие программы вычисления экспоненты и натурального логарифма. Вычисление квадратного корня S тогда производится с помощью свойств логарифмов (

Или в более общем случае:
Знаменатель дроби n соответствует степени корня. В случае квадратного корня знаменатель равен 2. То же самое тождество используется для вычисления квадратного корня с помощью таблиц логарифмов или логарифмических линеек.
Такой метод вычисления квадратного корня удобен для калькуляторов, поскольку они обычно не критичны ко времени выполнения операции. Однако ресурсоемкость данного метода делает его малопригодным для использования в ЭВМ, где простые арифметические операции должны обладать минимальными задержками. Тем не менее описанный метод вычисления квадратного корня применялся в ЭВМ ZX Spectrum.
Итеративный метод с двумя переменными[править | править код]
Этот метод применим для поиска квадратного корня из 

Это, однако, не является существенным ограничением для вычислений на компьютерах, поскольку в представлениях двоичных чисел с плавающей запятой и с фиксированной запятой тривиально умножить 



Начальный шаг метода
Итерационные шаги
Тогда 

Заметим, что сходимость 

Доказательство метода достаточно простое. Сначала перепишем итерационное определение 
.
Теперь «в лоб» доказывается, что
а потому сходимость 



Этот метод разработали около 1950 года М. В. Уилкс, Д. Дж. Уилер и С. Гилл[12] для использования в EDSAC, одном из первых электронных компьютеров[13]. Позднее метод был обобщён на неквадратные корни[14].
Итеративные методы вычисления обратного к квадратному корню числа[править | править код]
Далее приведены итеративные методы вычисления обратного к квадратному корню из S числа, то есть 


Алгоритм Гольдшмидта[править | править код]
Некоторые компьютеры используют алгоритм Гольдшмидта для одновременного вычисления 

Алгоритм Гольдшмидта находит 
Первый способ записи алгоритма Гольдшмидта начинается с
(обычно используется поиск в таблице)
и осуществляются итерации
пока 
,
.
Заметим, что можно опустить вычисление 


Второй способ, использующий операции совмещённого умножения-сложения начинается с
(обычно используется поиск в таблице)
и осуществляются итерации
пока 
.
Ряды Тейлора[править | править код]
Если N является приближением к 
Порядок сходимости равен числу используемых членов ряда. При использовании двух членов метод эквивалентен вавилонскому методу. При использовании трёх членов каждая итерация использует почти столько же операций, сколько использует приближение Бакхшали, но сходимость слабее. Поэтому этот метод не является особенно эффективным способом вычисления. Для максимизации скорости сходимости, следует выбрать N так, чтобы 
Разложение в цепную дробь[править | править код]
Квадратичные иррациональности (числа вида 


Применяя это выражение для 
Числитель/знаменатель разложения для непрерывных дробей (см. слева) затруднительно записывать, а также трудно укладывается в существующую систему форматирования документов. По этой причине была разработана специальная нотация для компактного представления целой и периодической частей непрерывных дробей. Одно из таких соглашений использует лексическую «ломаную линию» для представления черты между числителем и знаменателем, что позволяет записывать дробь горизонтально, а не вертикально:
Здесь каждая горизонтальная черта (в дроби) представлена тремя чертами — двумя вертикальными и одной горизонтальной, которые отделяют 

Ещё более компактная нотация имеет специальный вид
Для периодических непрерывных дробей (которыми являются все квадратные корни), повторяющаяся часть указывается лишь один раз с чертой над повторяющейся частью:
Для √2 значение 
Следуя этим путём мы получаем обобщённую непрерывную дробь[en] для квадратного корня

Первым шагом вычисления такой дроби для получения квадратного корня является подстановки для корня и выбор числа знаменателей. Например, в канонической форме 

Шаг 2. Непрерывная дробь свёртывается снизу вверх, один знаменатель за раз, чтобы получить рациональную дробь, числитель и знаменатель которой являются целыми числами. Процесс свёртывания тогда выглядит следующим образом (беря первые три знаменателя):
Наконец (шаг 3), делим числитель на знаменатель рациональной дроби, чтобы получить приближённое значение корня:
округлено до трёх знаков.
Действительное значение корня √2 равно 1,41 с точностью до трёх значащих цифр. Относительная ошибка равна 0,17%, так что рациональная дробь хороша почти до трёх знаков. Если брать больше знаменателей, получим последовательное улучшение приближения — четыре знаменателя дают дробь 
Непрерывные дроби доступны в таблицах по меньшей мере для малых чисел и общеизвестных констант. Для произвольных чисел в десятичной системе счисления предварительно вычисленные значения, скорее всего, бесполезны. Следующая таблица малых рациональных дробей, называемых подходящими дробями, полученных из канонических непрерывных дробей для нескольких констант:
| √S | цепная дробь | ~десятичное | Подходящие дроби |
|---|---|---|---|
| √2 | ![{displaystyle [1;{overline {2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/076639b7e958148e44b2dfe0bea22fca5b382c6f)
|
1,41421 | 
|
| √3 | ![{displaystyle [1;{overline {1,2}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/118ba741c0676d2c89508d125b151ab4d17b94eb)
|
1,73205 | 
|
| √5 | ![{displaystyle [2;{overline {4}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/574efb17309ec89c6733471fb7482deef730fafc)
|
2,23607 | 
|
| √6 | ![{displaystyle [2;{overline {2,4}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5f8f79da35588663e839e36b8447e741b651576)
|
2,44949 | 
|
| √10 | ![{displaystyle [3;{overline {6}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7e53c2d8b2dff31b1a66bf6179455be532d3a93)
|
3,16228 | 
|

|
![{displaystyle [1;1,3,2,1,1,6...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dc1ddad6bd13b951e89a900cadeaab3a1770c74)
|
1,77245 | 
|

|
![{displaystyle [1;1,1,1,5,1,1...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dc729725d22fec6931be55fdeb24281625abc18)
|
1,64872 | 
|

|
![{displaystyle [1;3,1,2,11,3,7...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c2b676231a4a5d8ae24101d610ec5465334869a)
|
1,27202 | 
|
Примечание: Перечислены все подходящие дроби вплоть до знаменателя 99.
В общем виде чем больше знаменатель рациональной дроби, тем лучше аппроксимация. Также можно доказать, что отсечение непрерывной дроби приводит к рациональной дроби, с лучшим приближением к корню любой дроби со знаменателем, меньшим или равным знаменателю этой дроби. Например, никакая дробь со знаменателем, не превосходящем 70, не будет так же хороша, как аппроксимация к √2 числом 99/70.
Метод последовательности Люка[править | править код]
Последовательность Люка первого рода 
и его характеристическим многочленом является
, он имеет дискриминант 
Всё это даёт следующее положительное значение
. Так что если мы хотим получить 






Наиболее эффективный способ вычисления 

Итог:
а тогда при 
Аппроксимации, зависящие от представления в виде числа с плавающей запятой[править | править код]
Число представляется в виде числа с плавающей запятой как 





Если взять лишь целую часть мантиссы, она может принимать значения от 1 до 99 и это можно использовать в качестве индекса в таблице из 99 предварительно вычисленных корней для завершения оценки. Компьютер, использующий шестнадцатеричное основание может потребовать большей таблицы, но при использовании основания 2 таблица будет состоять лишь из трёх величин — возможными битами целой части уточнённого представления мантиссы могут быть 01 (если степень чётная, так что нет никакого сдвига, и заметим, что нормализованное число с плавающей точкой всегда имеет ненулевую старшую цифру), или, если степень была нечётной, 10 или 11, это два первых бита исходной мантиссы. Тогда 6,25 (= 110,01 в двоичном представлении) нормализуется к 


Таблица с тремя элементами может быть расширена для включения дополнительных бит мантиссы. Однако в случае компьютеров вместо вычисления интерполяции в таблице часто лучше искать более простой способ вычислений, дающий те же результаты. Всё теперь зависит от точных деталей формата представления чисел и от операций, которые доступны для получения частей числа и работы с ними. Например, Фортран содержит функцию EXPONENT(x) для получения степени. Усилия, потраченные на получение хорошего начального приближения окупаются за счёт исключения дополнительных итераций процесса уточнения, которые потребовались бы в случае плохого приближения.
Многие компьютеры следуют стандарту IEEE для чисел с плавающей запятой[en] (или достаточно близкое представление) и очень быстрое приближение для квадратного корня может быть получено в качестве стартового значения метода Ньютона. Техника данного приближения вытекает из факта, что формат плавающего числа (по основанию два) аппроксимирует логарифм по основанию 2. То есть, 
Так что для 32-битного числа с плавающей запятой в формате IEEE (в котором степень имеет смещение[en] на 127[16]) вы можете получить приближённый логарифм путём интерпретации числа как 32-битного целого, умножения его на 
Например, число 1,0 в шестнадцатеричной системе имеет вид 0x3F800000, что можно представить как 



Чтобы получить квадратный корень, делим логарифм на 2 и преобразуем результат обратно. Ниже программа демонстрирует идею. Заметим, что младший бит порядка намеренно переводится в мантиссу. Одним из способов обоснования шагов этой программы, в предположении что 

/* Предполагаем, что плавающее число имеет формат IEEE 754 */ #include <stdint.h> float sqrt_approx(float z) { union { float f; uint32_t i; } val = {z}; /* Преобразуем тип не меняя битового представления */ /* * Для обоснования работы кода докажите, что * ((((val.i / 2^m) - b) / 2) + b) * 2^m = ((val.i - 2^m) / 2) + ((b + 1) / 2) * 2^m) * где * b = смещение степени * m = число бит в мантиссе */ val.i -= 1 << 23; /* Вычитаем 2^m. */ val.i >>= 1; /* Делим на 2. */ val.i += 1 << 29; /* Добавляем ((b + 1) / 2) * 2^m. */ return val.f; /* Интерпретируем снова как плавающее */ }
Три арифметические операции, образующие ядро функции можно представить в одну строку. Дополнительное уточнение может быть добавлено для уменьшения максимальной относительной ошибки. Таким образом, три операции, не включая приведение к вещественному, можно переписать как
val.i = (1 << 29) + (val.i >> 1) - (1 << 22) + a;
где a — смещение для уменьшения ошибок аппроксимации. Например, с a = 0 результаты точны для чётных степеней двойки 2 (например, 1,0), но для других чисел результат будет несколько великоват (например, 1,5 для 2,0 вместо 1,414… с ошибкой 6%). При a = −0x4B0D2 максимальная относительная ошибка сокращается до ±3,5%.
Если приближение нужно использовать как начальное значение для метода Ньютона в уравнении 
Обратное значение квадратного корня[править | править код]
Вариант описанной выше процедуры представлен ниже и он может быть использован для вычисления обратного к квадратному корню, то есть 
float invSqrt(float x) { float xhalf = 0.5f * x; union { float x; int i; } u; u.x = x; u.i = 0x5f375a86 - (u.i >> 1); /* Следующая строка может быть повторена произвольное число раз для увеличения точности */ u.x = u.x * (1.5f - xhalf * u.x * u.x); return u.x; }
Некоторые СБИС реализуют нахождение обратной величины к квадратному корню с помощью полиномиальной оценки с последующей итерацией Голдшмидта[18].
Корень из отрицательного или комплексного числа[править | править код]
Если 
Если 

Это можно проверить возведением в квадрат[19][20]. Здесь
является модулем числа S. Главный корень комплексного числа определяется как корень с неотрицательной вещественной частью.
См. также[править | править код]
- Алгоритм альфа max плюс бета min[en]
- Целочисленный квадратный корень
Примечания[править | править код]
- ↑ Кроме главного корня имеется отрицательный квадратный корень, равный по модулю главному корню, но с противоположным знаком, за исключением случая нуль, когда имеется два одинаковых корня, равных нулю.
- ↑ Множители два и шесть используются ввиду того, что они аппроксимируют среднее геометрическое нижнего и верхнего возможных значений с заданным числом знаков:
и
.
- ↑ Неокруглённая оценка имеет максимальную абсолютную ошибку 2,65 в точке 100 и максимальную относительную ошибку в 26,5% в точках y=1, 10 и 100
- ↑ Если число находится ровно посередине между двумя квадратами, наподобие 30,5, берём большее число, которое в нашем случае 6
- ↑ Это уравнение касательной прямой к y=x2 в точке y=1.
- ↑ Fowler, Robson, 1998, с. 376.
- ↑ Heath, 1921, с. 323–324.
- ↑ Bailey, Borwein, 2012, с. 646–657.
- ↑ Bucking down to the Bakhshali manuscript. Simply Curious blog (5 июня 2018). Дата обращения: 21 декабря 2020. Архивировано 26 октября 2020 года.
- ↑ Fast integer square root by Mr. Woo’s abacus algorithm (archived)
- ↑ Integer Square Root function. Дата обращения: 30 декабря 2021. Архивировано 30 сентября 2007 года.
- ↑ Wilkes, Wheeler, Gill, 1951.
- ↑ Campbell-Kelly, 2009.
- ↑ Gower, 1958, с. 142–143, 1958.
- ↑ Markstein, Peter (November 2004). Software Division and Square Root Using Goldschmidt’s Algorithms (PDF). 6th Conference on Real Numbers and Computers. Dagstuhl, Germany. CiteSeerX 10.1.1.85.9648. Архивировано (PDF) из оригинала 2022-04-28. Дата обращения 2021-12-30.
- ↑ К экспоненте числа добавляется 127, что позволяет интерпретировать экспоненту как число без знака.
- ↑ Fast Inverse Square Root Архивная копия от 6 февраля 2009 на Wayback Machine by Chris Lomont
- ↑
“High-Speed Double-Precision Computation of Reciprocal, Division, Square Root and Inverse Square Root”
by José-Alejandro Piñeiro and Javier Díaz Bruguera 2002 (abstract) - ↑ Abramowitz, Stegun, 1964, с. 17.
- ↑ Cooke, 2008, с. 59.
Литература[править | править код]
- David Fowler, Eleanor Robson. Square Root Approximations in Old Babylonian Mathematics: YBC 7289 in Context // Historia Mathematica. — 1998. — Т. 25, вып. 4. — doi:10.1006/hmat.1998.2209.
- Thomas Little Heath. A History of Greek Mathematics. — Oxford: Clarendon Press, 1921. — Т. 2. — С. 323–324.
- David Bailey, Jonathan Borwein. Ancient Indian Square Roots: An Exercise in Forensic Paleo-Mathematics // American Mathematical Monthly. — 2012. — Т. 119, вып. 8.
- Miltonn Abramowitz, Irene A. Stegun. Section 3.7.26 // Handbook of mathematical functions with formulas, graphs, and mathematical tables. — Courier Dover Publications, 1964. — С. 17. — ISBN 978-0-486-61272-0.
- J. C. Gower. A Note on an Iterative Method for Root Extraction // The Computer Journal. — 1958. — Т. 1 1, вып. 3.
- M. Campbell-Kelly. Origin of Computing // Scientific American. — 2009. — Сентябрь.
- Roger Cooke. Classical algebra: its nature, origins, and uses. — John Wiley and Sons, 2008. — ISBN 978-0-470-25952-8.
- M. V. Wilkes, D. J. Wheeler, S. Gill. The Preparation of Programs for an Electronic Digital Computer. — Addison-Wesley, 1951.
СсылкиWeisstein, Eric W. Square root algorithms (англ.) на сайте Wolfram MathWorld.[править | править код]
- Square roots by subtraction
- Integer Square Root Algorithm by Andrija Radović
- Personal Calculator Algorithms I : Square Roots (William E. Egbert), Hewlett-Packard Journal (may 1977) : page 22
- Калькулятор для обучения квадратному корню
Факт 1.
(bullet) Возьмем некоторое неотрицательное число (a) (то есть (ageqslant 0)). Тогда (арифметическим) квадратным корнем из числа (a) называется такое неотрицательное число (b), при возведении которого в квадрат мы получим число (a): [sqrt a=bquad text{то же самое, что }quad a=b^2] Из определения следует, что (ageqslant 0, bgeqslant 0). Эти ограничения являются важным условием существования квадратного корня и их следует запомнить!
Вспомним, что любое число при возведении в квадрат дает неотрицательный результат. То есть (100^2=10000geqslant 0) и ((-100)^2=10000geqslant 0).
(bullet) Чему равен (sqrt{25})? Мы знаем, что (5^2=25) и ((-5)^2=25). Так как по определению мы должны найти неотрицательное число, то (-5) не подходит, следовательно, (sqrt{25}=5) (так как (25=5^2)).
Нахождение значения (sqrt a) называется извлечением квадратного корня из числа (a), а число (a) называется подкоренным выражением.
(bullet) Исходя из определения, выражения (sqrt{-25}), (sqrt{-4}) и т.п. не имеют смысла.
Факт 2.
Для быстрых вычислений полезно будет выучить таблицу квадратов натуральных чисел от (1) до (20): [begin{array}{|ll|}
hline
1^2=1 & quad11^2=121 \
2^2=4 & quad12^2=144\
3^2=9 & quad13^2=169\
4^2=16 & quad14^2=196\
5^2=25 & quad15^2=225\
6^2=36 & quad16^2=256\
7^2=49 & quad17^2=289\
8^2=64 & quad18^2=324\
9^2=81 & quad19^2=361\
10^2=100& quad20^2=400\
hline end{array}]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
(bullet) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть [sqrt apmsqrt bne sqrt{apm b}] Таким образом, если вам нужно вычислить, например, (sqrt{25}+sqrt{49}), то первоначально вы должны найти значения (sqrt{25}) и (sqrt{49}), а затем их сложить. Следовательно, [sqrt{25}+sqrt{49}=5+7=12] Если значения (sqrt a) или (sqrt b) при сложении (sqrt
a+sqrt b) найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме (sqrt
2+ sqrt {49}) мы можем найти (sqrt{49}) – это (7), а вот (sqrt
2) никак преобразовать нельзя, поэтому (sqrt 2+sqrt{49}=sqrt
2+7). Дальше это выражение, к сожалению, упростить никак нельзя
(bullet) Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть [sqrt acdot sqrt b=sqrt{ab}quad text{и}quad
sqrt a:sqrt b=sqrt{a:b}] (при условии, что обе части равенств имеют смысл)
Пример: (sqrt{32}cdot sqrt 2=sqrt{32cdot
2}=sqrt{64}=8);
(sqrt{768}:sqrt3=sqrt{768:3}=sqrt{256}=16);
(sqrt{(-25)cdot (-64)}=sqrt{25cdot 64}=sqrt{25}cdot sqrt{64}=
5cdot 8=40).
(bullet) Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем (sqrt{44100}). Так как (44100:100=441), то (44100=100cdot 441). По признаку делимости число (441) делится на (9) (так как сумма его цифр равна 9 и делится на 9), следовательно, (441:9=49), то есть (441=9cdot 49).
Таким образом, мы получили: [sqrt{44100}=sqrt{9cdot 49cdot 100}=
sqrt9cdot sqrt{49}cdot sqrt{100}=3cdot 7cdot 10=210] Рассмотрим еще один пример: [sqrt{dfrac{32cdot 294}{27}}=
sqrt{dfrac{16cdot 2cdot 3cdot 49cdot 2}{9cdot 3}}= sqrt{
dfrac{16cdot4cdot49}{9}}=dfrac{sqrt{16}cdot sqrt4 cdot
sqrt{49}}{sqrt9}=dfrac{4cdot 2cdot 7}3=dfrac{56}3]
(bullet) Покажем, как вносить числа под знак квадратного корня на примере выражения (5sqrt2) (сокращенная запись от выражения (5cdot
sqrt2)). Так как (5=sqrt{25}), то [5sqrt2=sqrt{25}cdot sqrt2=sqrt{25cdot 2}=sqrt{50}] Заметим также, что, например,
1) (sqrt2+3sqrt2=4sqrt2),
2) (5sqrt3-sqrt3=4sqrt3)
3) (sqrt a+sqrt a=2sqrt a).
Почему так? Объясним на примере 1). Как вы уже поняли, как-то преобразовать число (sqrt2) мы не можем. Представим, что (sqrt2) – это некоторое число (a). Соответственно, выражение (sqrt2+3sqrt2) есть не что иное, как (a+3a) (одно число (a) плюс еще три таких же числа (a)). А мы знаем, что это равно четырем таким числам (a), то есть (4sqrt2).
Факт 4.
(bullet) Часто говорят “нельзя извлечь корень”, когда не удается избавиться от знака (sqrt {} ) корня (радикала) при нахождении значения какого-то числа. Например, извлечь корень из числа (16) можно, потому что (16=4^2), поэтому (sqrt{16}=4). А вот извлечь корень из числа (3), то есть найти (sqrt3), нельзя, потому что нет такого числа, которое в квадрате даст (3).
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа (sqrt3, 1+sqrt2, sqrt{15}) и т.п. являются иррациональными.
Также иррациональными являются числа (pi) (число “пи”, приблизительно равное (3,14)), (e) (это число называют числом Эйлера, приблизительно оно равно (2,7)) и т.д.
(bullet) Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой (mathbb{R}).
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
(bullet) Модуль вещественного числа (a) – это неотрицательное число (|a|), равное расстоянию от точки (a) до (0) на вещественной прямой. Например, (|3|) и (|-3|) равны 3, так как расстояния от точек (3) и (-3) до (0) одинаковы и равны (3). 
(bullet) Если (a) – неотрицательное число, то (|a|=a).
Пример: (|5|=5); (qquad |sqrt2|=sqrt2).
(bullet) Если (a) – отрицательное число, то (|a|=-a).
Пример: (|-5|=-(-5)=5); (qquad |-sqrt3|=-(-sqrt3)=sqrt3).
Говорят, что у отрицательных чисел модуль “съедает” минус, а положительные числа, а также число (0), модуль оставляет без изменений.
НО такое правило годится только для чисел. Если у вас под знаком модуля находится неизвестная (x) (или какая-то другая неизвестная), например, (|x|), про которую мы не знаем, положительная она, равна нулю или отрицательная, то избавиться от модуля мы не можем. В этом случае это выражение таким и остается: (|x|).
(bullet) Имеют место следующие формулы: [{large{sqrt{a^2}=|a|}}] [{large{(sqrt{a})^2=a}},
text{ при условии } ageqslant 0] Очень часто допускается такая ошибка: говорят, что (sqrt{a^2}) и ((sqrt a)^2) – одно и то же. Это верно только в том случае, когда (a) – положительное число или ноль. А вот если (a) – отрицательное число, то это неверно. Достаточно рассмотреть такой пример. Возьмем вместо (a) число (-1). Тогда (sqrt{(-1)^2}=sqrt{1}=1), а вот выражение ((sqrt {-1})^2) вообще не существует (ведь нельзя под знак корня помещать отрицательные числа!).
Поэтому обращаем ваше внимание на то, что (sqrt{a^2}) не равен ((sqrt a)^2)!
Пример: 1) (sqrt{left(-sqrt2right)^2}=|-sqrt2|=sqrt2), т.к. (-sqrt2<0);
(phantom{00000}) 2) ((sqrt{2})^2=2).
(bullet) Так как (sqrt{a^2}=|a|), то [sqrt{a^{2n}}=|a^n|] (выражение (2n) обозначает четное число)
То есть при извлечении корня из числа, находящегося в какой-то степени, эта степень уменьшается в два раза.
Пример:
1) (sqrt{4^6}=|4^3|=4^3=64)
2) (sqrt{(-25)^2}=|-25|=25) (заметим, что если модуль не поставить, то получится, что корень из числа равен (-25); но мы помним, что по определению корня такого быть не может: у нас всегда при извлечении корня должно получаться положительное число или ноль)
3) (sqrt{x^{16}}=|x^8|=x^8) (так как любое число в четной степени неотрицательно)
Факт 6.
Как сравнить два квадратных корня?
(bullet) Для квадратных корней верно: если (sqrt a<sqrt b), то (a<b); если (sqrt a=sqrt b), то (a=b).
Пример:
1) сравним (sqrt{50}) и (6sqrt2). Для начала преобразуем второе выражение в (sqrt{36}cdot sqrt2=sqrt{36cdot 2}=sqrt{72}). Таким образом, так как (50<72), то и (sqrt{50}<sqrt{72}). Следовательно, (sqrt{50}<6sqrt2).
2) Между какими целыми числами находится (sqrt{50})?
Так как (sqrt{49}=7), (sqrt{64}=8), а (49<50<64), то (7<sqrt{50}<8), то есть число (sqrt{50}) находится между числами (7) и (8).
3) Сравним (sqrt 2-1) и (0,5). Предположим, что (sqrt2-1>0,5): [begin{aligned}
&sqrt 2-1>0,5 big| +1quad text{(прибавим единицу к обеим
частям)}\[1ex]
&sqrt2>0,5+1 big| ^2 quadtext{(возведем обе части в
квадрат)}\[1ex]
&2>1,5^2\
&2>2,25 end{aligned}] Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и (sqrt 2-1<0,5).
Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве (-3<sqrt2) нельзя (убедитесь в этом сами)!
(bullet) Следует запомнить, что [begin{aligned}
&sqrt 2approx 1,4\[1ex]
&sqrt 3approx 1,7 end{aligned}] Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
(bullet) Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. Покажем, как это работает, на примере.
Возьмем (sqrt{28224}). Мы знаем, что (100^2=10,000), (200^2=40,000) и т.д. Заметим, что (28224) находится между (10,000) и (40,000). Следовательно, (sqrt{28224}) находится между (100) и (200).
Теперь определим, между какими “десятками” находится наше число (то есть, например, между (120) и (130)). Также из таблицы квадратов знаем, что (11^2=121), (12^2=144) и т.д., тогда (110^2=12100), (120^2=14400), (130^2=16900), (140^2=19600), (150^2=22500), (160^2=25600), (170^2=28900). Таким образом, мы видим, что (28224) находится между (160^2) и (170^2). Следовательно, число (sqrt{28224}) находится между (160) и (170).
Попробуем определить последнюю цифру. Давайте вспомним, какие однозначные числа при возведении в квадрат дают на конце (4)? Это (2^2) и (8^2). Следовательно, (sqrt{28224}) будет заканчиваться либо на 2, либо на 8. Проверим это. Найдем (162^2) и (168^2):
(162^2=162cdot 162=26224)
(168^2=168cdot 168=28224).
Следовательно, (sqrt{28224}=168). Вуаля!
Наличие квадратных корней в выражении усложняет процесс деления, однако существуют правила, с помощью которых работа с дробями становится значительно проще.
Единственное, что необходимо все время держать в голове — подкоренные выражения делятся на подкоренные выражения, а множители на множители. В процессе деления квадратных корней мы упрощаем дробь. Также, напомним, что корень может находиться в знаменателе.
Метод 1. Деление подкоренных выражений
Алгоритм действий:
Записать дробь
Если выражение не представлено в виде дроби, необходимо его так записать, потому так легче следовать принципу деления квадратных корней.
144÷36, это выражение следует переписать так: 14436
Использовать один знак корня
В случае если и в числителе, и знаменателе присутствует квадратные корни, необходимо записать их подкоренные выражения под одним знаком корня, чтобы сделать процесс решения проще.
Напоминаем, что подкоренным выражением (или числом) является выражением под знаком корня.
14436. Это выражение следует записать так: 14436
Разделить подкоренные выражения
Просто разделите одно выражение на другое, а результат запишите под знаком корня.
14436=4, запишем это выражение так: 14436=4
Упростить подкоренное выражение (если необходимо)
Если подкоренное выражение или один из множителей представляют собой полный квадрат, упрощайте такое выражение.
Напомним, что полным квадратом является число, которое представляет собой квадрат некоторого целого числа.
4 – полный квадрат, потому что 2×2=4. Из этого следует:
4=2×2=2. Поэтому 14436=4=2.
Метод 2. Разложение подкоренного выражения на множители
Алгоритм действий:
Записать дробь
Перепишите выражение в виде дроби (если оно представлено так). Это значительно облегчает процесс деления выражений с квадратными корнями, особенно при разложении на множители.
8÷36, переписываем так 836
Разложить на множители каждое из подкоренных выражений
Число под корнем разложите на множители, как и любое другое целое число, только множители запишите под знаком корня.
836=2×2×26×6
Упростить числитель и знаменатель дроби
Для этого следует вынести из-под знака корня множители, представляющие собой полные квадраты. Таким образом, множитель подкоренного выражения станет множителем перед знаком корня.
2266×62×2×2, из этого следует: 836=226
Рационализировать знаменатель (избавиться от корня)
В математике существуют правила, по которым оставлять корень в знаменателе — признак плохого тона, т.е. нельзя. Если в знаменателе присутствует квадратный корень, то избавляйтесь от него.
Умножьте числитель и знаменатель на квадратный корень, от которого необходимо избавиться.
В выражении 623 необходимо умножить числитель и знаменатель на 3, чтобы избавиться от него в знаменателе:
623×33=62×33×3=669=663
Упростить полученное выражение (если необходимо)
Если в числителе и знаменателе присутствуют числа, которые можно и нужно сократить. Упрощайте такие выражения, как и любую дробь.
26 упрощается до 13; таким образом 226упрощается до 123=23
Метод 3. Деление квадратных корней с множителями
Алгоритм действий:
Упростить множители
Напомним, что множители представляют собой числа, стоящие перед знаком корня. Для упрощения множителей понадобится разделить или сократить их. Подкоренные выражения не трогайте!
432616. Сначала сокращаем 46: делим на 2 и числитель, и знаменатель: 46=23.
Упростить квадратные корни
Если числитель нацело делится на знаменатель, то делите. Если нет, то упрощайте подкоренные выражения, как и любые другие.
32 делится нацело на 16, поэтому: 3216=2
Умножить упрощенные множители на упрощенные корни
Помним про правило: не оставлять в знаменателе корни. Поэтому просто перемножаем числитель и знаменатель на этот корень.
23×2=223
Рационализировать знаменатель (избавиться от корня в знаменателе)
4327. Следует умножить числитель и знаменатель на 7, чтобы избавиться от корня в знаменателе.
437×77=43×77×7=42149=4217
Метод 4. Деление на двучлен с квадратным корнем
Алгоритм действий:
Определить, находится ли двучлен (бином) в знаменателе
Напомним, что двучлен представляет собой выражение, которое включает 2 одночлена. Такой метод имеет место быть только в случаях, когда в знаменателе двучлен с квадратным корнем.
15+2— в знаменателе присутствует бином, поскольку есть два одночлена.
Найти выражение, сопряженное биному
Напомним, что сопряженный бином является двучленом с теми же одночленами, но с противоположными знаками. Чтобы упростить выражение и избавиться от корня в знаменателе, следует перемножить сопряженные биномы.
5+2и 5-2 – сопряженные биномы.
Умножить числитель и знаменатель на двучлен, который сопряжен биному в знаменателе
Такая опция поможет избавиться от корня в знаменателе, поскольку произведение сопряженных двучленов равняется разности квадратов каждого члена биномов: (a-b)(a+b)=a2-b2
15+2=1(5-2)(5-2)(5+2)=5-2(52-(2)2=5-225-2=5-223.
Из этого следует: 15+2=5-223.
Советы:
- Если вы работаете с квадратными корнями смешанных чисел, то преобразовывайте их в неправильную дробь.
- Отличие сложения и вычитания от деления — подкоренные выражения в случае деления не рекомендуется упрощать (за счет полных квадратов).
- Никогда (!) не оставляйте корень в знаменателе.
- Никаких десятичных дробей или смешанных перед корнем — необходимо преобразовать их в обыкновенную дробь, а потом упростить.
- В знаменателе сумма или разность двух одночленов? Умножьте такой бином на сопряженный ему двучлен и избавьтесь от корня в знаменателе.
Это умение очень пригодится на ЕГЭ и ОГЭ, потому как калькулятором пользоваться нельзя, подбором, умножая в столбик, получается долго и муторно, а в восьмой раз в туалет уже никто не выпустит.
Так что смотрим и запоминаем, чтобы потом научить своих детей, которым наверняка не рассказывали это в школе, но это сильно сэкономит время на экзаменах.
Этот способ подойдет для тех чисел, из которых корень извлекается целым числом. Именно поэтому этот способ очень удобен как раз для ОГЭ и ЕГЭ, потому как там не дают корни, из которых корень не извлекается (часть С не в счет).
Покажу на примерах. Кому удобнее смотреть видео, смотрите.
Допустим нам надо извлечь корень из числа 54756. Дальше листаем галерею, смотрим подписи к фотографиям и запоминаем алгоритм.
Второй пример. Извлечем корень из числа 259081. Попробуйте сами. На втором слайде будет решение.
На первый взгляд схема весьма непростая, но стоит один-два раза попробовать извлечь корни таким образом самостоятельно и вы будете щелкать такие задачи, как семечки. Попробуйте извлечь корень из 112225; 210681 и 998001.
С числами поменьше, всё ещё проще, даже писать ничего не придется. Можно в уме вычислять. Вот, например, как извлечь корень из 3136? Понятно, что грани две, поэтому в ответе двухзначное число. Первая цифра в ответе — это 5, потому что 5²=25, а 6²=36>31. Так как 3136 заканчивается на 6, а при возведении в квадрат шестерку могут давать только 4 или 6, ответом будет либо 54, либо 56. Как выбрать? Давайте вспомним чему равен 55². Если не помните, то это легко посчитать (подробно читайте тут), надо в конце записать 25, а в начале 5•6=30 Итого 55²=3025. 3025<3136, а так как корень должен извлекаться нацело, значит ответ 56.
Аналогично извлекаем корень из 4624. 6²=36, а 7²=49, поэтому первая цифра ответа — 6. При возведении в квадрат четверку на конце дают только 2 и 8, то есть ответ 62 или 68. Чтобы выбрать, мы должны сравнить подкоренное число с 65². 6•7=42, дописываем в конце 25 и получаем 65²=4225. 4225<4624 следовательно √4624=68.
Ну и последний корень попробуйте снова извлечь самостоятельно. Чему равен √2116? Проверьте себя по картинке ниже.
И не забываем о том, что у меня появился канал на Ютубе. Заходите в гости и подписывайтесь.
Ещё интересно: Два простых способа быстрого сложения и вычитания в уме
Простой и очень быстрый способ возведения в квадрат чисел, оканчивающихся на 5. Будешь считать быстрее калькулятора
90% европейских выпускников не смогли решить задачу, которую решили российские восьмиклассники












![{displaystyle {begin{aligned}{begin{array}{rlll}x_{0}&=6cdot 10^{2}&&=600{,}000\[0,3em]x_{1}&={frac {1}{2}}left(x_{0}+{frac {S}{x_{0}}}right)&={frac {1}{2}}left(600{,}000+{frac {125348}{600{,}000}}right)&=404{,}457\[0.3em]x_{2}&={frac {1}{2}}left(x_{1}+{frac {S}{x_{1}}}right)&={frac {1}{2}}left(404{,}457+{frac {125348}{404{,}457}}right)&=357{,}187\[0.3em]x_{3}&={frac {1}{2}}left(x_{2}+{frac {S}{x_{2}}}right)&={frac {1}{2}}left(357{,}187+{frac {125348}{357{,}187}}right)&=354{,}059\[0.3em]x_{4}&={frac {1}{2}}left(x_{3}+{frac {S}{x_{3}}}right)&={frac {1}{2}}left(354{,}059+{frac {125348}{354{,}059}}right)&=354{,}045\[0.3em]x_{5}&={frac {1}{2}}left(x_{4}+{frac {S}{x_{4}}}right)&={frac {1}{2}}left(354{,}045+{frac {125348}{354{,}045}}right)&=354{,}045end{array}}end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01b283c908a83bef269f36cd68c3feb7e857d33b)




















![{displaystyle {begin{aligned}&(a_{1}+a_{2}+a_{3}+dotsb +a_{n})^{2}\=&,a_{1}^{2}+2a_{1}a_{2}+a_{2}^{2}+2(a_{1}+a_{2})a_{3}+a_{3}^{2}+dotsb +a_{n-1}^{2}+2left(sum _{i=1}^{n-1}a_{i}right)a_{n}+a_{n}^{2}\=&,a_{1}^{2}+[2a_{1}+a_{2}]a_{2}+[2(a_{1}+a_{2})+a_{3}]a_{3}+dotsb +left[2left(sum _{i=1}^{n-1}a_{i}right)+a_{n}right]a_{n}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c9fc9912ec91d9fa1e6a5ca9c5d1c5b98ec6316)



![{displaystyle Y_{m}=[2P_{m-1}+a_{m}cdot 10^{n-m}]a_{m}cdot 10^{n-m}=left[20sum _{i=1}^{m-1}a_{i}cdot 10^{m-i-1}+a_{m}right]a_{m}cdot 10^{2(n-m)}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/665e9765734e1824ef3b9675155242ac283fef2f)






![{displaystyle {sqrt[{n}]{x}}=e^{{frac {1}{n}}ln x},,x>0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d95ffb1eb2d869962cc300a7bde538de29c69afd)




















![{displaystyle [a;2a,2a,2a,...]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/877c3c594b41a5acd82de511e9ef2999eb158359)
![{displaystyle [a;{overline {2a}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5b579e3cc5ede7bcb2db3f3b18b80dd1d2e9d3a)
















