Как найти положение центра масс маятника - Сайт, где вы сможете решить свои вопросы

Изучение свободных колебаний физического маятника Краткая теория.

Р
ассмотрим
колебательное движение физического
маятника.

Физический маятник
– твердое тело
произвольной формы, совершающее под
действием силы тяжести колебания вокруг
неподвижной горизонтальной оси, не
проходящей через центр масс тела.

Тело подвешено в точке О,
не совпадающей с
центром масс тела С (рис.1). Запишем
основной закон динамики вращательного
движения:

(1)

где I
– момент инерции тела относительно оси
вращения,

– угловое ускорение тела,

– момент силы тяжести,

–
радиус-вектор центра масс. Учитывая,
что проекция момента силы тяжести на
ось z
равна M_Z
= –mglsinφ,
получаем:

. (2)

При колебаниях, происходящих с малой
амплитудой, можно считать,

что sinφ≈φ.
Обозначим

,
тогда уравнение (2) запишется в виде:

. (3)

Решением этого уравнения
является гармоническая функция, например:

, (4)

где A
– амплитуда колебаний, ω₀
– циклическая частота, ₀
– начальная фаза колебаний.

Непосредственной подстановкой можно
убедиться, что функция (4) является
решением уравнения (3).

Период колебаний маятника определяется
по формуле:

, (5)

при малых углах отклонения:

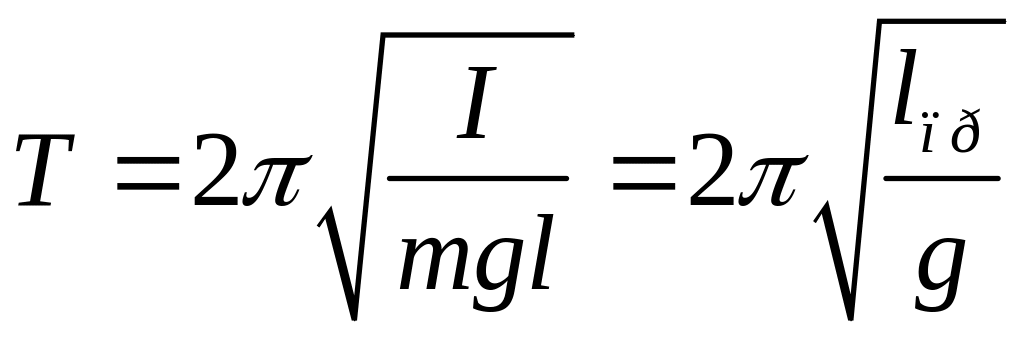
, (6)

где l_пр
– приведенная длина маятника, то есть
длина такого математического маятника,
период колебаний которого равен периоду
колебаний физического.

Определим положение центра
масс маятника аналитически. Обозначим
расстояние между опорами оборотного
маятника L.
Тогда на основании
(6) момент инерции маятника равен:

, (7)

где l
– расстояние от точки подвеса до центра
масс, T₁
– период колебаний маятника.

Для оборотного маятника справедлива
формула:

. (8)

Воспользуемся теоремой
Штейнера для определения момента инерции
тела при параллельном переносе оси
вращения:

. (9)

где I₀
– момент инерции относительно оси,
проходящей через центр масс тела.

Для оборотного маятника имеем:

. (10)

Из (10) вычитаем (9), вместо
моментов инерции тала поставляем их
значения из (8) и (7). После преобразований
получаем:

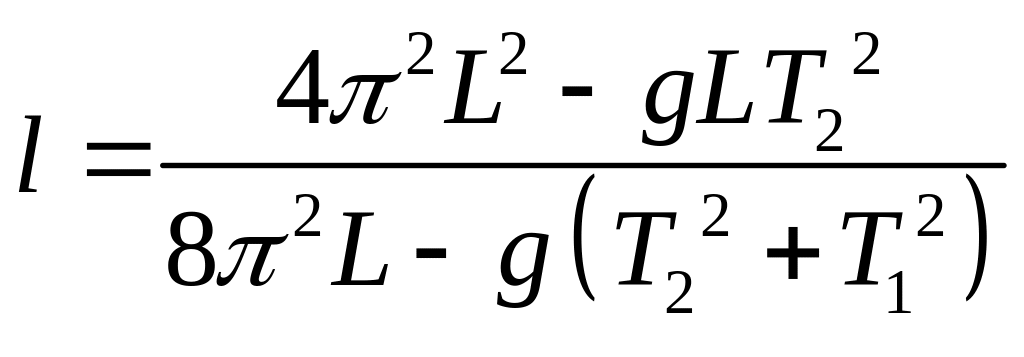
. (11)

Определив положение центра
масс несложно определить и моменты
инерции относительно двух осей вращения,
по формулам (7) и (8).

Перепишем соотношение (6) с
учетом теоремы Штейнера:

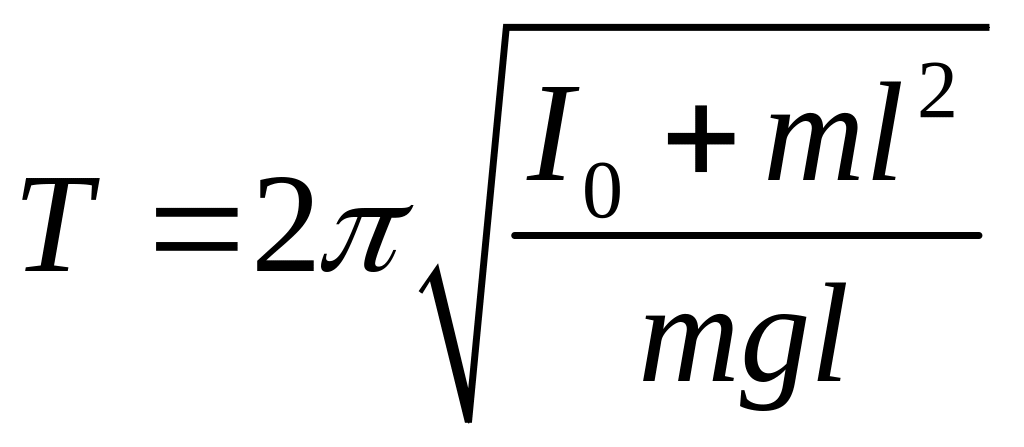
. (12)

Если положение грузов
маятника таково, что его период не
изменяется при обращении, то

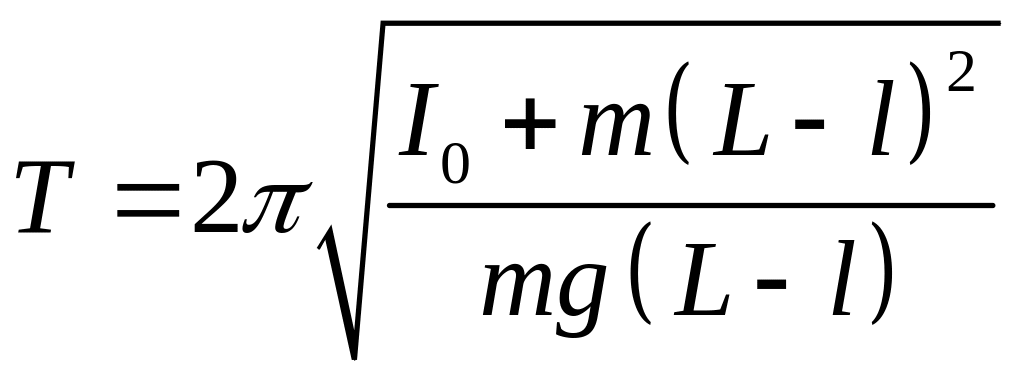
. (13)

С учетом (9) и (10) имеем

и

. (14)

Разность между двумя последними
выражениями дает:

. (15)

Экспериментальная установка.

О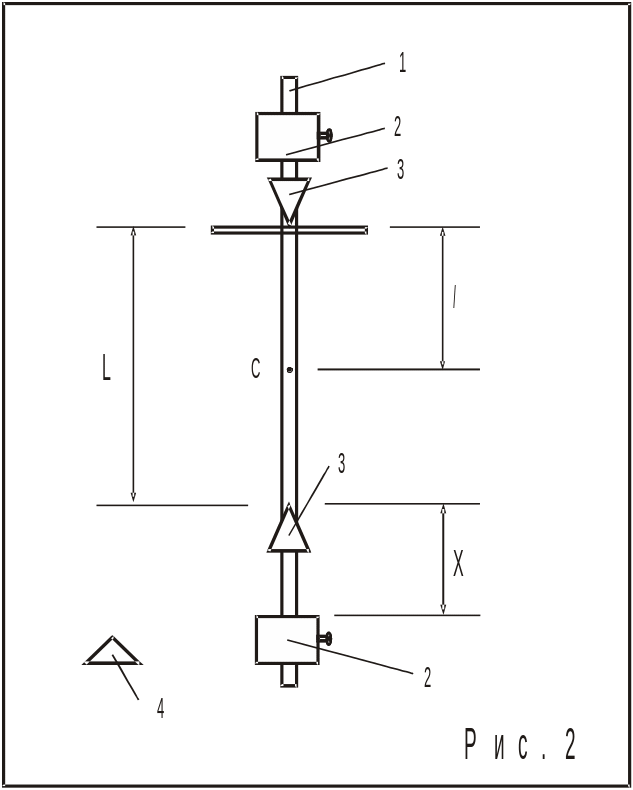
борудование:
физический маятник,
математический маятник, опорная призма,
секундомер, линейка, весы с разновесами.

Физический
маятник (рис.2) представляет
собой металлический стержень 1, на
котором крепятся две опоры 3 и грузы 2.
Положение центра масс определяется с
помощью опорной призмы 4. Расстояние
измеряются
при помощи линейки. Для определения
периода колебаний используется
секундомер.

Проведение эксперимента.

Задание
1. Определение момента инерции
физического маятника и его приведенной
длины.

Определите
массу физического маятника.
Произвольно
установите грузы на металлическом
стержне.
Экспериментально,
используя опорную призму, установите
положение центра масс
маятника. Измерьте расстояние l
от
одной из опор до центра масс.
Измерьте
время 20-30 колебаний маятника небольшой
амплитуды и вычислите
их период. Результаты занесите в таблицу
1.
Рядом
с физическим маятником подвесьте
математический маятник такой длины,
чтобы период его колебаний равнялся
периоду колебаний физического
маятника. Измерьте приведенную длину
l_пр.
Используя
формулу (6) вычислите момент инерции
маятника относительно оси, проходящей
через точку опоры и перпендикулярной
плоскости колебаний
маятника. Вычислите приведенную длину
l‘_пр.
Определите
момент инерции маятника относительно
оси, проходящей через
другую опору, и соответствующие
экспериментальные и теоретические
значения приведенной длины.
Аналитическим
методом найдите погрешность определения
момента инерции,
результат запишите в виде I
= (I₀
± ΔI).
Приведите пример вычислений всех
расчетных величин.

Таблица 1.

Опыт	Результаты измерений	Вычисления
m	l	n	t	T	l_пр	I	ΔI	l‘_пр

1
2

Задание
2. Определение положения центра масс
физического маятника
методом обращения.

Используя
данные, полученные в задании 1, теоретически
установите положение центра масс
маятника, сравните полученное значение
с найденным
экспериментально. Результаты вычислений
внесите в таблицу 2.
Определите погрешность проведенных
вычислений, считая истинным положение
центра масс, полученное экспериментально.

Приведите пример вычислений всех
расчетных величин.

Таблица 2.

T₁

ΔT₁

T₂

ΔT₂

ΔL

Δg

Δπ

lΔ

δl

Задание 3. Определение
ускорения силы тяжести оборотным
маятником.

Зафиксируйте положение одного из
грузов.
Перемещая
второй груз, подберите такое его
положение, при котором период
маятника не изменяется при его обращении.
Измерьте
период колебаний, измеряя время 20-30
полных колебаний для маятника на обеих
опорах, вычислите среднее значение
периода.
Результаты измерений и вычислений
занесите в таблицу 3.
Аналитически
рассчитайте погрешность определения
ускорения свободного падения оборотным
маятником.
Приведите пример вычисления.

Таблица 3.

Результаты измерений	Результаты вычислений
n₁	t₁	T₁	n₂	t₂	T₂	L	T	ΔT	g	Δg	δg

Задание
4. Изучение зависимости момента инерции
маятника от положения
подвижного груза.

Установите
произвольно один из грузов и зафиксируйте
его положение.

Установите
второй груз в крайнее положение. Запишите
его координату x.
Измерьте
период колебаний маятника Т₁,
расстояние от оси вращения до центра
масс l₁
и приведенную длину l_пр1
маятника описанным выше способом.
Вычислите
момент инерции маятника I₁
относительно оси вращения. Аналитически
найдите его погрешность Δ
I₁.
Повторите
измерения для другой опоры, найдя Т₂,
l₂,
l_пр2,
I₂
и ΔI₂.
Результат занесите
в таблицу 4.
Последовательно
перемещая груз на 1-2 см, занося его
координату в таблицу, проведите 10
опытов, определяя все перечисленные
величины.

Приведите пример вычисления всех
расчетных величин.
Постройте
графики Т₁
= Т₁(х),
и
Т₂
=
Т₂(x)
в одной системе координат.

По
графику установите положение груза,
при котором Т₁
= Т₂,
установите его
в это положение и убедитесь в равенстве
периодов.
Экспериментально установите
приведенную длину маятника, сравните
ее
с расстоянием между
опорами.
Постройте графики I₁
= I₁(х),
и I₂
= I₂(х)
в одной системе координат
и проанализируйте их.

Таблица 3.

Опыт	Результаты измерений	Вычисления
x	T	l	l_пр	I	Δ I

Опора 1
1..10
Опора 2
1..10

Заключение.

Укажите
при каком положении грузов периоды
колебаний маятника на обоих
опорах одинаковы. Как при этом соотносятся
расстояние между опорами
и приведенная длина маятника?
Охарактеризуйте зависимость периода
колебаний
(момента инерции) маятника от положения
груза на оси вращения и
объясните этот результат на качественном
уровне.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Андрей Геннадьевич Блохин

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Сущность понятия «центр масс»

Понятие “центр масс” широко используется в физике для решения задач, связанных с движением тел. Например, математический маятник удобно представить себе как подвешенное на нити тело, вся масса которого сконцентрирована в единой точке. В законе всемирного тяготения тоже речь идет о расстоянии не между телами, а между центрами тел, под каковыми подразумеваются именно центры масс, а не геометрические центры.

Определение 1

Центр масс – точка, характеризующая размещение и движение исследуемой системы как единого целого.

Признаком центра масс является то, что если тело подвесить, закрепив за эту точку, оно останется в покое, т.е. не будет раскачиваться или вращаться относительно этого центра. В простейшем случае, если речь идет о симметричном теле с равномерной плотностью, центр масс находится на пересечении осей симметрии рассматриваемого тела. Например, если взять линейку длиной 30 см, то ее центр масс будет расположен на отметке “15 см”. Подложив карандаш под эту отметку, легко привести линейку в положение равновесия.

На практике далеко не все тела, центр масс которых нужно найти, являются симметричными и однородными по плотности. Более того, многие исследуемые объекты представляют собой системы из нескольких тел с различными геометрическими и химическими характеристиками. Для расчетов их разбивают на элементарные фрагменты и производят вычисления поэтапно.

Нахождение координат центра масс

Определение 2

Центр масс двух тел с точечными массами $m_1$ и $m_2$ и координатами на координатной прямой $x_1$ и $x_2$ находится в точке, делящей расстояние между этими телами на отрезки с длинами обратно пропорциональными массам рассматриваемых тел.

Отсюда следует, что чем массивнее тело в такой элементарной системе, тем ближе оно к общему центру масс.

Расстояние между точечными телами равно:

$Delta x = x_2 – x_1$

Пропорция между массами и расстояниями, согласно определению:

$frac{l_1}{l_2} = frac{m_2}{m_1}$,

«Как найти координаты центра масс» 👇

где $l_1$, $l_2$ – расстояния от соответствующих тел до центра масс.

Выразив, длины через координаты

$l_1 = x_c – x_1; l_2 = x_2 – x_c$,

центр масс можно определить как

$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$.

где $x_c$ – координата центра тяжести.

Разложив любую сложную систему на множество элементарных тел с точечными массами, можно обобщить изложенный принцип в виде формулы (для оси абсцисс):

$x_c = frac{sumlimits^N_{i=1}{m_i cdot x_i}}{sumlimits^N_{i=1}{m_i}}$

В большинстве случаев центр масс требуется найти не на координатной прямой, а в двух- или трехмерной системе координат. Для дополнительных осей координаты центра масс ($y_c$, $z_c$) находят по аналогичному принципу.

Замечание 1

Центр тяжести системы тел представляет собой точку, подобную центру масс, но рассчитывается не для масс, а для весов (обусловленных гравитацией сил), действующих на точечные тела, входящие в систему. Центр тяжести определяется так же, как и центр масс, если размеры системы малы в сравнении с радиусом планеты Земля. Он в большинстве случаев с достаточной для практики точностью совпадает с центром масс рассматриваемой системы.

Пример 1

Найти центр масс двух линеек, изготовленных из одинакового материала, одинаковой толщины и ширины, левые концы линеек совмещены. Длины линеек – 10 и 30 см. Толщиной линеек можно пренебречь.

Поскольку толщиной можно пренебречь, найти нужно лишь координату центра масс по оси $x$.

Разобьем мысленно систему на два отрезка. Первый – где толщина линеек складывается. Его координаты – $[0, 10]$. Второй отрезок – где длинная линейка продолжается одна. Его координаты – $[10, 30]$. Примем за единицу измерения массу одного погонного сантиметра линейки. Тогда масса второго фрагмента:

$m_2 = 30 – 10 = 20$

На каждый сантиметр первого фрагмента приходится вдвое больше массы, поскольку там сложены две линейки:

$m_1 = 10 cdot 2 = 20$

Центры масс отрезков находятся на их осях симметрии, т.е. на середине длины каждого:

$x_{c1} = frac{10}{2} = 5$;

$x_{c2} = 10 + frac{20}{2} = 20$

Подставим значения в формулу:

$x_c = frac{m_1 cdot x_1 + m_2 cdot x_2}{m_1 + m_2}$

$x_c = frac{20 cdot 5 + 20 cdot 20}{20 +20} = frac{100 + 400}{40} = 12, 5$

Ответ: центр масс находится на расстоянии 12,5 см от левого конца системы линеек.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 июля 2022 года; проверки требует 1 правка.

Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Дифференциальное уравнение движения физического маятника[править | править код]

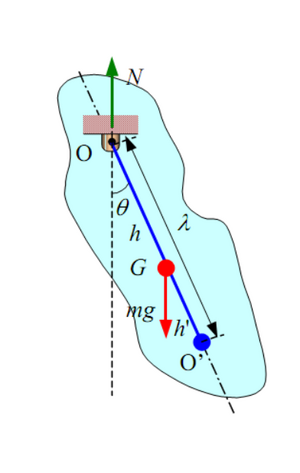
Момент инерции относительно оси, проходящей через точку подвеса, по теореме Штейнера:

${displaystyle I=I_{0}+mh^{2}=mleft(r^{2}+h^{2}right)}$

где I_0 — момент инерции относительно оси, проходящей через центр тяжести; — эффективный радиус инерции относительно оси, проходящей через центр тяжести.

Динамическое уравнение произвольного вращения твёрдого тела:

${displaystyle I{frac {d^{2}theta }{dt^{2}}}=-M_{s}}$

где M_s — суммарный момент сил, действующих на тело относительно оси вращения.

${displaystyle M_{s}=M+M_{f}}$

где — момент сил, вызванный силой тяжести; ${displaystyle M_{f}}$ — момент сил, вызванный силами трения среды.

Момент, вызванный силой тяжести, зависит от угла отклонения тела от положения равновесия:

Если пренебречь сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести:

$I{frac {d^{2}theta }{dt^{2}}}=-mghsin theta$

Если разделить обе части уравнения на и положить

${displaystyle lambda ={frac {r^{2}+h^{2}}{h}}={frac {r^{2}}{h}}+h}$

получим:

${displaystyle lambda {frac {d^{2}theta }{dt^{2}}}=-gsin theta }$

Такое уравнение аналогично уравнению колебаний математического маятника длиной lambda . Величина lambda называется приведённой длиной физического маятника.

Центр качания физического маятника. Теорема Гюйгенса[править | править код]

Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.

Поместим на луче, проходящем от точки подвеса через центр тяжести, точку на расстоянии lambda от точки подвеса. Эта точка и будет центром качания маятника.

Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром тяжести. Тогда момент инерции относительно оси подвеса будет равен ${displaystyle I=mlambda ^{2}}$ , а момент силы тяжести относительно той же оси . При этом уравнение движения не изменится.

Согласно теореме Гюйгенса,

Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.

Вычислим приведённую длину для нового маятника:

${displaystyle lambda _{1}={frac {r^{2}}{r^{2}/h}}+{frac {r^{2}}{h}}=h+{frac {r^{2}}{h}}=lambda }$

Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.

Период колебаний физического маятника[править | править код]

Наиболее общий случай[править | править код]

Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания.

Для этого умножим левую ${displaystyle lambda {frac {d^{2}theta }{dt^{2}}}=lambda {frac {d}{dt}}left({frac {dtheta }{dt}}right)}$ и правую часть этого уравнения на dtheta . Тогда:

${displaystyle lambda {frac {dtheta }{dt}}dleft({frac {dtheta }{dt}}right)=-gsin theta ,dtheta }$

Интегрируя это уравнение, получаем:

${displaystyle lambda left({frac {dtheta }{dt}}right)^{2}=2gcos theta +C}$

где — произвольная постоянная. Её можно найти из условия, что в ситуациях, когда , должно быть ${displaystyle {frac {dtheta }{dt}}=0}$ ( alpha — максимальный угол отклонения). Получаем:

Подставляем и преобразовываем получившееся уравнение:

${displaystyle {frac {dtheta }{dt}}=2{sqrt {frac {g}{lambda }}}{sqrt {sin ^{2}{frac {alpha }{2}}-sin ^{2}{frac {theta }{2}}}}.}$

Отделяем переменные и интегрируем это уравнение:

${displaystyle {sqrt {frac {g}{lambda }}}t=int limits _{0}^{frac {theta }{2}}{frac {dleft({frac {theta }{2}}right)}{sqrt {sin ^{2}{frac {alpha }{2}}-sin ^{2}{frac {theta }{2}}}}}}$

Удобно сделать замену переменной полагая $sin {frac {theta }{2}}=sin {frac {alpha }{2}}sin varphi$ . Тогда искомое уравнение принимает вид:

${displaystyle t={sqrt {frac {lambda }{g}}}int limits _{0}^{varphi }{frac {dvarphi }{sqrt {1-sin ^{2}{frac {alpha }{2}}sin ^{2}varphi }}}={sqrt {frac {lambda }{g}}}Fleft(varphi setminus alpha /2right).}$

Здесь — нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:

${displaystyle T=4{sqrt {frac {lambda }{g}}},int limits _{0}^{pi /2}{frac {dvarphi }{sqrt {1-sin ^{2}{frac {alpha }{2}}sin ^{2}varphi }}}=4{sqrt {frac {lambda }{g}}},Kleft(sin {frac {alpha }{2}}right).}$

Здесь $Kleft(sin {frac {alpha }{2}}right)$ — полный нормальный эллиптический интеграл Лежандра 1-го рода. Раскладывая его в ряд, можно получить удобную для практических вычислений формулу:

${displaystyle T=2pi {sqrt {frac {lambda }{g}}}left{1+left({frac {1}{2}}right)^{2}sin ^{2}left({frac {alpha }{2}}right)+left({frac {1cdot 3}{2cdot 4}}right)^{2}sin ^{4}left({frac {alpha }{2}}right)+dots +left[{frac {left(2n-1right)!!}{left(2nright)!!}}right]^{2}sin ^{2n}left({frac {alpha }{2}}right)+dots right}.}$

Период малых колебаний физического маятника[править | править код]

Если — случай малых максимальных угловых отклонений от равновесия — то так как разложение синуса в ряд Маклорена ${displaystyle sin theta approx theta -theta ^{3}/3dots }$ и уравнения движения переходит в уравнение гармонического осциллятора без трения:

${displaystyle lambda {frac {d^{2}theta }{dt^{2}}}=-gtheta .}$

Период колебания маятника в этом случае:

${displaystyle T=2pi {sqrt {frac {lambda }{g}}}.}$

В иной формулировке: если амплитуда колебаний alpha мала, то корень в знаменателе эллиптического интеграла приближённо равен единице. Такой интеграл легко берётся, и получается хорошо известная формула малых колебаний:

${displaystyle T=2pi {sqrt {frac {lambda }{g}}}=2pi {sqrt {frac {I}{mgh}}}.}$

Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.

Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах отклонения до 1 радиана (≈57°):

${displaystyle Tapprox 2pi {sqrt {frac {lambda }{g}}}left(1+{frac {1}{4}}sin ^{2}left({frac {alpha }{2}}right)right)={frac {pi }{4}}{sqrt {frac {lambda }{g}}}left(9-cos {alpha }right).}$

См. также[править | править код]

Математический маятник
Маятник Дубошинского

Ссылки[править | править код]

маятник — статья из Большой советской энциклопедии.

Источник

Методика проведения эксперимента

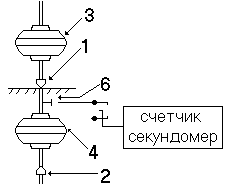
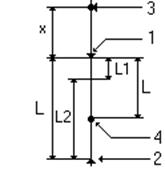
Обратный маятник состоит из стального стержня, на котором закрепляются опоры 1
и 2 в виде призм и грузы 3 и 4. Время N полных колебаний
маятника измеряются секундомерами. В автоматическом режиме секундомер
включается при срабатывании фотоэлемента датчика 6, выключается кнопкой СТОП.

Метод оборотного маятника основан на
сопряженности двух его точек: подвеса и центра касания. Путем изменения
расстояния между грузами (перемещением груза 3) добиваются такого расстояния,
чтобы период колебания маятника при его переворачивании не менялся. При этом
расстояние между опорами будет приведенной длиной маятника .

Теоретически рассчитать положение центра
масс физического маятника можно для упрощении модели маятника, состоящей из
невесомого стержня с закрепленным на нем материальными точками 3 и 4.

Порядок выполнения работы

Исходные данные:

Расстояние между спорами L=0.312м

Расстояние от опоры 1 до груза 4 l=0.15м

Масса маятника m=1.4м

Будем передвигать груз 3 и измерять время
12 полных колебаний, а результат записывать в таблицу, в которой:

x – расстояние от груза 3 до опоры 1

t1 – время 12 полных колебаний маятника,
подвешенного за опору 1

t2 – время 12 полных колебаний маятника,
подвешенного за опору 2.

№ эксперимента	х, м	t1, c	T2, c
1	0.04	12.60	13.10
2	0.05	13.02	13.50
3	0.06	13.30	13.50
4	0.07	14.61	14.50
5	0.08	14.83	14.34

Построим зависимость времени колебаний
маятника на опорах 1 и 2 от положения груза 3.

По точки пересечения графиков находим хпр=0.0625м.

Приведенная длина физического маятника
определяется по формуле: .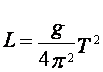

Необходимо найти .
Для этого установим груз 3 в положение хпр=0.062м
и определим время 12 колебаний 12 маятника,
повторим опыт несколько раз:

Источник

Изучение свободных колебаний физического маятника Краткая теория.

Экспериментальная установка.

Проведение эксперимента.

Сущность понятия «центр масс»

Нахождение координат центра масс

Дифференциальное уравнение движения физического маятника[править | править код]

Центр качания физического маятника. Теорема Гюйгенса[править | править код]

Период колебаний физического маятника[править | править код]

Наиболее общий случай[править | править код]

Период малых колебаний физического маятника[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Методика проведения эксперимента

<img loading="lazy" decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" width="165" height="173" src="http://files3.vunivere.ru/workbase/00/00/14/62/images/image052.jpg" />Порядок выполнения работы

х, м

Вам также может понравиться

Как найти валентность атома элемента

Как найти средний ндс

Разбойник майнкрафт как найти

Добавить комментарий Отменить ответ

Порядок выполнения работы