Как найти положение главных центральных осей

Центробежный момент инерции сечения относительно осей, из которых хотя бы одна есть ось симметрии, равен нулю. Действительно, каждому элементу площади в правой половине симметричного сечения (рис. 4.11) всегда соответствует такой же элемент в левой половине. Ординаты центров тяжести этих двух элементов одинаковы, а абсциссы равны по величине, но противоположны по знаку. Поэтому интегралы по площади левой и правой части сечения противоположны по знаку, а их сумма, представляющая собой центробежный момент инерции сечения, равна нулю.

Следовательно, если сечение имеет хотя бы одну ось симметрии, то эта ось является одной из главных центральных осей инерции. Любая перпендикулярная к ней ось также является главной, а проходящая, кроме того, через центр тяжести — второй главной центральной осью инерции. Поэтому при определении положения главных осей надо прежде всего обращать внимание на наличие осей симметрии.

Если сечение не имеет осей симметрии, то сначала выбирается рациональная система осей координат, затем вычисляются моменты инерции относительно этих осей и далее по формуле (4.26) определяется угол а, на который нужно повернуть исходные оси, чтобы они стали главными. При положительном оси у и надо поворачивать на угол а против часовой стрелки, а при отрицательном — по часовой стрелке.

Рассмотрим несколько примеров определения главных центральных осей инерции и главных моментов инерции сечений.

Пример. Определить главные центральные оси и главные моменты инерции для сечения, представленного на рис. 4.12.

Решение. Сечение имеет две оси симметрии Следовательно, эти оси являются искомыми главными центральными осями инерции сечения. Дополннм сечение до полного квадрата и определим вычитанием из момента инерции квадрата со стороной 4 см моментов инерции квадратов со стороной 1 см. Учитывая, что по доказанному выше моменты инерции квадратов относительно всех центральных осей одинаковы,

Рис. 4.11

Рис. 4.12

Рис. 4.13

Рис. 4.14

При вычислении необходимо применить формулу (4.12)

Итак, Заметим, что осью максимального главного Момента инерции всегда будет та, от которой более удалены элементы площади сечения.

Пример. Определить моменты инерции относительно главных нейтральных осей инерции (рис. 4.13).

Решение. Совместим оси и у с горизонтальным и вертикальным участками средней линии уголка и определим положение его центра тяжести:

Проведем через центр тяжести оси и вычислим моменты инерции уголка относительно этих осей. Разбивая уголок на два прямоугольника, как показано на рис. 4.13, с помощью формул (4.12) получаем:

Определим по формуле (4.27) угол а, на который надо повернуть центральные оси чтобы они совпали с главными центральными осями инерции уголка;

Как видно из рис. 4.13, при повороте на угол ось совпадает с первой, а ось второй главной центральной осью инерции уголка (элементы данной фигуры расположены ближе к оси чем к оси 1).

Главные моменты инерции и вычислим по формуле (4.28);

Следовательно,

Пример. Определить главные моменты инерции тонкостенного профиля по» стоянной толщины представленного на рис. 4.14.

Решение. Проведем оси и у, как показано на рис. 4.14, и определим положение центра тяжести профиля

где площади и статические моменты полукольца, вертикального и, горизонтального прямоугольников

Следовательно,

Определим моменты инерции относительно главных центральных осей инерции

При вычислении поступим так. Сначала определим момент инерции всего сечения относительно оси а затем по формулам (4.12) перейдем к центральной оси Используя результаты разд. 4.4, получим

Первое слагаемое в квадратных скобках, момент инерции горизонтального элемента относительно его собственной центральной оси — весьма мало по сравнению со всеми остальными слагаемыми, так как содержит малую величину в третьей степени.

Такими слагаемыми при расчете тонкостенных сечений обычно пренебрегают, Поэтому

Момент инерции относительно оси

Определяем
координаты точек С₁
и С₂
относительно системы z₁C₁y₁.

Точка
С₁:

=0;=0.

Точка
С₂
:
;.

Общая
площадь фигуры

Координата
центра тяжести по оси y

.

Координата
центра тяжести по оси z

.

П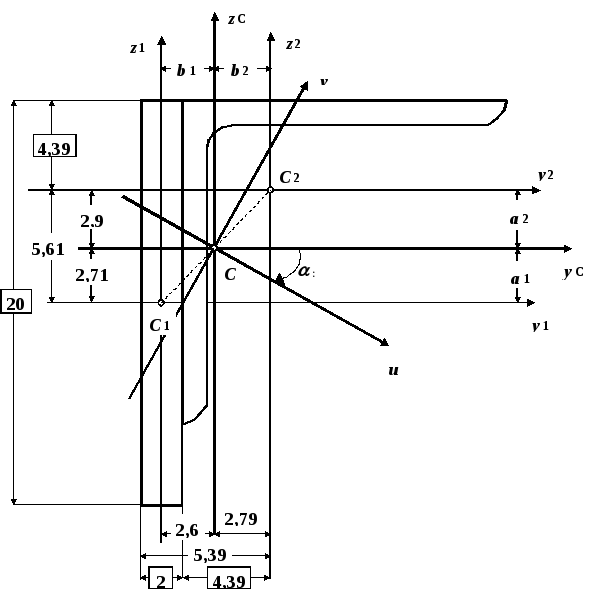роводим
центральные осиy
_C
, z
_C
параллельно
осям y
₁ , z₁
, как это
показано на рис.11.

Рис.11

Замечание. Центр
тяжести составной фигуры (точка С) всегда
должен лежать на

прямой
линии, соединяющей точка С₁
и С₂
(см. рис.11).

Теперь
y
_C,
z
_C

основная система координат.

2.Определение величин осевых и центробежного моментов инерции относительно центральных осей

Момент
инерции составной фигуры относительно
оси y
_C
равен сумме моментов инерции первой и
второй фигур

.

Момент
инерции первой фигуры относительно
оси y
_C
равен моменту инерции относительно оси
y
₁ плюс
площадь этой фигуры на квадрат расстояния
между осями y
₁ и y
_C
(используем формулы параллельного
переноса осей)

;

(см.
рис.11).

Момент
инерции второй фигуры относительно оси
y
_C

;

(см.
рис.11).

.

Момент
инерции составной фигуры относительно
оси z
_C
равен сумме моментов инерции первой и
второй фигур

.

;

(см.
рис.11).

Момент
инерции второй фигуры относительно оси
y
_C

;

(см.
рис.11).

.

Центробежный
момент инерции составной фигуры
относительно осей y
_C,
z
_C
равен сумме центробежных моментов
инерции первой и второй фигур

.

;

;

.

Моменты инерции
относительно центральных осей найдены

3. Определение направления главных центральных осей

Направление
главных центральных осей определяется
по формуле:

.

Знак
“ –“ показывает, что угол
откладывается
от осиy
_C
по ходу часовой стрелки (для “ + “ –
против хода часовой стрелки).

Проводим
главные центральные оси u
,v
, как это
показано на рис.11.

4. Определение
величин осевых моментов инерции
относительно

главных центральных
осей

Моменты инерции относительно главных
центральных осей вычисляются по следующим
формулам:

Так как
,
то

Наибольший из моментов инерции при
повороте осей возрастает, достигая
максимального значения, а меньший момент
инерции убывает, достигая минимального
значения, при этом сумма осевых моментов
инерции относительно двух взаимно
перпендикулярных осей остается
постоянной, т.е.

=const.

Используем последнее
соотношение в качестве проверки

==.

Задача 3

Для заданных двух
схем балок (рис.12,15) требуется:

1.Для
каждого участка балки составить выражения
поперечных сил (Q)
и изги-

бающих
моментов(M)
, используя метод сечений. Построить их
эпюры.

2.Определить опасное
сечение по нормальным напряжениям.

3.Из условия
прочности по методу допускаемых
напряжений при изгибе

подобрать:

а) для схемы (а)
деревянную балку круглого поперечного
сечения, приняв

допускаемое
нормальное напряжение 


= 10МПа;

б) для схемы (б)
стальную балку двутаврового поперечного
сечения, приняв

допускаемое
нормальное напряжение 


= 160МПа.

4. Проверить
прочность балок.

Схема
а)

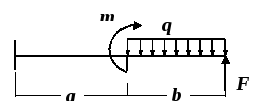Исходные
данные:

a=2
м;
b=2
м;
q=10
кН/м;

m=8
кНм;
F=15
кН;

  =
10МПа=10.

Рис.12

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Определить главные центральные моменты инерции, осевые моменты сопротивления  сечения, составленного из стандартных профилей проката.

Сечение состоит из двух неравнополочных уголков 75×50х5 (маркировка в мм) и швеллера № 16 (№ швеллера говорит о его высоте в см).

1. Определим положение центра тяжести сечения.

Сечение симметрично относительно оси у, проводим её как ось – главную и центральную. Координата х_С=0. Для нахождения у_С проводим случайную ось х′ (выбранную случайным образом). Обозначим центры тяжести всех профилей и выпишем необходимые характеристики профилей из сортамента прокатной стали.

Фигуры 1,2 – уголки 75×50х5

А₁=А₂=6,11 см²

I_х1= I_х2=34,8 см⁴

I_у1= I_у2=12,5 см⁴

Фигура 3 – швеллер №16

А₃=18,1 см²,    

I_х3=747 см⁴, 

I_у3=63,3 см⁴.

Покажем на схеме и определим координаты у для профилей

у₁ = у₂ = у₀ =2,39 см,

у₁= –z₀ =-1,8 см.

Определим координату у_С по формуле

 ,

где А_i – площадь каждого профиля,

      у_i – координата.

Проводим главную центральную ось х вниз от оси х′ на 0,11 см, наносим т.С – центр тяжести всего сечения.

2. Определяем главные центральные моменты инерции по формулам перехода:

,

где I_xi , I_yi — моменты инерции каждой фигуры;

А_i – площадь сечения каждой фигуры;

а_i – расстояние от центра тяжести каждой фигуры до главной центральной оси х;

b_i – расстояние от центра тяжести каждой фигуры до главной центральной оси у.

Определяем а_i (смотрим схему)

а₁ = а₂ = у₁+|у_С|= 2,39 + 0,11 = 2,5см,

а₃= — (|у₃|-|у_С|) = -1,69см.

Определяем I_х. Следует обратить внимание на то, что фигура 3 – швеллер – повернут, поэтому, для определения I_х следует из сортамента взять I_у швеллера.

I_х3=63,3см⁴

Определяем I_у.  Для швеллера (повернут)  I_у3 =  I_х = 747см⁴.

Определим размеры b_i, показываем на схеме.

b₁= –х₀ = -1,17см,

b₂= х₀ = 1,17см,

b₃=0, т.к. центр тяжести швеллера лежит на оси у.

3. Определим осевые моменты сопротивления сечения по формулам:

Из схемы видно ,что

Тогда

Определить главные центральные моменты инерции сечения геометрической формы.

1. Определим положение центра тяжести сечения.

Сечение симметрично относительно оси у, поэтому нанесем ось у – ось, на которой находится центр тяжести всего сечения. Координата х_С=0, значит, следует определить координату у_С.

Выберем случайную ось х′ — внизу сечения.

Разобьем сечение на простые фигуры:

фигура 1 – прямоугольник с основанием 8 см и высотой 6 см, отмечаем центр тяжести прямоугольника – т. С₁

фигура 2 – равнобедренный треугольник с основанием 8 см и высотой 3 см, отмечаем его центр тяжести – т. С₂.

Теперь  вычислим площади каждой фигуры и определим  координаты у каждой фигуры, затем координаты нанесем на схему

Прямоугольник

Треугольник

Теперь определим координату центра тяжести всего сечения по формуле:

Тогда

Отмечаем у_С на схеме, центр тяжести всего сечения – т.С — и проводим через эту точку главную центральную ось х.

По формулам перехода определяем главные центральные моменты инерции сечения:

,

где I_xi  , I_yi  — моменты инерции каждой фигуры;

А_i – площадь сечения каждой фигуры;

а_i – расстояние от центра тяжести каждой фигуры до главной центральной оси х;

b_i – расстояние от центра тяжести каждой фигуры до главной центральной оси у.

Фигура 1 – прямоугольник

Расстояние а₁ от С₁ до оси х покажем на схеме. Из схемы видно, что а₁=- ( у_С – у₁ )= -0,8 см. Так как С₁ находится на оси у, то b₁=0.

Фигура 2 – треугольник

Находим а₂ =  у₂ – у_С = 7 — 3,8= 3,2 см, отмечаем на схеме.

b₂=0, т.к. С₂ находится на оси у.

Подставляем значения в формулы перехода и определяем:

— главный центральный момент инерции сечения относительно оси х

— главный центральный момент инерции сечения относительно оси у

Таким образом,

Для заданного поперечного сечения, состоящего из швеллера и равнобокого (равнополочного) уголка   требуется определить главные центральные моменты инерции

1)  Вычерчиваем сечение в масштабе.

2)  Разбиваем на простейшие фигуры:

       1. Швеллер №30 (пользуемся сортаментом прокатных профилей):

   2. Уголок :

3)  В каждой фигуре найти собственный центр тяжести С₁ и С_{2   ,}провести собственные оси.

4)  Выбрать вспомогательные оси  .

5) Относительно вспомогательных осей определить центр тяжести всей фигуры:

Через найденный центр тяжести проводим центральные оси.

6) Находим моменты инерции всей фигуры относительно центральных осей, используя формулы перехода между параллельными осями

При определении центробежного момента инерции следует помнить ,что если фигура имеет хотя бы одну ось симметрии, то эта ось является главной, вторая ось, перпендикулярная ей, тоже главная. Центробежный момент относительно главных осей равен 0. Таким образом, для швеллера  

Для уголка  см⁴,  знак зависит от расположения уголка (см. Таблицы «Знак центробежного момента для уголков»). В нашем случае он положительный.

Здесь: а_i – расстояния между центральной осью Х и собственным центром тяжести каждой фигуры,

b_i – расстояние между центральной осью Y и собственным центром тяжести каждой фигуры 

Как видим из вычислений, центробежный момент инерции сечения значит, центральные оси Х;Y не являются главными!

7) Определим положение главных осeй через угол α₀:

Знак «-» означает, что надо повернуть оси Х, У по часовой стрелке.

8) Определим главные моменты инерции сечения

 9) Проверка: Сумма моментов инерции относительно любых двух взаимно перпендикулярных осей есть величина постоянная:

Проверка выполняется.

Найти главные центральные моменты инерции.

1. Подготовка исходных данных.

Из сортамента выписываем:

— для двутавра №10:

— для швеллера №20:

Нумеруем составные части, показываем их центры тяжести (С₁, С₂, С₃) и собственные центральные оси каждой из них (х₁,у₁; х₂,у₂; х₃,у₃).

2.  Поскольку сечение имеет одну ось симметрии, то она – одна из главных центральных (у₀). Найдем положение центра тяжести на этой оси. Для этого выберем вспомогательную ось х‘, перпендикулярную оси симметрии, и реализуем формулу:

которая и определит расстояние от оси х‘ до искомого центра тяжести.

Тогда А=А₁+А₂+А₃=2×20+14,3+28,83=83,15 см²,

тогда

Показываем на схеме центр тяжести «С» и проводим вторую главную центральную ось х₀.

Ординаты собственных центров тяжести простых фигур в системе главных центральных осей:

3. Вычисляем главные центральные моменты инерции

Итак, 

Определить главные центральные моменты инерции сечения.

Составные простые части сечения: прямоугольник 100×60см (I),  полукруг r=30см  (IIи III), треугольник 100×30см (IV). 

Вертикальная ось симметрии у₀ является одной из главных центральных осей.

1. Найдем положение центра тяжести сечения на оси симметрии. Для этого выберем вспомогательную ось х‘, перпендикулярную оси симметрии. Пусть она совпадает с осями: х₁, х₂, х₃

.

Общая площадь А = А₁ — А₂ — А₃ + А₄ = 6000 – 1415 – 1415 + 1500 = 4670см².

Статический момент относительно вспомогательной оси х‘:

Тогда

значит, центр тяжести сечения располагается на 12,8см выше вспомогательной оси х‘.

2. Вычисляем осевые моменты инерции    

Они и будут главными центральными моментами инерции сечения.

Здесь применялись формулы:

Найти главные центральные моменты инерции сечения, состоящего из листа 40×2см и двух уголков №14/9.

Исходные данные из сортамента для неравнобокого уголка №14/9.

Сечение имеет одну ось симметрии. Она – одна из главных центральных. Обозначаем её х₀. Чтобы показать вторую главную центральную ось, надо найти положение центра тяжести на оси симметрии:

Выбираем вспомогательную ось у‘, перпендикулярную к оси симметрии и вычисляем статический момент сложного сечения относительно этой оси:

Проводим главную центральную ось у₀ через найденный центр тяжести. 

Вычисляем непосредственно главные центральные моменты инерции:

Таким образом, 

Требуется найти главные центральные моменты инерции.

Сечение имеет две оси симметрии. Следовательно, центр тяжести совпадает с точкой пересечения этих осей, а сами они оказываются главными центральными осями.

Остается лишь вычислить осевые моменты инерции относительно осей х₀ и у₀.

«Разбиваем» сечение на простые фигуры: прямоугольник 6×8см и два круга r=1см. Тогда:

Итак

,

Требуется определить величины главных центральных моментов инерции.

Сечение имеет одну ось  симметрии.

На основании первого признака главных осей для симметричных сечений можно утверждать, что ось симметрии является одной из главных центральных осей. Обозначаем ее «у₀». Значит, вторая главная центральная ось, перпендикулярная оси симметрии, должна проходить через центр тяжести сечения.

Следовательно, нам достаточно только найти положение центра тяжести на оси симметрии, а для этого необходимо вычислить одну лишь координату его по формуле:

С этой целью выбираем вспомогательную ось х‘, «разбиваем» сложное сечение на прямоугольник со сторонами 10 и 4см и треугольник с основанием 4см и высотой 3см.

Тогда:

Проводим через найденный центр тяжести вторую главную центральную ось х₀.

Расстояние между осями х₁ и х₀: а₁=5 — 4,3 =0,7см, а расстояние между осями х₂ и х₀: а₂=10 – 1 — 4,3 = 4,7см.

Таким образом, положение главных центральных осей найдено, осталось вычислить величины главных центральных моментов инерции:

х‘, у‘ – вспомогательные оси при определении положения центра тяжести сечения,

S_х’, S_у’ – статические моменты относительно вспомогательных осей,

х_с, у_с – координаты центра тяжести сечения, а также и обозначение случайных (т.е. не главных) центральных осей,

х₀, у₀ – главные центральные оси,

α₀ – угол поворота главных центральных осей от случайных центральных осей х_с и у_с,

, — главные центральные моменты инерции,

с_i – центры тяжести отдельных фигур, из которых состоит сечение сложной формы,

х_i, у_i – собственные центральные оси отдельных фигур, а также и координаты центров тяжести отдельных фигур в системе вспомогательных осей х‘, у‘,

а_i, в_i – расстояния между собственными центральными осями отдельных фигур х_i, у_i и случайными центральными осями всего сечения х_с, у_с.

Требуется определить положение главных центральных осей и величины главных центральных моментов инерции.

Сечение имеет сложную форму, состоит их 4^х простых фигур:

I – швеллера №30^а,

II – прямоугольника 2×40см,

III – двутавра №20^а,

IV – равнобокого уголка №12 (d=10мм).

Всё начинается с подготовки исходных данных. С этой целью необходимо сделать выписки из таблиц Сортамента прокатных сечений (см. рубрику «Таблицы»).

Этап 0. Подготовительный

Фигура I. Швеллер №30^а

Фигура II – прямоугольник 2×40см, В сортаменте прокатной стали этой фигуры нет, поскольку все геометрические характеристики ее свободно вычисляются

Фигура III. Двутавр №20^а.

Фигура IV. Равнобокий уголок №12 (d=10мм).

Пользуясь данными сортамента, на схеме сечения, вычерченной в достаточно крупном масштабе, показываем положение центров тяжести каждой из фигур и собственные центральные оси х_i, у_i.

Этап 1. Определение положения центра тяжести сечения. Сечение не имеет осей симметрии. Поэтому придётся определять две координаты центра тяжести, используя формулы:

Для реализации этих формул выбираем вспомогательные оси х‘ и у‘ (см.схему сечения).

Площади отдельных фигур: А₁=43,89см², А₂=2×40=80см²,

А₃=35,5см², А₄=23,3см².

Координаты центров тяжести отдельных фигур:

Площадь всего сечения А=182,7см².

Тогда координаты собственных центров тяжести отдельных фигур в системе случайных центральных осей х_с, у_сбудут:

а₁=2,66см,                            b₁=-7,5см

а₂=-2,34см,                           b₂=-1,93см

а₃=-7,34см,                           b₃=9,07см

а₄=14,33см,                           b₄=2,4см.

Этап 2.  Определение моментов инерции относительно случайных центральных осей  х_с, у_с.

Справочные сведения о знаке собственного центробежного момента инерции уголка (равнобокого и неравнобокого):

Справочные сведения для определения собственного центробежного момента инерции неравнобокого уголка:  

Этап 3. Определение положения главных центральных осей

Положительный угол  α₀ соответствует повороту против часовой стрелки главных осей относительно случайных (см.схему).

Этап 4. Определение величин главных центральных моментов инерции

Правило: Ось с максимальным главным моментом инерции «тяготеет» к более тяжелой случайной оси. Поэтому в нашем случае:

тогда 

Проверки.

1. Выполнение закона суммы осевых моментов инерции.

Для этого сравним

.

получаем:

Разница в последней цифре дает незначительную погрешность <<5%, что вполне допустимо в инженерных расчетах.

2. Проверка правильности вычислений.

Суть ее в том, что если все сделано правильно, то центробежный момент инерции сечения относительно найденных нами главных осей должен равняться нулю.

Подставляя сюда    и sin13˚20’=0,2306,                                                    cos13˚20’=0,9730,имеем

погрешность составляет:

И эта проверка выполняется.

Зачем нужен момент инерции сечения

Несмотря на то, что наука о прочности давно уже шагнула вперёд, и давно уже развиваются многие её направления (строительная механика, механика разрушения, теория упругости и другие), а также несмотря на то, что всё чаще расчеты сложных конструкций выполняются при помощи метода конечного элемента посредством специализированных программных комплексов, прикидочные расчеты на основе методов сопромата не утратили своей актуальности. Ведь именно они, во-первых, позволяют дать оценку прочности конструкции «в полевых условиях» (без трудоёмкого построения конечно-элементной модели, без сложных математических выкладок), а во-вторых — позволяют это сделать достаточно быстро.

В основном, расчеты в сопротивлении материалов имеют целью проверить общую (а не местную) прочность балок. Поэтому расчетная схема принимается упрощенной, и многими конструктивными элементами, даже являющимися концентраторами напряжений, в ней пренебрегают. Тем не менее, несмотря на ряд упрощений в схеме и принятые допущения (гипотезы, принятые для построения теории сопротивления материалов), в этой науке разработаны методы, позволяющие с довольно большой точностью определить опасные сечения и напряжения, возникающие в них.

Вообще, поперечное сечение балки может представлять собой тавр, швеллер, двутавр, круг, прямоугольник, кольцо, полый прямоугольник и т.п. или может быть составным, т.е. составленным из нескольких однотипных или различных профилей. От его формы и размеров зависит прочность и жесткость балки. Площадь поперечного сечения является важной характеристикой, но знать только лишь её достаточно разве что для задач на центральное растяжение. Если же балка испытывает изгиб или кручение, то знать только лишь площадь поперечного сечения оказывается недостаточно. Балка может «проходить» (т.е. обладать достаточной прочностью и жесткостью) с одним типом сечения и «не проходить» с другим типом сечения такой же площади. В процессе решения задач по сопромату, касающихся определения напряжений в балке при её изгибе или кручении, проверке устойчивости сжатых стержней, а также при решении некоторых других задач требуется знать не только площадь, но и другие геометрические характеристики сечения (момент инерции площади сечения, момент сопротивления площади сечения, полярный момент инерции площади сечения). Во-первых, они требуются для решения конкретной задачи об определении напряжений в данной балке с заданными размерами поперечного сечения. Во-вторых, они нужны для выполнения сравнительного анализа разных типов сечений (например, выбора среди нескольких различных сечений с одинаковой площадью именно того сечения, которое будет лучше сопротивляться изгибу или кручению), для подбора оптимального сечения для балки, работающей в конкретно заданных условиях. Поскольку нахождение геометрических характеристик сечения требует определенных знаний и практических навыков, в любом учебнике или справочнике по сопромату выделен раздел, посвященный определению этих характеристик, а в любом задачнике по сопромату приведены задачи по нахождению момента инерции или момента сопротивления сечения.

Что такое момент инерции сечения

Обычно, когда речь идёт о геометрических характеристиках сечения, слово «площадь» опускают, чтобы не было нагромождения слов, и говорят не «момент инерции площади сечения», «момент сопротивления площади сечения», а просто «момент инерции сечения», «момент сопротивления сечения» или даже просто «момент инерции», «момент сопротивления». При этом различают осевой, полярный и центробежный момент инерции площади сечения.

Осевой момент инерции площади фигуры (сечения) — это интеграл произведений элементарных площадок данного сечения на квадраты их расстояний от рассматриваемой оси. Другое, менее распространенное его название – экваториальный момент инерции. Величина осевого момента инерции всегда положительна.

Полярный момент инерции площади фигуры (сечения) относительно данной точки (полюса) — это интеграл произведений элементарных площадок на квадраты их расстояний от полюса. Величина полярного момента инерции всегда положительна.

Центробежный момент инерции площади фигуры — это интеграл произведений элементарных площадок на их расстояния от координатных осей. В зависимости от положения осей центробежный момент инерции может быть положительным или отрицательным, а также равным нулю. При повороте осей вокруг начала координат на 90 градусов знак центробежного момента инерции меняется на обратный.

Задавая вопросы «в чем измеряется момент инерции», «какова единица измерения момента инерции», «как обозначается момент инерции» необходимо четко представлять, что именно имеется в виду: момент инерции сечения (о котором идёт речь в сопромате и, в частности, в настоящей статье) или же момент инерции тела (который упоминается в физике и в теории механизмов и машин). Размерность момента инерции сечения – это размерность длины в четвертой степени (например, см⁴, м⁴, мм⁴). Моменты инерции сечений стандартных профилей (швеллеров, уголков, тавров, двутавров) приведены в справочных таблицах в размерности «см⁴». При необходимости, данную в таблице величину можно представить в другой единице измерения. Обычно при решении задач возникает необходимость перевода этой величины в «мм⁴». Обозначается момент инерции сечения буквой I с нижним индексом, который указывает, относительно какой оси вычислена данная характеристика (например, I_x, I_y). Момент сопротивления сечения обозначается буквой W, также с нижним индексом, указывающим на ось, относительно которой дана эта величина (например, W_x, W_y). 

Что такое главные оси

Главные оси инерции – оси, относительно которых центробежный момент инерции равен нулю.

Главные центральные оси — главные оси, проходящие через центр тяжести сечения.

Как найти момент инерции сечения

При вычислении момента инерции сечения можно воспользоваться непосредственно определением момента инерции и вычислить эту характеристику сечения путём нахождения интеграла по площади. Так и поступают при нахождении момента инерции треугольника, круга, прямоугольника, кругового сектора и других простых фигур.

Обозначив характерные размеры сечения через параметры (т.е. буквами) и выполнив соответствующее интегрирование по площади, получают формулы для определения моментов инерции этих сечений. Ход решения показан, например, в учебнике по сопромату Г.С. Писаренко на примере вывода формул для определения момента инерции прямоугольника, треугольника, кругового сектора и эллипса. Такие формулы приведены во многих справочниках по сопромату (например, в книге Писаренко Г.С., Яковлев А.П. Матвеев В.В. Справочник по сопротивлению материалов. – К: Наукова думка, 1975, на страницах 24 — 77) для многих типов сечений (квадрат, полый квадрат, прямоугольник, полый прямоугольник, прямоугольник с круглым отверстием, прямоугольник с двумя отверстиями, прямоугольник с полукруглыми вырезами, повернутый прямоугольник, крестовина, корытное сечение, треугольник, трапеция, круг, кольцо, круговое незамкнутое тонкостенное кольцо, полукруг, четверть круга, круговой сектор, круговой сегмент, полукольцо, сектор кольца, круг с лыской, правильный шестиугольник, правильный многоугольник, круговое сечение с одной или с двумя шпоночными канавками, эллипс, полуэллипс, четверть эллипса, полый эллипс, параболический сегмент, параболический полусегмент, круговой треугольник, сечение железнодорожного рельса). Готовыми формулами из справочника пользоваться намного проще, чем выводить каждый раз нужную формулу самостоятельно путём интегрирования.

В этом же справочнике приведены и формулы для приближенного вычисления геометрических характеристик (F, I, W) сечений стандартных прокатных профилей: уголков (равнобокого и неравнобокого), швеллера, тавра, двутавра, однако на практике этими формулами пользуются весьма редко, т.к. все необходимые характеристики стандартных сечений уже вычислены и приведены в соответствующих нормативных документах (см. ГОСТ 8240-97 для швеллеров, ГОСТ 8509-93 для равнополочных уголков, ГОСТ 8510-86 для неравнополочных уголков, ГОСТ 26020-83 и ГОСТ 8239-89 для двутавров). Выдержки из перечисленных выше стандартов приведены во многих справочниках, учебниках и решебниках по сопромату.

Скачать примеры решения задач, касающиеся того, как найти момент инерции и момент сопротивления, можно здесь (бесплатно, без регистрации):

При вычислении моментов инерции сложных сечений их разбивают на отдельные простые части, моменты инерции которых известны.

Момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями.

Центробежный момент инерции относительно любой системы прямоугольных осей равен центробежному моменту инерции относительно системы центральных осей, параллельных данным, плюс произведение площади фигуры на координаты ее центра тяжести в новых осях.

При повороте прямоугольных осей сумма осевых моментов инерции не изменяется и равна полярному моменту инерции относительно начала координат.

Момент инерции фигуры относительно какой-либо оси можно представить в виде произведения площади фигуры на квадрат некоторой величины, называемой радиусом инерции.

Осевым моментом сопротивления называется отношение момента инерции относительно данной оси к расстоянию до наиболее удаленной точки поперечного сечения.

Размерность моментов сопротивления – единица длины в кубе (например, см³, м³, мм³).

Практическое значение имеют моменты сопротивления относительно главных центральных осей, которые обычно называются просто моментами сопротивления. Полярным моментом сопротивления называется отношение полярного момента инерции к расстоянию от полюса до наиболее удаленной точки сечения.

Источники:

• Н.М. Беляев. Сопротивление материалов.
•  Г.С. Писаренко, А.П. Яковлев, В.В. Матвеев. Справочник по сопротивлению материалов.
• А.В. Александров, В.Д. Потапов, Б.П. Державин. Сопротивление материалов.
• reshusam.ucoz.ru — Примеры определения моментов инерции сечений.

Дополнительно на Геноне:

• Что такое сопромат