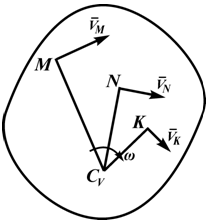
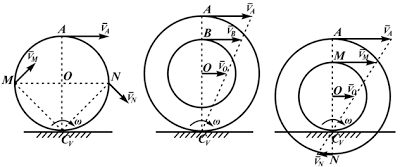
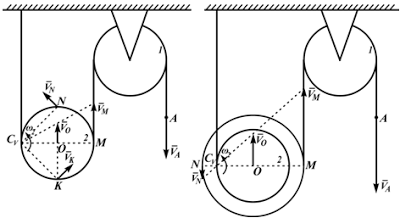
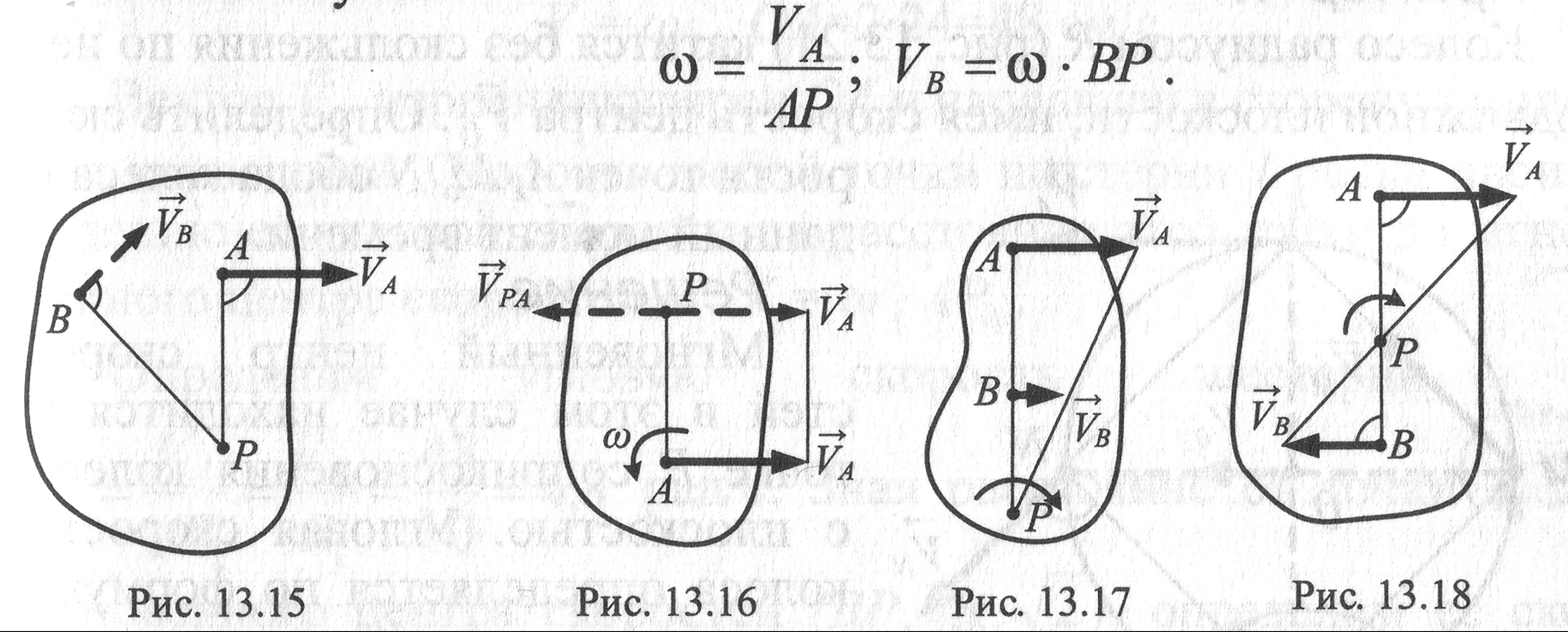
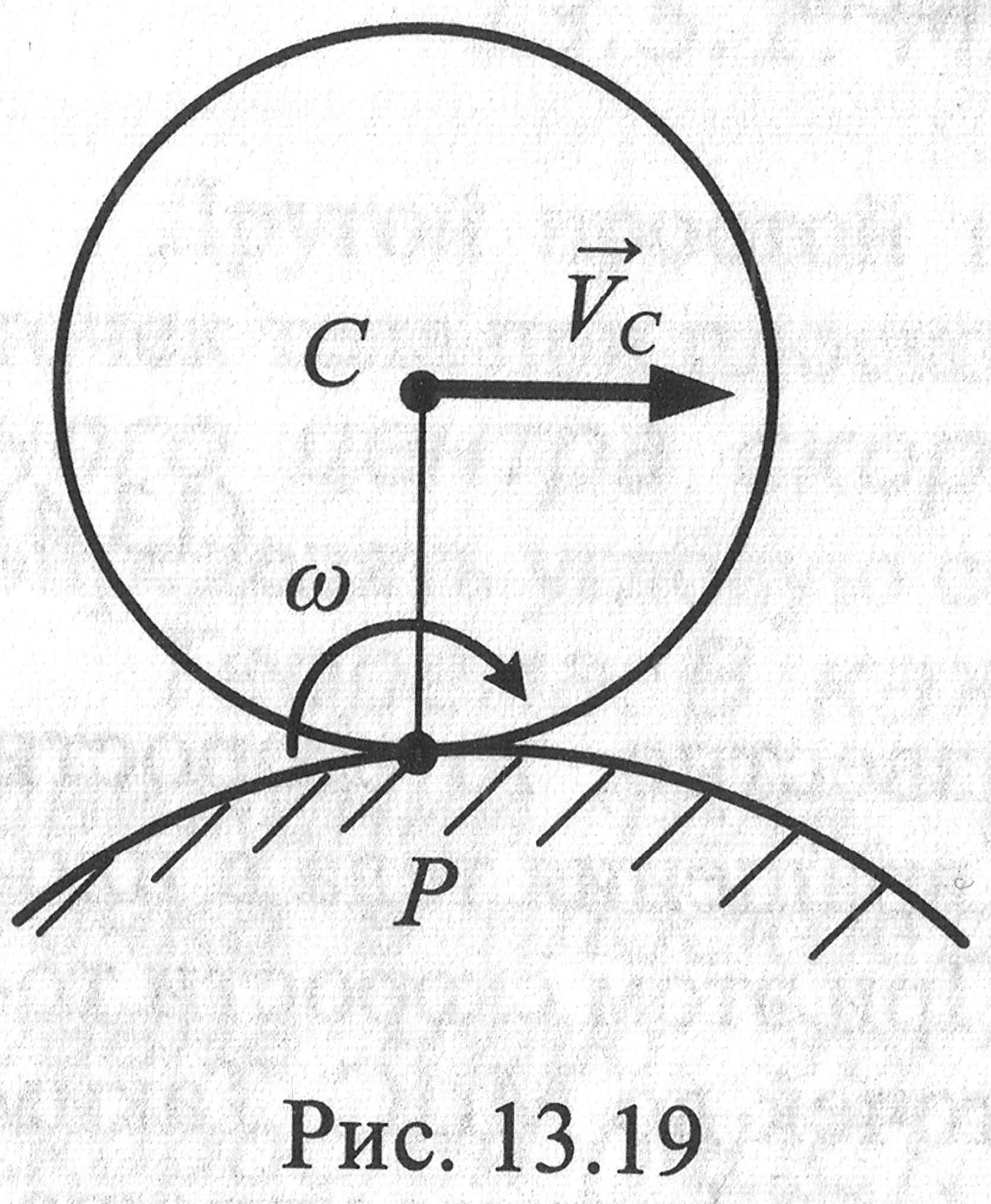
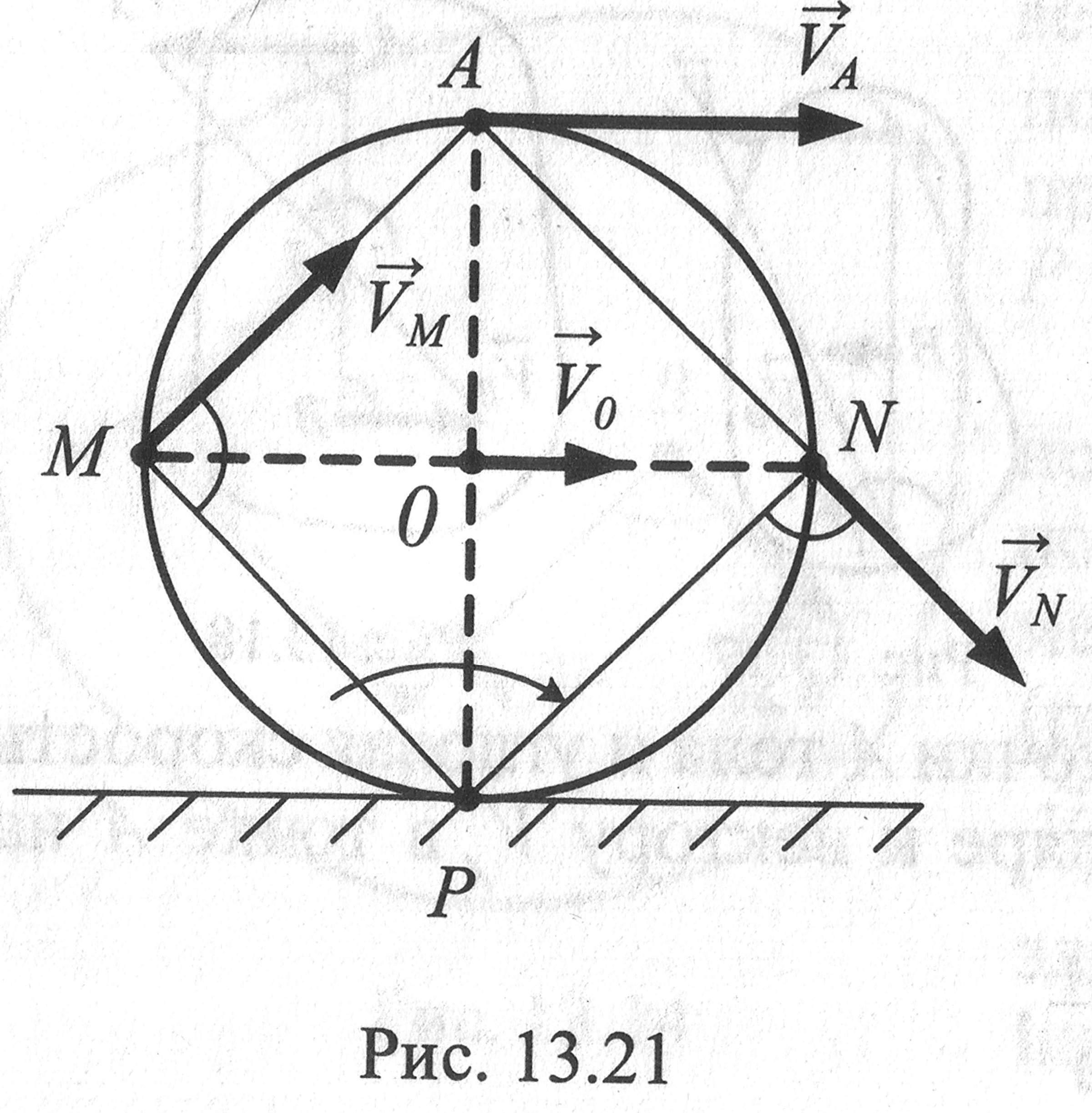
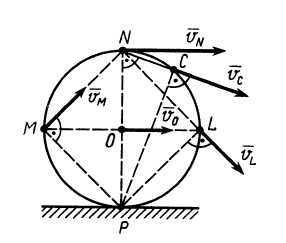
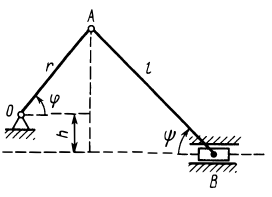
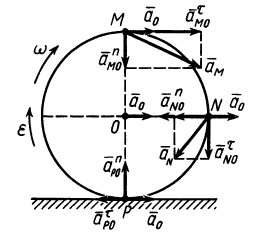
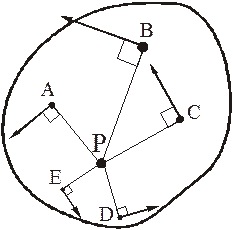
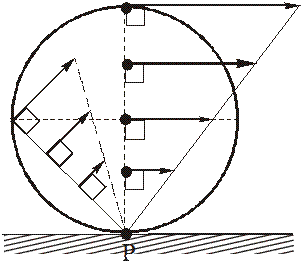
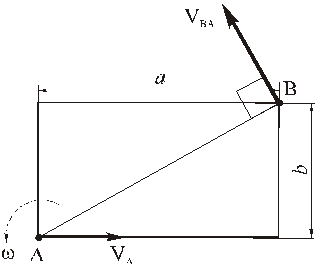
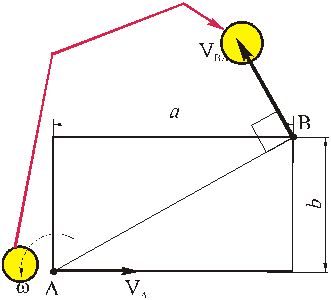
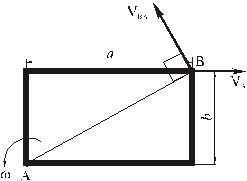
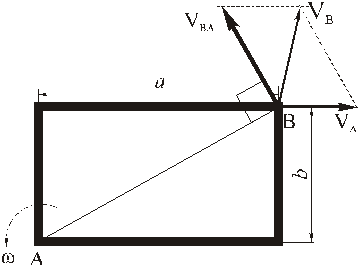
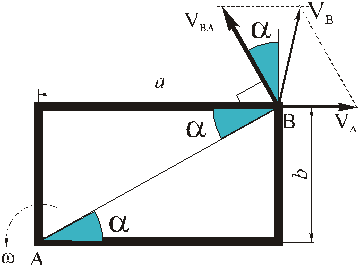
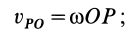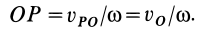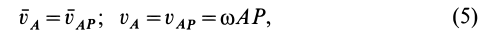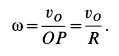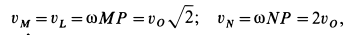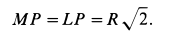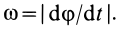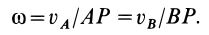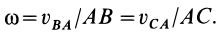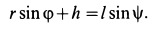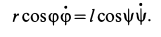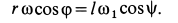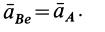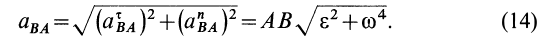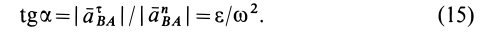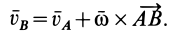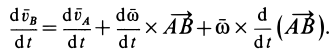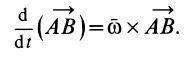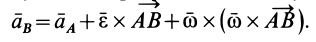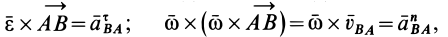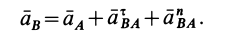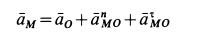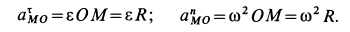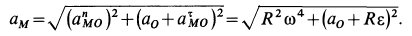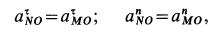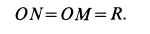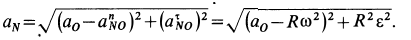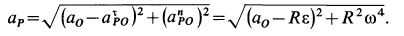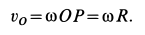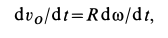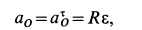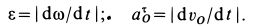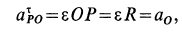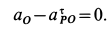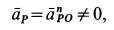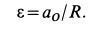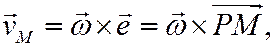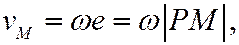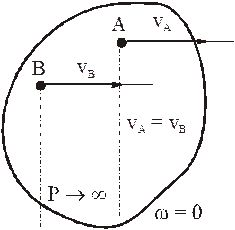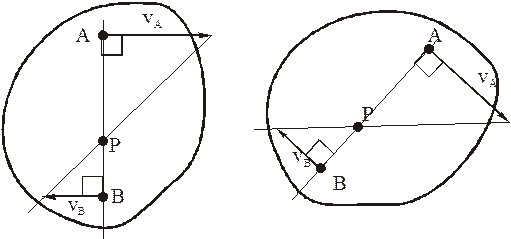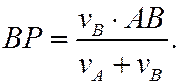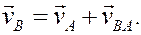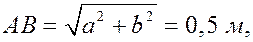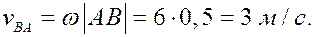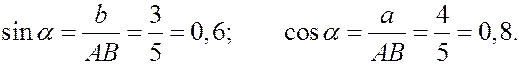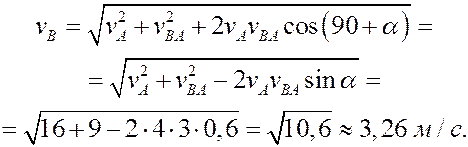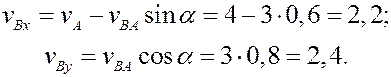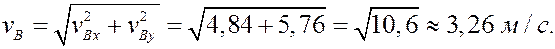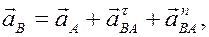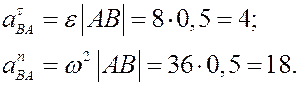Рассмотрим формулы и примеры определения положения мгновенного центра скоростей (МЦС) для различных твердых тел и механизмов при плоскопараллельном движении.
Теорема Эйлера-Шаля доказывает, что любое непоступательное перемещение фигуры в плоскости можно осуществить поворотом вокруг некоторого неподвижного центра.
В соответствии с этим легко доказывается, что при плоскопараллельном движении в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю.
Эту точку называют мгновенным центром скоростей (МЦС). В учебниках эту точку пишут с индексом V, например PV, CV.
Рисунок 2.16
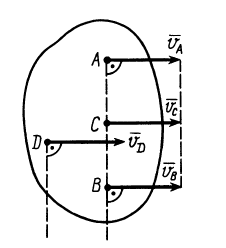
При определении положения МЦС скорость любой точки может быть записана: VM = VCv + VMCv , где точка CV выбрана за полюс. Поскольку это МЦС и VCv=0, то скорость любой точки определяется как скорость при вращении вокруг мгновенного центра скоростей:
VM=VCv+ VMCv=VMCv , VM=VMCv=ω∙CVM,
VN=VCv+ VNCv=VNCv , VN =VNCv=ω∙CVN,
VK=VCv+ VKCv=VKCv , VK=VKCv=ω∙CVK.
Из рисунка 2.16 видно, что МЦС лежит в точке пересечения перпендикуляров, проведённых к скоростям точек, при этом всегда справедливо соотношение:
VM/CVM=VN/CVN=VK/CVK=ω
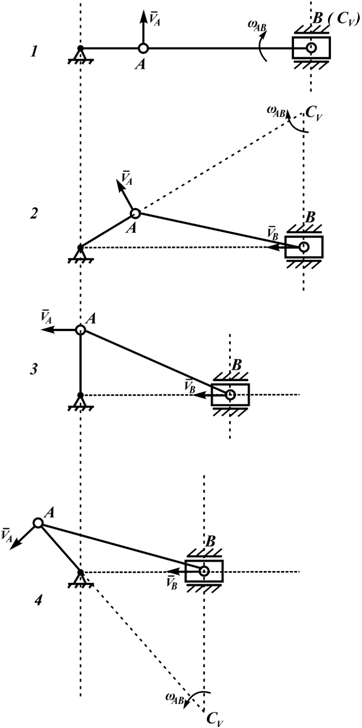
Рисунок 2.17
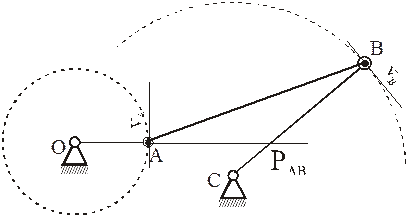
На рисунке 2.17 показаны примеры определения положения МЦС детали кривошипно-шатунного механизма и приведены формулы для расчета скоростей точек.
- CV совпадает с точкой B, VB=0. Шатун вращается вокруг точки B,
ωAB=VA/ACV=VA/AB; - VA/ACV=VB/BCV=ωAB;
- МЦС лежит в «бесконечности»:
VA/∞=VB/∞=ωAB=0, VB=VA; - VA/ACV=VB/BCV=ωAB.
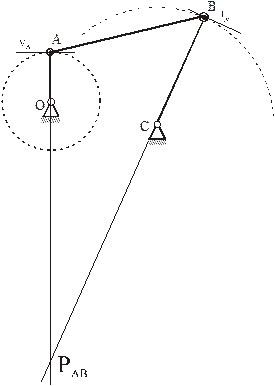
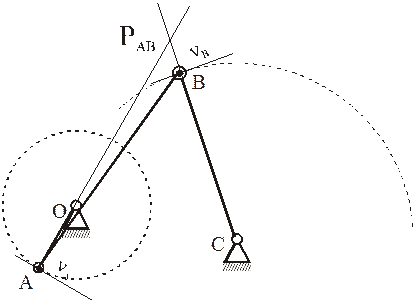
На рисунках 2.18 — 2.21 приведены примеры определения положения МЦС.
VA/ACV=VB/BCV=ω
Рисунок 2.18
VB||VA
В этом случае МЦС находится в «бесконечности», т.е.
ω=VA/∞=VB/∞=ωAB=0, VB=VA
Рисунок 2.19
Рисунок 2.20
- VA/2R=V0/R=VM/(R√2)=ω,
- VA/2R=V0/R=VB/(R+r)=ω,
- VA/(R+r)=V0/r=VN/(R-r)=ω
Формулы справедливы при отсутствии проскальзывания в точке CV.
а б
Рисунок 2.21
Для «а»:
VM=VA
VM/MCV=V0/OCV=VN/NCV=VK/KCV=ω2
Для «б»:
VA=VM
VM/MCV=V0/OCV=VN/NCV=ω2
Примеры решения задач >
Ускорение точки в плоскопараллельном движении >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
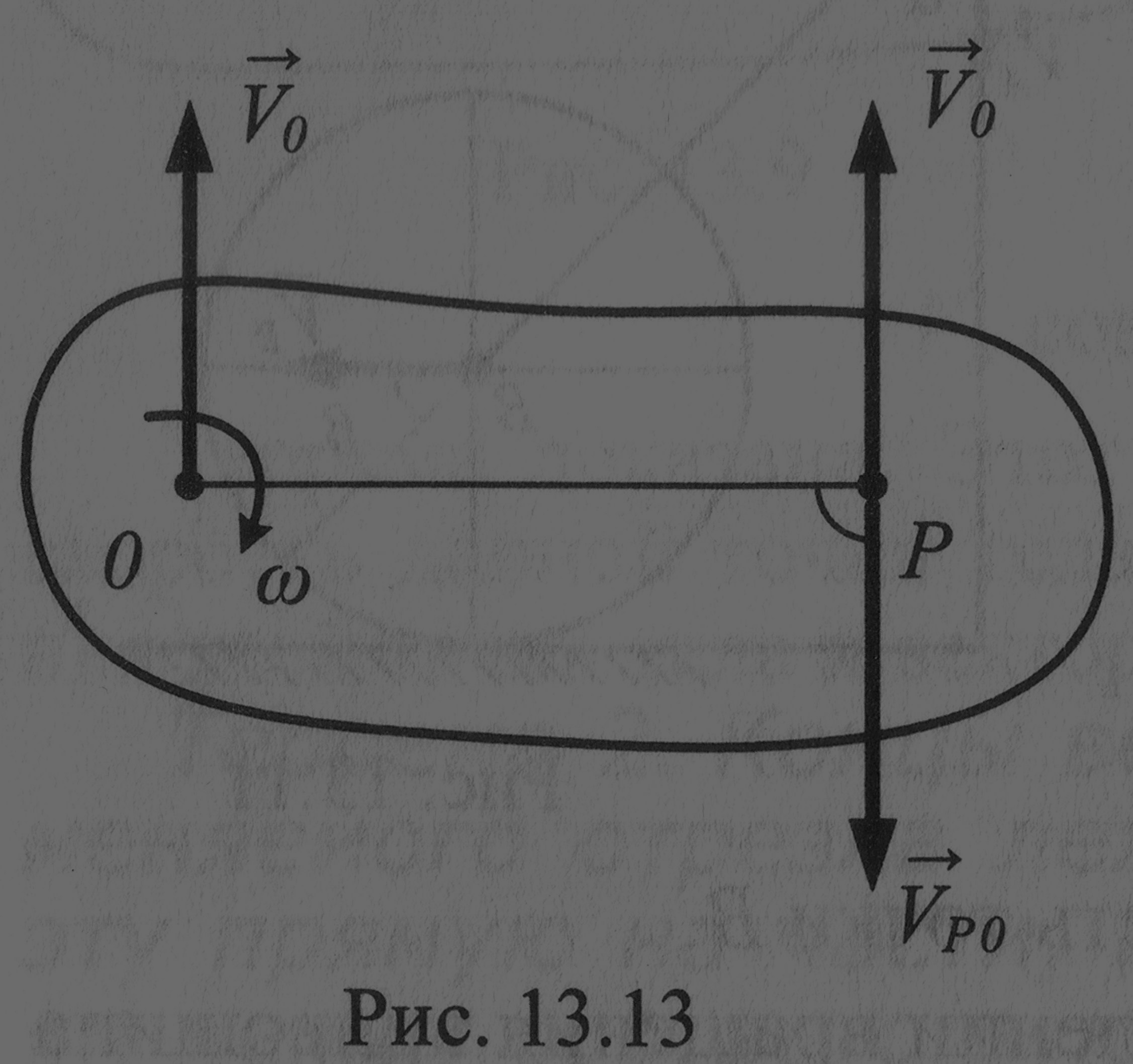
Теорема. В
каждый момент времени при плоском
движении тела, если
,имеется
единственная точка в плоскости его
движения, скорость которой равна нулю.
Эту
точку называют мгновенным
центром скоростей
(МЦС).
Обозначим
её Р.
Для
доказательства теоремы обратимся к
теореме о сложении скоростей . На рис.
точка О имеет
скорость
,
а тело – угловую скорость
заданного
направления. Требуется найти такую
точку Р, скорость которой равна нулю.
Для этого запишем теорему, удовлетворяя
заданное условие
=
0.
Равенство нулю этого выражения возможно
в том случае, если векторы
и
будут в точке
Р равны
по модулю и
противоположны друг другу по направлению:.
Если
;
,
то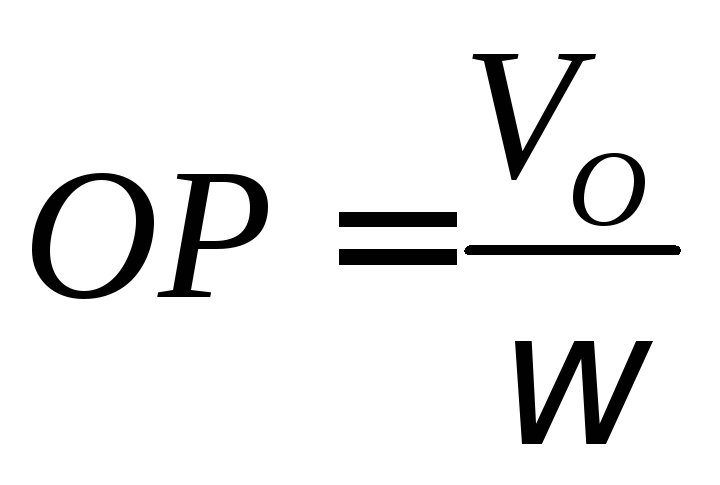
Таким образом,
точка Р –
МЦС на рис.
находится на перпендикуляре к вектору
справа на
расстоянии ОР.
Именно в
этой точке векторыи
равны друг
другу по модулю и противоположны по
направлению, поэтому скорость точки Р
равна нулю.
Если положение
МЦС известно, то, приняв его за полюс Р,
можно
определить скорость, например, точки А
следующим
образом:
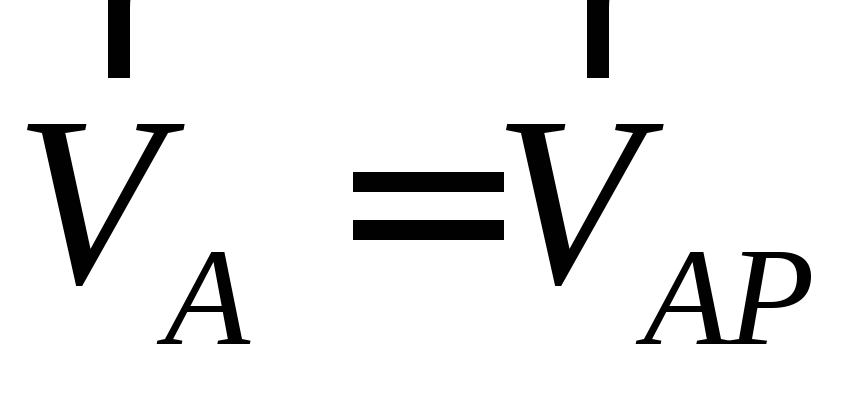
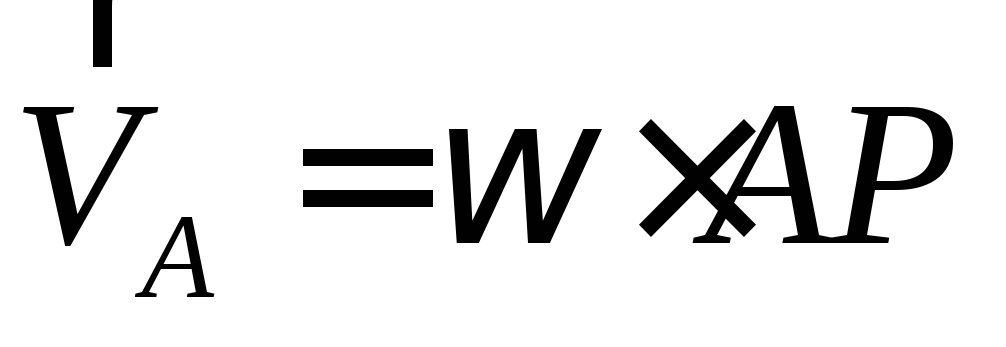

здесь AP
– радиус, на котором вращается точка А
относительно МЦС.
Скорость точки В
вычислим аналогично:
;
;
.
Из полученных
выражений для
и
имеем

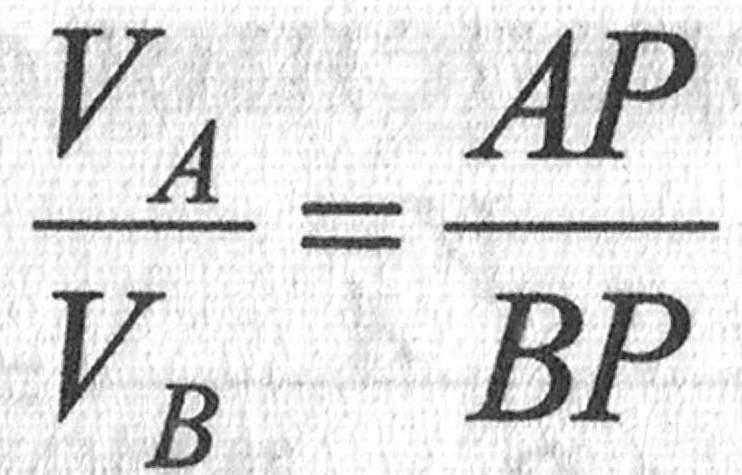
Следовательно,
если положение МЦС известно, то скорости
точек тела вычисляют так же, как и в
случае вращения тела в плоскости вокруг
МЦС с угловой скоростью
.
При этом
скорости точек тела пропорциональны
расстояниям от точек до МЦС. Таким
образом, задача расчёта скоростей точек
плоской фигуры упрощается, если известно
положение мгновенного центра скоростей
тела в любой момент времени.
Способы нахождения мгновенного центра скоростей
В некоторых случаях
из условия движения удаётся сразу
указать точку плоской фигуры, скорость
которой в рассматриваемый момент времени
равна нулю. Эти точки и являются
мгновенными центрами скоростей. В других
наиболее общих случаях положения МЦС
определяют, рассматривая параметры
движения тела и скорости
двух точек тела.
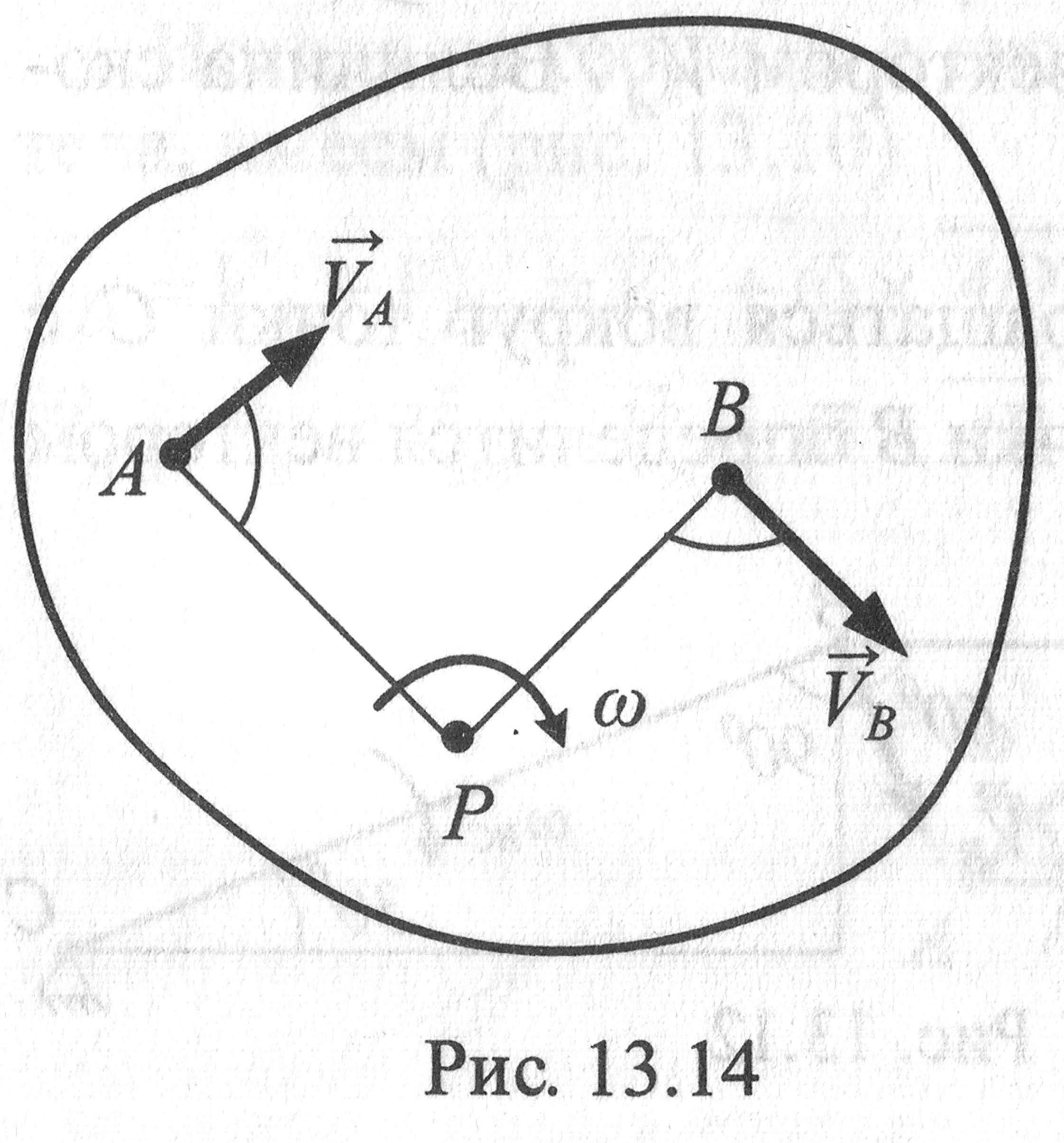
Вариант
1.
Известна
скорость точки А
и направление
скорости точки В.
МЦС находится
на пересечении перпендикуляров к
скоростям, проведённых в точках А
и В
.
В этом случае
Вариант
2. Известна
скорость точки А тела и угловая скорость
. МЦС находится на перпендикуляре к
векторув
точке А на расстоянии АРАР=
Вариант
3.Известны
длина отрезка АВ, скорости
и
двух точек тела, которые перпендикулярны
к отрезку АВ и направлены в одну сторону
МЦС находится на
продолжении отрезка АВ в точке пересечения
с прямой, проведенной через концы
векторов
и
.
Для определениясоставляем
выражение

откуда
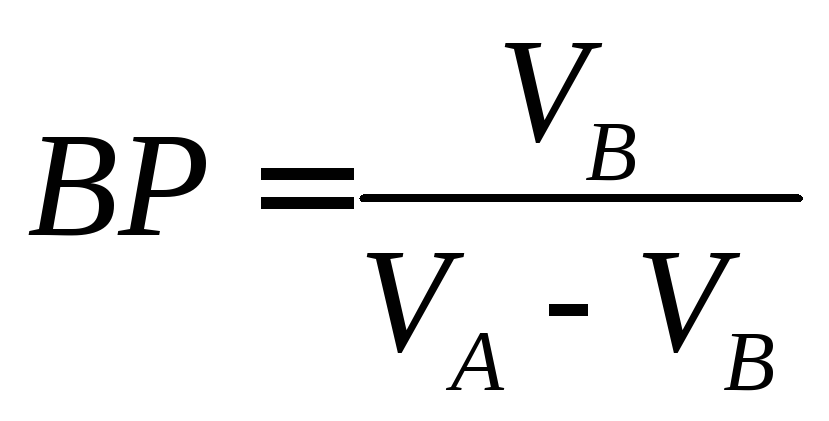
Вариант
4.
Известны
длина отрезка АВ, скоростии
двух точек тела, которые перпендикулярны
отрезку АВ и направлены в разные стороны
МЦС находится
внутри отрезка АВ. Для определения
составляем
выражение
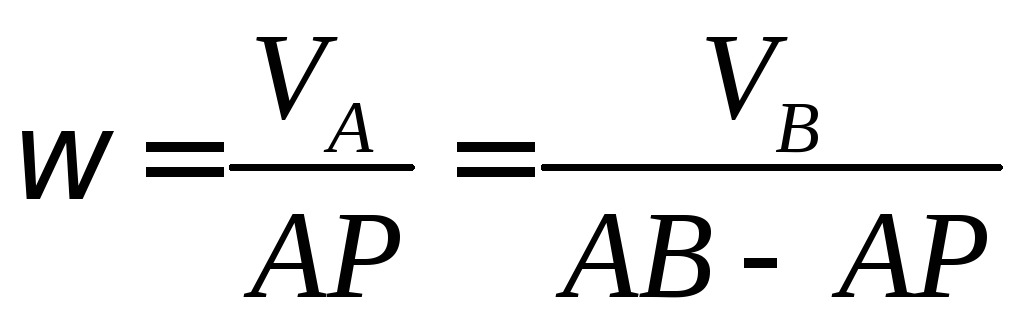
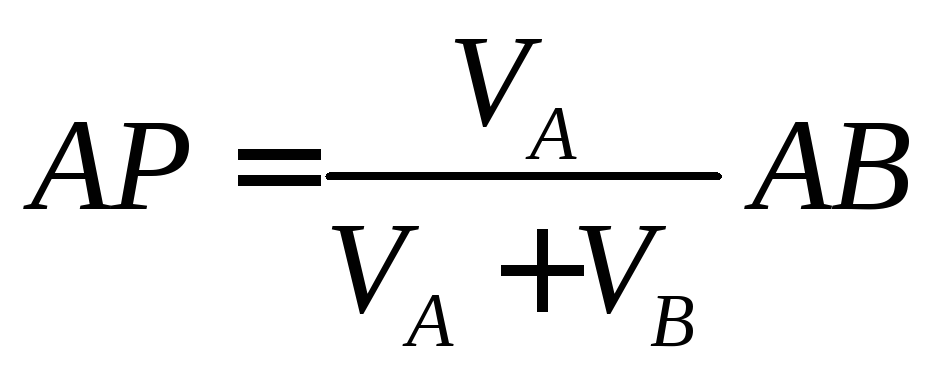
Вариант
5. На рис.
тело перекатывается без проскальзывания
по поверхности неподвижного тела. МЦС
находится в точке соприкосновения тел
в точке Р.
Вариант
6. На рис.
скорости двух точек тела параллельны.
В этом случае МЦС находится в бесконечности,
т.е. отсутствует. Тело совершает мгновенное
поступательное движение, тогда скорости
двух точек и всех других точек тела
одинаковы, а их ускорения в общем случае
могут быть разными.
Задача
3. Колесо
радиусом R
катится без скольжения по неподвижной
плоскости, имея скорость центра
.
Определить скорости точек А,M,
N
обода колеса в данный момент времени.
Решение.
Мгновенный центр
скоростей в этом случае находится в
точке Р соприкосновения колеса с
плоскостью. Угловая скорость колеса
определяется по формуле
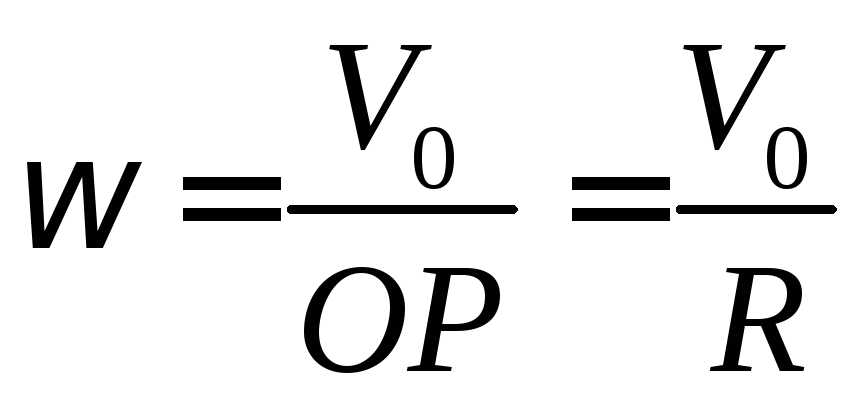
Скорости указанных точек определим с
помощью МЦС:;
,
т.к.MP=NP=R.
Скорости точек
колеса направлены по перпендикулярам
к отрезкам прямых, соединяющих мгновенный
центр скоростей с рассматриваемыми
точками в направлении вращения.
Задача 4.
Для механизма, изображенного на рис.,
найти скорости точек А, В, С, угловые
скорости шатуна ВС и колеса 1 в момент
времени, когда кривошип ОА находится в
горизонтальном положении, а шатун ВС
вертикален, если угловая скорость
кривошипа
рад/c;
ОА=24 см; ВС=30
см;
=10
см.
Для механизма,
изображенного на рис., найти скорости
точек А, В, С, угловые скорости шатуна
ВС и колеса 1 в момент времени, когда
кривошип ОА находится в горизонтальном
положении, а шатун ВС вертикален, если
угловая скорость кривошипа
рад/c;
ОА=24 см; ВС=30
см;
=10
см.
Решение.
Заданный плоский
механизм включает следующие звенья:
кривошип ОА, подвижную шестерню 1, шатун
ВС и ползун С. Шестерня 1 катится по
поверхности неподвижной шестерни 2 без
скольжения, совершая плоское движение,
поэтому мгновенный центр скоростей
шестерни
1 находится в точке их соприкосновения.
Используя угловую
скорость кривошипа ОА, определим скорость
точки А – конца кривошипа ОА и центра
шестерни 1:
см/c/
Вектор
перпендикулярен
ОА и направлен в сторону вращения
кривошипа. Скорость любой точки шестерни
1 равна произведению её угловой скорости
на расстояние этой точки до мгновенного
центра скоростей
:
=
.
Определим угловую
скорость шестерни 1:

Зная расстояние от точки В до мгновенного
центра скоростей (),
определим её скорость:
Скорость
направлена
перпендикулярно отрезку
в сторону
вращения шестерни 1 вокруг мгновенного
центра скоростей. Направление вращения
шестерни 1
установим,
исходя из направления скорости
,
которая является вращательной скоростью
относительно мгновенного центра
скоростей
.
Шатун ВС
совершает
плоское движение. Мгновенный центр
скоростей
шатуна
находится в точке пересечения
перпендикуляра к скорости точки В,
являющегося продолжением отрезка
,
и перпендикуляра
к скорости ползуна С, совершающего
прямолинейное движение вдоль направляющей,
наклоненной к горизонту под углом 45°.
Скорости всех
точек шатуна являются вращательными
вокруг мгновенного центра скоростей
,
поэтому
=
;
.
Из равнобедренного
прямоугольного треугольника
найдём, что
см.
Тогда
=67,88
см/с. Угловую скорость шатуна ВС
найдём
используя скорость точки В:
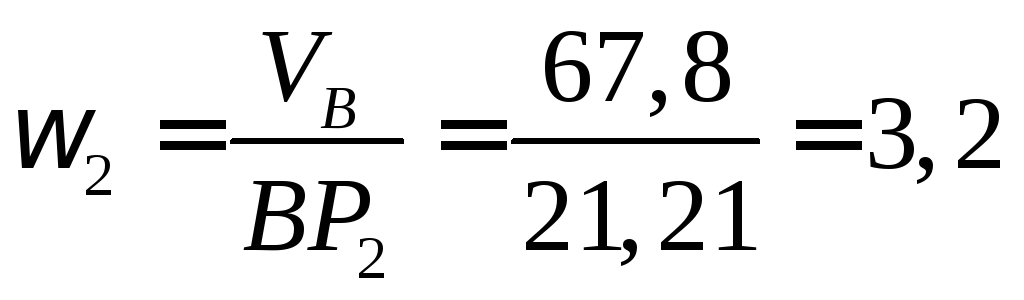
Вектор скорости
точки С
направлен
перпендикулярно к
в сторону
вращения шатуна ВС
вокруг
мгновенного центра скоростей
.
Направление
вращения шатуна установим, исходя из
направления скорости точки В, которая
является вращательной скоростью
относительно мгновенного центра
скоростей
.
Задача
5. В
положении механизма, схема которого
приведена на рис. 14, определить угловую
скорость шатуна АВ
и скорости точек В
и С,
если
=
2 рад/с,
ОА
= 0,2 м, АВ
= 1,6 м,
ВС
= 0,8 м,
h
= 0,8 м.
Решение. Найдем
скорость точки А:
Рис. 14
Скорость ползуна
В
должна: быть направлена по прямой
КВ.
Мгновенный центр шатуна АВ
находится
в точке Р
пересечения перпендикуляров.
Восстановленных к направлениям векторов
скоростей точек А
и В.
Угловая скорость
шатуна АВ
равна
.
Определим
величины АР,
ВР,
СР:
,
.
Тогда
равносторонний:
.
Находим
рад/с,
м/с,
м/с.
Направление
угловой скорости шатуна
определяется по направлению вращения
вектора
скорости точки
А
относительно мгновенного центра
скоростей. Угловая скорость шатуна
АВ
направлена по часовой стрелке. Скорости
точек В
и С
должны показывать такое же направление.
Для построения вектора
восстанавливаем перпендикуляр к отрезку
СР
и направляем вектор
в соответствии с направлением
.
Ответ.
= 0,29 рад/с,
= 0,23 м/с.
Задача 6. Колесо
катится без скольжения по прямолинейному
рельсу. Скорость цен-: тра колеса равна
20 м/с,
радиус
колеса 1 м.
Найти скорости точек А,
В, D
и угловую скорость колеса (рис. 15).
Решение.
Мгновенный центр скоростей находится
в точке Р
соприкосновения колеса и неподвижной
поверхности:
рад/с.
Угловая скорость
направлена по часовой стрелке. Определим
расстояние точек А,
В, D до МЦС:
м,
м,
м/с,
м/с.
Вектор
перпендикулярен прямойАР,
а вектор
перпендикулярен прямойВР.
Вектор
перпендикуляренDP.
Направления векторов
,
,
должны соответствовать угловой
скорости колеса (рис. 15).
Рис. 15
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 марта 2018 года; проверки требуют 2 правки.
Мгнове́нный центр скоросте́й — при плоскопараллельном движении абсолютно твёрдого тела точка, связанная с этим телом, которая имеет следующие свойства: а) её скорость в данный момент времени равна нулю; б) относительно неё в данный момент времени вращается тело. Она существует в любой момент времени, но её положение меняется со временем за исключением одного случая — вращательного движения.
Положение мгновенного центра скоростей[править | править код]
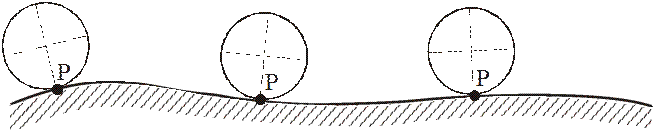
Рис. 1. При качении колеса по горизонтальной дороге мгновенный центр скоростей находится в точке касания колеса и дороги — в точке А. 


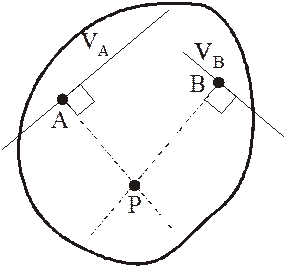
Для того, чтобы определить положение мгновенного центра скоростей, необходимо знать направления скоростей любых двух различных точек тела, скорости которых не параллельны. Тогда для определения положения мгновенного центра скоростей необходимо провести перпендикуляры к прямым, параллельным линейным скоростям выбранных точек тела. В точке пересечения этих перпендикуляров и будет находиться мгновенный центр скоростей.
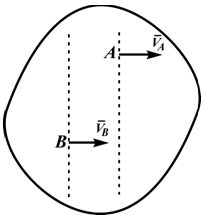
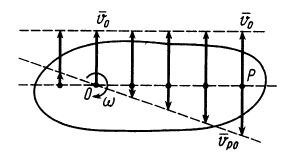
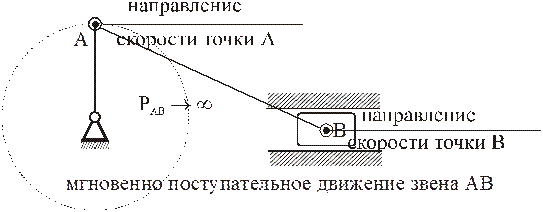
В том случае, если векторы линейных скоростей[1] двух различных точек тела параллельны друг другу, и отрезок, соединяющий эти точки, не перпендикулярен векторам этих скоростей, то перпендикуляры к этим векторам также параллельны. В этом случае говорят, что мгновенный центр скоростей находится в бесконечности, и тело движется мгновенно поступательно.
Если известны скорости двух точек, и эти скорости параллельны друг другу, и кроме того, указанные точки лежат на прямой, перпендикулярной скоростям, то положение мгновенного центра скоростей определяется так, как показано на рис. 2.
Положение мгновенного центра скоростей в общем случае не совпадает с положением мгновенного центра ускорений. Однако в некоторых случаях, например, при чисто вращательном движении, положения этих двух точек могут совпадать.
Рис. 2. Векторы скоростей точек колеса, лежащих на прямой РМ, образуют подобные треугольники; мгновенный центр скоростей находится в точке Р
Более общий случай сферического движения[править | править код]
Согласно теореме вращения Эйлера, любое вращающееся трёхмерное тело, имеющее неподвижную точку, также имеет и ось вращения. Таким образом, в более общем случае вращения трёхмерного тела говорят о мгновенной оси вращения.
Рис. 3. Чтобы определить положение мгновенного центра скоростей для шатуна в кривошипно-шатунном механизме, обычно необходимо провести перпендикуляры к векторам скоростей концов шатуна; мгновенный центр скоростей обозначен как CIR
Пример решения задачи[править | править код]
Найдём скорость точки K для колеса, показанного на рисунке 1, если задана скорость центра колеса (точки С), его радиус и угол АСК:



Решение
Найдём сначала угловую скорость колеса в данный момент времени при его вращении вокруг мгновенного центра скоростей (вокруг точки А):

Теперь, зная угловую скорость, найдём скорость точки К:

Чтобы найти численное значение 

или, учтя, что 

Вынесем R за знак корня:

Подставив заданые в условии численные значения, найдём:

Тогда, зная расстояние КА, можем найти численное значение скорости 

Ответ: 
Заметим, что для решения задачи знать численное значение R не обязательно.
Действительно, подставляя в формулу (*) выражения для 

Применение понятия мгновенного центра скоростей[править | править код]
Данное понятие используется при анализе движения звеньев кривошипно-шатунного механизма (рис. 3). Например, если известна постоянная угловая скорость вращающегося кривошипа (на рисунке 3 показан красным цветом), то скорость поршня не будет постоянной по модулю. Чтобы вычислить скорость поршня в разных положениях и построить соответствующий график, можно воспользоваться понятием мгновенного центра скоростей[2]. В свою очередь кривошипно-шатунные механизмы применяются в двигателях внутреннего сгорания, поршневых насосах, поворотных гидродвигателях и многих других устройствах. Таким образом, использование понятия мгновенного центра скоростей позволяет производить расчёты, необходимые для выбора оптимальной конструкции указанных механизмов.
Движения коленного, локтевого, плечевого и др. суставов биофизики также исследуют с помощью мгновенного центра скоростей.
Улучшения тормозных характеристик автомобилей можно добиться путём выбора оптимальной конструкции педалей тормоза и соответствующих кинематических расчётов, проведённых с помощью мгновенного центра скоростей.
Примечания[править | править код]
- ↑ Показанные на рис. 1 скорости являются линейными
- ↑ Скорости поршня в разных положениях можно также рассчитать графически с помощью плана скоростей
Литература[править | править код]
- Тарг С. М. Краткий курс теоретической механики. Учеб. для втузов.— 10-е изд., перераб. и доп. — М.: Высш. шк., 1986.— 416 с, ил.
- Основной курс теоретической механики (часть первая) Н. Н. Бухгольц, изд-во «Наука», Главная редакция физико-математической литературы, Москва, 1972, 468 стр.
Содержание:
Мгновенный центр скоростей:
В каждый момент времени при плоском движении фигуры в ее плоскости, если 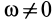
Для доказательства этой теоремы достаточно указать способ нахождения мгновенного центра скоростей, если известны по модулю и направлению скорость какой-либо точки 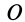
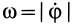
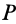
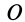
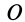
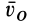
Рис. 46
Итак, если 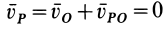
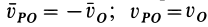
Ho
следовательно,
Таким образом, мгновенный центр скоростей находится на перпендикуляре к скорости 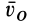
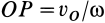
Мгновенный центр скоростей является единственной точкой плоской фигуры для данного момента времени. В другой момент времени мгновенным центром является уже другая точка плоской фигуры.
Если мгновенный центр известен, то, приняв его за полюс и учитывая, что скорость его в этом случае равна нулю, согласно (3) и (4), для точки 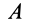
где 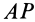
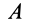
По направлению скорость 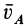
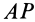
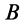
причем скорость 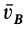
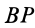
Из (5) и (6) имеем
и
Следовательно, если мгновенный центр скоростей известен, то скорости точек плоской фигуры при ее движении в своей плоскости вычисляют так же, как и в случае вращения фигуры в рассматриваемый момент вокруг своего мгновенного центра скоростей с угловой скоростью 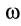
Для нахождения скоростей точек тела при его плоском движении обычно предварительно находят мгновенный центр скоростей. Но можно применить формулу, выражающую зависимость между скоростями двух точек тела.
Рассмотрим способы нахождения мгновенного центра скоростей. Существует два основных способа его нахождения: из механических условий задачи и по скоростям точек плоской фигуры.
В некоторых случаях удается сразу указать точку плоской фигуры, скорость которой в рассматриваемый момент равна нулю. Эти точки в таких задачах и являются мгновенными центрами скоростей. Так, в случае качения без скольжения одного тела по поверхности другого неподвижного тела точка соприкосновения поверхностей тел и является мгновенным центром скоростей.
Рис. 47
Рис. 48
Например, при качении без скольжения колеса по неподвижной прямой линии (см. рис. 52) и одного колеса по неподвижному другому колесу (см. рис. 61) мгновенный центр скоростей находится в точках соприкосновения колеса с прямой и соответственно колеса с колесом. В общем случае, если известны скорости двух точек плоской фигуры (рис. 47), мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям этих точек.
В том случае, когда точки лежат на общем перпендикуляре к скоростям этих точек, скорости точек параллельны и концы их лежат на одной прямой, проведенной через мгновенный центр скоростей (рис. 48 и 49), так как скорости точек пропорциональны расстояниям от этих точек до мгновенного центра скоростей. Если скорости двух точек, расположенных на общем перпендикуляре к этим скоростям, еще и равны (рис. 50), то имеем мгновенное поступательное движение плоской фигуры, при котором скорости всех точек фигуры одинаковы по модулю и направлению. Угловая скорость плоской фигуры при мгновенном поступательном движении равна нулю, и в этом случае, согласно формуле (7), мгновенный центр скоростей находится в бесконечности.
Рис. 49
Рис. 50
Рис. 51
Рис. 52
Заметим, что при мгновенном поступательном движении только скорости точек одинаковы, а их ускорения в общем случае различны. Невозможен случай, когда скорости двух точек, не лежащих на общем перпендикуляре к скоростям, не равны друг другу по модулю, но параллельны (рис. 51), так как для него не выполняется теорема о проекциях скоростей двух точек тела на прямую, соединяющую эти точки.
Пример:
Колесо радиусом 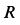
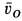
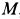
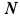
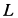
Решение. Мгновенный центр скоростей в этом случае находится в точке 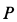
По формуле (5) для скоростей указанных точек имеем
так как
Скорости точек колеса направлены по перпендикулярам к отрезкам прямых, соединяющих мгновенный центр скоростей с рассматриваемыми точками.
Вычисление угловой скорости при плоском движении
Угловую скорость плоской фигуры при плоском движении можно вычислить, согласно ее определению, как
Затем ее можно определить по формуле (7):
Чтобы определить угловую скорость, надо скорость какой-либо точки плоской фигуры разделить на расстояние от этой точки до мгновенного центра скоростей. Направление вращения определяем по направлению скорости какой-либо точки, считая, что плоская фигура в данный момент вращается вокруг мгновенного центра скоростей с угловой скоростью 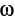
Рис. 53
Угловую скорость при плоском движении можно вычислить путем предварительного нахождения скорости какой-либо точки плоской фигуры от вращения фигуры вокруг другой ее точки, принятой за полюс, например 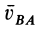
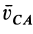
Знак угловой скорости определяют по направлению относительной скорости какой-либо точки фигуры от вращения фигуры вокруг другой ее точки, выбранной за полюс.
Применяют и другие способы определения угловой скорости. Так, если предварительно установить зависимость угла поворота плоской фигуры от линейных и угловых величин других плоских фигур тождественным соотношением, то, дифференцируя его по времени, получаем соотношение, из которого иногда удается определить искомую угловую скорость. Этот способ используют часто для нахождения зависимости угловых скоростей отдельных звеньев плоских механизмов.
Пример:
В кривошипно-шатунном механизме (рис. 53) даны длины кривошипа 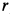
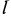
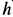
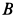
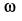
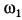
Решение. Положение кривошипа 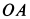
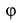
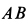
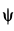
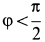
Дифференцируя это тождество по времени, получим
Но 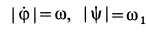
Полученное соотношение и является искомой зависимостью между угловыми скоростями кривошипа и шатуна. При 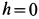
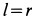
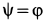
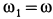
Направления вращений кривошипа и шатуна противоположны. При вращении кривошипа против часовой стрелки шатун вращается по часовой стрелке.
Ускорения точек тела при плоском движении
Рассматривая плоское движение плоской фигуры как сложное, состоящее из переносного поступательного вместе с полюсом 
Рис. 54
Так как переносное движение является поступательным вместе с точкой 
Относительное ускорение 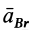
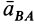
т. е. ускорение какой-либо точки плоской фигуры при плоском движении равно векторной сумме ускорения полюса и ускорения этой точки от вращательного движения плоской фигуры вокруг полюса.
Ускорение от относительного вращательного движения вокруг полюса, как и в случае вращения тела вокруг неподвижной оси, состоит из касательной и нормальной составляющих 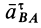
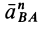
причем
и _________
Касательное относительное ускорение 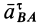
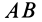
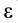
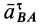
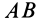
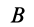
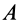
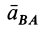
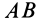
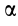
Из формулы (15) следует, что угол 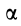
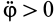
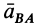
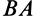
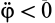
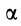
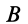
Формулу (10), определяющую зависимость ускорений двух точек плоской фигуры, можно получить непосредственным дифференцированием векторного равенства для скоростей, справедливого в любой момент времени. Имеем
Продифференцируем по времени обе части этого равенства, учитывая изменения векторных величин относительно неподвижной системы координат (полные производные). Получаем
Здесь 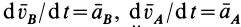
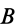
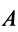
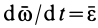
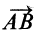
Объединяя полученные результаты, получаем
Рассуждения, аналогичные тем, которые проведены для скорости 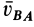
т. е. 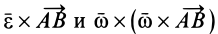
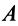
- Заказать решение задач по теоретической механике
Пример:
Колесо радиусом 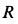
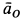
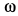
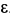
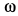
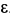
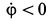
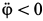
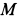
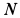
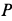
Решение. Ускорение точки 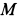
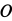
и аналогичным формулам для точек 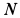
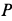
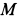
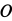
Рис. 55
Ускорение 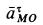
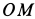
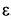
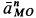
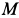
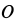
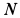
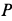
Так как для точки 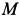
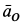
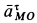
Для точки
так как
Окончательно для точки 
Для точки 
В том случае, когда колесо катится без скольжения, точка 
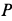
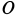
Дифференцируя по времени обе части этого тождества и приравнивая результат дифференцирования, получим
или
так как точка 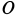
Учитывая, что
имеем
Следовательно, при качении колеса по прямой без скольжения
т. е. ускорение мгновенного центра скоростей, скорость которого равна нулю, не равно нулю.
Если угловое ускорение не задано, то при отсутствии скольжения колеса по прямой его можно определить по формуле
- Мгновенный центр ускорений
- Мгновенный центр вращения
- Вращение твердого тела вокруг неподвижной точки
- Сложное движение точки
- Пространственная система сил
- Центр тяжести
- Кинематика точки
- Плоское движение твердого тела
Мгновенный центр скоростей (МЦС) и его определение. Определение скоростей точек тела с помощью МЦС



Мгновенным центром скоростей (МЦС) называется такая точка плоской фигуры, скорость которой в данный момент времени равна нулю.
При любом непоступательном движении плоской фигуры такая точка всегда существует. Действительно,
Пусть в данный момент времени известно положение МЦС фигуры. Тогда, принимая его за полюс и учитывая, что 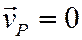
т.е. знание МЦС упрощает определение скоростей точек плоской фигуры, т.к. сразу позволяет определить модуль скорости по формуле (5) и направление: 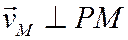
Таким образом, при известном МЦС вектор скорости любой точки плоской фигуры равен
модуль определяется по формуле
направлен вектор к отрезку РМ, соединяющему МЦС с данной точкой М, в сторону вращения фигуры вокруг МЦС.
В силу вышесказанного, возникает важная задача об определении положения МЦС плоской фигуры.
Положение мгновенного центра скоростей плоской фигуры может быть найдено, если:
1) задан закон движения (1) плоской фигуры (МЦС определяется с помощью дифференциальных равенств);
2) известны направления скоростей двух точек плоской фигуры, или их траектории.
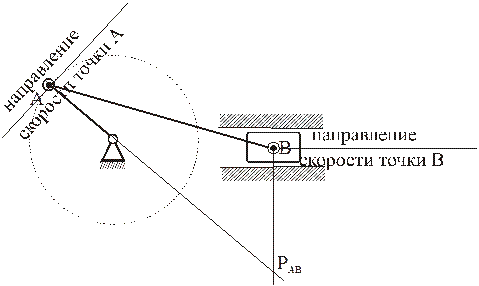
Рассмотрим только случай 2). Пусть известны направления скоростей двух точек А и В фигуры. Тогда для нахождения МЦС надо из этих точек опустить перпендикуляры к направлениям скоростей. В точке пересечения этих перпендикуляров и будет МЦС.
Частные случаи определения МЦС.
а) скорости точек параллельны, но точки не лежат на общем перпендикуляре к скоростям
Ясно, что в этом случае перпендикуляры к скоростям параллельны, 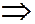
Замечание. Не путать мгновенно поступательное движение с поступательным: при поступательном движении скорости и ускорения всех точек равны между собой в любой момент времени, а при мгновенно поступательном равны только скорости всех точек (но не ускорения – они не равны друг другу!) и только в данный момент.
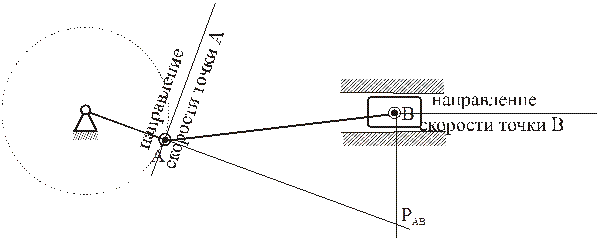
б) скорости двух точек фигуры параллельны, направлены в одну сторону и их модули не равны друг другу, а точки лежат на одном перпендикуляре к скоростям
В этом случае одних направлений скоростей не достаточно: должны быть известны и их модули.
Для нахождения МЦС надо концы векторов скоростей соединить прямой линией: в точке её пересечения с продолжением отрезка АВ и будет МЦС.
Если известно расстояние АВ, то легко получить
в) то же, что и в предыдущем случае, но векторы скоростей направлены в разные стороны; в этом случае модули скоростей могут быть и равны между собой, но должны быть известны.
Нахождение МЦС также аналогично предыдущему: концы векторов скоростей соединяем прямой линией – в точке её пересечения с отрезком АВ будет МЦС.
Если задано расстояние АВ, то аналогично пункту б) можно найти
г) качение колеса без скольжения по любой гладкой неподвижной поверхности.
Если колесо всё время остаётся в вертикальной плоскости, и отсутствуют повороты вокруг вертикальной оси, то оно совершает плоскопараллельное движение. В этом случае положение МЦС сразу известно: в точке контакта колеса с поверхностью. Действительно, если нет скольжения, то скорость точки контакта равна скорости соответствующей точки поверхности, т.е. нулю (поверхность неподвижна). По определению МЦС – здесь он и находится.
В связи с этим, интересно посмотреть распределение скоростей точек катящегося без скольжения колеса:
скорость верхней точки колеса в два раза больше скорости его центра!
Примеры определения МЦС для шатуна АВ кривошипно-ползунного механизма.
Определение МЦС для шатуна АВ кривошипно-коромыслового механизма:
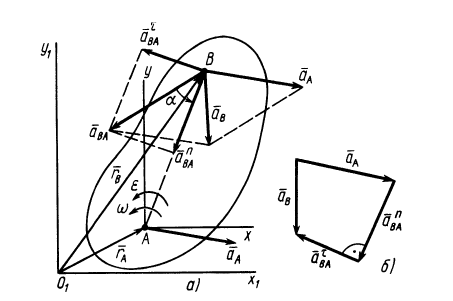
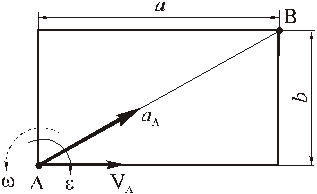
Рассмотрим пример определения скорости и ускорения точки плоской фигуры.
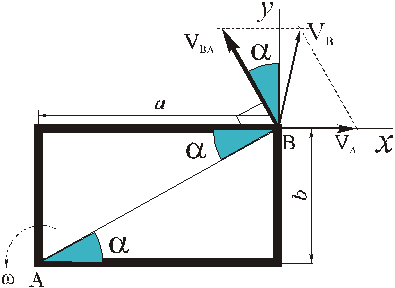
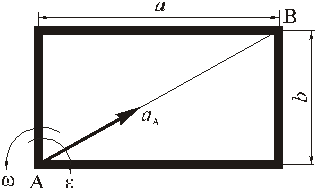
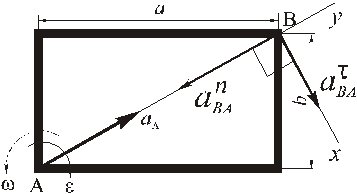
Прямоугольная пластина со сторонами a = 0,4 м и b = 0,3 м движется в своей плоскости. В данный момент времени скорость точки А пластины равна по модулю vA = 4 м/с, модуль ускорения этой точки равен aA = 3 м/с 2 , модули угловой скорости и углового ускорения фигуры равны соответственно 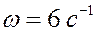
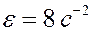
Определить скорость и ускорение точки B плоской фигуры в этот момент времени.

РЕШЕНИЕ. Принимая за полюс точку А, для определения скорости точки B используем формулу (4):
Вычислив расстояние АВ
по формуле (5) найдём модуль скорости точки В при её вращении вокруг полюса А
Изображаем вектор 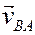
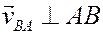
(стрелка вектора 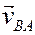
Вектор 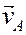
согласно равенству (4) складываем векторы 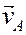
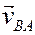
Для определения модуля скорости находим 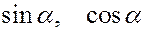
Теперь модуль скорости можно найти двумя способами:
по теореме косинусов (формула (6))
При определении скорости вторым способом выбираем оси координат
и проектируем (4) на эти оси:
Ускорение точки В определяем по формуле (8)
принимая за полюс точку А с известным ускорением.
По формулам (10) и (12) находим модули ускорений
Изображаем векторы этих ускорений:
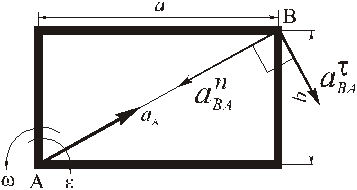
Так как согласно (8) для определения вектора ускорения точки В надо складывать три вектора, то выбираем оси координат
и проектируем (8) на эти оси:
Модуль ускорения будет
Геометрически (на рисунке) вектор ускорения строится при помощи «векторного многоугольника»: от заданной точки в выбранном масштабе последовательно откладываются векторы так, что конец предыдущего вектора является началом следующего; сумма векторов – вектор, идущий из заданной точки в конец последнего вектора.
Зная скорость точки А и угловую скорость фигуры можно найти положение мгновенного центра скоростей. Из равенства (15) следует
Используя доказательство существования МЦС, получаем.
Источник
Б) Метод определения мгновенного центра скоростей
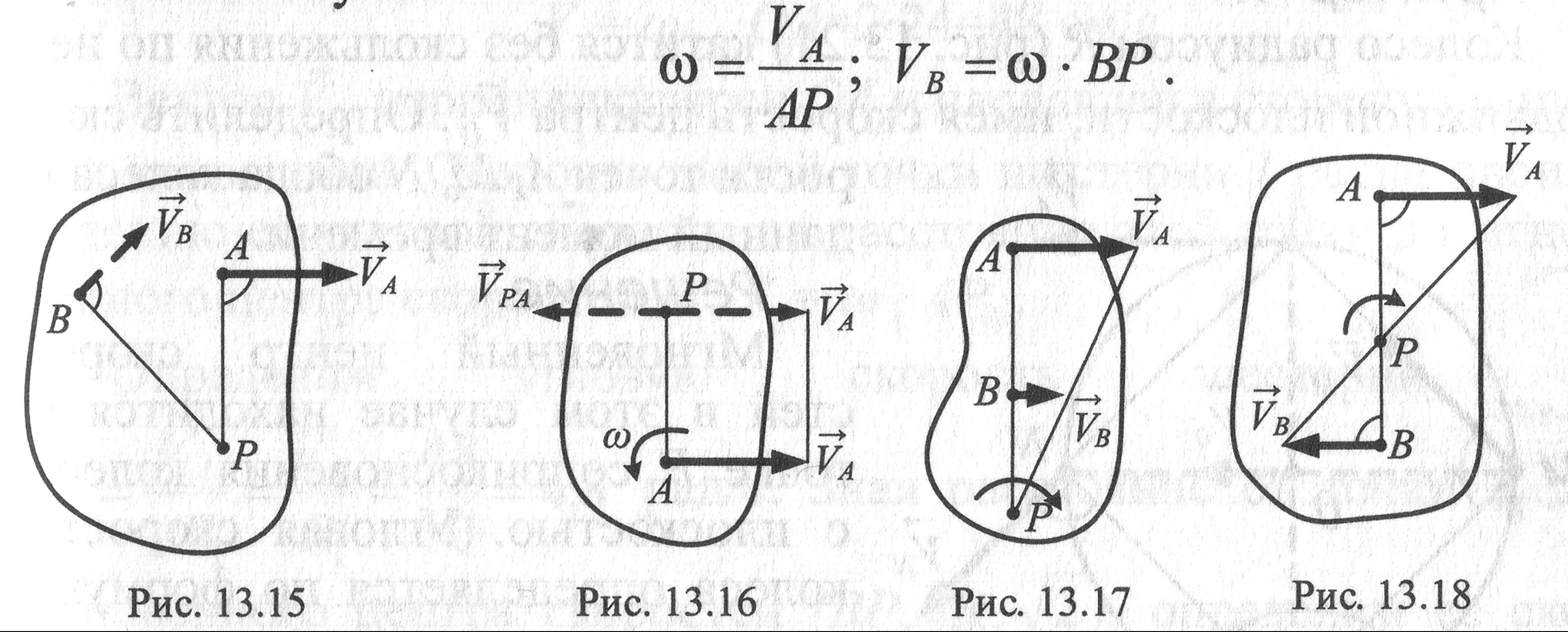
Скорость любой точки тела можно определять с помощью мгновенного центра скоростей. При этом сложное движение представляют в виде цепи вращений вокруг разных центров.
Задача сводится к определению положения мгновенного центра вращений (скоростей) (рис. 12.4).
Рис.12.4. Метод определения мгновенного центра скоростей
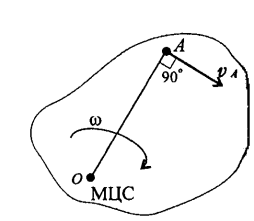
Мгновенным центром скоростей (МЦС) является точка на плоскости, абсолютная скорость которой в данный момент равна нулю.
Вокруг этой точки тело совершает поворот со скоростью ω
Скорость точки А в данный момент равна
т.к. vA — линейная скорость точки А, вращающейся вокруг МЦС.
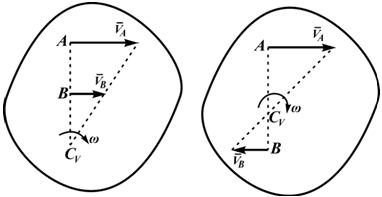
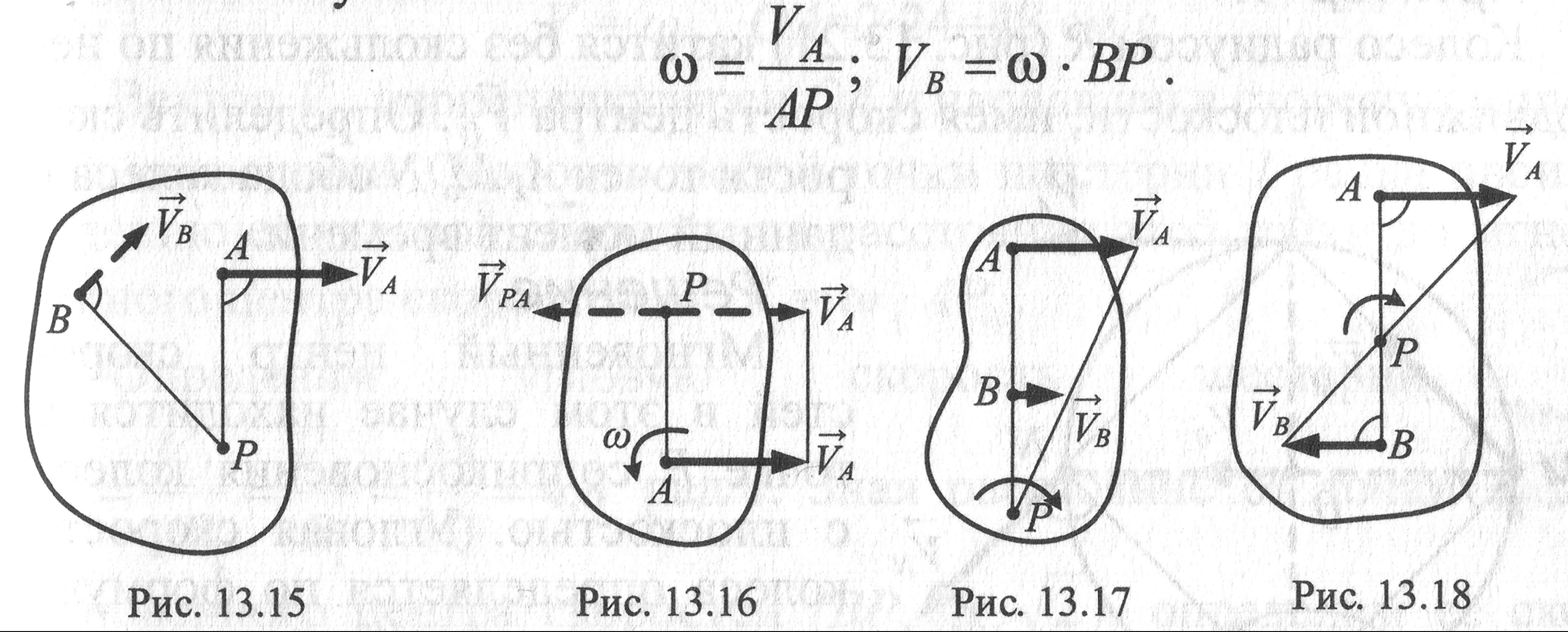
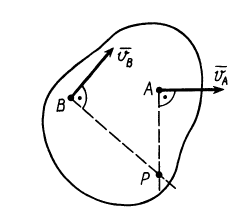
Существуют три способа определения положения мгновенного центра скоростей.
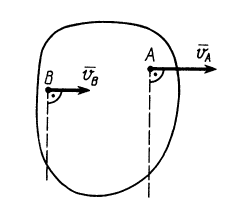
Первый способ.Известна скорость одной точки тела vA иугловая скорость вращения тела ω (рис. 12.5).
Точку О находим на перпендикуляре к вектору скорости vA
Соединяем точку О с точкой Д замеряем расстояние ОБ,
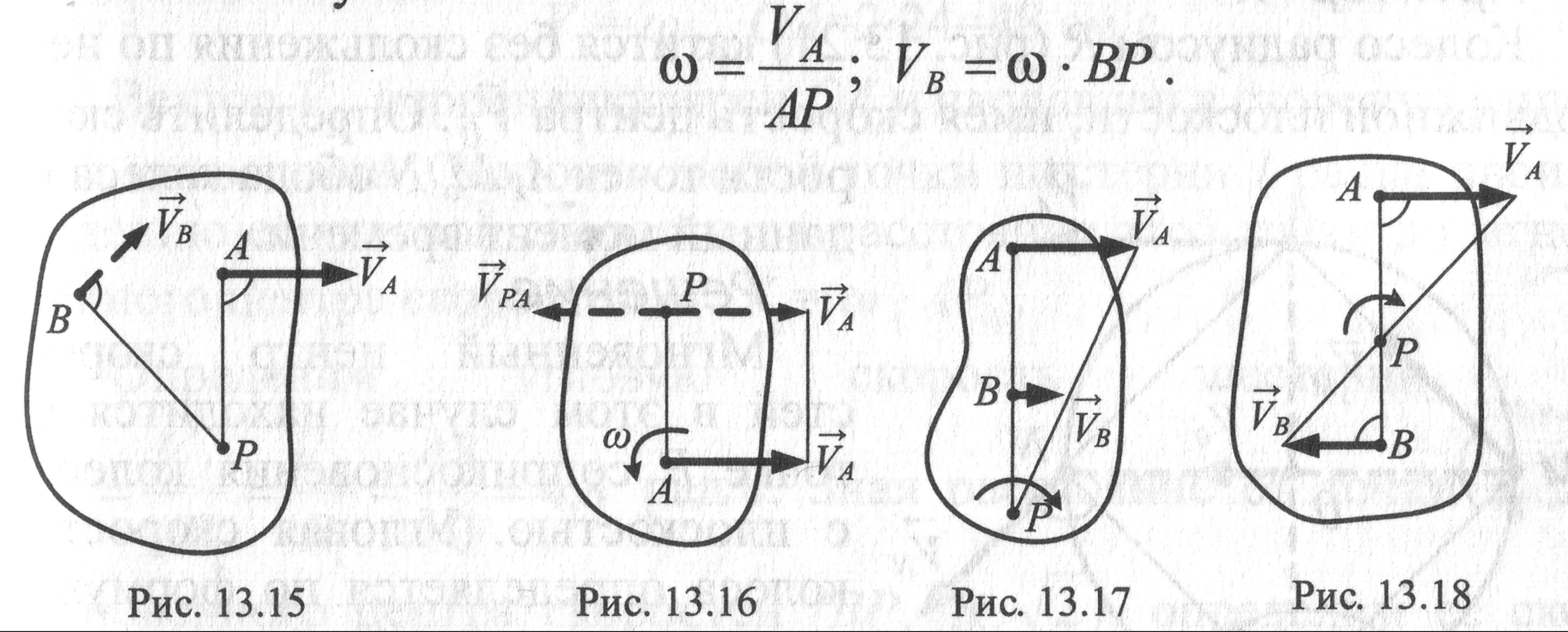
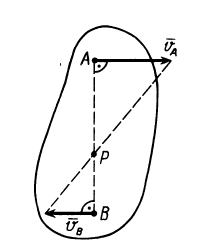
Второй способ.Известны скорости двух точек тела vA и v В и они не параллельны
Проводим из точек А и В два перпендикуляра к известным векторам скоростей.
На пересечении перпендикуляров находим МЦС. Далее можно
найти скорость любой точки С.
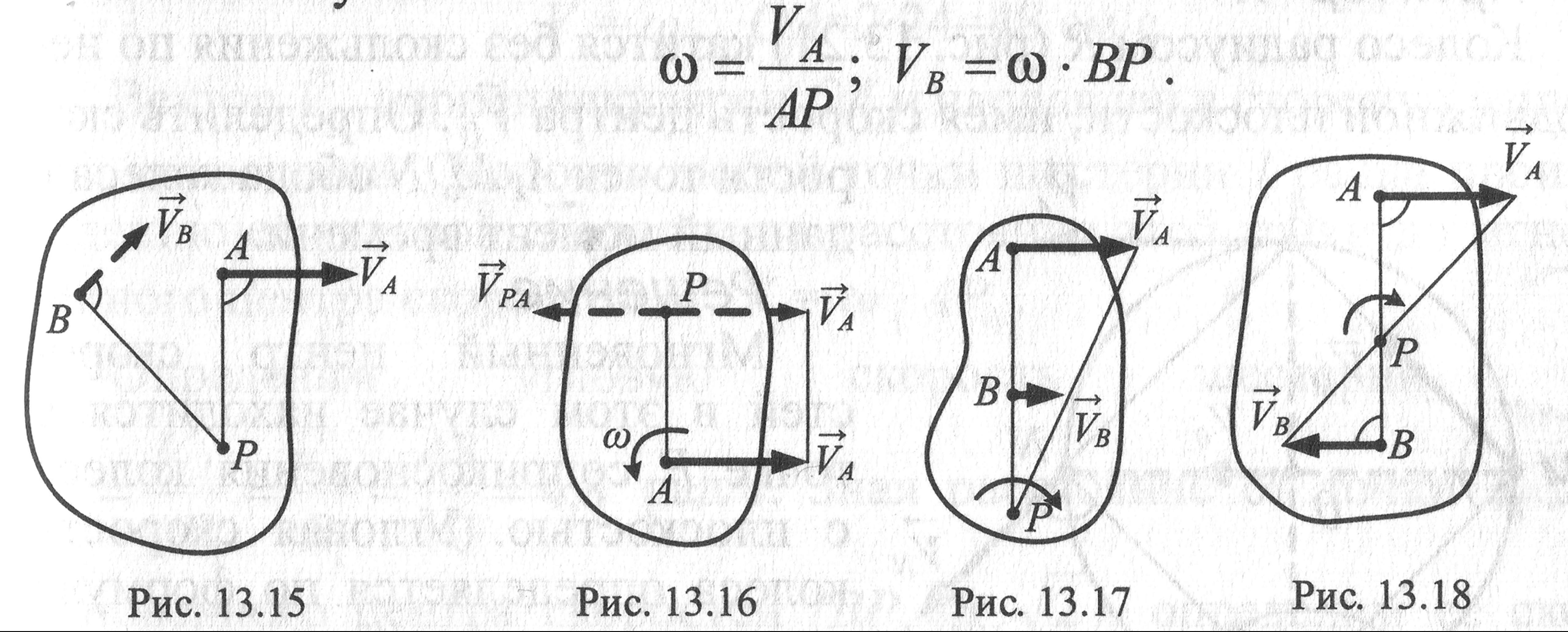
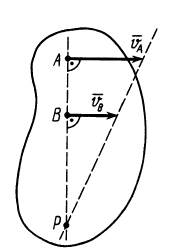
Третий способ.Известны скорости двух точек тела, и они параллельны (vA || v В)
Соединяем концы векторов, МЦС находится на пересечении линии, соединяющей концы векторов с линией АВ (рис. 12.7). При поступательном движении тела (рис. 12.7в) МЦС отсутствует.
Занятие 13. (2 часа) Основные понятия и аксиомы динамики. Понятия о трении.
Содержание и задачи динамики
Динамика — раздел теоретической механики, в котором устанавливается связь между движением тел и действующими на них силами.
В динамике решают два типа задач:
— определяют параметры движения по заданным силам;
— определяют силы, действующие на тело, по заданным кинематическим параметрам движения.
При поступательном движении все точки тела движутся одинаково, поэтому тело можно принять за материальную точку.
Если размеры тела малы по сравнению с траекторией, его тоже можно рассматривать как материальную точку, при этом точка совпадает с центром тяжести тела.
При вращательном движении тела точки могут двигаться неодинаково, в этом случае некоторые положения динамики можно применять только к отдельным точкам, а материальный объект рассматривать как совокупность материальных точек.
Поэтому динамику делят на динамику точки и динамику материальной системы.
Аксиомы динамики
Законы динамики обобщают результаты многочисленных опытов и наблюдений. Законы динамики, которые принято рассматривать как аксиомы, были сформулированы Ньютоном, но первый и четвертый законы были известны Галилею. Механику, основанную на этих законах, называют классической механикой.
Источник