Как найти положение передней главной плоскости

Переднее и заднее фокусные расстояния.

Р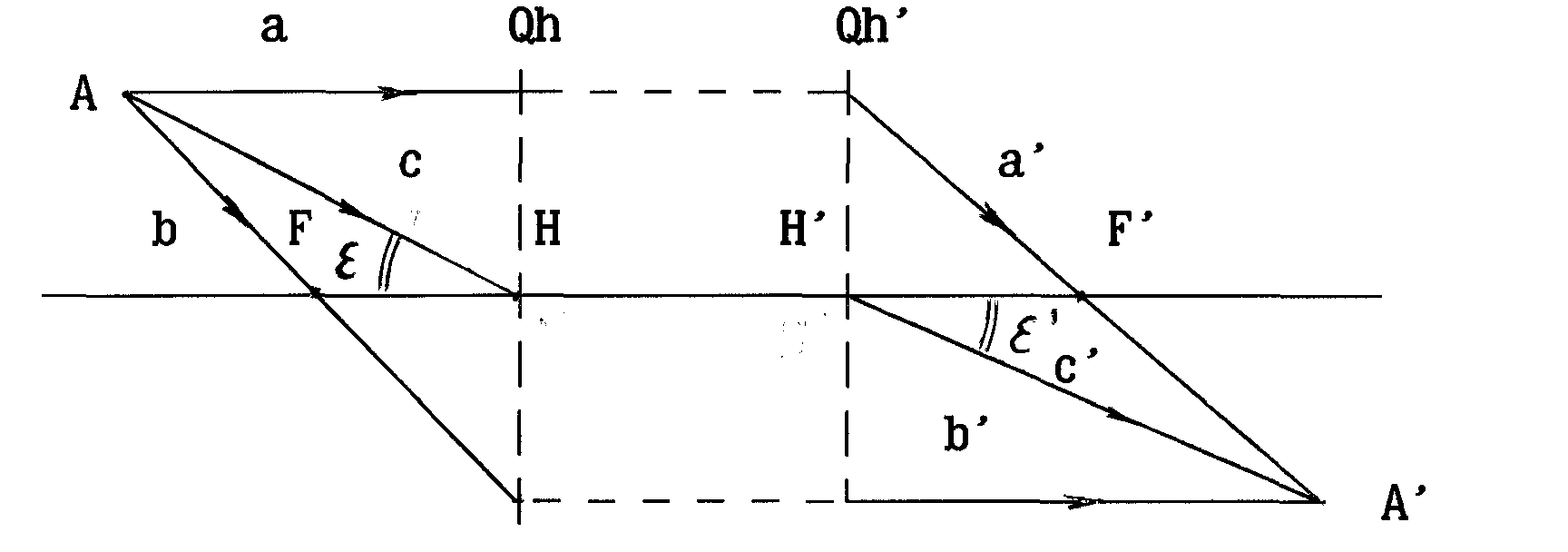асстояниеHFот передней главной
точкиНдо переднего фокусаFявляется передним фокусным расстоянием
оптической системы – f,

Рис.7. Графическое
определение положения главных плоскостей
и фокусов оптической системы: а – задних,
б – передних.

а расстояние
H‘F‘-от
задней главной точки Н’до заднего
фокусаF’ – задним фокусным
расстоянием f ′(рис.7).

Фокусные расстояния
отсчитывают от соответствующих главных
точек с учетом правила знаков. Если
оптическая система находится в однородной
среде, например в воздухе ( n=n‘ = 1), тоf ′ =
–f, т.е. фокусные расстояния равны по
абсолютному значению.

В общем случае –
f ^′ / f
= n/n‘.Так какn > 0 иn‘
> 0, то фокусные расстояния всегда имеют
разные знаки.

Обычно оптическую
систему характеризуют задним фокусным
расстоянием, поэтому, если f
′ > 0,то система
считается положительной, если

f
‘< 0,то – отрицательной.

Узловые точки оптической системы.

Точки предмета и
изображения, лежащие на оптической оси,
для которых угловое увеличение равно
плюс единице (
= +1), называются узловыми точками
оптической системыNиN

Будем в дальнейшем
рассматривать только оптические системы
расположенные в однородной среде, для
которых n=n
,f 
=f,
а следовательно, узловые точкиN,Nи главные точкиH,Hтакой системы
совпадают.

В этом случае
сопряженные лучи, проходящие через
главные точки HиHпараллельны друг другу (рис.8), т.е.
=‘.

Построение изображений и хода лучей в идеальной оптической системе.

Графическое решение
задачи построения изображения предмета
в оптической системе сводится к построению
изображения отдельных точек предмета,
а в конечном итоге к построению хода
лучей через оптическую систему. При
этом используются свойства кардинальных
элементов идеальной оптической
системы.Для построения любой точки
предмета достаточно построить ход хотя
бы двух лучей, проходящих через предметную
точку. Точка пересечения этих лучей
после прохождения их через оптическую
систему будет изображением предметной
точки.

Обычно для построения
используют так называемые характерные
лучи, ход которых в оптической системе
хорошо известен, т.е. лучи, проходящие
через фокусы и главные (узловые) точки
оптической системы

Луч (а),проходящий
через предметную точку (А) и падающий
на систему параллельно оптической оси,
после преломления на задней главной
плоскости (Oh)’проходит через задний фокус (F‘).

Луч (b),
проходящий через предметную точку и
передний фокус, после преломления на
передней главной плоскости идет
параллельно оптической оси.

Л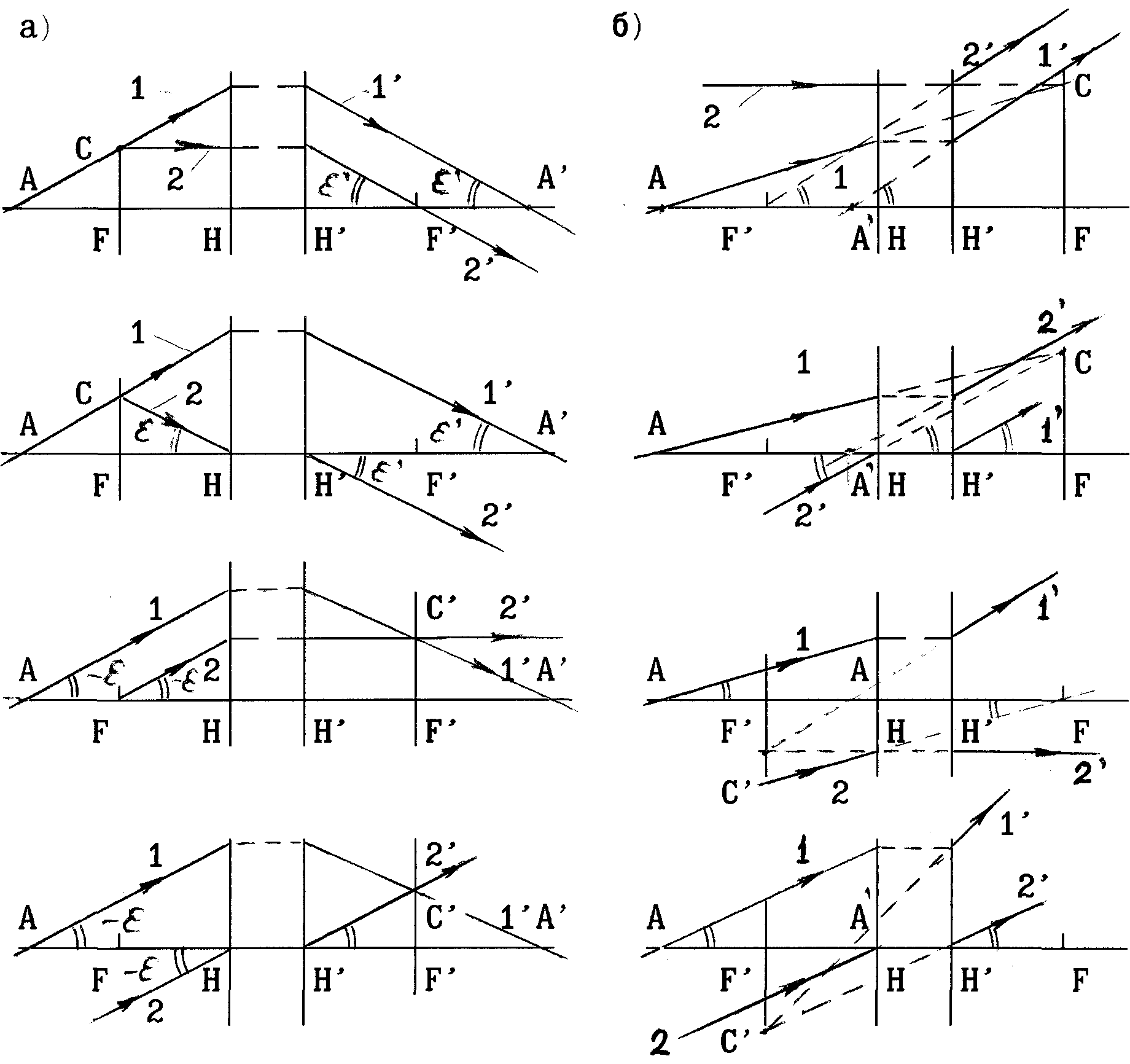уч
(c), проходящий через
предметную точку и переднюю главную
(узловую) точку, выходит из задней главной
(узловой) точки параллельно падающему
лучу (=)
.

Этими тремя лучами
удобно пользоваться, если предметная
точка расположена вне оптической оси.
Если же точка расположена на оптической
оси, то все три описанных выше луча
совпадают с оптической осью.

Поэтому для
построения изображения точки, расположенной
на оптической оси, необходимо построить
ход хотя бы одного луча, пересекающего
оптическую ось в предметной точке, и
найти точку пересечения этого луча
после выхода из оптической системы с
оптической осью. Эта точка и будет
изображением исходной предметной точки.

Рис.9. Построение
хода лучей в положительной (а) и
отрицательной (б) оптической системе.
1– заданный луч,2 –вспомогательный
луч.

На рис.9 показаны
четыре способа построения хода лучей
через положительную и отрицательную
оптические системы. Для построения
используются вспомогательные лучи,
проходящие через фокусы или главные
точки.

Точки, общие для
заданного и вспомогательного лучей в
передней фокальной плоскости, обозначены
точкой С,а точки общие для тех же
лучей в задней фокальной плоскости
обозначены соответственно через С‘.Лучи, выходящие из точек С,после
прохождения оптической системы будут
параллельными между собой. Параллельные
лучи, падающие на оптическую систему
соберутся в точке С’.

Соседние файлы в предмете Физика

• #
• #
• #
• #
• #
• #
• #
• #
• #

Предложите, как улучшить StudyLib

(Для жалоб на нарушения авторских прав, используйте

другую форму
)

2018-07-01   

Найти положение главных плоскостей, фокусное расстояние и знак оптической силы выпукло-вогнутой толстой стеклянной линзы, у которой:

а) толщина равна $d$, а радиусы кривизны поверхностей одинаковы и равны $R$;

б) преломляющие поверхности концентрические с радиусами кривизны $R_{1}$ и $R_{2}$ ($R_{2} > R_{1}$).

Решение:

(a) Сила линзы (как в задаче 8216)

$Phi = frac{n – 1}{R} – frac{n – 1}{R} – frac{d}{n} left ( frac{n – 1}{R} right ) left ( – frac{n – 1}{R} right ) = frac{d(n – 1)^{2} }{nR^{2} } > 0$.

Основные плоскости расположены на стороне выпуклой поверхности на расстоянии $d$ друг от друга, причем передняя главная плоскость удалена от выпуклой поверхности линзы на расстояние $R / (n – 1)$.

(б) $Phi = – frac{n – 1}{R_{1} } + frac{n + 1}{R_{2} } + frac{R_{2} – R_{1} }{n} frac{(n – 1)^{2}}{R_{1}R_{2} } = frac{(n – 1)(R_{2} – R_{1}) }{R_{2}R_{1} } left ( – 1 + frac{n – 1}{n} right ) = – frac{n – 1}{n} left ( frac{1}{R_{1} } – frac{1}{R_{2} } right ) < 0$

Обе основные плоскости проходят через общий центр кривизны поверхностей линзы.

Сложение оптических систем

Эффективность метода Гаусса наиболее ярко проявляется при анализе оптических систем состоящих из более чем одной преломляющей поверхности. Каждая такая поверхность является элементом оптической системы. Например, линза представляет собой систему двух преломляющих поверхностей. Рассмотрим систему из двух элементов. Каждый из них можно заменить системой главных плоскостей H1, H1‘ и H2, H2‘, относительно которых определены точки переднего и заднего фокусов F1, F1‘ и F2, F2‘ с соответствующими фокусными расстояниями f1, f1‘ и f2, f2‘. Расположение элементов относительно друг друга будем характеризовать расстоянием Δ между задней главной плоскостью H1′ первого элемента и передней главной плоскостью H2 второго элемента. Показатель среды перед передней главной плоскостью первого элемента n₁, показатель преломления среды между элементами – n, показатель преломления среды после задней главной плоскости второго элемента – n₂.

Получившаяся система, в свою очередь, будет характеризоваться своей системой главных плоскостей H, H’, положением фокусов F, F’. Требуется найти оптическую силу получившейся системы, а также положение ее главных плоскостей и фокусов относительно главных плоскостей составляющих ее элементов.

Рис. 11. Построение изображения в системе из двух элементов, отстоящих на расстоянии d друг от друга по главной оптической оси, показатель преломления между элементами n

Свет из точки А главной поверхности H сложной системы должен попасть в точку A’ задней поверхности H’. В эту точку он должен попадать, выходя из А в любом направлении к H’. Выберем одно из них, удобное для решения нашей задачи. Пусть луч 1из А проходит через передний фокус сложной системы, тогда по второму правилу идеальной оптической системы на выходе из второго элемента луч света 3должен идти параллельно главной оптической оси. Но из второго элемента луч света будет выходить параллельно оптической оси, только тогда, если на этот элемент луч света 2попадает, пройдя через передний фокус этого элемента (согласно второму правилу).

Из рисунка видно, что для подобных прямоугольных треугольников с общей вершиной в F справедливо равенство

= (16)

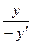
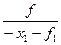
Из подобия прямоугольных треугольников с общей вершиной в F2 следует равенство

= (17)

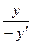
Из равенства левых частей в (16) и (17) следует

f = f₂ (18)

С другой стороны для первого элемента точка F является источником, а точка F2 – ее изображением. Тогда для этого элемента справедлива формула Ньютона (5), которая для используемых в рисунке обозначений записывается следующим образом: x₁×D= f₁ × f¢₁. Из этого равенства получаем выражение

x₁ = (19)

где Δ = d + f2 – f1′. После подстановки (19) в (18) находим переднее фокусное расстояние сложной системы

f = 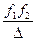. (20)

По определению фокусное расстояние сложной системы определяется через переднее фокусное расстояние формулой:

Ф = = = =d + + (21)

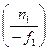
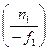
С учетом выражений для оптической силы первого и второго элементов системы: Ф₁ = 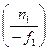и Ф₂ = , получаем формулу для оптической силы системы из двух элементов:

Ф = — Ф₁ Ф₂ + Ф₁ + Ф₂. (22)

Найдем положение Х передней главной плоскости Н сложной системы относительно передней главной плоскости первого элемента: –X = f – x₁ – f₁. После подстановки (19) и (20), находим искомое выражение

X = . (23)

Чтобы получить выражения для фокусного расстояния заднего фокуса сложной системы, а также для положения Х’ ее задней главной плоскости относительно задней плоскости второго элемента можно воспользоваться принципом взаимности, т.е. предположить, что источник находится в точке A’ и повторить всю цепочку рассуждений. Тогда можно легко найти соответствующие выражения:

f¢ = — (24)

X¢ = — . (25)

Таким образом, система из двух элементов может быть заменена одним эквивалентным ей элементом с характеристиками, определяемыми уравнениями (20), (22)–(25). Если система состоит из трех элементов, то сначала два соседних заменяются одним эквивалентным элементом с характеристиками (20), (22)–(25), а затем производят сложение эквивалентного элемента с третьим. Как видим, в качестве элемента оптической системы может выступать как одна преломляющая поверхность, так и система таких поверхностей, например, линза. Поэтому все результаты сложения элементов оптической системы, полученные выше, будут справедливы не только для двух преломляющих поверхностей, но и для двух линз, или двух систем, состоящих из линз.

Таким образом, для системы, представляющей собой сумму двух элементов уравнение связи (9) будет иметь следующий вид:

— = Ф, (26)

где оптическая сила Φ определяется выражением (22).

Линза представляет собой прозрачную однородную среду ограниченную двумя преломляющими поверхностями. Преломляющие поверхности могут иметь сферическую форму или плоскую (в последнее время используют и несферические поверхности). Как линзу можно рассматривать каплю дождя, стеклянный шар, стеклянный аквариум, заполненный водой и т.п.

Все виды линз делят на собирающие и рассеивающие. Если параллельные лучи после прохождения линзы сходятся в одной точке, то такая линза называется собирающей или положительной. Если же параллельные лучи после прохождения линзы расходятся, то такие линзы называют рассеивающие или отрицательной.

Рис. 12. а) собирающая двояковыпуклая линза, параллельные лучи сходятся в заднем фокусе, находящемся за линзой; б) рассеивающая двояковогнутая линза, параллельные лучи после линзы расходятся так, как будто они вышли из фокуса линзы, расположенного перед ней. Видно, что фокус находится на пересечении продолжений лучей

Все линзы, у которых толщина в середине больше чем толщина по краям, будут собирающими. Если же у линзы толщина увеличивается от середины к краям, то такая линза будет рассеивающей.

Процедура построения изображения в линзе зависит от того, можно ли ее считать тонкой или нет. Если каждая из сферических поверхностей, образующих линзу, имеет радиус много больший, чем толщина d в середине линзы, то такую линзу можно считать тонкой.

Тонкая линза

Для тонкой линзы можно считать d = 0. Тогда положения главных плоскостей линзы Х = Х’ = 0 совпадают с ее центром (см (23),(25)). Оптическая сила линзы в этом случае представляет собой сумму оптических сил ее преломляющих поверхностей

Ф = + , а уравнение связи (26) для тонкой линзы можно записать следующим образом:

— = + , (27)

где n₁ – показатель преломления среды перед передней поверхностью линзы, n₂ – показатель преломления среды после задней поверхности линзы, n – показатель преломления материла, из которого изготовлена линза. Если с обеих сторон линзы среда одна и та же n₁ = n₂ то (27) упрощается

— = . (28)

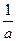
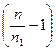
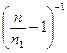
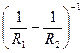
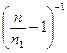
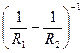
Из (28) следует, что, если a = ∞, то заднее фокусное расстояние f¢ = a¢ = , если же a’ = ∞, то переднее фокусное расстояние -f = a¢ = . То есть у тонкой линзы в однородной среде переднее и заднее фокусные расстояния равны.

Из (28) можно видеть, что для стеклянных собирающих линз в воздухе Φ > 0. Действительно, например, для двояковыпуклой линзы по правилу знаков R1 > 0, а R2 0, поэтому выражение во второй скобке в (28) имеет отрицательный знак.

Часто, для тонких линз уравнение (28) записывают в следующем виде

+ = Ф.

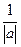
Это уравнение называют уравнением тонкой линзы, здесь Ф = 1/f . Напомним, что а – расстояние от линзы до предмета, а а’ – расстояние от линзы до изображения. Эти расстояния отсчитываются от центральной части линзы с учетом правила знаков: расстояние, отсчитываемое против хода, луча берется со знаком «–». Можно видеть, в случае собирающей линзы – Ф > 0, поэтому равенство выполняется при всех значениях a‘>0, а также при a‘ |a|. То есть изображение собирающей линзы может находиться и за линзой по ходу лучей, и перед ней (когда a‘ 3

Не нашли, что искали? Воспользуйтесь поиском по сайту:

Источник