Как найти положение солнца на эклиптике

Ещё с давних времён люди с большим интересом следили за происходящим на небе. С помощью небесных объектов люди ориентировались на местности. Ещё позже земледельцы и скотоводы задумались о создании календаря, поскольку сельскохозяйственные работы требовали последовательности и периодичности. В то время были сделаны первые научные выводы на основе многолетних наблюдений за Солнцем и Луной: люди заметили цикличность перемещения космических тел и особенности их движения.

Определение и значение

Одной из важных составляющих для понимания процессов Солнечной системы считается эклиптика объектов. Если говорить о Земле, то эклиптика планеты – это воображаемая плоскость, очерченная орбитой движения за год. Проще говоря, это вся плоскость на расстоянии от Земли до Солнца, ограждённая полным орбитальным оборотом вокруг звезды.

Существует понятие «эклиптики» и для самого Солнца – это плоскость, образованная при движении звёзды в космическом пространстве при прохождении 12 созвездий. Важно отметить, что эклиптическая плоскость Солнца совпадает с плоскостями эклиптики всех планет Солнечной системы.

Ещё древние цивилизации использовали наблюдения за движением Солнца в земледелии. Как правило, они селились вблизи больших рек, таких как Янцзы, Евфрат, Нил и другие. Люди понимали, что при смене сезонов менялись не только климатические условия, но и расположения Солнца на небосводе.  В то время было замечено отклонение траектории движения светила, которое повторялось примерно раз в 365 суток – годичный цикл.

Учёные античности отмечали, что Солнце движется по двум линиям. Первая ежедневная – перемещение с востока на запад и вторая, делающая проекцию на небесную сферу, что и положило начало понятию «эклиптика».

Впервые наклон планеты в 23 градуса 51 минуту высчитал ещё в третьем веке до нашей эры исследователь-астроном – Эратосфен. Независимо от движения по орбите или смены сезонов, Земля всегда сохраняет этот угол наклона.

Точки координат

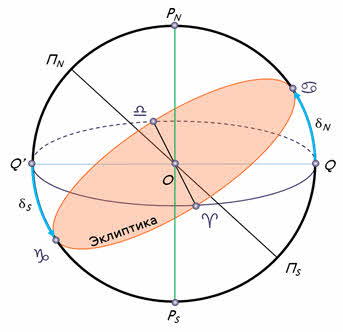
В современной астрономии круг эклиптики используют в качестве основной системы координат в движении Земли и Солнца. В системе эклиптических координат, широту измеряют расстоянием от южного до северного полюса эклиптики, а долготу с запада на восток. За полюс эклиптики принимают точку, где пересекается плоскость с перпендикуляром.

Вся плоскость эклиптики разрезается на две одинаковые части экватором. Противоположные точки экватора называются узлами или равноденствиями. На средине орбитального пути между равноденствиями находятся точки зимнего и летнего солнцестояния.

Линия равноденствий, она же небесный экватор – это воображаемая плоскость, расположенная перпендикулярно к оси вращения нашей планеты. Все околоземные спутники работают именно в этой плоскости. Если взглянуть на звёздную карту, то линия, идущая с запада на восток, будет экватором.

В понятии эклиптики, экватор называют ещё линией равенства. Такое название было дано неспроста, поскольку звёзды, которые расположены в данной области, находятся над горизонтом столько же времени, сколько и те, что пребывают ниже горизонта. Такая же ситуация наблюдается и с Солнцем, дважды в год в точках равноденствий.

Небесный экватор совпадает с плоскостью эклиптики и образует угол в 23º 27′. Это и есть наклон эклиптики. Данный угол наклона является постоянным на протяжении миллионов лет. При этом учёные выяснили, что он уменьшается каждое столетие на 48». Процесс уменьшение угла будет длиться ещё несколько тысяч лет, пока не будет достигнуто минимальное положение в 22° 54′.

Солнцестояние и равноденствие

Только на 47° поверхности планеты Земли, солнечные лучи падают перпендикулярно. Это объясняется сферической формой Земли и углом наклона. Крайняя северная точка перпендикулярного падения солнечного света находится на широте 23º 27′ и называется тропиком Рака. Южное полушарие имеет такую же крайнюю точку 23º 27′ южной широты и называется тропик Козерога. Это крайние точки воображаемой линии, по которой движется Солнце на протяжении года. Нахождение Солнца над этими точками называют солнцестояниями. В этот момент фиксируется самый длинный световой день и самая короткая ночь.

Название точек было взято от названий созвездий: южное полушарие – Козерог и северное – Рак. Точки пересечения эклиптики и небесного экватора совпадают весной в созвездии Рыбы, а осенью в созвездии Девы. Именно в этих точках осуществляется равномерное освещение Земли – это и будут равноденствия, когда продолжительность ночи равна продолжительности светового дня. При годичном перемещении Земли на орбите, момент равноденствия наступает 21 сентября и 21 марта.

Равноденствия смещаются во времени. Учёные установили, что момент равноденствий наступает на 20 минут 24 секунды ранее, чем это было в предыдущем звёздном году. Это периодическое явление, которое приходит в изначальное положение каждые 25 776 лет. В космической механике равноденствия немного смещаются, но всё же возвращаются на исходные места.

Происхождение плоскости орбит

Солнце и все планеты Солнечной системы расположены в одной плоскости, и это неслучайно. Причина такого положения кроется в процессах зарождения и формирования объектов нашей планетной системы.

Установлено, что наша родительская звезда появилась в результате скопления и уплотнения межзвёздного материала (пыли и газа), который остался от звёзд предыдущего поколения. В момент импульса исходные вещества начинают вращаться. В результате центробежных сил формируется огромный диск, который отталкивает материал от оси вращения.

Гравитационные, гидродинамические и магнитные процессы приводят к нестабильному вращению и как результат – скопление большого количества материи в центре диска. За счёт быстрого увеличения материал достигает критической массы, что и порождает гравитационный коллапс и запускает термоядерные процессы.

Начало термоядерных реакций запускает излучение протозвезды в космическое пространство. Импульсы фотонов и солнечный ветер приводят к тому, что протопланетный газопылевой диск, оставшийся после формирования Солнца, начинает видоизменяться. Гравитация и радиационное давление приводит к сдуванию материи и объединения её в большие фракции, образовывая планеты, спутники, кометы и астероиды, которые собирают дополнительный материал на своих орбитах.

Расположения всех объектов Солнечной системы в одной плоскости объясняется формированием их из первичного диска материи, размещённой в одной плоскости.

Путь Солнца по зодиакальным созвездиям

Вдоль всей эклиптики расположено 13 созвездий, которые проходит Солнце на своём годичном пути. Все они имеют названия животных, которые получили ещё с древних времён.

Предлагаем ознакомиться с таблицей всех созвездий, которые пересекает эклиптика.

№	Название: русское/латынь	Даты пребывания Солнца в созвездии	Время прохождения Солнца по созвездию в сутках
1	Овен/Aries	с 19 апреля по 13 мая	25
2	Телец/Taurus	с 14 мая по 19 июня	37
3	Близнецы/Gemini	с 20 июня по 20 июля	31
4	Рак/Cancer	с 21 июля по 9 августа	21
5	Лев/Leo	с 10 августа по 15 сентября	37
6	Дева/Virgo	с 16 сентября по 30 октября	45
7	Весы/Libra	с 31 октября по 22 ноября	23
8	Скорпион/Scorpius	с 23 ноября по 29 ноября	7
9	Змееносец/Ophiuchus	с 30 ноября по 17 декабря	18
10	Стрелец/Sagittarius	с 18 декабря по 19 января	32
11	Козерог/Capricornus	с 20 января по 15 февраля	28
12	Водолей/Aquarius	с 16 февраля по 11 марта	24
13	Рыбы/Pisces	с 12 марта по 18 апреля	38

Эклиптика планет Солнечной системы, Луны и других небесных тел

Если с углом наклона Земли и её траекторией движения на орбите всё понятно, то изучение других планет является приоритетным и интересным для современной астрономии. Исследования показывают, что все планеты Солнечной системы, за исключением карликовых, вращаются в одной плоскости с незначительными отклонениями.  Предлагаем вам ознакомиться с отклонением угла вращения планет от эклиптики.

Название планеты	Угол наклона к плоскости эклиптики
Земля	0°
Уран	0,77°
Юпитер	1,31°
Нептун	1,77°
Марс	1,85°
Сатурн	2,49°
Венера	3,39°
Меркурий	7,01°

Как видно из таблицы, больше всех от общей плоскости вращения отклоняется Меркурий.  При этом даже газовые гиганты, за исключением Сатурна практически идеально лежат на плоскости эклиптики. Если говорить о маломассивных объектах, таких как карликовые планеты, астероиды или кометы, то их орбиты могут существенно отличаться от общего положения. К примеру, карликовая планета Эрида имеет очень вытянутую орбиту своего движения и может находиться ближе к Солнцу, чем Плутон. Благодаря этому, её угол к плоскости эклиптики равен 45°

Эклиптика в небе

Чтобы прослеживать за эклиптикой в небе, необходимо осмыслить, что это путь, по которому движется Луна, Солнце и другие планеты, при наблюдении с Земли. Воображаемую линию лучше всего получится визуализировать при ясном звёздном небе перед полнолунием.

Для этого наблюдатель должен находиться на открытой местности после заката Солнца. Важно, чтобы небосвод был безоблачным и чистым, что позволит определить эклиптическую линию, обращая внимание на следующие особенности.

• Прямо над закатом Солнца, можно увидеть хорошо освещённую Венеру.
• Луна будет расположена чуть выше горизонта с восточной стороны.
• Третьей точкой наблюдения может стать Марс, который будет немного выше Луны.
• Спустя 2 часа после заката на востоке появится четвёртая точка – Сатурн.

Если между всеми указанными точками провести воображаемую линию мы и получим эклиптику.  Важно подчеркнуть, что вышеупомянутые космические тела не находятся строго на одной линии. Все же их орбиты почти в одной плоскости с Землей. Данное несоответствие и объясняет, почему солнечные затмения не происходят ежемесячно.

Эклиптика в литературе

Даже в литературных произведениях есть упоминания об эклиптике. В частности, в серии рассказов «О пилоте Пирксе», автор Станислав Лема использует астрономический термин. В произведении всем космическим кораблям запрещено посещать плоскость эклиптики. Но главному герою пилоту Пирксу в силу своих обязанностей нужно лететь через эклиптику, где он и обнаруживает огромный заброшенный инопланетный корабль, прибывший вместе с метеоритным потоком.

The position of the Sun in the sky is a function of both the time and the geographic location of observation on Earth’s surface. As Earth orbits the Sun over the course of a year, the Sun appears to move with respect to the fixed stars on the celestial sphere, along a circular path called the ecliptic.

Earth’s rotation about its axis causes diurnal motion, so that the Sun appears to move across the sky in a Sun path that depends on the observer’s geographic latitude. The time when the Sun transits the observer’s meridian depends on the geographic longitude.

To find the Sun’s position for a given location at a given time, one may therefore proceed in three steps as follows:^[1][2]

1. calculate the Sun’s position in the ecliptic coordinate system,
2. convert to the equatorial coordinate system, and
3. convert to the horizontal coordinate system, for the observer’s local time and location. This is the coordinate system normally used to calculate the position of the Sun in terms of solar zenith angle and solar azimuth angle, and the two parameters can be used to depict the Sun path.^[3]

This calculation is useful in astronomy, navigation, surveying, meteorology, climatology, solar energy, and sundial design.

Approximate position[edit]

Ecliptic coordinates[edit]

These equations, from the Astronomical Almanac,^[4][5]
can be used to calculate the apparent coordinates of the Sun, mean equinox and ecliptic of date, to a precision of about 0°.01 (36″), for dates between 1950 and 2050. These equations are coded into a Fortran 90 routine in Ref.^[3] and are used to calculate the solar zenith angle and solar azimuth angle as observed from the surface of the Earth.

Start by calculating n, the number of days (positive or negative, including fractional days) since Greenwich noon, Terrestrial Time, on 1 January 2000 (J2000.0). If the Julian date for the desired time is known, then

The mean longitude of the Sun, corrected for the aberration of light, is:

The mean anomaly of the Sun (actually, of the Earth in its orbit around the Sun, but it is convenient to pretend the Sun orbits the Earth), is:

Put and in the range 0° to 360° by adding or subtracting multiples of 360° as needed.

Finally, the ecliptic longitude of the Sun is:

The ecliptic latitude of the Sun is nearly:

,

as the ecliptic latitude of the Sun never exceeds 0.00033°,^[6]

and the distance of the Sun from the Earth, in astronomical units, is:

.

Obliquity of the ecliptic[edit]

Where the obliquity of the ecliptic is not obtained elsewhere, it can be approximated:

Equatorial coordinates[edit]

, and form a complete position of the Sun in the ecliptic coordinate system. This can be converted to the equatorial coordinate system by calculating the obliquity of the ecliptic, , and continuing:

Right ascension,

, where is in the same quadrant as ,

To get RA at the right quadrant on computer programs use double argument Arctan function such as ATAN2(y,x)

and declination,

.

Rectangular equatorial coordinates[edit]

Right-handed rectangular equatorial coordinates in astronomical units are:

Where axis is in the direction of the March equinox, the axis towards June Solstice, and the axis towards the North celestial pole.^[7]

Horizontal coordinates[edit]

Declination of the Sun as seen from Earth [edit]

The Sun appears to move northward during the northern spring, crossing the celestial equator on the March equinox. Its declination reaches a maximum equal to the angle of Earth’s axial tilt (23.44°)^[8][9] on the June solstice, then decreases until reaching its minimum (−23.44°) on the December solstice, when its value is the negative of the axial tilt. This variation produces the seasons.

A line graph of the Sun’s declination during a year resembles a sine wave with an amplitude of 23.44°, but one lobe of the wave is several days longer than the other, among other differences.

The following phenomena would occur if Earth were a perfect sphere, in a circular orbit around the Sun, and if its axis is tilted 90°, so that the axis itself is on the orbital plane (similar to Uranus). At one date in the year, the Sun would be directly overhead at the North Pole, so its declination would be +90°. For the next few months, the subsolar point would move toward the South Pole at constant speed, crossing the circles of latitude at a constant rate, so that the solar declination would decrease linearly with time. Eventually, the Sun would be directly above the South Pole, with a declination of −90°; then it would start to move northward at a constant speed. Thus, the graph of solar declination, as seen from this highly tilted Earth, would resemble a triangle wave rather than a sine wave, zigzagging between plus and minus 90°, with linear segments between the maxima and minima.

If the 90° axial tilt is decreased, then the absolute maximum and minimum values of the declination would decrease, to equal the axial tilt. Also, the shapes of the maxima and minima on the graph would become less acute, being curved to resemble the maxima and minima of a sine wave. However, even when the axial tilt equals that of the actual Earth, the maxima and minima remain more acute than those of a sine wave.

In reality, Earth’s orbit is elliptical. Earth moves more rapidly around the Sun near perihelion, in early January, than near aphelion, in early July. This makes processes like the variation of the solar declination happen faster in January than in July. On the graph, this makes the minima more acute than the maxima. Also, since perihelion and aphelion do not happen on the exact dates as the solstices, the maxima and minima are slightly asymmetrical. The rates of change before and after are not quite equal.

The graph of apparent solar declination is therefore different in several ways from a sine wave. Calculating it accurately involves some complexity, as shown below.

Calculations[edit]

The declination of the Sun, δ_☉, is the angle between the rays of the Sun and the plane of the Earth’s equator. The Earth’s axial tilt (called the obliquity of the ecliptic by astronomers) is the angle between the Earth’s axis and a line perpendicular to the Earth’s orbit. The Earth’s axial tilt changes slowly over thousands of years but its current value of about ε = 23°26′ is nearly constant, so the change in solar declination during one year is nearly the same as during the next year.

At the solstices, the angle between the rays of the Sun and the plane of the Earth’s equator reaches its maximum value of 23°26′. Therefore, δ_☉ = +23°26′ at the northern summer solstice and δ_☉ = −23°26′ at the southern summer solstice.

At the moment of each equinox, the center of the Sun appears to pass through the celestial equator, and δ_☉ is 0°.

The Sun’s declination at any given moment is calculated by:

where EL is the ecliptic longitude (essentially, the Earth’s position in its orbit). Since the Earth’s orbital eccentricity is small, its orbit can be approximated as a circle which causes up to 1° of error. The circle approximation means the EL would be 90° ahead of the solstices in Earth’s orbit (at the equinoxes), so that sin(EL) can be written as sin(90+NDS)=cos(NDS) where NDS is the number of days after the December solstice. By also using the approximation that arcsin[sin(d)·cos(NDS)] is close to d·cos(NDS), the following frequently used formula is obtained:

where N is the day of the year beginning with N=0 at midnight Universal Time (UT) as January 1 begins (i.e. the days part of the ordinal date −1). The number 10, in (N+10), is the approximate number of days after the December solstice to January 1. This equation overestimates the declination near the September equinox by up to +1.5°. The sine function approximation by itself leads to an error of up to 0.26° and has been discouraged for use in solar energy applications.^[2] The 1971 Spencer formula^[10] (based on a Fourier series) is also discouraged for having an error of up to 0.28°.^[11] An additional error of up to 0.5° can occur in all equations around the equinoxes if not using a decimal place when selecting N to adjust for the time after UT midnight for the beginning of that day. So the above equation can have up to 2.0° of error, about four times the Sun’s angular width, depending on how it is used.

The declination can be more accurately calculated by not making the two approximations, using the parameters of the Earth’s orbit to more accurately estimate EL:^[12]

which can be simplified by evaluating constants to:

N is the number of days since midnight UT as January 1 begins (i.e. the days part of the ordinal date −1) and can include decimals to adjust for local times later or earlier in the day. The number 2, in (N-2), is the approximate number of days after January 1 to the Earth’s perihelion. The number 0.0167 is the current value of the eccentricity of the Earth’s orbit. The eccentricity varies very slowly over time, but for dates fairly close to the present, it can be considered to be constant. The largest errors in this equation are less than ± 0.2°, but are less than ± 0.03° for a given year if the number 10 is adjusted up or down in fractional days as determined by how far the previous year’s December solstice occurred before or after noon on December 22. These accuracies are compared to NOAA’s advanced calculations^[13][14] which are based on the 1999 Jean Meeus algorithm that is accurate to within 0.01°.^[15]

(The above formula is related to a reasonably simple and accurate calculation of the Equation of Time, which is described here.)

More complicated algorithms^[16][17] correct for changes to the ecliptic longitude by using terms in addition to the 1st-order eccentricity correction above. They also correct the 23.44° obliquity which changes very slightly with time. Corrections may also include the effects of the moon in offsetting the Earth’s position from the center of the pair’s orbit around the Sun. After obtaining the declination relative to the center of the Earth, a further correction for parallax is applied, which depends on the observer’s distance away from the center of the Earth. This correction is less than 0.0025°. The error in calculating the position of the center of the Sun can be less than 0.00015°. For comparison, the Sun’s width is about 0.5°.

Atmospheric refraction[edit]

The declination calculations described above do not include the effects of the refraction of light in the atmosphere, which causes the apparent angle of elevation of the Sun as seen by an observer to be higher than the actual angle of elevation, especially at low Sun elevations.^[2] For example, when the Sun is at an elevation of 10°, it appears to be at 10.1°. The Sun’s declination can be used, along with its right ascension, to calculate its azimuth and also its true elevation, which can then be corrected for refraction to give its apparent position.^[2][14][18]

Equation of time[edit]

In addition to the annual north–south oscillation of the Sun’s apparent position, corresponding to the variation of its declination described above, there is also a smaller but more complex oscillation in the east–west direction. This is caused by the tilt of the Earth’s axis, and also by changes in the speed of its orbital motion around the Sun produced by the elliptical shape of the orbit.^[2] The principal effects of this east–west oscillation are variations in the timing of events such as sunrise and sunset, and in the reading of a sundial compared with a clock showing local mean time. As the graph shows, a sundial can be up to about 16 minutes fast or slow, compared with a clock. Since the Earth rotates at a mean speed of one degree every four minutes, relative to the Sun, this 16-minute displacement corresponds to a shift eastward or westward of about four degrees in the apparent position of the Sun, compared with its mean position. A westward shift causes the sundial to be ahead of the clock.

Since the main effect of this oscillation concerns time, it is called the equation of time, using the word “equation” in a somewhat archaic sense meaning “correction”. The oscillation is measured in units of time, minutes and seconds, corresponding to the amount that a sundial would be ahead of a clock. The equation of time can be positive or negative.

Analemma[edit]

An analemma is a diagram that shows the annual variation of the Sun’s position on the celestial sphere, relative to its mean position, as seen from a fixed location on Earth. (The word analemma is also occasionally, but rarely, used in other contexts.) It can be considered as an image of the Sun’s apparent motion during a year, which resembles a figure-8. An analemma can be pictured by superimposing photographs taken at the same time of day, a few days apart for a year.

An analemma can also be considered as a graph of the Sun’s declination, usually plotted vertically, against the equation of time, plotted horizontally. Usually, the scales are chosen so that equal distances on the diagram represent equal angles in both directions on the celestial sphere. Thus 4 minutes (more precisely 3 minutes, 56 seconds), in the equation of time, are represented by the same distance as 1° in the declination, since Earth rotates at a mean speed of 1° every 4 minutes, relative to the Sun.

An analemma is drawn as it would be seen in the sky by an observer looking upward. If north is shown at the top, then west is to the right. This is usually done even when the analemma is marked on a geographical globe, on which the continents, etc., are shown with west to the left.

Some analemmas are marked to show the position of the Sun on the graph on various dates, a few days apart, throughout the year. This enables the analemma to be used to make simple analog computations of quantities such as the times and azimuths of sunrise and sunset. Analemmas without date markings are used to correct the time indicated by sundials.^[19]

Light-time effects[edit]

We see light from the Sun about 20 angle seconds from where the Sun is when the light is seen. See Solar annual aberration.

See also[edit]

References[edit]

External links[edit]

• Solar Position Algorithm, at National Renewable Energy Laboratory’s Renewable Resource Data Center website.
• Sun Position Calculator, at pveducation.org. An interactive calculator showing the Sun’s path in the sky.
• NOAA Solar Calculator, at the NOAA Earth System Research Laboratory’s Global Monitoring Division website.
• NOAA’s declination and sun position calculator
• HORIZONS System, at the JPL website. Very accurate positions of Solar System objects based on the JPL DE series ephemerides.
• General ephemerides of the solar system bodies, at the IMCCE website. Positions of Solar System objects based on the INPOP series ephemerides.
• Solar position in R. Insol package.

Обновлено: 22.05.2023

В мире нет ничего особенного. Никакого волшебства. Только физика.

Чак Паланик

Вопросы к экзамену

Для всех групп технического профиля

Учу детей тому, как надо учиться

Часто сталкиваюсь с тем, что дети не верят в то, что могут учиться и научиться, считают, что учиться очень трудно.

Урок 03. Годичное движение Солнца по небу. Эклиптика. Движение и фазы Луны. Время и календарь.

Наименование разделов и тем

Содержание учебного материала, лабораторные работы и практические занятия, самостоятельная работа обучающихся

Объем часов

Уровень освоения

Годичное движение Солнца по небу. Эклиптика. Движение и фазы Луны.

Видимое годичное движение Солнца. Эклиптика. Видимое движение и фазы Луны. Затмения Солнца и Луны.

Воспроизведение определений терминов и понятий (кульминация Солнца, эклиптика). Объяснение наблюдаемых невооруженным глазом движения Солнца на различных географических широтах, движение и фазы Луны, причины затмений Луны и Солнца.

Время и календарь. Точное время и определение географической долготы.

Тема 2.2. Годичное движение Солнца по небу. Эклиптика. Движение и фазы Луны.

2.2.1. Видимое годичное движение Солнца. Эклиптика.

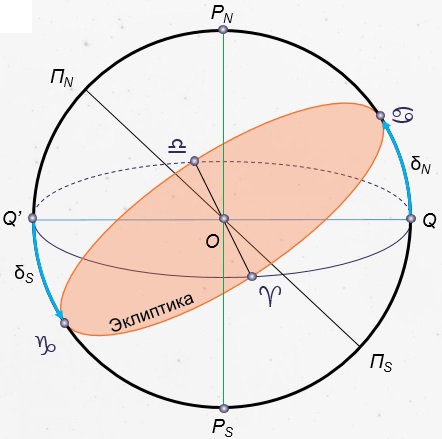
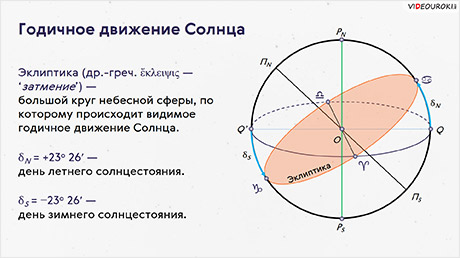
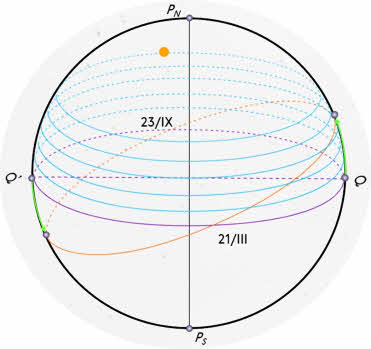
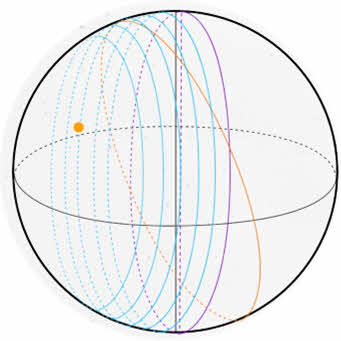
Еще в глубокой древности, наблюдая за Солнцем, люди обнаружили, что его полуденная высота в течение года меняется, как меняется и вид звездного неба: в полночь над южной частью горизонта в различное время года видны звезды разных созвездий — те, которые видны летом, не видны зимой, и наоборот. На основе этих наблюдений был сделан вывод о том, что Солнце перемещается по небу, переходя из одного созвездия в другое, и завершает полный оборот в течение года. Круг небесной сферы, по которому происходит видимое годичное движение Солнца, назвали эклиптикой.

Эклиптика (др.-греч. ἔκλειψις — ‘затмение’) — большой круг небесной сферы, по которому происходит видимое годичное движение Солнца.

Как вы уже знаете, перемещение Солнца на фоне звезд — явление кажущееся. Происходит оно вследствие годичного обращения Земли вокруг Солнца.

Поэтому эклиптика представляет собой тот круг небесной сферы, по которому она пересекается с плоскостью земной орбиты. За сутки Земля проходит примерно 1/365 часть своей орбиты. Вследствие этого Солнце перемещается на небе примерно на 1° за каждые сутки. Промежуток времени, в течение которого оно обходит полный круг по небесной сфере, назвали годом.

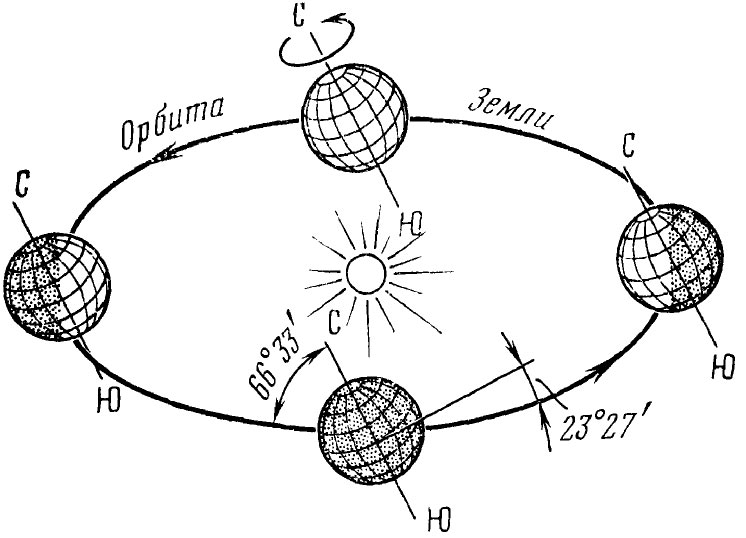
Из курса географии вам известно, что ось вращения Земли наклонена к плоскости ее орбиты под углом 66°30′. Следовательно, земной экватор имеет по отношению к плоскости орбиты наклон, равный 23°30′. Таков наклон эклиптики к небесному экватору, который она пересекает в двух точках: весеннего и осеннего равноденствий.

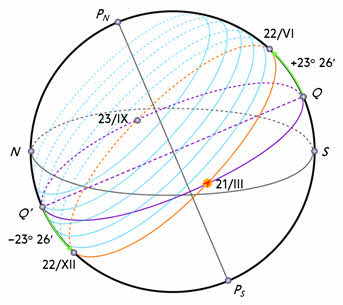
В эти дни (обычно — 21 марта и 23 сентября) Солнце находится на небесном экваторе и имеет склонение 0°. Оба полушария Земли освещаются Солнцем одинаково: граница дня и ночи проходит точно через полюса, и день равен ночи во всех пунктах Земли. В день летнего солнцестояния (22 июня) Земля повернута к Солнцу своим Северным полушарием. Здесь стоит лето, на Северном полюсе — полярный день, а на остальной территории полушария дни длиннее ночи. В день летнего солнцестояния Солнце поднимается над плоскостью земного (и небесного) экватора на 23°30′. В день зимнего солнцестояния (22 декабря), когда Северное полушарие освещается хуже всего, Солнце находится ниже небесного экватора на такой же угол 23°30′.

♈- точка весеннего равноденствия. 21 марта (день равняется ночи ).
Координаты Солнца: α ¤=0ч, δ ¤=0о
Обозначения сохранилось со времен Гиппарха, когда эта точка находилась в созвездии ОВНА → сейчас находится в созвездии РЫБ, В 2602г перейдет в созвездие ВОДОЛЕЯ.

♋ – день летнего солнцестояния. 22 июня (самый длинный день и самая короткая ночь).
Координаты Солнца: α¤=6ч, ¤=+23о26′
Обозначение созвездия Рака сохранилось со времен Гиппарха, когда эта точка находилась в созвездии Близнецов, затем была в созвездии Рака, а с 1988г перешла в созвездие Тельца.

♎ – день осеннего равноденствия. 23 сентября (день равен ночи).
Координаты Солнца: α ¤=12ч, δ t size=”2″ ¤=0о
Обозначение созвездия Весы сохранилось как обозначение символа правосудия при императоре Августе (63г до НЭ – 14г НЭ), сейчас в созвездии Девы, а в 2442г перейдет в созвездие Льва.

♑ – день зимнего солнцестояния. 22 декабря (самый короткий день и самая длинная ночь).
Координаты Солнца: α¤=18ч, δ¤=-23о26′
Обозначение созвездия Козерог сохранилось со времен Гиппарха, когда эта точка находилась в созвездии Козерога, сейчас в созвездии Стрельца, а в 2272г перейдет в созвездие Змееносца.

В зависимости от положения Солнца на эклиптике меняется его высота над горизонтом в полдень — момент верхней кульминации. Измерив полуденную высоту Солнца и зная его склонение в этот день, можно вычислить географическую широту места наблюдения. Этот способ издавна использовался для определения местоположения наблюдателя на суше и на море.

Суточные пути Солнца в дни равноденствий и солнцестояний на полюсе Земли, на ее экваторе и в средних широтах показаны на рисунке.

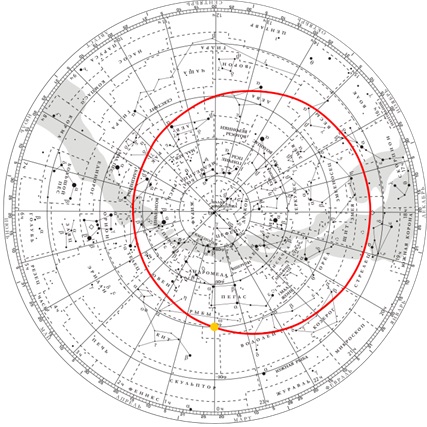
Определите положение Солнца на эклиптике и его экваториальные координаты на сегодняшний день.
Для этого достаточно мысленно провести прямую от полюса мира к соотвеисивующей дате на краю карты (приложить тинейку). Солнце должно располагается на эклиптике в точке ее пересечения с этой прямой

Склонение -16,5 град. Прямое восхождение 14 ч 52 мин. Созвездие — Весы.

ИЗУЧЕНИЕ ВИДИМОГО ГОДОВОГО ДВИЖЕНИЯ СОЛНЦА С ПОМОЩЬЮ ПОДВИЖНОЙ КАРТЫ ЗВЕЗДНОГО НЕБА

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке “Файлы работы” в формате PDF

Видимое годовое движение Солнца можно изучить с помощью подвижной карты звездного неба.

Подвижная карта звездного неба представляет собой круглую звездную карту небольших размеров, с помощью которой можно предельно просто определить, какие космические объекты можно наблюдать в данном месте в данное время. Она позволяет определять положение созвездий и ярчайших объектов в зависимости от следующих параметров: географической широты, из которой предполагается вести наблюдения, даты и времени наблюдения. Также по ней можно определять прямое восхождение и склонение светил.

Соответственно с помощью подвижной карты и звездного атласа можно изучить астрономическую закономерность, связанную с обращением Земли вокруг Солнца.

Нам требуется по подвижной карте звездного неба выяснить изменения условий видимости зодиакальных и прилегающих к ним созвездий на протяжении года и разобраться в причинах этого изменения.

По подвижной карте звездного неба нужно взять сначала, например, время года – весна. Находим середину весны (15 апреля), на карту сверху накладываем круг и совмещаем, допустим, с Утром (6 ч). По видимому срезу карты выписываем созвездия, которые видны утром 15 апреля. Далее совмещаем Вечер (18 ч) с 15 апреля и ,соответственно, выписываем те созвездия, которые видны. Затем 15 апреля совмещаем с Ночью (0 ч) и выписываем.

Для того, чтобы проследить за изменениями условий видимости зодиакальных и прилегающих к ним созвездий, те же самые (выше описанные) действия проделываем с оставшимися временами года: лето, осень, зима.

Еще мы можем устанавливать названия и границы зодиакальных созвездий и указывать те из них, в которых находятся основные точки эклиптики, определять среднюю продолжительность перемещения Солнца на фоне каждого зодиакального созвездия. Для этого понадобится карта звездного атласа.

Для каждого из 12 зодиакальных созвездий по карте звездного атласа находим прямое восхождение и склонение.

Склонением светила δ принято называть угол при центре сферы между плоскостью небесного экватора и направлением на светило. Изменяется склонение в пределах от 0 до ±90°. Знак указывает на то, ниже или выше относительно небесного экватора отсчитывается склонение светила.

Под прямым восхождением α светила понимают сферический угол при полюсе мира между колюром равноденствий и кругом склонения светила, считаемый в сторону, противоположную счету часовых углов, т.е. против суточного вращения сферы. Угол α измеряется дугой небесного экватора от точки весеннего равноденствия ϒ до круга склонения светила против хода часовой стрелки и изменяется от 0 до 24 h .

Записываем границы созвездий по прямому восхождению α и по склонению δ.

Далее по карте звездного неба смотрим, в какое время года можно наблюдать рассматриваемое созвездие. По той же карте звездного неба примерно определяем временные границы нахождения созвездия на небосклоне. Следовательно, можно делать выводы о продолжительности наблюдения созвездий (в сутках) [1], [3], [4].

Примеры:

1. Задание: Определить наклонение эклиптики около 3000 лет назад, если по наблюдениям в ту эпоху в некотором месте северного полушария Земли полуденная высота Солнца в день летнего солнцестояния равнялась +63°48′, а в день зимнего солнцестояния +16°00′ к югу от зенита. Данные наблюдений приведены в Таблице 1.

Посмотрев данный видеоурок, вы вспомните, что называется эклиптикой. Также мы с вами выясним, каковы особенности суточного движения Солнца на различных широтах.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.

Получите невероятные возможности

Конспект урока “Годичное движение Солнца по небу. Эклиптика”

Солнце так же, как и другие звёзды, описывает свой путь по небесной сфере. Находясь в средних широтах, мы можем каждое утро наблюдать за тем, как оно появляется из-за горизонта в восточной части неба. Затем постепенно поднимается над горизонтом и, наконец, в полдень достигает наивысшего положения на небе. После этого Солнце постепенно опускается, приближаясь к горизонту, и заходит в западной части неба.

Ещё в глубокой древности люди, наблюдавшие за перемещением Солнца по небу, обнаружили, что его полуденная высота меняется с течением года, как меняется и вид звёздного неба.

Если в течение года ежедневно отмечать положение Солнце на небесной сфере в момент его кульминации (то есть указывать его склонение и прямое восхождение), то мы получим большой круг, представляющий проекцию видимого пути центра солнечного диска в течение года. Этот круг древними греками был назван эклиптикой, что переводится, как ‘затмение’.

Конечно же, перемещение Солнца на фоне звёзд — это кажущееся явление. И вызвано оно вращением Земли вокруг Солнца. То есть, по сути, в плоскости эклиптики лежит путь Земли вокруг Солнца — её орбита.

Мы уже с вами говорили о том, что эклиптика пересекает небесный экватор в двух точках: в точке весеннего равноденствия (точка овна) и в точке осеннего равноденствия (точка весов).

Кроме точек равноденствия, на эклиптике выделяют ещё две промежуточные точки, в которых склонение Солнца бывает наибольшим и наименьшим. Эти точки получили название точек солнцестояния. В точке летнего солнцестояния (она ещё называется точкой рака) Солнце имеет максимальное склонение — +23 о 26’. В точке зимнего солнцестояния (точка козерога) склонение Солнца минимально и составляет –23 о 26’.

Созвездия, по которым проходит эклиптика получили названия эклиптические.

Ещё в Древней Месопота́мии было замечено, что Солнце, при своём видимом годовом движении проходит через 12 созвездий: Овен, Телец, Близнецы, Рак, Лев, Дева, Весы, Скорпион, Стрелец, Козерог, Водолей и Рыбы.

Изначально эклиптические знаки зодиака совпадали с зодиакальными, так как ещё не было чёткого разделения созвездий. Начало отсчёта знаков зодиака было установлено от точки весеннего равноденствия. А зодиакальные созвездия делили эклиптику на 12 равных частей.

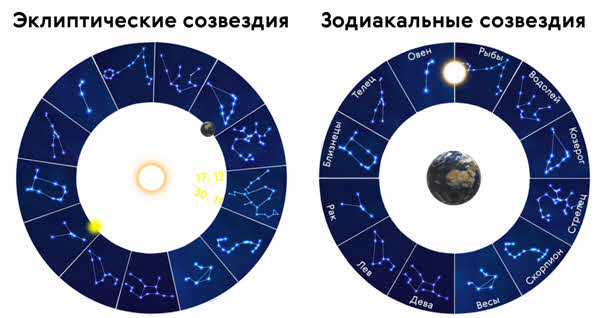
Сейчас же зодиакальные и эклиптические созвездия не совпадают: зодиакальных созвездий 12, а эклиптических — 13 (в них добавлено созвездие Змееносца, в котором Солнце находится с 30 ноября по 17 декабря. Помимо этого, из-за прецессии земной оси, точки весеннего и осеннего равноденствий постоянно смещается.

Прецессия (или предварение равноденствий) — это явление, возникающее из-за медленного раскачивания оси вращения земного шара. В этом цикле созвездия идут в обратную сторону, по сравнение с обычным годичным циклом. При этом получается, что точка весеннего равноденствия примерно каждые 2150 лет смещается на один знак зодиака по ходу часовой стрелки. Так с 4300 года по 2150 год до нашей эры эта точка располагалась в созвездии Тельца (эра Тельца), с 2150 года до нашей эры по 1 год нашей эры — в созвездии овна. Соответственно, сейчас, точка весеннего равноденствия находится в Рыбах.

После солнцестояния следует уменьшение склонения Солнца и длинный день начинает постепенно убывать до тех пор, пока день и ночь не сравняются (то есть примерно до 23 сентября).

После прохождения точки осеннего равноденствия, Солнце меняет своё склонение на южное. В Северном полушарии день продолжает убывать, а в Южном, наоборот, возрастает. И это будет продолжаться до тех пор, пока Солнце не достигнет точки зимнего солнцестояния (примерно до 22 декабря). Здесь Солнце опять примерно 4 дня практически не будет изменять своего склонения. В это время в Северном полушарии наблюдаются самые короткие дни и самые длинные ночи. В Южном наоборот, в разгаре лето и самый длинный день.

Через 4 дня, для наблюдателя в Северном полушарии, склонение Солнца начнёт постепенно увеличиваться и, примерно, через три месяца светило опять придёт в точку весеннего равноденствия.

Теперь давайте переместимся на Северный полюс. Здесь суточное движение Солнца практически параллельно горизонту. Поэтому в течение полугода Солнце не заходит, описывая круги над горизонтом — наблюдается полярный день.

Через полгода склонение Солнца поменяет свой знак на минус, на Северном полюсе начнётся полярная ночь. Она также будет длиться около полугода.

Переместимся на экватор. Здесь наше Солнце, как и все другие светила, восходит и заходит перпендикулярно плоскости истинного горизонта. Поэтому на экваторе день всегда равен ночи.

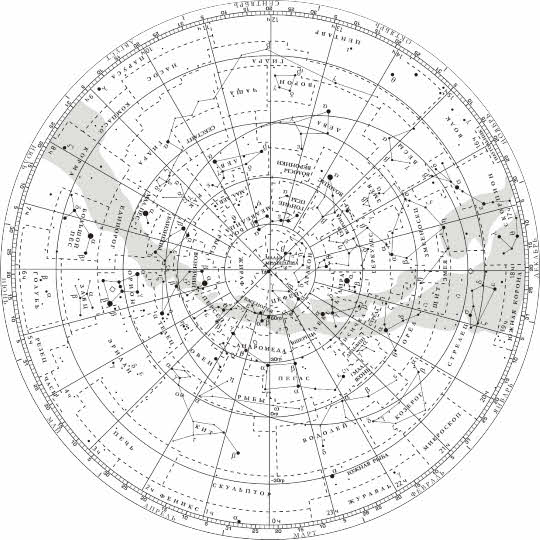
Теперь давайте обратимся к карте звёздного неба и немного поработаем с ней. Итак, мы уже знаем, что карта звёздного неба представляет собой проекцию небесной сферы на плоскость с нанесёнными на неё объектами в экваториальной системе координат. Напомним, что в центре карты располагается северный полюс мира. Рядом с ним Полярная звезда. Сетка экваториальных координат представлена на карте радиально расходящимися от центра лучами и концентрическими окружностями. На краю карты, возле каждого луча, написаны числа, обозначающие прямое восхождение (от нуля до двадцати трёх часов).

Склонение отсчитывается по этим лучам от окружности, которая изображает небесный экватор и имеет обозначение ноль градусов.

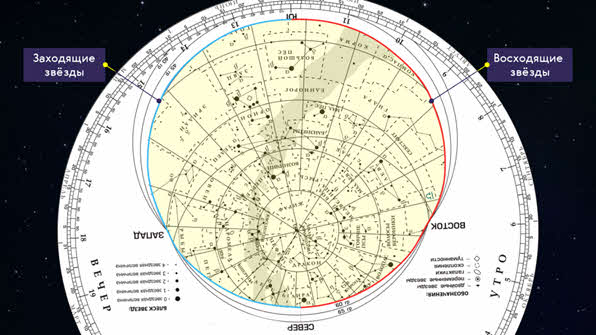
Для того, чтобы по карте звёздного неба определять вид неба в любое время суток выбранной даты года, к ней прилагается накладной круг, внутри которого начерчены оцифрованные пересекающиеся овалы, а по наружному краю круга нанесена шкала с делениями, которые соответствуют часам суток.

В накладном круге делается вырез по тому овалу, который является наиболее близким к широте места наблюдения. Полученный контур выреза будет представлять собой горизонт с основными его точками: севера, юга, запада и востока.

Для определения вида звёздного неба в конкретный момент времени на интересующую нас дату, необходимо совместить накладной круг и карту так, чтобы штрих момента времени совпал со штрихом этой даты. Тогда в отверстие накладного круга вы увидите звёздное небо на нужный вам день и час.

На контуре выреза, между его точками Ю, В и С, расположатся звезды, которые восходят в этот момент, а между точками Ю, 3 и С — звезды, которые заходят. Те звёзды, которые закрыл накладной круг, будут не видны.

Однако с помощью подвижной карты можно определять не только моменты восхода и захода звёзд, но и других светил, в том числе, и Солнца.

Как мы говорили, видимый годовой путь Солнца среди звёзд называется эклиптикой. На карте она представлена овалом, который несколько смещён относительно Северного полюса мира. Точки пересечения эклиптики с небесным экватором называются точками весеннего и осеннего равноденствия (они обозначены символами овна и весов). Две другие точки — точки летнего и зимнего солнцестояний — на нашей карте обозначены кружочком и ромбиком соответственно.

Чтобы можно было определять время восхода и захода Солнца или планет, необходимо предварительно нанести их положение на карту. Для Солнца это не составляет большого труда: достаточно приложить линейку к Северному полюсу мира и штриху заданной даты. Точка пересечения линейки с эклиптикой покажет положение Солнца на эту дату.

Теперь давайте с помощью подвижной карты звёздного неба определим экваториальные координаты Солнца, например, на 18 октября. А также найдём примерное время его восхода и захода на эту дату.

Чтобы понять принцип видимого движения Солнца и других светил на небесной сфере, рассмотрим сперва истинное движение Земли. Земля является одной из планет солнечной системы. Она непрерывно вращается вокруг своей оси.

Период вращения ее равен одним суткам, поэтому наблюдателю, находящемуся на Земле, кажется, что все небесные светила обращаются вокруг Земли с востока на запад с тем же периодом.

Наклон оси вращения Земли к плоскости орбиты

Но Земля не только вращается вокруг своей оси, но и обращается также вокруг Солнца по эллиптической орбите. Полный оборот вокруг Солнца она совершает за один год. Ось вращения Земли наклонена к плоскости орбиты под углом 66°33′. Положение оси в пространстве при движении Земли вокруг Солнца все время остается почти неизменным. Поэтому Северное и Южное полушария попеременно бывают обращены в сторону Солнца, в результате чего на Земле происходит смена времен года.

При наблюдении неба можно заметить, что звезды на протяжении многих лет неизменно сохраняют свое вза­имное расположение.

Звезды “неподвижны” лишь потому, что находятся очень далеко от нас. Расстояние до них так велико, что с любой точки земной орбиты они видны одинаково.

А вот тела же солнечной системы — Солнце, Луна и планеты, которые нахо­дятся сравнительно недалеко от Земли, и смену их положений мы можем легко заметить. Таким образом, Солнце наравне со всеми светила­ми участвует в суточном движении и одновременно имеет собст­венное видимое движение (оно называется годовым движением), обусловленное движением Земли вокруг Солнца.

Представьте себе картину – Луна взяла и исчезла с орбиты Земли. Чем нам может грозить такой поворот событий? Подробнее об этом

Видимое годовое движение Солнца на небесной сфере

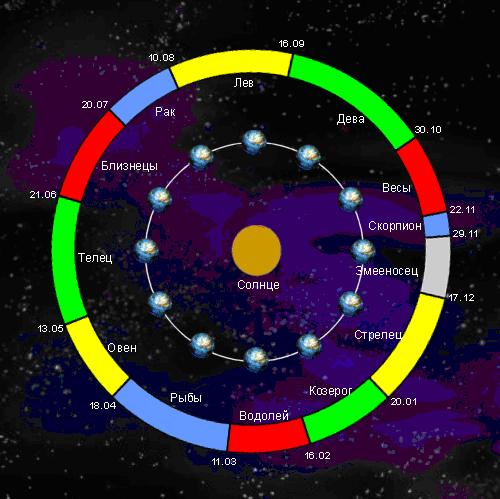
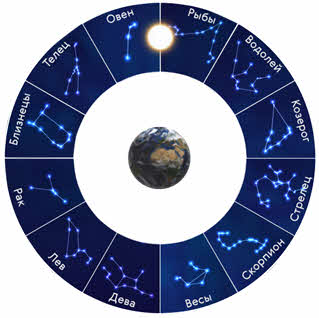
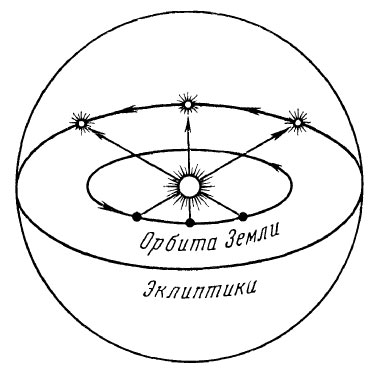
Наиболее просто годовое движение Солнца можно объяснить по рисунку приведенному ниже. Из этого ри­сунка видно, что в зависимости от положения Земли на орбите наблюдатель с Земли будет видеть Солнце на фоне разных со­звездий. Ему будет казаться, что оно все время перемещается по небесной сфере. Это движение является отражением обращения Земли вокруг Солнца. За год Солнце сделает полный оборот.

Что представляет собой эклиптика

Большой круг на небесной сфере, по которому происходит ви­димое годовое движение Солнца, называется эклиптикой. Эклиптика — слово греческое и в переводе означает затмение. Этот круг назвали так потому, что затмения Солнца и Луны про­исходят только тогда, когда оба светила находятся на этом круге.

Следует отметить, что плоскость эклиптики совпадает с плос­костью орбиты Земли.

Видимое годовое движение Солнца по эк­липтике происходит в том же направлении, в котором Земля движется по орбите вокруг Солнца, т. е. оно перемещается к востоку. В течение года Солнце последовательно проходит по эк­липтике 12 созвездий, которые образуют пояс Зодиака и называются зодиакальными.

Пояс Зодиака образуют следующие созвездия: Рыбы, Овен, Телец, Близнецы, Рак, Лев, Дева, Весы, Скорпион, Стрелец, Ко­зерог и Водолей. Вследствие того, что плоскость земного экватора наклоне­на к плоскости орбиты Земли на 23°27 ‘ , плоскость небесного эк­ватора также наклонена к плоскости эклиптики на угол е=23°27′.

Наклон эклиптики к экватору не сохраняется постоян­ным (вследствие воздействия на Землю сил притяжения Солнца и Луны), поэтому в 1896 г. при утверждении астрономических постоянных ре­шено было наклон эклиптики к экватору считать усредненно равным 23°27’8″,26.

Небесный экватор и плоскость эклиптики

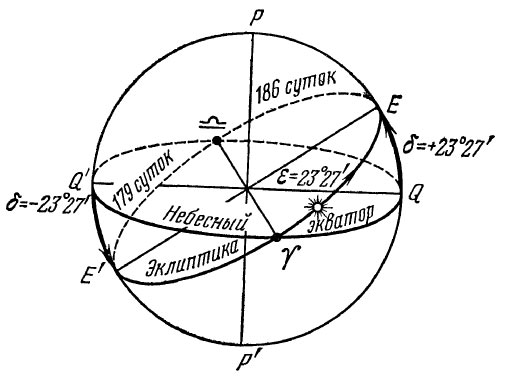
Эклиптика пересекается с небесным экватором в двух точках, которые называются точками весеннего и осеннего равноденствий. Точку весеннего равноденствия принято обозначать знаком созвездия Овен Т, а точку осеннего равноденствия — знаком созвездия Весов —. Солнце в этих точках соответственно бывает 21 марта и 23 сентября. В эти дни на Земле день равен ночи, Солнце точно восходит в точке восто­ка и заходит в точке запада.

Точки весеннего и осеннего равноденствия – места пересечения экватора и плоскости эклиптики

Точки эклиптики, отстоящие от точек равноденствий на 90°, называются точками солнцестояний. Точка Е на эклип­тике, в которой Солнце занимает самое высокое положение отно­сительно небесного экватора, называется точкой летнего солнцестояния, а точка Е’, в которой оно занимает самое низкое поло­жение, называется точкой зимнего солнцестояния.

В точке летне­го солнцестояния Солнце бывает 22 июня, а в точке зимнего солнцестояния — 22 декабря. В течение нескольких дней, близ­ких к датам солнцестояний, полуденная высота Солнца остается почти неизменной, в связи с чем эти точки и получили такое на­звание. Когда Солнце находится в точке летнего солнцестояния день в Северном полушарии самый длинный, а ночь самая корот­кая, а когда оно находится в точке зимнего солнцестояния — на­оборот.

В день летнего солнцестояния точки восхода и захода Солнца максимально удалены к северу от точек востока и запада на го­ризонте, а в день зимнего солнцестояния они имеют наибольшее удаление к югу.

Движение Солнца по эклиптике приводит к непрерывному из­менению его экваториальных координат, ежедневному изменению полуденной высоты и перемещению по горизонту точек восхода и захода.

Известно, что склонение Солнца отсчитывается от плоскости небесного экватора, а прямое восхождение — от точки весеннего равноденствия. Поэтому когда Солнце находится в точке весен­него равноденствия, его склонение и прямое восхождение равны нулю. В течение года склонение Солнца в настоящий период из­меняется от +23°26′ до —23°26′, переходя два раза в год через нуль, а прямое восхождение от 0 до 360°.

Солнце имеет форму шара или сплюснуто у полюсов? Давайте разберемся! Подробнее об этом

Экваториальные координаты Солнца в течение года

Экваториальные координаты Солнца в течение года изменя­ются неравномерно. Происходит это вследствие неравномерности движения Солнца по эклиптике и движения Солнца по эклиптике и наклона эклиптики к экватору. Половину своего видимого годо­вого пути Солнце проходит за 186 суток с 21 марта по 23 сентяб­ря, а вторую половину за 179 суток с 23 сентября по 21 марта.

Неравномерность движения Сол­нца по эклиптике связана с тем, что Земля на протяжении всего периода обращения вокруг Солнца движется по орбите не с оди­наковой скоростью. Солнце находится в одном из фокусов эллип­тической орбиты Земли.

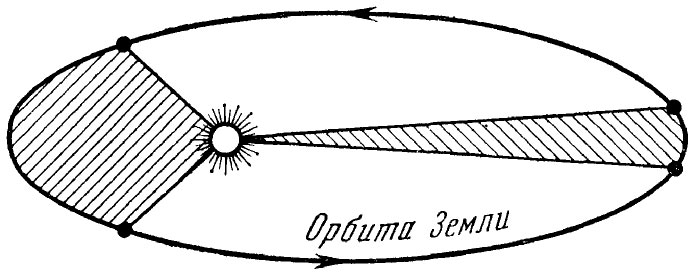
движение Земли по орбите

Из второго закона Кеплера известно, что линия, соединяющая Солнце и планету, за равные промежутки времени описывает равные площади. Согласно этому закону Земля, находясь ближе всего к Солнцу, т. е. в перигелии, движется быстрее, а находясь дальше всего от Солнца, т. е. в афелии — медленнее.

Ближе к Солнцу Земля бывает зимой, а летом — дальше. Поэтому в зим­ние дни она движется по орбите быстрее, чем в летние. Вследст­вие этого суточное изменение прямого восхождения Солнца в день зимнего солнцестояния равно 1°07′, тогда как в день летнего солнцестояния оно равно только 1°02′.

Различие скоростей движения Земли в каждой точке орбиты вызывает неравномерность изменения не только прямого восхож­дения, но и склонения Солнца. Однако за счет наклона эк­липтики к экватору его изменение имеет другой характер. Наиболее быстро склонение Солнца изменяется вблизи точек равноденствия, а у точек солнцестояния оно почти не из­меняется.

Знание характера изменения экваториальных координат Солн­ца позволяет производить приближенный расчет прямого восхож­дения и склонения Солнца.

Для выполнения такого расчета бе­рут ближайшую дату с известными экваториальными координа­тами Солнца. Затем учитывают, что прямое восхождение Солнца за сутки изменяется в среднем на 1°, а склонение Солнца в тече­ние месяца до и после прохождения точек равноденствия изме­няется на 0,4° в сутки; в течение месяца перед солнцестояниями и после них — на 0,1° в сутки, а в течение промежуточных меся­цев между указанными — на 0,3°.

Читайте также:

  

• Что такое финансовый кризис кратко

  

• Какие потребности личности удовлетворяет религия кратко

  

• План урока скорость распространения света

  

• Что является активной частью опорно двигательного аппарата 8 класс биология кратко

  

• Какие территории утратила германия после поражения в первой мировой войне кратко

Солнце так же, как и другие
звёзды, описывает свой путь по небесной сфере. Находясь в средних широтах, мы
можем каждое утро наблюдать за тем, как оно появляется из-за горизонта в
восточной части неба. Затем постепенно поднимается над горизонтом и, наконец, в
полдень достигает наивысшего положения на небе. После этого Солнце постепенно
опускается, приближаясь к горизонту, и заходит в западной части неба.

Ещё в глубокой древности люди,
наблюдавшие за перемещением Солнца по небу, обнаружили, что его полуденная
высота меняется с течением года, как меняется и вид звёздного неба.

Если в течение года ежедневно
отмечать положение Солнце на небесной сфере в момент его кульминации (то есть
указывать его склонение и прямое восхождение), то мы получим большой круг,
представляющий проекцию видимого пути центра солнечного диска в течение года.
Этот круг древними греками был назван эклиптикой, что переводится, как ‘затмение’.

Конечно же, перемещение Солнца
на фоне звёзд — это кажущееся явление. И вызвано оно вращением Земли вокруг
Солнца. То есть, по сути, в плоскости эклиптики лежит путь Земли вокруг Солнца
— её орбита.

Мы уже с вами говорили о том,
что эклиптика пересекает небесный экватор в двух точках: в точке весеннего
равноденствия (точка овна) и в точке осеннего равноденствия (точка весов).

Кроме точек равноденствия, на
эклиптике выделяют ещё две промежуточные точки, в которых склонение Солнца
бывает наибольшим и наименьшим. Эти точки получили название точек солнцестояния.
В точке летнего солнцестояния (она ещё называется точкой рака)
Солнце имеет максимальное склонение — +23^о 26’. В точке зимнего
солнцестояния (точка козерога) склонение Солнца минимально и составляет –23^о
26’.

Созвездия, по которым проходит
эклиптика получили названия эклиптические.

Ещё в Древней
Месопота́мии было замечено, что Солнце, при своём видимом годовом движении
проходит через 12 созвездий: Овен, Телец, Близнецы, Рак, Лев, Дева, Весы,
Скорпион, Стрелец, Козерог, Водолей и Рыбы.

Позже, древние греки назвали
этот пояс Поясом Зодиака. Дословно это переводится, как «круг из
животных». И действительно, если посмотреть на названия зодиакальных созвездий,
то несложно увидеть, что их половина в классическом греческом зодиаке
представлена в виде животных (помимо мифологических существ).

Изначально эклиптические знаки
зодиака совпадали с зодиакальными, так как ещё не было чёткого разделения
созвездий. Начало отсчёта знаков зодиака было установлено от точки весеннего
равноденствия. А зодиакальные созвездия делили эклиптику на 12 равных частей.

Сейчас же зодиакальные и
эклиптические созвездия не совпадают: зодиакальных созвездий 12, а
эклиптических — 13 (в них добавлено созвездие Змееносца, в котором Солнце
находится с 30 ноября по 17 декабря. Помимо этого, из-за прецессии земной оси,
точки весеннего и осеннего равноденствий постоянно смещается.

Прецессия (или предварение
равноденствий) — это явление,
возникающее из-за медленного раскачивания оси вращения земного шара. В этом
цикле созвездия идут в обратную сторону, по сравнение с обычным годичным
циклом. При этом получается, что точка весеннего равноденствия примерно каждые
2150 лет смещается на один знак зодиака по ходу часовой стрелки. Так с 4300
года по 2150 год до нашей эры эта точка располагалась в созвездии Тельца (эра
Тельца), с 2150 года до нашей эры по 1 год нашей эры — в созвездии овна.
Соответственно, сейчас, точка весеннего равноденствия находится в Рыбах.

Как мы уже упоминали, за
начало движение Солнца по эклиптике принимается день весеннего равноденствия
(около 21 марта). Суточная параллель Солнца под влиянием его годового движения
непрерывно смещается на шаг склонения. Поэтому общее движение Солнца на небе
происходит как бы по спирали, которая является результатом сложения суточного и
годового движения. Итак, двигаясь по спирали, Солнце увеличивает своё склонение
примерно на 15 минут в сутки. При этом продолжительность светового дня в
Северном полушарии растёт, а в Южном — убывает. Это увеличение будет
происходить до тех пор, пока склонение Солнца не достигнет +23^о 26’,
что произойдёт примерно 22 июня, в день летнего солнцестояния. Название
«солнцестояние» связано с тем, что в это время (примерно 4 дня) Солнце
практически не изменяет своего склонения (то есть как бы «стоит»).

После солнцестояния следует
уменьшение склонения Солнца и длинный день начинает постепенно убывать до тех
пор, пока день и ночь не сравняются (то есть примерно до 23 сентября).

После прохождения точки
осеннего равноденствия, Солнце меняет своё склонение на южное. В Северном
полушарии день продолжает убывать, а в Южном, наоборот, возрастает. И это будет
продолжаться до тех пор, пока Солнце не достигнет точки зимнего солнцестояния
(примерно до 22 декабря). Здесь Солнце опять примерно 4 дня практически не будет
изменять своего склонения. В это время в Северном полушарии наблюдаются самые
короткие дни и самые длинные ночи. В Южном наоборот, в разгаре лето и самый длинный
день.

Через 4 дня, для наблюдателя в
Северном полушарии, склонение Солнца начнёт постепенно увеличиваться и,
примерно, через три месяца светило опять придёт в точку весеннего
равноденствия.

Теперь давайте переместимся на
Северный полюс. Здесь суточное движение Солнца практически параллельно
горизонту. Поэтому в течение полугода Солнце не заходит, описывая круги над
горизонтом — наблюдается полярный день.

Через полгода склонение Солнца
поменяет свой знак на минус, на Северном полюсе начнётся полярная ночь. Она
также будет длиться около полугода.

Переместимся на экватор. Здесь
наше Солнце, как и все другие светила, восходит и заходит перпендикулярно
плоскости истинного горизонта. Поэтому на экваторе день всегда равен ночи.

Теперь давайте обратимся к
карте звёздного неба и немного поработаем с ней. Итак, мы уже знаем, что карта
звёздного неба представляет собой проекцию небесной сферы на плоскость с
нанесёнными на неё объектами в экваториальной системе координат. Напомним, что
в центре карты располагается северный полюс мира. Рядом с ним Полярная звезда. Сетка
экваториальных координат представлена на карте радиально расходящимися от
центра лучами и концентрическими окружностями. На краю карты, возле каждого
луча, написаны числа, обозначающие прямое восхождение (от нуля до двадцати трёх
часов).

Склонение отсчитывается по
этим лучам от окружности, которая изображает небесный экватор и имеет
обозначение ноль градусов.

Для того, чтобы по карте
звёздного неба определять вид неба в любое время суток выбранной даты года, к
ней прилагается накладной круг, внутри которого начерчены оцифрованные
пересекающиеся овалы, а по наружному краю круга нанесена шкала с делениями,
которые соответствуют часам суток.

В накладном круге делается
вырез по тому овалу, который является наиболее близким к широте места
наблюдения. Полученный контур выреза будет представлять собой горизонт с
основными его точками: севера, юга, запада и востока.

Для определения вида звёздного
неба в конкретный момент времени на интересующую нас дату, необходимо
совместить накладной круг и карту так, чтобы штрих момента времени совпал со
штрихом этой даты. Тогда в отверстие накладного круга вы увидите звёздное небо
на нужный вам день и час.

На контуре выреза, между его
точками Ю, В и С, расположатся звезды, которые восходят в этот момент, а между
точками Ю, 3 и С — звезды, которые заходят. Те звёзды, которые закрыл накладной
круг, будут не видны.

Однако с помощью подвижной
карты можно определять не только моменты восхода и захода звёзд, но и других
светил, в том числе, и Солнца.

Как мы говорили, видимый
годовой путь Солнца среди звёзд называется эклиптикой. На карте она
представлена овалом, который несколько смещён относительно Северного полюса
мира. Точки пересечения эклиптики с небесным экватором называются точками
весеннего и осеннего равноденствия (они обозначены символами овна и весов). Две
другие точки — точки летнего и зимнего солнцестояний — на нашей карте
обозначены кружочком и ромбиком соответственно.

Чтобы можно было определять
время восхода и захода Солнца или планет, необходимо предварительно нанести их
положение на карту. Для Солнца это не составляет большого труда: достаточно
приложить линейку к Северному полюсу мира и штриху заданной даты. Точка
пересечения линейки с эклиптикой покажет положение Солнца на эту дату.

Теперь давайте с помощью
подвижной карты звёздного неба определим экваториальные координаты Солнца,
например, на 18 октября. А также найдём примерное время его восхода и захода на
эту дату.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.