Определение координаты движущегося тела

Как определить координаты движущегося тела? Для этого необходимо знать такие понятия, как механическое движение, пройденный путь, скорость, перемещение.
Механическое движение
При механическом движении происходит изменение положения тела в пространстве относительно других тел за промежуток времени. Оно бывает равномерным и неравномерным.
Равномерное движение
При равномерном движении тело за равные промежутки времени проходит одинаковые расстояния (т.е. движется с постоянной скоростью).
Путь, пройденный при равномерном движении равен: Sx=Vxt=x-xо
Следовательно, при равномерном движении координата тела изменяется по следующей зависимости:
Где:
- Xо – начальная координата тела;
- X – координата в момент времени t;
- Vx – проекция скорости на ось X.
Неравномерное движение
Неравномерное движение – движение, при котором тело за равные промежутки времени проходит неодинаковые расстояния (движется с непостоянной скоростью), то есть движется с ускорением.
Если тело движется неравномерно, то скорость тела в разные моменты отличается не только по величине, но и (или) по направлению. Средняя скорость тела при неравномерном движении определяется по формуле: V (ср)= S (весь)/t (весь)
Ускорение – величина, показывающая, как изменяется скорость за 1 секунду.
Следовательно, скорость в любой момент времени можно найти следующим образом:
V=Vо+at
Если скорость с течением времени увеличивается, то a больше 0, если скорость с течением времени уменьшается, то a меньше 0.
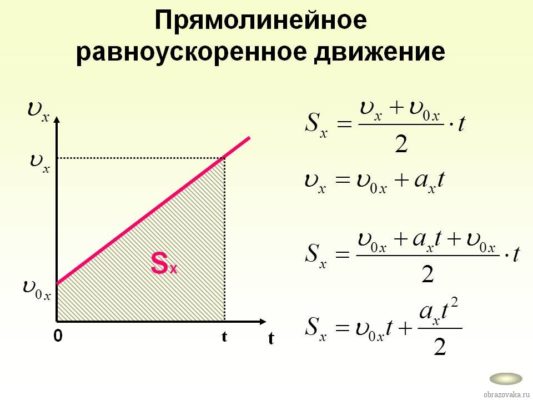
Как найти путь при равноускоренном движении?
Пройденный путь численно равен площади под графиком. То есть Sx=(Vox+Vx)t/2
Скорость в любой момент времени равна Vx=Vox+axt, следовательно Sx=Voxt+axt2/2
Так как перемещение тела равно разности конечной и начальной координат (Sx=X-Xo), то координата в любой момент времени вычисляется по формуле X=Xo+Sx, или
X=Xo+Voxt+axt2/2
Движение тела по вертикали
Если тело движется по вертикали, а не по горизонтали, то такое движение всегда является равноускоренным. Когда тело падает вниз, то падает оно всегда с одинаковым ускорением – ускорением свободного падения. Оно всегда одинаковое: g=9,8 м/кв.с.
При движении по вертикали формула скорости приобретает вид: Vy=Voy+gt,
где Vy и Voy – проекции начальной и конечной скоростей на ось OY.
Координату же можно рассчитать по формуле: Y=Yo+Voyt+gt2/2
Движение тела по окружности
При движении по окружности численное значение скорости может и не изменяться, но поскольку обязательно изменяется направление, то движение по окружности – это всегда равноускоренное движение.
Что мы узнали?
Тема «Определение координаты движущего тела», которую изучают в 9 классе, поможет ученикам систематизировать информацию о том, что движение может быть равномерным и неравномерным. Так же для того чтобы знать пройденный путь, нужно выбрать тело отсчета и использовать прибор для отсчета времени.
Оценка доклада
А какая ваша оценка?
Наверняка каждый из вас неоднократно договаривался с другом, родителями или учителем о встрече. При этом всегда возникал вопрос: где встретиться? Хорошо, если намеченное место встречи было известно, и вы могли его назвать или показать. Но как быть, если вы договариваетесь о месте встречи по телефону или сообщаете о нем в письме?
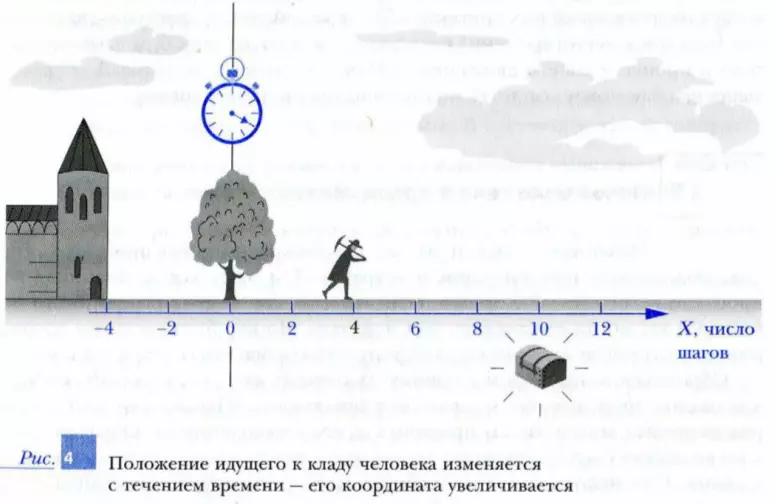
Обратимся за примером к одному из древних авторов, который сообщал в послании другу, как найти зарытый в землю клад. «Найдя одинокий дуб перед воротами моего замка, прижмись к его стволу спиной. Обратив лицо к восходящему Солнцу, отсчитай десять шагов вперед, и ты окажешься над искомым». При использовании подобного наставления трудно не найти спрятанный сундук с сокровищами. Ясно, что найти клад было бы значительно труднее, если бы в послании говорилось, что надо отсчитать десять шагов от замка, а не от достаточно малого по размерам конкретного места — дуба.
Вдумаемся, что использовал автор послания. Во-первых, он указал точку на поверхности Земли перед своим замком (дуб), от которого надо начинать поиск. Физики говорят, что было указано тело отсчета и начало отсчета (земля вокруг замка и дуб соответственно). Во-вторых, он указал направление (восходящее Солнце, т. е. восток) и расстояние от начала отсчета до искомого места вдоль этого направления, выраженное в единицах длины — шагах. Говоря иначе, он ввел ось координат, связанную с телом отсчета.
Телом отсчета называют тело, относительно которого определяют положение остальных тел. Некоторую точку этого тела называют началом отсчета и присваивают этой точке координату нуль. Из начала отсчета в нужном направлении проводят координатную ось. Отметим, что расстояние между любыми точками тела отсчета должно быть неизменным.
Обратим внимание, что ось координат имеет:
- начало отсчета (в данном случае — дуб);
- положительное направление (восходящее Солнце — восток);
- нанесенные на нее метки, соответствующие выбранной единице длины (шаг).
Теперь любой точке на этой оси можно приписать конкретное число, равное расстоянию в заданных единицах длины (шагах) от начала отсчета до этой точки. Это число называют координатой точки по этой оси. Например, точка, где находится клад (рис. 4), имеет координату по этой оси xкл = 10 шагов. А точка, в которой находится изображенный на рисунке человек, имеет координату xч = 4 шага. Координата дуба xд = 0. Отметим еще раз, что точку с нулевой координатой называют началом отсчета.
Координаты точек, которые находятся на оси от начала отсчета в направлении, противоположном положительному, считают отрицательными. Поэтому координата стены у ворот замка на рис. 4 имеет отрицательное значение xс = -4 шага.
Подведем итог нашим рассуждениям. Чтобы описать положение конкретной точки (или тела, замененного этой точкой), следует:
- выбрать тело отсчета, относительно которого будем проводить дальнейшее описание;
- ввести ось координат, связанную с этим телом отсчета, начало отсчета (ось имеет направление, начало отсчета и единицу длины);
- указать координату интересующей нас точки.
Отметим, что для нахождения искомого места необходимо использовать все три понятия: тело отсчета, координатная ось и координата. Скажем, если кто-то из вас предложит другу встретиться завтра в точке с координатой x = 18, не указав ни тела отсчета, ни оси, ни единицы длины вдоль этой оси, то встречи, скорее всего, не будет. Однако если вы договоритесь с одноклассниками встретиться в 10 метрах на север от памятника А. С. Пушкину на Тверском бульваре, например, 18 марта этого года в 10 часов утра, то, будете уверены, никто не заблудится.
Обратим внимание на то, что в последнем условии помимо места указано время встречи. Любое устройство, предназначенное для отсчета времени, называют часами.
Часы — это любое устройство для отсчета времени.
Пользуясь часами, можно ответить и на другой интересующий нас вопрос — когда? То есть в какой момент времени должна, например, произойти встреча в заданной точке пространства.
Можно сказать, что, взяв часы, мы тем самым вводим еще одну ось — ось времени, на которой, как на секундомере, нанесены метки, соответствующие выбранной единице времени, например секунде.
Точно так же, как на оси координат, на оси времени должно быть отмечено начало отсчета — нулевая точка. Это может быть, например, момент включения секундомера.
Совокупность тела отсчета, с которым связана ось координат, и часов называют системой отсчета.
Имея систему отсчета, мы можем ответить на вопросы: «Где и когда находится интересующее нас тело?».
Итоги
Для того чтобы описать положение данного тела в пространстве, необходимо:
- выбрать тело отсчета и начало отсчета на нем;
- связать с ним координатную ось, проходящую через начало отсчета в нужном направлении, и указать единицу длины.
При этом расстояние от начала отсчета до данного тела, выраженное в выбранных единицах длины и взятое с соответствующим знаком, называют координатой этого тела.
Поступив так, мы будем говорить, что описали положение данного тела относительно выбранного тела отсчета.
Если мы выберем в качестве тела отсчета другое тело или другую ось координат, то и координат данного тела может стать другой.
Совокупность тела отсчета, с которым связана ось координат, и часов называют системой отсчета.
Вопросы
- Что такое ось координат, координата точки, тело отсчета, часы?
- Что такое система отсчета?
- Что и в какой последовательности нужно сделать для того, чтобы описать положение тела в пространстве?
- Расскажите, как выбирают тело отсчета и начало отсчета. Объясните, почему в качестве тела отсчета нельзя выбрать точечное тело. Перед ответом на последний вопрос скажите, какое минимальное число точек определяет положение прямой линии.
Упражнения
- Опишите положение (найдите координаты): а) дуба; б) человека; в) клада, изображенных на рис. 4, если в качестве начала отсчета выбрать: стену у ворот замка; клад.
- Опишите систему отсчета, позволяющую задать на местности координаты (место) и время встречи одноклассников. Для выполнения упражнения используйте компас, часы, рулетку. Какие физические модели вы будете применять при выполнении упражнения?
Введение
Представьте: вы изо всей силы бросили мяч. Как определить, где он будет находиться через две секунды? Можно подождать две секунды и просто посмотреть, где он. Но, даже не глядя, вы приблизительно можете предсказать, где будет мяч: бросок был сильнее обычного, направлен под большим углом к горизонту, значит, полетит высоко, но недалеко… Используя законы физики, можно будет точно определить положение нашего мяча.
Определить положение движущегося тела в любой момент времени – это и есть основная задача кинематики.
Система отсчета
Начнем с того, что у нас есть тело: как определить его положение, как объяснить кому-то, где оно находится? Об автомобиле мы скажем: он на дороге за 150 метров перед светофором или на 100 метров за перекрестком (см. рис. 1).
Рис. 1. Определение местоположения машины
Или на трассе за 30 км к югу от Москвы. О телефоне на столе скажем: он сантиметров на 30 правее клавиатуры или рядом с дальним углом стола (см. рис. 2).
Рис. 2. Положение телефона на столе
Заметьте: мы не сможем определить положение автомобиля, не упомянув другие объекты, не привязавшись к ним: светофор, город, клавиатуру. Мы определяем положение, или координаты, всегда относительно чего-то.
Координаты – это набор данных, по которому определяется положение того или иного объекта, его адрес.
Примеры упорядоченных и неупорядоченных имен
Координата тела – это его адрес, по которому мы его можем найти. Он упорядоченный. Например, зная ряд и место, мы точно определяем, где находится наше место в зале кинотеатра (см. рис. 3).
Рис. 3. Зал кинотеатра
Буквой и цифрой, например e2, точно задается положение фигуры на шахматной доске (см. рис. 4).
Рис. 4. Положение фигуры на доске
Зная адрес дома, например улица Солнечная 14, мы будем искать его на этой улице, на четной стороне, между домами 12 и 16 (см. рис. 5).
Рис. 5. Поиск дома
Названия улиц не упорядочены, мы не будем искать Солнечную улицу по алфавиту между улицами Розовой и Тургенева. Также не упорядочены номера телефонов, номерные знаки автомобилей (см. рис. 6).
Рис. 6. Неупорядоченные имена
Эти номера, идущие подряд, – это лишь совпадение, не означающее соседства.
Мы можем задать положение тела в разных системах координат, как нам удобно. Для того же автомобиля, можно задать точные географические координаты (широту и долготу) (см. рис. 7).
Рис. 7. Долгота и широта местности
Можно выбрать любую точку в городе и считать, сколько километров нужно проехать на юг и сколько на восток, чтобы найти автомобиль (см. рис. 8).
Рис. 8. Местоположение относительно точки
Причем если мы выберем разные такие точки, то получим разные координаты, хотя они будут задавать положение одного и того же автомобиля.
Итак, положение тела относительно разных тел в разных системах координат будет разным. А что такое движение? Движение – это изменение положения тела со временем. Поэтому описывать движение мы будем в разных системах отсчета по-разному, и нет смысла рассматривать движение тела без системы отсчета.
Например, как движется стакан с чаем на столе в поезде, если сам поезд едет? Смотря относительно чего. Относительно стола или пассажира, сидящего рядом на сидении, стакан покоится (см. рис. 9).
Рис. 9. Движение стакана относительно пассажира
Относительно дерева около железной дороги стакан движется вместе с поездом (см. рис. 10).
Рис. 10. Движение стакана вместе с поездом относительно дерева
Относительно земной оси стакан и поезд вместе со всеми точками земной поверхности будут еще и двигаться по окружности (см. рис. 11).
Рис. 11. Движение стакана с вращением Земли относительно земной оси
Поэтому нет смысла говорить о движении вообще, движение рассматривается в привязке к системе отсчета.
Наблюдение и вычисление
Всё, что мы знаем о движении тела, можно разделить на наблюдаемое и вычисляемое. Вспомним пример с мячом, который мы бросили. Наблюдаемое – это его положение в выбранной системе координат, когда мы его только бросаем (см. рис. 12).
Рис. 12. Наблюдение
Это момент времени, когда мы его бросили; время, которое прошло после броска. Пусть на мяче нет спидометра, который показал бы скорость мяча, но ее модуль, как и направление, тоже можно узнать, используя, например, замедленную съемку.
С помощью наблюдаемых данных мы можем предсказать, например, что мяч через 5 секунд упадет за 20 м от места броска или через 3 секунды попадет в верхушку дерева. Положение мяча в любой момент времени – это в нашем случае вычисляемые данные.
Что определяет каждое новое положение движущегося тела? Его определяет перемещение, потому что перемещение – это вектор, характеризующий изменение положения. Если начало вектора совместить с начальным положением тела, то конец вектора укажет на новое положение переместившегося тела (см. рис. 13).
Рис. 13. Вектор перемещения
Нахождение координаты тела по перемещению
Рассмотрим несколько примеров на определение координаты движущегося тела по его перемещению.
Пусть тело двигалось прямолинейно из точки 1 в точку 2. Построим вектор перемещения и обозначим его (см. рис. 14).
Рис. 14. Перемещение тела
Тело двигалось вдоль одной прямой, значит, нам будет достаточно одной оси координат, направленной вдоль перемещения тела. Допустим, мы наблюдаем за движением со стороны, совместим начало отсчета с наблюдателем.
Перемещение – вектор, удобнее работать с проекциями векторов на оси координат (у нас она одна). – проекция вектора
(см. рис. 15).
Рис. 15. Проекция вектора
Как определить координату начальной точки, точки 1? Опускаем перпендикуляр из точки 1 на ось координат. Этот перпендикуляр пересечет ось и отметит на оси координату точки 1. Так же определяем координату точки 2 (см. рис. 16).
Рис. 16. Опускаем перпендикуляры на ось ОХ
Проекция перемещения равна:
При таком направлении оси и перемещения будет по модулю равна самому перемещению
.
Зная начальную координату и перемещение, найти конечную координату тела – дело математики:
Уравнение
Уравнение – это равенство, содержащее неизвестный член. В чем его смысл?
Любая задача заключается в том, что что-то нам известно, а что-то – нет, и неизвестное нужно найти. Например, тело из некоторой точки переместилось на 6 м в направлении оси координат и оказалось в точке с координатой 9 (см. рис. 17).
Рис. 17. Начальное положение точки
Как найти, из какой точки тело начало движение?
У нас есть закономерность: проекция перемещения – это разность конечной и начальной координат:
Смысл уравнения будет в том, что перемещение и конечную координату мы знаем () и можем подставить эти значения, а начальную координату не знаем, она будет неизвестным в этом уравнении:
И уже решая уравнение, мы получим ответ: начальная координата .
Перемещение и направление оси не совпадают по направлению
Рассмотрим другой случай: перемещение направлено в сторону, противоположную направлению оси координат.
Координаты начальной и конечной точек определяются так же, как и раньше, – опускаются перпендикуляры на ось (см. рис. 18).
Рис. 18. Ось направлена в другую сторону
Проекция перемещения (ничего не меняется) равна:
Обратите внимание, что больше, чем
, и проекция перемещения
, когда она направлена против оси координат, будет отрицательной.
Конечная координата тела из уравнения для проекции перемещения равна:
Как видим, ничего не меняется: в проекции на ось координат конечное положение равно начальному положению плюс проекция перемещения. В зависимости от того, в какую сторону тело переместилось, проекция перемещения будет положительной или отрицательной в данной системе координат.
Перемещение и ось координат находятся под углом друг к другу
Рассмотрим случай, когда перемещение и ось координат направлены под углом друг к другу. Теперь одной оси координат нам недостаточно, нужна вторая ось (см. рис. 19).
Рис. 19. Ось направлена в другую сторону
Теперь перемещение будет иметь ненулевую проекцию на каждую ось координат. Эти проекции перемещения будут определяться, как и раньше:
Заметьте, модуль каждой из проекций в этом случае меньше модуля перемещения. Модуль перемещения можем легко найти, используя теорему Пифагора. Видно, что если построить прямоугольный треугольник (см. рис. 20), то его катеты будут равны и
, а гипотенуза равна модулю перемещения
или, как часто записывают, просто
.
Рис. 20. Треугольник Пифагора
Тогда по теореме Пифагора запишем:
Задача
Автомобиль находится в 4 км к востоку от гаража. Воспользуйтесь одной осью координат, направленной на восток, с началом отсчета в гараже. Укажите координату автомобиля в заданной системе через 3 минуты, если автомобиль этим временем ехал со скоростью 0,5 км/мин на запад.
В задаче ничего не сказано о том, что автомобиль поворачивал или изменял скорость, поэтому считаем движение равномерным прямолинейным.
Изобразим систему координат: начало координат у гаража, ось х направлена на восток (см. рис. 21).
Рис. 21. Направление оси Ох
Автомобиль изначально был в точке и двигался по условию задачи на запад (см. рис. 22).
Рис. 22. Движение автомобиля на запад
Проекция перемещения, как мы неоднократно писали, равна:
Мы знаем, что автомобиль проезжал по 0,5 км каждую минуту, значит, чтобы найти суммарное перемещение, нужно скорость умножить на количество минут
:
На этом физика закончилась, осталось математически выразить искомую координату. Выразим ее из первого уравнения:
Подставим перемещение:
Осталось подставить числа и получить ответ. Не забывайте, что автомобиль двигался на запад против направления оси х, это значит, что проекция скорости отрицательна: .
Задача решена.
Итоги
Главное, чем мы сегодня пользовались для определения координаты, – выражение для проекции перемещения:
И из него мы уже выражали координату:
При этом сама проекция перемещения может быть задана, может вычисляться как , как в было в задаче о равномерном прямолинейном движении, может вычисляться сложнее, что нам еще предстоит изучить, но в любом случае координату движущегося тела (где тело оказалось) можно определить по начальной координате (где тело было) и по проекции перемещения (куда переместилось).
На этом наш урок окончен, до свидания!
Список литературы
- Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. – 2-е издание, передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Перышкин А.В., Гутник Е.М. Физика: 9 класс. Учебник для общеобразовательных учреждений. – 14-е изд. – М.: Дрофа, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «Class-fizika.narod.ru» (Источник)
- Интернет-портал «Av-physics.narod.ru» (Источник)
- Интернет-портал «Class-fizika.narod.ru» (Источник)
Домашнее задание
- Что такое перемещение, путь, траектория?
- Как можно определить координаты тела?
- Запишите формулу для определения проекции перемещения.
- Как будет определяться модуль перемещения, если перемещение имеет проекции на две оси координат?
I. Механика
Тестирование онлайн
Положение предметов в пространстве. Тело отсчета.
Предлагаю игру: выбрать предмет в комнате и описать его местонахождение. Выполнить это так, чтобы угадывающий не смог ошибиться. Вышло? А что выйдет из описания, если другие тела не использовать? Останутся выражения: “слева от…”, “над …” и подобное. Положение тела можно задать только относительно какого-нибудь другого тела.
Местонахождение клада: “Стань у восточного угла крайнего дома села лицом на север и, пройдя 120 шагов, повернись лицом на восток и пройди 200 шагов. В этом месте вырой яму в 10 локтей и найдешь 100 слитков золота”. Клад найти невозможно, иначе его давно откопали бы. Почему? Тело, относительно которого совершается описание не определено, неизвестно в каком селе находится тот самый дом. Необходимо точно определиться с телом, которое возьмется за основу нашего будущего описания. Такое тело в физике называется телом отсчета. Его можно выбрать произвольно. Например, попробуйте выбрать два различных тела отсчета и относительно их описать местонахождение компьютера в комнате. Выйдет два непохожих друг на друга описания.
Система координат
Рассмотрим картинку. Где находится дерево, относительно велосипедиста I, велосипедиста II и нас, смотрящих на монитор?
Относительно тела отсчета – велосипедист I – дерево находится справа, относительно тела отсчета – велосипедист II – дерево находится слева, относительно нас оно впереди. Одно и то же тело – дерево, находящееся постоянно в одном и том же месте, одновременно и “слева”, и “справа” и “впереди”. Проблема не только в том, что выбраны различные тела отсчета. Рассмотрим его расположение относительно велосипедиста I.
На этом рисунке дерево справа от велосипедиста I
На этом рисунке дерево слева от велосипедиста I
Дерево и велосипедист не меняли своего месторасположения в пространстве, однако дерево одновременно может быть “слева” и “справа”. Для того, чтобы избавиться от неоднозначности описания самого направления, выберем определенное направление за положительное, противоположное выбранному будет отрицательным. Выбранное направление обозначают осью со стрелкой, стрелка указывает положительное направление. В нашем примере выберем и обозначим два направления. Слева направо (ось, по которой движется велосипедист), и от нас внутрь монитора к дереву – это второе положительное направление. Если первое, выбранное нами направление, обозначить за X, второе – за Y, получим двухмерную систему координат.
Относительно нас велосипедист движется в отрицательном направлении по оси X, дерево находится в положительном направлении по оси Y
Относительно нас велосипедист движется в положительном направлении по оси X, дерево находится в положительном направлении по оси Y
А теперь определите, какой предмет в комнате находится в 2 метрах в положительном направлении по оси X (справа от вас), и в 3 метрах в отрицательном направлении по оси Y (позади вас). (2;-3) – координаты этого тела. Первой цифрой “2” принято обозначать расположение по оси X, вторая цифра “-3” указывает расположение по оси Y. Она отрицательная, потому что по оси Y находится не в стороне дерева, а в противоположной стороне. После того, как выбрано тело отсчета и направления, месторасположение любого предмета будет описано однозначно. Если вы повернетесь спиной к монитору, справа и позади вас будет уже другой предмет, но и координаты у него будут другие (-2;3). Таким образом, координаты точно и однозначно определяют расположение предмета.
Пространство, в котором мы живем, – пространство трех измерений, как говорят, трехмерное пространство. Кроме того, что тело может находится “справа” (“слева”), “впереди” (“позади”), оно может быть еще “выше” или “ниже” вас. Это третье направление – принято обозначать его осью Z
Можно ли выбирать не такие направления осей? Можно. Но нельзя менять их направления в течение решения, например, одной задачи. Можно ли выбрать другие названия осей? Можно, но вы рискуете тем, что вас не поймут другие, лучше так не поступать. Можно ли поменять местами ось X с осью Y? Можно, но не путайтесь в координатах: (x;y).
При прямолинейном движении тела для определения его положения достаточно одной координатной оси.
Для описания движения на плоскости используется прямоугольная система координат, состоящая из двух взаимно перпендикулярных осей (декартовая система координат).
С помощью трехмерной системы координат можно определить положение тела в пространстве.
Подробнее о системе координат и проекциях
Система отсчета
Каждое тело в любой момент времени занимает определенное положение в пространстве относительно других тел. Определять его положение уже умеем. Если с течением времени положение тела не изменяется, то оно покоится. Если же с течением времени положение тела изменяется, то это означает, что тело движется. Все в мире происходит где-то и когда-то: в пространстве (где?) и во времени (когда?). Если к телу отсчета, системе координат, которые определяют положение тела, добавить способ измерения времени – часы, получим систему отсчета. При помощи которой можно оценить движется или покоится тело.
Относительность движения
Космонавт вышел в открытый космос. В состоянии покоя или движения он находится? Если рассматривать его относительно друга космонавта, находящегося рядом, он будет покоиться. А если относительно наблюдателя на Земле, космонавт движется с огромной скоростью. Аналогично с поездкой в поезде. Относительно людей в поезде вы неподвижно сидите и читаете книгу. Но относительно людей, которые остались дома, вы двигаетесь со скоростью поезда.
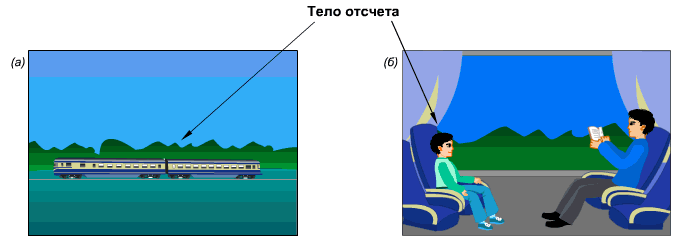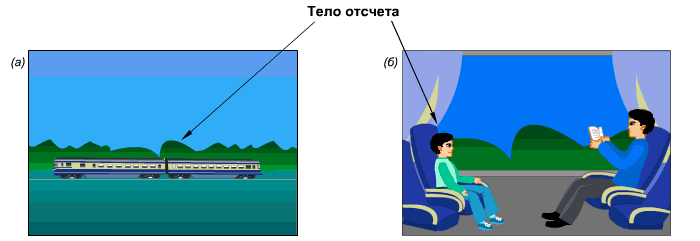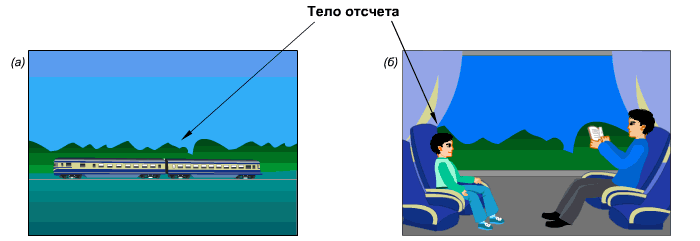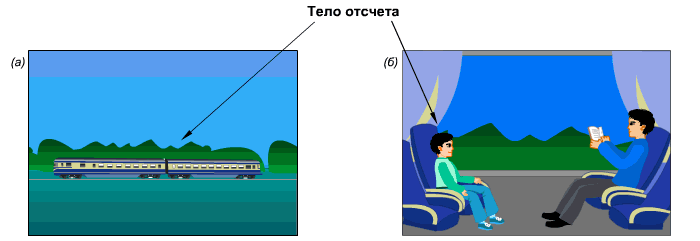
Примеры выбора тела отсчета, относительно которого на рисунке а) поезд движется (относительно деревьев), на рисунке б) поезд покоится относительно мальчика.
Сидя в вагоне, ожидаем отправления. В окне наблюдаем за электричкой на параллельном пути. Когда она начинает двигаться, трудно определить кто движется – наш вагон или электричка за окном. Для того, чтобы определиться, необходимо оценить движемся ли мы относительно других неподвижных предметов за окном. Мы оцениваем состояние нашего вагона относительно различных систем отсчета.
Изменение перемещения и скорости в разных системах отсчета
Перемещение и скорость изменяются при переходе из одной системы отсчета в другую.
Скорость человека относительно земли (неподвижной системы отсчета) различная в первом и втором случаях.
Правило сложения скоростей: Скорость тела относительно неподвижной системы отсчета – это векторная сумма скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной.
Аналогично вектора перемещения. Правило сложения перемещений: Перемещение тела относительно неподвижной системы отсчета – это векторная сумма перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной.
Пусть человек идет по вагону по направлению (или против) движения поезда. Человек – тело. Земля – неподвижная система отсчета. Вагон – подвижная система отсчета.
|
Вектора подвижной со и тела относительно подвижной со совпадают по направлению |
Вектора подвижной со и тела относительно подвижной со противоположные по направлению |
Изменение траектории в разных системах отсчета
Траектория движения тела относительна. Например, рассмотрим пропеллер вертолета, спускающегося на Землю. Точка на пропеллере описывает окружность в системе отсчета, связанного с вертолетом. Траектория движения этой точки в системе отсчета, связанной с Землей, представляет собой винтовую линию.
Поступательное движение
Движение тела – это изменение его положения в пространстве относительно других тел с течением времени. Каждое тело имеет определенные размеры, иногда разные точки тела находятся в разных местах пространства. Как же определить положение всех точек тела?
НО! Иногда нет необходимости указывать положение каждой точки тела. Рассмотрим подобные случаи. Например, это не нужно делать, когда все точки тела движутся одинаково.
Одинаково движутся все токи чемодана, машины.
Движение тела, при котором все его точки движутся одинаково, называется поступательным
Материальная точка
Не нужно описывать движение каждой точки тела и тогда, когда его размеры очень малы по сравнению с расстоянием, которое оно проходит. Например, корабль, преодолевающий океан. Астрономы при описании движения планет и небесных тел друг относительно друга не учитывают их размеров и их собственное движение. Несмотря на то, что, например, Земля громадная, относительно расстояния до Солнца она ничтожно мала.
Нет необходимости рассматривать движение каждой точки тела, когда они не влияют на движение тела всего целиком. Такое тело можно представлять точкой. Все вещество тела как бы сосредотачиваем в точку. Получаем модель тела, без размеров, но она имеет массу. Это и есть материальная точка.
Одно и то же тело при одних его движениях можно считать материальной точкой, при других – нельзя. Например, когда мальчик идет из дома в школу и при этом проходит расстояние 1 км, то в этом движении его можно считать материальной точкой. Но когда тот же мальчик выполняет зарядку, то точкой его считать уже нельзя.
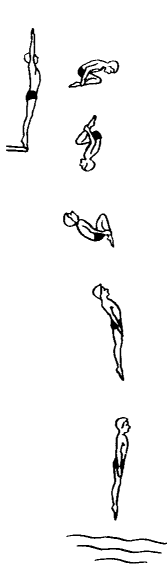
Рассмотрим движущихся спортсменов
В этом случае можно спортсмена моделировать материальной точкой
В случае прыжка спортсмена в воду (рисунок справа) нельзя моделировать его в точку, так как от любого положения рук и ног зависит движение всего тела
Главное запомнить
1) Положение тела в пространстве определяется относительно тела отсчета;
2) Необходимо задать оси (их направления), т.е. систему координат, которая определяет координаты тела;
3) Движение тела определяется относительно системы отсчета;
4) В разных системах отсчета скорость тела может быть разной;
5) Что такое материальная точка
Видеодемонстрация относительности движения
Сложение скоростей
Упражнения
Мимо стоящего велосипедиста проезжает колонна движущихся с одинаковой скоростью машин. Движется ли каждая из машин относительно велосипедиста? Движется ли машина относительно другой машин? Движется ли велосипедист относительно машины?
Из центра горизонтально расположенного вращающегося диска по его поверхности пущен шарик. Каковы траектории шарика относительно Земли и диска?
Чему равно перемещение какой-либо точки, находящейся на краю диска радиусом R при его повороте относительно подставки на 600? на 1800? Решить в системах отсчета, связанных с подставкой и диском.
Почему дождевые капли в безветренную погоду оставляют наклонные прямые полосы на стеклах равномерно движущегося поезда?
Каким образом можно определить скорость бега, если тренироваться на беговой дорожке со сломанным автоматическим определением скорости? Ведь относительно стен зала не пробегаешь ни одного метра.
Эскалатор метро движется вверх со скоростью 0,75 м/с. а) С какой скоростью и в каком направлении надо идти по эскалатору, чтобы быть все время на уровне одного из фонарей освещения туннеля? б) С какой скоростью относительно поднимающейся лестницы надо было бы передвигаться, чтобы опускаться вниз со скоростью пассажиров, неподвижно стоящих на другой опускающейся лестнице?
Какую систему координат следует выбрать (одномерную, двухмерную, трехмерную) для определения положения таких тел:
1. трактор в поле;
2. поезд;
3. люстра в комнате;
4. лифт;
5. подводная лодка;
6. шахматная фигура
На
прошлом уроке мы с вами говорили о пути и перемещении тела. Давайте вспомним,
что путь — это скалярная величина, равная длине траектории, которую
описывает тело за некоторый промежуток времени.
А
перемещением называется направленный отрезок прямой, соединяющий
начальное и конечное положения тела.
Так
как перемещение — это векторная величина, то есть имеет модуль и направление,
то складывать и вычитать перемещения необходимо по правилам сложения и
вычитания векторов. Однако при решении большинства задач, используется понятие
не вектора, а проекции вектора на ось координат.
—
А что такое проекция вектора и каковы её свойства?
На
это вопрос мы с вами и попытаемся сегодня ответить. Начнём с простого — с
понятия проекция точки на ось. Проекция точки — это основание
перпендикуляра, опущенного из данной точки на ось.
На
представленном рисунке точка А1 — это проекция точки А
на ось Ox,
а точка B1 —
проекция точки B
на
ось Oy.
Теперь
разберёмся с проекцией вектора на ось. Согласно определению, проекция
вектора на ось — это длина отрезка между проекциями начала и конца вектора на
эту ось, взятая со знаком «плюс» или «минус».
Знак
«плюс» берут, если угол между вектором и осью острый, а «минус» — если угол
тупой.
Обозначать
проекцию вектора будем той же буквой, что и вектор, но с индексом внизу
(например, ax
— это проекция вектора a
на ось Ox).
—
А если вектор перпендикулярен оси?
Тогда
проекция этого вектора равна нулю.
Проекцию
вектора можно выразить через его модуль и угол между вектором и осью. Итак,
пусть у нас есть вектор a
направленный под некоторым острым углом к координатной оси Ox. Укажем проекцию этого вектора на
ось.
У
нас с вами получился прямоугольный треугольник, гипотенуза которого равна длине
вектора a,
а катет AB1
— это проекция вектора a
на
ось Ox.
Тогда,
на основании определения косинуса острого угла, мы можем записать, что проекция
вектора на ось равна модулю вектора, умноженному на косинус угла между вектором
и осью:
Это
правило справедливо при любых значениях угла φ. Например,
для углов, больше 90о, косинус угла φ отрицательный. Тогда по
формуле получается, что проекция вектора на ось также отрицательна, как и
должно быть по определению проекции.
—
А можно ли найти модуль и направление вектора по его проекциям на координатные
оси?
Чтобы
ответить на этот вопрос рассмотрим вектор, лежащий в плоскости xOy.
Вектор, лежащий в заданной плоскости, определяется двумя проекциями на оси
координат.
Обратим
внимание на важное свойство проекций: проекция суммы векторов на ось равна
сумме их проекций на эту ось.
Но
вернёмся к нашему прошлому уроку. На нём мы с вами говорили о том, что
положение тела, которое совершило некоторое перемещение, можно найти
графически. Для этого достаточно отложить вектор перемещения от начального
положения этого тела. Однако в большинстве случаев необходимо уметь вычислять
положение тела, то есть уметь определять его координаты. Давайте на примере
решения задачи посмотрим, как можно определить координату движущегося тела,
зная координату его начального положения и вектор перемещения.
Итак,
два поезда идут по параллельным путям в противоположных направлениях и
встречаются в шестидесяти километрах к востоку от железнодорожного вокзала.
Продолжив движение через некоторое время t первый поезд удалился от места
встречи на 50 километров в восточном направлении, а второй — на 80 километров в
западном. Определите координаты каждого поезда относительно вокзала и
расстояние между ними через промежуток времени t.