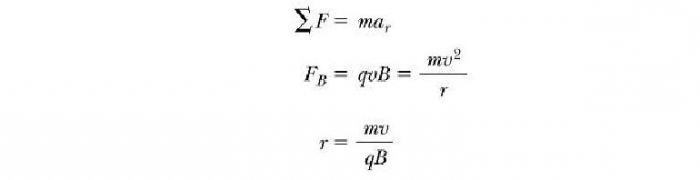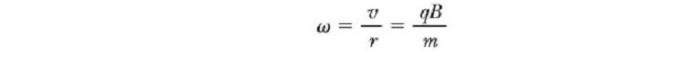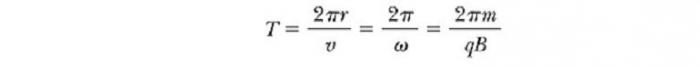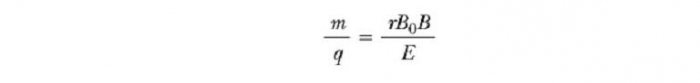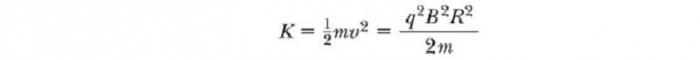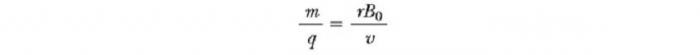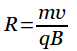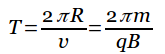Как найти положительно заряженную частицу

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

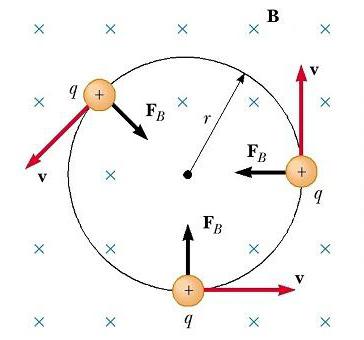
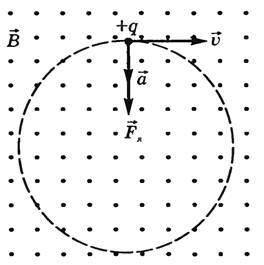
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Движение частицы под углом к вектору магнитного поля

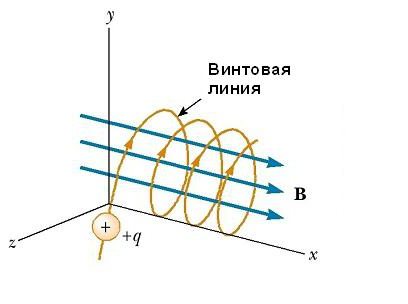
Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у² + ν_z²).

Неоднородное магнитное поле: как в нем движутся частицы

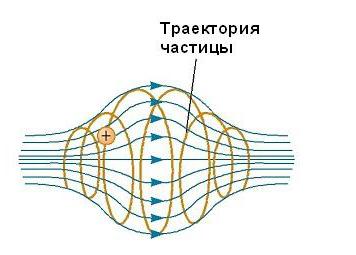
Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

Заряженная частица стартует с одного конца винтовой линии, накрученной вдоль силовых линий, и движется вдоль нее, пока не достигнет другого конца, где она поворачивает свой ​​путь обратно. Эта конфигурация известна как “магнитная бутылка”, поскольку заряженные частицы могут быть захвачены в нее. Она была использована, чтобы ограничить плазму, газ, состоящий из ионов и электронов. Такая схема плазменного заключения может выполнять ключевую роль в контроле ядерного синтеза, процессе, который представит нам почти бесконечный источник энергии. К сожалению, “магнитная бутылка” имеет свои проблемы. Если в ловушке большое число частиц, столкновения между ними вызывают утечку их из системы.

Как Земля влияет на движение космических частиц

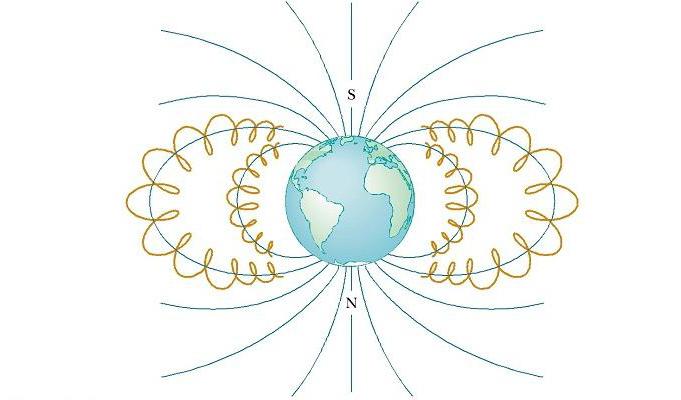
Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

Селектор скоростей

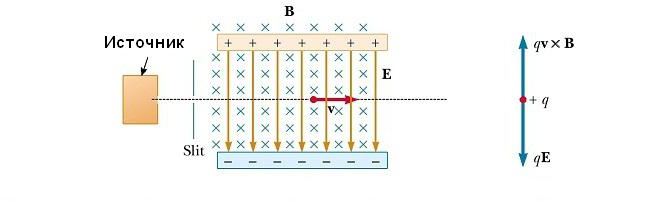
Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Для положительного q магнитная сила F_B=qv х В направлена вверх, а электрическая сила qE – вниз. Когда величины двух полей выбраны так, что qE = qvB, то частица движется по прямой горизонтальной линии через область поля. Из выражения qE = qvB мы находим, что только частицы, имеющие скорость v=E/B, проходят без отклонения через взаимно перпендикулярные электрическое и магнитное поля. Сила F_B, действующая на частицы, движущиеся со скоростью большей, чем v=E/B, оказывается больше электрической, и они отклоняются вверх. Те же из них, которые движутся с меньшей скоростью, отклоняются вниз.

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

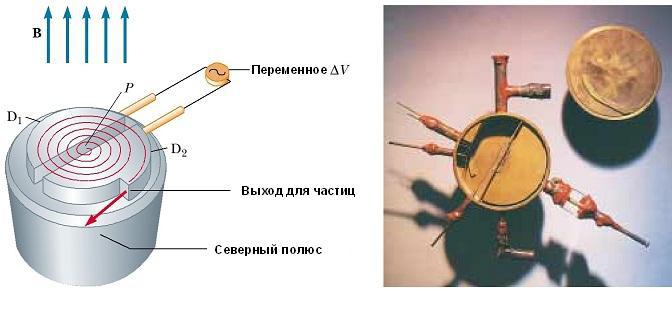
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т – время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один “удар” через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы – ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

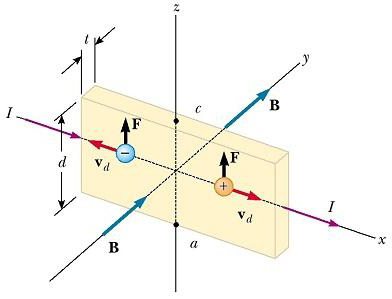
Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Однородное поле B приложено в направлении у. Если носителями заряда являются электроны, движущиеся вдоль оси х со скоростью дрейфа v_d, то они испытывают направленную вверх (с учетом отрицательного q) магнитную силу F_B = qv_d х B, отклоняются вверх и накапливаются на верхнем краю плоского проводника, в результате чего появляется избыток положительного заряда на нижнем краю. Это накопление заряда на краях увеличивается до тех пор, пока электрическая сила, появившаяся в результате разделения зарядов, не уравновешивает магнитную силу, действующую на носители. Когда это равновесие будет достигнуто, электроны больше не отклоняются вверх. Чувствительный вольтметр или потенциометр, подключенный к верхней и нижней граням проводника, может измерить разность потенциалов, известную как ЭДС Холла.

Как найти заряд частицы по окружности

Заряженная частица движется в магнитном поле по окружности со скоростью v = 10 6 м/с. Индукция магнитного поля B = 0,3 Тл. Радиус окружности R = 4 см. Найти заряд q частицы, если известно, что ее энергия W = 12 кэВ

Дано:

W = 12 кэВ = 1,92·10 -15 Дж

Решение:

На частицу, движущуюся в магнитном поле действует сила Лоренца

которая является центростремительной

Ответ:

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Движение частицы под углом к вектору магнитного поля

Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

Неоднородное магнитное поле: как в нем движутся частицы

Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

Как Земля влияет на движение космических частиц

Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

Селектор скоростей

Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

и затем, используя уравнение v=E/B, мы находим, что

Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т – время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один “удар” через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы – ν = qBR /m. Следовательно, ее кинетическая энергия

Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

Особенности формулы заряда q

Время на чтение:

Электрический заряд – это основа работы любого электронного прибора и та величина, без которой невозможно посчитать ни один важный показатель в электродинамике и электростатике. Подробная расшифровка термина, описание формулы нахождения электрического заряда и образец решения типовой задачи приведены в данной статье.

Что такое электрический заряд q

Электрический заряд, обозначаемый в международной системе единиц буквами q и Q, считается скалярной физической величиной, которая определяет свойство частицы или тела выступать в качестве источника электромагнитного поля и вступать в прямое взаимодействие с ним. В физике существует несколько видов электромагнитных заряженных частиц, и они называются положительными или отрицательными. Обе единицы измеряются в Кулонах, а найти их можно путём вычисления произведения одного Ампера с одной секундой.

Понятие из учебного пособия

Формула нахождения заряда

Определить искомую величину можно из физико-математической формулы силы тока. В соответствии с ней, нужно перемножить силу тока на время его прохождения по проводнику. Количество заряда можно узнать через формулу +-ne, где n служит целым числом, а е равно значению = -1,6*10^-19 Кулон.

Обратите внимание! Формула заряда является следствием прямой зависимости напряженности электромагнитного поля от потенциала его частицы, что является основным правилом нахождения емкости заряженного конденсатора и величины энергии, накопленной в нём. Кроме того, вычислить количество заряда можно через силу Лоренца.

Как вычислять с помощью законов

Поскольку q и Q являются скалярными единицами, вычислить их с помощью законов можно через точные формулы, выведенные известными учеными-физиками. К примеру, в соответствии с законом Кулона, можно найти величину и силовое направление взаимодействия заряженных частиц между несколькими неподвижными телами.

Закон сохранения

Все элементарные частицы подразделяются на нейтральные или заряженные. Они вступают во взаимодействие друг с другом внутри электромагнитного поля. Частицы, которые имеют одноименный электрон, отталкиваются, а разноименный – притягиваются. В первом случае наблюдается избыток электронов, а во втором – их недостаток. Оба типа частиц заряжаются посредством электризации. На практике, при возникновении данного явления, заряженные частицы равны по модулю, несмотря на противоположность знаков. Когда разные частицы притягиваются, то между ними происходит электризация и сохранение электрона. При этом, сумма всех изолированных системных частиц не изменяется, то есть, q + q + q…= const.

Закон сохранения

Закон Кулона

Выше было сказано, что электрические заряженные микрочастицы бывают как положительными, так и отрицательными, а их наличие подтверждается силовым взаимодействием, которое с помощью экспериментов на весах описал в 1785 году О. Кулон, создав свой физико-математический закон.

Закон Кулона представляет собой физическую закономерность, которая описывает взаимодействие наэлектризованных частиц между не электризованными, в зависимости от промежутка между ними. В соответствии с этой формулировкой, чем больше электронов имеет частица, тем ближе она расположена к другой элементарной единице заряда, и, соответственно, сила возрастает.

Обратите внимание! При увеличении расстояния между частицами, сал их взаимодействия неизменно убывает. В математической формуле это выглядит так: F1 = F2 = K*(q1*q2/r2), где q1 и q2 считаются модулями заряженных микрочастиц, k является коэффициентом пропорциональности, который зависит от системного выбора единицы, а r — расстоянием.

Образец решения задач по теме «Электрический заряд»

Ниже приведены образцы решения простых задач по электростатике, в частности, на закон Кулона.

Задача 1. Несколько одинаковых заряженных шаров имеют показатели q1 = 6 микрокулон и q2 = -18 микрокулон. Они располагаются друг от друга на 36 сантиметров (0,36 метров). Насколько будет меняться сила их взаимодействия при соприкосновении друг с другом и разведении в сторону?

Чтобы решить эту задачу, нужно воспользоваться эл заряд формулой F=K*(q1*q2/r2), подставив вместо букв известные величины. В результате, выйдет число 7,5.

Задача 2. Маленькие одинаковые шары находятся на промежутке в 0,15 метра и притягиваются с силой 1 микроньютон. Задача состоит в определении первоначальных зарядов шаров.

Чтобы решить вторую задачу, нужно использовать ту же формулу Кулона, но немного видоизмененную: F=kq2/r2. Затем вывести из правила показатель q2. Он будет равен Fr2/k. Подставив известные значения и выполнив несложные расчеты, получится цифры в 10^-7 или 10 микрокулон.

Формула для решения

В целом, электрический заряд представляет собой физическую скалярную величину, которая определяет способность тел являться источником электромагнитного поля и участвовать во взаимодействии с ним. Отыскать величину, которая обозначается буквами q и Q, для решения задач или для выполнения другой работы, можно через закон сохранения, Кулона и представленные выше основные физические формулы.

[spoiler title=”источники:”]

http://www.syl.ru/article/203046/new_dvijenie-zaryajennoy-chastitsyi-v-magnitnom-pole-formulyi-dvijenie-zaryajennyih-chastits-v-odnorodnom-magnitnom-pole

http://rusenergetics.ru/polezno-znat/formula-zaryada

[/spoiler]

1. Движение вдоль линий напряженности

Рассмотрим сначала случай, когда действующей на тело силой тяжести можно пренебречь по сравнению с силой, которая действует на тело со стороны электрического поля. Это всегда имеет место, когда речь идет о движении заряженных микрочастиц, например электронов. Напомним, кстати, что электрон имеет отрицательный заряд, а протон – положительный.

? 1. Объясните, почему при рассмотрении движения частицы в электрическом поле нельзя пренебрегать массой частицы даже в том случае, когда сила тяжести пренебрежимо мала по сравнению с силой, действующей на частицу со стороны электрического поля.

? 2. Заряженная частица движется в однородном электрическом поле. Что можно сказать о начальной скорости этой частицы, если траектория ее движения – прямолинейная?

Рассмотрим, как при таком движении изменяется кинетическая и потенциальная энергия частицы.

? 3. Электрон движется прямолинейно в однородном электрическом поле из точки с потенциалом 700 В в точку с потенциалом 200 В.
а) Совпадает ли направление начальной скорости электрона с направлением линий напряженности поля или эти направления противоположны?
б) Как изменилась полная энергия электрона?
в) Чему равно изменение потенциальной энергии электрона?
г) Чему равно изменение кинетической энергии электрона?
д) Какова минимальная начальная скорость электрона?

При движении в электрическом поле заряженная частица может изменить направление движения на противоположное.

? 4. Электрон влетает в однородное электрическое поле с начальной скоростью 8 * 10⁶ м/с. Потенциал поля в точке, в которую влетает электрон, равен 500 В. Направление начальной скорости электрона совпадает с направлением линий напряженности поля.
а) До точки с каким минимальным значением потенциала поля долетит электрон?
б) С какой по модулю скоростью электрон вернется в начальную точку?
в) Чему равна напряженность поля, если электрон вернулся в начальную точку через 9,1 * 10^-9 с?
г) Чему равен путь, пройденный электроном до его возвращения в начальную точку?

Сравним движение в одном и том же поле двух частиц с одинаковыми по модулю зарядами, но с различными массами.

? 5. Электрон и протон находятся на одной линии напряженности однородного электрического поля на расстоянии 1 см друг от друга. Они начинают двигаться из состояния покоя в противоположные стороны.
а) Чему равна напряженность поля, если через 10^-8 с расстояние между частицами стало равным 9,8 см?
б) На какое расстояние от своей начальной точки удалился к этому моменту протон?
в) Чему равны в этот момент скорости электрона и протона?

2. Движение заряженной частицы в конденсаторе

Если силой тяжести можно пренебречь по сравнению с силой, действующей на заряженную частицу со стороны электрического поля, то ее движение в поле конденсатора будет аналогично движению тела, брошенного горизонтально или под углом к горизонту, только роль силы тяжести будет играть сила, действующая на заряженную частицу со стороны электрического поля.

? 6. По какой траектории будет двигаться заряженная частица в однородном электрическом поле, если ее начальная скорость направлена под углом к линиям напряженности поля?

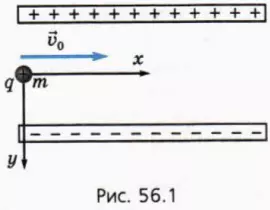
При рассмотрении тела, брошенного горизонтально или под углом к горизонту, мы использовали горизонтально направленную ось координат x и вертикально направленную ось y. В данном случае также удобно ввести оси координат x и y, как показано на рисунке 56.1.

Если начальная скорость частицы направлена горизонтально, направление оси y удобно выбрать так, чтобы проекция силы, действующей на эту частицу со стороны электрического поля конденсатора, была положительной. Начало координат совместим с начальным положением частицы.

? 7. Частица с зарядом q и массой m влетает в электрическое поле плоского конденсатора в точке, находящейся посередине между пластинами (рис. 56.1). Пластины конденсатора расположены горизонтально. Расстояние между пластинами равно d, длина пластин l, напряжение между пластинами U. Начальная скорость частицы равна по модулю v0 и направлена горизонтально.
а) Чему равны проекции ускорения частицы на оси координат при ее движении внутри конденсатора?
б) Как зависят от времени проекции скорости частицы?
в) Как зависят от времени координаты частицы?
г) Сколько времени частица будет лететь сквозь весь конденсатор, если не столкнется с его пластиной?
д) При каком соотношении между указанными выше параметрами частица пролетит сквозь весь конденсатор и вылетит из него?
е) Чему равен тангенс угла между скоростью частицы и горизонталью в тот момент, когда частица вылетает из конденсатора?
ж) Чему равен модуль скорости частицы, когда она вылетает из конденсатора?

? 8. Электрон влетает в конденсатор посередине между его пластинами со скоростью, направленной параллельно пластинам. Расстояние между пластинами равно 1 см, длина пластин 10 см. Начальная скорость электрона 5 * 10⁷ м/с.
а) Какова должна быть разность потенциалов между пластинами конденсатора, чтобы электрон не пролетел сквозь весь конденсатор?
б) На какую пластину в таком случае попадет электрон?
в) На каком расстоянии от положительной пластины будет находиться электрон в момент вылета из конденсатора, если напряжение между его пластинами равно 100 В?
г) Чему в этом случае будет равен тангенс угла между скоростью электрона и горизонталью в момент его вылета из конденсатора?
д) Как в этом случае изменится потенциальная энергия электрона за время его движения в конденсаторе?
е) На сколько процентов увеличится кинетическая энергия электрона за время движения в конденсаторе?

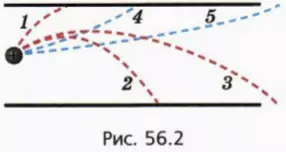
Рассмотрим случай, когда начальная скорость частицы направлена под углом к пластинам конденсатора.

Возможные типы траектории движения частицы схематически изображены на рисунке 56.2. Для определенности мы выбрали положительно заряженную частицу.

? 9. Каков знак заряда верхней пластины конденсатора, если положительно заряженная частица движется по одной из траекторий, изображенных красным пунктиром? синим пунктиром?

3. Движение заряженного тела в электрическом поле с учетом силы тяжести

Рассмотрим теперь случай, когда надо учитывать не только силу, действующую на тело со стороны электрического поля, но и силу тяжести.

? 10. Две большие пластины заряженного плоского конденсатора расположены вертикально (рис. 56.3). Разность потенциалов между пластинами равна U, а расстояние между ними равно d. Посередине между пластинами находится шарик с зарядом q и массой m. В начальный момент шарик покоится. Через некоторое время после того, как шарик отпустили, он столкнулся с одной из пластин конденсатора. Направим оси координат, как показано на рисунке.
56.3
а) Чему равна по модулю сила, действующая на шарик со стороны электрического поля?
б) Чему равна проекция ускорения шарика на ось х?
в) Через какой промежуток времени шарик столкнется с пластиной? Каков знак заряда этой пластины?
г) Насколько уменьшится высота шарика над землей к моменту столкновения по сравнению с его начальной высотой?
д) Какова форма траектории шарика?
е) Чему равно ускорение шарика во время движения?
ж) Чему равна скорость шарика в момент столкновения с пластиной?

Дополнительно вопросы и задания

11. Крупинка массой 10^-5 г влетает в электрическое поле горизонтально расположенного плоского конденсатора в точке, находящейся посередине между пластинами. Верхняя пластина конденсатора заряжена положительно. Начальная скорость крупинки направлена горизонтально. Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение между пластинами 1 кВ. Начальная скорость пылинки 6 м/с. Заряд крупинки равен по модулю 3 * 10^-12 Кл.
а) Чему равно отношение модулей силы тяжести и силы, действующей на крупинку со стороны электрического поля? При каком знаке заряда крупинки эти силы направлены одинаково?
б) Чему равно и как направлено ускорение крупинки, если у нее избыток электронов? недостаток электронов?
в) При каком знаке заряда крупинки она пролетит конденсатор насквозь?

12. Заряженная частица влетает в однородное электрическое поле с начальной скоростью, перпендикулярной линиям напряженности поля. В момент вылета из поля направление ее скорости составляет угол 60º с направлением начальной скорости. Во сколько раз увеличилась кинетическая энергия частицы при движении в электрическом поле? Считайте, что силой тяжести можно пренебречь.

Движение заряженных
частиц в магнитном поле.

На
заряженную частицу в электростатическом
поле действует кулоновская сила, которую
можно найти, зная напряженность поля в
данной точке:  .
Эта сила сообщает ускорение

  

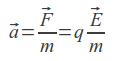
где
m — масса заряженной частицы. Как видно,
направление ускорения будет совпадать
с направлением  ,
если заряд частицы положителен (q > 0),
и будет противоположно  ,
если заряд отрицателен (q<0).

Если
электростатическое поле однородное
(  =
const), то ускорение  a= const и частица
будет совершать равноускоренное
движение (при
отсутствии других сил).

Вид
траектории частицы зависит от начальных
условий. Если вначале заряженная частица
покоилась  или
ее начальная скорость сонаправлена с
ускорением , то частица будет совершать
равноускоренное прямолинейное движение
вдоль поля и ее скорость будет расти.
Если  ,
то частица будет тормозиться в этом
поле.

Если
угол между начальной скоростью и
ускорением острый 0 < α < 90° (или тупой),
то заряженная
частица  будет
двигаться по параболе.  

Во
всех случаях при движении заряженной
частицы будет изменяться модуль скорости,
а следовательно, и кинетическая энергия
частицы.

1.  Заряженная
частица влетает в магнитное поле со
скоростью , направленной вдоль поля
 или противоположно  направлению
магнитной индукции поля  .

В
этих случаях сила Лоренца     и
частица будет продолжать двигаться
равномерно прямолинейно.

2.
Заряженная частица движется перпендикулярно
линиям магнитной индукции

тогда
сила Лоренца  ,
следовательно, и сообщаемое ускорение
будут постоянны по модулю и перпендикулярны
к скорости частицы.

В
результате частица
будет двигаться по окружности ,
радиус которой можно найти на основании
второго закона Ньютона:

  

Отношение
     —
называют удельным зарядом частицы.

  

Период
вращения частицы

то
есть период вращения не зависит от
скорости частицы и радиуса траектории.

3.
Скорость заряженной частицы направлена
под углом  к вектору.

  

Движение
частицы можно представить в виде
суперпозиции равномерного прямолинейного
движения вдоль поля со скоростью  и
движения по окружности с постоянной по
модулю скоростью  в плоскости,
перпендикулярной полю.

Радиус
окружности определяется аналогично
предыдущему случаю, только надо  заменить
 на  ,
то есть

В
результате сложения этих движений
возникает движение по винтовой линии,
ось которой параллельна магнитному
полю. Шаг винтовой линии

Направление,
в котором закручивается спираль, зависит
от знака заряда частицы.

Если
скорость заряженной частицы составляет
угол α с направлением вектора
   неоднородного
магнитного поля, индукция которого
возрастает в направлении движения
частицы, тο R и h уменьшаются с ростом B.
На этом основана фокусировка заряженных
частиц в магнитном поле.

Если
на движущуюся заряженную частицу помимо
магнитного поля с индукцией  действует
одновременно и электростатическое поле
с напряженностью , то равнодействующая
сила, приложенная к частице, равна
векторной сумме электрической силы и
силы Лоренца:  .
Характер движения и вид траектории
зависят в данном случае от соотношения
этих сил и от направления электростатического
и магнитного полей.

Соседние файлы в папке fizika

• #
• #
• #
• #
• #
• #
• #
• #
• #

III. Основы электродинамики

Тестирование онлайн

Электрический заряд

Нам приходится буквально отлеплять одну от другой свежевыстиранные и доставаемые из сушилки вещи, или когда мы никак не можем привести в порядок наэлектризованные и буквально встающие дыбом волосы. А кто не пробовал подвесить воздушный шарик к потолку, после трения его о голову? Подобное притяжение и отталкивание является проявлением статического электричества. Подобные действия называются электризацией.

Статическое электричество объясняется существованием в природе электрического заряда. Заряд является неотъемлемым свойством элементарных частиц. Заряд, который возникает на стекле при трении его о шелк, условно называют положительным, а заряд, возникающий на эбоните при трении о шерсть, – отрицательным.

Рассмотрим атом. Атом состоит из ядра и, летающих вокруг него, электронов (на рисунке синие частицы). Ядро состоит из протонов (красные) и нейтронов (черные).

.

Носителем отрицательного заряда является электрон, положительного – протон. Нейтрон – нейтральная частица, не имеет заряда.

Величина элементарного заряда – электрона или протона, имеет постоянное значение и равна

Весь атом нейтрально заряжен, если количество протонов соответствует электронам. Что произойдет, если один электрон оторвется и улетит? У атома станет на один протон больше, то есть положительных частиц больше, чем отрицательных. Такой атом называют положительным ионом. А если присоединится один электрон лишний – получим отрицательный ион. Электроны, оторвавшись, могут не присоединятся, а некоторое время свободно перемещаться, создавая отрицательный заряд. Таким образом, в веществе свободными носителями заряда являются электроны, положительные ионы и отрицательные ионы.

Для того, чтобы имелся свободный протон, необходимо, чтобы разрушилось ядро, а это означает разрушение атома целиком. Такие способы получения электрического заряды мы рассматривать не будем.

Тело становится заряженным, когда оно содержит избыток одних или иных заряженных частиц (электронов, положительных или отрицательных ионов).

Величина заряда тела кратна элементарному заряду. Например, если в теле 25 свободных электронов, а остальные атомы являются нейтральными, то тело заряжено отрицательно и его заряд составляет . Элементарный заряд не делим – это свойство называется дискретностью

Одноименные заряды (два положительных или два отрицательных) отталкиваются, разноименные (положительный и отрицательный) – притягиваются

Точечный заряд – это материальная точка, которая имеет электрический заряд.

Закон сохранения электрического заряда

Замкнутая система тел в электричестве – это такая система тел, когда между внешними телами нет обмена электрическими зарядами.

Алгебраическая сумма электрических зарядов тел или частиц остается постоянной при любых процессах, происходящих в электрически замкнутой системе.

На рисунке пример закона сохранения электрического заряда. На первой картинке два тела разноименного заряда. На втором рисунке те же тела после соприкосновения. На третьем рисунке в электрически замкнутую систему внесли третье нейтральное тело и тела привели во взаимодействие друг с другом.

В каждой ситуации алгебраическая сумма заряда (с учетом знака заряда) остается постоянной.

Главное запомнить

1) Элементарный электрический заряд – электрон и протон
2) Величина элементарного заряда постоянна
3) Положительный и отрицательный заряды и их взаимодействие
4) Носителями свободных зарядов являются электроны, положительные ионы и отрицательные ионы
5) Электрический заряд дискретен
6) Закон сохранения электрического заряда

Дополнительные источники*