Механическая работа – это одна из основных скалярных величин в физике. В рамках стандартной школьной программы она изучается в седьмом классе в разделе механики. Механическая работа – один из способов изменения внутренней энергии тела или субстанции (например, газа или жидкости) наряду с такими формами теплопередачи, как теплопроводность, конвекция и излучение, которые изучаются в разделе тепловых явлений.
Что такое работа в физике – определение и формула
Механическая работа – это количество энергии, которое нужно затратить для того, чтобы тело начало равномерно замедляющееся движение и прошло некоторую дистанцию.
В физике механической работой называется произведение силы, которая действует на некоторое тело, на расстояние, которое оно проходит под ее воздействием:
A = F * S
В более сложных случаях в формуле появляется и третья величина – косинус угла, под которым друг к другу расположены векторы движения и приложенной силы. Найти ее значение можно по формуле:
A = F * S * cosA
В чем измеряется работа
Физические единицы, в которых выражается механическая работа, – Джоули.
Существуют разные способы для ее практического измерения, которые зависят от типа произведенного движения. При этом в формулу работы подставляют значение силы в Ньютонах и расстояния в метрах. Угол между векторами измеряют в математических единицах – градусах.
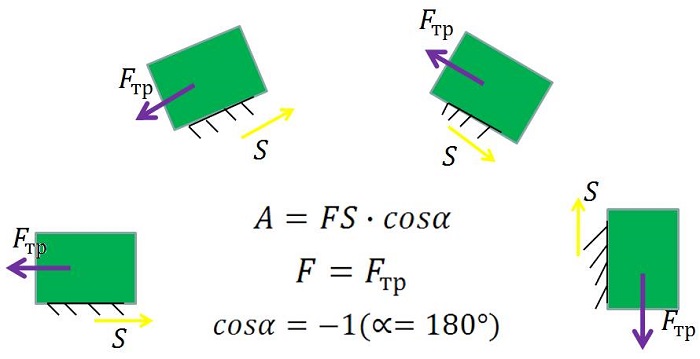
Работа силы трения
При условиях, существующих на Земле, на любое движущееся тело оказывает воздействие сила трения, замедляющая его движение. Чаще всего это трение поверхности, по которой движется объект. Это очевидно из того факта, что при воздействии постоянной силы на тело его скорость окажется переменной.
Следовательно, должна быть и другая сила, противодействующая ей – и это сила трения. Если система координат выбрана по направлению движения тела, то ее числовое значение будет отрицательным.
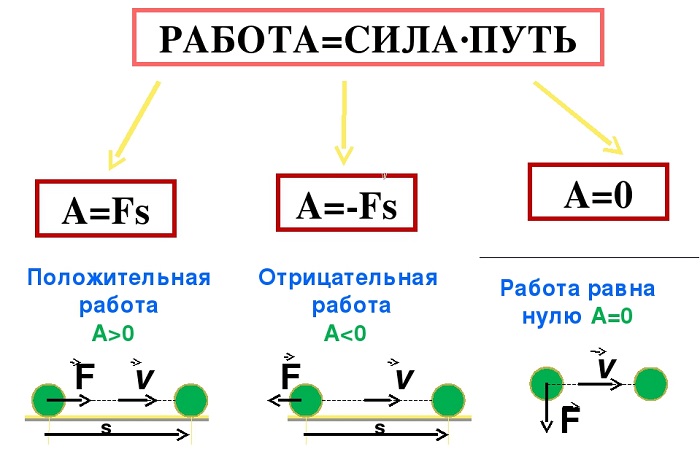
Положительная и отрицательная работа
Числовое значение работы, которую совершает сила, может становиться отрицательным в случае если ее вектор противоположен вектору скорости.
Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае она будет называться противодействующей.
Полезная или затраченная работа
У тела, совершающего одно и то же действие, есть два значения работы. Первая из них, полезная, вычисляется по обычной формуле.
Вторая, затраченная, по своему понятию не имеет общей формулы для вычисления и измеряется практически. Эта разница между совершенной в реальности работой и той, которая должна была быть совершена в теории, равна коэффициенту полезного действия – КПД. Он вычисляется так:
КПД = А полезная / А затраченная,
и выражается в процентах. КПД всегда меньше 100.
Мощность
Среднее количество работы, совершаемой за единицу времени (секунду), характеризует такую величину, как мощность. Формула для ее вычисления выглядит так:
Р = A / t
В качестве работы можно подставить люблю известную формулу для ее вычисления в зависимости от ситуации. Ответ будет выражен в Ваттах.
Однако при равномерном движении можно использовать и другую формулу:
Р = F * v
Подставив вместо обычной скорости мгновенную, можно получить значение мгновенной мощности.
Примеры решения задач
Рассмотрим несколько простых задач на нахождение механической работы.
Задача 1
Какую работу совершает подъемный механизм, поднимающий десятикилограммовый блок на высоту 50 метров.
Решение:
Для того, чтобы поднять тело, необходимо преодолеть действующую на него силу тяжести. То есть F, с которой поднимают блок, равна той, с которой он притягивается к земле. Так как последняя равна m * g, то для нахождения конечного результата понадобится только одна измененная версия стандартной формулы, упомянутой выше: A = S * m * g.
При помощи простой математики найдем числовой ответ:
A = 50 м * 10 кг * 10 Н/кг;
A = 5000 Дж.
Ответ: 5000 Дж.
Впрочем, не всегда речь идет о силе тяжести.
Задача 2
Какая работа совершается силой упругости, когда пружина с жесткостью 10 Н/м, сжатая на 20 см, возвращается в исходное состояние? Система замкнута, нет никаких внешних сил, воздействующих на пружину.
Решение:
Для начала нужно найти саму F упругости, которая совершает работу. Ее формула – F = x * |k|, где x – это длина, на которую сжимается или растягивается пружина, а k – коэффициент ее жесткости. Перемещение пружины равно ее деформации, и следовательно, конечная формула в этом случае будет выглядеть так: A = S * x * k = x * x * k = x^2 * k.
Далее при помощи элементарных вычислений рассчитаем ответ:
A = (0,2 м)^2 * 10 Н/м = 0,04 * 10 = 0,4 Дж.
Ответ: 0,4 Дж.
Но во всех задачах по данной теме траектория движения тела прямая.
Задача 3
Рассчитайте, какова сила, действующая на колесо, если на то, чтобы совершить полный оборот, ему требуется 10 кДж. Диаметр диска равен 40 см, а толщина шины – 10 см.
Решение:
В этом случае нам нужно найти не А, а F, но сделать это можно при помощи все той же формулы. Возьмем точку на поверхности колеса. Предположим, что при вращательном движении ее вектор будет противоположен вектору приложения силы, а значит косинусом в формуле вновь можно пренебречь. Таким образом, за один оборот колеса точка пройдет расстояние, равное длине окружности, которую можно вычислить как 2πr или πd. Диаметр окружности можно найти из предоставленных данных: он равен сумме диаметра диска и удвоенной толщины шины, то есть 40 см + 2 * 10 см = 40 см + 20 см = 60 см = 0,6 м.
Теперь, когда мы можем вычислить расстояние, у нас есть все данные для того, чтобы приступить к нахождению силы.
Формула работы для этого случая будет такой: A = F * π * d, то силу, соответственно, можно будет выразить как F = A / (π * d).
В таком случае:
F = 10 кДж / (3,14 * 0,6 м) = 10000 Дж / 1,884 м = ~ 5308 Н.
Ответ: 5308 Н.
В завершение решим самый сложный вариант задачи, включающий в себя все, о чем говорилось выше.
Задача 4
Автомобиль Фольксваген весом 2500 кг заезжает на гору. Какова должна быть его минимальная скорость, чтобы удержаться на горе, если сила тяги равна 10 кН, время работы двигателя – 10 с, КПД – 30%, а угол наклона горы – 60 градусов. Трением и прочими силами пренебречь.
Решение:
На первый взгляд задача может показаться сложной, но для ее решения используются только простые известные формулы.
Запишем условие в более наглядном виде.
Дано:
m = 2500 кг;
F = 10000 H;
t = 10 с;
КПД = 30%;
угол A = 1500 (60+90, т. к. сила тяжести приложена под углом 90 к горизонтали);
V – ?
Выведение формулы:
Шаг 1. По условию A1 (силы тяжести) = А2 (тяги).
A1 = mg;
A2 = P * t / КПД.
То есть mg = P * t / КПД.
Шаг 2. P = F * V * cosA.
Шаг 3. Общая формула: mg = F * V * cosA * t / КПД.
V = (m * g * КПД) / (F * t * cosA).
Числовое решение:
V = (2500 кг * 10 Н/кг * 30%) / (10000 H * 10 с * cos150);
V = (2500 кг * 10 Н/кг * 0,3) / (10000 H * 10 с * cos60);
V = 7500 / 50000;
V = 0,15 м/с.
Ответ: 0,15 м/с.
2010-03-24 22:30
Если сила, приложенная к телу, совершает положительную работу, то скорость тела увеличивается. Действительно, в этом случае сила, а значит, и ускорение, направлены по скорости, увеличивая ее. Если же сила совершает отрицательную работу, то ускорение направлено против скорости и скорость тела убывает.
Допустим, что мы бросили тело в вертикальном направлении. Пока тело летит вверх, сила тяжести совершает над телом отрицательную работу и скорость тела уменьшается до нуля. Достигнув верхней точки, тело начинает двигаться ускоренно вниз. Сила тяжести совершает при этом положительную работу.
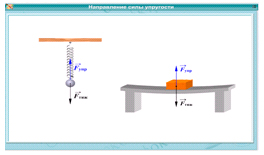
Если на движущееся тело действуют две противоположно направленные силы, то одна из них совершает положительную, а другая — отрицательную работу. Например, если на нерастянутую пружину подвесить груз (рис. 159) и дать ему возможность опускаться, то сила тяжести
, действующая на груз, будет совершать положительную работу, так как груз будет двигаться в направлении этой силы. В то же время сила
, с которой пружина действует на груз, будет совершать отрицательную работу.

Рис. 159. При опускании груза работа силы
положительна, а силы
отрицательна
Когда мы поднимаем некоторый груз, нам приходится преодолевать действие силы тяжести, притягивающей груз к Земле. В этом случае работа силы тяжести отрицательна. Положительна работа, которую мы затрачиваем на преодоление силы тяжести. Иногда эту работу называют работой, совершаемой против силы тяжести. Аналогично, в случае, когда на тело действуют две противоположно направленные силы
и
, то работа одной из них, скажем
будет положительна, а работа другой, т. е. силы
, будет отрицательна. Можно сказать, что работа силы
совершается против силы
. Подчеркнем, что в случае, когда работа некоторой силы
отрицательна, работа, совершаемая какой-то другой силой против силы
, будет положительна.
Сила, перемещающая тело, совершает работу. Работа – это разность энергии тела в начале процесса и в его конце. А мощность – это работа за одну секунду. Коэффициент полезного действия (КПД) – это дробное число. Максимальный КПД равен единице, однако, часто, КПД меньше единицы.
Работы силы, формула
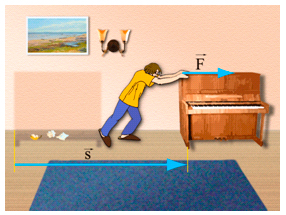
Сила, приложенная к телу и перемещающая его, совершает работу (рис. 1).
Рис. 1. Сила перемещает тело и совершает работу
Работа силы — это скалярное произведение вектора силы на вектор перемещения.
Работу, совершаемую силой, можно посчитать, используя векторный или скалярный вид записи такой формулы:
Векторный вид записи
[ large boxed{ A = left( vec{F} , vec{S} right) }]
Для решения задач правую часть этой формулы удобно записывать в скалярном виде:
[ large boxed{ A = left| vec{F} right| cdot left| vec{S} right| cdot cos(alpha) }]
( F left( H right) ) – сила, перемещающая тело;
( S left( text{м} right) ) – перемещение тела под действием силы;
( alpha ) – угол между вектором силы и вектором перемещения тела;
Работу обозначают символом (A) и измеряют в Джоулях. Работа – это скалярная величина.
В случае, когда сила постоянная, формула позволяет рассчитать работу, совершенную силой за полное время ее действия.
Если сила изменяется со временем, то в каждый конкретный момент времени будем получать мгновенную работу. Эти, мгновенные значения для разных моментов времени будут различаться.
Рассмотрим несколько случаев, следующих из формулы:
- Когда угол между силой и перемещением острый, работа силы положительная;
- А если угол тупой — работа отрицательная, так как косинус тупого угла отрицательный;
- Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
Работа — разность кинетической энергии
Работу можно рассчитать еще одним способом — измеряя кинетическую энергию тела в начале и в конце процесса движения. Рассмотрим такой пример. Пусть автомобиль, движется по горизонтальной прямой и, при этом увеличивает свою скорость (рис. 2). Масса автомобиля 1000 кг. В начале его скорость равнялась 1 м/с. После разгона скорость автомобиля равна 10 метрам в секунду. Найдем работу, которую пришлось проделать, чтобы ускорить этот автомобиль.
Рис. 2. Автомобиль движется прямолинейно и увеличивает свою скорость
Для этого посчитаем энергию движения автомобиля в начале и в конце разгона.
( E_{k1} left(text{Дж} right) ) – начальная кинетическая энергия машины;
( E_{k2} left(text{Дж} right) ) – конечная кинетическая энергия машины;
( m left( text{кг}right) ) – масса автомобиля;
( displaystyle v left( frac{text{м}}{c}right) ) – скорость, с которой машина движется.
Кинетическую энергию будем вычислять, используя формулу:
[ large E_{k} = m cdot frac{v^{2}}{2} ]
[ large E_{k1} = 1000 cdot frac{1^{2}}{2} = 500 left(text{Дж} right) ]
[ large E_{k2} = 1000 cdot frac{10^{2}}{2} = 50000 left(text{Дж} right) ]
Теперь найдем разницу кинетической энергии в конце и вначале разгона.
[ large boxed{ A = Delta E_{k} }]
[ large Delta E_{k} = E_{k2} — E_{k1} ]
[ large Delta E_{k} = 50000 – 500 = 49500 left(text{Дж} right) ]
Значит, работа, которую потребовалось совершить, чтобы разогнать машину массой 1000 кг от скорости 1 м/с до скорости 10 м/с, равняется 49500 Джоулям.
Примечание: Работа – это разность энергии в конце процесса и в его начале. Можно находить разность кинетической энергии, а можно — разность энергии потенциальной.
[ large boxed{ A = Delta E }]
Работа силы тяжести — разность потенциальной энергии
Рассмотрим теперь следующий пример. Яблоко массой 0,2 кг упало на садовый стол с ветки, находящейся на высоте 3 метра от поверхности земли. Столешница располагается на высоте 1 метр от поверхности (рис. 3). Найдем работу силы тяжести в этом процессе.
Рис. 3. На рисунке указано начальное 1 положение тела (яблока) и его конечное 2 положение, отмечены высоты для подсчета работы по вертикальному перемещению тела
Посчитаем потенциальную энергию яблока до его падения и энергию яблока на столешнице.
( E_{p1} left(text{Дж} right) ) – начальная потенциальная энергия яблока;
( E_{p2} left(text{Дж} right) ) – конечная потенциальная энергия яблока;
Примечание: Работу можно рассчитать через разность потенциальной энергии тела.
Потенциальную энергию будем вычислять, используя формулу:
[ large E_{p} = m cdot g cdot h]
( m left( text{кг}right) ) – масса яблока;
Величина ( displaystyle g approx 10 left(frac{text{м}}{c^{2}} right) ) – ускорение свободного падения.
( h left( text{м}right) ) – высота, на которой находится яблоко относительно поверхности земли.
Начальная высота яблока над поверхностью земли равна 3 метрам
[ large E_{p2} = 0,2 cdot 10 cdot 3 = 6 left(text{Дж} right) ]
Потенциальная энергия яблока на столе
[ large E_{p1} = 0,2 cdot 10 cdot 1 = 2 left(text{Дж} right) ]
Теперь найдем разницу потенциальной энергии яблока в конце падения и перед его началом.
[ large Delta E_{p} = E_{p2} — E_{p1} ]
[ large Delta E_{p} = 2 – 6 = — 4 left(text{Дж} right) ]
Важно помнить: Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
Чтобы работа получилась положительной, в правой части формулы перед ( Delta E_{p}) дополнительно допишем знак «минус».
[ large boxed{ A = — Delta E_{p} }]
Значит, работа, которую потребовалось совершить силе тяжести, чтобы яблоко массой 0,2 кг упало с высоты 3 м на высоту 1 метр, равняется 4 Джоулям.
Примечания:
- Если тело падает на землю, работа силы тяжести положительна;
- Когда мы поднимаем тело над землей, мы совершаем работу против силы тяжести. Наша работа при этом положительна, а работа силы тяжести будет отрицательной;
- Сила тяжести относится к консервативным силам. Для консервативных сил перед разностью потенциальной энергии мы дописываем знак «минус»;
- Работа силы тяжести не зависит от траектории, по которой двигалось тело;
- Работа для силы (displaystyle F_{text{тяж}}) зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени.
Рисунок 4 иллюстрирует факт, что для силы (displaystyle F_{text{тяж}}) работа зависит только от разности высот и не зависит от траектории, по которой тело двигалось.
Рис. 4. Разность высот между начальным и конечным положением тела во всех случаях на рисунке одинакова, поэтому, работа силы тяжести для представленных случаев будет одинаковой
Мощность
В механике мощность часто обозначают символами N или P и измеряют в Ваттах в честь шотландского изобретателя Джеймса Уатта.
Примечание: Символ (vec{N}) используется для обозначения силы реакции опоры — она измеряется в Ньютонах и является векторной величиной. Чтобы не возникло путаницы, мощность вместо N будем обозначать символом P. Символ P – первая буква в английском слове power – мощность.
Мощность – это работа, совершенная за одну секунду (энергия, затраченная за 1 сек).
Расчет работы осуществляем, используя любую из формул:
[ large A = Delta E_{k} ]
[ large A = Delta E_{p} ]
[ large A = F cdot S cdot cos(alpha) ]
Разделив эту работу на время, в течение которого она совершалась, получим мощность.
[ large boxed{ P = frac{A}{Delta t} }]
Если работа совершалась равными частями за одинаковые интервалы времени – мощность будет постоянной величиной.
Мощность переменная, когда в некоторые интервалы времени совершалось больше работы.
Еще одна формула для расчета мощности
Есть еще один способ расчета мощности, когда сила перемещает тело и при этом скорость тела не меняется:
[ large P = left( vec{F} , vec{v} right) ]
Формулу можно записать в скалярном виде:
[ large P = left| vec{F} right| cdot left| vec{v} right| cdot cos(alpha) ]
( F left( H right) ) – сила, перемещающая тело;
( displaystyle v left( frac{text{м}}{c} right) ) – скорость тела;
( alpha ) – угол между вектором силы и вектором скорости тела;
Когда векторы (vec{F}) и (vec{v}) параллельны, запись формулы упрощается:
[ large boxed{ P = F cdot v }]
Примечание: Такую формулу для расчета мощности можно получить из выражения для работы силы, разделив обе части этого выражения на время, в течение которого работа совершалась (а если точнее, найдя производную обеих частей уравнения).
КПД
КПД – коэффициент полезного действия. Обычно обозначают греческим символом (eta) «эта». Единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах.
Примечания:
- Процент – это дробь, у которой в знаменателе число 100.
- КПД — это либо правильная дробь, или дробь, равная единице.
Вычисляют коэффициент (eta) для какого-либо устройства, механизма или процесса.
[ large boxed{ eta = frac{ A_{text{полезная}}}{ A_{text{вся}}} }]
(eta) – КПД;
( large A_{text{полезная}} left(text{Дж} right)) – полезная работа;
(large A_{text{вся}} left(text{Дж} right)) – вся затраченная для выполнения работы энергия;
Примечание: КПД часто меньше единицы, так как всегда есть потери энергии. Коэффициент полезного действия не может быть больше единицы, так как это противоречит закону сохранения энергии.
[ large boxed{ eta leq 1 }]
Величина (eta) является дробной величиной. Если числитель и знаменатель дроби разделить на одно и то же число, полученная дробь будет равна исходной. Используя этот факт, можно вычислять КПД, используя мощности:
[ large boxed{ eta = frac{ P_{text{полезная}}}{ P_{text{вся затраченная}}} }]
Выводы
- Сила, приложенная к телу и перемещающая его, совершает работу;
- Когда угол между силой и перемещением острый, работа силы положительная, а если угол тупой — работа отрицательная; Если же угол прямой – работа равна нулю. Сила, перпендикулярная перемещению, работу не совершает!
- Работу можно вычислить, измеряя кинетическую энергию тела в начале и в конце его движения;
- Вычислить работу можно через разность потенциальной энергии тела в начальной и в конечной высотах над землей;
- Когда тело падает на землю, его потенциальная энергия уменьшается. Сила тяжести при этом совершает положительную работу!
- Мы совершаем работу против силы тяжести, когда поднимаем тело над землей. При этом наша работа положительная, а работа силы тяжести — отрицательная;
- Сила тяжести — это консервативная сила. Поэтому, работа силы (displaystyle F_{text{тяж}}) не зависит от траектории, по которой двигалось тело, а зависит только от разности высот, в которых тело находилось в конечный и начальный моменты времени;
- Мощность – это работа, совершенная за одну секунду, или затраченная за 1 сек. энергия;
- Коэффициент полезного действия обозначают греческим символом (eta) «эта», единиц измерения не имеет, выражается либо десятичной дробью, либо в процентах;
- КПД — это либо правильная дробь, или дробь, равная единице.
- Можно вычислять КПД, подставляя в формулу работу, или мощности
Конспект по физике для 7 класса «Механическая работа». ВЫ УЗНАЕТЕ: Что такое механическая работа. Как рассчитать механическую работу. Когда механическая работа положительна, когда отрицательна и когда равна нулю. ВСПОМНИТЕ: Что такое сила? Каковы единицы силы?
Конспекты по физике Учебник физики Тесты по физике
Механическая работа
В обыденной жизни словом «работа» мы называем различные действия человека или технического устройства. Например, мы говорим: работает учитель, работает врач, работает грузчик, работает холодильник, pa6oтaeт компьютер. Хотя мы прекрасно понимаем, что речь идёт о разных вещах, и не стремимся сравнить результаты работы грузчика с результатами работы компьютера.
Если обозначить величины: работа — А, сила, действующая на тело, — F и пройденный путь – s, то работу рассчитывают по формуле A = Fs, если направление силы совпадает с направлением движения тела. В старших классах вы узнаете, как вычислять работу силы, направлен ной под углом к направлению движения тела.
ПРИМЕРЫ МЕХАНИЧЕСКОЙ РАБОТЫ
В физике термин «работа» или «механическая работа» — это определённая физическая величина, которую можно измерить.
Автомобиль движется по автомагистрали благодаря силе тяги работающего двигателя. Мяч под действием силы тяжести падает на поверхность Земли. В этих примерах на тела действуют силы, изменяется их скорость и положение в пространстве — совершается механическая работа.
Во всех технических устройствах, от самых простых до крайне сложных, всегда действуют силы, которые совершают работу при движении механизма или отдельных его частей. Так, например, в старинных паровых машинах сила давления пара на поршень совершает работу при движении поршня. А в современных электрических двигателях силы взаимодействия электрических токов совершают работу при вращении мотора.
ОПРЕДЕЛЕНИЕ МЕХАНИЧЕСКОЙ РАБОТЫ
Считается, что механическая работа совершается, когда тело движется под действием силы. Таким образом, в физике понятие работы напрямую связано с силой (нет силы — нет работы). Поэтому принято говорить о работе некоторой силы.
Механической работой называют физическую величину, зависящую от численного значения и направления силы и от перемещения точки се приложения. Механическая работа совершается только тогда, когда на тело действует сила и тело перемещается под действием этой силы. Следовательно, механическая работа прямо пропорциональна приложенной силе и прямо пропорциональна пути.
Таким образом, в самом простом случае работа равна произведению силы, действующей на тело, на путь, пройденный телом под действием этой силы: работа = сила х путь.
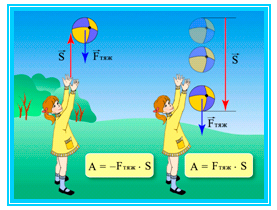
Если направление силы совпадает с направлением движения тела, то данная сила совершает положительную работу. Например, мы везём по снегу санки, и направление приложенной нами силы совпадает с направлением движения.
В этом случае сила совершает положительную работу, которую определяют по формуле А = Fs.
Если движение тела происходит в направлении, противоположном направлению приложенной силы, то данная сила совершает отрицательную работу. Отрицательная работа, например, совершается силой трения скольжения в случае, когда сапки, скатившись с горы, движутся по снегу вплоть до полной остановки. В данном случае работа будет определяться по формуле А = –Fs.
Если направление силы, действующей на тело, перпендикулярно направлению движения, то эта сила работы не совершает, работа равна нулю.
ЕДИНИЦА РАБОТЫ
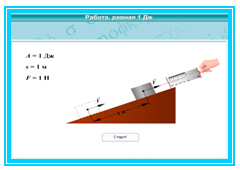
За единицу работы принимают работу, совершаемую силой в 1 Н, на пути, равном 1 м. Единица работы — джоуль (Дж) названа в честь английского ученого Джеймса Джоуля.
1 Дж = 1 Н•м.
Также часто используют килоджоули и миллиджоули: 1 кДж = 1000 Дж, 1 мДж = 0,001 Дж.
СИТУАЦИИ, В КОТОРЫХ МЕХАНИЧЕСКАЯ РАБОТА НЕ СОВЕРШАЕТСЯ
Мы уже знаем, что если сила действует перпендикулярно направлению движения тела, то работа этой силы равна нулю. А в каких ещё случаях работа может быть равна нулю? Очевидно, что в случае, когда равны нулю либо силы, действующие на тело, либо под действием сил тело не перемещается.
Например, после выключения двигателя ракета, летящая в открытом космосе, продолжает движение по инерции. В этом случае нет действующей на тело силы и механическая работа не совершается.
Если мы стараемся сдвинуть с места тяжёлый предмет, но сила, с которой мы на него действуем, меньше максимально возможной в этом случае силы трения покоя, то предмет останется на месте. Поэтому, несмотря на нашу усталость, механической работы не совершалось, так как не было перемещения тела.
Как бы ни было тяжело мифологическому герою Атланту, держащему на плечах небесный свод, механической работы при этом он не совершал, так как небесный свод в этом случае не двигался.
ДЛЯ СПРАВКИ:
Джеймс Прескотт Джоуль (1818–1889). Английский физик, член Лондонского королевского общества.
Вы смотрели Конспект по физике для 7 класса «Механическая работа»: Что такое механическая работа. Как рассчитать механическую работу. Когда механическая работа положительна, когда отрицательна и когда равна нулю.
Вернуться к Списку конспектов по физике (В оглавление).
Пройти онлайн-тест «»
Работа – это главное в жизни. От всех
неприятностей, от всех бед можно найти только
одно избавление – в работе.
Эрнест Хемингуэй
Оборудование: компьютер, проектор,
электронные учебные пособия “Физика 7 класс”.
УМК “Сферы”. Москва. Просвещение, 2009., Библиотека
наглядных пособий Физика 7-11 классы. ООО “Дрофа”,
2004 г.
1. Организационный момент. Целеполагание.
Учитель зачитывает высказывания великих людей
о работе (слайд 2).
Вопрос: Ребята, что вы понимаете под словом
работа?
Ответ: Процесс получения какого-либо
продукта.
Ответ: В обыденной жизни под словом “работа”
мы понимаем различные действия человека,
механизма.
А какая из физических величин необходима
человеку для совершения работы?
Ответ: Сила.
Итак, ребята, сегодня на уроке вы узнаете:
- Что такое механическая работа;
- Как рассчитать механическую работу;
- Когда механическая работа положительна, когда
отрицательна и когда равна нулю.
Сегодня на уроке вы вспомните:
- Что такое сила;
- От чего зависит результат действия силы;
- Какие силы бывают и как они направлены (слайд 3).
2. Актуализация знаний
Ребята, а какие силы были изучены нами в этом
учебном году?
Ответ: сила тяжести, сила упругости, вес
тела, сила трения. Давайте вспомним понятие
“силы” и виды сил, о которых мы узнали в 7 классе.
Вопрос: Что такое сила? От чего зависит
результат действия силы?
Ответ: Сила – векторная физическая величина
и результат её действия зависит от трёх
характеристик: направления, точки приложения,
модуля (слайд 4).
Рис. 1
Сила трения.
Одна из самых любимых детских сказок – сказка
“Репка”. Сегодня мы рассмотрим её с научной
точки зрения и увидим, что для того чтобы
объяснить некоторые события в сказках нужно
знать физику.
Ученик: Посадил дед репку. Выросла репка
большая-пребольшая, тяжёлая-претяжёлая,
разрослась она во все стороны, грунт потеснила.
Поэтому-то очень плотный контакт у её клубня с
почвой получился. Пошёл дед репку тянуть. Тянет –
потянет – вытянуть не может. Сила тяги деда
меньше той предельной силы, которая по
поверхности соприкосновения репы с землёй
возникает. Она называется…….!? (Cилой Трения
покоя).
Вопрос: Какая сила мешала дедушке
самостоятельно вытянуть репку?
Ответ: Сила трения покоя.
Вопрос: Какие ещё силы трения вам известны?
Когда они возникают? Куда направлены?
Ответ: Сила трения скольжения, сила трения
качения. Направлены в сторону противоположную
движению, против внешней силы (слайд 5).
Вопрос: Какая ещё сила действовала на всех
героев сказки “Репка”?
Ответ: Сила тяжести.
Сила тяжести
Ребята, давайте посмотрим фрагмент мультфильма
и ответим на вопросы к нему.
(Слайд 6: фрагмент из мультфильма Незнайка).
Вопрос: Может ли такое случиться в земных
условиях? Если нет, то почему?
Ответ: Нет, так как на земле существует сила
тяжести, которая действует на любой предмет и
притягивает его к Земле.
Вопрос: Куда направлена сила тяжести?
Ответ: Всегда к Земле.
Вопрос: Что предлагал найти Незнайка?
Ответ: Вес.
Вопрос: Что такое вес?
Ответ: Вес-это сила, которая вследствие
притяжения к Земле действует на опору или подвес
со стороны тела?
Вопрос: А в земных условиях человек не
может пребывать в невесомости?
Ответ: Может, при полёте вниз, но при этом на
него действует сила тяжести, он не будет парить, а
будет притягиваться к Земле (слайд 7).
Рис. 2
Вопрос: Почему капли дождя падают на Землю? (Слайд
8)
Рис. 3
Ответ: На них действует сила тяжести.
Сила упругости.
Посмотрим следующий фрагмент и ответим на вопрос:
какая сила возникает в этом случае? (Слайд 9:
фрагмент из мультфильма “Добрыня Никитич”)
Ответ: сила упругости, возникает при
деформациях тел, т.е. при изменении формы и объёма
тела.
Вопрос: Как направлена сила упругости?
Ответ: Всегда в сторону, противоположную
деформации.
Под действием силы тяжести многие тела падают
на землю. Но, всё же, действие силы тяжести не
всегда приводит к движению тела. Например, кирпич
лежит на опоре и не падает.
Почему?
Ответ: На кирпич со стороны опоры действует
сила упругости, которая равна по модулю силе
тяжести, направлена в противоположную сторону и
уравновешивает её (слайд 10).
Рис. 4
Вывод: Одновременно на одно и то же тело
может действовать несколько сил (слайд 11).
Рис.5
Работа с опорным конспектом (ОК) (слайд 12)
Один учащийся располагает силы на доске,
остальные в рабочих тетрадях.
Рис. 6
3. Изучение нового материала.
3.1.Объяснение нового материала.
Мы вспомнили все силы неслучайно. Тема нашего
урока “Механическая работа”. Как мы выяснили в
начале урока, без силы никакая работа
совершаться не может.
Под работой человек понимает различные
действия, приводящие к получению “продукта”.
Например, мы говорим: работает учитель, работает
компьютер, работает трактор, холодильник. Мы
понимает, что речь идёт о разных вещах, и не
стремимся сравнивать работу грузчика с работой
компьютера. Что же такое работа с точки
зрения физики, точнее, что такое механическая
работа? Давайте посмотрим анимацию
“Механическая работа” (слайд 13).
Итак, в физике механическая работа – это
величина, которую можно измерить. Под
механической работой понимают связь между силой,
действующей на тело и его перемещением или
движением тела под действием силы.
Считается, что механическая работа
совершается, когда тело движется под действием
силы.
Таким образом, в физике понятие работы напрямую
связано с силой (нет силы, нет работы). Поэтому
принято говорить о работе некоторой силы.
Нетрудно понять, что чем большая сила действует
на тело и чем длиннее путь, который проходит тело
под действием этой силы, тем большая совершается
работа.
Механическая работа прямо пропорциональна
приложенной силе и прямо пропорциональна
пройденному пути.
Формула работы (слайд 14).
Рис. 7
Работа – физическая величина и, следовательно,
у неё есть единица измерения (слайды 15-16).
Рис. 8
1Н*м = 1 Дж – единица измерения работы названа в
честь английского физика Джеймса Прескотта
Джоуля.
За единицу работы принимают работу,
совершаемую силой в 1 Н на пути 1 м.
1 кДж=1000 Дж
3.2. Рефлексия
Наступило время проверить как вы усвоили
понятие механической работы.
Совершается ли механическая работа в следующих
случаях? (Примеры совершения и не совершения
механической работы слайды 17-22).
Если мы пытаемся сдвинуть с места тяжёлый
предмет, но сила, с которой мы на него действуем
меньше силы трения покоя, то предмет остаётся на
месте. В этом случае, несмотря на нашу усталость,
мы не совершаем механической работы, так как нет
перемещения тела. Как бы не было тяжело
мифологическому герою Атланту удерживать на
плечах небесный свод, Атлант не совершает
механической работы, так как небесный свод в этом
случае не двигался.
Механическая работа равна нулю в случае, когда
равны нулю либо силы, действующие на тело, либо
под действием сил тело не перемещается.
Рис. 9
(Заполнение опорного конспекта урока, слайд 23)
3.3. Расширение знаний о физической величине
Знак работы.
Мы выяснили, что работа может быть равной нулю.
(Приведу примеры из жизни: не выучил урок –
работа равна нулю; выучил урок – выполнил
полезную работу; набросал на пол фантики от
конфет – совершил работу отрицательную).
Оказывается, механическая работа, может быть
отрицательной и положительной. Рассмотрим, в
каких случаях и какая по знаку работа
совершается (анимация “Положительная,
отрицательная работы и работа, равная нулю”, слайд
24).
Рис. 10
Вопрос: Какая из известных вам сил, всегда
совершает отрицательную работу?
Ответ: Сила трения.
(Показываю движение деревянного бруска по
плоскости и выясняем, что сила тяги совершает
положительную работу, сила трения –
отрицательную. Задаю вопросы: Совершает ли
работу сила тяжести? Как направлена сила тяжести
по отношению к перемещению бруска? Делаем вывод,
что работа силы равна нулю, если она направлена
перпендикулярно перемещению).
Дополним ОК.
Рис. 11
Проверим, как вы усвоили понятия положительной
и отрицательной работы.
1. Какой знак работы силы тяжести в каждом
случае?
Рис. 12
2. Какую работу совершают сила трения и внешняя
сила?
Рис. 13
4. Закрепление изученного
Тест по теме “Механическая работа”
- Что такое механическая работа?
- К неподвижному массивному телу массой 100 кг
приложена сила 200 Н. При этом положение тела не
изменилось. Чему равна работа силы? - Какая из перечисленных ниже единиц принята за
единицу работы? - Тело под действием силы 40 Н переместилось на 2
метра. Чему равна работа? - Какую работу совершает сила трения при попытке
человека сдвинуть с места тяжёлый шкаф?
З) Произведение силы на скорость тела
Е) Отношение пути ко времени движения тела
Р) Произведение силы на путь, пройденный по
направлению силы
Г) 20000 Дж
Е) 0 Дж
Ж) 20 Дж
П) Ньютон
Н) Метр
Ш) Джоуль
И) 80 Дж
К) 20 Н
Л) 0 Дж
И) Равную нулю
К) Положительную
Л) Отрицательную
Если результатом является слово “решил”, то ты
молодец!
6. Подведение итогов урока. Постановка
домашнего задания.
Дома: п. 53, задание 17 (1) – экспериментальное.
Задача: Бочка заполнена водой. Пользуясь
ведром, половину воды из бочки вычерпала девочка.
Оставшуюся часть воды – мальчик. Одинаковую ли
работу совершили девочка и мальчик? Ответ
обоснуйте.
Тест (Приложение)