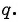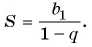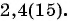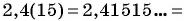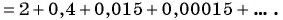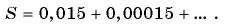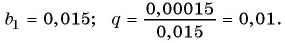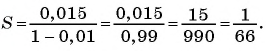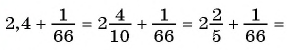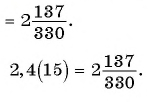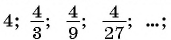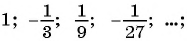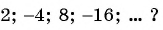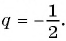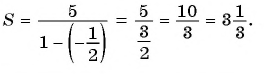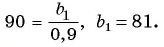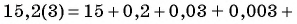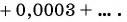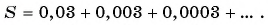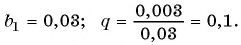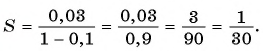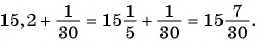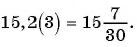Прогрессия — это последовательность величин, каждая последующая из них находится в некоторой, общей для всей прогрессии, зависимости от предыдущей.
Содержание:
Числовая последовательность
В жизни мы часто встречаемся с функциями, областью определения которых является множество натуральных чисел. Например, стоимость проезда в пригородном транспорте зависит от дальности поездки и задается функцией
Функция стоимости проезда задана таблично, областью определения функции является множество натуральных чисел 
Примером числовой последовательности является последовательность положительных четных чисел: 2; 4; 6; 8; … . Число 2 — первый член последовательности, число 4 — второй и т. д. Ясно, что на 5-м месте будет число 10 (пятый член последовательности), а на 100-м — число 200 (сотый член последовательности).
Еще один пример — последовательность чисел, обратных натуральным числам: 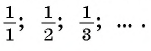
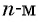
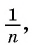
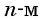
Последовательности могут быть конечными и бесконечными. Например, последовательность двузначных чисел 10; 11; …; 99 является конечной, так как содержит конечное число членов. А последовательность нечетных натуральных чисел — бесконечная.
Определение числовой последовательности
Определение:
Числовой последовательностью называется функция, определенная на множестве 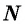
Числа, образующие последовательность (значения функции), называются членами последовательности. Они записываются буквами с индексами, обозначающими номер члена последовательности: 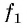
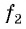
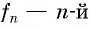
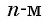
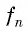
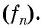
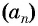
Если 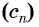
Последовательности, так же как и функции, могут быть заданы различными способами.
Аналитический способ — это задание последовательности с помощью формулы ее 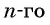
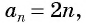
С помощью формулы 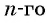
Например, пусть последовательность 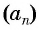
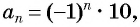
Чтобы найти некоторый член последовательности с помощью формулы 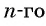
Для задания последовательностей часто используется рекуррентный способ (от лат. recurrentis — возвращающийся). Он заключается в вычислении следующих членов последовательности по предыдущим.
Например, условия 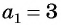
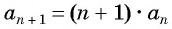
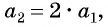
Пример №1
Найдите несколько членов последовательности 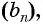
Решение:
Запишем несколько членов этой последовательности в ряд: 1; 1; 2; 3; 5; … .
Полученную последовательность чисел называют последовательностью Фибоначчи по имени итальянского математика Леонардо Фибоначчи (1180—1240).
Формула n-го члена последовательности
Пример №2
Последовательность 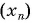
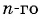
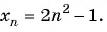
Решение:
Пример №3
Последовательность задана формулой 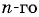
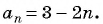
а) -2; б) -7?
Решение:
Для того чтобы определить, является ли число членом последовательности, нужно определить, имеет ли натуральные корни уравнение:
а) 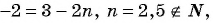
б) 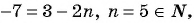
Пример №4
Для каких членов последовательности 
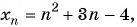
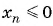
Решение:
Подставим в неравенство 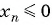
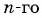
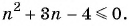
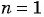
Рекуррентный способ задания последовательности
Пример №5
Запишите 5 первых членов последовательности 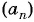
Решение:
Пример №6
Запишите несколько первых членов последовательности 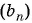
Задайте эту последовательность формулой 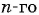
Решение:
Получим следующую последовательность: 8; -8; 8; -8; …. На нечетных местах этой последовательности стоят члены, равные числу 8, а на четных — числу -8, значит, формула 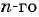
Арифметическая прогрессия
Рассмотрим задачу. В горной местности температура воздуха летом при подъеме на каждые 100 м в среднем понижается на 0,7 °С. У подножия горы температура равна 26 °С. Найдите температуру воздуха на высоте 100 м; 200 м; 300 м.
Решение:
Температура воздуха на высоте 100 м равна 26 °С – 0,7 °С = 25,3 °С. На высоте 200 м температура будет равна 25,3 °С – 0,7 °С = 24,6 °С, а на высоте 300 м — 24,6 °С – 0,7 °С = 23,9 °С.
Ответ: 25,3 °С; 24,6 °С; 23,9 °С.
Решая задачу, мы получили последовательность 26; 25,3; 24,6; … . Каждый член этой последовательности равен предыдущему, сложенному с числом -0,7. Многие практические задачи приводят к последовательностям такого вида. Они называются арифметическими прогрессиями (от лат. progression — движение вперед).
Определение арифметической прогрессией
Определение:
Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же для данной последовательности числом, т. е.
Число 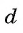
Из равенства 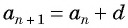
Чтобы задать арифметическую прогрессию 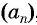
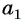
Например, если 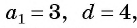
Если 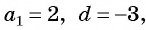
Если 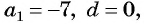
Чтобы вычислить любой член арифметической прогрессии, не вычисляя все предыдущие члены, используют формулу 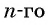
Выведем эту формулу. Если 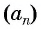
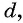
Сложим эти равенства:
После упрощения получим:
Так как число слагаемых 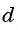
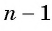
Получили формулу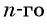
Формула 
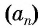
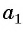
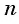
Пример №7
Последовательность 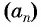
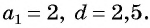
Решение:
По формуле 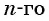
Ответ: 249,5.
Пример №8
Последовательность 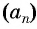
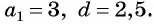
Решение:
а) По условию 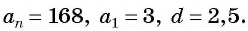
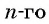
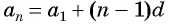
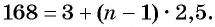
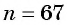
б) Подставим значения 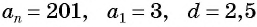
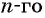
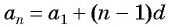
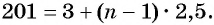
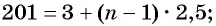
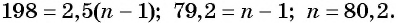
Ответ: а) число 168 является членом этой прогрессии; б) число 201 не является членом этой прогрессии.
Характеристическое свойство арифметической прогрессии
В арифметической прогрессии каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего (соседних с ним)
членов, т. е. 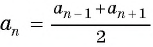
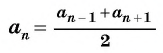
Доказательство. В арифметической прогрессии 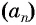
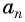
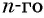
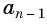
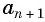
Найдем их среднее арифметическое:
Справедливо и обратное утверждение:
если в последовательности каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего (соседних с ним) членов, то последовательность является арифметической прогрессией.
Доказательство:
Пусть в некоторой числовой последовательности 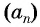
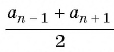
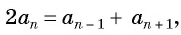
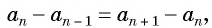
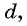
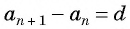
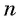
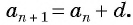
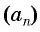
Оба утверждения можно объединить в одно, которое называется характеристическим свойством арифметической прогрессии:
числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов:
Пример №9
Проверьте, является ли арифметической прогрессией последовательность, заданная формулой
Решение:
Запишем для 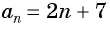
Найдем среднее арифметическое этих членов:
По характеристическому свойству арифметической прогрессии последовательность 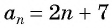
Решение арифметической прогрессии
Пример №10
Последовательность 2; 12; 22; … является арифметической прогрессией. Продолжите последовательность.
Решение:
Так как последовательность является арифметической прогрессией, то найдем ее разность 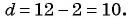
Пример №11
Известны члены арифметической прогрессии: 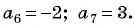
Решение:
Найдем разность арифметической прогрессии:
Формула n-го члена арифметической прогрессии
Пример №12
Последовательность 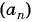
Решение:
По формуле 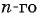
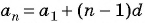
Пример №13
Запишите формулу 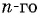
Решение:
По условию 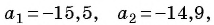
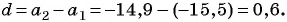
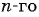
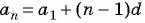
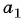
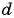
Подставим 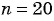
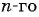
Пример №14
В арифметической прогрессии 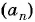
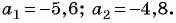
Решение:
Так как 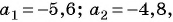
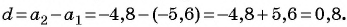
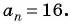
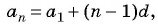
Пример №15
В арифметической прогрессии 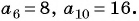
Решение:
По условию
Решим систему уравнений
Вычтем из второго уравнения первое, получим 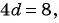
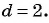
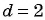
Характеристическое свойство арифметической прогрессии
Пример №16
Найдите восьмой член арифметической прогрессии 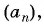
Решение:
По характеристическому свойству арифметической прогрессии 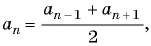
Пример №17
При каком значении 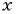
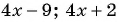
Решение:
По характеристическому свойству прогрессии последовательность является арифметической прогрессией, если каждый ее член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов:
Решим полученное уравнение:
Формула суммы n первых членов арифметической прогрессии
Рассмотрим задачу. Двое друзей решили улучшить знание английского языка и каждый день учить на 3 новых слова больше, чем в предыдущий. Сколько слов выучит каждый из друзей за 10 дней, если они начнут с одного слова?
Для решения этой задачи нужно найти сумму десяти первых членов арифметической прогрессии 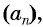
Возникает вопрос: как найти эту сумму, не вычисляя всех десяти членов прогрессии?
В общем виде эта задача приводит к необходимости вывода формулы суммы 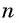
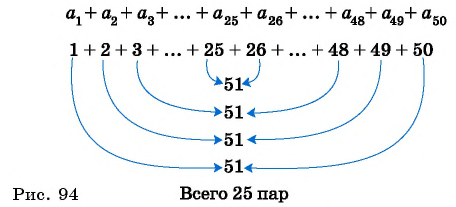
Для того чтобы вывести эту формулу, докажем свойство: суммы двух членов конечной арифметической прогрессии, равноудаленных от ее концов, равны между собой и равны сумме первого и последнего ее членов, т. е.
В общем виде:
Доказательство:
Преобразуем слагаемые в левой части равенства, воспользовавшись формулой 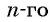
Тогда получим:
С помощью доказанного свойства найдем, например, сумму всех натуральных чисел от 1 до 50.
Натуральные числа от 1 до 50 составляют арифметическую прогрессию 1; 2; 3; …; 50. Первый член этой прогрессии равен 1, последний равен 50. Всего в этой прогрессии 50 членов.
Поскольку 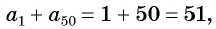
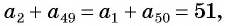
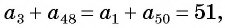
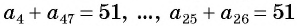
Выведем формулу суммы 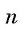
Обозначим 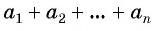
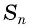
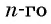
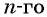
Сложим эти два равенства и получим:
По свойству 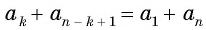
Число всех таких пар сумм равно 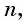
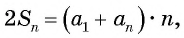
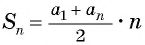
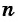
Идея такого доказательства принадлежит выдающемуся немецкому математику К. Гауссу (1777—1855).
Формулу суммы 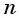
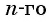
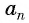
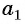
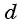
Если известен первый член прогрессии и разность, то удобно использовать формулу
Применим эту формулу к задаче о количестве выученных иностранных слов и получим: 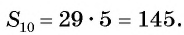
Пример №18
Найдите сумму пятидесяти первых членов арифметической прогрессии 3; 7; 11; 15; … .
Решение:
В этой прогрессии первый член равен 3, а разность 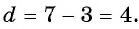
для и получим:
Ответ: 5050.
Пример №19
В арифметической прогрессии 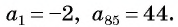
Решение:
Применим формулу суммы 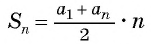
Ответ: 1785.
Пример №20
Найдите сумму шести первых членов арифметической прогрессии, если ее первый член равен -2, а разность прогрессии равна 0,4.
Решение:
Воспользуемся формулой
так как 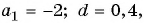
Пример №21
Найдите сумму 4 + 7 + 10+ … + 100, если ее слагаемые — последовательные члены арифметической прогрессии.
Решение:
Последовательность 4, 7, 10, …, 100 является арифметической прогрессией, в которой 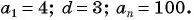
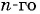
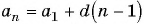
Воспользуемся формулой суммы 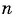
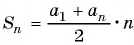
Пример №22
Найдите количество членов арифметической прогрессии, зная, что их сумма равна 430, первый член прогрессии равен -7, а разность прогрессии равна 3.
Решение:
Воспользуемся формулой суммы 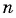
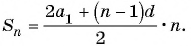
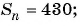
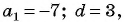
Так как 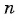
Пример №23
В арифметической прогрессии 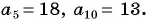
Решение:
Найдем 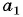
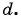
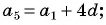
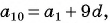
Решим полученную систему способом сложения:
Тогда
Примем четвертый член данной прогрессии за первый член некоторой другой прогрессии, тогда семнадцатый член данной прогрессии станет четырнадцатым (17 – 4 + 1 = 14) членом новой прогрессии. Искомая сумма равна:
Пример №24
Найдите сумму всех четных натуральных чисел, не превосходящих 300, которые при делении на 13 дают в остатке 5.
Решение:
Первое число в последовательности всех четных натуральных чисел, не превосходящих 300, которые при делении на 13 дают в остатке 5, — это число 18. Каждое следующее число равно предыдущему, сложенному с числом 26. Последнее четное число, которое при делении на 13 дает в остатке 5, — это число 278. Поскольку рассматриваются только четные числа, то разность прогрессии равна 26. Найдем номер числа прогрессии, равного 278: 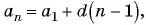
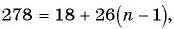
Геометрическая прогрессия
Рассмотрим задачу. Вкладчик положил в банк 1000 р. на
депозит, по которому сумма вклада увеличивается ежегодно на 5 %. Какая сумма будет у него через 1 год, 2 года, 6 лет?
Решение:
Начальная сумма в 1000 р. через год увеличится на 5 % и составит 105 % от 1000 р. Найдем 105 % = 1,05 от 1000 р.: 1000 • 1,05 = 1050 (р.).
Через два года сумма вклада станет равной 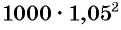
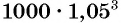
Через шесть лет сумма будет равна
Многие практические задачи приводят к последовательностям такого вида. Они называются геометрическими прогрессиями.
Определение геометрической прогрессии
Определение:
Геометрической прогрессией называется числовая последовательность, первый член которой отличен от нуля, а каждый следующий, начиная со второго, равен предыдущему, умноженному на одно и то же для данной последовательности число, не равное нулю, т. е.
Число 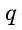
Из равенства 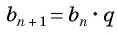
Чтобы задать геометрическую прогрессию 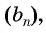
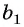
Например, если 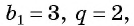
Если 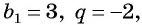
Если 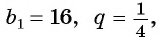
вид
Если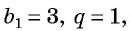
Чтобы вычислить любой член геометрической прогрессии, не вычисляя все предыдущие члены, используют формулу 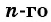
Выведем эту формулу. Если 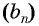
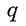
Перемножим эти равенства между собой:
Разделим обе части равенства на произведение 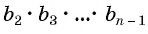
Так как число множителей 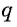
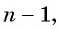
Получили формулу 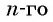
Формула 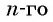
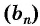
Пример №25
Последовательность 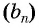
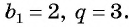
Решение:
По формуле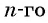
Ответ: 4374.
Пример №26
Последовательность 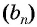
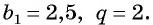
Решение:
По условию 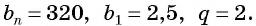
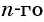
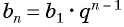
Решим это уравнение:
Так как 8 — натуральное число, то число 320 является членом этой прогрессии с номером 8.
Ответ: число 320 является членом этой прогрессии.
- Заказать решение задач по высшей математике
Характеристическое свойство геометрической прогрессии
В геометрической прогрессии модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего (соседних с ним) ее членов, т. е. 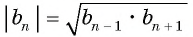
или 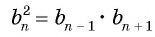
Доказательство:
В геометрической прогрессии 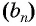
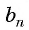
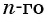
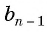
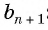
Найдем среднее пропорциональное (среднее геометрическое) соседних с 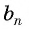
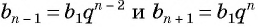
Выполним преобразования в правой части равенства:
откуда получим, что
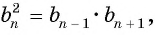
Справедливо и обратное утверждение:
- если в последовательности чисел, отличных от нуля, модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего (соседних с ним) ее членов, то последовательность является геометрической прогрессией.
Доказательство:
Пусть в некоторой числовой последовательности 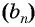
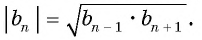
Тогда 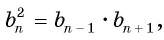
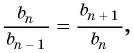
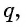
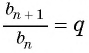
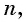
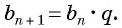
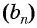
Оба утверждения можно объединить в одно, которое называется характеристическим свойством геометрической прогрессии:
- числовая последовательность, все члены которой отличны от нуля, является геометрической прогрессией тогда и только тогда, когда модуль каждого ее члена, начиная со второго, равен среднему пропорциональному предыдущего и последующего ее членов:
Пример №27
Проверьте, является ли геометрической прогрессией последовательность, заданная формулой
Решение:
Запишем для 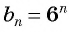
Найдем среднее пропорциональное этих членов:
По характеристическому свойству геометрической прогрессии последовательность 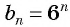
Решение геометрической прогрессии
Пример №28
Последовательность 2; 10; 50; … является геометрической прогрессией. Продолжите последовательность.
Решение:
Так как последовательность является геометрической прогрессией, то найдем ее знаменатель 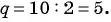
Пример №29
Известны члены геометрической прогрессии:
Найдите знаменатель этой прогрессии.
Решение:
Так как знаменатель геометрической прогрессии равен отношению любого ее члена к предыдущему, то
Формула n-го члена геометрической прогрессии:
Пример №30
Последовательность 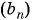
Решение:
По формуле 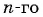
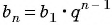
Пример №31
Запишите формулу 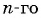
Решение:
По условию 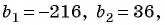
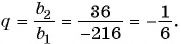
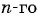
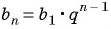
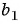
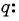
Подставим 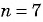
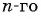
Пример №32
Найдите номер члена геометрической прогрессии 0,1; 0,3; …, равного 218,7.
Решение:
Найдем знаменатель прогрессии:
Известно, что 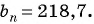
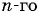
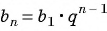
Пример №33
Найдите знаменатель и первый член геометрической прогрессии 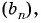
Решение:
По условию
Составим систему уравнений
Разделим второе уравнение на первое и получим:
Подставим это значение 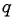
Характеристическое свойство геометрической прогрессии
Пример №34
Найдите сорок девятый член геометрической прогрессии, если сорок восьмой ее член равен 4, а пятидесятый ее член равен 9.
Решение:
Воспользуемся характеристическим свойством геометрической прогрессии 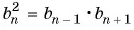
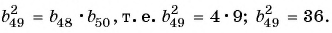
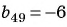
Пример №35
При каком значении 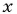
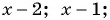
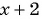
Решение:
По характеристическому свойству прогрессии последовательность является геометрической прогрессией, если каждый ее член, начиная со второго, равен среднему пропорциональному предыдущего и последующего членов:
Решим полученное уравнение:
Формула суммы n первых членов геометрической прогрессии
Немало легенд связано с геометрической прогрессией.
Наиболее известная из них рассказывает об изобретателе шахмат.
По легенде, когда создатель шахмат показал свое изобретение правителю страны, тому так понравилась игра, что он дал изобретателю право самому выбрать награду. Мудрец попросил у правителя за первую клетку шахматной доски заплатить ему одно зерно пшеницы, за вторую — два, за третью — четыре и т. д., удваивая количество зерен на каждой следующей клетке (рис. 96).
Правитель быстро согласился и приказал казначею выдать мудрецу нужное количество зерна. Однако когда казначей показал расчеты, то оказалось, что расплатиться невозможно, разве только осушить моря и океаны и засеять все пшеницей.
Число зерен, которое попросил мудрец, равно сумме членов геометрической прогрессии 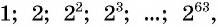
Выведем формулу, по которой можно находить сумму 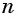
Обозначим сумму 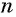
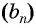
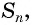
Умножим обе части этого равенства на знаменатель прогрессии 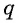
Вычтем из второго равенства первое и получим:
т. e. 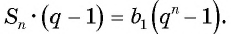
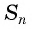
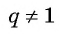
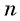
Если 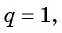
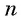
Формула суммы n первых членов геометрической прогрессии:
Вычислим по формуле суммы 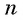
Первый член геометрической прогрессии 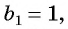
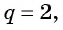
Тогда
Такого количества пшеницы человечество не собрало за всю свою историю.
Пример №36
Найдите сумму десяти первых членов геометрической прогрессии 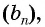
Решение:
Применим формулу суммы 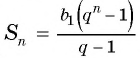
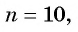
Ответ: 511,5.
Пример №37
Найдите сумму двенадцати первых членов геометрической прогрессии 3; -6; 12; -24; … .
Решение:
Подставим в формулу 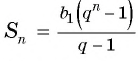
Ответ. -4095.
Пример №38
Найдите сумму пяти первых членов геометрической прогрессии 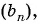
Решение:
Найдем знаменатель и первый член геометрической прогрессии:
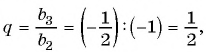
По формуле 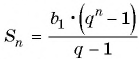
Пример №39
Сумма членов геометрической прогрессии равна 605. Найдите количество членов прогрессии, если
Решение:
Подставим в формулу 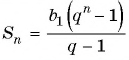
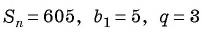
Пример №40
В геометрической прогрессии 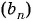

Решение:
Найдем знаменатель прогрессии:
Подставим в формулу 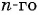
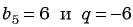
По формуле 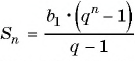
Пример №41
В геометрической прогрессии 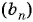
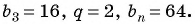
Решение:
Зная, что третий член геометрической прогрессии равен 16, а ее знаменатель равен 2, по формуле 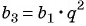
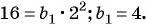
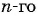
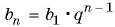
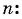
По формуле суммы 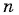
Сумма бесконечно убывающей геометрической прогрессии
Любую обыкновенную дробь можно записать в виде десятичной дроби — конечной или бесконечной периодической дроби. Например, 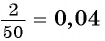
Вы рассматривали правило записи конечной десятичной дроби в виде обыкновенной дроби (например, 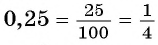
Выясним, как бесконечную периодическую десятичную дробь записать в виде обыкновенной дроби.
Рассмотрим, например, бесконечную периодическую десятичную дробь 0,(7) = 0,7777… . Определим, какой обыкновенной дроби равно это число.
Запишем дробь 0,(7) в виде суммы разрядных слагаемых:
В данном случае необходимо найти сумму бесконечного числа слагаемых.
Слагаемые этой суммы являются членами бесконечной
геометрической прогрессии со знаменателем 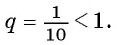
Определение. Бесконечно убывающей геометрической прогрессией называется такая бесконечная геометрическая прогрессия, у которой знаменатель
Например, геометрическая прогрессия 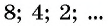
Геометрическая прогрессия 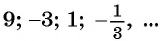
Для того чтобы представить бесконечную периодическую десятичную дробь в виде обыкновенной, нужно найти сумму бесконечно убывающей геометрической прогрессии. Ее обозначают буквой 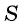
Покажем идею вывода формулы суммы бесконечно убывающей геометрической прогрессии.
Рассмотрим бесконечную геометрическую прогрессию 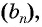
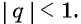
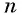
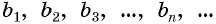
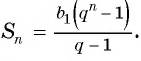
Представим, что п неограниченно возрастает (говорят, что стремится к бесконечности, и записывают 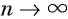
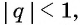
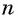
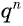
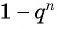
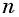
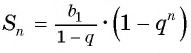
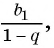
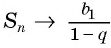
Число 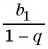
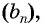
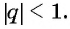
Обозначим сумму бесконечно убывающей геометрической прогрессии буквой 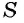
Вычислим по этой формуле сумму разрядных слагаемых:
Слагаемые этой суммы образуют бесконечно убывающую геометрическую прогрессию 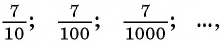
а знаменатель равен
Сумма бесконечно убывающей геометрической прогрессии:
Так как 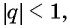
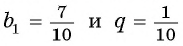
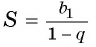
Значит,
Таким образом, бесконечную периодическую десятичную дробь 0,(7) можно записать в виде обыкновенной дроби 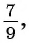
Таким же способом можно любую бесконечную периодическую десятичную дробь представить в виде обыкновенной дроби.
Чтобы записать бесконечную периодическую десятичную дробь в виде обыкновенной дроби, нужно:
- Представить число в виде суммы разрядных слагаемых.
- Выделить сумму бесконечно убывающей геометрической прогрессии.
- Указать первый член
, и найти знаменатель этой прогрессии
- Найти сумму бесконечно убывающей геометрической прогрессии по формуле
- Вычислить сумму первых слагаемых и найденного значения суммы бесконечно убывающей геометрической прогрессии.
Запишите в виде обыкновенной дроби число
(1)
(2)
(3)
(4)
(5)
Бесконечно убывающая геометрическая прогрессия
Пример №42
В бесконечной геометрической прогрессии 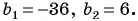
Решение:
Найдем знаменатель прогрессии: 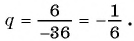
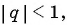
Пример №43
Является ли бесконечно убывающей геометрическая прогрессия:
а)
б)
в)
Решение:
а) Каждый член этой геометрической прогрессии, начиная со второго, равен предыдущему, умноженному на число 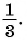
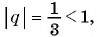
б) Поскольку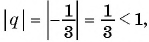
в) Знаменатель прогрессии 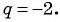
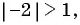
Пример №44
Найдите сумму бесконечно убывающей геометрической прогрессии, в которой 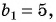
Решение:
По формуле 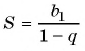
Пример №45
В бесконечно убывающей геометрической прогрессии 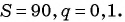
Решение:
В формулу суммы бесконечно убывающей геометрической прогрессии 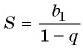
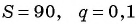
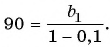
Пример №46
Запишите бесконечную периодическую десятичную дробь 15,2(3) в виде обыкновенной дроби.
Решение:
(1)
(2)
(3)
(4)
(5)
- Единичная окружность – в тригонометрии
- Определение синуса и косинуса произвольного угла
- Определение тангенса и котангенса произвольного угла
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Наибольшее и наименьшее значения функции
- Раскрытие неопределенностей
- Дробно-рациональные уравнения
- Дробно-рациональные неравенства
Числовой последовательностью называют ряд чисел, полученных по некоторому правилу или формуле.
Например, правило «все положительные четные числа по возрастанию начиная с двойки» задает последовательность: (2; 4; 6; 8; 10…) А правило «первое число равно (3), а каждое следующее число в два раза больше предыдущего» формирует последовательность: (3; 6; 12; 24; 48….)
Ниже разобраны несколько разных способов задания числовых последовательностей.
Числа, образующие последовательность, называются ее членами
(или элементами). И каждое из этих чисел имеет свой порядковый номер.
Например, в последовательности (3; 6; 12; 24; 48…) тройка является первым членом (порядковый номер – один), шестерка – вторым (ее номер по порядку равен двум), двенадцать – третьим и т.д.
В математике последовательность обозначают маленькой латинской буквой, а каждый отдельный ее элемент – той же буквой с числовым индексом равным порядковому номеру этого элемента.
То есть, если последовательность (3; 6; 12; 24; 48…) обозначить как (a_n), то можно записать, что (a_1=3), (a_2=6), (a_3=12), (a_4=24) и так далее.
Иными словами, для последовательности (a_n={ 3;: 6; :12; : 24; : 48; : 96; : 192; : 384…}).
|
порядковый номер элемента |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
(8) |
… |
|
обозначение элемента |
(a_1) |
(a_2) |
(a_3) |
(a_4) |
(a_5) |
(a_6) |
(a_7) |
(a_8) |
… |
|
значение элемента |
(3) |
(6) |
(12) |
(24) |
(48) |
(96) |
(192) |
(384) |
… |
Отметим, что членами последовательности необязательно должны быть различные числа. Она может состоять из одних и тех же чисел, например, выглядеть вот так: (1; : 1; : 1; : 1…) .
Способы задания числовых последовательностей
Все способы формирования числовых последовательностей можно разделить на три большие группы:
– I способ: словесный. Здесь все просто – в буквальном смысле словами описывается каким образом можно вычислить элементы искомой последовательности.
Пример: Напишите первые пять членов последовательности квадратов натуральных чисел.
Решение: Натуральными называют числа, возникающие естественным образом при счете количества предметов, то есть: (1; : 2; : 3; : 4; : 5) и т.д. Нашу же последовательность формируют квадраты этих чисел, то есть (1^2;: 2^2; : 3^2; : 4^2; : 5^2…) . Таким образом, имеем ответ: (1; : 4; : 9; : 16; : 25…)
Ответ: (1; : 4; : 9; : 16; : 25…)
Отметим, что последовательности в начале статьи заданы именно словесным способом.
– II способ: аналитический (формулой энного члена). Тут значение каждого элемента последовательности вычисляется по некоторой формуле, в которую подставляется порядковый номер этого элемента.
Пример: Последовательность задана формулой: (b_n=frac{n-1}{n^2}). Вычислите первые пять членов этой последовательности.
Решение: Вычислим (b_1). Это первый член последовательности, то есть его порядковый номер (n) равен единице. Тогда его значение равно (b_1=frac{1-1}{1^2} =frac{0}{1}=0).
У второго члена (n=2), то есть его значение равно (b_2=frac{2-1}{2^2} =frac{1}{4}).
Третий ((n=3)): (b_3=frac{3-1}{3^2} =frac{2}{9}).
Четвертый ((n=4)): (b_4=frac{4-1}{4^2} =frac{3}{16}).
Пятый ((n=5)): (b_5=frac{5-1}{5^2} =frac{4}{25}) .
Готово. Можно писать ответ.
Ответ: (b_n= {0; : frac{1}{4}; : frac{2}{9}; : frac{3}{16}; : frac{4}{25}…}).
Обратите внимание, что при таком задании последовательности, значение каждого элемента зависит только от его порядкового номера. И поэтому, если нам нужно вычислить, например, пятнадцатый элемент, мы можем это сделать сразу, не вычисляя предыдущие четырнадцать.
Пример: Последовательность задана формулой: (a_n=8+5n-n^2). Вычислите (a_9).
Решение: Нужно вычислить значение девятого элемента, то есть порядковый номер (n=9). Подставляем в формулу: (a_9=8+5·9-9^2=8+45-81=-28).
Ответ: (a_9=-28).
III способ: рекуррентное соотношение. Звучит страшно, но суть проста – здесь дается начало последовательности (один или несколько первых элементов) и правило, по которому из предыдущего (или нескольких предыдущих) членов последовательности можно вычислить следующий.
Пример: Последовательность задана условиями: (c_1=4), (c_{n+1}=c_n+3). Вычислите первые пять членов этой последовательности.
Решение: Первый член нам известен: (c_1=4).
Второй мы получим, подставив в формулу вместо (n) единицу: (c_{1+1}=c_1+3)
(c_2=c_1+3=4+3=7)
Третий ((n=2)): (c_{2+1}=c_2+3 )
(c_3=c_2+3=7+3=10).
Четвертый ((n=3)): (c_{3+1}=c_3+3)
(c_4=c_3+3=10+3=13).
Пятый ((n=4)): (c_{4+1}=c_4+3)
(c_5=c_4+3=13+3=16).
Нужные пять элементов вычислены. Теперь можно записывать ответ.
Ответ: (c_n={4; : 7; : 10; : 13; : 16…}).
В этом примере мы по сути получали следующий элемент из предыдущего путем прибавления к предыдущему тройки. Логично, ведь формула (c_{n+1}=c_n+3) требовала именно этого. В ней (c_n) – это предыдущий элемент, а (c_{n+1}) – следующий за ним (ведь его номер на единицу больше).
На практике могут встречаться более сложные формулы, в которых следующий элемент вычисляется из двух, трех или даже большего количества предыдущих.
Пример: У последовательности известны первые два элемента (z_1=2;) (z_2=5). Так же известна формула следующего элемента (z_{n+2}=3z_{n+1}-z_n). Вычислите значения третьего, четвертого и пятого членов.
Решение: Слева будем писать текущую последовательность, а справа вести вычисления очередного элемента.
|
Последовательность на данный момент: |
Вычисления: |
||||||||||||
|
Так как формула дана для элемента с номером (n+2), то чтобы найти (z_3) нужно подставлять вместо (n) единицу:
|
||||||||||||
|
Теперь найдем (z_4), подставив вместо (n) двойку: (z_{2+2}=3z_{2+1}-z_2) (z_4=3z_3-z_2=3·13-5=34) |
||||||||||||
|
Наконец вычисляем (z_5), подставляя вместо (n) тройку: (z_{3+2}=3z_{3+1}-z_3) (z_5=3z_4-z_3=3·34-13=89) |
||||||||||||
|
Готово. Можно писать ответ. |
Ответ: (c_3=13); (c_4=34); (c_5=89).
Важное отличие рекуррентного способа задания последовательности от аналитического – при рекуррентном мы не можем посчитать следующий элемент, не зная предыдущих. То есть, если нам нужно вычислить, например, пятнадцатый элемент, придется сначала вычислить все, что идут до него.
Как определить является ли число элементом последовательности?
Во всех предыдущих примерах мы находили значения элементов последовательности – чему равен третий, пятый или девятый член. Иначе говоря, выясняли какое именно число стоит в последовательности на таком-то месте.
Но в практике встречается также обратная задача – значение известно и надо выяснить, есть ли оно среди элементов некоторой последовательности? А если есть, то на каком месте?
Пример (ОГЭ): Какое из чисел ниже есть среди членов последовательности (a_n=n^2-n):
а) (1) б) (3) в) (6) г) (10) ?
Решение: Из условия задачи понятно, что одно из этих чисел точно является элементом последовательности. Поэтому мы можем просто вычислять элементы по очереди, пока не найдем нужный:
(a_1=1^2-1=0) – мимо.
(a_2=2^2-2=2) – тоже не то.
(a_3=3^2-3=6) – есть!
Нужный элемент найден.
Ответ: (6).
Такой метод решения годится только если заранее известно, что элемент точно в последовательности есть. Потому что если его вдруг там нет – это можно проверять вечность, последовательность ведь бесконечна!
Поэтому в такой ситуации пользуются следующим алгоритмом:
-
Подставляют заданное число в формулу (n) -го члена вместо (a_n);
-
Решая полученное уравнение, находят неизвестное (n);
-
Если (n) – натуральное, то данное число – член последовательности.
Пример: Выяснить, является ли число (3) членом последовательности (a_n=)(frac{51+2n}{n+4}) ?
Решение:
|
(a_n=)(frac{51+2n}{n+4}) |
Если число (3) – член последовательности, то значит при некотором значении (n), формула (frac{51+2n}{n+4}) должна дать нам тройку. Найдем это (n) по алгоритму выше. |
|
(3=)(frac{51+2n}{n+4}) |
Решаем это уравнение. Умножаем левую и правую части на знаменатель ((n+4)). |
|
(3cdot (n+4)=51+2n) |
Получилось линейное уравнение. Раскрываем скобки слева. |
|
(3n+12=51+2n) |
Собираем неизвестные слева, числа справа… |
|
(3n-2n=51-12) |
…и приводим подобные слагаемые. |
|
(n=39) |
Готово. Найденное значение – это то число, которое надо подставить вместо (n) в формулу (frac{51+2n}{n+4}), чтоб получилось тройка (можете проверить это сами). Значит (39)-ый член последовательности равен трем. |
Ответ: Да, число (3) является элементом данной последовательности.
Смотри также:
Арифметическая прогрессия
Геометрическая прогрессия
Download Article
Download Article
An arithmetic sequence is any list of numbers that differ, from one to the next, by a constant amount. For example, the list of even numbers, 
If you know you are working with an arithmetic sequence, you may be asked to find the very next term from a given list. You may also be asked to fill in a gap where a term is missing. Finally, you might want to know, for example, the 100th term, without actually writing out all 100 terms. A few simple steps can help you do any of these.
-
1
Find the common difference for the sequence. When you are presented with a list of numbers, you may be told that the list is an arithmetic sequence, or you may need to figure that out for yourself. The first step is the same in either case. Select the first two consecutive terms in the list. Subtract the first term from the second term. The result is the common difference of your sequence.[2]
-
2
Check that the common difference is consistent. Finding the common difference for just the first two terms does not ensure that your list is an arithmetic sequence. You need to make sure that the difference is consistent for the whole list.[3]
Check the difference by subtracting two different consecutive terms in the list. If the result is consistent for one or two other pairs of terms, then you probably have an arithmetic sequence.Advertisement
-
3
Add the common difference to the last given term. Finding the next term of an arithmetic sequence after you know the common difference is easy. Simply add the common difference to the last term of the list, and you will get the next number.[4]
Advertisement
-
1
Verify that you are starting with an arithmetic sequence. In some cases, you may have a list of numbers with a missing term in the middle. Begin, as before, by checking that your list is an arithmetic sequence. Select any two consecutive terms and find the difference between them. Then check this against two other consecutive terms in the list. If the differences are the same, you can presume that you are working with an arithmetic sequence and proceed.
-
2
Add the common difference to the term before the space. This is similar to adding a term to the end of a sequence. Find the term that immediately precedes the space in your sequence. This is the “last” number that you know. Add your common difference to this term, to find the number that should fill in the space.[5]
-
3
Subtract the common difference from the term following the space. To be sure that you have the correct answer, check from the other direction. An arithmetic sequence should be consistent going in either direction. If you move from left to right and add 4, then going in the opposite direction, from right to left, you would do the opposite and subtract 4.[6]
-
4
Compare your results. The two results that you get, from adding up from the bottom or from subtracting down from the top should match. If they do, then you have found the value for the missing term. If they do not, then you need to check your work. You may not have a true arithmetic sequence.
Advertisement
-
1
Identify the first term of the sequence. Not every sequence begins with the numbers 0 or 1. Look at the list of numbers that you have and find the first term. This is your starting point, which can be designated using variables as a(1).
-
2
Define your common difference as d. Find the common difference for the sequence as before. In this working example, the common difference is
, which is 5. Checking with other terms in the sequence provides the same result. We will note this common difference with the algebraic variable d.[7]
-
3
Use the explicit formula. An explicit formula is an algebraic equation that you can use to find any term of an arithmetic sequence, without having to write out the full list. The explicit formula for an algebraic sequence is
.[8]
- The term a(n) can be read as “the nth term of a,” where n represents which number in the list you want to find and a(n) is the actual value of that number. For example, if you are asked to find the 100th item in an arithmetic sequence, then n will be 100. Note that n is 100, in this example, but a(n) will be the value of the 100th term, not the number 100 itself.
-
4
Fill in your information to solve the problem. Using the explicit formula for your sequence, fill in the information that you know to find the term that you need.[9]
Advertisement
-
1
Rearrange the explicit formula to solve for other variables. Using the explicit formula[10]
and some basic algebra, you can find several pieces of information about an arithmetic sequence. In its original form,, the explicit formula is designed to solve for an and give you the nth term of a sequence. However, you can algebraically manipulate this formula and solve for any of the variables.
-
2
Find the first term of a sequence. You may know that the 50th term of an arithmetic sequence is 300, and you know that the terms have been increasing by 7 (the “common difference”), but you want to find out what the first term of the sequence was. Use the revised explicit formula that solves for a1 to find your answer.[11]
- Use the equation
, and fill in the information that you know. Since you know that the 50th term is 300, then n=50, n-1=49 and a(n)=300. You also are given that the common difference, d, is 7. Therefore, the formula becomes
. This works out to
. The sequence that you have began at 43, and counted up by 7. Therefore, it looks like 43,50,57,64,71,78…293,300.
- Use the equation
-
3
Find the length of a sequence. Suppose you know all about the start and end of an arithmetic sequence, but you need to find out how long it is. Use the revised formula
.[12]
- Suppose you know that a given arithmetic sequence begins at 100 and increases by 13. You are also told that the final term is 2,856. To find the length of the sequence, use the terms a1=100, d=13, and a(n)=2856. Insert these terms into the formula to give
. If you work this out, you get
, which equals 212+1, which is 213. There are 213 terms in that sequence.
- This sample sequence would look like 100, 113, 126, 139… 2843, 2856.
- Suppose you know that a given arithmetic sequence begins at 100 and increases by 13. You are also told that the final term is 2,856. To find the length of the sequence, use the terms a1=100, d=13, and a(n)=2856. Insert these terms into the formula to give
Advertisement
Add New Question
-
Question
Given only the 10th and 15th term, how do I find the first three terms?
Subtract the 10th term from the 15th term and divide by 5: that gives you D, the difference between any two consecutive terms. Multiply D by 9, and subtract that amount from the 10th term; that gives you the first term.
-
Question
What is the formula for the sequence 8,16,32,64,___?
This is not an arithmetic sequence. Look up geometric sequences for whatever formula you’re interested in.
-
Question
How do I calculate the 5 terms of an arithmetic sequence if the first term is 8 and the last term is 100?
Subtract 8 from 100 = 92. Divide 92 by 4 (because with five terms there will be four intervals between the first and last term). That gives you 23, the size of each interval. So the sequence begins with 8 and has a common difference of 23.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
-
There are different kinds of sequences of numbers. Do not assume that a list of numbers is an arithmetic sequence. Always check at least two pairs of terms, or preferably three or four, to find the common difference between terms.
Advertisement
Video
-
Remember that d can be either positive or negative, depending if it is being added or subtracted.
Thanks for submitting a tip for review!
Advertisement
About This Article
Article SummaryX
To find a term in an arithmetic sequence, determine the common difference by subtracting the first number from the second number. Then, confirm that the difference is consistent between each number in the sequence by repeating the above equation with the second and third numbers, the third and fourth numbers, and so on. Once you’ve confirmed the common difference, all you have to do to find the missing number is add the common difference to preceding term in the sequence. If you want to learn how to find a term later on in a sequence of numbers, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 339,698 times.
Did this article help you?
Числовая последовательность
Определение 1. Числовой последовательностью называется функция, аргументом которой является множество всех натуральных чисел, или множество первых n натуральных чисел.
Обозначается числовая последовательность так:
или
где 
Последовательности можно задавать тремя способами: словестно, аналитически и рекуррентно.
При словестном задании последовательности, описывается из каких элементов она состоит.
Последовательность нечетных чисел:
Последовательность простых чисел :
и т.д.
Последовательности (1) и (2) мы задали словестно.
Последовательность называется заданной аналитически, если указана формула ее n-го члена.
Последовательность нечетных чисел аналитически задается формулой
Действительно. Взяв для n значения 1, 2, 3, … мы получим последовательность (1).
Отметим, что последовательность простых чисел невозможно задать аналитически.
Последовательность задана рекуррентно, если указан метод вычисления n – го члена, при известных предыдущих членах последовательности.
Пример задания рекуррентной последовательности:
В этой последовательности
Определение 2. Числовая последовательность, в котором все члены равны называется стационарным.
Пример стационарной последовательности:
Возрастающие и убывающие последовательности
Определение 3. Последовательность, в которой каждый последующий член (кроме первого) больше предыдующего, называется возрастающей:
Определение 4. Последовательность, в которой каждый последующий член (кроме первого) меньше предыдующего, называется убывающей:
Возрастающие и убывающие последовательности называются также монотонными последовательностями.
Пример 1. Выяснить, монотонна ли последовательность
Решение. Запишем n+1 член последовательности (подставим вместо n, n+1):
Найдем разность членов 

или
Так как n=1,2,3,… то правая часть уравнения (3) положительна. Тогда:
или
Таким образом, каждый последующий член последовательности больше предыдующего. Следовательно последовательность является возрастающим (и монотонным).
Пример 2. Выяснить, при каких значениях a последовательность (bn) является возрастающей и при каких, убывающей:
Решение. Запишем n+1 член последовательности (вместо n подставим n+1):
Найдем разность членов 

или
Посмотрим на правую часть выражения (4). Если a<10, то 


т.е. имеем дело с последовательностью
Очевидно, что последовательность (5) не является монотонной. Она является стационарной последовательностью.
Ограниченные и неограниченные последовательности
Определение 5. Последовательность (yn) называется ограниченной сверху, если существует такое число k, что yn<k при любом n.
Определение 6. Последовательность (yn) называется ограниченной снизу, если существует такое число k, что yn>k при любом n.
Определение 7. Последовательность (yn) называется ограниченной, если она ограничена и сверху, и снизу.
Пример 3. Показать, что последовательность (an) является монотоннной и ограниченной:
Решение. Запишем n+1 член последовательности (вместо n подставим n+1):
Найдем разность членов 

или
Правая часть равенства (6) положительна при любых натуральных чисел n. Следовательно последовательно (an) возрастающая (и монотонная).
Далее, сделаем эквивалентное преобразование для проследовательности (5):
или
Из выражения (7) видно, что при любых n an≤1. Т.е. хотя последовательность возрастает, то остается меньше числа 1 (ограничена сверху). Запишем несколько членов данной последовательности, задав n=1,2,3,…
Так как последовательность возрастающая, то все члены последовательности не меньше 
Сходящиеся и расходящиеся последовательности
Рассмотрим две числовые последовательности:
На координатной прямой изобразим члены этих последовательностей:
Как можно заметить из рисунков Рис.1 и Рис.2, члены последовательности 



Предел числовой последовательности
Точка, к которой приближаются члены последовательности при увеличении n, называется пределом последовательности. Для последовательности (10) пределом является число 0. Более строго предел последовательности определяется так:
Определение 8. Число k называют пределом последовательности (yn), если для любой заранее выбранной окресности точки k, можно выбрать такой номер n0, чтобы все члены последовательности, начиная с номера n0 содержались в указанной окрестности.
Если k является пределом последовательности (yn), то пишут 


Обозначают это так:
Выраженние (11) читается так: предел проследовательности 
Изложим некоторые пояснения к определению 8.
Пусть выполнено (11). Возьмем окрестность точки k, т.е. интервал 


Если же взять другую окресность 

Пример 4. Дана полследовательность (yn):
Доказать, что 
Решение. Найдем любую окрестность точки 0. Пусть ее радиус равен r. Тогда всегда можно выбирать n0 так, чтобы 
Пусть, например, r=0.001. Вычислим n‘ из уравнения
Имеем:
В качестве n0 берем 501. Имеем:
или
Запишем члены последовательности (12) начиная с номера 501:
Далее, учитывая (13), имеем:
Следовательно, все члены последовательности (12) начиная с номера 501 попадают в окресность 
Пример 5. Дана полследовательность (yn):
Доказать, что 
Решение. Найдем любую окрестность точки 2. Пусть ее радиус равен r. Тогда всегда можно выбирать n0 так, чтобы
Рашим (15) относительно n0:
Получили
Неравенство в (17) всегда выполняется так как n0 натуральное число, а правая часть неравенства отрицательно (это означает, что 

Запишем члены последовательности, начиная с номера 2000:
Легко проверить, что 
Пример 6. Найти предел последовательности
Решение. Выполним некоторые преобразования выражения (18):
Тогда последовательность (18) можно переписать так:
Как видно из (19), пройдя по членам последовательности слева направо, из числа 1 вычитается все меньшее и меньшее положительное число. Т.е. последовательность приближается к числу 1. Тогда 1 является пределом последовательности (19) и (18):
На Рис. 3 представлена функция 
Свойства сходящихся последовательностей
Сходящиеся последовательности обладают рядом свойств.
Свойство 1. Если последовательность сходится, то только к одному пределу.
Свойство 2. Если последовательность сходится, то она ограничена.
Свойство 3. Если последовательность монотонна и ограничена, то она сходится (теорема Вейерштрасса).
Предел стационарной последовательности равен значению любого члена последовательности:
Теорема. Если 
1. Предел суммы равен сумме пределов:
2. Предел произведения равен произведению пределов:
3. Предел частного равен частному пределов:
(при c≠0).
4. Постоянный множитель можно вывести за знак предела:
Пример 7. Найти предел последовательности:
Решение. Так как 
Пример 8. Найти предел последовательности:
Решение. Применив правило “предел суммы” теоремы, получим
Пример 9. Вычислить:
Решение. Делим числитель и знаменатель дроби на наивысшую из имеющихся степень переменного n. Далее используем правило “предел суммы” для числителя и знаменателя и правило “предел частного”:
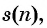

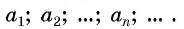
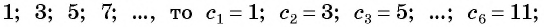
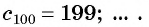
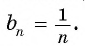
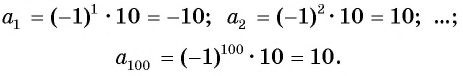
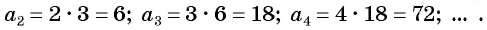
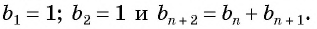
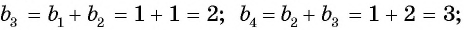
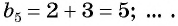
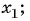
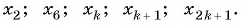
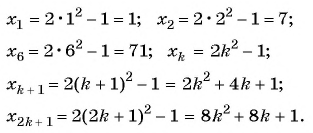
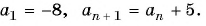
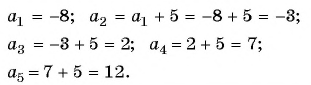
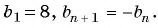
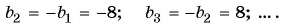
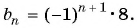
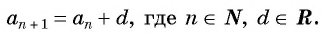
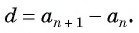
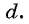
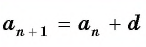
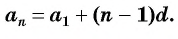
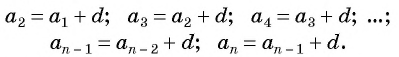
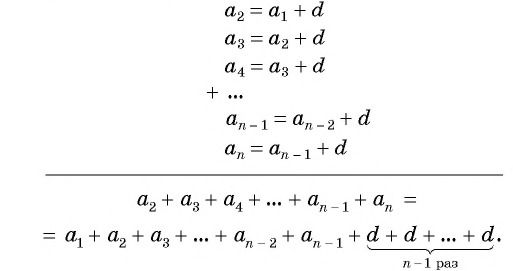
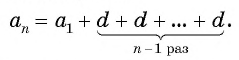
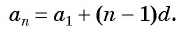

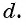
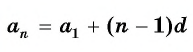
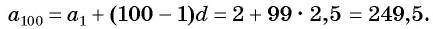
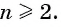
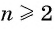
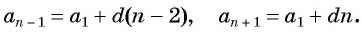
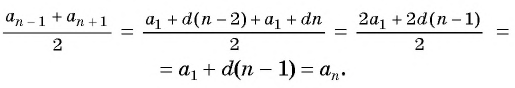
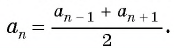
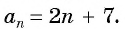
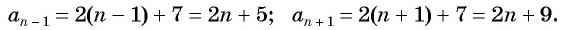
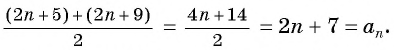
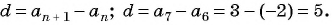
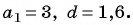
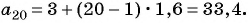
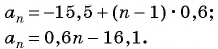
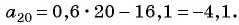
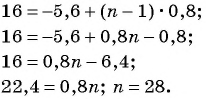
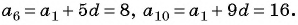
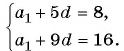
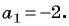
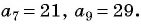
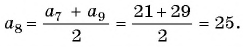
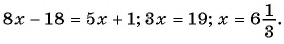
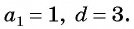
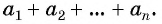
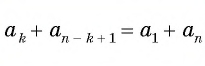
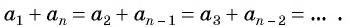
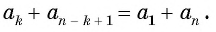
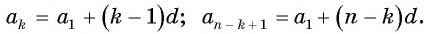
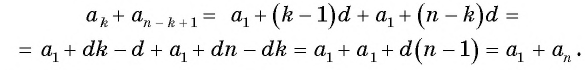
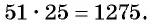
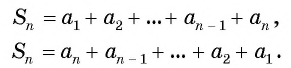
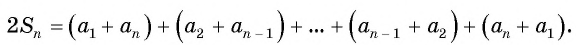
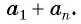
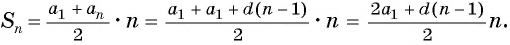
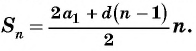
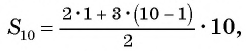

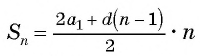
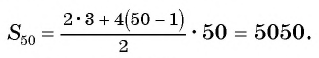
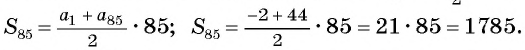
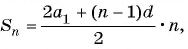
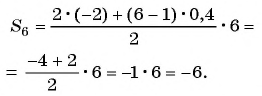
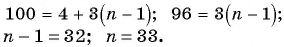
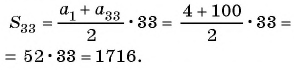
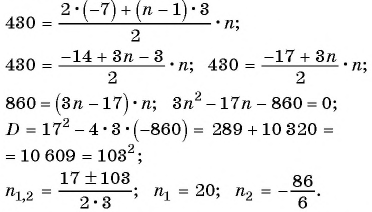
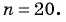
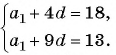
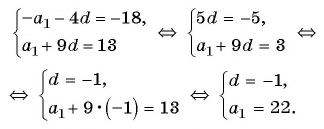
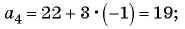
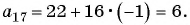
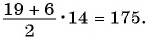
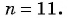
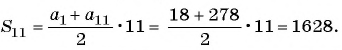
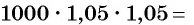
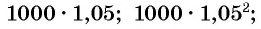
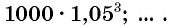
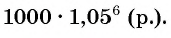
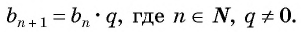
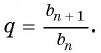
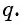
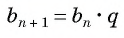
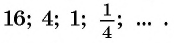
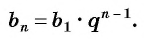
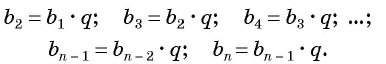
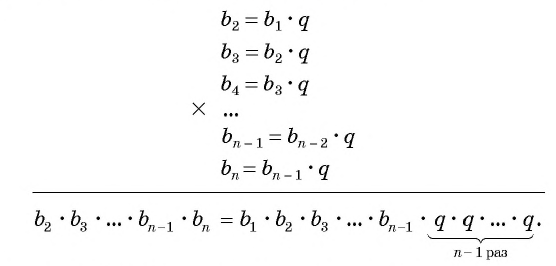
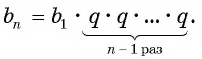
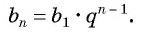
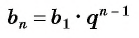
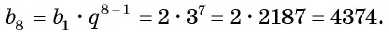
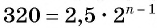
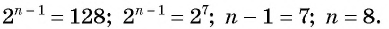
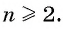
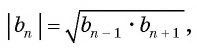
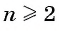
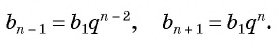
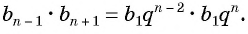
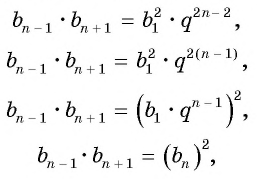
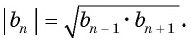
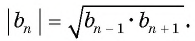
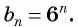
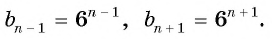
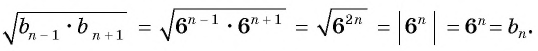
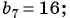
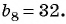
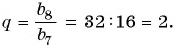
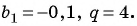
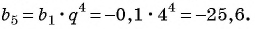
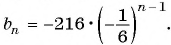
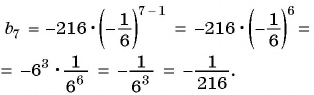
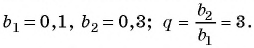
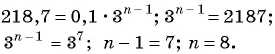
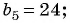
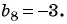
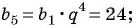
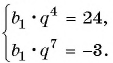
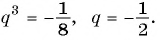
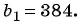
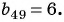
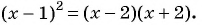
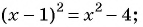
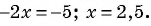

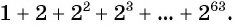
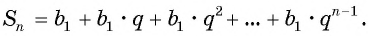
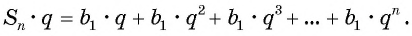
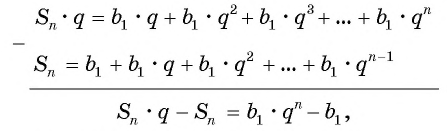
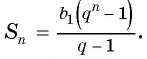
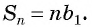
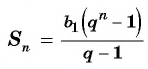
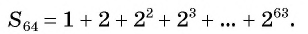
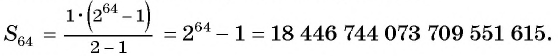
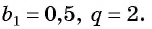
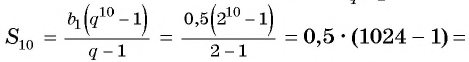
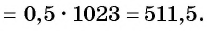
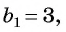
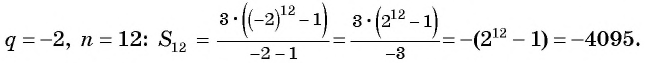
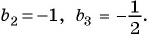
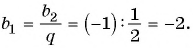
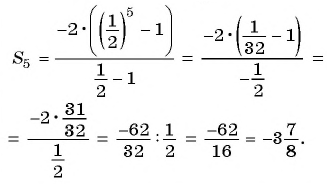
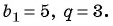
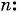
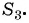
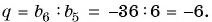
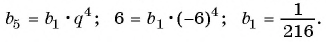
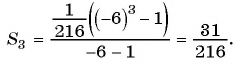
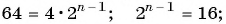
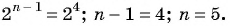
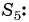
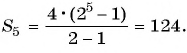
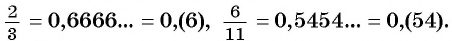
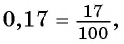
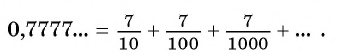
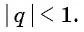
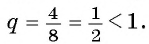
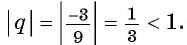
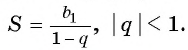
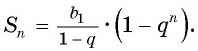
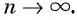
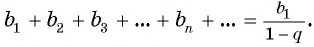
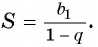
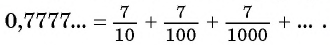
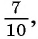
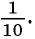
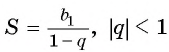
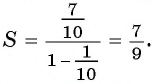
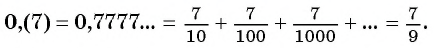
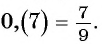
 , и найти знаменатель этой прогрессии
, и найти знаменатель этой прогрессии