Как найти полуоси эллипса по уравнению онлайн - Сайт, где вы сможете решить свои вопросы

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	– twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{”}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	–
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

ось:9x^2+4y^2=1
ось:16x^2+25y^2=100
ось:25x^2+4y^2+100x-40y=400
ось:frac{(x-1)^2}{9}+frac{y^2}{5}=100
Показать больше

Описание

Пошаговый расчет оси эллипса по заданному уравнению

ellipse-function-axis-calculator

Блог-сообщения, имеющие отношение к Symbolab

Practice Makes Perfect

Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

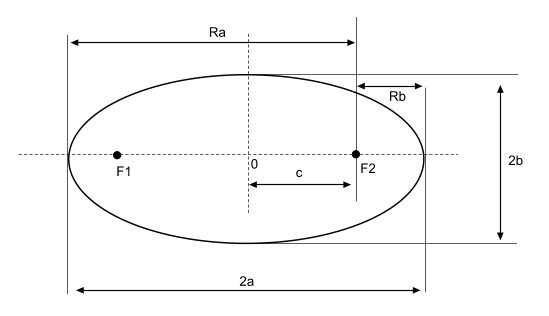
Полуось эллипса

Свойства

a, b – полуоси
c, d – оси
P – окружность
S – площадь

Полуоси эллипса представляют собой его радиусы, расположенные относительно друг друга под углом 90 градусов. Чтобы значения полуосей были актуальными для расчета площади и длины окружности, отрезки должны лежать на осях симметрии эллипса. Значения полуосей эллипса можно взять из уравнения, задающего его в плоскости. Чтобы найти полуоси эллипса, необходимо извлечь квадратный корень из соответствующих знаменателей.
x^2/a^2 +y^2/b^2 =1

Тогда, зная полуоси эллипса, можно найти его площадь и периметр по следующим формулам.
S=πab
P=4 (πab+(a-b))/(a+b)

Источник

Каноническое уравнение эллипса по двум точкам

Две точки с координатами

Первая координата

Вторая координата

Каноническое уравнение эллипса

Большая полуось эллипса

Малая полуось эллипса

Эксцентриситет эллипса

Фокусное/фокальное расстояние

Коэффициент сжатия

Координаты первого фокуса F1(x1:y1)

Координаты второго фокуса F2(x2:y2)

Фокальный параметр

Перифокусное расстояние

Апофокусное расстояние

Уравнение эллипса в каноническом виде имеет вот такой вид.

$?frac{x^2}{a^2}+frac{y^2}{b^2}=1$

Так как тут всего две переменных, то логично предположить, что по двум заданным точкам мы всегда сможем построить формулу эллипса.

Для расчета поставленной задачи воспользуемся материалом расчет кривой второго порядка на плоскости, который и позволит легко и быстро получить результат.

Кроме этого, на этой странице мы получим следующую информацию.

Фокальный параметр – половина длины хорды, проходящей через фокус и перпендикулярной большой оси эллипса

$p=cfrac{1-e^2}{e}$

Значение полуосей – большая полуось и малая полуось ( Естественно это в том случае, когда эллипс вытянут вдоль оси абсцисс)

$a=frac{b}{sqrt{1-e^2}}$

Эксцентриситет – коэффициент, показывающий насколько его фигура отличается от окружности

$e=frac{c}{a}$

Фокальное расстояние

c=ae

Коэффициент сжатия – отношение длин малой и большой полуосей

Перифокусное расстояние

$Ra=cfrac{1+e}{e}$

Апофокусное расстояние

$Rb=cfrac{1-e}{e}$

Примеры задач

Cоставить каноническое уравнение эллипса по двум точкам $Ra=cfrac{1+e}{e}$

Ввводим данные в калькулятор, не забывая что квадратный корень у нас обозначается sqrt

и получаем результат

Каноническое уравнение эллипса

Большая полуось эллипса

8.48528137423857

Малая полуось эллипса

5.656854249492381

Эксцентриситет эллипса

0.8958064164776166

Фокусное/фокальное расстояние

32.2490309931942

Коэффициент сжатия

0.4444444444444444

Координаты первого фокуса F1(x1:y1)

-16.1245154965971 : 0

Координаты второго фокуса F2(x2:y2)

16.1245154965971 : 0

Фокальный параметр

3.5555555555555554

Перифокусное расстояние

1.875484503402901

Апофокусное расстояние

34.1245154965971

И еще один пример

Даны две точки с координатами (3:2) и (4:-9) построить каноническое уравнение эллипса.

Если мы введем данные в калькулятор получим

Большая полуось эллипса

5.877538136328849

Малая полуось эллипса

NaN

Как видно, одна из осей не может быть определена, так как нам придется брать корень квадратный из отрицательного числа, а следовательно одна из осей будет комплексным числом, что быть не может.

Таким образом по этим двум точкам, нельзя построить эллипс.

А что же можно построить? Перейдя по ссылке данной в начале статьи, мы можем увидеть что это каноническое уравнение гиперболы.

$frac{x^2}{a^2}-frac{y^2}{b^2}=1$

Более подробно, про гиперболу есть отдельный калькулятор Каноническое уравнение гиперболы по двум точкам

Удачных расчетов!

Источник

Большая полуось эллипса Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Большая ось эллипса: 20 метр –> 20 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

10 метр –> Конверсия не требуется

10+ Большая ось эллипса Калькуляторы

Большая полуось эллипса формула

Большая полуось эллипса = Большая ось эллипса/2

a = 2a/2

Что такое эллипс?

Эллипс в основном представляет собой коническое сечение. Если мы разрезаем прямой круговой конус плоскостью под углом, большим, чем полуугол конуса. Геометрически эллипс — это совокупность всех точек на плоскости, сумма расстояний до которых от двух фиксированных точек является константой. Эти фиксированные точки являются фокусами эллипса. Наибольшая хорда эллипса является большой осью, а хорда, проходящая через центр и перпендикулярно большой оси, является малой осью эллипса. Окружность является частным случаем эллипса, в котором оба фокуса совпадают в центре, и поэтому обе большие и малые оси становятся равными по длине, которая называется диаметром окружности.

Источник

Господин Экзамен

Другие калькуляторы

График неявной функции
Поверхность, заданная уравнением

Канонический вид/
Уравнение эллипса

Каноническое уравнение эллипса

⚟

График:

x: [,
]

y: [,
]

z: [,
]

Качество:

(Кол-во точек на оси)

Тип построения:

Источник

Номер Строки

Полуось эллипса

Свойства

Каноническое уравнение эллипса по двум точкам

Примеры задач

Большая полуось эллипса Решение

10+ Большая ось эллипса Калькуляторы

Большая полуось эллипса формула

Что такое эллипс?

Другие калькуляторы

Каноническое уравнение эллипса

График:

Качество:

Тип построения:

Вам также может понравиться

Как составить планы на год чтобы они сбылись

Taobao как найти посредника

Как найти результаты опроса в гугл форме

Добавить комментарий Отменить ответ