Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6dc9dabc886f8f5b • Your IP : 85.95.188.35 • Performance & security by Cloudflare
Как найти полу периметр?
Как найти Полупериметр если есть периметр?
Если периметр – это сумма длин всех сторон фигуры, то полупериметр – сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках – (a+b)).
Как найти площадь треугольника зная его периметр?
Площадь треугольника = a * h/2. Периметр треугольника = a + b + c.
Как найти Полупериметр трапеции?
Трапеция – это четырехугольник с двумя параллельными сторонами. Чтобы найти периметр трапеции, нужно сложить длины всех четырех сторон. Зачастую в задачах длины некоторых сторон не даны, но известны другие величины, например, высота или угол трапеции.
Что такое площадь треугольника 3 класс?
Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.
Что такое площадь 3 класс?
Площадь – внутренняя часть любой плоской геометрической фигуры. Квадрат – это прямоугольник, у которого все стороны равны. . Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Формулы определения периметра, площади и сторон треугольника
Треугольник — это элементарная геометрическая фигура, содержащая минимально возможное количество составляющих — три.
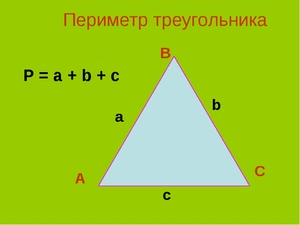
Точки соприкосновения сторон являются вершинами его углов, обозначаются заглавными латинскими символами A; B и C. Отрезки между вершинами являются сторонами или гранями треугольника и обозначаются названиями этих вершин: AB; BC; CA или прописной буквой противолежащего угла (вершины): AB=c; BC=a; CA=b.
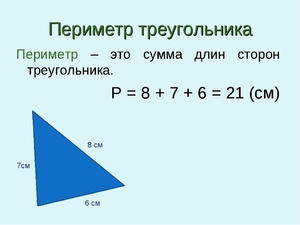
Периметр равен длине всех сторон фигуры, у треугольника он равен сумме трех сторон:
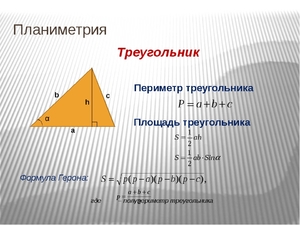
Высота треугольника — это перпендикуляр от прямой, на которой лежит основание, до одноименной вершины, обозначается h.
Площадь составляет величину поверхности, заключенной внутри фигуры, обозначается S. Произведение основания на высоту дает значение площади. Ее можно определить и по формуле Герона:
Из этого видео вы узнаете, как найти площадь треугольника.
Классификация треугольников
Треугольник состоит из сторон и углов, сумма его углов всегда равна 180 градусов: A+B+C=180°.
- Равноугольный: все вершины равны 60°, будет и равносторонним.
- Равнобедренный: при равенстве двух граней углы на основании равны.
- Разноугольный: все вершины разные, ребра у него тоже разные.
- Прямоугольный: один угол равен 90°, примыкающие грани называются катеты, противолежащая — гипотенуза. Бывает равнобедренным (катеты равны) или разноугольным (катеты разные).
- Тупоугольный: один угол больше 90°. Может быть равнобедренным или разноугольным.
Описание
Чтобы описать любой треугольник, достаточно указать:
- Одну сторону и прилегающие к ней углы.
- Две стороны и угол между ними.
- Три стороны.
Данных из любого пункта достаточно для построения заданной фигуры и вычисления всех ее параметров, используя теорему косинусов:
Подставляя известные значения, получим уравнение, решив которое узнаем неизвестные величины.
Cos90°=0, поэтому для прямоугольного треугольника c*c=a*a+b*b, где a и b — катеты, c — гипотенуза, сторона, лежащая напротив прямого угла.
Примеры
Известно, что одна грань равна 9 см и прилегающие углы по 60 градусов. Тогда из того, что сумма углов всегда равна 180°, получаем: 180=60+60+x; x=180—120=60. Все три вершины по 60°, значит, все стороны равны. Периметр составляет P=9+9+9=27 см, полупериметр p=13,5 см. Чтобы найти высоту, нужно опустить перпендикуляр из вершины на основание, получим прямоугольный треугольник с гипотенузой 9 см, катетом 4,5 см и катетом неизвестной длины, равным искомой высоте: 9*9—4,5*4,5=60,75=h 2 .
Высота равна корню квадратному из 60,75 или 7,79422863406 см. Умножаем основание на высоту, делим пополам и получаем площадь: 7,79422863406*9/2=35,074028853 см 2 . Если находить площадь по формуле Герона через полупериметр и ребра, ответ будет одинаковый:
S=√(13,5·(13,5—9)·(13,5—9)·(13,5—9))=35,074028853 см 2 .
Следующий пример с разносторонним треугольником. Дано: AB=12 см, BC=10 см, CA=8 см. Требуется найти периметр и площадь фигуры. P=a+b+c=BC+CA+AB=10 см+8 см+12 см=30 см. Площадь находим по формуле Герона, подставляя в нее уже известные значения, учитывая, что p=0,5Р; p=15 см. S=√(p·(p—a)·(p—b)·(p—c))=√(15·(15—10)·(15—8)·(15—12))=√15·5·7·3=√1575=39,686269666 см 2 .
Рассмотрим пример, когда известны два катета прямоугольного треугольника. Допустим, они имеют значения два и четыре метра. Тогда гипотенуза будет равна корню квадратному из суммы квадратов катетов √2 2 +4 2 =4,472135955 м. Периметр 2+4+4,472135955=10,472135955. Площадь равна половине произведения катетов S=2·4=8м 2 .
Когда известны две стороны и угол между ними, остается найти только третью сторону по теореме косинусов. Пусть известные стороны составляют значения 16 и 28 метров, а угол между ними будет в 60 градусов, тогда третья сторона будет равна корню квадратному из этого выражения 16 2 +28 2 — 2·16·28·0,5, что составит значение в 24,3310501212 м. Периметр равен 16+28+24,3310501212=68,3310501212≈68,33 м. Полупериметр будет 34,165 м. Подставляя полученные значения в формулу Герона, найдем площадь S=√(34,165·(34,165—16)·(34,165—28)·(34,165—24,33))=193,982314238 м 2 .
Если известно три параметра любого треугольника — два угла и сторона или две стороны и угол между ними, то ничего особенно сложного в нахождении неизвестных параметров треугольника — периметра, площади или высоты — нет. Нужно только внимательно производить простые вычисления. Иногда можно проявить и смекалку, разбив фигуру на несколько более простых в вычислении, например, прямоугольных треугольников. В каждом конкретном случае все зависит от исходных данных. Все формулы и вычисления, приведенные выше, верны для плоских фигур; для расположенных на сферической поверхности ход вычислений будет иным.
Видео
Это видео поможет вам закрепить полученные знания.
[spoiler title=”источники:”]
http://fcessentuki.ru/kak-naiti-polu-perimetr
http://liveposts.ru/articles/education-articles/matematika/formuly-opredeleniya-perimetra-ploshhadi-i-storon-treugolnika
[/spoiler]
Содержание
- – Как найти Полупериметр если есть периметр?
- – Как найти площадь треугольника зная его периметр?
- – Как найти Полупериметр трапеции?
- – Что такое площадь треугольника 3 класс?
- – Что такое площадь 3 класс?
Чтобы найти полупериметр треугольника, нужно сложить длины всех его сторон, и полученный результат разделить на два.
Как найти Полупериметр если есть периметр?
Если периметр – это сумма длин всех сторон фигуры, то полупериметр – сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках – (a+b)).
Как найти площадь треугольника зная его периметр?
Площадь треугольника = a * h/2. Периметр треугольника = a + b + c.
Как найти Полупериметр трапеции?
Трапеция – это четырехугольник с двумя параллельными сторонами. Чтобы найти периметр трапеции, нужно сложить длины всех четырех сторон. Зачастую в задачах длины некоторых сторон не даны, но известны другие величины, например, высота или угол трапеции.
Что такое площадь треугольника 3 класс?
Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.
Что такое площадь 3 класс?
Площадь – внутренняя часть любой плоской геометрической фигуры. Квадрат – это прямоугольник, у которого все стороны равны. … Квадратный сантиметр – квадрат со стороной 1 сантиметр.
Интересные материалы:
Как долго принимать аллохол?
Как долго проходят симптомы цистита?
Как долго проходит корочка от Микроблейдинга?
Как долго проходит красный загар?
Как долго растет груша?
Как долго шпаклевать стены?
Как долго сходят корочки после Пудрового напыления бровей?
Как долго смывается тоник для волос?
Как долго смывается тоник с волос?
Как долго смывается тонировка с волос?
Содержание материала
- Треугольники [ править ]
- Видео
- Если известны длины трех сторон
- Для прямоугольного треугольника
- Площадь треугольника по гипотенузе и острому углу
- Площадь прямоугольного треугольника по катету и прилежащему углу
- Если он равнобедренный
- Как найти Полупериметр трапеции?
Треугольники [ править ]
В любом треугольнике расстояние вдоль границы треугольника от вершины до точки на противоположном крае, которой касается вневписанная окружность, равно полупериметру.
Полупериметр чаще всего используется для треугольников; формула для полупериметра треугольника со сторонами a , b и c имеет вид
Видео
Если известны длины трех сторон
Делайте так:
- Найдите периметр. Для этого сложите все три стороны.
- Найдите полупериметр – разделите периметр на два. Запомните значение.
- Отнимите от полупериметра длину первой стороны. Запомните.
- Отнимите от полупериметра длину второй стороны. Тоже запомните.
- Отнимите от полупериметра длину третьей стороны. И ее запомните.
- Умножьте полупериметр на каждое из этих чисел (разницу с первой, второй и третьей стороной).
- Найдите квадратный корень.

Эта формула еще называется формулой Герона. Возьмите на заметку, если вдруг учитель спросит.
Для прямоугольного треугольника
Для прямоугольного треугольника чаще всего используют одну формулу — половину произведения катетов. Потому что их всегда можно найти с помощью правил тригонометрии или теоремы Пифагора.
, где , — стороны.

Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.

Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.

Катетом принято называть одну из двух сторон, образующих прямой угол.
Если он равнобедренный
То есть у него равны боковые стороны. В таком случае надо провести высоту к основанию (той стороне, которая не равна «бедрам»), перемножить высоту с основанием и поделить результат на два.

Как найти Полупериметр трапеции?
Трапеция – это четырехугольник с двумя параллельными сторонами. Чтобы найти периметр трапеции, нужно сложить длины всех четырех сторон. Зачастую в задачах длины некоторых сторон не даны, но известны другие величины, например, высота или угол трапеции.
Теги
Лучший ответ
anastasia.kochura
Профи
(699)
12 лет назад
сложить все стороны и разделить на 2
Остальные ответы
Надя Кратко
Мастер
(1749)
12 лет назад
отмерь периметр, раздели на 2
Болеслав Звершхановский
Просветленный
(24068)
12 лет назад
Сложить все стороны и разделить пополам, ОДНАКО !!!
Kirill ___________
Ученик
(123)
12 лет назад
Полупериметр — половина периметра. а периметр – это сумма длин всех сторон.
Сергей Свиридов
Гуру
(3081)
12 лет назад
Полупериметр равностороннего треугольника = сторона + основание/2
Игорь
Мастер
(2205)
12 лет назад
Надо объем треугольника разделить на его площадь.
Коржавин
Знаток
(281)
12 лет назад
Пройти по длинной стороне!
|
периметр равен 36, а диагональ 13, как найти площадь?
Прости, но я в своём репертуаре первым делом беру тетрадь в клеточку и черчу на новом листе условный прямоугольник. Из одного угла в противоположный протягиваем диагональ – это её длина нам известна и равна 13. Пусть у нас всё будет в метрах, чтобы не применять условные единицы.
Теперь, чтобы найти площадь (S), нам необходимо определить стороны геометрической фигуры. Но нам известна их удвоенная сумма – периметр и сумма квадратов – она будет равна квадрату диагонали. Как ни крути, а одним действием вычислить не удаётся. Видимо, потребуется строить систему уравнений, которую и решать в итоге.А выглядит она следующим образом:
В первой строке можно разделить обе стороны равенства на 2, а во второй возведём 13 в квадрат.
Теперь нам не составит большого труда выразить длину одной из сторон через другую. Сделать это позволяет первая из приведённых формул. Мы, например, просто вычтем из каждой половинки значение (y):
После этого не трудно подставить полученное выражение во вторую формулу вместо (a). Это позволит нам остаться в вычислениях один на один с неизвестным значением (b):
И тут меня осенило – мы ведь вплотную приблизились к решению квадратного уравнения. Об этом явно свидетельствуют следующие преобразования формулы:
Как решаются такие уравнения? Кто помнит? А что такое “Дискриминант”? Тоже забыли? Давайте вспоминать вместе. И в первую очередь эту саму D, которая равна b²-4ac, где abc – коэффициенты в полученной нами формуле (a = 2, b = -36, c = 155). В итоге:
Дискриминант больше нуля и это свидетельствует о том, что нам удастся отыскать два корня этого уравнения.
Я надеюсь, что вы поняли, что за значения мы получили? Это ведь стороны искомого прямоугольника. Одну из них можно оставить “игреком”, а вторую обозначить “иксом”. Вам остаётся лишь перемножить два дробных числа, чтобы получить значение площади = 77.5 квадратных метров. Не верите? Что же, давайте перепроверим. И для этого вернёмся к теореме Пифагора, согласно которой:
Всё сходится. система выбрала этот ответ лучшим
Артём Денисов более года назад Наиболее простой способ решить задачку – найти стороны и перемножить их. Поскольку соотношение сторон нам неизвестно, то их необходимо определить (сделаем это с помощью длины гипотенузы и диагонали). Сумма 2-х сторон треугольника, который составляет половину площади прямоугольника:
БОльшая сторона равна разности полупериметра (18) и меньшей стороны. Выразим площадь в формуле через полупериметр (полупериметр² – диагональ² / 2). На двойку делим потому, что именно такое количество равных треугольников в прямоугольнике. Решение:
Ответ: площадь равна 77.5.
Sagavaha более года назад Самое простое решение – это найти стороны и умножить их одна на другую. Но вот нам не известно соотношение сторон, именно тут нам и пригодится и длина гипотенузы/диагонали прямоугольника из условия. Сумма двух сторон треугольника, составляющего половину площади прямоугольника равна полупериметру – 36:2=18 Большая сторона a будет равна разности полупериметра 18 и меньшей стороны b, но считать их точное число нам не обязательно, так как можно просто выразить площадь в формуле через полупериметр, который у нас есть. Площадь S=(полупериметр в квадрате (18Х18) – диагональ в квадрате (d^2), и всё это делим пополам, так как треугольника два и они равны. (324-169):2=77,5 Это и будет наш ответ
Марина Вологда более года назад Чтобы правильно ответить на вопрос, давайте вспомним, что такое периметр, диагональ и площадь, которую нам необходимо найти. Итак, мы знаем, что диагональ у нас равна 13 (пусть будет см). Известен нам и периметр, который равен 36 см. Нам надо найти площадь прямоугольника. Площадь прямоугольника можно найти по формуле, где нужны значения диагонали и стороны.
Нам не обойтись без формулы Пифагора, а также формулы периметра.
По второй формуле находим одну из сторон, получая следующую формулу:
Упрощаем все:
Вычисляем дискриминант квадратного уравнения, выглядит эта формула вот так:
А теперь подставляем известные нам данные: D= 8*13² – 36² = 56 Применяя формулы для выявления сторон прямоугольника, у нас получается вот такое уровнение:
Ну и площадь теперь найти не проблематично, для этого 10,87 * 7,13 = 77,5 Krustall более года назад Здесь надо искать что-то простое, поэтому советую решить таким образом, найти стороны прямоугольника и перемножить их одну за другой. Но пропорцию не знаем, тут пригодится длина гипотенузы/диагонали прямоугольника из условия задачи. Сумма двух сторон треугольника, равная половине площади прямоугольника, равна половине длины окружности – 36:2=18. Большая сторона А будет равна разнице между половиной периметра18 и меньшей стороной В, но не нужно считать их точное количество, потому что мы можем просто выразить площадь в формуле через имеющуюся у нас половину периметра. Площадь равна (половина круга в квадрате (18Х18) – диагональ в квадрате (d^2) и делим все это пополам, так как треугольников два и они равны (324-169): 2 = 77,5.
Преследующий более года назад Как найти площадь прямоугольника, если известны периметр и диагональ?Вроде бы вопрос со школьной программы, но когда прошли годы – тяжело и вспомнить. А лично мне – вообще тяжело давалась геометрия, по этому я обратился с этим вопросом к другу, который просто обожает этот предмет. Лично мне тяжело далось понять, но автору вопроса должна эта информация помочь. Нужно следовать правилу:
периметр Q диагональ E найти R Q = 2(a+b) E² = a² + b² R = ab a² + b² = a² + b² + 2ab – 2ab = (a+b)² – 2ab =E² 2ab = (a+b)² – d²(a+b) = P/2 (a+b)² = Q² / 4 2ab = (Q² / 4) – d² R = (Q² / 8) – (E² / 2) Применив формулу к данным, что периметр равен 36, а диагональ 13 – площадь прямоугольника будет ровна 77.5 квадратных метров.
Viridi более года назад Для того чтобы найти площадь прямоугольника нужно знать несколько исходных данных. В каждом классе школы, в которых есть предмет геометрия, первоначальные данные усложняются с каждым разом. самое простое – это конечно искать площадь, зная величину его сторон, но в вопросе приведено более сложное задание. При его решении мы будем использовать теорему Пифагора. Пусть катеты фигуры будут обозначены латинскими буквами a и b. В результате некоторых математических приёмов мы получим вот такое решение: Чтобы найти площадь фигуры, в данном случае прямоугольника, нужно знать чему равно произведение a и b. Как мы видим, площадь прямоугольника в конечном итоге получилась равно числу 77, 5. Судя, по предыдущим ответам, где в ответе аналогичная цифра, мы решили всё правильно.
Sanch001 более года назад P.s. В задаче не указаны единицы измерения, поэтому для примера я возьму сантиметры ( см ). Для того чтобы найти площадь прямоугольника при известных периметре и диагонали, первым делом нужно найти полупериметр. Для его нахождения необходимо периметр прямоугольника поделить по полам: 36 : 2 = 18 см Рассмотрим один из треугольников полупериметра: катеты нам не известны, гипотенуза равна 13 см. Назовём две стороны (катеты) как a и b. Тогда по теореме Пифагора следует что: a² + b² = 169см ( 13² ) Теперь выразим длину одной стороны относительно другой: x = 18 – y. Далее приобразовываем формулы: (18² – 2 * 18 * y + y²) + y² = 169 324 – 36 * y + 2 * y² = 169 2 * y² – 36 * y + 324 – 169 = 0 2 * y² – 36 * y + 155 = 0 Решаем через Дискриминант чисел: D = 36² – 4 * 2 * 155 = 1296 – 1240 = 56 y1 = (-b – √D)/2a = 7.1291713066 y2 = (-b + √D)/2a = 10.8708286934 7.1291713066 * 10.8708286934 = 75,4 см². Давайте проверим: 7.1291713066² + 10.8708286934² = 13² 50.8250835188+118.174916481 ≈ 169 Ответ: площадь прямоугольника 75,4 см².
Валерий Альбертович 3 года назад Чтобы решить такое задание, воспользуемся теоремой Пифагора. Т.к. у нас есть диагональ в прямоугольнике, то она образует (“делит”) из прямоугольника два прямоугольных треугольника, стороны в котором мы и сможем найти по теореме Пифагора. Пусть a и b – катеты прямоугольного треугольника, диагональ (d) нам известна, она в данном случае является гипотенузой. Тогда: d^2 = a^2 + b^2 => a^2 + b^2 = 13^2 = 169 P прям. = 2(a+b) = 36 => a + b = P/2 = 36/2 = 18 Площадь прямоугольника вычисляется по формуле: S = a*b Воспользуемся формулой: S = ((P/2)^2 – d^2)/2, подставим S = (18^2 – 13^2)/2 = (324 – 169)/2 = 155/2 = 77,5 Ответ: 77,5 Rafail 4 года назад Обозначим стороны прямоугольника х и у. По теореме Пифагора х^2+y^2=13^2=169. Р=2*(х+у). отсюда х+у=Р/2 (в данном случае 36/2=18). Возведём выражение (х+у) в квадрат. x^2+2*x*y+y^2=324. Отсюда получаем: S=х*у(324-169)/2=77,5. |















