Вневписанные окружности
Теорема 1 . В любом треугольнике биссектрисы двух внешних углов и биссектриса внутреннего угла, не смежного с ними, пересекаются в одной точке.
Доказательство . Рассмотрим произвольный треугольник ABC и продолжим, например, стороны BA и BC за точки A и C соответственно (рис.1).
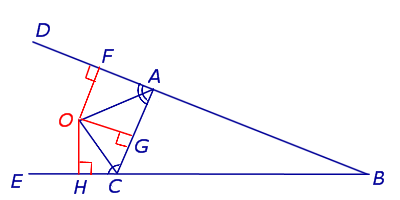

Проведём биссектрисы углов DAC и ECA , которые являются внешними углами треугольника ABC . Обозначим точку пересечения этих биссектрис буквой O . Докажем, что точка O лежит на биссектрисе угла ABC , который является внутренним углом треугольника ABC , не смежным с внешними углами DAC и ECA . С этой целью опустим из точки O перпендикуляры OF , OG и OH на прямые AB , AC и BC соответственно. Поскольку AO – биссектриса угла DAC , то справедливо равенство:
Следовательно, справедливо равенство
Замечание 1 . В ходе доказательства теоремы 1 мы установили, что справедливы равенства
откуда вытекает, что точки F , G и H лежат на одной окружности с центром в точке O .
Определение . Окружность называют окружностью, вневписанной в треугольник , или вневписанной окружностью, если она касается касается одной стороны треугольника и продолжений двух других сторон (рис.2).
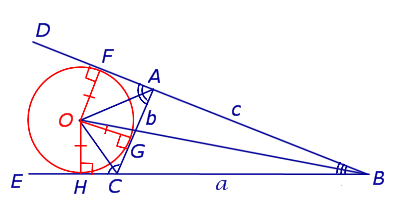
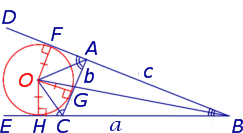
Замечание 2 . У каждого треугольника существуют три вневписанных окружности. На рисунке 2 изображена одна из них.
Замечание 3 . Центр вневписанной окружности, изображенной на рисунке 2, лежит на биссектрисе угла B , а окружность касается стороны b . Для удобства обозначений и терминологии будем называть эту окружность вневписанной окружностью, касающейся стороны b , и обозначать её радиус символом rb .
Теорема 2 . Пусть вневписанная окружность касается стороны AC треугольника ABC . Тогда отрезки касательных касательных от вершины B до точек касания с вневписанной окружностью равны полупериметру треугольника.
Доказательство . Снова рассмотрим рисунок 2 и докажем, что выполнено равенство
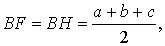
где a, b, c – стороны треугольника ABC . Действительно, отрезки AG и AF равны, как отрезки касательных к окружности, выходящих из точки A . Отрезки CG и CH равны, как отрезки касательных к окружности, выходящих из точки C . Отрезки BF и BH равны, как отрезки касательных к окружности, выходящих из точки B . Отсюда получаем:

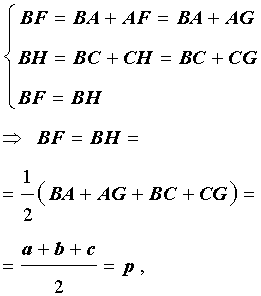
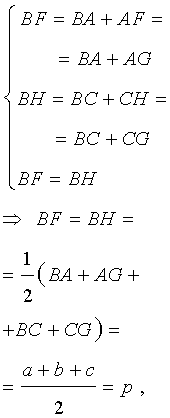
где буквой p обозначен полупериметр треугольника ABC . Теорема 2 доказана.
Теорема 3 . Радиус вневписанной окружности , касающейся стороны b , вычисляется по формуле
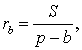
где буквой S обозначена площадь треугольника ABC , а буквой p обозначен полупериметр треугольника ABC .
Доказательство . Снова рассмотрим рисунок 2 и заметим, что выполнены равенства
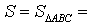

Следовательно, справедливо равенство
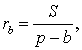
что и требовалось доказать.
Следствие . Радиусы двух других вневписанных в треугольник ABC окружностей вычисляются по формулам:
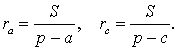
Теорема 4 . Если обозначить буквой r радиус вписанной в треугольник ABC окружности, то будет справедлива формула:
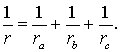
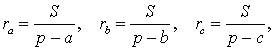
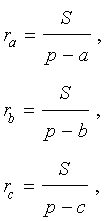
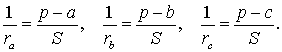
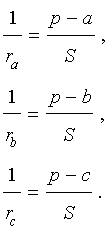
Складывая эти формулы и воспользовавшись формулой для радиуса вписанной окружности
 ,
,
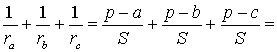
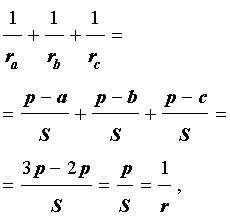
что и требовалось доказать.
Теорема 5 . Площадь треугольника можно вычислить по формуле
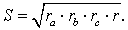
Доказательство . Перемножим формулы
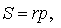
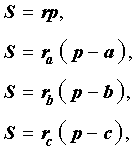
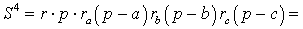
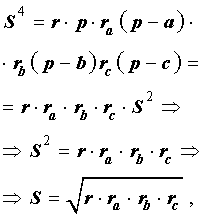
что и требовалось доказать.
Теорема 6 . Если обозначить буквой R радиус описанной около треугольника ABC окружности, то будет справедлива формула:
Доказательство . Воспользовавшись формулами для радиусов вписанной и вневписанных окружностей, а также формулой Герона, получим
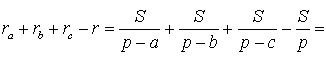
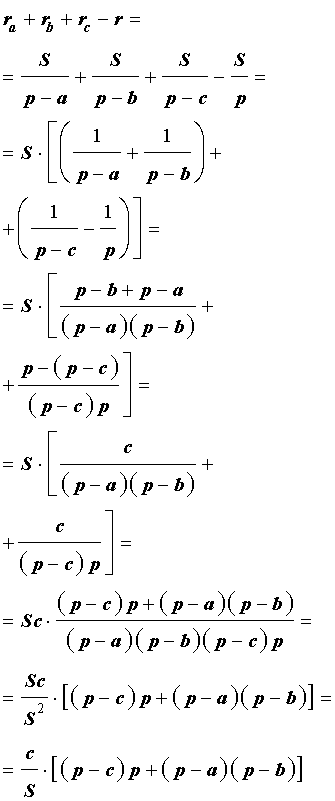
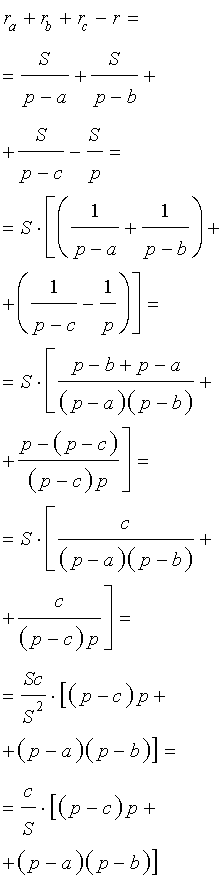
Преобразуем выражение, стоящее в квадратной скобке:
Длина окружности

О чем эта статья:
6 класс, 9 класс, ЕГЭ/ОГЭ
Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так – l
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Как найти длину окружности через диаметр
Хорда — это отрезок, который соединяет две точки окружности.
Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:
π— число пи — математическая константа, примерно равная 3,14
d — диаметр окружности
Как найти длину окружности через радиус
Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:
π — число пи, примерно равное 3,14
r – радиус окружности
Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.
Как вычислить длину окружности через площадь круга
Если вам известна площадь круга, вы также можете узнать длину окружности:
π — число пи, примерно равное 3,14
S — площадь круга
Как найти длину окружности через диагональ вписанного прямоугольника
Как измерить окружность, если в нее вписан прямоугольник:
π — число пи, примерно равное 3,14
d — диагональ прямоугольника
Как вычислить длину окружности через сторону описанного квадрата
Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:
π – математическая константа, примерно равная 3,14
a – сторона квадрата
Как найти длину окружности через стороны и площадь вписанного треугольника
Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:
π — математическая константа, она примерно равна 3,14
a — первая сторона треугольника
b — вторая сторона треугольника
c — третья сторона треугольника
S — площадь треугольника
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.
Формула вычисления длины окружности:
π — математическая константа, примерно равная 3,14
a — сторона многоугольника
N — количество сторон многоугольника
Задачи для решения
Давайте тренироваться! Двигаемся от простого к сложному:
Задача 1. Найти длину окружности, диаметр которой равен 5 см.
Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:
Подставляем туда известные переменные и получается, что длина окружности равна
Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм
Решение. Радиус окружности равен Подставим туда наши переменные и получим
Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.
Обучение на курсах по математике поможет закрепить полученные знания на практике.
Периметр прямоугольника
Периметр прямоугольника — это сумма
всех сторон прямоугольника.
Периметр прямоугольника можно рассчитать
через четыре стороны, через смежные стороны,
через диагональ, через площадь,
через радиус описанной окружности.
Самый простой способ найти периметр
прямоугольника, это сложить все стороны.
Также, исходя из свойства прямоугольника, — «противоположные
стороны равны и параллельны», можно сказать, что периметр
численно равен удвоенной сумме ширины и высоты — двух
смежных сторон прямоугольника.
Кроме этих двух способов периметр прямоугольника
можно найти через другие величины. Например, через
площадь прямоугольника, диагональ прямоугольника, и так далее.
В прямоугольник невозможно вписать окружность,
поэтому выразить периметр через вписанную
окружность не получится.
Единицы измерения периметра прямоугольника:
км, м, дм, см, мм.
Формулы периметра прямоугольника
- Периметр прямоугольника через четыре стороны
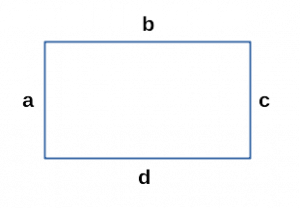
a, b, c, d — стороны прямоугольника;
a || c, b || d;
a = c, b = d;
Периметр прямоугольника через смежные стороны 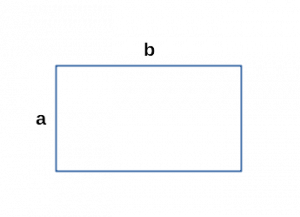
a, b — смежные стороны;
a ≠ b;
Периметр прямоугольника через любую сторону и диагональ 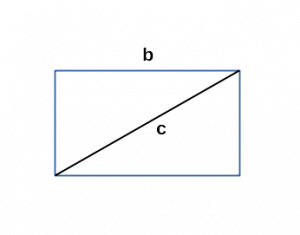
b — любая сторона;
c — диагональ;
Периметр прямоугольника через любую сторону и площадь 
b — любая сторона;
S — площадь;
Периметр прямоугольника через любую сторону и радиус описанной окружности 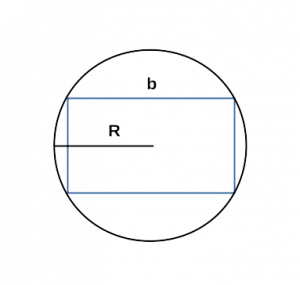
b — любая сторона;
R — радиус описанной окружности;
Полупериметр
Полупериметр — это половина периметра.
Обозначается латинской буквой p.
Чтобы найти полупериметр нужно разделить
периметр на два, или домножить периметр на 0.5.
[ p = frac
<2>= P cdot 0.5 ]
Полупериметр применяется в некоторых формулах
нахождения разных величин прямоугольника. Вместо того,
чтобы вычислять периметр, в таких формулах
удобней вычислять полупериметр.
Основные определения и величины
Длина прямоугольника — это длинная сторона
/ наибольшая сторона прямоугольника.
Обозначается латинской буквой a.
Ширина прямоугольника — это широкая сторона
/ наименьшая сторона прямоугольника.
Обозначается латинской буквой b.
Сторона прямоугольника — это ширина или длина прямоугольника,
в зависимости от численного значения длины стороны.
Обозначается латинской буквой a или b.
Диагональ прямоугольника — это отрезок, соединяющий
противоположные стороны прямоугольника.
Обозначается латинской буквой c или d.
Средняя линия прямоугольника — это отрезок, соединяющий
наименьшие параллельные стороны прямоугольника друг с
другом, причем делящий их пополам на равные отрезки.
Обозначается латинской буквой l.
Радиус описанной окружности прямоугольника — это отрезок,
соединяющий центр описанной около треугольника
окружности и произвольную точку на окружности.
Обозначается латинской буквой R.
Высота прямоугольника — это любая сторона прямоугольника,
а также любой отрезок в прямоугольнике, образующий угол в 90 градусов.
Обозначается латинской буквой h.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/dlina-okruzhnosti
http://colibrus.ru/perimetr-pryamougolnika/
[/spoiler]
Длина (периметр) окружности калькулятор онлайн умеет вычислять длину восемью способами:
- По радиусу.
- По диаметру.
- По площади окружности.
- По диагонали вписанного прямоугольника.
- По стороне описанного квадрата.
- По сторонам и площади описанного треугольника.
- По площади вписанного треугольника.
- По стороне вписанного многогранника.
Сделав расчет периметра на этом онлайн калькуляторе Вы получите не только ответ, но и детальное, пошаговое решение с выводом формул и промежуточных действий.
Длина окружности или периметр окружности – это длина кривой из множества точек которая ограничивает собой круг.
Длина окружности может быть найдена по длине пути, который проедет круг сделав один полный оборот.
Как найти длину окружности?
Найти длину окружности очень просто на нашем онлайн калькуляторе. Так же длина может быть найдена самостоятельно по формулам. Выбор нужной формулы зависит от того какие данные известны.
1) По радиусу
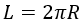
где R – радиус окружности.
2) По диаметру
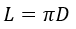
где D – диаметр окружности.
3) По площади окружности
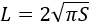
ггде S – площадь окружности.
4) По диагонали вписанного прямоугольника
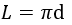
где d – диагональ вписанного прямоугольника.
5) По стороне описанного квадрата
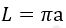
где a – сторона описанного квадрата.
6) По сторонам и площади описанного треугольника
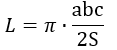
где a,b,c – стороны описанного треугольника, S – его площадь.
7) По площади вписанного треугольника
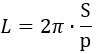
где p – полупериметр вписанного треугольника, S – его площадь.
8) По стороне вписанного многогранника
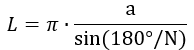
где a – сторона вписанного многогранника, N – количество сторон.
Скачать все формулы в формате Word
8 способов найти длину окружности
Выбирайте формулу, ориентируясь на известные величины.
1. Как найти длину окружности через диаметр
Просто умножьте диаметр на число пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d —диаметр окружности.
2. Как найти длину окружности через радиус
Умножьте число пи на два радиуса.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- r — радиус окружности.
3. Как вычислить длину окружности через площадь круга
Умножьте число пи на четыре площади круга.
Найдите корень из результата.
- O — искомая длина окружности.
- S – площадь круга. Напомним, кругом называют плоскость внутри окружности.
- π (пи) — константа, равная 3,14.
4. Как найти длину окружности через диагональ вписанного прямоугольника
Умножьте число пи на диагональ.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- d – любая диагональ прямоугольника.
5. Как вычислить длину окружности через сторону описанного квадрата
Умножьте число пи на сторону квадрата.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- a – любая сторона квадрата.
6. Как найти длину окружности через стороны и площадь вписанного треугольника
Перемножьте стороны треугольника.
Поделите результат на площадь и на два.
Умножьте полученное число на пи.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- a, b, c – стороны треугольника.
7. Как найти длину окружности через площадь и полупериметр описанного треугольника
Поделите площадь треугольника на его полупериметр.
Умножьте результат на число пи и на два.
- O — искомая длина окружности.
- π (пи) — константа, равная 3,14.
- S – площадь треугольника.
- p – полупериметр треугольника (равен половине от суммы всех сторон).
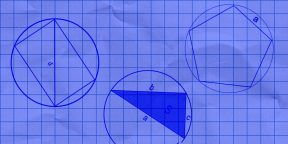
8. Как вычислить длину окружности через сторону вписанного правильного многоугольника
Разделите 180 градусов на количество сторон многоугольника.
Найдите синус полученного числа.
Разделите сторону многоугольника на результат.
Умножьте получившееся число на пи.
- O — искомая длина окружности.
- a — сторона правильного многоугольника. Напомним, в правильном многоугольнике все стороны равны.
- π (пи) — константа, равная 3,14.
- N — количество сторон многоугольника. К примеру, если в задаче фигурирует пятиугольник, как на изображении выше, N будет равняться 5.
Читайте также 📐✏️🎓
- Как найти периметр прямоугольника
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Вычисление длины окружности
При решении задач и в повседневной жизни можно встретить множество предметов круглой формы, в связи с чем возникает необходимость в их измерении. К примеру, для расчета объема материала, необходимого для производства круглого стакана определенного размера, потребуется построить и найти длину его окружности.
Определение
Окружность представляет собой замкнутую плоскую кривую, состоящую из всех точек на плоскости, которые равноудалены от заданной точки.
Рассматриваемая в рамках этого определения точка является центром окружности. Если соединить центр с любой точкой, принадлежащей окружности, то получится радиус. Радиусом также называют длину данного отрезка.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Радиус окружности является прямым отрезком, который выходит из центра окружности и проведен до ее границы.
Таким образом, радиус окружности соединяет ее центр с точкой, расположенной на этой окружности. Для обозначения радиуса используют r.
Определение
Диаметр окружности – является прямым отрезком, который соединяет две точки, расположенные на границе окружности, и проходит через центр этой окружности.
Данный параметр обозначают D или d.
Как рассчитать через диаметр или радиус
Длина окружности также является периметром этой окружности. Для расчета длины или периметра круга необходимо знать диаметр или радиус.
Формулы для вычисления длины окружности:
(L = pi DL=pi D)
(L = 2 pi rL=2pi r)
где L – является длиной окружности;
D – определяется, как диаметр окружности;
r – представляет собой радиус окружности;
(pi) – это число Пи, равное примерно 3,14.
Исходя из представленных формул для расчета длины окружности, можно вывести соотношение радиуса и диаметра окружности:
(D = 2rD=2r)
Основные формулы с пояснением
Обладая информацией о радиусе и диаметре окружности, достаточно просто рассчитать ее длину. Однако не во всех задачах присутствуют эти данные. Есть ряд примеров, в которых определить длину окружности необходимо с помощью параметров другой геометрической фигуры.
Вычисление длины окружности через площадь круга
В том случае, когда известна площадь круга, можно рассчитать длину окружности по формуле:
(L=sqrt{S4pi })
где (pi) — является числом пи, значение которого равно 3,14;
S — определяет площадь круга
Расчет длины окружности через диагональ вписанного прямоугольника
В задачах можно встретить примеры вписанного в окружность прямоугольника.
В этом случае длина окружности рассчитывается по формуле:
(L=pi * d)
где ( pi) — является числом пи, значение которого равно 3,14;
d — является диагональю рассматриваемого прямоугольника.
Как вычислить длину окружности через сторону описанного квадрата
В том случае, когда окружность вписана в квадрат с прямыми углами, сторона которого известна, можно определить длину этой окружности.
(L=pi * a)
где (pi ) — является числом пи, значение которого равно 3,14;
a — определяет длину стороны квадрата
Расчет длины окружности с помощью сторон и площади вписанного треугольника
Предположим, что в окружность вписан треугольник. Если имеется информация о всех его трех сторонах, а также площади, то можно рассчитать длину окружности, оперируя следующей формулой:
(L=pi *frac{abc}{2S})
где (pi) — математическая константа со значением 3,14;
a — является первой стороной треугольника;
b — является второй стороной треугольника;
с – является третьей стороной треугольника;
S – определяется, как площадь рассматриваемого треугольника.
Способ нахождения длины окружности при известной площади и полупериметру описанного треугольника
Представим, что в какой-то треугольник вписана окружность. Известно значение площади треугольники и его полупериметр. Необходимо рассчитать длину окружности. Следует заметить, что периметром треугольника называют сумму всех его сторон, а полупериметр составляет половину этой суммы. Таким образом, для нахождения полупериметра нужно определить периметр треугольника и разделить его на два.
Формула расчета длины окружности:
(L=2pi *frac{S}{p})
где (pi) — математическая константа со значением 3,14;
S — является площадью треугольника;
p — представляет собой полупериметр треугольника.
Как вычислить длину окружности через сторону вписанного правильного многоугольника
Когда в окружность вписан правильный многоугольник, в первую очередь стоит сосчитать количество его сторон. Также требуется знать длину стороны этой геометрической фигуры. Стороны правильного многоугольника одинаковы, как у квадрата. В этом случае формула для расчета длины окружности имеет вид:
(L=pi *frac{a}{sin frac({180}{N})})
где (pi) — математическая константа со значением 3,14;
a — это сторона многоугольника;
N — определяет количество сторон многоугольника.
Примеры решения задач
Задача 1
Необходимо рассчитать, какова длина окружности, если ее диаметр составляет 5 см.
Решение
При известном диаметре окружности можно рассчитать ее длину с помощью формулы:
(L = pi D)
Подставив известные из условия задачи значения, получим:
(L = pi D = 3,14 * 5 = 15,7) (см)
Ответ: длина окружности равна 15,7 см.
Задача 2
Требуется определить длину окружности, описанной вокруг правильного треугольника, сторона которого составляет (a=4sqrt{3}) дм.
Решение
Радиус окружности составляет:
(R=frac{a}{sqrt{3}})
При подстановке переменных формула будет изменена:
(R=frac{4sqrt{3}}{sqrt{3}})
При известном радиусе окружности можно рассчитать длину рассматриваемой окружности, используя соответствующую формулу:
(L = 2 pi r=2 pi *4=2*3,14*4=25,12) (дм)
Ответ: длина окружности составляет 25,12 дм.
Задача 3
Дана окружность, радиус которой равен 2 см. Требуется рассчитать длину окружности.
Решение
(L = pi d)
d=2 *r= 4
L = 3.14 * 4 = 12,56 (см)
Ответ: длина окружности равна 12,56 см.
Задача 4
Имеется окружность с радиусом 3 см. Необходимо определить длину данной окружности.
Решение
(L = pi d)
L = 3.14 * 3 = 9,42 (см)
Ответ: длина окружности составляет 9,42 см.
Формы труб
Автор Антон
Дата
Авг 26, 2016
0
2 145
Поделиться
Если возникают неполадки в водопроводе, канализации или газовой коммуникации, то приходится заменять и устанавливать новый фрагмент трубопровода. Для реализации операции в домашних условиях учатся находить диаметр труб, вооружившись подручными средствами. Выбирают конкретный метод обмера, опираясь на габариты изделий и расположение трубопровода.

- LiveJournal
- Blogger
Диаметр трубы можно узнать самостоятельно, нужно знать всего лишь несколько простых способов
- Как в домашних условиях определить овальность трубы большого диаметра
- Правильное измерение диаметра трубы в 3 этапа
- Обмер крупного изделия рулеткой, линейкой, штангенциркулем и без него
- Проверка диаметра труб и остальных параметров в условиях производства: наружный, внутренний показатель
Вычисление диаметра окружности с использованием радиуса, длины окружности или площади круга
-

1
Если вам известен радиус окружности, то, для того чтобы узнать диаметр, удвойте его.
Радиус – это расстояние от центра окружности до любой точки, лежащей на ней. Например, если радиус окружности равен 4 см, то диаметр окружности составляет 4 см x 2, или 8 см.
-

2
Если вам известна длина окружности, то, для того чтобы вычислить диаметр, разделите ее на π.
Число π равно примерно 3,14; но чтобы получить наиболее точное значение, вам следует воспользоваться калькулятором. Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.
-

3
Если вам известна площадь круга, то для нахождения диаметра разделите ее на π и извлеките из результата квадратный корень, чтобы получить радиус; затем умножьте на 2 для получения диаметра.
Данное вычисление вытекает из формулы площади круга, A = πr2, преобразованной для нахождения диаметра. Например, если площадь круга равна 25 см2, разделите ее на число π и извлеките квадратный корень: √(25/3,14) = √7,96 = 2,82 см. Это радиус окружности. Умножьте его на 2, и вы получите диаметр: 2,82 х 2 = 5,64 см.
Как найти длину окружности через площадь и полупериметр описанного треугольника
Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.
Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.
где:
π — математическая константа, примерно равная 3,14
S — площадь треугольника
p — полупериметр треугольника

Формула вычисления длины/периметра
1. Через радиус
Периметр круга или длина окружности (C) равняется удвоенному произведению ее радиуса на число π:
C = 2 * π * r
Радиус (r) – это отрезок, который соединяет центр окружности и любую точку на ней.
2. Через диаметр
Периметр/длина окружности считается как произведение ее диаметра на число π:
C = π * d
Диаметр (d) равен двум радиусам (d=2r). Это отрезок, соединяющий две противоположные точки на окружности.
Примечание: в расчетах значение числа π округляется до 3,14.
Как в домашних условиях определить овальность трубы большого диаметра
- рулетка;
- калькулятор;
- линейка;
- штангенциркуль;
- мобильный телефон с камерой ли фотоаппарат;
- нитка или шнурок;
- предмет с измеренными сторонами (коробок спичек).
В каких единицах измерить показатели? В дюймах. Единица измерения равна 2,54 см. Когда требуется замена трубы, узнают диаметр снаружи и внутри. Первое значение учитывает производитель при формировании резьбы и спаек. Параметр зависит напрямую от толщины стенок изделия (разности показателей снаружи и внутри).
Узнаем, как произвести замеры труб в разной доступности и положении.

- LiveJournal
- Blogger
Выисление диаметра трубы
Изделие полностью доступно для обмера
Найти наружный диаметр помогает штангенциркуль. Если измеряют параметр изделия, торец которого виден и доступен, то разрешается воспользоваться линейкой либо рулеткой. Но запросы к точности вычислений должны быть минимальными. Выполняют следующие задачи.
- К краю изделия, к широкой части прикладывают измерительный инструмент.
- Отсчитывают количество частей, которые отвечают диаметру.
Методика позволяет узнать точный размер изделия. У малых труб узнается значение посредством уже привычного приспособления под названием штангенциркуль.
Правильное измерение диаметра трубы в 3 этапа
Производится поэтапно измерение диаметра трубы:
- Разъединяют ножки приспособления и прикладывают к концу трубы.
- Сдвигают ножки для плотного прилегания к внешним стенкам изделия.
- По шкале значений инструмента определяют показатель. Точность – до миллиметра.
Узнаем, как произвести измерение, если трубная продукция была смонтирована. Как поступить, если труба смонтирована
Для замера понадобится штангенциркуль. Ножки приспособления касаются широкого участка, боковой поверхности. Замер проводят, если длина ножек приспособления больше половины диаметра рассматриваемого изделия.
Если труба обладает большой толщиной, замеряют окружность посредством рулетки и делят на 3,14.
Вычисление площади круга и длины окружности, когда радиус или диаметр выражены переменными
-

1
Найдите радиус или диаметр окружности.
В некоторых задачах радиус или диаметр дается в виде выражения с участием переменной, например, г = (х + 7) или d = (х + 3). В этом случае вы можете найти площадь круга или длину окружности, но окончательный ответ будет также содержать переменную. Запишите радиус или диаметр так, как дается в задаче.
- Пример: вычислите длину окружности с радиусом (х + 1).
-

2
Напишите формулу с данным значением.
Вычисляя площадь круга или длину окружности, вы подставляете данное значение в соответствующую формулу. Сначала запишите формулу для вычисления площадь круга или длину окружности, а затем подставьте в нее значение диаметра или радиуса, выраженное переменной.
- Пример: вычислите длину окружности с радиусом (х + 1).
Напишите формулу: C = 2πr
- Подставьте данное значение: C = 2π(х + 1)
-

3
Вычислите длину окружности так, как если бы переменная была представлена числом.
На данный момент решите задачу, рассматривая переменную в качестве обычного числа. Возможно, вам придется использовать свойство дистрибутивности для упрощения окончательного ответа.
- Пример: вычислите длину окружности с радиусом (х + 1).
C = 2πr = 2π (х + 1) = 2πx + 2π1 = 2πx + 2π = 6,28x + 6,28
- Если вы знаете значение переменной «х», подставьте его в найденное выражение, чтобы получить численный ответ.
-

4
Попрактикуйтесь на нескольких примерах.
Теперь, когда вы знаете формулу, попробуйте решить несколько задач. Чем больше задач вы решите, тем быстрее научитесь справляться с ними.
- Найдите площадь круга с радиусом 2х. A = πr2 = π(2x)2 = π4×2 = 12,56×2
- Найдите площадь круга с диаметром (х + 2).
- A = π(d/2)2 = π((x +2)/2)2 = ((x +2)2/4)π
Окружности в архитектуре
Окружность — весьма совершенная форма, потому что каждая точка окружности находится на одном и том же расстоянии от ее центра. Как и другие совершенные формы, окружность часто используют архитекторы. Круг и окружность широко применяются в архитектуре, и это при том, что круглые здания строить труднее, чем здания прямоугольной формы. Поэтому для постройки круглых зданий всегда была нужна особая мотивация. Возможно, что самая серьезная мотивация была религиозной. Окружности и сферы можно найти практически в любой культуре, религии или системе верований в качестве магических знаков или символов. Многие культовые здания и сооружения являются окружностями в плане — например, буддийские ступы в форме полусферы или Стоунхендж.



Архитекторы считают окружность и сферу самыми совершенными из всех геометрических форм. Покрытия зданий в форме верхней части сферы, то есть купола, широко применяются в архитектуре и бывают различных форм и размеров. Они могут быть полусферическими или заостренной на вершине формы, или с конусным верхом, который можно увидеть в исламской архитектуре. Они могут иметь совершенную сферическую форму, как римские и византийские купола или могут плавно заостряться на вершине, и тогда купол становится похожим на луковицу, как в православных храмах или в архитектурных стилях Великих Моголов.




Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат: r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат: r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Обмер крупного изделия рулеткой, линейкой, штангенциркулем и без него

- LiveJournal
- Blogger
Обмер крупного изделия потребует тщательных расчетов
Трубу с солидными габаритами обмерить несложно. Для этого определяют окружность посредством рулетки либо шнура и находят диаметр заготовки по формуле D = L/число Пи. Первое значение – это диаметр трубы, второе – окружность. К примеру, окружность составляет 35,2 см, тогда D равняется 11, 2 сантиметра или 112 мм (35,2:3,14). Что делать при полной недоступности элемента
Не найден доступ к трубам? Обмеры осуществляют методом копирования. Небольшой объект с известными габаритами приставляют к поверхности изделия и фотографируют. По полученному фотоснимку производят вычисления. Видимая толщина элемента определятся до миллиметра. Подсчеты переводят в реальный размер, ссылаясь на масштаб съемки. Диаметр труб необходимо измерять с большой точностью, так как от этого показателя зависят многие функции трубопроводных коммуникаций.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Окружность в технике
Невозможно представить себе технику без колес и других деталей в форме окружности. Некоторые из них (например, шасси самолетов и колеса автомобилей) хорошо видны. Другие спрятаны в компьютерах, стиральных и посудомоечных машинах, холодильниках, турбинах и другом оборудовании.




Таблица. Длина окружности диаметра D.
Таблица. Длина окружности диаметра D. Пример: длина окружности диаметра 1,523 = 4475+9= 4,784
Таблица. Длина окружности диаметра D.
| D | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 |
| 1,0 | 3,142 | 3,173 | 3,204 | 3,236 | 3,267 | 3,299 | 3,330 | 3,362 | 3,393 | 3,424 | 3 | 6 | 9 | 13 | 16 |
| 1,1 | 3,456 | 3,487 | 3,519 | 3,550 | 3,581 | 3,613 | 3,644 | 3,676 | 3,707 | 3,738 | 3 | 6 | 9 | 13 | 16 |
| 1,2 | 3,770 | 3,801 | 3,833 | 3,864 | 3,896 | 3,927 | 3,958 | 3,990 | 4,021 | 4,053 | 3 | 6 | 9 | 13 | 16 |
| 1,3 | 4,084 | 4,115 | 4,147 | 4,178 | 4,210 | 4,241 | 4,273 | 4,304 | 4,335 | 4,367 | 3 | 6 | 9 | 13 | 16 |
| 1,4 | 4,398 | 4,430 | 4,461 | 4,492 | 4,524 | 4,555 | 4,587 | 4,618 | 4,650 | 4,681 | 3 | 6 | 9 | 13 | 16 |
| 1,5 | 4,712 | 4,744 | 4,775 | 4,807 | 4,838 | 4,869 | 4,901 | 4,932 | 4,964 | 4,995 | 3 | 6 | 9 | 13 | 16 |
| 1,6 | 5,027 | 5,058 | 5,089 | 5,121 | 5,152 | 5,184 | 5,215 | 5,246 | 5,278 | 5,309 | 3 | 6 | 9 | 13 | 16 |
| 1,7 | 5,341 | 5,372 | 5,404 | 5,435 | 5,466 | 5,498 | 5,529 | 5,561 | 5,592 | 5,623 | 3 | 6 | 9 | 13 | 16 |
| 1,8 | 5,655 | 5,686 | 5,718 | 5,749 | 5,781 | 5,812 | 5,843 | 5,875 | 5,906 | 5,938 | 3 | 6 | 9 | 13 | 16 |
| 1,9 | 5,969 | 6,000 | 6,032 | 6,063 | 6,095 | 6,126 | 6,158 | 6,189 | 6,220 | 6,252 | 3 | 6 | 9 | 13 | 16 |
| 2,0 | 6,283 | 6,315 | 6,346 | 6,377 | 6,409 | 6,440 | 6,472 | 6,503 | 6,535 | 6,566 | 3 | 6 | 9 | 13 | 16 |
| 2,1 | 6,597 | 6,629 | 6,660 | 6,692 | 6,723 | 6,754 | 6,786 | 6,817 | 6,849 | 6,880 | 3 | 6 | 9 | 13 | 16 |
| 2,2 | 6,912 | 6,943 | 6,974 | 7,006 | 7,037 | 7,069 | 7,100 | 7,131 | 7,163 | 7,194 | 3 | 6 | 9 | 13 | 16 |
| 2,3 | 7,226 | 7,257 | 7,288 | 7,320 | 7,351 | 7,383 | 7,414 | 7,446 | 7,477 | 7,508 | 3 | 6 | 9 | 13 | 16 |
| 2,4 | 7,540 | 7,571 | 7,603 | 7,634 | 7,665 | 7,697 | 7,728 | 7,760 | 7,791 | 7,823 | 3 | 6 | 9 | 13 | 16 |
| 2,5 | 7,854 | 7,885 | 7,917 | 7,948 | 7,980 | 8,011 | 8,042 | 8,074 | 8,105 | 8,137 | 3 | 6 | 9 | 13 | 16 |
| 2,6 | 8,168 | 8,200 | 8,231 | 8,262 | 8,294 | 8,325 | 8,357 | 8,388 | 8,419 | 8,451 | 3 | 6 | 9 | 13 | 16 |
| 2,7 | 8,482 | 8,514 | 8,545 | 8,577 | 8,608 | 8,639 | 8,671 | 8,702 | 8,734 | 8,765 | 3 | 6 | 9 | 13 | 16 |
| 2,8 | 8,796 | 8,828 | 8,859 | 8,891 | 8,922 | 8,954 | 8,985 | 9,016 | 9,048 | 9,079 | 3 | 6 | 9 | 13 | 16 |
| 2,9 | 9,111 | 9,142 | 9,173 | 9,205 | 9,236 | 9,268 | 9,299 | 9,331 | 9,362 | 9,393 | 3 | 6 | 9 | 13 | 16 |
| 3,0 | 9,425 | 9,456 | 9,488 | 9,519 | 9,550 | 9,582 | 9,613 | 9,645 | 9,676 | 9,708 | 3 | 6 | 9 | 13 | 16 |
| 3,1 | 9,739 | 9,770 | 9,802 | 9,833 | 9,865 | 9,896 | 9,927 | 9,959 | 9,990 | 10,022 | 3 | 6 | 9 | 13 | 16 |
| 3,2 | 10,053 | 10,085 | 10,116 | 10,147 | 10,179 | 10,210 | 10,242 | 10,273 | 10,304 | 10,336 | 3 | 6 | 9 | 13 | 16 |
| 3,3 | 10,367 | 10,399 | 10,430 | 10,462 | 10,493 | 10,524 | 10,556 | 10,587 | 10,619 | 10,650 | 3 | 6 | 9 | 13 | 16 |
| 3,4 | 10,681 | 10,713 | 10,744 | 10,776 | 10,807 | 10,838 | 10,870 | 10,901 | 10,933 | 10,964 | 3 | 6 | 9 | 13 | 16 |
| 3,5 | 10,996 | 11,027 | 11,058 | 11,090 | 11,121 | 11,153 | 11,184 | 11,215 | 11,247 | 11,278 | 3 | 6 | 9 | 13 | 16 |
| 3,6 | 11,310 | 11,341 | 11,373 | 11,404 | 11,435 | 11,467 | 11,498 | 11,530 | 11,561 | 11,592 | 3 | 6 | 9 | 13 | 16 |
| 3,7 | 11,624 | 11,655 | 11,687 | 11,718 | 11,750 | 11,781 | 11,812 | 11,844 | 11,875 | 11,907 | 3 | 6 | 9 | 13 | 16 |
| 3,8 | 11,938 | 11,969 | 12,001 | 12,032 | 12,064 | 12,095 | 12,127 | 12,158 | 12,189 | 12,221 | 3 | 6 | 9 | 13 | 16 |
| 3,9 | 12,252 | 12,284 | 12,315 | 12,346 | 12,378 | 12,409 | 12,441 | 12,472 | 12,504 | 12,535 | 3 | 6 | 9 | 13 | 16 |
| 4,0 | 12,566 | 12,598 | 12,629 | 12,661 | 12,692 | 12,723 | 12,755 | 12,786 | 12,818 | 12,849 | 3 | 6 | 9 | 13 | 16 |
| 4,1 | 12,881 | 12,912 | 12,943 | 12,975 | 13,006 | 13,038 | 13,069 | 13,100 | 13,132 | 13,163 | 3 | 6 | 9 | 13 | 16 |
| 4,2 | 13,195 | 13,226 | 13,258 | 13,289 | 13,320 | 13,352 | 13,383 | 13,415 | 13,446 | 13,477 | 3 | 6 | 9 | 13 | 16 |
| 4,3 | 13,509 | 13,540 | 13,572 | 13,603 | 13,635 | 13,666 | 13,697 | 13,729 | 13,760 | 13,792 | 3 | 6 | 9 | 13 | 16 |
| 4,4 | 13,823 | 13,854 | 13,886 | 13,917 | 13,949 | 13,980 | 14,012 | 14,043 | 14,074 | 14,106 | 3 | 6 | 9 | 13 | 16 |
| 4,5 | 14,137 | 14,169 | 14,200 | 14,231 | 14,263 | 14,294 | 14,326 | 14,357 | 14,388 | 14,420 | 3 | 6 | 9 | 13 | 16 |
| 4,6 | 14,451 | 14,483 | 14,514 | 14,546 | 14,577 | 14,608 | 14,640 | 14,671 | 14,703 | 14,734 | 3 | 6 | 9 | 13 | 16 |
| 4,7 | 14,765 | 14,797 | 14,828 | 14,860 | 14,891 | 14,923 | 14,954 | 14,985 | 15,017 | 15,048 | 3 | 6 | 9 | 13 | 16 |
| 4,8 | 15,080 | 15,111 | 15,142 | 15,174 | 15,205 | 15,237 | 15,268 | 15,300 | 15,331 | 15,362 | 3 | 6 | 9 | 13 | 16 |
| 4,9 | 15,394 | 15,425 | 15,457 | 15,488 | 15,519 | 15,551 | 15,582 | 15,614 | 15,645 | 15,677 | 3 | 6 | 9 | 13 | 16 |
| 5,0 | 15,708 | 15,739 | 15,771 | 15,802 | 15,834 | 15,865 | 15,896 | 15,928 | 15,959 | 15,991 | 3 | 6 | 9 | 13 | 16 |
| 5,1 | 16,022 | 16,054 | 16,085 | 16,116 | 16,148 | 16,179 | 16,211 | 16,243 | 16,273 | 16,305 | 3 | 6 | 9 | 13 | 16 |
| 5,2 | 16,336 | 16,368 | 16,399 | 16,431 | 16,462 | 16,493 | 16,525 | 16,556 | 16,588 | 16,619 | 3 | 6 | 9 | 13 | 16 |
| 5,3 | 16,650 | 16,682 | 16,713 | 16,745 | 16,776 | 16,808 | 16,839 | 16,870 | 16,902 | 16,933 | 3 | 6 | 9 | 13 | 16 |
| 5,4 | 16,965 | 16,996 | 17,027 | 17,059 | 17,090 | 17,122 | 17,153 | 17,185 | 17,216 | 17,247 | 3 | 6 | 9 | 13 | 16 |
| 5,5 | 17,279 | 17,310 | 17,342 | 17,373 | 17,404 | 17,436 | 17,467 | 17,499 | 17,530 | 17,562 | 3 | 6 | 9 | 13 | 16 |
| 5,6 | 17,593 | 17,624 | 17,656 | 17,687 | 17,719 | 17,750 | 17,781 | 17,813 | 17,844 | 17,876 | 3 | 6 | 9 | 13 | 16 |
| 5,7 | 17,907 | 17,938 | 17,970 | 18,001 | 18,033 | 18,064 | 18,096 | 18,127 | 18,158 | 18,190 | 3 | 6 | 9 | 13 | 16 |
| 5,8 | 18,221 | 18,253 | 18,284 | 18,316 | 18,347 | 18,378 | 18,410 | 18,441 | 18,473 | 18,504 | 3 | 6 | 9 | 13 | 16 |
| 5,9 | 18,535 | 18,567 | 18,598 | 18,630 | 18,661 | 18,692 | 18,724 | 18,755 | 18,787 | 18,818 | 3 | 6 | 9 | 13 | 16 |
| 6,0 | 18,850 | 18,881 | 18,912 | 18,944 | 18,975 | 19,007 | 19,038 | 19,069 | 19,101 | 19,132 | 3 | 6 | 9 | 13 | 16 |
| 6,1 | 19,164 | 19,195 | 19,227 | 19,258 | 19,289 | 19,321 | 19,352 | 19,384 | 19,415 | 19,446 | 3 | 6 | 9 | 13 | 16 |
| 6,2 | 19,478 | 19,509 | 19,541 | 19,572 | 19,604 | 19,635 | 19,666 | 19,698 | 19,729 | 19,761 | 3 | 6 | 9 | 13 | 16 |
| 6,3 | 19,792 | 19,823 | 19,855 | 19,886 | 19,918 | 19,949 | 19,981 | 20,012 | 20,043 | 20,075 | 3 | 6 | 9 | 13 | 16 |
| 6,4 | 20,106 | 20,138 | 20,169 | 20,200 | 20,232 | 20,263 | 20,295 | 20,326 | 20,358 | 20,389 | 3 | 6 | 9 | 13 | 16 |
| 6,5 | 20,420 | 20,452 | 20,483 | 20,515 | 20,546 | 20,577 | 20,609 | 20,640 | 20,672 | 20,703 | 3 | 6 | 9 | 13 | 16 |
| 6,6 | 20,735 | 20,766 | 20,797 | 20,829 | 20,860 | 20,892 | 20,923 | 20,954 | 20,986 | 21,017 | 3 | 6 | 9 | 13 | 16 |
| 6,7 | 21,049 | 21,080 | 21,112 | 21,143 | 21,174 | 21,206 | 21,237 | 21,269 | 21,300 | 21,331 | 3 | 6 | 9 | 13 | 16 |
| 6,8 | 21,363 | 21,394 | 21,426 | 21,457 | 21,488 | 21,520 | 21,551 | 21,583 | 21,614 | 21,646 | 3 | 6 | 9 | 13 | 16 |
| 6,9 | 21,677 | 21,708 | 21,740 | 21,771 | 21,803 | 21,834 | 21,865 | 21,897 | 21,928 | 21,960 | 3 | 6 | 9 | 13 | 16 |
| 7,0 | 21,991 | 22,023 | 22,054 | 22,085 | 22,117 | 22,148 | 22,180 | 22,211 | 22,242 | 22,274 | 3 | 6 | 9 | 13 | 16 |
| 7,1 | 22,305 | 22,337 | 22,368 | 22,400 | 22,431 | 22,462 | 22,494 | 22,525 | 22,557 | 22,588 | 3 | 6 | 9 | 13 | 16 |
| 7,2 | 22,619 | 22,651 | 22,682 | 22,714 | 22,745 | 22,777 | 22,808 | 22,839 | 22,871 | 22,902 | 3 | 6 | 9 | 13 | 16 |
| 7,3 | 22,934 | 22,965 | 22,996 | 23,028 | 23,059 | 23,091 | 23,122 | 23,154 | 23,185 | 23,216 | 3 | 6 | 9 | 13 | 16 |
| 7,4 | 23,248 | 23,279 | 23,311 | 23,342 | 23,373 | 23,405 | 23,436 | 23,468 | 23,499 | 23,531 | 3 | 6 | 9 | 13 | 16 |
| 7,5 | 23,562 | 23,593 | 23,625 | 23,656 | 23,688 | 23,719 | 23,750 | 23,782 | 23,813 | 23,845 | 3 | 6 | 9 | 13 | 16 |
| 7,6 | 23,876 | 23,908 | 23,939 | 23,970 | 24,002 | 24,033 | 24,065 | 24,096 | 24,127 | 24,159 | 3 | 6 | 9 | 13 | 16 |
| 7,7 | 24,190 | 24,222 | 24,253 | 24,285 | 24,316 | 24,347 | 24,379 | 24,410 | 24,442 | 24,473 | 3 | 6 | 9 | 13 | 16 |
| 7,8 | 24,504 | 24,536 | 24,567 | 24,599 | 24,630 | 24,662 | 24,693 | 24,724 | 24,756 | 24,787 | 3 | 6 | 9 | 13 | 16 |
| 7,9 | 24,819 | 24,850 | 24,881 | 24,913 | 24,944 | 24,976 | 25,007 | 25,038 | 25,070 | 25,101 | 3 | 6 | 9 | 13 | 16 |
| 8,0 | 25,133 | 25,164 | 25,196 | 25,227 | 25,258 | 25,290 | 25,321 | 25,353 | 25,384 | 25,415 | 3 | 6 | 9 | 13 | 16 |
| 8,1 | 25,447 | 25,478 | 25,510 | 25,541 | 25,573 | 25,604 | 25,635 | 25,667 | 25,698 | 25,730 | 3 | 6 | 9 | 13 | 16 |
| 8,2 | 25,761 | 25,792 | 25,824 | 25,855 | 25,887 | 25,918 | 25,950 | 25,981 | 26,012 | 26,044 | 3 | 6 | 9 | 13 | 16 |
| 8,3 | 26,075 | 26,107 | 26,138 | 26,169 | 26,201 | 26,232 | 26,264 | 26,295 | 26,327 | 26,358 | 3 | 6 | 9 | 13 | 16 |
| 8,4 | 26,389 | 26,421 | 26,452 | 26,484 | 26,515 | 26,546 | 26,578 | 26,609 | 26,641 | 26,672 | 3 | 6 | 9 | 13 | 16 |
| 8,5 | 26,704 | 26,735 | 26,766 | 26,797 | 26,829 | 26,861 | 26,892 | 26,923 | 26,955 | 26,986 | 3 | 6 | 9 | 13 | 16 |
| 8,6 | 27,018 | 27,049 | 27,081 | 27,112 | 27,143 | 27,175 | 27,206 | 27,238 | 27,269 | 27,300 | 3 | 6 | 9 | 13 | 16 |
| 8,7 | 27,332 | 27,363 | 27,395 | 27,426 | 27,458 | 27,469 | 27,520 | 27,552 | 27,583 | 27,615 | 3 | 6 | 9 | 13 | 16 |
| 8,8 | 27,646 | 27,677 | 27,709 | 27,740 | 27,772 | 27,803 | 27,835 | 27,866 | 27,897 | 27,929 | 3 | 6 | 9 | 13 | 16 |
| 8,9 | 27,960 | 27,992 | 28,023 | 28,054 | 28,086 | 28,117 | 28,149 | 28,180 | 28,212 | 28,243 | 3 | 6 | 9 | 13 | 16 |
| 9,0 | 28,274 | 28,306 | 28,337 | 28,369 | 28,400 | 28,431 | 28,463 | 28,494 | 28,526 | 28,557 | 3 | 6 | 9 | 13 | 16 |
| 9,1 | 28,588 | 28,620 | 28,651 | 28,683 | 28,714 | 28,746 | 28,777 | 28,808 | 28,840 | 28,871 | 3 | 6 | 9 | 13 | 16 |
| 9,2 | 28,903 | 28,934 | 28,965 | 28,997 | 29,028 | 29,060 | 29,091 | 29,123 | 29,154 | 29,185 | 3 | 6 | 9 | 13 | 16 |
| 9,3 | 29,207 | 29,248 | 29,280 | 29,311 | 29,342 | 29,374 | 29,405 | 29,437 | 29,468 | 29,500 | 3 | 6 | 9 | 13 | 16 |
| 9,4 | 29,531 | 29,562 | 29,594 | 29,625 | 29,657 | 29,688 | 29,719 | 29,751 | 29,782 | 29,814 | 3 | 6 | 9 | 13 | 16 |
| 9,5 | 29,845 | 29,877 | 29,908 | 29,939 | 29,971 | 30,002 | 30,034 | 30,065 | 30,096 | 30,128 | 3 | 6 | 9 | 13 | 16 |
| 9,6 | 30,159 | 30,191 | 30,222 | 30,254 | 30,285 | 30,316 | 30,348 | 30,379 | 30,411 | 30,442 | 3 | 6 | 9 | 13 | 16 |
| 9,7 | 30,473 | 30,505 | 30,536 | 30,568 | 30,599 | 30,631 | 30,662 | 30,693 | 30,725 | 30,756 | 3 | 6 | 9 | 13 | 16 |
| 9,8 | 30,788 | 30,819 | 30,850 | 30,882 | 30,913 | 30,945 | 30,976 | 31,008 | 31,039 | 31,070 | 3 | 6 | 9 | 13 | 16 |
| 9,9 | 31,102 | 31,133 | 31,165 | 31,196 | 31,227 | 31,259 | 31,290 | 31,322 | 31,353 | 31,385 | 3 | 6 | 9 | 13 | 16 |
| 10,0 | 31,416 | ||||||||||||||
| d | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 2 | 3 | 4 | 5 |
( 2 оценки, среднее 5 из 5 )
