Как найти полупериметр окружности вписанной в треугольник - Сайт, где вы сможете решить свои вопросы

Радиус вписанной в треугольник окружности
рассчитать и выразить через периметр, площадь,
высоту, основание, стороны, диаметр. Формулы
радиуса окружности вписанной в треугольник.

Центр вписанной в треугольник окружности — это одна
из замечательных точек треугольника, она расположена
в точке пересечения биссектрис треугольника, её
иногда называют инцентром.

Центр вписанной окружности правильного треугольника — это
точка, где пересекаются высоты, медианы и биссектрисы.

В любой треугольник можно вписать только одну
окружность, которая находится внутри треугольника.
Центр вписанной окружности равноудален от всех
сторон треугольника. Точка, где окружность пересекается
со стороной треугольника, называется точкой касания.

Все отрезки, которые проведены от точки касания к центру
вписанной окружности имеют одинаковую длину.

Чтобы найти радиус окружности вписанной в треугольник
надо площадь разделить на полупериметр.

Диаметр вписанной окружности в треугольник численно
равен двум радиусам вписанной окружности. Радиус
вписанной окружности можно найти по разным
формулам, все зависит от того, какой треугольник.

Всего различают четыре вида треугольников:

Разносторонний / любой
Правильный / равносторонний
Равнобедренный / равнобочный
Прямоугольный / прямой

Содержание

Радиус вписанной окружности в любой треугольник
Радиус вписанной окружности в правильный треугольник
Радиус вписанной окружности в равнобедренный треугольник
Радиус вписанной окружности в прямоугольный треугольник

Радиус вписанной окружности в любой треугольник

Радиус вписанной окружности в любой треугольник через площадь и полупериметр
[ r = frac{S}{p} ]

S — площадь; p — полупериметр;
Радиус вписанной окружности в любой треугольник через все стороны и полупериметр
[ r = sqrtfrac{{(p-a)(p-b)(p-c)}}{p} ]

a, b, c — стороны; p — полупериметр;
Радиус вписанной окружности в любой треугольник через основание, высоту и полупериметр
[ r = frac{frac{1}{2}a cdot h}{p} ]

a — основание, сторона на которую падает высота; h — высота; p — полупериметр;
Радиус вписанной окружности в любой треугольник через диаметр вписанной окружности
[ r = frac{D}{2} ]

D — диаметр вписанной окружности;

Радиус вписанной окружности в правильный треугольник

Радиус вписанной окружности в правильный треугольник через сторону
[ r = frac{a}{2sqrt 3} ]

a — сторона;
Радиус вписанной окружности в правильный треугольник через радиус описанной окружности
[ r = frac{R}{2} ]

R — радиус описанной окружности;
Радиус вписанной окружности в правильный треугольник через диаметр вписанной окружности
[ r = frac{D}{2} ]

D — диаметр вписанной окружности;

Радиус вписанной окружности в равнобедренный треугольник

Радиус вписанной окружности в равнобедренный треугольник через боковые стороны и основание
[ r = frac{b}{2} cdot sqrt{frac{2a-b}{2a+b}} ]

a — боковая сторона; b — основание;
Радиус вписанной окружности в равнобедренный треугольник через высоту и основание
[ r = frac{bh}{b + sqrt{4h^2+b^2}} ]

b — основание; h — высота;
Радиус вписанной окружности в равнобедренный треугольник через диаметр вписанной окружности
[ r = frac{D}{2} ]

D — диаметр вписанной окружности;

Радиус вписанной окружности в прямоугольный треугольник

Радиус вписанной окружности в прямоугольный треугольник через два катета и гипотенузу
[ r = frac{a+b-c}{2} ]

a, b — катеты; с — гипотенуза.
Радиус вписанной окружности в прямоугольный треугольник через гипотенузу и два катета
[ r = frac{ab}{a+b+c} ]

c — гипотенуза; a, b — катеты;
Радиус вписанной окружности в прямоугольный треугольник через диаметр вписанной окружности
[ r = frac{D}{2} ]

D — диаметр вписанной окружности;

Вписанная окружность в треугольник — это окружность,
которая вписана в треугольник и касается всех его сторон.

Радиус вписанной окружности в треугольник — это отрезок,
проведенный от центра вписанной окружности до любой стороны.

Длина радиуса вписанной окружности, диаметра
вписанной окружности а также других величин
измеряется в мм, см, м, км и так далее.

В любом треугольнике все радиусы и диаметры
равны, имеют одинаковую длину.

Источник

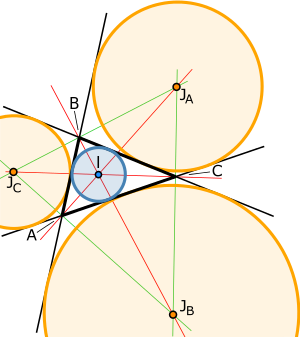
Треугольник (чёрный) с вписанной окружностью (синей), инцентр (I), вневписанными окружностями (оранжевые), эксцентры (J_A,J_B,J_C), внутренние биссектрисы (красные) и внешние биссектрисы (зелёные)

Вписанная в треугольник окружность — окружность внутри треугольника, касающаяся всех его сторон; наибольшая окружность, которая может находиться внутри треугольника. Центр этой окружности является точкой пересечения биссектрис треугольника и называется инцентром треугольника.

Вневписанная окружность треугольника — окружность, лежащая вне треугольника и касающаяся одной стороны треугольника и продолжения двух других сторон^[en]. Любой треугольник имеет три различные вневписанные окружности, каждая из которых касается своей стороны треугольника.
Центром вневписанной окружности является пересечение биссектрисы одного внутреннего угла^[en] и биссектрис двух других внешних углов^[en]. Поскольку биссектриса внутреннего угла перпендикулярна биссектрисе смежного внешнего угла, центр вписанной окружности вместе с тремя центрами вневписанных окружностей образуют ортоцентричную систему^[en]^[1].

Не все многоугольники с числом сторон более трёх имеют вписанную окружность. Те, которые имеют, называются описанными.

Связь с площадью треугольника[править | править код]

Радиусы вписанных и вневписанных окружностей имеют тесную связь с площадью треугольника^[2].

Вписанная окружность[править | править код]

Пусть имеет вписанную окружность радиуса r с центром I.
Пусть a — длина BC, b — длина AC, а c — длина AB.
Пусть вписанная окружность касается AB в некоторой точке C′, тогда
является прямым.
Тогда радиус C’I будет высотой треугольника
.
Таким образом,

имеет основание длины c и высоту r, а следовательно, его площадь равна
${tfrac {1}{2}}cr$ .
Подобным же образом

имеет площадь
${tfrac {1}{2}}br$
и

имеет площадь ${tfrac {1}{2}}ar$ .
Поскольку эти три треугольника разбивают , получаем, что

${displaystyle Delta ={frac {1}{2}}(a+b+c)r=pr,}$

где Delta — площадь , а ${displaystyle p={frac {1}{2}}(a+b+c)}$ — его полупериметр.

Чтобы получить альтернативную формулу, рассмотрим . Это прямоугольный треугольник, у которого один из катетов равен r, а другой равен ${displaystyle rcdot mathrm {ctg} {frac {angle A}{2}}}$ . То же самое верно для . Весь треугольник состоит из 6 таких треугольников, и общая площадь составляет:

${displaystyle Delta =r^{2}cdot (mathrm {ctg} {frac {angle A}{2}}+mathrm {ctg} {frac {angle B}{2}}+mathrm {ctg} {frac {angle C}{2}})}$

Вневписанные окружности[править | править код]

Пусть вневписанная окружность, касающаяся стороны AB, касается продолжения стороны AC в точке G, и пусть радиус этой окружности равен $r_{c}$ , а её центр — $I_{c}$ . Тогда $I_{c}G$ является высотой треугольника $triangle ACI_{c}$ ,
так что $triangle ACI_{c}$ имеет площадь ${tfrac {1}{2}}br_{c}$ . По тем же причинам
$triangle BCI_{c}$
имеет площадь
${tfrac {1}{2}}ar_{c}$ ,
а $triangle ABI_{c}$
имеет площадь
${tfrac {1}{2}}cr_{c}$ .
Тогда

${displaystyle Delta ={frac {1}{2}}(a+b-c)r_{c}=(p-c)r_{c}}$

Таким образом, ввиду симметрии,

${displaystyle Delta =pr=(p-a)r_{a}=(p-b)r_{b}=(p-c)r_{c}}$

По теореме косинусов получаем

$cos A={frac {b^{2}+c^{2}-a^{2}}{2bc}}$

Комбинируя это с тождеством $sin ^{2}A+cos ^{2}A=1$ , получим

$sin A={frac {sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2b^{2}c^{2}+2a^{2}c^{2}}}{2bc}}$

Но $Delta ={tfrac {1}{2}}bcsin A$ , так что

${displaystyle {begin{aligned}Delta &={frac {1}{4}}{sqrt {-a^{4}-b^{4}-c^{4}+2a^{2}b^{2}+2b^{2}c^{2}+2a^{2}c^{2}}}\&={frac {1}{4}}{sqrt {(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}\&={sqrt {p(p-a)(p-b)(p-c)}},end{aligned}}}$

и это формула Герона вычисления площади треугольника по его сторонам.

Комбинируя формулу Герона с , получим

${displaystyle r^{2}={frac {Delta ^{2}}{p^{2}}}={frac {(p-a)(p-b)(p-c)}{p}}}$

Аналогично, ${displaystyle (p-a)r_{a}=Delta }$ даёт

${displaystyle r_{a}^{2}={frac {p(p-b)(p-c)}{p-a}}}$

Из этих формул видно, что вневписанные окружности всегда больше вписанной и наибольшая окружность соответствует самой длинной стороне, а самая наименьшая из вневписанных окружностей соответствует самой маленькой стороне. Дальнейшее комбинирование формул приводит к:^[3]

$Delta ={sqrt {rr_{a}r_{b}r_{c}}}.$

Отношение площади вписанной окружности к площади треугольника меньше или равно ${frac {pi }{3{sqrt {3}}}}$ , и равенство достигается только на правильных треугольниках^[4].

Связанные построения[править | править код]

Окружность девяти точек и точка Фейербаха[править | править код]

Теорема Эйлера об окружности Эйлера. Середины отрезков высот от ортоцентра до вершин треугольника называются точками Эйлера. Основания медиан, основания высот и точки Эйлера лежат на одной окружности, называемой окружностью девяти точек^[5].

Теорема Фейербаха. Окружность девяти точек касается всех трёх вневписанных окружностей, а также вписанной окружности в четырёх разных точках. Одна из них – точка касания окружности Эйлера и вписанной окружности известна как точка Фейербаха.

Треугольник и точка Жергонна[править | править код]

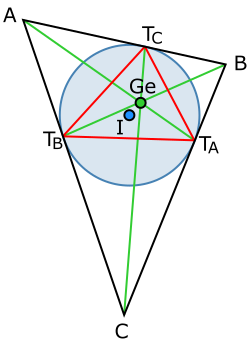
Треугольник ΔABC с вписанной окружностью (синяя), и её центр (синий, I), треугольник точек касания (красный, ΔT_aT_bT_c) и точка Жергонна (зелёная, Ge)

Треугольник Жергонна (для треугольника ABC) определяется тремя точками касания вписанной окружности на трёх сторонах.
Эти вершины обозначим T_A, и т. д..
Точка T_A лежит напротив вершины A.

Этот треугольник Жергонна T_AT_BT_C известен также как треугольник касаний треугольника ABC.

Три прямые AT_A, BT_B и CT_C пересекаются в одной точке — точке Жергонна и обозначается Ge — X(7). Точка Жергонна лежит внутри открытого ортоцентроидного круга^[en] с выколотым центром^[6].

Интересно, что точка Жергонна треугольника является точкой пересечения симедиан треугольника Жергонна. Полный набор свойств точки Жергонна можно найти в статье Декова^[7].

Трилинейные координаты вершин треугольника касаний задаются формулами

вершина $A=0:sec ^{2}left({frac {B}{2}}right):sec ^{2}left({frac {C}{2}}right)$
вершина $B=sec ^{2}left({frac {A}{2}}right):0:sec ^{2}left({frac {C}{2}}right)$
вершина $C=sec ^{2}left({frac {A}{2}}right):sec ^{2}left({frac {B}{2}}right):0$

Трилинейные координаты точки Жергонна

$sec ^{2}left({frac {A}{2}}right):sec ^{2}left({frac {B}{2}}right):sec ^{2}left({frac {C}{2}}right)$

или, эквивалентно, по теореме синусов,

${frac {bc}{b+c-a}}:{frac {ca}{c+a-b}}:{frac {ab}{a+b-c}}$

Точка Жергонна является изотомическим сопряжением точки Нагеля.

Треугольник и точка Нагеля[править | править код]

Треугольник Нагеля (см. рис. выше) для треугольника ABC определяется вершинами T_A, T_B и T_C, которые являются точками касания вневписанных окружностей треугольника ABC и точка X_A противоположна стороне A, и т. д. Описанная вокруг треугольника T_AT_BT_C окружность называется окружностью Мандарта (частный случай эллипса Мандарта). Три прямые AT_A, BT_B и CT_C делят периметр пополам и пересекаются в одной точке Нагеля Na — X(8).

Трилинейные координаты точек касания треугольника вневписанными окружностями задаются формулами

вершина $A=0:csc ^{2}left({frac {B}{2}}right):csc ^{2}left({frac {C}{2}}right)$
вершина $B=csc ^{2}left({frac {A}{2}}right):0:csc ^{2}left({frac {C}{2}}right)$
вершина $C=csc ^{2}left({frac {A}{2}}right):csc ^{2}left({frac {B}{2}}right):0$

Трилинейные координаты точки Нагеля задаются формулами

$csc ^{2}left({frac {A}{2}}right):csc ^{2}left({frac {B}{2}}right):csc ^{2}left({frac {C}{2}}right)$

или, эквивалентно, по теореме синусов,

${frac {b+c-a}{a}}:{frac {c+a-b}{b}}:{frac {a+b-c}{c}}$

Точка Нагеля является изотомическим сопряжением точки Жергонна.

Трилинейные координаты вписанных треугольников[править | править код]

Трилинейные координаты вершин треугольника, образованного основаниями биссектрис, задаются формулами

вершина
вершина
вершина

Трилинейные координаты треугольника, образованного точками касания сторон внеописанными окружностями, задаются формулами

вершина
вершина
вершина

Уравнения окружностей[править | править код]

Пусть x : y : z — координаты точки в трилинейных координатах, и пусть u = cos²(A/2), v = cos²(B/2), w = cos²(C/2). Четыре окружности, описанные выше, можно задать любым из двух указанных способов^[8]:

Вписанная окружность:

$u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}-2vwyz-2wuzx-2uvxy=0$

$pm {sqrt {x}}cos {frac {A}{2}}pm {sqrt {y}}cos {frac {B}{2}}pm {sqrt {z}}cos {frac {C}{2}}=0$

A-внешневписанная:

$u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}-2vwyz+2wuzx+2uvxy=0$

$pm {sqrt {-x}}cos {frac {A}{2}}pm {sqrt {y}}cos {frac {B}{2}}pm {sqrt {z}}cos {frac {C}{2}}=0$

B-внешневписанная:

$u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}+2vwyz-2wuzx+2uvxy=0$

$pm {sqrt {x}}cos {frac {A}{2}}pm {sqrt {-y}}cos {frac {B}{2}}pm {sqrt {z}}cos {frac {C}{2}}=0$

C-внешневписанная:

$u^{2}x^{2}+v^{2}y^{2}+w^{2}z^{2}+2vwyz+2wuzx-2uvxy=0$

$pm {sqrt {x}}cos {frac {A}{2}}pm {sqrt {y}}cos {frac {B}{2}}pm {sqrt {-z}}cos {frac {C}{2}}=0$

Другие свойства вписанной окружности[править | править код]

Некоторые формулы с радиусом вписанной окружности[править | править код]

Радиус вписанной окружности не больше одной девятой суммы высот треугольника^[9].

Неравенство Эйлера: радиус вписанной окружности не превосходит половины радиуса описанной окружности и равенство имеет место лишь для равностороннего треугольника^[10].

Предположим, что точки касания вписанной окружности делят стороны на отрезки длиной x и y, y и z, z и x. Тогда вписанная окружность имеет радиус^[11]

$r={sqrt {frac {xyz}{x+y+z}}}$

и площадь треугольника равна

Если высоты, опущенные на стороны a, b и c есть h_a, h_b и h_c, то радиус вписанной окружности r равен одной трети гармонического среднего этих высот, то есть

$r={frac {1}{h_{a}^{-1}+h_{b}^{-1}+h_{c}^{-1}}}.$

Произведение радиуса вписанной окружности r и радиуса описанной окружности R треугольника со сторонами a, b и c равен^[1]

$rR={frac {abc}{2(a+b+c)}}.$

Некоторые связи сторон, радиусов вписанной окружности и описанной окружностей^[12]:

$ab+bc+ca=s^{2}+(4R+r)r,$

$a^{2}+b^{2}+c^{2}=2s^{2}-2(4R+r)r.$

Любая прямая, проходящая через треугольник и делящая площадь треугольника и периметр пополам, проходит через центр вписанной окружности. Таких прямых может существовать три, две или одна^[13].

Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности^[14].

Формулы для расстояний до центра вписанной или вневписанной окружностей[править | править код]

Теорема Эйлера[править | править код]

Теорема Эйлера утверждает, что в треугольнике^[10]:

$(R-r_{in})^{2}=d^{2}+r_{in}^{2},$

где R и r_in являются радиусами описанной и вписанной окружностей соответственно, а d — расстояние между центрами этих окружностей.

Для вневписанных окружностей уравнение выглядит похоже:

$(R+r_{ex})^{2}=d^{2}+r_{ex}^{2},$

где r_ex — радиус одной из вневписанных окружностей, а d — расстояние между центрами описанной и вневписанной окружностей^[15]^[16]^[17]

Возводя в квадрат и приводя подобные из первой формулы Эйлера выше имеем:

Квадрат расстояния от центра вписанной окружности I до центра описанной O задаётся уравнением^[18]

$OI^{2}=d^{2}=R(R-2r_{in}),$

${displaystyle OI^{2}={frac {abc,}{a+b+c}}left[{frac {abc,}{(a+b-c),(a-b+c),(-a+b+c)}}-1right]}$

Аналогично для второй формулы:

$d^{2}=R(R+2r_{ex}).$

Другие формулы для расстояний до центра вписанной или вневписанной окружностей[править | править код]

Расстояние от центра вписанной окружности до центра N окружности девяти точек равно^[18]

$IN={frac {1}{2}}(R-2r)<{frac {1}{2}}R.$

Расстояние от вершины до точек касания вписанной окружности на прилегающих сторонах равно полусумме длин прилегающих сторон минус половина противолежащей стороны^[19]. Так, для вершины B и прилежащих точек касания T_A и T_C,

$BT_{A}=BT_{C}={frac {BC+AB-AC}{2}}.$

Если обозначить центр вписанной окружности треугольника ABC буквой I, мы получим^[20]

${frac {IAcdot IA}{CAcdot AB}}+{frac {IBcdot IB}{ABcdot BC}}+{frac {ICcdot IC}{BCcdot CA}}=1$

и^[21]

$IAcdot IBcdot IC=4Rr^{2}.$

Теорема Мансиона (составная часть Теоремы о трезубце). Середины трёх отрезков, соединяющих центр вписанной окружности с центрами вневписанных окружностей лежат на описанной окружности^[10].

Теорема Харкорта. Пусть треугольник задан своими вершинами A, B и C, противоположные вершинам стороны имеют длины a, b и c, площадь равна K и прямая касается вписанной в треугольник окружности в произвольной точке. Обозначим расстояния от вершин треугольника до прямой через a ‘, b ‘ и c ‘, при этом, если вершина и центр окружности лежат по разные стороны от прямой, расстояние считается отрицательным. Тогда

$aa^{prime }+bb^{prime }+cc^{prime }=2K.$

Другие свойства вневписанных окружностей[править | править код]

Следующее отношение выполняется для радиуса r вписанной окружности, радиуса R описанной окружности, полупериметра s и радиусов вневписанных окружностей r_a, r_b, r_c^[12]:

$r_{a}+r_{b}+r_{c}=4R+r,$

$r_{a}r_{b}+r_{b}r_{c}+r_{c}r_{a}=s^{2},$

$r_{a}^{2}+r_{b}^{2}+r_{c}^{2}=(4R+r)^{2}-2s^{2},$

Окружность, проходящая через центры вневписанных окружностей, имеет радиус 2R^[12].

Если H — ортоцентр треугольника ABC, то^[12]

$r_{a}+r_{b}+r_{c}+r=AH+BH+CH+2R,$

$r_{a}^{2}+r_{b}^{2}+r_{c}^{2}+r^{2}=AH^{2}+BH^{2}+CH^{2}+(2R)^{2}.$

Вершины A, B и C треугольника ABC являются основаниями высот треугольника J_AJ_B,J_C,

где J_AJ_B,J_C — центры вневписанных окружностей^[10].

Перпендикуляры, восставленные к сторонам треугольника в точках касания вневписанных окружностей, пересекаются в одной точке. Эта точка симметрична центру вписанной окружности относительно центра описанной окружности^[14].
Центр Шпикера треугольника является радикальным центром его вневписанных окружностей^[22]. Если из центра Шпикера треугольника провести 6 касательных к 3 вневписанным окружностям треугольника, то все их длины будут равны между собой.

Окружность Аполлония[править | править код]

Определение окружности Аполлония[править | править код]

Точка Аполлония и окружность Аполлония

Пусть дан треугольник ABC. Пусть вневписанные окружности треугольника ABC, противоположные вершинам A, B и C, есть соответственно E_A, E_B, E_C (см. рисунок). Тогда окружность Аполлония E (на рис. справа показана зеленым цветом) касается внутренним образом сразу трех вневписанных окружностей треугольника ABC в точках соответственно E_A, E_B и E_C (см. рисунок)^[23].

Радиус окружности Аполлония[править | править код]

Радиус окружности Аполлония равен ${frac {r^{2}+s^{2}}{4r}}$ , где r — радиус вписанной окружности и s — полупериметр треугольника^[24].

Определение точки Аполлония Ap[править | править код]

Точка Аполлония Ap в Энциклопедии центров треугольника у Кларка Кимберлинга (Encyclopedia of Triangle Centers (ETC)) именуется как центр треугольника под именем X(181).
Точка Аполлония Ap или X(181) определяется следующим образом:

Пусть A’ , B’ и C’ есть точки касания окружности Аполлония E с соответствтвующими вневписанными окружностями. Тогда прямые AA’ , BB’ и CC’ пересекаются в одной точке Ap, которую называют точкой Аполлония треугольника ABC.

Изогональное сопряжение[править | править код]

Изогональное сопряжение имеет ровно четыре неподвижные точки (то есть точки, которые сопряжены самим себе): центр вписанной окружности и центры вневписанных окружностей треугольника^[25].

Ортоцентр треугольника изогонально сопряжён центру описанной окружности этого треугольника^[25].

Обобщение на другие многоугольники[править | править код]

Некоторые (но не все) четырёхугольники имеют вписанную окружность. Они называются описанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важным является то, что суммы противоположных сторон равны. Это утверждение называется теоремой Пито.
Некоторые (но не все) четырёхугольники имеют вневписанную окружность. Они называются внеописанными четырёхугольниками. Среди свойств этих четырёхугольников наиболее важное свойство отмечает теорема Уркхарта. Она утверждает:
Если противоположные стороны выпуклого четырёхугольника ABCD пересекаются в точках E и F, то

{displaystyle AB+BC=AD+DCquad Leftrightarrow quad AE+EC=AF+FC.}

См. также[править | править код]

Вневписанная окружность
Внеописанный четырёхугольник
Вписанная окружность
Вписанные и описанные фигуры для треугольника
Вписанное коническое сечение^[en]
Вписанная сфера
Высота треугольника
Замечательные точки треугольника
Инцентр или Центр вписанной окружности
Окружность
Описанная окружность
Описанный четырёхугольник
Ортоцентр
Степень точки относительно окружности
Теорема Мансиона
Теорема о трезубце
Теорема Тебо 2 и 3
Теорема Харкорта
Точки Аполлония
Степень точки относительно окружности
Центр Шпикера
Центроид
Центроид треугольника
Эллипс Мандарта
Эллипс Штейнера

Примечания[править | править код]

↑ ¹ ² Roger A. Johnson. Advanced Euclidean Geometry. — Dover, 2007 (оригинал — 1929).. — С. 189, #298(d).
↑ H.S.M. Coxeter. Introduction to Geometry. — 2. — Wiley, 1961..
↑ Marcus Baker. A collection of formulae for the area of a plane triangle. — January 1885. — Т. part 1, vol. 1(6). — С. 134-138.. См. также часть 2 в томе. 2(1), Сентябрь 1885, 11-18.)
↑ D. Minda, S. Phelps. Triangles, ellipses, and cubic polynomials // American Mathematical Monthly. — October 2008. — Вып. 115. — С. 679-689: Theorem 4.1..
↑ С. И. Зетель. Новая геометрия треугольника. — Москва: УЧПЕДГИЗ, 1962. — С. 52-53 Глава III.
↑ Christopher J. Bradley, Geoff C. Smith. The locations of triangle centers // Forum Geometricorum. — 2006. — Вып. 6. — С. 57-70..
↑ Deko Dekov. Computer-generated Mathematics : The Gergonne Point // Journal of Computer-generated Euclidean Geometry. — 2009. — Т. 1. — С. 1–14.. Архивировано 5 ноября 2010 года.
↑ William Allen Whitworth. Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions. — 2012. — С. 210-215. — (Forgotten Books).
↑ Alfred S. Posamentier, Ingmar Lehmann. The Secrets of Triangles. — Prometheus Books, 2012. — С. 289.
↑ ¹ ² ³ ⁴ А. Д. Куланин, С. Н. Федин. Геометрия треугольника в задачах. — М.: Книжный дом «ЛИБРОКОМ», 2009. — ISBN 978-5-397-00786-3.
↑ Thomas Chu. The Pentagon. — Spring, 2005. — С. 45, задача 584..
↑ ¹ ² ³ ⁴ Amy Bell. Hansen’s right triangle theorem, its converse and a generalization // Forum Geometricorum. — 2006. — Вып. 6. — С. 335–342.
↑ Dimitrios Kodokostas. Triangle Equalizers // Mathematics Magazine. — 2010. — Вып. 83, April. — С. 141-146..
↑ ¹ ² Мякишев, 2002, с. 11, п. 5.
↑ Roger Nelson. Euler’s triangle inequality via proof without words // Mathematics Magazine. — February 2008. — Вып. 81(1). — С. 58-61.
↑ R. A. Johnson. Modern Geometry. — Boston: Houghton Mifflin, 1929. — С. 187.
↑ Lev Emelyanov, Tatiana Emelyanova. Euler’s formula and Poncelet’s porism // Forum Geometricorum. — 2001. — Вып. 1. — С. 137–140..
↑ ¹ ² ³ William N. Franzsen. The distance from the incenter to the Euler line // Forum Geometricorum. — 2011. — Т. 11. — С. 231–236..
↑ Mathematical Gazette, July 2003, 323—324.
↑ Patricia R. Allaire, Junmin Zhou, Haishen Yao. Proving a nineteenth century ellipse identity // Mathematical Gazette. — 2012. — Вып. 96, March. — С. 161-165..
↑ Nathan Altshiller-Court. College Geometry. — Dover Publications, 1980. — С. 121,#84.
↑ Odenhal, 2010, с. 35—40.
↑ Darij Grinberg, Paul Yiu. The Apollonius Circle as a Tucker Circle // Forum Geometricorum. — 2002. — Вып. 2. — С. 175-182.
↑ Milorad R. Stevanovi´c. The Apollonius circle and related triangle centers // Forum Geometricorum. — 2003. — Вып. 3. — С. 187-195..
↑ ¹ ² В. В. Прасолов. Точки Брокара и изогональное сопряжение. — М.: МЦНПО, 2000. — (Библиотека «Математическое просвещение»). — ISBN 5-900916-49-9.

Литература[править | править код]

Мякишев А.Г. Элементы геометрии треугольника. — М.: МЦНМО, 2002.
Clark Kimberling. Triangle Centers and Central Triangles // Congressus Numerantium. — 1998. — Вып. 129. — С. i-xxv, 1-295.
Sándor Kiss. The Orthic-of-Intouch and Intouch-of-Orthic Triangles // Congressus Numerantium. — 2006. — Вып. 6. — С. 171—177.
Boris Odenhal. Some triangle centers associated with the circles tangent to the excircles // Forum Geometricorum. — 2010. — Т. 10.

Ссылки[править | править код]

Derivation of formula for radius of incircle of a triangle
Weisstein, Eric W. Incircle (англ.) на сайте Wolfram MathWorld.

Сайты с интерактивным содержанием[править | править код]

Triangle incenter Triangle incircle Incircle of a regular polygon With interactive animations
Constructing a triangle’s incenter / incircle with compass and straightedge An interactive animated demonstration
Equal Incircles Theorem at cut-the-knot
Five Incircles Theorem at cut-the-knot
Pairs of Incircles in a Quadrilateral at cut-the-knot
An interactive Java applet for the incenter

Источник

Как найти радиус вписанной окружности треугольника

Содержание:

Окружность, вписанная в треугольник — как найти радиус
Свойства вписанной в треугольник окружности
- Первое свойство
- Второе свойство
- Третье свойство
Формулы вычисления радиуса вписанной окружности
- Произвольный треугольник
- Прямоугольный треугольник
- Равнобедренный треугольник
- Равносторонний треугольник
Как найти через высоту или стороны, примеры решения

Окружность, вписанная в треугольник — как найти радиус

Определение

Вписанной в треугольник окружностью называют такую окружность, которая занимает внутреннее пространство геометрической фигуры, соприкасаясь со всеми ее сторонами.

В таком случае грани треугольника представляют собой касательные к этой окружности. Сама геометрическая фигура с тремя углами считается описанной вокруг рассматриваемой окружности.

Вписанная окружность

Источник: people-ask.ru

Свойства вписанной в треугольник окружности

Окружность, которую вписали в треугольник, обладает определенными свойствами. Основные из них можно записать таким образом:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Центр окружности, которую вписали в треугольник, совпадает с точкой пересечения биссектрис этой геометрической фигуры.
Во внутреннее пространство любого треугольника можно вписать лишь одну окружность.
Формула радиуса окружности, который вписали во многоугольник с тремя углами, будет иметь такой вид:

Радиус

Источник: people-ask.ru

В представленной формуле радиуса окружности использованы следующие величины:

S – является площадью треугольника;
р – представляет собой полупериметр геометрической фигуры;
a, b, c – являются сторонами треугольника.

Перечисленные свойства необходимо доказать.

Первое свойство

Требуется доказать, что центр окружности, которую вписали в фигуру с тремя углами, совпадает с точкой пересечения биссектрис.

Доказательство построено в несколько этапов:

Необходимо опустить из центральной точки окружности перпендикулярные прямые OL, OK и OM, которые опускаются на стороны треугольника АВС. Из вершин треугольника следует провести прямые, соединяющие их с центром фигуры OA, OC и OB.

3 Доказательство

Источник: people-ask.ru

Далее можно рассмотреть пару треугольников AOM и AOK. Можно отметить, что они являются прямоугольными, так как OM и OK являются перпендикулярами к сторонам AC и AB. Гипотенуза OA является общей для пары этих фигур.
Исходя из того, что касательная к окружности является перпендикуляром к радиусу, который проведен в точку касания, согласно свойству касательной к окружности, то катеты OМ и OК представляют собой радиусы окружности и, следовательно, равны.
Согласно полученным утверждениям, можно сделать вывод о равенстве прямоугольных треугольников AOМ и AOК по гипотенузе и катету. Таким образом, углы OAМ и OAК тоже равны. Получается, что OA является биссектрисой угла BAC.
Аналогично можно доказать, что OC является биссектрисой угла ACB, а OB – биссектрисой угла ABC.
Таким образом, биссектрисы треугольника совпадают в одной точке, которая представляет собой центр вписанной окружности.

Данное свойство окружности доказано.

Второе свойство

Необходимо представить доказательства свойства окружности, согласно которому в любой треугольник можно вписать окружность, причем только одну.

Доказательство состоит из нескольких этапов:

Окружность получится вписать в треугольник в том случае, когда существует точка, удаленная на равные расстояния от сторон геометрической фигуры.
Можно построить пару биссектрис ОА и ОС. Из точки, в которой они пересекаются, необходимо опустить перпендикулярные прямые OK, OL и OM ко всем граням многоугольника с тремя углами ABC.

4 Второе свойство

Источник: people-ask.ru

Затем следует рассмотреть пару треугольников AOK и AOM.
Эти фигуры обладают общей гипотенузой АО. Углы OAK и OAM равны, так как OA является биссектрисой угла KAM. Углы OKA и OMA прямые, то есть также равны, так как OK и OM являются перпендикулярами к сторонам AB и AC.
Исходя из того, что две пары углов равны, можно сделать вывод о равенстве третьей пары AOM и AOK.
Таким образом, получилось подтвердить равенство треугольников AOK и AOM по стороне AO и двум углам, которые к ней прилегают.

5 Второе свойство

Источник: people-ask.ru

Удалось определить равенство сторон ОМ и ОК, то есть они удалены на одинаковое расстояние от сторон геометрической фигуры АС и АВ.
Аналогично можно доказать, что OM и OL равны, то есть равноудалены от граней AC и BC.
Таким образом, точка равноудалена от сторон треугольника, что делает ее центром окружности, которая вписана в этот многоугольник.
Аналогичным способом можно определить точку во внутреннем пространстве любой геометрической фигуры с тремя углами, которая будет удалена на равные расстояния от его сторон, и представляет собой центр окружности, вписанной в этот треугольник.
Исходя из вышесказанного, можно сделать вывод о том, что в любой треугольник можно вписать окружность.
Необходимо заметить, что центральная точка окружности совпадает с точкой, в которой пересекаются биссектрисы треугольника.
Можно допустить ситуацию, при которой в геометрическую фигуру с тремя углами можно вписать две и более окружности.
Необходимо провести три прямые из вершин геометрической фигуры к центральной точке окружности, вписанной в нее, и опустить перпендикулярные прямые к каждой грани треугольника. Таким образом, будет доказано, что рассматриваемая окружность лежит на пересечении биссектрис треугольника, согласно доказательству ее первого свойства.
Получим совпадение центральной точки окружности и центра первой окружности, которая уже была вписана в этот треугольник, а ее радиус соответствует перпендикуляру, опущенному на сторону треугольника так же, как и в первом случае. Можно сделать вывод о совпадении этих окружностей.
Аналогично любая другая окружность, вписанная в геометрическую фигуру с тремя углами, будет совпадать с первой окружностью.
Таким образом, в треугольник получается вписать лишь одну окружность.

Свойство доказано.

Третье свойство

Требуется доказать, что радиус окружности, которую вписали в геометрическую фигуру с тремя углами, представляет собой отношение площади треугольника к полупериметру:

6 Формула

Источник: people-ask.ru

Кроме того, необходимо представить доказательства следующему равенству:

7 Формула

Источник: people-ask.ru

Доказательство:

8 Треугольник

Источник: people-ask.ru

Следует рассмотреть произвольный треугольник АВС, стороны которого соответствуют a, b и c. Для расчета полупериметра данного треугольника целесообразно использовать формулу:

9 Формула

Источник: people-ask.ru

Центральная точка окружности совпадает с точкой пересечения биссектрис геометрической фигуры с тремя углами. Прямые OA, OB и OC, которые соединяют O с вершинами треугольника АВС, разделяют геометрическую фигуру на три части: AOC, COB, BOA. Площадь треугольника ABC представляет собой сумму площадей этих трех частей.

10 Формула

Источник: people-ask.ru

Исходя из того, что площадь какого-либо треугольника представляет собой половину произведения его основания на высоту, а высота треугольников AOC, COB, BOA рассчитывается, как радиус окружности r, то площади треугольников AOC, COB и BOA можно определить по формулам:

11 Формула

Источник: people-ask.ru

Далее необходимо представить площадь S геометрической фигуры АВС, как сумму площадей нескольких треугольников:

12 Формула

Источник: people-ask.ru

Следует отметить, что второй множитель является полупериметром геометрической фигуры с тремя углами АВС, что можно записать в виде равенства:

13 Формула

Источник: people-ask.ru

14 Формула

Источник: people-ask.ru

Таким образом, доказано равенство радиуса вписанной окружности и отношения площади треугольника к полупериметру.
Можно записать формулу Герона, смысл которой заключается в следующем: площадь треугольника (S) равняется квадратному корню из произведения его полупериметра (p) на разности полупериметра и каждой из его сторон (a, b, c)

15 Формула

Источник: people-ask.ru

Далее следует преобразовать формулу для расчета радиуса:

16 Формула

Источник: people-ask.ru

Свойство окружности доказано.

Формулы вычисления радиуса вписанной окружности

Параметры окружности, которую вписали в геометрическую фигуру с тремя углами, можно рассчитать с помощью стандартных формул. Радиус окружности будет определен в зависимости от типа треугольника.

Произвольный треугольник

Определить радиус окружности, которая вписана в какой-либо треугольник, можно, как удвоенную площадь треугольника, поделенную на его периметр.

17 Формула

Источник: microexcel.ru

В данном случае, a, b, c являются сторонами геометрической фигуры с тремя углами, S – ее площадь.

Прямоугольный треугольник

Радиус окружности, которую вписали в треугольник с прямым углом, представляет собой дробь с числителем в виде суммы катетов за минусом гипотезы и знаменателем, равным числу 2.

18 Формула

Источник: microexcel.ru

В формуле a и b являются катетами, c – гипотенузой треугольника.

Равнобедренный треугольник

Радиус окружности, которая вписана в равнобедренный треугольник, определяют по формуле:

19 Формула

Источник: microexcel.ru

В этом случае a – боковые стороны, b – основание треугольника.

Равносторонний треугольник

Расчет радиуса окружности, которая вписана в правильный или равносторонний треугольник, выполняют по формуле:

20 Формула

Источник: microexcel.ru

где a – сторона геометрической фигуры с тремя углами.

Как найти через высоту или стороны, примеры решения

Задача 1

Имеется геометрическая фигура с тремя углами, стороны которой составляют 5, 7 и 10 см. Требуется определить радиус окружности, которая вписана в этот треугольник.

Решение

В первую очередь необходимо определить, какова площадь треугольника. Для этого можно воспользоваться формулой Герона:

21 Формула

Источник: microexcel.ru

Затем применим формулу для расчета радиуса круга:

22 Формула

Источник: microexcel.ru

Ответ: радиус окружности составляет примерно 1,48 см.

Задача 2

Необходимо рассчитать радиус окружности, которая вписана в равнобедренный треугольник. Боковые стороны геометрической фигуры составляют 16 см, а основание равно 7 см.

Решение

Следует использовать подходящую формулу для расчета радиуса, подставив в нее известные величины:

23 Формула

Источник: microexcel.ru

Ответ: радиус окружности примерно равен 2,8 см.

Источник

Как найти площадь треугольника через радиус вписанной окружности?

Площадь треугольника равна произведению радиуса вписанной в этот треугольник окружности на на его полупериметр.

Формула для нахождения площади треугольника через радиус вписанной окружности:

$[p = frac{{a + b + c}}{2}]$

Дано:

∆ ABC,

окружность (O; r) — вписанная,

AB=c, BC=a, AC=b,

$[p = frac{{a + b + c}}{2}]$

Доказать:

$[{S_{Delta ABC}} = pr]$

Доказательство:

Рассмотрим треугольник AOC.

(как радиус, проведенный в точку касания).

Следовательно, OF — высота треугольника AOC.

По формуле

$[S = frac{1}{2}a{h_a}]$

$[{S_{Delta AOC}} = frac{1}{2}AC cdot OF = frac{1}{2}br.]$

Аналогично найдем

площади

треугольников

AOB и BOC:

$[{S_{Delta AOB}} = frac{1}{2}AB cdot OD = frac{1}{2}cr,]$

$[{S_{Delta BOC}} = frac{1}{2}BC cdot OK = frac{1}{2}ar.]$

Так как площадь треугольника ABC равна сумме площадей этих треугольников, то

$[{S_{Delta ABC}} = {S_{Delta AOC}} + {S_{Delta AOB}} + {S_{Delta BOC}} = ]$

$[ = frac{1}{2}br + frac{1}{2}cr+frac{1}{2}ar = frac{{a + b + c}}{2} cdot r = pr.]$

Что и требовалось доказать.

Если требуется найти площадь треугольника через его периметр, формулу записывают так:

$[S = frac{1}{2}P cdot r,]$

где P — периметр треугольника, r — радиус вписанной в этот треугольник окружности.

Источник

Вписанная окружность и отрезки сторон треугольника

Давай представим, что мы откуда-то узнали все три стороны треугольника.

okruzhnost vpisannaya v treugolnik otrezki

Можно ли найти как-то отрезочки ( displaystyle AK), ( displaystyle KC), ( displaystyle BL) и.д. —отрезки, на которые точки касания разбивают стороны треугольника?

Представь себе, можно, и даже очень легко. Для этого нужно знать только то, что отрезки касательных, проведённых из одной точки, равны (если ещё не успел это узнать – загляни в тему «Касательные, касающиеся окружности»).

Итак, начнём поиск!

Посмотри внимательно: из точки ( displaystyle A) проведено две касательных, значит их отрезки ( displaystyle AK) и ( displaystyle AM) равны.

Мы обозначим их «( displaystyle x)».

Далее, точно так же:

( displaystyle BM=BL=y) (обозначили).

( displaystyle CK=CL=z) (обозначили).

okruzhnost vpisannaya v treugolnik otrezki 1

Теперь вспомним-ка, что мы знаем длины всех трёх сторон треугольника. Обозначим эти длины «( displaystyle a)», «( displaystyle b)», «( displaystyle c)» — смотри на рисунок. Что же теперь получилось?

А вот, например, отрезок «( displaystyle a)» состоит из двух отрезков «( displaystyle y)» и «( displaystyle z)», да и отрезки «( displaystyle b)» и «( displaystyle c)» тоже из чего-то состоят. Запишем это всё сразу:

( displaystyle left{ begin{array}{l}y+z=a\x+z=b\x+y=cend{array} right.)

Ух ты! Выход в алгебру! Три уравнения и три неизвестных! Сейчас решим!

Сложим первые два уравнения и вычтем третье:

( displaystyle left{ begin{array}{l}y+z=a\x+z=b\x+y=cend{array} right.Rightarrow x+y+2z-left( x+y right)=a+b-c), то есть:

( displaystyle z=frac{a+b-c}{2})

А теперь сложим первое и третье уравнение и вычтем второе:

( displaystyle left{ begin{array}{l}y+z=a\x+z=b\x+y=cend{array} right.Rightarrow y+z+x+y-left( x+z right)=a+c-b), то есть:

( displaystyle y=frac{a+c-b}{2})

И последний шаг: сложим второе и третье, а потом вычтем первое.

( displaystyle left{ begin{array}{l}y+z=a\x+z=b\x+y=cend{array} right.Rightarrow x=frac{b+c-a}{2})

( displaystyle x=frac{b+c-a}{2})

Ну вот, всё нашли:

( displaystyle x=frac{b+c-a}{2};y=frac{a+c-b}{2};~z=frac{a+b-c}{2})

Очень много плюсов и минусов – аж в глазах рябит. Как же это запомнить? А оказывается, очень просто. Смотри-ка на картинку и формулу сразу.

okruzhnost vpisannaya v treugolnik otrezki 2

( displaystyle x=frac{b+c-a}{2})

Секрет вот в чём: те стороны, на которых есть «( displaystyle x)» («( displaystyle b)» и «( displaystyle c)») будут с плюсом, а та сторона, где нет «( displaystyle x)» (это «( displaystyle a)»), будет с минусом.

Ну, а пополам поделить всё хозяйство. С другими буквами точно так же

( displaystyle y=frac{a+c-b}{2})

На «( displaystyle a)» и «( displaystyle c)» есть «( displaystyle y)» — они с плюсом, на «( displaystyle b)» нет «( displaystyle y)» — она с минусом

( displaystyle z=frac{a+b-c}{2})

На «( displaystyle a)» и «( displaystyle b)» есть «( displaystyle z)» — они с плюсом, на «( displaystyle c)» нет «( displaystyle z)» — она с минусом.

Источник

Радиус вписанной окружности в любой треугольник

Радиус вписанной окружности в правильный треугольник

Радиус вписанной окружности в равнобедренный треугольник

Радиус вписанной окружности в прямоугольный треугольник

Связь с площадью треугольника[править | править код]

Вписанная окружность[править | править код]

Вневписанные окружности[править | править код]

Связанные построения[править | править код]

Окружность девяти точек и точка Фейербаха[править | править код]

Треугольник и точка Жергонна[править | править код]

Треугольник и точка Нагеля[править | править код]

Трилинейные координаты вписанных треугольников[править | править код]

Уравнения окружностей[править | править код]

Другие свойства вписанной окружности[править | править код]

Некоторые формулы с радиусом вписанной окружности[править | править код]

Формулы для расстояний до центра вписанной или вневписанной окружностей[править | править код]

Теорема Эйлера[править | править код]

Другие формулы для расстояний до центра вписанной или вневписанной окружностей[править | править код]

Другие свойства вневписанных окружностей[править | править код]

Окружность Аполлония[править | править код]

Определение окружности Аполлония[править | править код]

Радиус окружности Аполлония[править | править код]

Определение точки Аполлония Ap[править | править код]

Изогональное сопряжение[править | править код]

Обобщение на другие многоугольники[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Сайты с интерактивным содержанием[править | править код]

Как найти радиус вписанной окружности треугольника

Окружность, вписанная в треугольник — как найти радиус

Свойства вписанной в треугольник окружности

Первое свойство

Второе свойство

Третье свойство

Формулы вычисления радиуса вписанной окружности

Произвольный треугольник

Прямоугольный треугольник

Равнобедренный треугольник

Равносторонний треугольник

Как найти через высоту или стороны, примеры решения

Вписанная окружность и отрезки сторон треугольника

Вам также может понравиться

Как найти проводку под штукатуркой мультиметром

Текст на тему как мы лепили снеговика 3 класс по картинке составить

Fix the errors below and try again ets2 как исправить

Добавить комментарий Отменить ответ