Как найти полупериметр правильного треугольника

Как найти полупериметр правильного треугольника

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6dc9c5486d93164e • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Площадь треугольника через стороны

Площадь треугольника через стороны — это
площадь треугольника, которая выражена через
три стороны треугольника и полупериметр.

Полупериметр — это половина суммы
длин всех сторон треугольника.

Площадь любого треугольника можно рассчитать по
разным формулам. Одна из популярных формул:

С помощью этой формулы можно найти площадь
треугольника зная длину основания и высоту.
Но, иногда требуется найти площадь треугольника,
зная только стороны треугольника. Так, как у
каждого треугольника три стороны, то соответственно
три длины. Но, как же найти площадь?

Площадь треугольника через стороны легко рассчитать
зная Формулу Герона.Герон — греческий математик, в
честь которого и была названа эта формула. В чем суть
формулы Герона? Как найти площадь треугольника через длины сторон?

Площадь произвольного треугольника равна квадратному
корню из произведения полупериметра на разницу
между полупериметром и стороной a, полупериметром
и стороной b, полупериметром и стороной c.

Можно сделать вывод, что, чтобы рассчитать площадь треугольника
по Формуле Герона, нужно знать все стороны данного треугольника.

Формула Герона:

a, b, c — длины сторон треугольника;
p — полупериметр;
S — площадь;

Формула полупериметра:

Обобщение площади треугольника через стороны:

Подставив в вышеперечисленные формулы длины всех сторон,
можно найти площадь любого треугольника. С помощью формулы
площади треугольника через три стороны, можно также
найти не только площадь, но и периметр.

Как найти площадь треугольника

На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.

Треугольник – это многоугольник с тремя сторонами.

По формуле Герона

Формула Герона для нахождения площади треугольника:

Через основание и высоту

Формула нахождения площади треугольника с помощью половины его основания и высоту:

Через две стороны и угол

Формула нахождения площади треугольника через две стороны и угол между ними:

Через сторону и два прилежащих угла

Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:

Площадь прямоугольного треугольника

Прямоугольный треугольник – треугольник у которого один из углов прямой, т.е. равен 90°.

Формула нахождения площади прямоугольного треугольника через катеты:

Площадь равнобедренного треугольника через стороны

Равнобедренный треугольник – треугольник, в котором две стороны равны. А значит, равны и два угла.

Формула нахождения площади равнобедренного треугольника через две стороны:

Площадь равнобедренного треугольника через основание и угол

Формула нахождения площади равнобедренного треугольника через основание и угол:

Площадь равностороннего треугольника через стороны

Равносторонний треугольник – треугольник, в котором все стороны равны, а каждый угол равен 60°.

Формула нахождения площади равностороннего треугольника через сторону:

Площадь равностороннего треугольника через высоту

Формула нахождения площади равностороннего треугольника через высоту:

Площадь равностороннего треугольника через радиус вписанной окружности

Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:

Площадь равностороннего треугольника через радиус описанной окружности

Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:

Площадь треугольника через радиус описанной окружности и три стороны

Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:

Площадь треугольника через радиус вписанной окружности и три стороны

Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:

[spoiler title=”источники:”]

http://colibrus.ru/ploschad-treugolnika-cherez-storony/

http://mozgan.ru/Geometry/AreaTriangle

[/spoiler]

Источник

Полупериметр многоугольника — это половина его периметра. Хотя полупериметр является очень простой производной периметра, он столь часто появляется в формулах для треугольников и других геометрических фигур, что ему выделили отдельное наименование. Если полупериметр оказывается в какой-либо формуле, его, обычно, обозначают буквой p.

Треугольники[править | править код]

В любом треугольнике расстояние вдоль сторон от вершины до точки касания вневписанной окружности на противоположной стороне равно полупериметру.

Полупериметр чаще всего используется для треугольников. Формула полупериметра для треугольника со сторонами a, b и c

{displaystyle p={frac {a+b+c}{2}}.}

Свойства[править | править код]

В любом треугольнике вершина и точка касания вневписанной окружности на противоположной стороне делят периметр треугольника на две равные части, то есть на два пути, длина каждого из которых равна полупериметру. На рисунке показаны стороны A, B, C и точки касания A’, B’, C’, тогда

{displaystyle p=|AB|+|A'B|=|AB|+|AB'|=|AC|+|A'C|}

{displaystyle =|AC|+|AC'|=|BC|+|B'C|=|BC|+|BC'|.}

Три отрезка, соединяющих вершины с противоположными точками касания, пересекаются в одной точке — точке Нагеля.

Если рассмотреть отрезки, соединяющие середины сторон с точками, отстоящими (вдоль сторон) от этой середины на полупериметр, то эти отрезки пересекаются в одной точке — центре окружности Шпикера, которая является окружностью, вписанной в медианный треугольник[en]. Центр Шпикера является центром тяжести сторон треугольника.

Прямая, проходящая через центр вписанной окружности треугольника делит периметр пополам в том и только в том случае, когда она делит пополам площадь.

Полупериметр треугольника равен периметру его медианного треугольника[en].

Из неравенства треугольника вытекает, что длина наибольшей стороны треугольника не превосходит полупериметр.

Формулы с полупериметром[править | править код]

Площадь K любого треугольника является произведением радиуса его вписанной окружности и полупериметра:

{displaystyle K=pr.}

Площадь треугольника можно вычислить исходя из его полупериметра и длин сторон a, b, c по формуле Герона:

{displaystyle K={sqrt {pleft(p-aright)left(p-bright)left(p-cright)}}.}

Радиус описанной окружности R треугольника можно также вычислить из его полупериметра и длин сторон:

{displaystyle R={frac {abc}{4{sqrt {p(p-a)(p-b)(p-c)}}}}.}

Эту формулу можно вывести из теоремы синусов.

Радиус вписанной окружности равен

{displaystyle r={sqrt {frac {(p-a)(p-b)(p-c)}{p}}}.}

Теорема котангенсов даёт котангенсы половин углов в вершинах треугольника в терминах полупериметра, сторон и радиуса вписанной окрухности.

Длина биссектрисы внутреннего угла, противоположного стороне a, равна[1]

{displaystyle t_{a}={frac {2{sqrt {bcs(p-a)}}}{b+c}}.}

В прямоугольном треугольнике радиус вневписанной окружности на гипотенузе равен полупериметру. Полупериметр равен сумме радиуса вписанной окружности и удвоенного радиуса описанной. Площадь прямоугольного треугольника равна {displaystyle (p-a)(p-b)}, где a и b — катеты.

Четырёхугольники[править | править код]

Формула для полупериметра четырёхугольника со сторонами a, b, c и d

{displaystyle p={frac {a+b+c+d}{2}}.}

Одна из формул для треугольников, использующая полупериметр, применима также и к описанным четырёхугольникам, которые имеют вписанную окружность и сумма длин противоположных сторон которых равна полупериметру. А именно, это формула площади фигуры:

{displaystyle K=pr.}

Простейшая форма формулы Брахмагупты для площади четырехугольника вписанного в окружность имеет вид, близкий к формуле Герона для площади треугольника:

{displaystyle K={sqrt {left(p-aright)left(p-bright)left(p-cright)left(p-dright)}}.}

Соотношение Бретшнайдера обобщает формулу для всех выпуклых четырёхугольников:

{displaystyle K={sqrt {(p-a)(p-b)(p-c)(p-d)-abcdcdot cos ^{2}left({frac {alpha +gamma }{2}}right)}},}

где alpha и gamma  — два противоположных угла.

Четыре стороны бицентрального четырёхугольника[en] являются четырьмя решениями уравнения четвёртой степени, параметрами которого являются полупериметр, радиус вписанной окружности и радиус описанной.

Правильные многоугольники[править | править код]

Площадь выпуклого правильного многоугольника равна произведению его полупериметра на расстояние от центра до одной из сторон.

Примечания[править | править код]

  1. ↑ Johnson, 2007, с. 70.

Литература[править | править код]

  • Roger A. Johnson. Advanced Euclidean Geometry. — Dover Publ., 2007. (Переиздание книги 1929 года)

Ссылки[править | править код]

  • Weisstein, Eric W. Semiperimeter (англ.) на сайте Wolfram MathWorld.
Источник

Полупериметр равностороннего треугольника Калькулятор

Search
Дом математика ↺
математика Геометрия ↺
Геометрия 2D геометрия ↺
2D геометрия Треугольник ↺
Треугольник Равносторонний треугольник ↺
Равносторонний треугольник Полупериметр равностороннего треугольника ↺

✖Длина ребра равностороннего треугольника — это длина одной из сторон равностороннего треугольника. В равностороннем треугольнике все три стороны равны.ⓘ Длина ребра равностороннего треугольника [le]

+10%

-10%

✖Полупериметр равностороннего треугольника равен половине суммы длин всех сторон треугольника.ⓘ Полупериметр равностороннего треугольника [s]

⎘ копия

Полупериметр равностороннего треугольника Решение

ШАГ 0: Сводка предварительного расчета

ШАГ 1. Преобразование входов в базовый блок

Длина ребра равностороннего треугольника: 8 метр –> 8 метр Конверсия не требуется

ШАГ 2: Оцените формулу

ШАГ 3: Преобразуйте результат в единицу вывода

12 метр –> Конверсия не требуется




9 Полупериметр равностороннего треугольника Калькуляторы




9 Важные формулы равностороннего треугольника Калькуляторы

Полупериметр равностороннего треугольника формула

Полупериметр равностороннего треугольника = (3*Длина ребра равностороннего треугольника)/2

s = (3*le)/2

Что такое равносторонний треугольник?

Равносторонний треугольник в геометрии — это треугольник, у которого все три стороны имеют одинаковую длину. В знакомой евклидовой геометрии равносторонний треугольник также является равноугольным; то есть все три внутренних угла также конгруэнтны друг другу и равны 60 ° каждый.

Как рассчитывается полупериметр?

Его полупериметр вычисляется по формуле S = 3a/2, где S — полупериметр равностороннего треугольника, а a — длина стороны треугольника.

Источник

Правильный треугольник

Правильный треугольник — это такой треугольник у которого все три стороны равны и его три угла равны.

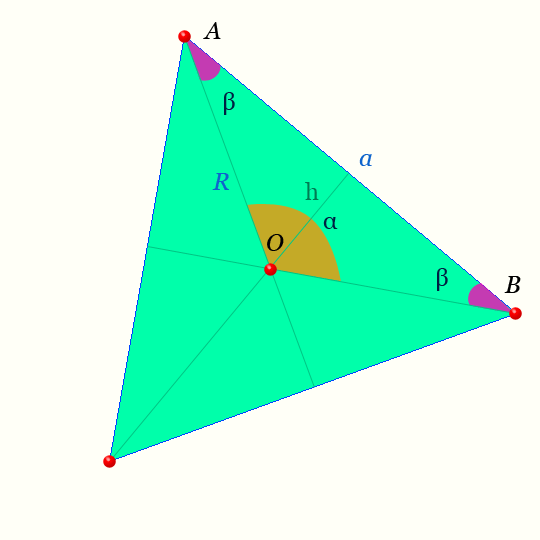
Правильный треугольник

Правильный треугольник

Центр правильного треугольника — на рисунке точка O равноудалена от вершин.

Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.

Отрезки OA, OB — радиусы правильного треугольника.

Обозначения на рисунке для правильного треугольника

n=3 число сторон и вершин правильного треугольника, шт
α центральный угол правильного треугольника, радианы, °
β половина внутреннего угла правильного треугольника, радианы, °
γ внутренний угол правильного треугольника, радианы, °
a сторона правильного треугольника, м
R радиусы правильного треугольника, м
p полупериметр правильного треугольника, м
L периметр правильного треугольника, м
h апофемы правильного треугольника, м

Основные формулы для правильного треугольника

Периметр правильного треугольника

[ L = 3a ]

Полупериметр правильного треугольника

[ p = frac{3}{2}a ]

Центральный угол правильного треугольника в радианах

[ α = frac{2}{3}π ]

Центральный угол правильного треугольника в градусах

[ α = frac{360°}{3} = 120° ]

Половина внутреннего угла правильного треугольника в радианах

[ β = frac{1}{6}π ]

Половина внутреннего угла правильного треугольника в градусах

[ β = frac{180°}{6} = 30° ]

Внутренний угол правильного треугольника в радианах

[ γ = 2β = frac{π}{3} ]

Внутренний угол правильного треугольника в градусах

[ γ = frac{180°}{3} = 60° ]

Площадь правильного треугольника

[ S = ph = frac{3}{2}ha ]

Или учитывая формулу Площади равностороннего треугольника получим

[S=frac{sqrt{3}}{4}a^2]

Правильный треугольник

 стр. 267
Источник

Лучший ответ

anastasia.kochura

Профи

(699)


12 лет назад

сложить все стороны и разделить на 2

Остальные ответы

Надя Кратко

Мастер

(1749)


12 лет назад

отмерь периметр, раздели на 2

Болеслав Звершхановский

Просветленный

(24068)


12 лет назад

Сложить все стороны и разделить пополам, ОДНАКО !!!

Kirill ___________

Ученик

(123)


12 лет назад

Полупериметр — половина периметра. а периметр – это сумма длин всех сторон.

Сергей Свиридов

Гуру

(3081)


12 лет назад

Полупериметр равностороннего треугольника = сторона + основание/2

Игорь

Мастер

(2205)


12 лет назад

Надо объем треугольника разделить на его площадь.

Коржавин

Знаток

(281)


12 лет назад

Пройти по длинной стороне!

Источник

Добавить комментарий