Призма
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.
Многоугольники $ABCD$ и $A_1B_1C_1D_1$ – называются основаниями призмы.
Параллелограммы $АА_1В_1В, ВВ_1С_1С$ и т.д.- боковыми гранями.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
$С_1Н$ – высота
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
Формулы вычисления объема и площади поверхности призмы:
Чтобы были понятны формулы, введем обозначения:
$P_{осн}$ – периметр основания;
$S_{осн}$ – площадь основания;
$S_{бок}$ – площадь боковой поверхности;
$S_{п.п}$ – площадь полной поверхности;
$h$ – высота призмы.
$S_{бок}=P_{осн}·h$
$S_{п.п}=S_{бок}+2S_{осн}$
$V=S_{осн}·h$
В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.
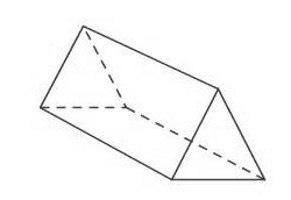
В основании лежит треугольник.
- $S={a·h_a}/{2}$, где $h_a$ – высота, проведенная к стороне $а$
- $S={a·b·sinα}/{2}$, где $a,b$ – соседние стороны, $α$ – угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ – это полупериметр $p={a+b+c}/{2}$
- $S=p·r$, где $r$ – радиус вписанной окружности
- $S={a·b·c}/{4R}$, где $R$ – радиус описанной окружности
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ – катеты прямоугольного треугольника.
В основании лежит четырехугольник
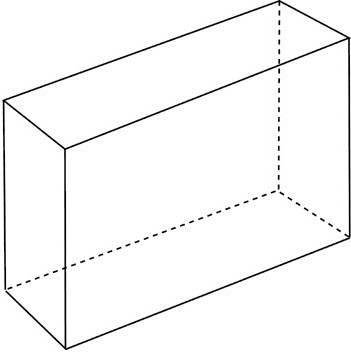
1. Прямоугольник
$S=a·b$, где $а$ и $b$ – смежные стороны.
2. Ромб
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ – диагонали ромба
$S=a^2·sinα$, где $а$ – длина стороны ромба, а $α$ – угол между соседними сторонами.
3. Трапеция
$S={(a+b)·h}/{2}$, где $а$ и $b$ – основания трапеции, $h$ – высота трапеции.
Прямая призма называется правильной, если ее основания – правильные многоугольники.
Рассмотрим площади правильных многоугольников:
1. Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ – длина стороны.
2. Квадрат
$S=a^2$, где $а$ – сторона квадрата.
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
$S=6·S_{треугольника}={6·a^2√3}/{4}={3·a^2√3}/{2}$, где $а$ – сторона правильного шестиугольника.
Пример:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $10$ и $24$, а её боковое ребро равно $20$.
Решение:
Построим прямую призму, в основании которой лежит ромб.
Распишем формулу площади полной поверхности:
$S_{п.п}=S_{бок}+2S_{осн}=P_{осн}·h+2S_{ромба}$
В прямой призме высота равна боковому ребру, следовательно, $h=С_1С=20$
Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.
Диагонали точкой пересечения делятся пополам, поэтому катеты прямоугольного треугольника равны $5$ и $12$.
$АВ=√{5^2+12^2}=√{25+144}=√{169}=13$
$Р=13·4=52$
Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.
$S_{основания}={d_1·d_2}/{2}={10·24}/{2}=120$
Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:
$S_{п.п}=P_{осн}·h+2S_{ромба}=52·20+2·120=1040+240=1280$
Ответ: $1280$
Цилиндр – это та же призма, в основании которой лежит круг.
$S_{бок}=P_{осн}·h=2πRh$
$S_{п.п}=S_{бок}+2S_{осн}=2πRh+2πR^2=2πR(h+R)$
$V=S_{осн}·h=πR^2 h$
Подобные призмы: при увеличении всех линейных размеров призмы в $k$ раз, её объём увеличится в $k^3$ раз.
Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ – средняя линия, так как соединяет середины соседних сторон.
$MN {//} AC, MN = {AC}/{2}$
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ – коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
$AC^2+BC^2=AB^2$
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ – противолежащий катет; $ВС$ – прилежащий катет.
Для острого угла $А: ВС$ – противолежащий катет; $АС$ – прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | ${1}/{2}$ | ${√2}/{2}$ | ${√3}/{2}$ |
| $cosα$ | ${√3}/{2}$ | ${√2}/{2}$ | ${1}/{2}$ |
| $tgα$ | ${√3}/{3}$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | ${√3}/{3}$ |
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ – радиус описанной около треугольника окружности.
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα;$
$b^2=a^2+c^2-2·a·c·cosβ;$
$c^2=b^2+a^2-2·b·a·cosγ.$
Содержание
- Как найти периметр призмы
- Что такое призма?
- Периметр призмы
- Зачем вам нужно рассчитывать периметр призмы?
- Пример задачи: периметр прямоугольной призмы
- Как найти площадь прямоугольной призмы
- Как найти площадь треугольной призмы
- Как найти высоту призмы
- Призма
- Призма
- Формулы вычисления объема и площади поверхности призмы:
- В основании лежит треугольник.
- В основании лежит четырехугольник
- 1. Прямоугольник
- 2. Ромб
- 3. Трапеция
- Рассмотрим площади правильных многоугольников:
- Подобие треугольников
- Прямоугольный треугольник и его свойства:
- Теорема Пифагора
- Теорема синусов
- Теорема косинусов
Как найти периметр призмы
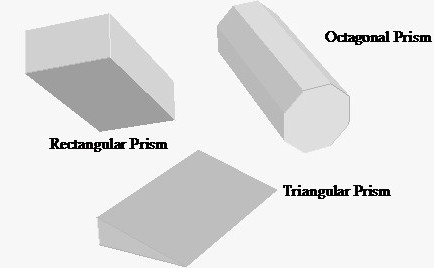
Вы можете увидеть призмы как на уроке математики, так и на протяжении всей вашей повседневной жизни. Кирпич — это прямоугольная призма. Упаковка апельсинового сока — это тип призмы. Коробка из ткани представляет собой прямоугольную призму. Амбары представляют собой тип пятиугольной призмы. Пентагон — это пятиугольная призма. Аквариум представляет собой прямоугольную призму. Этот список можно продолжать и продолжать.
Призмы по определению — это сплошные объекты с одинаковыми концевыми формами, одинаковыми сечениями и плоскими боковыми гранями (без кривых) И хотя большинство математических задач и примеров из реальной жизни, касающихся вычислений призмы, связаны с формулой объема или формулой площади поверхности, прежде чем вы сможете это сделать, вам нужно сначала понять один расчет: периметр призмы.
Что такое призма?
Общее определение призмы — это трехмерная сплошная форма, которая имеет следующие характеристики:
- Это многогранник (то есть это сплошная фигура).
- Поперечное сечение объекта является одинаковым по всей длине объекта.
- Это параллелограмм (четырехсторонняя форма, в которой противоположные стороны параллельны друг другу).
- Грани объекта плоские (без изогнутых граней).
- Две концевые формы идентичны.
Название призмы происходит от формы двух концов, которые известны как основания. Это может быть любая форма (кроме кривых или кругов). Например, призма с треугольными основаниями называется треугольной призмой. Призма с прямоугольными основаниями называется прямоугольной призмой. Этот список можно продолжить.
Рассматривая характеристики призм, это исключает сферы, цилиндры и конусы как призмы, потому что они имеют изогнутые грани. Это также устраняет пирамиды, потому что они не имеют одинаковых основных форм или идентичных поперечных сечений повсюду.
Периметр призмы
Говоря о периметре призмы, вы на самом деле имеете в виду периметр базовой формы. Периметр основания призмы такой же, как периметр вдоль любого поперечного сечения призмы, поскольку все поперечные сечения одинаковы по всей длине призмы.
Периметр измеряет сумму длин любого многоугольника. Таким образом, для каждого типа призмы вы найдете сумму длин любой формы, являющейся основанием, и это будет периметр призмы.
Например, формула для нахождения периметра треугольной призмы будет суммой трех длин треугольника, составляющего основание, или:
Периметр треугольника = a + b + c, где a , b и c — три длины треугольника.
Это будет периметр формулы прямоугольной призмы:
Периметр прямоугольника: 2l + 2w, где l — длина прямоугольника, а w — ширина.
Примените стандартные расчеты периметра к базовой форме призмы, и это даст вам периметр.
Зачем вам нужно рассчитывать периметр призмы?
Поиск периметра призмы не кажется слишком сложным, если вы понимаете, о чем идет речь. Однако периметр является важным расчетом, который учитывает формулы площади и объема поверхности для некоторых призм.
Например, это формула для определения площади поверхности правой призмы (правая призма имеет идентичные основания и стороны, которые все прямоугольные):
Площадь поверхности = 2b + ph
где b равно площади основания, p равно периметру основания, а h равно высоте призмы. Вы можете видеть этот периметр, необходимый для определения площади поверхности.
Пример задачи: периметр прямоугольной призмы
Допустим, у вас есть проблема с правильной прямоугольной призмой, и вас попросили найти периметр. Вам даны следующие значения:
Чтобы найти периметр, используйте формулу для нахождения периметра прямоугольной призмы, поскольку имя говорит о том, что основание представляет собой прямоугольник:
Периметр = 2l + 2w = 2 (75 см) + 2 (10 см) = 150 см + 20 см = 170 см
Затем вы можете продолжить, чтобы найти площадь поверхности, потому что у вас есть высота, у вас есть периметр основания, и это считается, что эта призма является правой призмой.
Площадь основания равна длине × ширине (как всегда для прямоугольника), которая равна:
Площадь основания = 75 см × 10 см = 750 см 2
Теперь у вас есть все значения для расчета площади поверхности:
Площадь поверхности = 2b + ph = 2 (750 см 2 ) + 170 см (5 см) = 1500 см 2 + 850 см = 2350 см 2
Как найти площадь прямоугольной призмы
Два одинаковых конца прямоугольной призмы являются прямоугольниками, и в результате четыре стороны между концами также являются двумя парами одинаковых прямоугольников. Поскольку прямоугольная призма имеет шесть прямоугольных граней или сторон, площадь ее поверхности является суммой шести граней, и поскольку каждая грань имеет одинаковую противоположность, .
Как найти площадь треугольной призмы
Призма определяется как сплошная фигура с равномерным поперечным сечением. Существует много различных типов призм, от прямоугольных до круглых и треугольных. Вы можете найти площадь поверхности любого типа призмы с простой формулой, и треугольные призмы не являются исключением. Может быть полезно понять, как рассчитать .
Как найти высоту призмы
Два основания призмы могут определять ее форму, но высота призмы определяет ее размер. Призмы — это многогранники, трехмерные тела с двумя одинаковыми и параллельными многоугольными основаниями или концами. Высота призмы — это расстояние между двумя ее основаниями и является важным измерением при расчете .
Источник
Призма
Призма
Призма – это многогранник, состоящий из двух равных многоугольников, расположенных в параллельных плоскостях, и $n$-го количества параллелограммов.
Многоугольники $ABCD$ и $A_1B_1C_1D_1$ – называются основаниями призмы.
Параллелограммы $АА_1В_1В, ВВ_1С_1С$ и т.д.- боковыми гранями.
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.
Формулы вычисления объема и площади поверхности призмы:
Чтобы были понятны формулы, введем обозначения:
$S_<бок>$ — площадь боковой поверхности;
$S_<п.п>$ — площадь полной поверхности;
В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.
В основании лежит треугольник.
- $S=/<2>$, где $h_a$ — высота, проведенная к стороне $а$
- $S=/<2>$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√$, где $р$ — это полупериметр $p=/<2>$
- $S=p·r$, где $r$ — радиус вписанной окружности
- $S=/<4r>$, где $R$ — радиус описанной окружности
- Для прямоугольного треугольника $S=/<2>$, где $а$ и $b$ — катеты прямоугольного треугольника.
В основании лежит четырехугольник
1. Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
2. Ромб
$S=/<2>$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
3. Трапеция
$S=<(a+b)·h>/<2>$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Прямая призма называется правильной, если ее основания – правильные многоугольники.
Рассмотрим площади правильных многоугольников:
1. Для равностороннего треугольника $S=/<4>$, где $а$ — длина стороны.
$S=a^2$, где $а$ — сторона квадрата.
3. Правильный шестиугольник
Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:
Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными $10$ и $24$, а её боковое ребро равно $20$.
Построим прямую призму, в основании которой лежит ромб.
Распишем формулу площади полной поверхности:
В прямой призме высота равна боковому ребру, следовательно, $h=С_1С=20$
Чтобы найти периметр основания, надо узнать сторону ромба. Рассмотрим один из прямоугольных треугольников, получившихся, при пересечении диагоналей и воспользуемся теоремой Пифагора.
Диагонали точкой пересечения делятся пополам, поэтому катеты прямоугольного треугольника равны $5$ и $12$.
Теперь найдем площадь основания: площадь ромба равна половине произведения его диагоналей.
Далее подставим все найденные величины в формулу полной поверхности и вычислим ее:
Цилиндр — это та же призма, в основании которой лежит круг.
Подобные призмы: при увеличении всех линейных размеров призмы в $k$ раз, её объём увеличится в $k^3$ раз.
Средняя линия треугольника параллельна основанию и равна его половине.
$MN$ — средняя линия, так как соединяет середины соседних сторон.
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Прямоугольный треугольник и его свойства:
В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.
Некоторые свойства прямоугольного треугольника:
- Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
- Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
Теорема Пифагора
В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.
Соотношение между сторонами и углами в прямоугольном треугольнике:
В прямоугольном треугольнике $АВС$, с прямым углом $С$
Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.
Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.
- Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
- Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
- В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
- Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
- Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения
Значения тригонометрических функций некоторых углов:
| $α$ | $30$ | $45$ | $60$ |
| $sinα$ | $<1>/<2>$ | $<√2>/<2>$ | $<√3>/<2>$ |
| $cosα$ | $<√3>/<2>$ | $<√2>/<2>$ | $<1>/<2>$ |
| $tgα$ | $<√3>/<3>$ | $1$ | $√3$ |
| $ctgα$ | $√3$ | $1$ | $<√3>/<3>$ |
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Источник
Разные призмы непохожи друг на друга. В то же время у них много общего. Чтобы найти площадь основания призмы, потребуется разобраться в том, какой вид оно имеет.
Общая теория
Призмой является любой многогранник, боковые стороны которого имеют вид параллелограмма. При этом в ее основании может оказаться любой многогранник – от треугольника до n-угольника. Причем основания призмы всегда равны друг другу. Что не относится к боковым граням — они могут существенно различаться по размерам.
При решении задач встречается не только площадь основания призмы. Может потребоваться знание боковой поверхности, то есть всех граней, которые не являются основаниями. Полной поверхностью уже будет объединение всех граней, которые составляют призму.
Иногда в задачах фигурирует высота. Она является перпендикуляром к основаниям. Диагональю многогранника является отрезок, который соединяет попарно две любые вершины, не принадлежащие одной грани.
Следует отметить, что площадь основания прямой призмы или наклонной не зависит от угла между ними и боковыми гранями. Если у них одинаковые фигуры в верхней и нижней гранях, то их площади будут равными.
Треугольная призма
Она имеет в основании фигуру, имеющую три вершины, то есть треугольник. Он, как известно, бывает разным. Если треугольник прямоугольный, то достаточно вспомнить, что его площадь определяется половиной произведения катетов.
Математическая запись выглядит так: S = ½ ав.
Чтобы узнать площадь основания треугольной призмы в общем виде, пригодятся формулы: Герона и та, в которой берется половина стороны на высоту, проведенную к ней.
Первая формула должна быть записана так: S = √(р (р-а) (р-в) (р-с)). В этой записи присутствует полупериметр (р), то есть сумма трех сторон, разделенная на два.
Вторая: S = ½ на * а.
Если требуется узнать площадь основания треугольной призмы, которая является правильной, то треугольник оказывается равносторонним. Для него существует своя формула: S = ¼ а2 * √3.
Четырехугольная призма
Ее основанием является любой из известных четырехугольников. Это может быть прямоугольник или квадрат, параллелепипед или ромб. В каждом случае для того, чтобы вычислить площадь основания призмы, будет нужна своя формула.
Если основание — прямоугольник, то его площадь определяется так: S = ав, где а, в — стороны прямоугольника.
Когда речь идет о четырехугольной призме, то площадь основания правильной призмы вычисляется по формуле для квадрата. Потому что именно он оказывается лежащим в основании. S = а2.
В случае когда основание — это параллелепипед, будет нужно такое равенство: S = а * на. Бывает такое, что даны сторона параллелепипеда и один из углов. Тогда для вычисления высоты потребуется воспользоваться дополнительной формулой: на = в * sin А. Причем угол А прилегает к стороне «в», а высота на противолежащая к этому углу.
Если в основании призмы лежит ромб, то для определения его площади будет нужна та же формула, что для параллелограмма (так как он является его частным случаем). Но можно воспользоваться и такой: S = ½ d1 d2. Здесь d1 и d2 – две диагонали ромба.
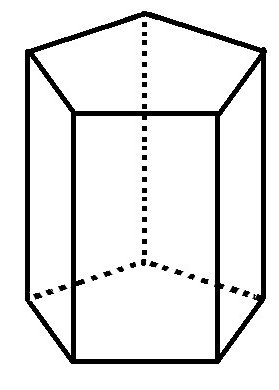
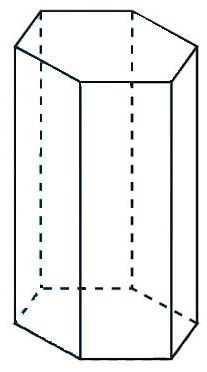
Правильная пятиугольная призма
Этот случай предполагает разбиение многоугольника на треугольники, площади которых узнать проще. Хотя бывает, что фигуры могут быть с другим количеством вершин.
Поскольку основание призмы — правильный пятиугольник, то он может быть разделен на пять равносторонних треугольников. Тогда площадь основания призмы равна площади одного такого треугольника (формулу можно посмотреть выше), умноженной на пять.
Правильная шестиугольная призма
По принципу, описанному для пятиугольной призмы, удается разбить шестиугольник основания на 6 равносторонних треугольников. Формула площади основания такой призмы подобна предыдущей. Только в ней площадь равностороннего треугольника следует умножать на шесть.
Выглядеть формула будет таким образом: S = 3/2 а2 * √3.
Задачи
№ 1. Дана правильная прямая четырехугольная призма. Ее диагональ равна 22 см, высота многогранника — 14 см. Вычислить площадь основания призмы и всей поверхности.
Решение. Основанием призмы является квадрат, но его сторона не известна. Найти ее значение можно из диагонали квадрата (х), которая связана с диагональю призмы (d) и ее высотой (н). х2 = d2 – н2. С другой стороны, этот отрезок «х» является гипотенузой в треугольнике, катеты которого равны стороне квадрата. То есть х2 = а2 + а2. Таким образом получается, что а2 = (d2 – н2)/2.
Подставить вместо d число 22, а «н» заменить его значением — 14, то получается, что сторона квадрата равна 12 см. Теперь просто узнать площадь основания: 12 * 12 = 144 см2.
Чтобы узнать площадь всей поверхности, нужно сложить удвоенное значение площади основания и учетверенную боковую. Последнюю легко найти по формуле для прямоугольника: перемножить высоту многогранника и сторону основания. То есть 14 и 12, это число будет равно 168 см2. Общая площадь поверхности призмы оказывается 960 см2.
Ответ. Площадь основания призмы равна 144 см2. Всей поверхности – 960 см2.
№ 2. Дана правильная треугольная призма. В основании лежит треугольник со стороной 6 см. При этом диагональ боковой грани составляет 10 см. Вычислить площади: основания и боковой поверхности.
Решение. Так как призма правильная, то ее основанием является равносторонний треугольник. Поэтому его площадь оказывается равна 6 в квадрате, умноженному на ¼ и на корень квадратный из 3. Простое вычисление приводит к результату: 9√3 см2. Это площадь одного основания призмы.
Все боковые грани одинаковые и представляют собой прямоугольники со сторонами 6 и 10 см. Чтобы вычислить их площади, достаточно перемножить эти числа. Потом умножить их на три, потому что боковых граней у призмы именно столько. Тогда площадь боковой поверхности оказывается раной 180 см2.
Ответ. Площади: основания – 9√3 см2, боковой поверхности призмы – 180 см2.
Призма. Формулы и свойства призмы
Определение.
Призма — это многогранная объемная фигура, которая состоит из двух одинаковых плоских многоугольников (основ), находящихся в двух параллельных плоскостях, а другие грани (боковые грани) – параллелограммы, что имеют общие стороны с этими многоугольниками.
Определение. Основы призмы – две грани, которые являются равными параллельными плоскими многоугольниками (ABCEF, GMNJK).
Определение. Боковые грани призмы – все остальные грани за исключением основ.
Определение. Боковая поверхность призмы – совокупность всех боковых граней призмы.
Определение. Поверхность призмы – это совокупность поверхностей двух оснований и боковой поверхности.
Определение. Боковое ребро призмы – общая сторона двух боковых граней.
Определение. Высота – это перпендикуляр, который соединяет две основы призмы под прямым углом.
Определение. Диагональ основания призмы – это отрезок, соединяющий две не соседние вершины, принадлежащие этой же основе.
Определение. Диагональ боковой грани призмы – это отрезок, соединяющий две противоположные вершины, лежащие на одной боковой грани однако принадлежат различным основам.
Определение. Диагональ призмы (AN) – это отрезок, соединяющий две вершины, лежащие на разных основаниях, но не лежат на одной боковой стороне.
Определение. Диагональное сечение – это пересечение призмы плоскостью, проходящей через диагональ основания призмы и боковое ребро. Треугольная призма (в основе призмы треугольники) не имеет диагональных сечений.
Определение. Перпендикулярное сечение – это пересечение призмы плоскостью, пересекающей боковые ребра призмы под прямым углом.
Определение. Прямая призма – это призма, в которой все боковые грани перпендикулярны к основанию. Высота равна длине бокового ребра.
Определение. Наклонная призма – это призма, в которой боковые грани не перпендикулярны к основанию.
Определение. Правильная призма – это призма, в которой основы являются правильными многоугольниками. Правильная призма может быть, как прямой, так и наклонной.
Определение. Усечённая призма – это призма, в которой две основы не параллельны (рис. 2). Усечённая призма может быть, как прямой, так наклонной.
Объём призмы
Формула. Объём призмы через площадь основания и высоту:
V = SоснH
Формула. Объём наклонной призмы через площадь перпендикулярного сечения и длину бокового ребра:
V = SпL
Формула.
Объём правильной прямой призмы через высоту (h), длину стороны (a) и количество сторон (n):
Площадь поверхности призмы
Формула. Площадь боковой поверхности призмы через периметр основания и высоту:
Sb = P·h
Формула. Площадь поверхности призмы через площадь основания, периметр основания и высоту:
S = 2Soсн + P·h
Формула.
Площадь поверхности правильной призмы через высоту (h), длину стороны (a) и количество сторон (n):
| S = | n | a2ctg | π | + nah |
| 2 | n |
Основные свойства призмы
Основы призмы – равные многоугольники.
Боковые грани призмы – параллелограммы.
Боковые ребра призмы параллельны и равны между собой.
Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.
Высота прямой призмы равна длине бокового ребра.
Высота наклонной призмы всегда меньше длины ребра.
В прямой призме гранями могут быть прямоугольниками или квадратами.

tayberi
+10
Ответ дан
8 лет назад
Математика
5 – 9 классы
Сторона основания прямой треугольной примы 3см, 4см и 5 см. Высота призмы равно половине периметра основания. Найди её объём?
Ответ
0/5
(0 оценок)
1

mrVladislav
8 лет назад
Светило науки – 124 ответа – 0 раз оказано помощи
Формула объема призмы V=S(основания)*h
S(основания)=
p=
p=
S(основания)=
h=p
V=6*6=
Оцените пользу ответа
Ответ
2.5/5
(2 оценки)
1
Xpomic
8 лет назад
Светило науки – 8 ответов – 0 раз оказано помощи
Находим полупериметр треугольника р=(3+4+5)/2=6 см. h=p=6 см. Площадь треугольника по формуле Герона S=[p(p-a)(p-b)(p-c)]^1/2=[6*3*2*1]^1/2=36^1/2=6 см. Объем призмы V=S*h=6*6=36см^2
Оцените пользу ответа

Мозг
Отвечающий
Остались вопросы?
Задать вопрос