Please wait.
We are checking your browser. mathvox.ru
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d9e25b15dfe068a • Your IP : 85.95.188.35 • Performance & security by Cloudflare
Периметр прямоугольника

Периметр прямоугольника — это сумма
всех сторон прямоугольника.
Периметр прямоугольника можно рассчитать
через четыре стороны, через смежные стороны,
через диагональ, через площадь,
через радиус описанной окружности.
Самый простой способ найти периметр
прямоугольника, это сложить все стороны.
Также, исходя из свойства прямоугольника, — «противоположные
стороны равны и параллельны», можно сказать, что периметр
численно равен удвоенной сумме ширины и высоты — двух
смежных сторон прямоугольника.
Кроме этих двух способов периметр прямоугольника
можно найти через другие величины. Например, через
площадь прямоугольника, диагональ прямоугольника, и так далее.
В прямоугольник невозможно вписать окружность,
поэтому выразить периметр через вписанную
окружность не получится.
Единицы измерения периметра прямоугольника:
км, м, дм, см, мм.
Формулы периметра прямоугольника
- Периметр прямоугольника через четыре стороны
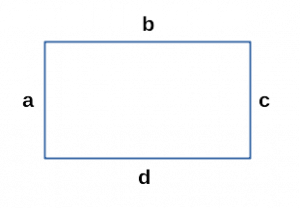
a, b, c, d — стороны прямоугольника;
a || c, b || d;
a = c, b = d;
Периметр прямоугольника через смежные стороны 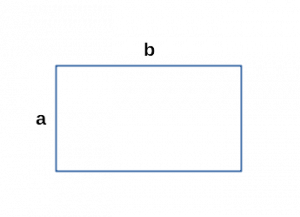
a, b — смежные стороны;
a ≠ b;
Периметр прямоугольника через любую сторону и диагональ 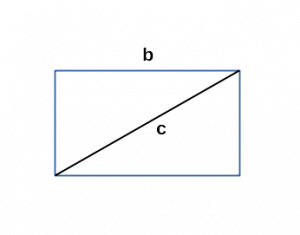
b — любая сторона;
c — диагональ;
Периметр прямоугольника через любую сторону и площадь 
b — любая сторона;
S — площадь;
Периметр прямоугольника через любую сторону и радиус описанной окружности 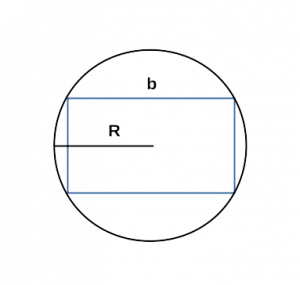
b — любая сторона;
R — радиус описанной окружности;
Полупериметр
Полупериметр — это половина периметра.
Обозначается латинской буквой p.
Чтобы найти полупериметр нужно разделить
периметр на два, или домножить периметр на 0.5.
[ p = frac
<2>= P cdot 0.5 ]
Полупериметр применяется в некоторых формулах
нахождения разных величин прямоугольника. Вместо того,
чтобы вычислять периметр, в таких формулах
удобней вычислять полупериметр.
Основные определения и величины
Длина прямоугольника — это длинная сторона
/ наибольшая сторона прямоугольника.
Обозначается латинской буквой a.
Ширина прямоугольника — это широкая сторона
/ наименьшая сторона прямоугольника.
Обозначается латинской буквой b.
Сторона прямоугольника — это ширина или длина прямоугольника,
в зависимости от численного значения длины стороны.
Обозначается латинской буквой a или b.
Диагональ прямоугольника — это отрезок, соединяющий
противоположные стороны прямоугольника.
Обозначается латинской буквой c или d.
Средняя линия прямоугольника — это отрезок, соединяющий
наименьшие параллельные стороны прямоугольника друг с
другом, причем делящий их пополам на равные отрезки.
Обозначается латинской буквой l.
Радиус описанной окружности прямоугольника — это отрезок,
соединяющий центр описанной около треугольника
окружности и произвольную точку на окружности.
Обозначается латинской буквой R.
Высота прямоугольника — это любая сторона прямоугольника,
а также любой отрезок в прямоугольнике, образующий угол в 90 градусов.
Обозначается латинской буквой h.
Как найти периметр треугольника

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.
Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
В чем измеряется периметр:
Как узнать периметр треугольника
Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.
Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.
P = a + b + c, где a, b, c — длина стороны.
Если известна площадь и радиус вписанной окружности:
P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.
Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:
P = √ b 2 + с 2 – 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.
Если известна одна сторона в равностороннем треугольнике:
P = 3 * a, где a — длина стороны.
Все стороны в равносторонней фигуре равны.
Если известна боковая сторона и основание в равнобедренном треугольнике:
P = 2 * a + b, где a — боковая сторона, b — основание.
Боковые стороны в равнобедренной фигуре равны.
Если известна боковая сторона и высота в равнобедренном треугольнике:
P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.
Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.
Если известны катеты в прямоугольном треугольнике:
P = √ a 2 + b 2 + (a + b), где a, b — катеты.
Катет — одна из двух сторон, которые образуют прямой угол.
Если известны катет и гипотенуза в прямоугольном треугольнике:
P = √ c 2 – a 2 + (a + c), где a — любой катет, c — гипотенуза.
Гипотенуза — сторона, которая лежит напротив прямого угла.
Скачать онлайн таблицу
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.
[spoiler title=”источники:”]
http://colibrus.ru/perimetr-pryamougolnika/
http://skysmart.ru/articles/mathematic/perimetr-treugolnika
[/spoiler]
Запишите данное утверждение и ответы на поставленные вопросы на математическом языке.
Периметр P прямоугольника равен удвоенной сумме сторон a и b.
а) Чему равен полупериметр p прямоугольника?
б) Как найти сторону прямоугольника, зная полупериметр и другую его сторону?
в) Как найти сторону прямоугольника, зная периметр и другую его сторону?
г) Чему равен периметр квадрата со стороной a?

reshalka.com
ГДЗ учебник по алгебре 7 класс Мордкович. §2. Что такое математический язык. Номер №2.14.
Решение а
p
=
P
2
=
2
(
a
+
b
)
2
=
a
+
b
− полупериметр прямоугольника.
Решение б
p = a + b − полупериметр прямоугольника;
a = p − b − одна сторона прямоугольника;
b = p − a − вторая сторона прямоугольника.
Решение в
P = 2(a + b) − периметр прямоугольника
P = 2a + 2b
2a = P − 2b
a
=
P
−
2
b
2
a
=
P
2
−
b
− одна сторона прямоугольника;
b
=
P
2
−
a
− вторая сторона прямоугольника.
Решение г
P = 2(a + b) − периметр прямоугольника;
a = b − в квадрате все стороны равны;
P = 2(a + a) = 2 * 2a = 4a − периметр квадрата.
а) Полупериметр прямоугольника равен сумме длины и ширины. Так же полупериметр равен половине периметра.
р = а + b, где р – полупериметр, а – длина, b – ширина.
б) Чтобы найти неизвестную сторону, нужно из полупериметра вычесть известную сторону.
а = р – b.
b = р – а.
в) Чтобы найти неизвестную сторону, нужно разделить периметр на 2 и вычесть известную сторону
а = (Р : 2) – b, где Р – периметр.
b = (Р : 2) – а.
г) В квадрате 4-е равные стороны.
Р = 4а, где Р – периметр квадрата, а – сторона квадрата.
|
периметр равен 36, а диагональ 13, как найти площадь?
Прости, но я в своём репертуаре первым делом беру тетрадь в клеточку и черчу на новом листе условный прямоугольник. Из одного угла в противоположный протягиваем диагональ – это её длина нам известна и равна 13. Пусть у нас всё будет в метрах, чтобы не применять условные единицы.
Теперь, чтобы найти площадь (S), нам необходимо определить стороны геометрической фигуры. Но нам известна их удвоенная сумма – периметр и сумма квадратов – она будет равна квадрату диагонали. Как ни крути, а одним действием вычислить не удаётся. Видимо, потребуется строить систему уравнений, которую и решать в итоге.А выглядит она следующим образом:
В первой строке можно разделить обе стороны равенства на 2, а во второй возведём 13 в квадрат.
Теперь нам не составит большого труда выразить длину одной из сторон через другую. Сделать это позволяет первая из приведённых формул. Мы, например, просто вычтем из каждой половинки значение (y):
После этого не трудно подставить полученное выражение во вторую формулу вместо (a). Это позволит нам остаться в вычислениях один на один с неизвестным значением (b):
И тут меня осенило – мы ведь вплотную приблизились к решению квадратного уравнения. Об этом явно свидетельствуют следующие преобразования формулы:
Как решаются такие уравнения? Кто помнит? А что такое “Дискриминант”? Тоже забыли? Давайте вспоминать вместе. И в первую очередь эту саму D, которая равна b²-4ac, где abc – коэффициенты в полученной нами формуле (a = 2, b = -36, c = 155). В итоге:
Дискриминант больше нуля и это свидетельствует о том, что нам удастся отыскать два корня этого уравнения.
Я надеюсь, что вы поняли, что за значения мы получили? Это ведь стороны искомого прямоугольника. Одну из них можно оставить “игреком”, а вторую обозначить “иксом”. Вам остаётся лишь перемножить два дробных числа, чтобы получить значение площади = 77.5 квадратных метров. Не верите? Что же, давайте перепроверим. И для этого вернёмся к теореме Пифагора, согласно которой:
Всё сходится. система выбрала этот ответ лучшим
Артём Денисов более года назад Наиболее простой способ решить задачку – найти стороны и перемножить их. Поскольку соотношение сторон нам неизвестно, то их необходимо определить (сделаем это с помощью длины гипотенузы и диагонали). Сумма 2-х сторон треугольника, который составляет половину площади прямоугольника:
БОльшая сторона равна разности полупериметра (18) и меньшей стороны. Выразим площадь в формуле через полупериметр (полупериметр² – диагональ² / 2). На двойку делим потому, что именно такое количество равных треугольников в прямоугольнике. Решение:
Ответ: площадь равна 77.5.
Sagavaha более года назад Самое простое решение – это найти стороны и умножить их одна на другую. Но вот нам не известно соотношение сторон, именно тут нам и пригодится и длина гипотенузы/диагонали прямоугольника из условия. Сумма двух сторон треугольника, составляющего половину площади прямоугольника равна полупериметру – 36:2=18 Большая сторона a будет равна разности полупериметра 18 и меньшей стороны b, но считать их точное число нам не обязательно, так как можно просто выразить площадь в формуле через полупериметр, который у нас есть. Площадь S=(полупериметр в квадрате (18Х18) – диагональ в квадрате (d^2), и всё это делим пополам, так как треугольника два и они равны. (324-169):2=77,5 Это и будет наш ответ
Марина Вологда более года назад Чтобы правильно ответить на вопрос, давайте вспомним, что такое периметр, диагональ и площадь, которую нам необходимо найти. Итак, мы знаем, что диагональ у нас равна 13 (пусть будет см). Известен нам и периметр, который равен 36 см. Нам надо найти площадь прямоугольника. Площадь прямоугольника можно найти по формуле, где нужны значения диагонали и стороны.
Нам не обойтись без формулы Пифагора, а также формулы периметра.
По второй формуле находим одну из сторон, получая следующую формулу:
Упрощаем все:
Вычисляем дискриминант квадратного уравнения, выглядит эта формула вот так:
А теперь подставляем известные нам данные: D= 8*13² – 36² = 56 Применяя формулы для выявления сторон прямоугольника, у нас получается вот такое уровнение:
Ну и площадь теперь найти не проблематично, для этого 10,87 * 7,13 = 77,5 Krustall более года назад Здесь надо искать что-то простое, поэтому советую решить таким образом, найти стороны прямоугольника и перемножить их одну за другой. Но пропорцию не знаем, тут пригодится длина гипотенузы/диагонали прямоугольника из условия задачи. Сумма двух сторон треугольника, равная половине площади прямоугольника, равна половине длины окружности – 36:2=18. Большая сторона А будет равна разнице между половиной периметра18 и меньшей стороной В, но не нужно считать их точное количество, потому что мы можем просто выразить площадь в формуле через имеющуюся у нас половину периметра. Площадь равна (половина круга в квадрате (18Х18) – диагональ в квадрате (d^2) и делим все это пополам, так как треугольников два и они равны (324-169): 2 = 77,5.
Преследующий более года назад Как найти площадь прямоугольника, если известны периметр и диагональ?Вроде бы вопрос со школьной программы, но когда прошли годы – тяжело и вспомнить. А лично мне – вообще тяжело давалась геометрия, по этому я обратился с этим вопросом к другу, который просто обожает этот предмет. Лично мне тяжело далось понять, но автору вопроса должна эта информация помочь. Нужно следовать правилу:
периметр Q диагональ E найти R Q = 2(a+b) E² = a² + b² R = ab a² + b² = a² + b² + 2ab – 2ab = (a+b)² – 2ab =E² 2ab = (a+b)² – d²(a+b) = P/2 (a+b)² = Q² / 4 2ab = (Q² / 4) – d² R = (Q² / 8) – (E² / 2) Применив формулу к данным, что периметр равен 36, а диагональ 13 – площадь прямоугольника будет ровна 77.5 квадратных метров.
Viridi более года назад Для того чтобы найти площадь прямоугольника нужно знать несколько исходных данных. В каждом классе школы, в которых есть предмет геометрия, первоначальные данные усложняются с каждым разом. самое простое – это конечно искать площадь, зная величину его сторон, но в вопросе приведено более сложное задание. При его решении мы будем использовать теорему Пифагора. Пусть катеты фигуры будут обозначены латинскими буквами a и b. В результате некоторых математических приёмов мы получим вот такое решение: Чтобы найти площадь фигуры, в данном случае прямоугольника, нужно знать чему равно произведение a и b. Как мы видим, площадь прямоугольника в конечном итоге получилась равно числу 77, 5. Судя, по предыдущим ответам, где в ответе аналогичная цифра, мы решили всё правильно.
Sanch001 более года назад P.s. В задаче не указаны единицы измерения, поэтому для примера я возьму сантиметры ( см ). Для того чтобы найти площадь прямоугольника при известных периметре и диагонали, первым делом нужно найти полупериметр. Для его нахождения необходимо периметр прямоугольника поделить по полам: 36 : 2 = 18 см Рассмотрим один из треугольников полупериметра: катеты нам не известны, гипотенуза равна 13 см. Назовём две стороны (катеты) как a и b. Тогда по теореме Пифагора следует что: a² + b² = 169см ( 13² ) Теперь выразим длину одной стороны относительно другой: x = 18 – y. Далее приобразовываем формулы: (18² – 2 * 18 * y + y²) + y² = 169 324 – 36 * y + 2 * y² = 169 2 * y² – 36 * y + 324 – 169 = 0 2 * y² – 36 * y + 155 = 0 Решаем через Дискриминант чисел: D = 36² – 4 * 2 * 155 = 1296 – 1240 = 56 y1 = (-b – √D)/2a = 7.1291713066 y2 = (-b + √D)/2a = 10.8708286934 7.1291713066 * 10.8708286934 = 75,4 см². Давайте проверим: 7.1291713066² + 10.8708286934² = 13² 50.8250835188+118.174916481 ≈ 169 Ответ: площадь прямоугольника 75,4 см².
Валерий Альбертович 3 года назад Чтобы решить такое задание, воспользуемся теоремой Пифагора. Т.к. у нас есть диагональ в прямоугольнике, то она образует (“делит”) из прямоугольника два прямоугольных треугольника, стороны в котором мы и сможем найти по теореме Пифагора. Пусть a и b – катеты прямоугольного треугольника, диагональ (d) нам известна, она в данном случае является гипотенузой. Тогда: d^2 = a^2 + b^2 => a^2 + b^2 = 13^2 = 169 P прям. = 2(a+b) = 36 => a + b = P/2 = 36/2 = 18 Площадь прямоугольника вычисляется по формуле: S = a*b Воспользуемся формулой: S = ((P/2)^2 – d^2)/2, подставим S = (18^2 – 13^2)/2 = (324 – 169)/2 = 155/2 = 77,5 Ответ: 77,5 Rafail 4 года назад Обозначим стороны прямоугольника х и у. По теореме Пифагора х^2+y^2=13^2=169. Р=2*(х+у). отсюда х+у=Р/2 (в данном случае 36/2=18). Возведём выражение (х+у) в квадрат. x^2+2*x*y+y^2=324. Отсюда получаем: S=х*у(324-169)/2=77,5. |

Запишите на математическом языке:
Периметр P прямоугольника равен удвоенной сумме его сторон a и b.
1. Чему равен полупериметр p прямоугольника?
2. Как найти сторону прямоугольника, зная полупериметр и другую его сторону?
3. Как найти сторону прямоугольника, зная периметр и другую его сторону?
4. Чему равен периметр квадрата со стороной a?

Светило науки – 6 ответов – 69 раз оказано помощи
P=2(a+b)
1)a) p=a+b
2)Полупериметр минус известная сторона(a=p-b; b=p-a )
3)вычесть из периметра удвоенную известную сторону, получившийся ответ разделить на два. например периметр 20, известная сторона 6. неизвестная сторона равна (20 – (6 * 2)) / 2 = 4(a=P/2-b; b=P/2-a )
4)периметр равен а * 4(P=4a)














