Как найти полупериметр прямоугольника равен

Запишите данное утверждение и ответы на поставленные вопросы на математическом языке.
Периметр P прямоугольника равен удвоенной сумме сторон a и b.
а) Чему равен полупериметр p прямоугольника?
б) Как найти сторону прямоугольника, зная полупериметр и другую его сторону?
в) Как найти сторону прямоугольника, зная периметр и другую его сторону?
г) Чему равен периметр квадрата со стороной a?

Периметр прямоугольника — это сумма
всех сторон прямоугольника.

Периметр прямоугольника можно рассчитать
через четыре стороны, через смежные стороны,
через диагональ, через площадь,
через радиус описанной окружности.

Самый простой способ найти периметр
прямоугольника, это сложить все стороны.

Также, исходя из свойства прямоугольника, — «противоположные
стороны равны и параллельны», можно сказать, что периметр
численно равен удвоенной сумме ширины и высоты — двух
смежных сторон прямоугольника.

Кроме этих двух способов периметр прямоугольника
можно найти через другие величины. Например, через
площадь прямоугольника, диагональ прямоугольника, и так далее.

В прямоугольник невозможно вписать окружность,
поэтому выразить периметр через вписанную
окружность не получится.

Единицы измерения периметра прямоугольника:
км, м, дм, см, мм.

Формулы периметра прямоугольника

1. Периметр прямоугольника через четыре стороны
   

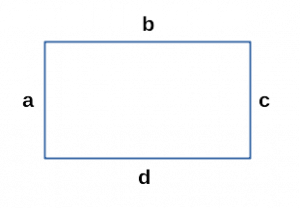
   [ P = a + b + c + d ]

   a, b, c, d — стороны прямоугольника;
   a || c, b || d;
   a = c, b = d;

2. Периметр прямоугольника через смежные стороны
   

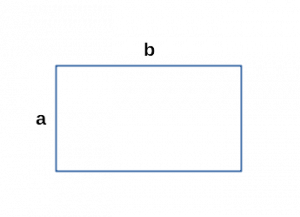
   [ P = 2a + 2b = 2(a+b) ]

   a, b — смежные стороны;
   a ≠ b;

3. Периметр прямоугольника через любую сторону и диагональ
   

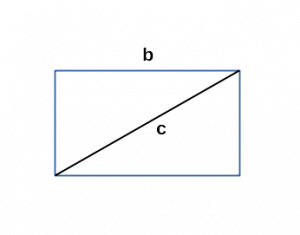
   [ P = 2(b + (sqrt{c^2-b^2})) ]

   b — любая сторона;
   c — диагональ;

4. Периметр прямоугольника через любую сторону и площадь
   

   [ P = 2 * (b + S : b) ]

   b — любая сторона;
   S — площадь;

5. Периметр прямоугольника через любую сторону и радиус описанной окружности
   

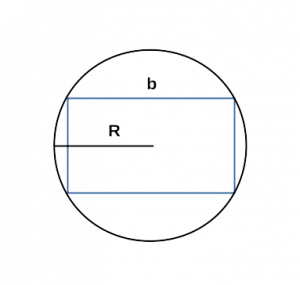
   [ P = 2 cdot (b + sqrt{4R^2 — b^2}), ]

   b — любая сторона;
   R — радиус описанной окружности;

Полупериметр

Полупериметр — это половина периметра.

Обозначается латинской буквой p.

Чтобы найти полупериметр нужно разделить
периметр на два, или домножить периметр на 0.5.

[ p = frac{P}{2} = P cdot 0.5 ]

Полупериметр применяется в некоторых формулах
нахождения разных величин прямоугольника. Вместо того,
чтобы вычислять периметр, в таких формулах
удобней вычислять полупериметр.

Основные определения и величины

Длина прямоугольника — это длинная сторона
/ наибольшая сторона прямоугольника.

Обозначается латинской буквой a.

Ширина прямоугольника — это широкая сторона
/ наименьшая сторона прямоугольника.

Обозначается латинской буквой b.

Сторона прямоугольника — это ширина или длина прямоугольника,
в зависимости от численного значения длины стороны.

Обозначается латинской буквой a или b.

Диагональ прямоугольника — это отрезок, соединяющий
противоположные стороны прямоугольника.

Обозначается латинской буквой c или d.

Средняя линия прямоугольника — это отрезок, соединяющий
наименьшие параллельные стороны прямоугольника друг с
другом, причем делящий их пополам на равные отрезки.

Обозначается латинской буквой l.

Радиус описанной окружности прямоугольника — это отрезок,
соединяющий центр описанной около треугольника
окружности и произвольную точку на окружности.

Обозначается латинской буквой R.

Высота прямоугольника — это любая сторона прямоугольника,
а также любой отрезок в прямоугольнике, образующий угол в 90 градусов.

Обозначается латинской буквой h.

Полупериметр многоугольника — это половина его периметра. Хотя полупериметр является очень простой производной периметра, он столь часто появляется в формулах для треугольников и других геометрических фигур, что ему выделили отдельное наименование. Если полупериметр оказывается в какой-либо формуле, его, обычно, обозначают буквой p.

Треугольники[править | править код]

Полупериметр чаще всего используется для треугольников. Формула полупериметра для треугольника со сторонами a, b и c

Свойства[править | править код]

В любом треугольнике вершина и точка касания вневписанной окружности на противоположной стороне делят периметр треугольника на две равные части, то есть на два пути, длина каждого из которых равна полупериметру. На рисунке показаны стороны A, B, C и точки касания A’, B’, C’, тогда

Три отрезка, соединяющих вершины с противоположными точками касания, пересекаются в одной точке — точке Нагеля.

Если рассмотреть отрезки, соединяющие середины сторон с точками, отстоящими (вдоль сторон) от этой середины на полупериметр, то эти отрезки пересекаются в одной точке — центре окружности Шпикера, которая является окружностью, вписанной в медианный треугольник^[en]. Центр Шпикера является центром тяжести сторон треугольника.

Прямая, проходящая через центр вписанной окружности треугольника делит периметр пополам в том и только в том случае, когда она делит пополам площадь.

Полупериметр треугольника равен периметру его медианного треугольника^[en].

Из неравенства треугольника вытекает, что длина наибольшей стороны треугольника не превосходит полупериметр.

Формулы с полупериметром[править | править код]

Площадь K любого треугольника является произведением радиуса его вписанной окружности и полупериметра:

Площадь треугольника можно вычислить исходя из его полупериметра и длин сторон a, b, c по формуле Герона:

Радиус описанной окружности R треугольника можно также вычислить из его полупериметра и длин сторон:

Эту формулу можно вывести из теоремы синусов.

Радиус вписанной окружности равен

Теорема котангенсов даёт котангенсы половин углов в вершинах треугольника в терминах полупериметра, сторон и радиуса вписанной окрухности.

Длина биссектрисы внутреннего угла, противоположного стороне a, равна^[1]

В прямоугольном треугольнике радиус вневписанной окружности на гипотенузе равен полупериметру. Полупериметр равен сумме радиуса вписанной окружности и удвоенного радиуса описанной. Площадь прямоугольного треугольника равна , где a и b — катеты.

Четырёхугольники[править | править код]

Формула для полупериметра четырёхугольника со сторонами a, b, c и d

Одна из формул для треугольников, использующая полупериметр, применима также и к описанным четырёхугольникам, которые имеют вписанную окружность и сумма длин противоположных сторон которых равна полупериметру. А именно, это формула площади фигуры:

Простейшая форма формулы Брахмагупты для площади четырехугольника вписанного в окружность имеет вид, близкий к формуле Герона для площади треугольника:

Соотношение Бретшнайдера обобщает формулу для всех выпуклых четырёхугольников:

где и  — два противоположных угла.

Четыре стороны бицентрального четырёхугольника^[en] являются четырьмя решениями уравнения четвёртой степени, параметрами которого являются полупериметр, радиус вписанной окружности и радиус описанной.

Правильные многоугольники[править | править код]

Площадь выпуклого правильного многоугольника равна произведению его полупериметра на расстояние от центра до одной из сторон.

Примечания[править | править код]

Литература[править | править код]

• Roger A. Johnson. Advanced Euclidean Geometry. — Dover Publ., 2007. (Переиздание книги 1929 года)

Ссылки[править | править код]

• Weisstein, Eric W. Semiperimeter (англ.) на сайте Wolfram MathWorld.

а) Полупериметр прямоугольника равен сумме длины и ширины. Так же полупериметр равен половине периметра.

 р  =  а + b,         где     р – полупериметр,   а – длина,  b – ширина.

б) Чтобы найти неизвестную сторону, нужно из полупериметра вычесть известную сторону.

 а  =  р – b.

 b  =  р – а.

в) Чтобы найти неизвестную сторону, нужно разделить периметр на 2 и вычесть известную сторону

 а  =  (Р : 2) – b,                 где   Р – периметр.

 b  =  (Р : 2) – а.

г) В квадрате 4-е равные стороны.

 Р  =  4а,        где   Р – периметр квадрата,     а – сторона квадрата.