Как найти полупериметр треугольника прямоугольного

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6d9e25b15dfe068a • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Периметр прямоугольника

Периметр прямоугольника — это сумма
всех сторон прямоугольника.

Периметр прямоугольника можно рассчитать
через четыре стороны, через смежные стороны,
через диагональ, через площадь,
через радиус описанной окружности.

Самый простой способ найти периметр
прямоугольника, это сложить все стороны.

Также, исходя из свойства прямоугольника, — «противоположные
стороны равны и параллельны», можно сказать, что периметр
численно равен удвоенной сумме ширины и высоты — двух
смежных сторон прямоугольника.

Кроме этих двух способов периметр прямоугольника
можно найти через другие величины. Например, через
площадь прямоугольника, диагональ прямоугольника, и так далее.

В прямоугольник невозможно вписать окружность,
поэтому выразить периметр через вписанную
окружность не получится.

Единицы измерения периметра прямоугольника:
км, м, дм, см, мм.

Формулы периметра прямоугольника

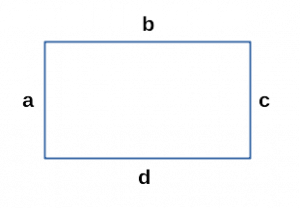
1. Периметр прямоугольника через четыре стороны
   

a, b, c, d — стороны прямоугольника;
a || c, b || d;
a = c, b = d;
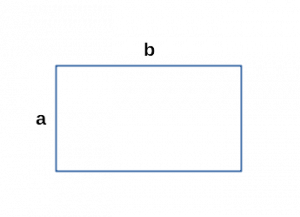
Периметр прямоугольника через смежные стороны

a, b — смежные стороны;
a ≠ b;
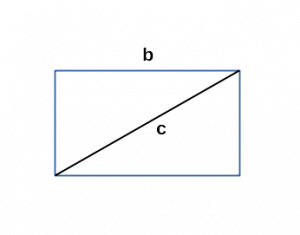
Периметр прямоугольника через любую сторону и диагональ

b — любая сторона;
c — диагональ;
Периметр прямоугольника через любую сторону и площадь

b — любая сторона;
S — площадь;
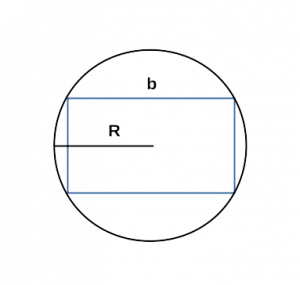
Периметр прямоугольника через любую сторону и радиус описанной окружности

b — любая сторона;
R — радиус описанной окружности;

Полупериметр

Полупериметр — это половина периметра.

Обозначается латинской буквой p.

Чтобы найти полупериметр нужно разделить
периметр на два, или домножить периметр на 0.5.

[ p = frac

<2>= P cdot 0.5 ]

Полупериметр применяется в некоторых формулах
нахождения разных величин прямоугольника. Вместо того,
чтобы вычислять периметр, в таких формулах
удобней вычислять полупериметр.

Основные определения и величины

Длина прямоугольника — это длинная сторона
/ наибольшая сторона прямоугольника.

Обозначается латинской буквой a.

Ширина прямоугольника — это широкая сторона
/ наименьшая сторона прямоугольника.

Обозначается латинской буквой b.

Сторона прямоугольника — это ширина или длина прямоугольника,
в зависимости от численного значения длины стороны.

Обозначается латинской буквой a или b.

Диагональ прямоугольника — это отрезок, соединяющий
противоположные стороны прямоугольника.

Обозначается латинской буквой c или d.

Средняя линия прямоугольника — это отрезок, соединяющий
наименьшие параллельные стороны прямоугольника друг с
другом, причем делящий их пополам на равные отрезки.

Обозначается латинской буквой l.

Радиус описанной окружности прямоугольника — это отрезок,
соединяющий центр описанной около треугольника
окружности и произвольную точку на окружности.

Обозначается латинской буквой R.

Высота прямоугольника — это любая сторона прямоугольника,
а также любой отрезок в прямоугольнике, образующий угол в 90 градусов.

Обозначается латинской буквой h.

Как найти периметр треугольника

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение

Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской буквой P. Под «P» удобно писать маленькими буквами название фигуры, чтобы не запутаться в задачах и ходе решении.

Важно, чтобы все параметры были переданы в одной единице длины, иначе мы не сможем подсчитать результат. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.

В чем измеряется периметр:

Как узнать периметр треугольника

Рассмотрим какие существуют формулы, и при каких известных исходных данных их можно применять.

Если известны три стороны, то периметр треугольника равен их сумме. Этот способ проходят во втором классе.

P = a + b + c, где a, b, c — длина стороны.

Если известна площадь и радиус вписанной окружности:

P = 2 * S : r, где S — площадь, r — радиус вписанной окружности.

Если известны две стороны и угол между ними, вычислить периметр треугольника можно так:

P = √ b 2 + с 2 – 2 * b * с * cosα + (b + с), где b, с — известные стороны, α — угол между известными сторонами.

Если известна одна сторона в равностороннем треугольнике:

P = 3 * a, где a — длина стороны.

Все стороны в равносторонней фигуре равны.

Если известна боковая сторона и основание в равнобедренном треугольнике:

P = 2 * a + b, где a — боковая сторона, b — основание.

Боковые стороны в равнобедренной фигуре равны.

Если известна боковая сторона и высота в равнобедренном треугольнике:

P = 2 * (√ a 2 + h 2 ) + 2 * a, где a — боковая сторона, h — высота.

Высотой принято называть отрезок, который вышел из вершины и опустился на основание. В равнобедренной фигуре высота делит основание пополам.

Если известны катеты в прямоугольном треугольнике:

P = √ a 2 + b 2 + (a + b), где a, b — катеты.

Катет — одна из двух сторон, которые образуют прямой угол.

Если известны катет и гипотенуза в прямоугольном треугольнике:

P = √ c 2 – a 2 + (a + c), где a — любой катет, c — гипотенуза.

Гипотенуза — сторона, которая лежит напротив прямого угла.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

[spoiler title=”источники:”]

http://colibrus.ru/perimetr-pryamougolnika/

http://skysmart.ru/articles/mathematic/perimetr-treugolnika

[/spoiler]

Полупериметр многоугольника — это половина его периметра. Хотя полупериметр является очень простой производной периметра, он столь часто появляется в формулах для треугольников и других геометрических фигур, что ему выделили отдельное наименование. Если полупериметр оказывается в какой-либо формуле, его, обычно, обозначают буквой p.

Треугольники[править | править код]

Полупериметр чаще всего используется для треугольников. Формула полупериметра для треугольника со сторонами a, b и c

Свойства[править | править код]

В любом треугольнике вершина и точка касания вневписанной окружности на противоположной стороне делят периметр треугольника на две равные части, то есть на два пути, длина каждого из которых равна полупериметру. На рисунке показаны стороны A, B, C и точки касания A’, B’, C’, тогда

Три отрезка, соединяющих вершины с противоположными точками касания, пересекаются в одной точке — точке Нагеля.

Если рассмотреть отрезки, соединяющие середины сторон с точками, отстоящими (вдоль сторон) от этой середины на полупериметр, то эти отрезки пересекаются в одной точке — центре окружности Шпикера, которая является окружностью, вписанной в медианный треугольник^[en]. Центр Шпикера является центром тяжести сторон треугольника.

Прямая, проходящая через центр вписанной окружности треугольника делит периметр пополам в том и только в том случае, когда она делит пополам площадь.

Полупериметр треугольника равен периметру его медианного треугольника^[en].

Из неравенства треугольника вытекает, что длина наибольшей стороны треугольника не превосходит полупериметр.

Формулы с полупериметром[править | править код]

Площадь K любого треугольника является произведением радиуса его вписанной окружности и полупериметра:

Площадь треугольника можно вычислить исходя из его полупериметра и длин сторон a, b, c по формуле Герона:

Радиус описанной окружности R треугольника можно также вычислить из его полупериметра и длин сторон:

Эту формулу можно вывести из теоремы синусов.

Радиус вписанной окружности равен

Теорема котангенсов даёт котангенсы половин углов в вершинах треугольника в терминах полупериметра, сторон и радиуса вписанной окрухности.

Длина биссектрисы внутреннего угла, противоположного стороне a, равна^[1]

В прямоугольном треугольнике радиус вневписанной окружности на гипотенузе равен полупериметру. Полупериметр равен сумме радиуса вписанной окружности и удвоенного радиуса описанной. Площадь прямоугольного треугольника равна , где a и b — катеты.

Четырёхугольники[править | править код]

Формула для полупериметра четырёхугольника со сторонами a, b, c и d

Одна из формул для треугольников, использующая полупериметр, применима также и к описанным четырёхугольникам, которые имеют вписанную окружность и сумма длин противоположных сторон которых равна полупериметру. А именно, это формула площади фигуры:

Простейшая форма формулы Брахмагупты для площади четырехугольника вписанного в окружность имеет вид, близкий к формуле Герона для площади треугольника:

Соотношение Бретшнайдера обобщает формулу для всех выпуклых четырёхугольников:

где и  — два противоположных угла.

Четыре стороны бицентрального четырёхугольника^[en] являются четырьмя решениями уравнения четвёртой степени, параметрами которого являются полупериметр, радиус вписанной окружности и радиус описанной.

Правильные многоугольники[править | править код]

Площадь выпуклого правильного многоугольника равна произведению его полупериметра на расстояние от центра до одной из сторон.

Примечания[править | править код]

Литература[править | править код]

• Roger A. Johnson. Advanced Euclidean Geometry. — Dover Publ., 2007. (Переиздание книги 1929 года)

Ссылки[править | править код]

• Weisstein, Eric W. Semiperimeter (англ.) на сайте Wolfram MathWorld.

Прямоугольный треугольник – это треугольник, у которого один из углов прямой (90°).

Другие виды треугольников:

• равнобедренные треугольники;
• равносторонние треугольники.

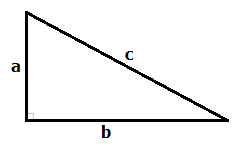
Любой прямоугольный треугольник характеризуется катетами a и b и гипотенузой c (см. рисунок).

Катет – это сторона прямоугольного треугольника, образующая прямой угол с другой стороной (также катетом).

Гипотенуза – это сторона прямоугольного треугольника, лежащая напротив прямого угла.

Именно эти характеристики используются в формулах прямоугольного треугольника при вычислении площади, периметра, а также радиусов вписанной и описанной окружностей.

Формула радиуса вписанной окружности для прямоугольного треугольника

Радиус вписанной окружности r можно вычислить, зная стороны прямоугольного треугольника:

r = (a + b – c)/2

Формула радиуса описанной окружности для прямоугольного треугольника

Радиус описанной окружности R можно вычислить, зная гипотенузу прямоугольного треугольника:

R = c/2

Формула периметра прямоугольного треугольника

Периметр P прямоугольного треугольника можно получить, зная его стороны:

P = a + b + c

При вычислении площади прямоугольного треугольника часто требуется знать его полупериметр:

p = P/2 = (a + b + c)/2

Формулы площади прямоугольного треугольника

При вычислении площади прямоугольного треугольника можно пользоваться формулами, которые применяются для вычисления площади произвольного треугольника, так как прямоугольный треугольник является частным случаем для треугольников.

Площадь прямоугольного треугольника S можно вычислить, зная его катеты a и b:

S = 1/2 ⋅ a ⋅ b

Еще одна формула позволяет вычислить площадь прямоугольного треугольника по его катетам a и b и полупериметру p (формула Герона):

S = (p – a) ⋅ (p – b)