Определение
7.10. Степенью
вершины v
для неориентированного графа, обозначается
d(v),
называется количество ребер, инцидентных
этой вершине. Вершина степени 0 называется
изолированной.
Вершина степени 1 называется висячей.
Определение
7.11. Полустепенью
исхода вершины
v
для орграфа
называется количество дуг, для которых
v
является начальной вершиной, обозначается
![]() .
.
Полустепенью
захода
вершины v
называется количество дуг, для которых
v
является конечной вершиной, обозначается
![]() .
.
Если![]() ,
,
то вершинаv
называется истоком.
Если
![]() ,
,
то вершинаv
называется стоком.
Теорема 7.2.
(Теорема
Эйлера)
Сумма степеней вершин графа равна
удвоенному количеству ребер:
![]() .
.
Доказательство.
При подсчете суммы степеней вершин
каждое ребро учитывается два раза: для
одного конца ребра и для другого.
Следствие 1.
Число вершин нечетной степени четно.
Доказательство.
По теореме Эйлера сумма степеней всех
вершин – четное число. Сумма степеней
вершин четной степени четна, значит,
сумма степеней вершин нечетной степени
также четна, следовательно, их четное
число.
Следствие 2.
Сумма полустепеней вершин орграфа
равна удвоенному количеству дуг:
![]() .
.
Доказательство.
Сумма полустепеней вершин орграфа
равна сумме степеней вершин графа,
полученного из орграфа забыванием
ориентации дуг.
Пример 7.5.
Определить степени вершин данного
графа.

Пример 7.6.
Определить полустепени исхода и захода
данного орграфа.

7.5. Представление (способы задания) графов.
-
Граф
как алгебраическая система:
модель, носителем
которой является множество вершин, а
отношение – бинарное отношение смежности
вершин.
< {a,b,c,d};
– множество
вершин
{(a,b),(b,a),(b,c),(c,b),(a,c),(c,a),(c,d),(d,c)}
– множество
рёбер
>
-
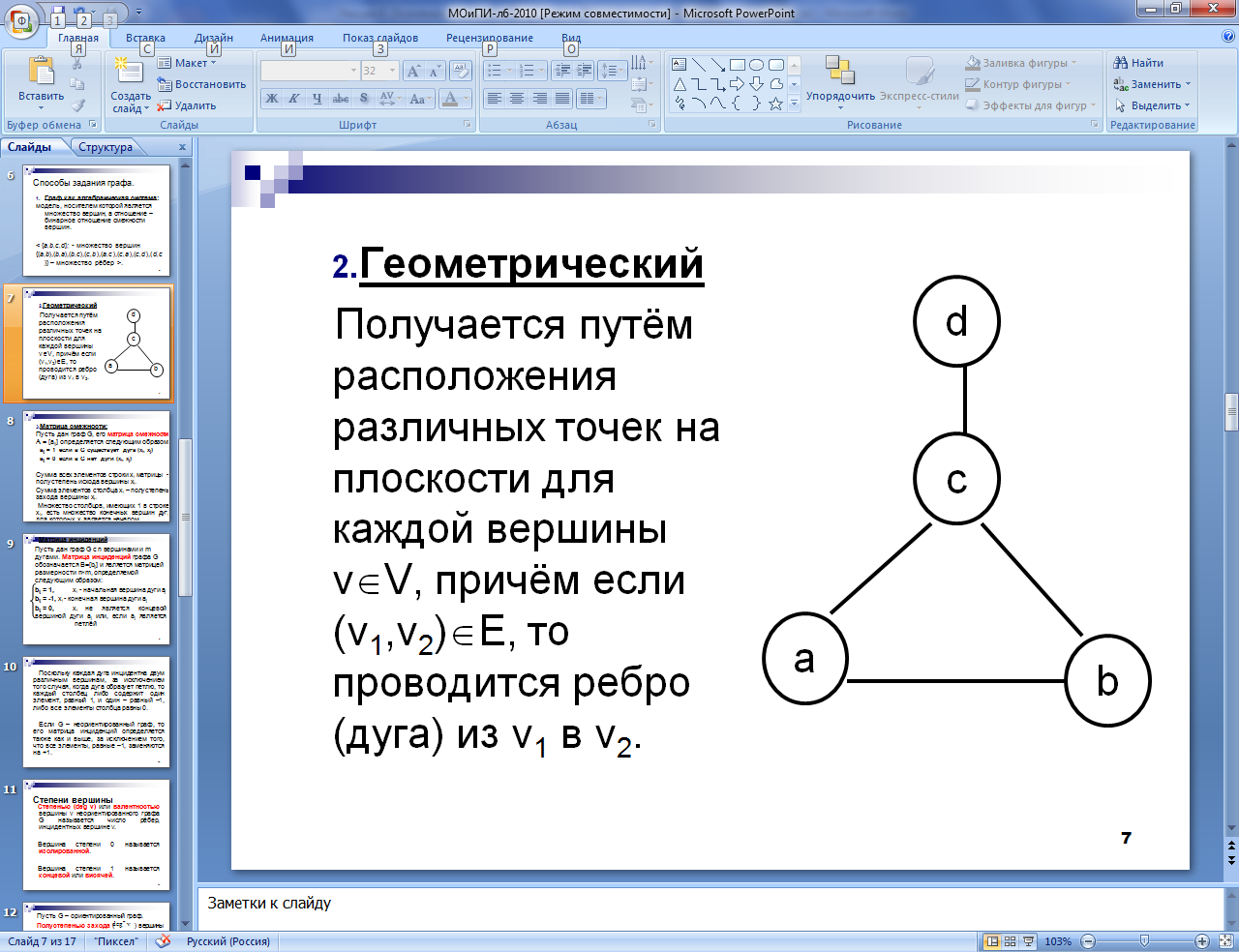
Геометрический
Получается путём
расположения различных точек на
плоскости для каждой вершины vÎV,
причём если (v1,v2)ÎЕ,
то проводится ребро (дуга) из v1
в v2.
Для представления
в компьютере чаще всего граф задается
либо матрицей
смежности,
либо матрицей
инциденций.
Матрицей
смежности вершин неориентированного
графа
G,
содержащего n
вершин, называют квадратную матрицу
A=aij
n-го
порядка, у которой строки и столбцы
матрицы соответствуют вершинам
неориентированного графа.
Элементы aij
матрицы A
равны числу ребер, направленных из i-й
вершины в j-ю.
В случае неориентированного
графа G
ему вместе с ребром (vi,
vj)
принадлежит и ребро (vj,
vi),
поэтому матрица смежности вершин
A=aij
будет симметрична относительно главной
диагонали.
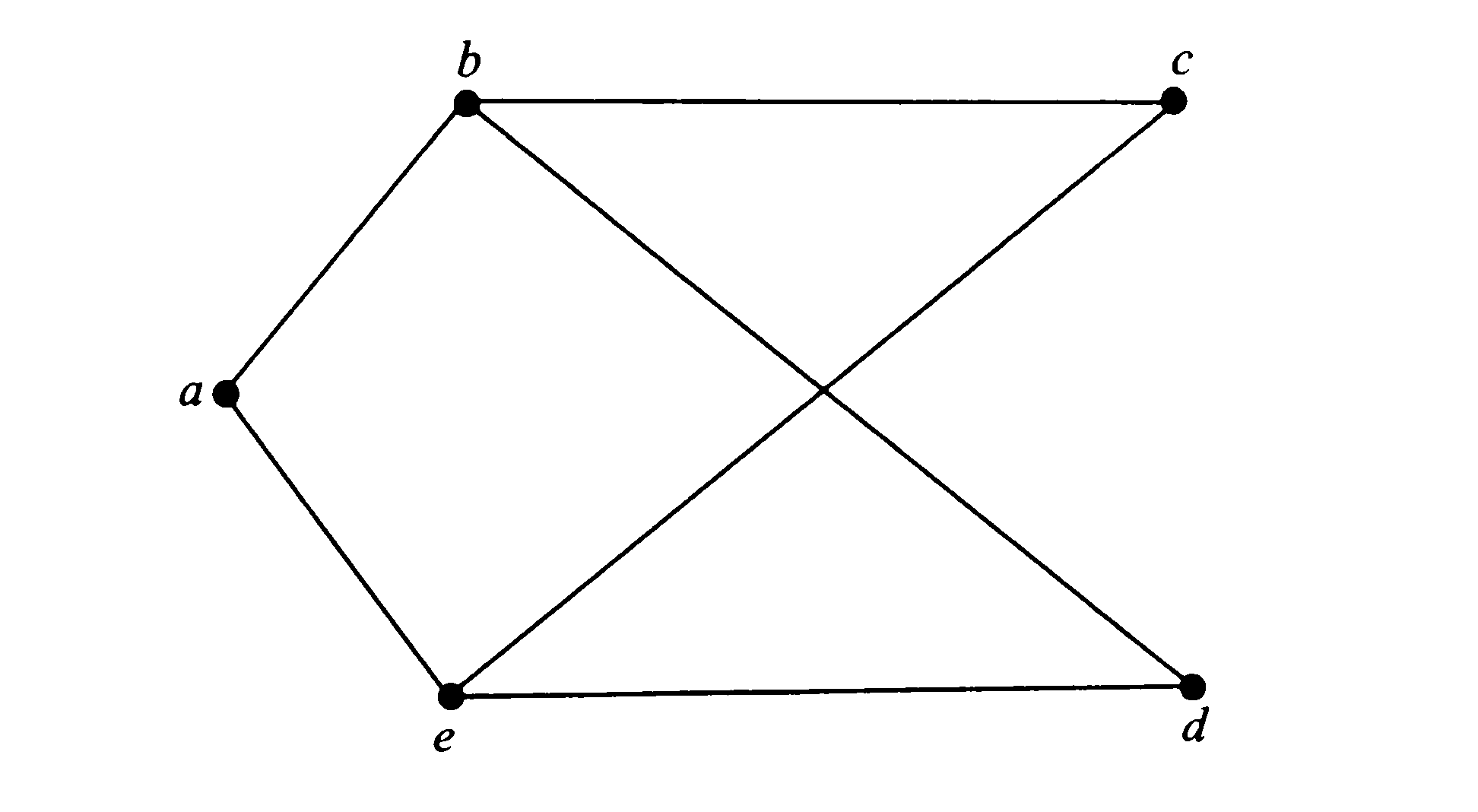
ПРИМЕР.
Граф: множество вершин V
= {a,b,c,d,e}
Множество
ребер
Е
= {{а, b},
{а, е}, {b,
c},
{b,
d},
{c,
e},
{d,e}},

Матрица смежности
симметрична относительно главной
диагонали.
На главной диагонали
стоит 1 (символ Л) из-за
нерефлексивности
отношения на множестве вершин (EÍV´V)
Логическая матрица
отношения на множестве вершин графа,
которое задается его ребрами.
a b c d
b c d
a 0 1 0 1
b 1 0 1 1
с 0 1 0 1
d 1 1 1 0
простой
граф
a b c d
a 1 1 0 1
b 1 0 3 0
c 0 3 0 2
d 1 0 2 0
граф
с кратными
рёбрами
и петлёй

Определение
7.12. Матрица
смежности вершин орграфа
G,
содержащего n
вершин-
это квадратная матрица A=aij
n-го
порядка, у которой строки и столбцы
матрицы соответствуют вершинам орграфа.
Элементы aij
матрицы A
равны числу дуг, направленных из i-й
вершины в j-ю.
Если орграф состоит из однократных
дуг, то элементы матрицы равны либо 0,
либо 1.
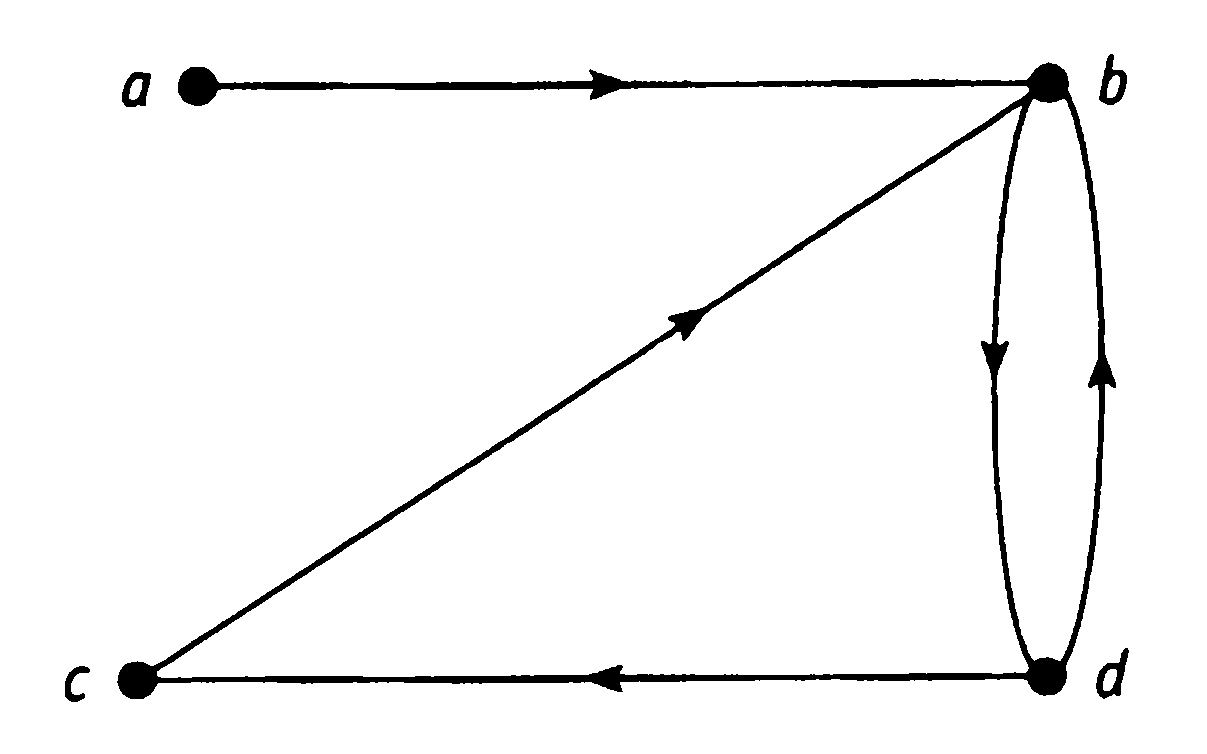
Матрица
смежности:
Пусть дан граф G,
его матрица
смежности
А = [aij]
определяется следующим образом:
aij
= 1 если в G
существует дуга (xi,
xj)
aij
= 0 если в G
нет дуги (xi,
xj)
![]()
![]()

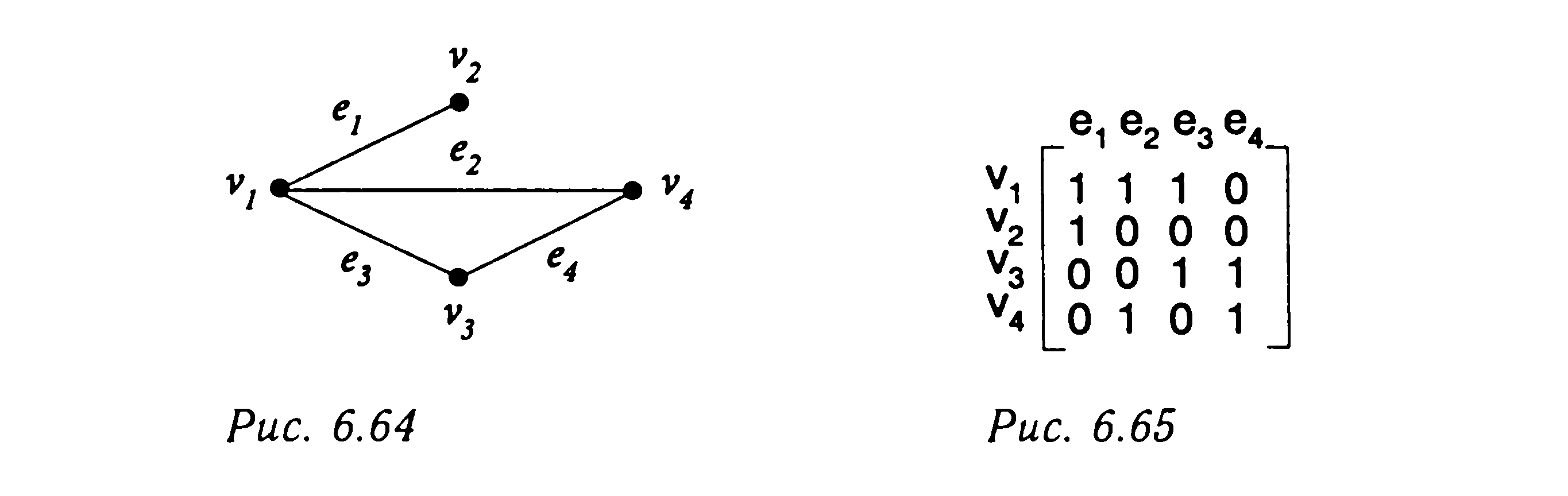
Определение
7.14. Матрицей
инциденций (инцидентности) неориентированного
графа с
![]() вершинами
вершинами
и
![]() ребрами
ребрами
называется
матрица
![]() размерности
размерности![]() ,
,
строки которой соответствуют вершинам,
а столбцы – ребрам. Элементы![]() матрицы инциденций неориентированного
матрицы инциденций неориентированного
графа равны 1, если вершина![]() инцидентна ребру
инцидентна ребру![]() ,
,
и 0 в противном случае.
Матрицей
инциденций (инцидентности) орграфа с
![]() вершинами
вершинами
и
![]() дугами
дугами
называется
матрица
![]() размерностиnm,
размерностиnm,
строки которой соответствуют вершинам,
а столбцы -дугам
орграфа.
Элементы cij
равны
1, если дуга ej
исходит из i-й
вершины;
–1, если дуга ej
заходит в i-ю
вершину;
0, если дуга не
инцидентна i-й
вершине
Поскольку каждая
дуга инцидентна двум различным вершинам,
за исключением того случая, когда дуга
образует петлю, то каждый столбец либо
содержит один элемент, равный 1, и один
– равный –1, либо все элементы столбца
равны 0.
Степень вершины
равна сумме элементов строки, обозначенной
этой вершиной, так как каждая единица
в этой строке представляет инцидентность
этой вершины ребру.
В каждом столбце
также будут две единицы, так как каждое
ребро инцидентно двум вершинам.
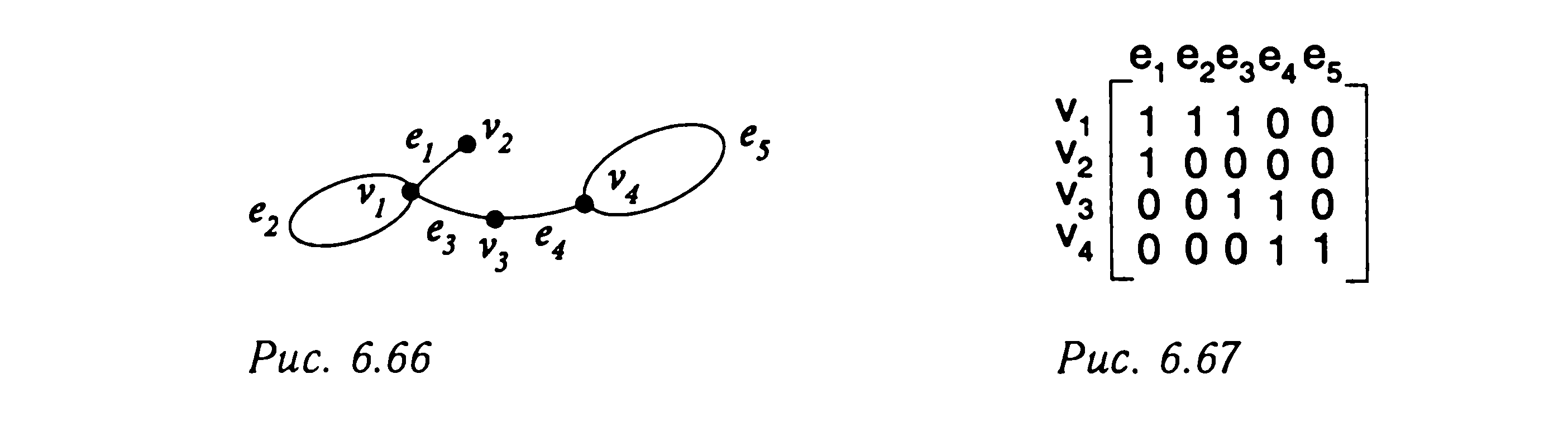
Матрицы инцидентности
не имеют большого значения при
рассмотрении ориентированных графов,
т.к. они не содержат информации о том,
как ребро ориентировано.
Поэтому, используя
матрицу инцидентности, нельзя восстановить
ориентированный граф.
Такую возможность
обеспечивает матрица смежности,
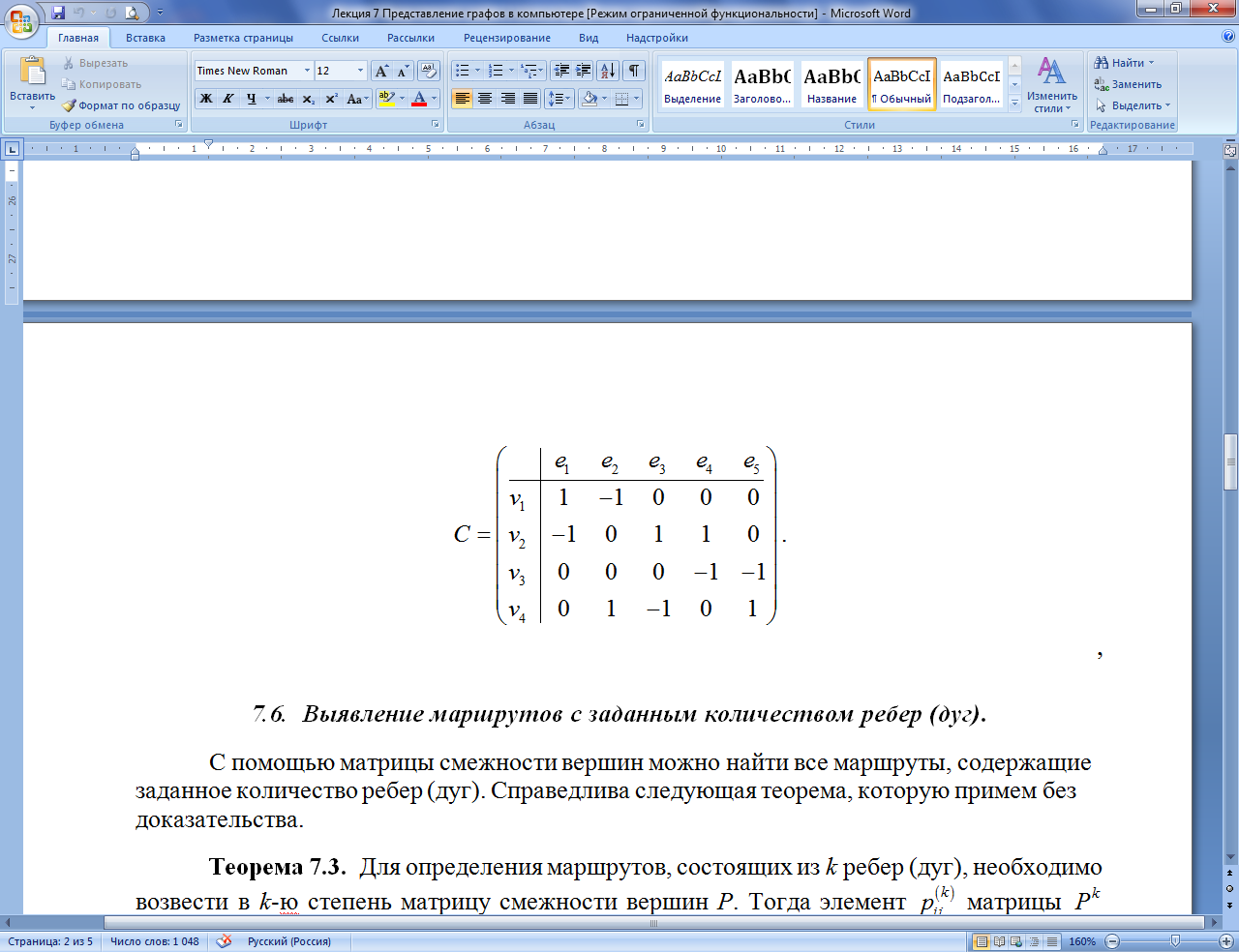
Пример
7.7.1.
Для заданного неориентированного
графа построить матрицы смежностей и
матрицу инциденций.
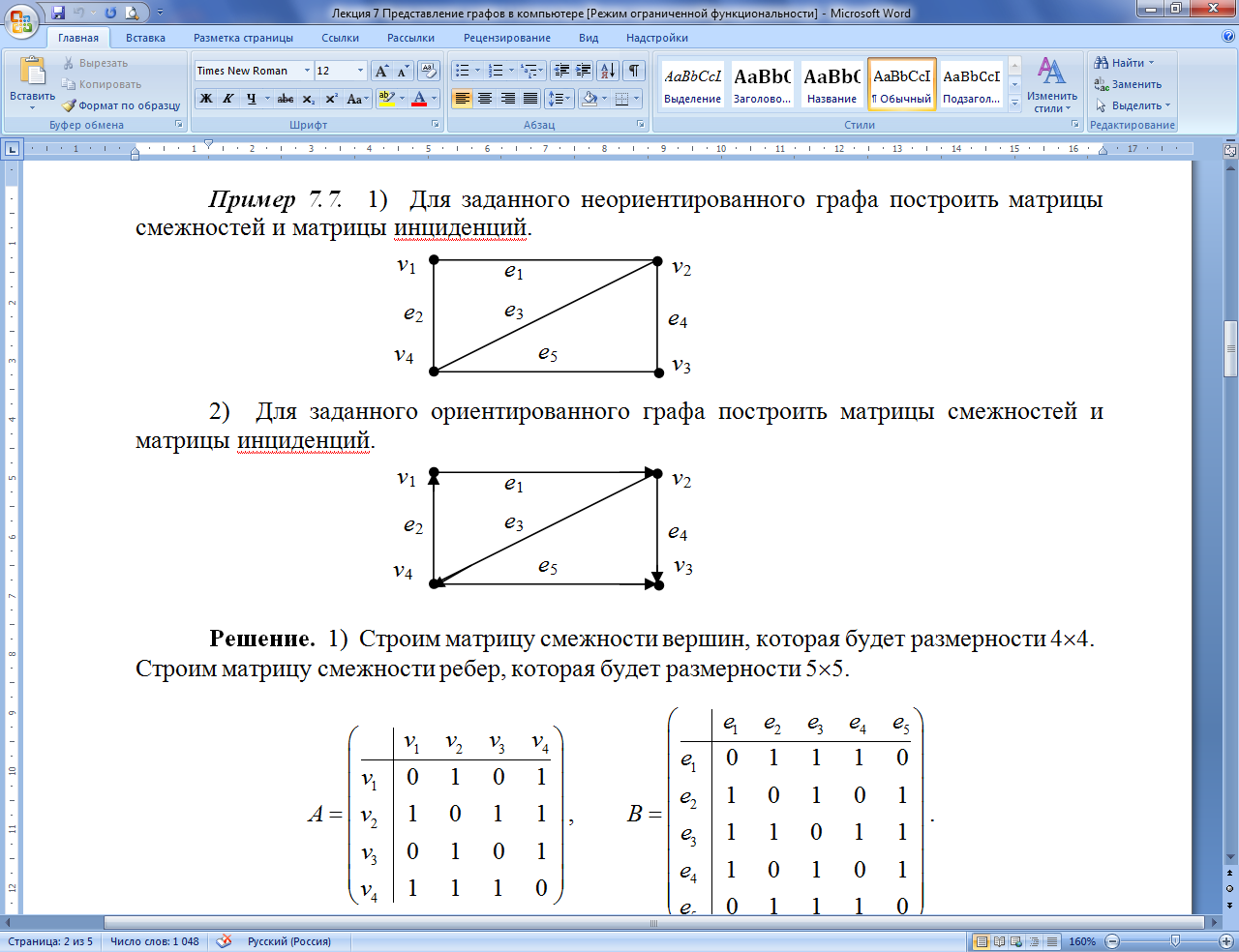
Решение.
1) Строим матрицу смежности вершин,
которая будет размерности 44.
Строим матрицу смежности ребер, которая
будет размерности 55.


2) Строим матрицу
инциденций, которая будет размерности
45.
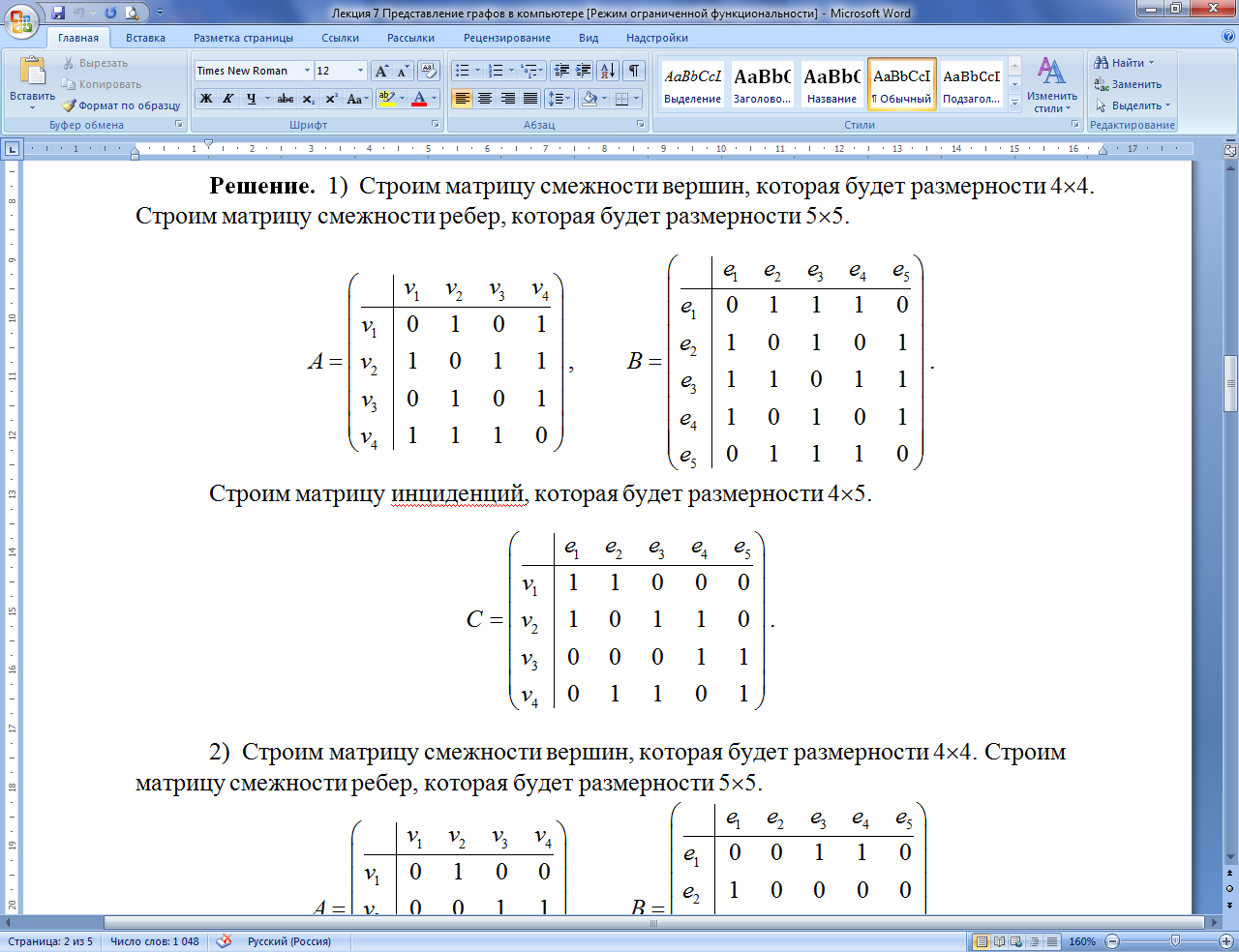
Пример
7.7.2.
Для заданного ориентированного графа
построить матрицы смежностей и матрицу
инциденций.
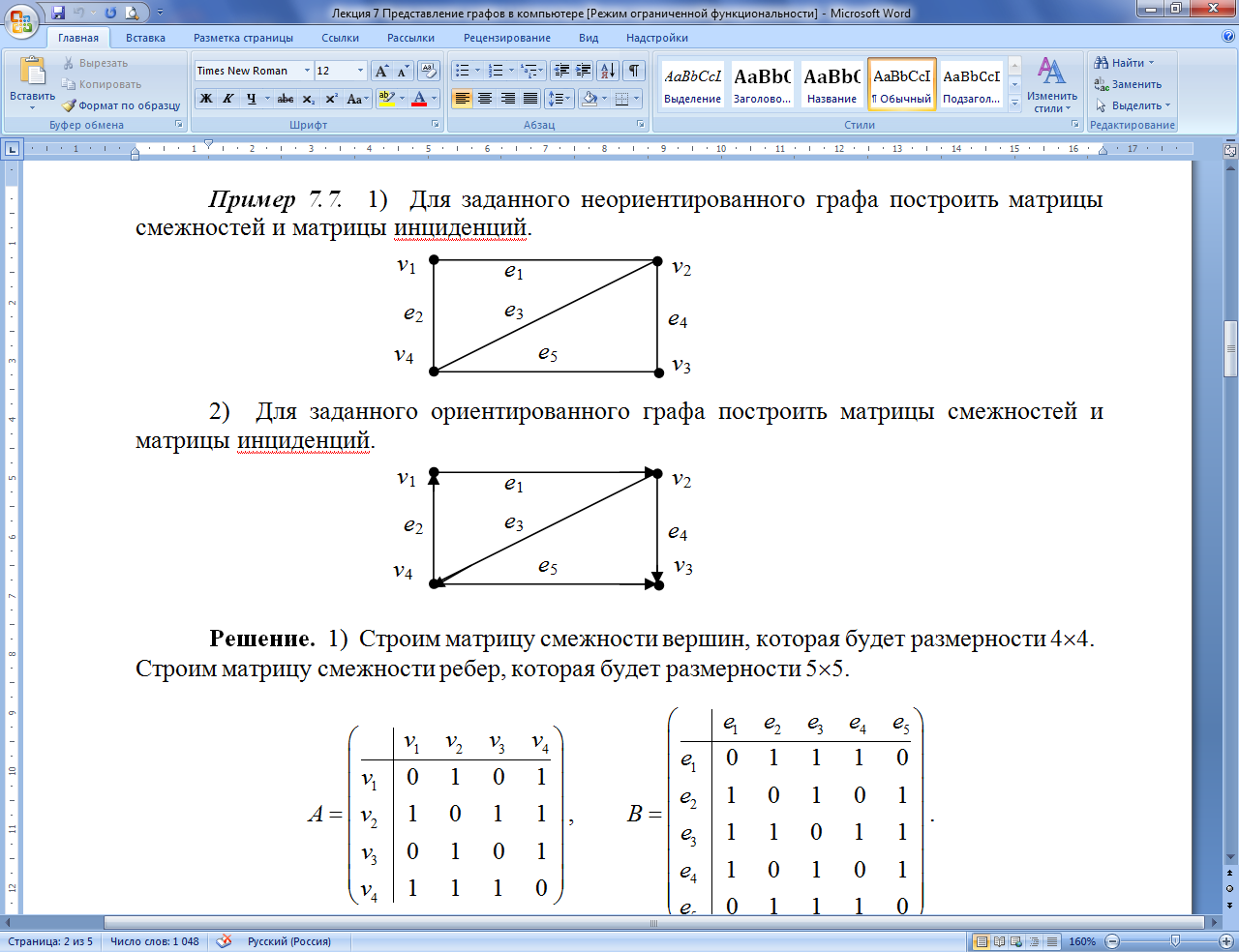
Решение.
1) Строим матрицу смежности вершин,
которая будет размерности 44.
Строим матрицу смежности ребер, которая
будет размерности 55.

2) Строим матрицу
инциденций, которая будет размерности
45.
Соседние файлы в папке Лекции_2
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Теория графов. Термины и определения в картинках
Время на прочтение
5 мин
Количество просмотров 94K

В этой статье мы познакомимся с основными терминами и определениями Теории графов. Каждый термин схематично показан на картинках.
Самый объёмный модуль на курсе «Алгоритмы и структуры данных» посвящён теории графов.
Граф – это топологичекая модель, которая состоит из множества вершин и множества соединяющих их рёбер. При этом значение имеет только сам факт, какая вершина с какой соединена.
Например, граф на рисунке состоит из 8 вершин и 8 рёбер.

Очень многие задачи могут быть решены используя богатую библиотеку алгоритмов теории графов. Для этого достаточно лишь принять объекты за вершины, а связь между ними – за рёбра, после чего весь арсенал алгоритмов теории графов к вашим услугам: нахождение маршрута от одного объекта к другому, поиск связанных компонент, вычисление кратчайших путей, поиск сети максимального потока и многое другое.
В этой статье мы познакомимся с основными терминами и определениями теории графов. На курсе “Алгоритмы и Структуры данных” в компании Отус “Теория графов” изучается в самом объёмном модуле из 6 вебинаров, где мы изучаем десяток самых популярных алгоритмов.
Вершина – точка в графе, отдельный объект, для топологической модели графа не имеет значения координата вершины, её расположение, цвет, вкус, размер; однако при решении некоторых задачах вершины могут раскрашиваться в разные цвета или сохранять числовые значения.
Ребро – неупорядоченная пара двух вершин, которые связаны друг с другом. Эти вершины называются концевыми точками или концами ребра. При этом важен сам факт наличия связи, каким именно образом осуществляется эта связь и по какой дороге – не имеет значения; однако рёбра может быть присвоен “вес”, что позволит говорить о “нагруженном графе” и решать задачи оптимизации.
Инцидентность – вершина и ребро называются инцидентными, если вершина является для этого ребра концевой. Обратите внимание, что термин “инцидентность” применим только к вершине и ребру.
Смежность вершин – две вершины называются смежными, если они инцидентны одному ребру.
Смежность рёбер – два ребра называются смежными, если они инцедентны одной вершине.
Говоря проще – две вершины смежные, если они соединены ребром, два ребра смежные – если они соединены вершиной.

Петля – ребро, инцидентное одной вершине. Ребро, которое замыкается на одной вершине.
Псевдограф – граф с петлями. С такими графами не очень удобно работать, потому что переходя по петле мы остаёмся в той же самой вершине, поэтому у него есть своё название.

Кратные рёбра – рёбра, имеющие одинаковые концевые вершины, по другому их называют ещё параллельными.
Мультиграф – граф с кратными рёбрами.
Псевдомультиграф – граф с петлями и кратными рёбрами.

Степень вершины – это количество рёбер, инцидентных указанной вершине. По-другому – количество рёбер, исходящих из вершины. Петля увеливает степень вершины на 2.
Изолированная вершина – вершина с нулевой степенью.
Висячая вершина – вершина со степенью 1.

Подграф. Если в исходном графе выделить несколько вершин и несколько рёбер (между выбранными вершинами), то мы получим подграф исходного графа.

Идея подграфов используется во многих алгоритмах, например, сначала создаётся подграф их всех вершин без рёбер, а потом дополняется выбранными рёбрами.
Полный граф – это граф, в котором каждые две вершины соединены одним ребром.

Сколько рёбер в полном графе? Это известная задача о рукопожатиях: собралось N человек (вершин) и каждый с каждым обменялся рукопожатием (ребро), сколько всего было рукопожатий? Вычисляется как сумма чисел от 1 до N – каждый новый участник должен пожать руку всем присутствующим, вычисляется по формуле: N * (N – 1) / 2.
Регулярный граф – граф, в котором степени всех вершин одинаковые.

Двудольный граф – если все вершины графа можно разделить на два множества таким образом, что каждое ребро соединяет вершины из разных множеств, то такой граф называется двудольным. Например, клиент-серверное приложение содержит множество запросов (рёбер) между клиентом и сервером, но нет запросов внутри клиента или внутри сервера.

Планарный граф. Если граф можно разместить на плоскости таким образом, чтобы рёбра не пересекались, то он называется “планарным графом” или “плоским графом”.

Если это невозможно сделать, то граф называется “непланарным”.
Минимальные непланарные графы – это полный граф К5 из 5 вершин и полный двудольный граф К3,3 из 3+3 вершин (известная задача о 3 соседях и 3 колодцах). Если какой-либо граф в качестве подграфа содержит К5 или К3,3, то он является непланарным.

Путь или Маршрут – это последовательность смежных рёбер. Обычно путь задаётся перечислением вершин, по которым он пролегает.
Длина пути – количество рёбер в пути.
Цепь – маршрут без повторяющихся рёбер.
Простая цепь – цепь без повторяющихся вершин.

Цикл или Контур – цепь, в котором последняя вершина совпадает с первой.
Длина цикла – количество рёбер в цикле.
Самый короткий цикл – это петля.

Цикл Эйлера – цикл, проходящий по каждому ребру ровно один раз. Эйлер доказал, что такой цикл существует тогда, и только тогда, когда все вершины в связанном графе имеют чётную степень.

Цикл Гамильтона – цикл, проходящий через все вершины графа по одному разу. Другими словами – это простой цикл, в который входят все вершины графа.

Взвешенный граф – граф, в котором у каждого ребра и/или каждой вершины есть “вес” – некоторое число, которое может обозначать длину пути, его стоимость и т. п. Для взвешенного графа составляются различные алгоритмы оптимизации, например поиск кратчайшего пути.

Пока ещё не придуман алгоритм, который за полиномиальное время нашёл бы кратчайший цикл Гамильтона в полном нагруженном графе, однако есть несколько приближённых алгоритмов, которые за приемлимое время находят если не кратчайший, то очень короткий цикл, эти алгоритмы мы также рассматриваем на курсе Отуса – “Алгоритмы и структуры данных”.
Связный граф – граф, в котором существует путь между любыми двумия вершинами.
Дерево – связный граф без циклов.
Между любыми двумя вершинами дерева существует единственный путь.
Деревья часто используются для организации иерархической структуры данных, например, при создании двоичных деревьев поиска или кучи, в этом случае одну вершину дерева называют корнем.

Лес – граф, в котором несколько деревьев.

Ориентированный граф или Орграф – граф, в котором рёбра имеют направления.
Дуга – направленные рёбра в ориентированном графе.

Полустепень захода вершины – количество дуг, заходящих в эту вершину.
Исток – вершина с нулевой полустепенью захода.
Полустепень исхода вершины – количество дуг, исходящих из этой вершины
Сток – вершина с нулевой полустепенью исхода.

Компонента связности – множество таких вершин графа, что между любыми двумя вершинами существует маршрут.

Компонента сильной связности – максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам.
Компонента слабой связности – максимальное множество вершин орграфа, между любыми двумя вершинами которого существует путь по дугам без учёта направления (по дугам можно двигаться в любом направлении).

Мост – ребро, при удалении которого, количество связанных компонент графа увеличивается.

Это только основные термины и определения теории графов, которые мы рассматриваем на первом вебинаре модуля “Теория графов”. Цель статьи – дать наглядное и понятное представление об этих терминах, для чего и были нарисованы эти картинки.
-
Узнать о курсе подробнее
-
Записаться на интенсив: “Алгоритм сжатия данных – код Хаффмана. Создание Архиватора.”. День 1
-
Записаться на интенсив: “Алгоритм сжатия данных – код Хаффмана. Создание Архиватора.”. День 2
Основные понятия и определения.
Пара (V(G), E(G)) называется простым графом, если V(G) – непустое конечное множество элементов, называемых вершинами (или узлами, или точками), а E(G) – конечное множество неупорядоченных пар различных элементов из V(G), называемых ребрами (или линиями). В простом графе данную пару вершин может соединять не более чем одно ребро.
Между элементами множества вершин и множества ребер определено отношение инцидентности. Говорят, что ребро е инцидентно вершинам v1, v2, если оно соединяет эти вершины и наоборот, каждая из вершин v1, v2 инцидентна ребру е.
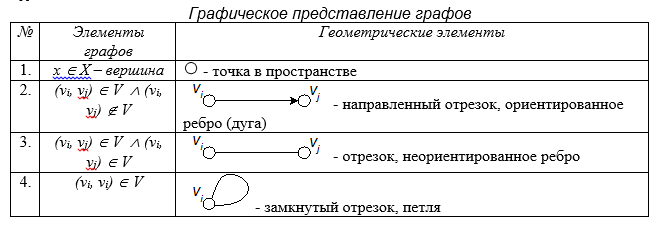
Часто бывает удобно снять ограничение, состоящее в том, что ребро должно соединять две различные вершины, и допустить существование петель.
Получающийся при этом объект, в котором могут быть и кратные ребра и петли называется графом (псевдографом).
Псевдограф без петель называется мультиграфом.
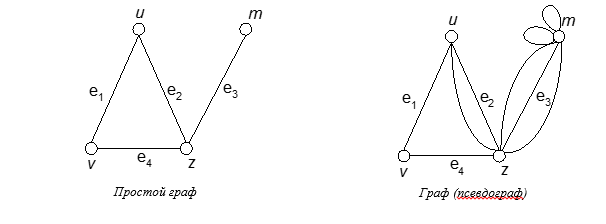
Подграфом графа G называется граф, все вершины и ребра которого содержатся среди вершин и ребер графа G. Подграф называется собственным, если он отличен от самого графа.
Кратностью ребер называют количество одинаковых пар.
пример 
Мультиграф в котором ни одна пара не встречается более одного раза называется графом.
Две вершины называются смежными, если существует ребро, концами которого они являются. Два ребра называются смежными, если они имеют общую вершину.
Смежные вершины – вершины, инцидентные одной дуге.
Смежные дуги – это дуги инцидентные одной вершине.
Степени вершин и полустепени исхода и захода.
Степенью вершины v графа G называется число ребер графа, которым инцидентна эта вершина.
Вершина, локальная степень которой равна 0, называется изолированной; степень которой равна 1 – висячей.
Полустепенью исхода (захода) вершины v орграфа D называется число дуг орграфа D, исходящих из вершины v (заходящих в вершину v).
Количество вершин и ребер в графе G обозначим соответственно через n(G) и m(G), а количество вершин и дуг в орграфе D – через n(D) и m(D).
Для любого псевдографа G выполняется равенство 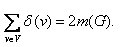
(Cумма степеней всех вершин = удвоенное количество ребер в графе)
Для любого ориентированного псевдографа D выполняется равенство 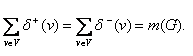
(Cумма полустепеней исхода и захода всех вершин = количество ребер в графе)
Два графа G1 и G2 называются изоморфными, если существует взаимно однозначное соответствие между множествами их вершин, обладающее тем свойством, что число ребер, соединяющих любые две вершины в G1, равно число ребер, соединяющих соответствующие вершины в G2.
Операция подразбиения (измельчения) дуги (u, v) в орграфе D = (V, E) состоит в удалении из Е дуги (u, v), добавлении к V новой вершины w и добавлении к Е | {(u, v)} двух дуг (u, w), (w, v). Аналогично определяется операция подразбиения ребра в графах.
Орграф D1 называется подразбиением орграфа D2, если орграф D1 можно получить из D2 путем последовательного применения операции подразбиения дуг. Аналогично определяется подразбиение графа.
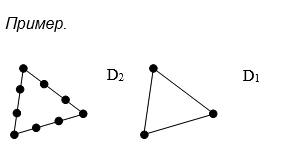
Орграфы D1, D2 называются гомеоморфными, если существуют их подразбиения, являющиеся изоморфными.
Матрицы смежностей и инциденций вершин графов и орграфов.
Матрицей смежности орграфа D называется квадратная матрица A(D)=[aij] порядка n, у которой
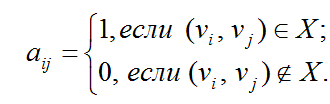
Матрицей инцидентности орграфа D называется (nxm) –матрица B(D)=[bij], у которой

Матрицей смежности графа G называется квадратная матрица A(G)=[aij] порядка n, у которой
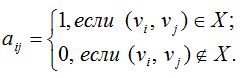
Матрицей инцидентности графа G называется (nxm) –матрица B(G)=[bij], у которой

Основные свойства матриц смежности:
- Матрица смежностей вершин неориентированного графа A (G) является квадратной и симметричной относительно главной диагонали.
- Элементами матрицы A (G) являются целые положительные числа и число ноль.
- Сумма элементов матрицы A (G) по i-й строке (или по i-му столбцу) равна степени соответствующей вершины δ ( xi ).
Из определения следует, что сумма элементов i-й строки матрицы A (G)орграфа равна полустепени исхода δ+ ( xi ), а по i-му столбцу – полустепени захода δ¯ ( xi ).
Свойства матрицы инцидентности неориентированного графа:
- Сумма элементов матрицы на i-й строке равна δ ( xi ).
- Сумма элементов матрицы по i-му столбцу равна 2.
Матрица инцидентности орграфа G обладает следующими свойствами:
- Сумма строк матрицы B(G) является нулевой строкой.
- Любая строка матрицы B(G) является линейной комбинацией остальных строк.
- Ранг матрицы B(G) равен p-1.
Основные типы графов.
Граф, у которого множество ребер пусто, называется вполне несвязным (или пустым) графом. Вполне несвязный граф обозначают Nn.
Простой граф, в котором любые две вершины смежны, называется полным. Полный граф обозначают Кn.

Граф, у которого все вершины имеют одну и ту же локальную степень n, называется регулярным (или однородным) степени n. Регулярные графы степени 3 называются кубическими (или трехвалентными). Среди регулярных графов особенно интересны так называемые платоновы графы – графы, образованные вершинами и ребрами пяти правильных многогранников – Платоновых тел: тетраэдра, куба, октаэдра, додекаэдра и икосаэдра.
Допустим, что множество вершин графа G можно разбить на два непересекающихся подмножества V1 и V2 так, что каждое ребро в G соединяет какую-нибудь вершину из V1 с какой-нибудь вершиной из V2, тогда данный граф называется двудольным.
Если в двудольном графе каждая вершина из V1 соединена с каждой вершиной из V2, то граф называется полным двудольным.
Граф называется связным, если его нельзя представить в виде объединения двух графов, и несвязным в противном случае.
Очевидно, что всякий несвязный граф можно представить в виде объединения конечного числа связных графов – каждый из таких связных графов называется компонентой связности графа.
Определение. Связный регулярный граф степени 2 называется циклическим графом.
Смешанный граф – Граф, содержащий как ориентированные, так и неориентированные рёбра
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 июня 2021 года; проверки требуют 3 правки.

Рис. 1. Граф, на вершинах которого отмечены степени.
Степень (валентность) вершины графа — количество рёбер графа 

При подсчёте степени ребро-петля учитывается дважды.[1]
Степень вершины обычно обозначается как 

Максимальная и минимальная степень вершин графа G обозначаются соответственно Δ(G) и δ(G).
На рис. 1 максимальная степень равна 5, минимальная — 0.
В регулярном графе степени всех вершин одинаковы, поэтому в данном случае можно говорить о степени графа.
Лемма о рукопожатиях[править | править код]
По формуле суммы степеней для графа 
то есть сумма степеней вершин любого графа равна удвоенному числу его рёбер. Кроме того, из формулы следует, что в любом графе число вершин нечётной степени чётно. Данное утверждение (и сама формула) известны как лемма о рукопожатиях. Название происходит от известной математической задачи: необходимо доказать, что в любой группе число людей, пожавших руку нечётному числу других, чётно.
Последовательность степеней вершин[править | править код]

Рис. 2. Два неизоморфных графа с одинаковой последовательностью степеней (3, 2, 2, 2, 2, 1, 1, 1).
Последовательность степеней вершин неориентированного графа является невозрастающей последовательностью.[2] Для графа, изображённого на рис. 1, она имеет вид (5, 3, 3, 2, 2, 1, 0). Последовательность степеней вершин есть инвариант графа, поэтому у изоморфных графов она одинакова. Однако последовательность степеней вершин не является уникальной характеристикой графа: в некоторых случаях неизоморфные графы также обладают одинаковой последовательностью.
Проблема последовательности степеней заключается в нахождении некоторых или всех графов с заданной невозрастающей последовательностью, состоящей из натуральных чисел (нулевые степени при этом могут быть проигнорированы, так как их количество изменяется добавлением или удалением изолированных вершин). Последовательность, являющаяся последовательностью степеней какого-либо графа, называется графической (англ. graphical sequence). Из формулы суммы степеней следует, что любая последовательность с нечётной суммой (как, к примеру, 3, 3, 1) не может быть последовательностью степеней графа. Обратное также верно: если последовательность имеет чётную сумму, она представляет собой последовательность степеней мультиграфа. Построение такого графа осуществляется достаточно простым способом: необходимо объединить вершины нечётных степеней в пары, к оставшимся незаполненными вершинам следует добавить петли.
Сложнее реализовать простой граф с заданной последовательностью. Теорема Эрдёша — Галлаи утверждает, что невозрастающая последовательность di (при i = 1,…,n) может быть последовательностью простого графа только если её сумма чётна и выполняется неравенство
Например, последовательность (3, 3, 3, 1) не может являться последовательностью простого графа; она удовлетворяет неравенству Эрдёша — Галлаи только при k равном 1, но не при k равном 2 или 3.
Согласно критерию Гавела — Хакими, если невозрастающая последовательность (d1, d2, …, dn) это последовательность степеней простого графа, то (d2 − 1, d3 − 1, …, dd1+1 − 1, dd1+2, dd1+3, …, dn) некоторая последовательность степеней простого графа. Этот факт позволяет построить полиномиальный алгоритм нахождения простого графа с заданной реализуемой последовательностью.
Сопоставим исходной последовательности чисел вершины графа без ребер с требуемыми степенями. Указанное преобразование последовательностей задает как минимум одну вершину графа, все инцидентные ей ребра и множество вершин с новыми требуемыми дополнениями степеней. Упорядочивая оставшиеся вершины по невозрастанию дополнений степеней, получим невозрастающую последовательность степеней простого графа. Повторяя преобразование и упорядочение не более n-1 раза, получаем весь граф.
Проблема нахождения или оценки числа графов по заданной последовательности относится к области перечисления графов.
Частные значения[править | править код]

Рис. 3. Концевыми вершинами являются 4, 5, 6, 7, 10, 11 и 12.
- Вершина степени 0 называется изолированной.
- Вершина степени 1 называется концевой (англ. end vertex), висячей (англ. pendant vertex) или листом графа (англ. leaf vertex). Ребро, инцидентное такой вершине называется висячим (англ. terminal (pendant) edge, end-edge). На рис. 3 висячим ребром является {3,5}. Подобная терминология используется в изучении деревьев в общем и как структур данных.
- Вершина степени n-1 графа порядка n называется доминирующей (англ. dominating vertex).
Общие свойства[править | править код]
- Если все вершины графа имеют одинаковую степень k, граф называют k-регулярным или регулярным графом степени k. В этом случае сам граф имеет степень k.
- Эйлеров путь существует в неориентированном, связном графе тогда и только тогда, когда граф имеет 0 или 2 вершины нечётной степени. Если граф содержит 0 вершин нечётной степени, Эйлеров путь является циклом.
- Орграф является псевдолесом[неизвестный термин] только если полустепень исхода каждой вершины не больше 1. Функциональный граф — частный случай псевдолеса, в котором полустепени исхода всех вершин равны 1.
- Согласно теореме Брукса, хроматическое число любого графа за исключением клики или нечётного цикла не превышает максимальной степени его вершин (Δ). Согласно теореме Визинга, хроматический индекс любого графа не превышает Δ + 1.
- k-вырожденным графом называется граф, в котором каждый подграф имеет вершину степенью не больше k.
См. также[править | править код]
- Полустепень захода и полустепень исхода вершин ориентированных графов
- Распределение степеней
Примечания[править | править код]
- ↑ Дистель, стр. 5
- ↑ Дистель, стр. 278
Источники[править | править код]
- Дистель, Рейнхард (2005), Graph Theory (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-26183-4, <http://diestel-graph-theory.com/index.html>.
- Эрдёш, П. & Галлаи, T. (1960), Gráfok előírt fokszámú pontokkal, Matematikai Lapok Т. 11: 264—274, <http://www.renyi.hu/~p_erdos/1961-05.pdf>.
- Хакими, С. Л. (1962), On realizability of a set of integers as degrees of the vertices of a linear graph. I, Journal of the Society for Industrial and Applied Mathematics Т. 10: 496–506.
- Сирксма, Хирард & Хоохефен, Хан (1991), Seven criteria for integer sequences being graphic, Journal of Graph Theory Т. 15 (2): 223–231, DOI 10.1002/jgt.3190150209.
Степенью вершины V графа G называется число инцидентных ей рёбер, т. е. число рёбер, выходящих из данной вершины. (В случае псевдографов каждая петля добавляет 2 в степень вершины). Обозначается степень вершины V графа G: degGv или просто deg V, если ясно, о каком графе G идет речь.
Вершина степени 0 называется Изолированной. Вершина степени 1 называется Концевой (или Висячей). Ребро, инцидентное концевой вершине также
 Называется Концевым.
Называется Концевым.
Вершина V Графа G, смежная со всеми другими вершинами G, называется Доминирующей. Её степень degGv очевидно равна |G| –1.
Граф G называется Регулярным (или, по-другому, Однородным), если степени всех его вершин равны. Эта общая степень всех вершин регулярного графа G называется степенью регулярного графа G и обозначается deg G.
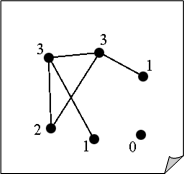
Последовательность степеней вершин графа G, записанная в каком либо порядке называется степенной последовательностью графа G. Например, граф на рисунке справа имеет степенную последовательность (3, 3, 1, 0, 1, 2).
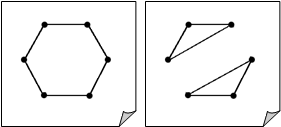 Понятно, что изоморфные графы имеют одинаковые (с точностью до порядка следования элементов) степенные последовательности. Однако, из этого совпадения степенных последовательностей двух графов ещё не следует их изоморфность. На следующих двух рисунках изображены два неизоморфных регулярных графа степени 2.
Понятно, что изоморфные графы имеют одинаковые (с точностью до порядка следования элементов) степенные последовательности. Однако, из этого совпадения степенных последовательностей двух графов ещё не следует их изоморфность. На следующих двух рисунках изображены два неизоморфных регулярных графа степени 2.
Таким образом, степенная последовательность не определяет граф полностью и не может
служить способом его задания.
Степенная последовательность не может быть произвольным набором чисел, а обладает определёнными свойствами.
Лемма 1 (“о рукопожатиях”). Сумма степеней всех вершин графа G есть число чётное, ровно в два раза большее числа рёбер графа G, т. е.
Доказательство: Действительно, подсчитаем количество рёбер графа G, просматривая поочередно все вершины графа G и считая рёбра выходящие из этих вершин. Так как из каждой вершины V выходит degGV рёбер, то мы получим сумму:
Но при этом каждое ребро будет учтено 2 раза: один раз, когда рассматривался один его конец, другой раз, когда — второй. Таким образом, лемма верна.
Из леммы 1 вытекает
Следствие. В любом графе число вершин нечётной степени является чётным.
Доказательство. В самом деле, иначе, если бы сумма целых чисел содержала нечётное число нечетных слагаемых, то она, очевидно, была бы нечётной, что противоречит лемме о рукопожатиях.
В ориентированных графах для каждой вершины V дополнительно рассматривается также полустепень исхода и полустепень захода. Полустепенью исхода вершины V называется число дуг графа G, для которых V Является началом, а Полустепенью захода – число дуг, для которых V является концом. Обозначаются полустепени захода и исхода графа G соответственно deg-V и deg+V. При этом полная степень degV = deg-V+ deg+V. Поскольку каждая дуга имеет ровно одно начало и один конец, то справедлива
Лемма 2. Сумма полустепеней исхода всех вершин графа G Равна сумме полустепеней захода, т. е.
| < Предыдущая | Следующая > |
|---|


