Средней
величиной называется статистический
показатель, который дает обобщенную
характеристику варьирующего признака
однородных единиц совокупности.
Для
относительной характеристики величины
варьирующего признака и внутреннего
строения рядов распределения пользуются
структурными средними, которые
представлены модой и медианой.
-
Мода
статистики называется такое значение
варьирующего признака, который
встречается в совокупности наиболее
часто.
В
дискретном ряду мода — это варианта с
наибольшей частотой.
Пример
расчета моды для дискретного ряда:
|
X |
F Число |
|
34 |
2 |
|
35 |
10 |
|
36 |
20 |
|
37 |
88 |
|
38 |
19 |
|
39 |
9 |
|
40 |
1 |
Мода
– 37
Мо
— мода
Если
ряд интервальный, то Мо рассчитывается
по формуле
Xmo
— нижняя граница модального интервала
-величина
модального интервала
fмо–
частота, соответствующая модальному
интервалу
fмо-1
—
частота, предшествующая модальному
интервалу.
fmo+1
—
частота интервала, следующая за модальным
Пример
расчета моды в интервальном ряду
|
d |
Интервал |
Количество |
|
1 |
330-370 |
4 |
|
2 |
371-410 |
4 |
|
3 |
411-450 |
5 |
|
4 |
451-490 |
4 |
|
5 |
491-530 |
3 |
Определяем
модальный интервал 411-150
-
Медиана.
Это величина, которая делит численность
упорядоченного вариационного ряда на
2 равные части. 1 часть имеет значение
варьирующего признака меньше средней,
др.больше.
Для
расчёта медианы в дискретном ряду
необходимо ранжировать (упорядочить),
то есть расположить все значения
показателя в порядке убывания и
возрастания.
Если
ряд с нечётным числом индивидуальной
величины, то медианой является величина
или варианта, находящаяся в центре
ряда.
1,
2, 2, 3,
5, 7, 10
(
Ме = 3)
А
если ряд с чётным числом индивидуальной
величины, то медиана будет средней
арифметической из двух смежных вариант,
лежащих в центре ряда.
1,
2, 2, (3,
5),
7, 10, 11
В
интервальном вариационном ряду порядок
нахождения следующий :
1)
располагаемое индивидуальное значение
признака (интервальна) групп по ранжиру
2)
определяем для данного ранжированного
ряда накопленные частоты
3)по
данным о накопленных частотах находим
медианный интервал
4)поскольку
медиана делит численность ряда пополам,
то следовательно, что величина её
находится там, где сумма накопленных
частот составляет половину или больше
половины всей суммы частот.
5)Далее
медиану рассчитываем по формуле:
– нижняя граница медиального ряда
ime–
величина медианного интервала
Σf
/ 2 –полусумма частот ряда
S
m-1
-сумма накопленных частот, предшествовавшие
медианный интервал
fme–
частота медианного ряда
– сумма накопленных частот, предшествующих
медиальному интервалу
Пример
расчета медианы для интервального ряда
|
X |
F |
|
|
|
I |
330-370 |
4 |
4 |
|
II |
371-410 |
4 |
8 |
|
III |
411-450 Медиальный |
||
|
IV |
451-490 |
4 |
17 |
|
V |
491-530 |
3 |
20 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Расчет моды
Теперь посмотрим, как рассчитать моду. Мода – это то значение в анализируемой совокупности данных, которое встречается чаще других, поэтому нужно посмотреть на частоты значений и отыскать максимальное из них. Например, в наборе данных 3, 4, 6, 7, 3, 5, 3, 4 модой будет значение 3 – повторяется чаще остальных. Это в дискретном ряду, и здесь все просто. Если данных много, то моду легче всего найти с помощью соответствующей гистограммы. Бывает так, что совокупность данных имеет бимодальное распределение.
Без диаграммы очень трудно понять, что в данных не один, а два центра. К примеру, на президентских выборах предпочтения сельских и городских жителей могут отличаться. Поэтому распределение доли отданных голосов за конкретного кандидата может быть «двугорбым». Первый «горб» – выбор городского населения, второй – сельского.
Немного сложнее с интервальными данными, когда вместо конкретных значений имеются интервалы. В этом случае говорят о модальном интервале (при анализе доходов населения, например), то есть интервале, частота которого максимальна относительно других интервалов. Однако и здесь можно отыскать конкретное модальное значение, хотя оно будет условным и примерным, так как нет точных исходных данных. Представим, что есть следующая таблица с распределением цен.
Для наглядности изобразим соответствующую диаграмму.
Требуется найти модальное значение цены.
Вначале нужно определить модальный интервал, который соответствует интервалу с наибольшей частотой. Найти его так же легко, как и моду в дискретном ряду. В нашем примере это третий интервал с ценой от 301 до 400 руб. На графике – самый высокий столбец. Теперь нужно определить конкретное значение цены, которое соответствует максимальному количеству. Точно и по факту сделать это невозможно, так как нет индивидуальных значений частот для каждой цены. Поэтому делается допущение о том, что интервалы выше и ниже модального в зависимости от своей частоты имеют разные вес и как бы перетягивают моду в свою сторону. Если частота интервала следующего за модальным больше, чем частота интервала перед модальным, то мода будет правее середины модального интервала и наоборот. Давайте еще раз посмотрим на рисунок, чтобы понять формулу, которую я напишу чуть ниже.
На рисунке отчетливо видно, что соотношение высоты столбцов, расположенных слева и справа от модального определяет близость моды к левому или правому краю модального интервала. Задача по расчету модального значения состоит в том, чтобы найти точку пересечения линий, соединяющих модальный столбец с соседними (как показано на рисунке пунктирными линиями) и нахождении соответствующего значения признака (в нашем примере цены). Зная основы геометрии (7-й класс), по данному рисунку нетрудно вывести формулу расчета моды в интервальном ряду.
Формула моды имеет следующий вид.
Где Мо – мода,
x – значение начала модального интервала,
h – размер модального интервала,
fМо – частота модального интервала,
fМо-1 – частота интервала, находящего перед модальным,
fМо1 – частота интервала, находящего после модального.
Второе слагаемое формулы моды соответствует длине красной линии на рисунке выше.
Рассчитаем моду для нашего примера.
Таким образом, мода интервального ряда представляет собой сумму, состоящую из значения начального уровня модального интервала и отрезка, который определяется соотношением частот ближайших интервалов от модального.
Видео
Мода и медиана
Модой называют элемент, который встречается в выборке чаще других.
Рассмотрим следующую выборку: шестеро спортсменов, а также время в секундах за которое они пробегают 100 метров
Элемент 14 встречается в выборке чаще других, поэтому элемент 14 назовем модой.
Рассмотрим еще одну выборку. Тех же спортсменов, а также смартфоны, которые им принадлежат
Элемент iphone встречается в выборке чаще других, значит элемент iphone является модой. Говоря простым языком, носить iphone модно.
Конечно элементы выборки в этот раз выражены не числами, а другими объектами (смартфонами), но для общего представления о моде этот пример вполне приемлем.
Рассмотрим следующую выборку: семеро спортсменов, а также их рост в сантиметрах:
Упорядочим данные в таблице так, чтобы рост спортсменов шел по возрастанию. Другими словами, построим спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 183, 184, 185, 188, 190
В получившейся выборке 7 элементов. Посередине этой выборки располагается элемент 184. Слева и справа от него по три элемента. Такой элемент как 184 называют медианой упорядоченной выборки.
Медианой упорядоченной выборки называют элемент, располагающийся посередине.
Отметим, что данное определение справедливо в случае, если количество элементов упорядоченной выборки является нечётным.
В рассмотренном выше примере, количество элементов упорядоченной выборки было нечётным. Это позволило нам быстро указать медиану
Но возможны случаи, когда количество элементов выборки чётно.
К примеру, рассмотрим выборку в которой не семеро спортсменов, а шестеро:
Построим этих шестерых спортсменов по росту:
Выпишем рост спортсменов отдельно:
180, 182, 184, 186, 188, 190
В данной выборке не получается указать элемент, который находился бы посередине. Если указать элемент 184 как медиану, то слева от этого элемента будут располагаться два элемента, а справа — три. Если как медиану указать элемент 186, то слева от этого элемента будут располагаться три элемента, а справа — два.
В таких случаях для определения медианы выборки, нужно взять два элемента выборки, находящихся посередине и найти их среднее арифметическое. Полученный результат будет являться медианой.
Вернемся к нашим спортсменам. В упорядоченной выборке 180, 182, 184, 186, 188, 190 посередине располагаются элементы 184 и 186
Найдем среднее арифметическое элементов 184 и 186
Элемент 185 является медианой выборки, несмотря на то, что этот элемент не является членом исходной и упорядоченной выборки. Спортсмена с ростом 185 нет среди остальных спортсменов. Рост в 185 см используется в данном случае для статистики, чтобы можно было сказать о том, что срединный рост спортсменов составляет 185 см.
Поэтому более точное определение медианы зависит от количества элементов в выборке.
Если количество элементов упорядоченной выборки нечётно, то медианой выборки называют элемент, располагающийся посередине.
Если количество элементов упорядоченной выборки чётно, то медианой выборки называют среднее арифметическое двух чисел, располагающихся посередине этой выборки.
Медиана и среднее арифметическое по сути являются «близкими родственниками», поскольку и то и другое используют для определения среднего значения. Например, для предыдущей упорядоченной выборки 180, 182, 184, 186, 188, 190 мы определили медиану, равную 185. Этот же результат можно получить путем определения среднего арифметического элементов 180, 182, 184, 186, 188, 190
Но медиана в некоторых случаях отражает более реальную ситуацию. Например, рассмотрим следующий пример:
Было подсчитано количество имеющихся очков у каждого спортсмена. В результате получилась следующая выборка:
0, 1, 1, 1, 2, 1, 2, 3, 5, 4, 5, 0, 1, 6, 1
Определим среднее арифметическое для данной выборки — получим значение 2,2
По данному значению можно сказать, что в среднем у спортсменов 2,2 очка
Теперь определим медиану для этой же выборки. Упорядочим элементы выборки и укажем элемент, находящийся посередине:
0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 3, 4, 5, 5, 6
В данном примере медиана лучше отражает реальную ситуацию, поскольку половина спортсменов имеет не более одного очка.
Среднее арифметическое
Понятие среднего значения часто используется в повседневной жизни.
Примеры:
- средняя зарплата жителей страны;
- средний балл учащихся;
- средняя скорость движения;
- средняя производительность труда.
Речь идет о среднем арифметическом — результате деления суммы элементов выборки на их количество.
Среднее арифметическое — это результат деления суммы элементов выборки на их количество.
Вернемся к нашему примеру
Узнаем сколько в среднем мы тратили в каждом из шести дней:
Теория для решения данных задач. Формулы для расчета моды и медианы
Модой в статистике называется величины признака (варианта), которая чаще всего встречается в данной совокупности.
Медианой в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам. Обозначают медиану символом.
Распределительные средние – мода и медиана, их сущность и способы исчисления.
Данные показатели относятся к группе распределительных средних и используются для формирования обобщающей характеристики величины варьирующего признака.
Мода 
– это наиболее часто встречающееся значение варьирующего признака в вариационном ряду. Модой распределения называется такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т.е. один из вариантов признака повторяется чаще, чем все другие. Для дискретного ряда (ряд, в котором значение варьирующего признака представлены отдельными числовыми показателями) модой является значение варьирующего признака обладающего наибольшей частотой. Для интервального ряда сначала определяется модальный интервал (т.е. содержащий моду), в случае интервального распределения с равными интервалами определяется по наибольшей частоте; с неравными интервалами – по наибольшей плотности, а определение моды требует проведения расчетов на основе следующих формул:
где:
— нижняя граница модального интервала;
— величина модального интервала;
— частота модального интервала;
— частота интервала, предшествующего модальному;
— частота интервала, следующего за модальным;
Медиана (Ме) — это значение варьирующего признака, приходящееся на середину ряда, расположенного в порядке возрастания или убывания числовых значений признака, т.е. величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда. Главное свойство медианы в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:
Для определения медианы в дискретном ряду при наличии частот, сначала исчисляется полусумма частот, а затем определяется какое значение варьирующего признака ей соответствует. При исчислении медианы интервального ряда сначала определяются медианы интервалов, а затем определяется какое значение варьирующего признака соответствует данной частоте. Для определения величины медианы используется формула:
где:
— нижняя граница медианного интервала;
— величина медианного интервала;
— накопленная частота интервала, предшествующего медианному;
— частота медианного интервала;
Медианный интервал не обязательно совпадает с модальным.
Моду и медиану в интервальном ряду распределения можно определить графически. Мода определяется по гистограмме распределения. Для этого выбирается самый высокий прямоугольник, который в данном случае является модальным. Затем правую вершину модального прямоугольника соединяют с правым верхним углом предыдущего прямоугольника. А левую вершину модального прямоугольника – с левым верхним углом последующего прямоугольника. Далее из точки их пересечения опускают перпендикуляр на ось абсцисс.
Теги
В статистических исследованиях довольно широко применяются средние величины. Их нахождение позволяет выявить типичное значение признака исследуемой совокупности. Например, типичный уровень доходов покупателей или возраст большинства клиентов компании. При этом вычисление, к примеру, среднего арифметического не всегда уместно.
Представим такую ситуацию: мы опросили 10 человек на предмет их уровня доходов. У 9-х доходы оказались примерно одинаковыми и составили 10 тыс. руб. Что касается 10-ого опрошенного, то оказалось, что его доход равняется 410 тыс. руб. в месяц. Если мы вычислим простое среднее арифметическое, то типичный доход будет равняться 50 тыс. руб.! Но это явно не так. В таких ситуациях более объективную и правдоподобную картину дает вычисление моды или медианы, которые относятся к структурным средним показателям.
Понятие медианы
Медиана (Me) — значение признака в исследуемом ряду величин, которое делит этот ряд на две равные части.
То есть половина (50%) всех значений в исследуемом ряду будет меньше медианы, а другая половина — больше ее. Поэтому медиану еще называют 50-й перцентиль или квантиль 0,5.
Формула для расчета медианы
Если значений немного, то медиану можно определить «на глазок». Для этого достаточно расположить все значения в порядке возрастания и найти середину.
Если число случаев четное и в центре ряда находятся два разных числа, то медианой будет среднее между ними (даже если такого значения нет в самом ряду исследуемых случаев). Например, в ряду 1 2 3 4 5 6, медианой будет 3,5.
Для нахождения медианы в более сложных случаях (по интервальным рядам) используется специальная формула:
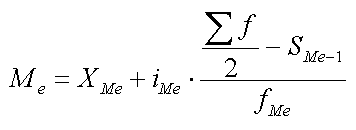
где: Me — медиана;
Xme — нижняя граница медианного интервала (того интервала, накопленная частота которого превышает полусумму всех частот);
ime — величина медианного интервала;
f — частота (сколько раз в ряду встречается то или иное значение);
Sme-1 — сумма частот интервалов предшествующих медианному интервалу;
fme — число значений в медианном интервале (его частота).
Пример вычисления медианы
Был проведен опрос среди покупателей с целью выяснить их типичный возраст. По результатам опроса было установлено, что: 25 покупателей имеют возраст до 20 лет; 32 покупателя — 20-40 лет; 18 покупателей — 40-60 лет; 15 покупателей — свыше 60 лет. Найдем медиану.
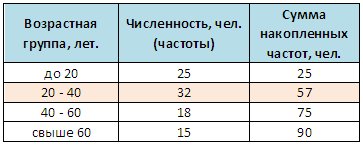
Сначала находим медианный интервал. Для этого вычисляем сумму частот: 25 + 32 + 18 + 15 = 90. Половина этой суммы — 45. Это соответствует возрастной группе 20-40 лет (т. к. полученная полусумма частот — 45, и накопленная частота 1-й группы меньше ее, а 3-ей — больше). Тогда нижняя граница медианного интервала — 20 (лет), а величина медианного интервала — 20 (40 лет за вычетом 20). Сумма частот интервалов предшествующих медианному интервалу — 25. Число значений в медианном интервале — 32 (количество покупателей в возрасте 20-40 лет).
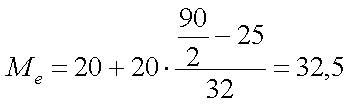
Расчетное значение медианы — 32,5. Округив его, получим средний возраст покупателя — 33 года.
Область применения медианы
При вычислении типичного признака неоднородных рядов, имеющих «выбросы» — значения во много раз отличающиеся от других значений ряда.
Особенности медианы
- Медиана обладает высокой робастностью, то есть нечувствительностью к неоднородностям и ошибкам выборки;
- Сумма разностей между членами ряда выборки и медианой меньше, чем сумма этих разностей с любой другой величиной. В том числе с арифметическим средним.
Источники
- Медиана // Википедия. URL: http://ru.wikipedia.org/wiki/Медиана_(статистика) (дата обращения: 23.10.2013)
- Минашкин В. Г. и др. Курс лекций по теории статистики. – М.: МЭСИ, 2001.
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Нашли опечатку? Помогите сделать статью лучше! Выделите орфографическую ошибку мышью и нажмите Ctrl + Enter.
Библиографическая запись для цитирования статьи по ГОСТ Р 7.0.5-2008:
Галяутдинов Р.Р. Медиана // Сайт преподавателя экономики. [2013]. URL: https://galyautdinov.ru/post/mediana (дата обращения: 18.05.2023).
Образец Практическая работа № 3 Средние величины
Задание 1Для компенсации потерь населения по вкладам в условиях инфляции коммерческий банк в течение года применял следующие процентный ставки:
| Месяцы | Январь-март | Апрель-май | Июнь-сентябрь | Октябрь-декабрь |
| Процентная ставка, % Х | ||||
| f |
Определите среднюю годовую ежемесячную процентную ставку Х.
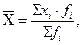= (22*3 + 21*2+ 18*4 + 15*3) / (3+2+4+3 ) = …..% среднегодовая процентная ставка
Задание 2 Имеются данные о финансовых показателях фирм за два периода:
|
№ фирмы |
Базисный период 2018 год |
Отчётный период 2019 |
|||
| Прибыль на одну акцию, руб. Х |
Количество акций, штук f |
Прибыль на одну акцию, руб. Х |
Сумма прибыли, тыс. руб. Х * f = W |
Количество акций, шт. f | |
| 8,5 | 9,5 | 6840/9,5=720 | |||
| 4,7 | 8,8 | ||||
Задание Определите среднюю прибыль на одну акцию по двум фирмам в каждом периоде.
Сумма прибыли / количество акций = Прибыль на одну акцию
2018 год 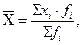= ( 8,5 *700 + 4.7 *500)/ (700+500) =…руб.
средняя прибыль на одну акцию в 2018 году
2019 год
А)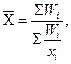 
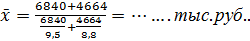средняя прибыль на одну акцию в 2019 году
Б) 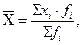= (9,5*720+8,8*530)/ (720 + 530) = средняя прибыль на одну акцию в 2019 году
Задание 3Обеспеченность населения города общей жилой площадью характеризуется следующими данными:
| Размер общей жилой площади на 1 члена семьи, м2 Х | до 8 | 8-12 | 12-16 | 16-20 | 20-24 | 24-28 | Свыше 28 |
| Число семей, d% |
Определите для населения города средний размер общей жилой площади на одного члена семьи. Определить моду и медиану
Решение
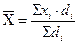= (22* 6 + 28* 10 + 30*14+12 *18 + 5*22 + 2*26+ 1*30) /100 = 1240 /100 = 12,4 м2 средний размер общей жилой площади на одного члена семьи изучаемой совокупности
∑di = 100%, или ∑di = 1;
| Размер общей жилой площади на 1 члена семьи, м2 Х | Число семей, % di |
Середина интервала X¢ |
X¢ × di | Сумма частот накопленным итогом |
| 4 до 8 8 – 4 = 4 |
(4+8)/2 = 6 | 6* 22 = 132 | 22 < 50 | |
| 8-12 h = 12 – 8 = 4 м2 медианный интервал |
(8+12)/2=10 | 10* 28 = 280 | 22+28 =50 | |
| 12-16 Модальный интервал Величина интервала 16-12 =4 |
30 наибольшее значение частоты, значит здесь лежит мода | – | ||
| 16-20 | – | |||
| 20-24 | – | |||
| 24-28 h = 28-24 = 4 |
– | |||
| 28 – 32 28 + 4 = 32 |
– | |||
| итого | – | – |
1240/100 = 12,4 м2
Определить моду
1. Определить модальный интервал (где лежит мода), в нашем примере это интервал 12-16
Можно сделать экспресс расчёт, т.е. найти середину модального интервала:
(12+16) /2 = 14 м2 Мода.
экспресс расчет, для более точного расчета, надо применять формулу:
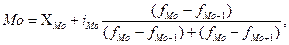= 12 + 4 ((30 – 28) / ((30 – 28) + (30 – 12))) = …м2 показатель, который наиболее часто встречается в совокупности.
Медиана это значение признак, которое делит совокупность на две равные части
Определить медиану В первую очередь находят медианный интервал. Чтобы определить медианный интервал, надо сделать два действия:
а) находим полусумму частот: Sd / 2 = 100% / 2 = 50%
б) суммируем частоты до тех пор, пока сумма частот не превысит полусумму (50%) или не будет ей равна.
в)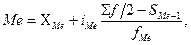 
= 8 + 4 * ((100/2 – 22)/28) = 12 м2 это значение признака, которое делит совокупность признаков на две равные части.
| Размер общей жилой площади на 1 члена семьи, кв. м Х | Число семей, % d | Сумма частот накопленным итогом |
| 4-8 | ||
| 8-12 Медина Величина интервала = 12-8=4 |
22+28 =50 | |
| 12-16 Мода | – | |
| 16-20 | – | |
| – | ||
Задание 4По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, тыс. руб. Х | До 100 | 100-300 | 300-500 | 500-700 | Свыше 700 |
| Число вкладчиков, тыс. чел. f |
Определите средний размер вклада. Определить моду и медиану
Решение
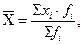= (50*40 +200*170+ 400*350+ 600*230 + 800*120) / (40+170+400+230+120)
Решение
| Размер вклада, тыс. руб. Х | Число вкладчиков, тыс. чел. f | Середина интервала X¢ | X¢ × fi | Сумма частот накопленным итогом |
| 0-100 100-200 = -100 |
(0+100) /2 = 50 | 50*40 =2000 | 40 < 455 | |
| 100-300 300-100 = 200 |
(100+300)/2 = 200 | 40 + 170 =210 < 455 | ||
| 300-500 Величина интервала 500-300=200 Мода Медиана |
|
|
40 + 170 + 350 = 560 > 455 |
|
| 500-700 700-500= 200 |
– | |||
| 700-900 700+200 = 900 |
– | |||
| итого | – | итого | – |
Решение
Определите средний размер вклада
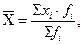= …….= …..тыс. руб.
Определить моду
1. Находим модальный интервал по самому большому размеру f.
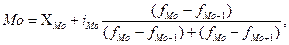Мо = 300 +200 *((350-170) / (350-170) + (350 – 230)) = … тыс. руб. размер вклада, который наиболее часто встречается в совокупности, т.е. моду
Определить медиану чтобы посчитать более точно, надо для расчета применить формулу:
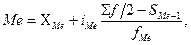
1. Определяем медианный интервал
а) находим полусумму частот: Sf / 2 = 910/2 = 455
б) суммируем частоты до тех пор, пока сумма частот не превысит полусумму (455) или не будет ей равна. 40+170 =210 +350 =560 > 455, значит в интервале 300-500 лежит медиана
2. Рассчитываем медиану по формуле
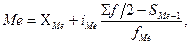= 300 + 200 *((455 – 210)/350) = 440 тыс. руб. это значение признака, которое делит совокупность на две равные части
Медиану можно рассчитать быстро (300+500)/2 = 400,
Структурные средние величины
Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:Кроме степенных средних в статистике для относительной характеристики величины варьирующего признака и внутреннего строения рядов распределения пользуются структурными средними, которые представлены ,в основном, модой и медианой.
где:
— значение моды
— нижняя граница модального интервала
— величина интервала
— частота модального интервала
— частота интервала, предшествующего модальному
— частота интервала, следующего за модальным
Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.
Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот , а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:
Ме = (n(число признаков в совокупности) + 1)/2,
в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).
При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:
где:
Пример. Найти моду и медиану.
| Возрастные группы | Число студентов | Сумма накопленных частот ΣS |
| До 20 лет | 346 | 346 |
| 20 — 25 | 872 | 1218 |
| 25 — 30 | 1054 | 2272 |
| 30 — 35 | 781 | 3053 |
| 35 — 40 | 212 | 3265 |
| 40 — 45 | 121 | 3386 |
| 45 лет и более | 76 | 3462 |
| Итого | 3462 |
Решение:
В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1054).
Рассчитаем величину моды:
Это значит что модальный возраст студентов равен 27 годам.
Вычислим медиану. Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части (Σfi/2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:
Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.
Кроме моды и медианы могут быть использованы такие показатели, как квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили — на 100 частей.
